Introduction

Solid-state batteries are poised to revolutionize the energy storage industry due to their potential for higher energy density, excellent safety and improved sustainability, which are critical for addressing the limitations of current lithium-ion batteries1,2. Solid-state electrolytes is the key to the solid state batteries, and hence has attracted tremendous research interest3,4,5,6,7,8,9,10. However, solid electrolytes still face critical challenges, particularly the low ion conductivity compared with liquid electrolytes. In this regard, sulfide electrolytes (e.g., LGPS-like and argyrodite) with fast ion transport are promising candidates for commercial application11,12. Usually, the ion conductivity of base electrolyte can be further improved by chemical doping (i.e., element substitution), which has been one of the most effective strategies for electrolyte optimization towards high-energy storage3,13. With proper doping, an optimal lithium ion concentration with maximum ion conductivity can be achieved when there are both abundant diffusing ions and vacant hopping sites. High entropy materials with extensive doping also introduce local structure distortion, which disturbs the ion packing and removes the degeneracy of hopping barriers3,14. For instance, heavily doped sulfide electrolytes, such as the Li9.54Si1.74P1.44S11.7Cl0.311, the Li9.54 [Si0.6Ge0.4]1.74P1.44S11.1Br0.3O0.67, etc., achieve much higher ion conductivity than their base compounds. Therefore, material optimization with doping engineering is an important strategy to achieve the high-performance solid electrolytes.

Traditionally, wide chemical space has to be explored experimentally to find the optimized composition, which is both costly and time-consuming. Atomistic simulation of electrolyte materials with atomic details can significantly accelerate this process by predicting ion conductivity of arbitrary compositions15. Atomistic simulation involves force field, which can be constructed either by fitting a physically informed model to experiments, or by first-principle quantum theory calculation. Empirical potentials, while being fast and efficient, are limited by their accuracy and generalizability across diverse material configurations and wide temperature ranges. Ab initio calculation achieves high accuracy, but the computational cost is exceedingly high. The simulation is usually limited to a few hundred atoms and several nanoseconds, insufficient for reliable simulation of solid electrolytes15.

Machine learning force fields (MLFF), such as DeePMD16,17, etc., enable ab initio accuracy at the computational cost of empirical force fields18,19,20. Trained over small scale ab initio calculations, the computation cost of MLFF scales linearly with atom count, supporting large-scale simulation. Previous works have shown MLFF can predict ion conductivity in solid electrolytes, a task previously intractable for empirical or ab initio methods21,22. However, conventional MLFFs lack generalizability across diverse chemical and configurational space, requiring costly retraining for each system, especially for complex doped electrolytes23. Universal force fields pre-trained across the periodic table, such as the DPA-224, MACE25, M3GNet26, CHGNet27, et al.23,28,29, are highly generalizable. However, these universal models are primarily trained on datasets consisting of equilibrium or near-equilibrium configurations. As a result, current universal force fields usually struggle to accurately predict out-of-equilibrium states critical to ionic transport, such as Li-hopping transition states, and lack the quantitative accuracy required for electrolytes simulation. To address this, it is imperative to develop a domain-specific model scheme which is highly accurate while retaining good generalizability within solid electrolyte chemistry.

Here, we introduce DPA-SSE, a domain-specific pre-trained deep potential model with attention mechanism that is specifically designed for sulfide electrolytes simulation. The DPA-SSE model includes 41 unique systems, among which are 26 sulfide compounds, thereby providing a solid platform for the study of sulfide electrolytes and beyond. Trained in extensive out-of-equilibrium configurations, the model accurately predicts the energy and atomic forces of sulfide electrolytes along dynamic trajectories, reproducing ion transport to ab initio accuracy. The DPA-SSE exhibits good generalizability. It accurately predicts solid solutions of arbitrary concentration, an important merit for sulfide electrolyte optimization. The pre-trained model can also be fine-tuned with minimal training data for downstream tasks. The fine-tuned model achieves similar performance with ten times fewer training data than the models trained from scratch. Moreover, a distillation scheme that generates simpler models to alleviate the high cost associated with pre-trained universal models in dynamic simulation is proposed. Combining high precision and good generalizability, the DPA-SSE could aid in the development of better sulfide electrolytes.

Results

Model overview

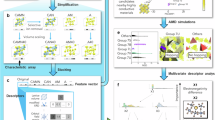
Figure1 provides a graphical representation of the training sets for the DPA-SSE model, as well as an overview of the model workflow. The training sets include three major types of sulfides electrolytes, namely, the LGPS-like compounds (Li10XY2S12; X = Ge, Sn, Si; Y = P, Ga, Sb, As), argyrodites (Li6PS5X; X = Cl, Br, I) and Li7P3S11. For solid batteries, the ability to operate at elevated temperatures is highly desirable, and MD simulations provide critical information regarding the thermal stability of solid electrolytes. To this end, the decomposition products of sulfide SEs are also required. By thermodynamic analysis, LGPS-like compounds decompose into Li2S, Y2S5 and XS2, while X = Ge, Sn, Si and Y = P, Ga, Sb, As; likewise, argyrodites decomposes to Li2S, P2S5 and LiX (X = Cl, Br, I). These compounds, as well as the lithium metal, are included in the training sets. In general, the training sets cover 15 elements and 41 different systems, including 26 chalcogenides, as presented in Fig. 1. DPA-SSE utilizes the DPA-224 framework, a sophisticated architecture with an attention mechanism designed for broad coverage across the periodic table and versatile applications. With the pre-trained DPA-SSE, one can perform atomic simulation of sulfide electrolytes, obtaining key properties of ion transport, thermodynamic stability, etc. If unfamiliar systems are encountered, DPA-SSE can be fine-tuned for downstream tasks with minimal additional data set by leveraging the transferable knowledge embedded within the pre-trained model. Usually, atomic simulation only involves a portion of the composition space covered by DPA-SSE. In these cases, lighter, faster DeePMD models can be generated from the pre-trained or fine-tuned DPA-SSE model for more efficient molecular dynamics simulation.

Fig. 1: Overview of the DPA-SSE model and its training dataset.
figure 1

The DPA-SSE model is pre-trained on a diverse dataset covering sulfide-based chemistries, with a focus on LGPS-like and argyrodite electrolytes. It can be efficiently fine-tuned for downstream tasks using minimal additional data. Furthermore, a distillation framework enables the generation of faster, lightweight DeePMD models from the pre-trained or fine-tuned DPA-SSE, enabling efficient molecular dynamics simulations for target systems.

Full size image

Model testing and performance

DPA-SSE can accurately predict the energies and forces of sulfide electrolytes of various configurations. In Fig. 2a, b, the predicted energy and force are plotted against the DFT calculation. The energy and force mean absolute error (MAE) converge to 1.58 meV/atom and 30.28 meV/Å on the test sets, respectively. To further validate DPA-SSE for the simulation of sulfide electrolytes, Fig. 2c, d test the energy and force MAE on six typical sulfide electrolytes, namely Li10XP2S12 (X = Ge, Sn, Si) and Li6PS5X (X = Cl, Br, I). The test data is constructed by performing long DeePMD simulations heating from 150 to 1150 K and labeling the trajectories with DFT calculation. For all test systems, the energy and force MAE are within 2 meV/atom and 30 meV/Å, respectively. This high accuracy ensures reliable simulation of sulfide electrolytes across a wide temperature range. For a comprehensive evaluation, benchmark tests on these sulfide electrolyte systems are also conducted for universal force fields which include MACE, M3GNet, as well as DPA-2-MP, a pre-trained DPA-2 model branch for the MPtrj dataset. Note that only conservative force fields are listed here. Conservative means that atomic forces are derivatives of the potential energy, which ensures energy conservation in the MD simulation and is fundamental in calculating dynamical properties such as ion diffusion30,31. As shown in Supplementary Fig. S1, the universal force fields perform reasonably well on low-temperature, near-equilibrium trajectories but have significant errors on the heating trajectories with many out-of-equilibrium configurations. A more detailed comparison of energy prediction by DPA-SSE and other universal force fields is presented in Supplementary Fig. S2. The result suggests that the energy of out-of-equilibrium configurations, such as those in the lithium-hopping event, is underestimated by universal force fields, and significantly higher ion transport may be obtained during dynamic simulations. This result shows the importance of the domain-specific DPA-SSE dataset, which includes a considerable amount of out-of-equilibrium configurations for both electrolyte materials and their subsystems. To further illustrate this point, we fine-tuned the universal force fields (MACE, M3GNet and DPA-2-MP) with DPA-SSE dataset, and test the performance of those fine-tuned models. It is worth noting that the universal force fields being tested are pre-trained with DFT dataset labeled using PBE functional, whereas the DPA-SSE dataset uses PBESol functional. Usually, the difference between PBE and PBESol data amounts to a moderate energy shift, which can be handled by updating the fitting network parameters as well as the element reference energy during fine-tuning. As shown in Fig. 2c, d, the accuracy of the fine-tuned models is significantly improved and is comparable to DPA-SSE for the dynamical trajectories of test systems. The fine-tuned M3GNet exhibits larger errors than fine-tuned MACE and DPA-2-MP, particularly in force predictions, likely due to its significantly smaller model size and less comprehensive pre-training dataset25,26. This highlights the critical role of extensive pre-training data and high model expressiveness for effective foundation models.

Fig. 2: Performance on test datasets.
figure 2

a, b Mean absolute errors (MAEs) of energy and force near equilibrium, compared to DFT calculations on the test datasets. Each color corresponds to one of the 41 distinct training systems. c, d Energy and force MAEs of DPA-SSE on heating trajectories of representative sulfide electrolytes from 150 K to 1150 K. For comparison, results from universal force fields fine-tuned on the DPA-SSE dataset are also shown.

Full size image

In addition to the benchmark tests for static energy and force prediction, DPA-SSE is also tested for lattice relaxation, as shown in Supplementary Fig. S4. The lattice constants of the relaxed structures fit well with the DFT calculations. DPA-SSE is also capable of predicting the thermal stability of sulfide electrolyte materials. In Supplementary Fig. S5, the formation energy of pseudo-binary system xLi2S(1-x)P2S5 as a function of composition is presented. The three unique compositions, Li7P3S11 (x = 0.7), Li3PS4 (x = 0.75) and Li7PS6 (x = 0.875) are all on the formation energy hull in this pseudo-binary phase diagram, which agree with DFT calculations.

Model generalizability

As mentioned in previous sections, chemical doping is a key strategy for electrolyte optimization, and atomistic simulations capable of predicting doped electrolytes may provide crucial guidance. Being generalizable is essential here, as no training set can cover the vast configuration space of solid solutions and doped compounds. To verify the generalizability of DPA-SSE, Li10(Ge, Sn, Si)P2S12 (L(Ge, Sn, Si)PS) and Li6PS5(Cl, Br, I) (LPS(Cl, Br, I)) solid solutions with random mixes of cation and anion atoms at various concentrations are constructed. For each configuration, an room temperature AIMD trajectory was produced and added to the test set. Figure 3a, b presents the energy and force prediction in the test sets. The energy and force MAE for solid solutions are 1.56 meV/atom and 29.15 meV/Å, respectively. The insets of Fig. 3a, b also show the distribution of energy and force MAE. The accuracy for solid solutions is on par with that for standard test sets as shown in Fig. 2, suggesting good generalizability for solid solution. To reveal the origin of predictability for solid solutions, the t-distributed stochastic neighbor embedding plot (t-SNE) for the data sets is presented in Fig. 3c. The t-SNE plot projects high-dimensional data distribution onto a 2D plane, visualizing the similarity of two data points by their distance. In Fig. 3c, points representing the solid solutions sit within the regions spanned by the training sets. Therefore, the generalizability can be attributed to the efficient sampling strategy for the training set and the advanced model architecture, which learned the essential features of solid solutions from constituent compounds.

Fig. 3: Generalizability to solid solutions.
figure 3

Mean absolute error and error distribution of a energy and b forces of Li10Ge1−x−ySnxSiyP2S12 (LXPS) and Li6PS5Cl1−x−yBrxIy (LPSX) solid solutions. These compounds are not present in the training sets. c The t-distributed stochastic neighbor embedding (t-SNE) representation of the training set and the test sets for solid solutions. The t-SNE plot measures the similarity of two data points by their relative distance in a 2-dimension plane. According to the t-SNE plot, data points within the training set have covered main features of the solid solutions.

Full size image

Model fine-tuning

As well as accurate “zero-shot" prediction for materials with complex composition, a transferable model easily adapts to downstream tasks by model fine-tuning, which requires much less training data than training from scratch. Here, we showcase the fine-tuning of DPA-SSE. 800 snapshots of a Li2B2S5 (mp-29410, denoted as LBS) compound, which is not included in the training set (Supplementary Fig. S6), are collected from the DP-GEN workflow as downstream data set32. The test set is constructed by 40 frames randomly chosen from the downstream data set. Figure 4a, b presents the energy and force prediction on LBS before and after model fine-tuning. The “zero-shot" energy and force prediction MAE are 162.65 meV/atom and 369.16 meV/Å, respectively. An obvious bias can be observed for the zero-shot energy prediction. After fine-tuning with 20 randomly selected samples, the energy bias is eliminated, and the energy mean absolute error (MAE) is reduced to 3.44 meV/atom. The force prediction also improves significantly’ achieving a MAE of 89.07 meV/Å. Figure 4c, d compares the energy and force convergence of randomly initialized and pre-trained models based on the size of training sets. Normalizing the training epochs by the number of data frames, we find that after fine-tuning with 60 frames, the pre-trained model outperforms the model trained from scratch using the complete training set of 760 frames. In this example, fine-tuning significantly reduces the amount of training data required, resulting in substantial savings on data generation. For comparison, the learning rate of the DPA-2-MP universal force field fine-tuned with DPA-SSE data is also presented in Fig. 4c, d. The DPA-2-MP-ft model, which shares the same model architecture with DPA-SSE, exhibits data efficiency similar to that of the specialized DPA-SSE model. In both cases, fine-tuning with a pre-trained model greatly accelerates the training process for unfamiliar compounds by utilizing the transferable knowledge obtained during pre-training.

Fig. 4: Efficiency of model fine-tuning.
figure 4

a, b Energy and force predictions for the L2B2S5 (mp-29410) system before and after fine-tuning the model using 20 data frames. The comparison highlights the sample efficiency of fine-tuning versus training from scratch. c, d Mean absolute errors (MAEs) of energy and force predictions as a function of the number of training frames for the L2B2S5 system. For reference, the learning curve of the pre-trained DPA-2-MP universal force field fine-tuned using DPA-SSE dataset is also shown.

Full size image

Nudged elastic band calculation and dynamic simulations

Large-scale dynamic simulation of solid electrolytes for a sufficiently long time can predict ion transport properties. For precise ion transport calculations, it is essential that the underlying force fields can accurately evaluate out-of-equilibrium configurations during Li+ ion hopping. Figure 5a, b presents the hopping barrier for the correlated Li+ motion along c-axis and within the ab-plane of LGPS electrolyte33,34. The diffusion path is optimized using nudged elastic band (NEB) method with the pre-trained DPA-SSE model. Along the NEB path, the Li+ hopping energy is calculated as 0.28 eV along the c-axis and 0.36 eV within the ab-plane, which agrees well with the DFT result using PBESol functional. To demonstrate the accuracy of DPA-SSE, Fig. 5c compares the calculated and experimental lithium ion diffusion coefficient D of LGPS from room temperature up to 1100 K. Clearly, the diffusion coefficients calculated by the DPA-SSE simulation are very close to those of the AIMD simulation. Similar results are also obtained for other LGPS-like electrolytes, as shown in Supplementary Fig. S8. Most noticeably, DPA-SSE enables an accurate simulation of sulfide electrolytes at room temperature, which agrees reasonably well with available experimental results. This is previously intractable for AIMD simulation due to the long simulation time required for convergence and the large simulation cell to mitigate the size effect35. For comparison, universal force fields (M3GNet, MACE, DPA-2-MP) fine-tuned with DPA-SSE dataset as well as their base models are also tested. It is noted that the DFT label of the three universal force fields uses PBE functional, instead of the PBESol used by DPA-SSE. To clarify potential ambiguity in simulation results due to the functional choice, lithium-hopping paths labeled with PBE calculations are presented in Fig. 5a, b. The difference in relative energy between frames in the lithium-hopping paths is very small for the two types of functional. A previous study by Huang et al. also suggests the PBE and PBESol functional only has a minor effect on the ionic transport simulation of sulfide electrolytes22. The universal force fields tend to underestimate the Li+ hopping barrier, which results in significantly higher Li+ diffusion coefficients, especially at ambient temperature36. After fine-tuning, these universal force fields predict hopping barriers with much improved accuracy and achieve quantitative results of Li+ diffusion coefficients similar to the DPA-SSE model. This observation may suggest fine-tuning as a viable future direction for building domain-specific models.

Fig. 5: Nudged elastic band (NEB) calculation of concerted Li transport in Li10GeP2S12 (LGPS) electrolytes.
figure 5

Hopping energy barrier of a the concerted Li+ ion motion along the c-axis and b the Li+ ion diffusion with a kick-off mechanism in the ab-plane of LGPS electrolyte. The hopping energy barriers calculated with universal force fields fine-tuned with DPA-SSE are presented for comparison, along with the results from the base models, indicated by thin dotted lines of the same color. NEB results by PBE DFT calculations are shown as red dotted lines. c Experimental and simulated diffusion coefficient (D) of LGPS electrolyte obtained from AIMD, DPA-SSE, fine-tuned universal force fields, and their base models.

Full size image

The ion transport of sulfide electrolytes can be modified by doping. Figure 6a plots the room temperature ion conductivity of Li10(SixGe1−x)P2S12 solid solutions using DPA-SSE model. The result agrees reasonably well with experimental measurements. Even without external doping, there might be an intrinsic disorder in the electrolyte materials that plays a key role in ion transport. The Li+ ion transport in the argyrodite electrolyte LPSX (X = Cl, Br, I) has been attributed to the S2−/X− anion site disorder37. Powder X-ray diffraction analysis reveals that a portion of the halide atoms at the 4c sites randomly exchange with an equal number of S atoms at the 4a sites, as shown in the inset of Fig. 6b38. Molecular dynamic simulations with DPA-SSE capture the correlation between anion site disorder and ion transport21. Figure 6b shows the time evolution of the mean square displacement (MSD) at room temperature of lithium ions in LPSCl with and without anion disorder. The lithium MSD converges after a few hundred picoseconds in the ordered phase; in the disordered phase, the lithium MSD increases with simulation steps, suggesting long-range ion transport. Hence, anion site disorder is essential for fast ion transport in argyrodites. Figure 6d also plots the potential energy of ordered and disordered LPSCl along the simulation trajectory. The disorder phase actually has lower potential energy, and is thus more favorable than the ordered phase. This result is in agreement with experimental synthesis of LPSCl electrolytes. Unlike LPSCl, LPSI in ordered phase exhibits lower potential energy as shown in Supplementary Fig. S8, which helps explain the significantly lower ion conductivity. The anion disorder critical to inonic transport in LPSCl electrolyte can be enhanced by substituting more S at the 4c sites with excess Cl atoms, which also introduces Li vacancies to keep stoichiometry39. In Supplementary Fig. S10a, ionic conductivity of Li6−xPS5−xCl1+x as a function of excess Cl doping is calculated with DPA-SSE. The result reveals the correlated effect of Li vacancy and stronger S/Cl mixing at 4c site that significantly improves ionic conductivity, which supports the experimental measurement39,40. An alternative strategy would be to replace the excess Cl with Br, and the ionic conductivity of Li6−xPS5−xClBrx calculated with DPA-SSE is presented in Supplementary Fig. S10b, along with experimental results41. The Br-doped LPSCl exhibits higher ionic conductivity than Cl doping at higher concentration, possibly due to the enhanced configurational entropy. In both examples, DPA-SSE accurately simulates the positive effect of excess halogen doping in LPSCl electrolyte.

Fig. 6: Molecular dynamic simulation of lithium ion transport in sulfide electrolytes.
figure 6

a Experimental and calculated room temperature ion conductivity of Li10SixGe1−xP2S12 solid solution at various concentrations. b The time evolution of lithium ion mean square displacement (MSD) for Li6PSCl5 in ordered and disordered anion-site configurations, the potential energy of the two configurations are also plotted. Experimental and calculated room temperature c ion conductivity and d hopping activation energy of five typical sulfide electrolytes.

Full size image

Considering the anion site disorder in argyrodites, Fig. 6c lists room temperature ion conductivity of five sulfide electrolytes calculated with DPA-SSE, showing excellent agreement with experiments. Assuming Arrhenius relations, activation energy Ea of lithium ion diffusion can be extracted from the temperature dependence of diffusion coefficient D. The activation energy for Li+ hopping is plotted in Fig. 6d. Evidently, the hopping barrier ΔE estimated by DPA-SSE is very close to the experimental measurement, consistent with the NEB calculations in Fig. 5.

Model distillation

Despite the high accuracy and good generalizability, DPA-SSE is still rather expensive for large-scale dynamic simulations. Usually, the simulation systems only represent a small portion of the chemical and configuration space covered by the pre-trained DPA-SSE model. In these cases, the complex model structure associated with the generalization becomes redundant and can be trade-off for better efficiency. To address this, a knowledge distillation scheme was proposed for DPA-SSE, as demonstrated in Supplementary Fig. S12a. Firstly, thousands of randomly perturbed structures are generated. To ensure the robustness of the distilled model for dynamic simulations, we run a few short MD simulations with the DPA-SSE model from the perturbed structures for picoseconds. The resulting trajectory was further perturbed to generate more out-of-equilibrium configurations. These configurations are labeled by the DPA-SSE model that effectively acts as a “teacher”, and those with excessive atomic forces (in this case more than 10 eV/Å) are filtered out. Then a standard DeePMD model with local descriptor, the “student” model, is trained for a million steps on the collected training set. Supplementary Fig. S10b, c compares the performance of the “teacher” and “student” models on the test set constructed from a 900 K AIMD trajectory. The energy and force MAE of the distilled model are 2.10 meV/atom and 48.44 meV/Å, respectively. For comparison, the energy and force MAE of the DPA-SSE “teacher” are 1.59 meV/atom and 30.0 meV/Å, respectively. Note that in addition to error inherent in the “teacher” model, the training process of the “student” model also induces errors. Thus, the accuracy of the distilled model would inevitably be affected compared with the original DPA-SSE. However, the extent of the induced error can be controlled within the acceptable range of less than 1 meV/atom and a few dozen meV/Åby including a sufficient number of data frames in the training dataset. Provided with a reliable and accurate “teacher” model, a robust distilled model can be obtained for only slight loss in accuracy, which can be easily out-weighted by the vastly improved simulation efficiency. The inset of Supplementary Fig. S12b compares the running efficiency of the pre-trained and distilled models. The benchmark test involves running a 900 K NVT simulation of an LGPS supercell consisting of 1350 atoms, on the same GPU processing unit. The distilled model is faster than the pre-trained model by at least two orders of magnitude. Figure 7 compares the efficiency of DPA-SSE, distilled DPA-SSE and other universal force fields. The efficiency of the distilled model can be further improved by hardware-acceleration, e.g., the non von-Neumann molecular dynamic (NVNMD) proposed by Mo et al.42. The NVNMD is revised from the standard DeePMD model and addresses the “memory bottleneck” issue by running on purpose-built hardwares of non von-Neumann architecture.

Fig. 7: Model efficiency for molecular dynamic simulation.
figure 7

The distilled DPA-SSE and fine-tuned universal force fields are tested on a computation node of a single V100 GPU unit and 12 CPU cores. The NVNMD model is tested on custom hardware with a specialized architecture for running molecular dynamics.

Full size image

Discussion

Ion conductivity is one of the most essential parameters of solid electrolytes. Atomistic simulation can be a valuable asset in the search for better electrolyte composition by screening candidate materials based on predicted ion conductivity. This may significantly accelerate the development process of solid electrolytes. To this end, the underlying force field of atomistic simulation must fulfill two requirements: First, it must be highly accurate even along out-of-equilibrium dynamic trajectories; secondly, it must be generalizable to doped electrolyte materials of complex composition. Traditional machine learning potentials or universal force fields trained on near-equilibrium data sets either lack generalizability or do not have sufficient accuracy. As shown in our comparative tests, the universal force fields overestimate the room temperature ion conductivity of sulfide electrolytes by more than an order of magnitude, thus falling short of the required accuracy.

In this work, we introduced the domain-specific pre-trained DPA-SSE model built for accurate simulation of sulfide electrolytes. Leveraging the extensive out-of-equilibrium training set and advanced model architecture, DPA-SSE model achieves high accuracy and good generalizability among sulfide electrolytes. We demonstrate the capability of DPA-SSE by the Li+ hopping barrier calculation using NEB method and accurately reproduce the experimental ion conductivity of sulfide electrolytes even with complex composition and intrinsic disorder such as the L(Si, Ge, Sn)PS and LPS(Cl, Br, I) solid solutions. In addition to direct application, DPA-SSE also serves as a basis platform for more specialized tasks. The model can be fine-tuned for downstream tasks, achieving the same performance as the model trained from scratch but with ten times less training data, as demonstrated in the example of an LBS system. When the chemical and composition space of the target electrolyte can be narrowed, the pretrained or fine-tuned DPA-SSE model can generate a faster and lighter DeePMD model through distillation. The distilled model is much more efficient in dynamic simulation as it truncates model parameters irrelevant to the target system.

Despite these advancements, further improvements can be achieved through several efforts. First, DPA-SSE encompasses only sulfide electrolytes, and the coverage and generalizability of the model may be further enhanced by incorporating other systems. Second, an automated workflow for model fine-tuning and distillation may greatly enhance the accessibility of DPA-SSE for field experts and industry users. This workflow should automatically validate the quality of fine-tuned models and the robustness of distilled models. In addition to predicting bulk electrolyte properties, interface models can also be generated on the basis of DPA-SSE. In solid batteries, the composition and structure of the interface between the electrolyte and electrode materials often differ significantly from bulk materials, which presents major challenges in ion conduction and chemical stability43. Machine learning force fields may play a pivotal role in understanding interfaces in atomistic detail, but training an interface force field is very difficult due to the complexity of the interface and the requirement for extensive DFT calculations. With the fine-tune workflow, interface models built upon the pre-trained DPA-SSE may greatly improve training efficiency and accelerate the interface design process. In conclusion, DPA-SSE enables accurate large-scale atomistic simulation of sulfide electrolytes within a wide chemical and configuration space. Our model not only accelerates the optimization of sulfide electrolytes but also serves as a platform model toward widespread applications of AI-driven techniques in solid electrolyte development.

Methods

Model design

The DPA-SSE model utilizes the DPA-224 framework, a sophisticated model designed with broad coverage across the periodic table in mind. By leveraging the innovative architecture design, DPA-2 exhibits remarkable transferability with sufficient training sets. In DPA-2, a local descriptor Di is constructed from the local structural and chemical environment for each atom, represented by a single atom channel fi, a rotation invariant atom pair channel gij and a rotation equivariant channel hij. The single- and pair-atom representation subsequently passes through multiple transformer layers to output the local descriptor Di which is invariant under lattice translation, rotation and atom permutation. For each type of downstream task, a neural network would fit the local descriptor to the outputs. In the case of atomistic simulation, Di is fitted to a local energy Ei, whose summation over atomic indices gives the potential energy, E(R) = ∑iEi(R), where R represents atomic configuration. The atomic forces are derived from the partial differentiation of potential energy with respect to atomic position, which naturally ensures force conservation.

Fine-tune and distillation

The pre-trained DPA-SSE model can be fine-tuned for downstream tasks, wherein the atomic descriptors Di are initialized by the pre-trained model. Thanks to the transferable knowledge, the fine-tuned model converges much faster than models trained from scratch. Due to the large number of model parameters, direct application of the fine-tuned DPA-SSE to dynamic simulation for long time steps can be inefficient, which is a common issue for universal models. Thus, a distillation strategy is devised. In this scheme, DPA-SSE model, the “teacher” model, essentially plays the role of an energy and force calculator, and a “student” model, usually a standard, lightweight DeePMD model using the local descriptor without the attention mechanism16,24,44, is trained with a large data set labeled by the DPA-SSE model. For the distilled LGPS model reported in this work, the detailed procedure of distillation is as follows: The perturbed LGPS structures are first generated using the dpdata module, and then labeled by the pre-trained DPA-SSE model. Five perturbed structures are randomly selected as the initial structure for a short DPA-SSE molecular dynamics simulation of 2000 steps at 900 K using the NPT thermostat at ambient pressure. The time step of the molecular dynamic simulation is 1 fs. One hundred frames are extracted from each trajectory, and each frame is further perturbed to generate more configurations. In total, the training set consists of 8579 frames of LGPS system. The test set is constructed from an 900K AIMD trajectory of NVT thermostat starting from the relaxed LGPS structure. A simple schematics of the distillation procedure is presented at Supplementary Fig. S12a.

Data generation

The training sets are produced by the standard DP-GEN workflow45. Initial configurations are constructed by sampling a short AIMD trajectory starting from a randomly perturbed structure. In subsequent training iterations, the training sets are collected through NPT simulations conducted over a temperature range of 0–1200 K and a pressure range of 0–2 GPa for extensive sampling of out-of-equilibrium configurations. Such a wide temperature and pressure range ensures extensive sampling of configurations relevant to MD simulation at heating temperature. The final training sets consist of 54,771 snapshots of various configurations with DFT energy, force and virial as labels. The labeling of training sets are carried out on VASP packages46 utilizing projector-augmented plane-wave (PAW) pseudopotentials with PBESol exchange-correlation functional47. The cutoff energy was set to 600 eV for plane-waves, and the convergence condition was set to 0.01 eV/Å for atomistic coordination relaxation. The Brillouin zone samplings were controlled by KSPACING in order to ensure the same k-point grid for all systems, and it is set to be 0.3.

Model training

The collected training sets are utilized to train the DPA-SSE model as mentioned before. The descriptor has two major components, a representation initializer (repinit) layer and 12 representation transformer (repformer) layers. The repinit layer consists of three hidden layers with 25, 50 and 100 neurons, respectively. The repformer layers serve to learn complex information within the latent space of data sets, enabling increasing model performance with the number of data frames. The learned descriptors are fitted to downstream tasks by a fitting network of three hidden layers each with 240 neurons. The transformer module generally implies a lower learning rate for training stability48. A low initial learning rate of 0.001 is chosen, which decays to 3.51 × 10−8 after 12,000,000 learning steps at an interval of 60,000 steps. We utilize the DPA-2 framework for single-task training. Specifically, we set the cutoff radius for the repinit layer to 9.0 Å. The input dimension for single-atom representations is fixed at 8. For the embedding connection, we employ a multilayer perceptron (MLP) consisting of three layers with 25, 50, and 100 neurons, respectively. Both types of layers are configured with four attention heads. The fitting network is composed of a three-layer MLP, each layer containing 240 neurons. Our training strategy starts with a learning rate of 2 × 10−4, undergoing exponential decay every 10,000 steps, eventually reducing to 3 × 10−8 at the 2,000,000 step. The prefactors for energy, force, and stress are adjusted alongside the learning rate. Specifically, the energy (virial) prefactor is scaled from 0.02 (0.2) to 1, while the force prefactor is adjusted from 1000 to 1. The more detailed training parameters can be found in our previous paper24, and we have made all the training sets and models available through the AIS-Square platform at here. We have created a notebook to help readers learn how to use open models for property calculation and model evaluation (https://bohrium.dp.tech/notebooks/71679486918).

The universal force fields, namely DPA-2-MP, MACE and M3GNet, are fine-tuned with the DPA-SSE dataset for 4 epochs in all cases, with 5% of frames randomly selected for validation. The DPA-2-MP (DPA-2.3.1-v3.0.0rc0) is pre-trained on a diverse dataset including MPtraj and millions of other data frames using a multi-task strategy, and it shares the same network structure with DPA-SSE. The MACE model being tested is the small version of MACE-MP-0a pre-trained on the MPtraj dataset25. The M3GNet model is fine-tuned using the matgl module (M3GNet-MP-2021.2.8-PES) instead of the original implementation49. For the learning rate test at Fig. 4, DPA-SSE, DPA-2-MP-ft and the randomly initialized DPA-2 model are all trained for 133 epochs, starting with a learning rate of 0.001, which finally decays to 3.51 × 10−8.

Ionic conductivity

The mean square displacement (MSD) of lithium ions after time period t can be calculated as \({\rm{MSD}}(t)=\frac{1}{N}\mathop{\sum }\nolimits_{i}^{N}| {r}_{i}(t)-{r}_{i}(0){| }^{2}\), where N is the number of lithium ions. Assuming Brownian motion, the diffusion coefficient D of lithium ions in 3-dimensional space can be deduced as \(D=\mathop{\lim }\nolimits_{t\to \infty }\frac{{\rm{MSD}}(t)}{6t}\). The Nernst–Einstein relation relates ionic conductivity σ at temperature T to the lithium diffusion coefficient if the correlation between ions is negligible, \(\sigma (T)=\frac{{(ze)}^{2}}{V{k}_{B}T}D\), where V the volume of simulation cell, ze the electronic charge for each lithium ion, and kB is the Boltzmann coefficient50. Ion conduction is a thermally activated process, and the activation energy Ea can be extrapolated by fitting the modified Arrhenius relation to the calculated ion conductivity at various temperatures, \(\sigma (T)={\sigma }_{0}{T}^{m}\exp (\frac{-{E}_{a}}{{k}_{B}T})\), with m typically equal to −1. The pre-factor σ0 is related to ion hopping entropy, distance, as well as attempt frequency in the simple case of uncorrelated ion hopping4. In practice, σ0Tm can be approximated as constant over temperatures.