Introduction

One of the most significant advances in molecular and materials simulation over the past decade has been the introduction of atomistic machine learning interatomic potentials (MLIPs)1,2,3,4. These methods can approach the accuracy of ab initio techniques while scaling to systems containing hundreds of thousands of atoms, opening the door to discoveries previously thought impossible5,6,7. This breakthrough relies generally on the assumption that the total energy of a system can be decomposed into atomic contributions. These contributions are modeled as a function of each atom’s local chemical environment within a defined cutoff radius, using ML techniques such as Neural Networks (NN)8,9 or Gaussian Process Regression (GPR)10,11.

However, due to their inherent locality approximation, these models are fundamentally limited by their inability to account for long-range interactions and non-local effects such as charge transfer. This is often unproblematic since long-range effects are effectively screened in isotropic condensed phase systems. It can become significant in systems involving polar interfaces or complex ionic interactions, however12. In such cases, local models reach the boundaries of their applicability.

To address these limitations, considerable effort is being devoted to developing methods that incorporate interactions beyond the cutoff of local descriptors. One promising approach involves the use of message-passing neural networks (MPNNs), which extend the effective receptive field of the models by propagating information through a graph representation of the atomistic structure. This enables such models to capture interactions over longer distances, alleviating some of the constraints imposed by the locality assumption9,13,14,15,16. However, message passing is not effective for describing truly long-range interactions as each additional layer increases the computational cost. Furthermore, the large receptive fields of these MLIPs makes parallelization across devices inefficient, precluding their application to very large systems 17.

As a consequence of this, models with an explicit physics-based representation of long-range interactions have been of great interest in recent years, including the long-distance equivariant (LODE) framework18,19 and its extensions20, BpopNN21, deep potential long-range (DPLR) models using charges obtained from maximally localized Wannier functions22, or self-consistent field neural networks (SCFNN)23. On a related note, there has also been significant work on developing MLIPs capable of capturing the effects of an external electric field (e.g. for electrochemical or spectroscopic applications), without explicitly predicting charges or directly modeling long-range interactions 24,25,26,27.

For electrostatics in particular, arguably the most adopted approach is to build MLIP models that self-consistently predict atomic charges or charge distributions by minimizing a charge-dependent energy expression. This enables a physically correct description of long-range interactions, but also automatically provides a means to include external fields and varying total charge states on the same footing. The earliest implementation of this concept in ML was introduced in the CENT models28,29,30, where Goedecker and co-workers combined a classical Charge Equilibration (QEq) method with environment-dependent electronegativities predicted by neural networks (NNs). This methodology was later advanced into the Fourth Generation High-Dimensional Neural Network Potentials (4G-HDNNP), where a local NN potential is combined with a CENT-like model fitted to reproduce Hirshfeld charges31,32. This idea was subsequently also used in other NN potentials33,34, linear Atomic Cluster Expansion models35, and the Kernel Charge Equilibration (kQEq) method. In the latter case, the models were directly trained on observables such as energies, forces or dipole moments 36,37.

QEq has thus been found to be highly effective as a building block of long-ranged ML models. Nonetheless, there are some known pathologies of this approach, which have been discussed in the context of classical force fields38. While ML-based charge equilibration models (ML-QEq) are in general much more expressive and accurate than their classical counterparts37, it has not been thoroughly investigated to what extent these pathologies are inherited. This paper aims to answer this question. To this end, we first summarize the known limtations of QEq and analyze to what extent they can be expected to carry over to ML-QEq models. Subsequently, we investigate critical cases numerically by applying ML-QEq methods to systems with varying total charge, cluster fragmentation and applied electric fields.

Results

Classical charge equilibration methods

QEq is widely used to compute partial atomic charges for classical MD simulations, enabling the treatment of long-range electrostatic interactions and polarization effects via electronegativity equalization. As detailed in the methods section, the central idea behind QEq and related approaches is that the charge distribution in a system can be obtained by minimizing a charge-dependent energy function. This function describes the interplay between the Coulomb interaction among the partial charges (favoring charge separation), the electronegativity differences between atoms (favoring flow of negative charge from electropositive to electronegative elements), and the electronic hardness of each atom (limiting the total amount of charge that can be accommodated by each atom).

While QEq yields reasonable charge distributions near equilibrium geometries, it is well known to overestimate charge transfer between dissociated atoms or molecules39,40. This is particularly drastic in the atomized limit, where the off-diagonal elements of the hardness matrix (see Methods section) vanish, so that the atomic charges become determined solely by differences in atomic electronegativities and the sum of the diagonal hardness terms. To eliminate spurious charge transfer in this limit, atomic electronegativities would need to asymptotically vanish, or hardness parameters diverge to infinity. Neither of these is possible within the standard QEq formalism, where both quantities are treated as elemental constants 41.

One of the conceptual predecessors to modern environment-dependent ML-QEq models is the Charge Transfer with Polarization Current Equilibration (QTPIE) method39,40. QTPIE addresses key deficiencies of conventional QEq by introducing charge transfer variables that represent polarization currents between atom pairs. The atomic partial charge qi is then obtained as a sum of pairwise charge transfers to and from atom i. Here, unphysical long-range charge transfer is mitigated by dampening the polarization current with the distance. Interestingly, this atom-pairwise approach was found to be equivalent to a more familiar QEq-like picture that uses overlap integrals Sij to renormalize the atomic electronegativities, making each atom’s effective electronegativity dependent on the local electronic environment just as in ML-QEq methods 41.

This analogy raises the question whether ML-QEq methods suffer from the same limitations as classical QEq, or whether they are mitigated by the use of environment-dependent electronegativities. To answer this question, we focus on two situations where (semi)local MLIPs cannot be applied, namely on systems with variable total charge and under applied electric fields, using water clusters as prototypical test systems.

Variable total charges

As a first example, we consider water clusters in different states of (de)protonation with total charges of −1, 0, and 1 e. A local potential with a sufficiently large cutoff could in principle infer the total charge from the number of hydrogen atoms in such clusters. However, this must fail when the clusters are dissociated into their molecular components by a distance larger than the cut-off radius of the local descriptor.

To prepare the dataset of water clusters, the local minima of neutral water clusters containing 3 to 10 molecules, as provided by Xantheas and coworkers42, were used as a starting point. To generate charged configurations, either a proton or a hydroxyl group was removed from each neutral cluster, resulting in positively and negatively charged configurations. Non-equilibrium configurations of these clusters were then generated through molecular dynamics (MD) simulations employing the semiempirical GFN2-xTB method43,44,45. Finally, expanded and contracted clusters were generated by displacing the molecules relative to each cluster’s center of mass by factors ranging from 0.9 to 5.0 (see Fig. 1). For all configurations thus obtained, energies and forces were computed with the hybrid PBE0 functional. A full overview of the dataset is provided in Supplementary Note 1, with RMSE values for validation and test sets in Supplementary Table 1.

Fig. 1: Charged and neutral water clusters.
figure 1

a Exemplary cluster in the equilibrium and dissociated state. b Learning curves for energies (blue) and forces (red). Mean and standard deviations for three random training sets are shown for each size. RMSEs are calculated on the validation set composed of 2000 randomly selected structures for each net charge state. c Relative distribution of energy errors for a test set composed of 5000 random structures for each net charge state (represented by different color bars), and the corresponding parity plot.

Full size image

Figure 1 presents learning curves for training an MLIP composed of a short-range Gaussian Approximation Potential (GAP) and a long-ranged kQEq model, with all general conclusions derived below being independent of this particular type of short-ranged MLIP architecture. Full details on architecture and training of these models are provided in the methods section. With sufficient training data, this MLIP can accurately predict energies and forces for all charge states and intermolecular distances, achieving RMSEs of 2 meV/atom and 49 meV/Å. The figure also shows the energy error distributions of the test set in terms of histograms and correlation plots comparing DFT and GAP+kQEq energies. Neutral clusters exhibit lower energy errors relative to charged ones, but also span a smaller energy range. Additionally, neutral clusters constitute the majority of the training set (55% of all structures) and are the only group for which local minima are included. Overall, the performance for all charge states is thus satisfactory.

Notably, this accuracy also translates to an accurate description of long-range interactions. This is shown for the example of dissociation curves for three representative clusters (each corresponding to a different total charge state) in Fig. 2. When comparing the DFT energy with that obtained from the GAP+kQEq model (for comparisons with standalone GAP and kQEq models see Supplementary Fig. 1 and Supplementary Note 2), we can see that the potential energy surface (PES) is accurately described across the entire range of inter-molecular distances, including interactions outside of the descriptor cutoff distance. However, at longer distances (i.e. beyond a two-fold expansion) the ML-curves display small energy fluctuations which are absent at the DFT level. These will be analyzed in more detail below.

Fig. 2: Cluster dissociation.
figure 2

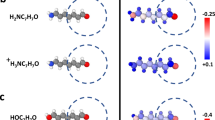
a Comparison between DFT (points) and the GAP+kQEq (full lines) energies. b Illustration of equilibrium and dissociated water clusters for each energy curve, where atoms are colored according to their atomic charges. For anionic and cationic clusters the OH− and H3O+ fragments are circled, respectively.

Full size image

It is worth noting that all models discussed so far have not been trained on reference atomic charges. This contrasts with common practice in the development of long-range MLIPs, where schemes such as Hirshfeld partitioning are often used to generate reference charges31,34,35. On the other hand, models where charges are considered solely as learnable weights in long-range energy expressions are becoming increasingly popular46,47. Indeed, given that the partial charges of atoms in molecules are not physical observables, ML charges obtained via fitting potential energy surfaces can nonetheless acquire a meaningful interpretation and reflect the underlying physics of the system. This is somewhat analogous to density representations obtained with Resolution-of-the-Identity (RI) and Density Fitting (DF) techniques in quantum chemistry, which can also differ significantly depending on whether an overlap (density-based) or Coulomb (energy-based) metric is used48. Indeed, it has been argued that charge partitioning schemes can be considered a primitive form of RI 49.

In order to judge the quality of the predicted charges, we therefore choose not to compare them to an (arbitrary) reference partitioning scheme. Instead, we consider how the sums of atomic charges for individual molecules fluctuate during the dissociation of the corresponding clusters. This provides insight into intermolecular charge transfer and polarization, which should be robustly captured by any reasonable partitioning. Figure 3 shows the evolution of the molecular charges for the dissociation of a representative test set cluster at each charge state. Here, we compare PBE0 Hirshfeld charges (top) with the kQEq charges of a model trained on energies and forces (center) and specialized kQEq models trained to reproduce Hirshfeld charges (bottom).

Fig. 3: Evolution of molecular charges during cluster dissociation.
figure 3

Charges are shown for each total charge state and DFT-based Hirshfeld partitioning (top), a GAP+kQEq model fitted on energies and forces (center), and kQEq models fitted on Hirshfeld charges (bottom). Different shades of lines represent different molecules in each cluster. Note that a single energy/force model was trained for all charge states, whereas individual models were trained for each charge state when fitting to charges.

Full size image

At first glance, all methods capture the same basic trends. The total charges are delocalized among all molecules in the equilibrium geometry. Upon dissociation, the charge localizes on one fragment (H3O+ or OH−, respectively), while the H2O molecules become charge neutral. Interestingly, even the DFT reference displays a small deviation from integer charges in this limit (particularly for the anionic cluster), due to the well known delocalization error50. Because a hybrid functional is used (and because the electronegativity differences between the fragments are relatively small) DFT does approximately recover the correct limit of integer charges in this case, however. Deviations are more pronounced in the ML models, with deviations of up to 0.05 elementary charges. They thus inherit the overdelocalization tendency from the underlying QEq model, which is much more pronounced than for hybrid DFT41. The models that are explicitly fitted on charges are actually slightly worse in this respect, indicating that this is a fundamental property of ML-QEq models and not related to the specific training setup.

Beyond these general trends, there are also notable differences in how the methods approach their asymptotic limits. In the DFT case, the molecular charges monotonically approach the asymptotic values, whereas the ML models show much more variation and even local minima and maxima in some cases. This is also related to the fact that QEq-based models can arbitrarily transfer charge between molecules, as long as this is variationally convenient. This leads to an exaggerated response of the charges to small perturbations in the electrostatic potential, and leads to the small energy fluctuations upon dissociation seen in Fig. 2.

External fields

One of the key advantages of variational charge equilibration methods is their inherent ability to dynamically adapt the atomic charges in response to external fields. This feature is particularly important for MLIPs intended for applications involving non-isotropic environments, such as interfaces in battery systems or electrocatalysis. Here, local fields can vary significantly and do not tend to cancel out in the course of MD simulations 12.

To assess the ability of QEq-based methods for accurately describing the PES in the presence of an external electric field, we selected a subset of 3030 non-equilibrium neutral water cluster configurations from the dataset described in the previous section. Based on this, a second dataset in which each configuration was subjected to a uniform external electric field was generated. These fields were defined based on a randomly oriented unit vector scaled by a randomly selected magnitude ranging from 0.01 to 0.2 V/Å. This range was chosen to reflect realistic conditions at electrode interfaces, where local field strengths can reach up to 0.2 V/Å24,51,52. Higher fields, particularly around 0.35 V/Å, are known to induce water molecule dissociation53, and were therefore avoided to remain within the regime of non-destructive field strengths53.

To explore optimal training strategies in this setting, we constructed training sets following two complementary approaches, depicted in Fig. 4. In the first case, a set of 100 field-perturbed data points was augmented with a varying number of field-free configurations. In the second case, a set of 100 field-free configurations was augmented with a varying number of field-perturbed configurations. This strategy was chosen in order to determine how training data points with and without a field help or hinder the predictive performance of the model for both kinds of data. This reveals that incorporating field-perturbed structures into the training set is crucial for achieving optimal performance for both field-free and perturbed systems. While adding field-free configurations also initially improves the performance for perturbed systems, this benefit quickly tapers off as more structures are added. In contrast, adding field-perturbed structures is beneficial to both field-free and field perturbed systems. Nevertheless, an accuracy gap between the field-perturbed and field-free structures remains.

Fig. 4: Learning curves for configurations with and without external fields.
figure 4

Shown are energy errors for a model trained on an initial set of 100 field-perturbed configurations, which is augmented by N field-free configurations (dashed lines) and a model trained on an initial set of 100 field-free configurations, which is augmented by N field-perturbed configurations (full lines). Color scheme: blue - test set of field-perturbed structures, red - test set of unperturbed structures.

Full size image

Based on these findings, a final model was trained using a dataset comprising 2000 field-perturbed and 1000 field-free configurations. While overall low errors (ca. 2 meV/atom for energies and 60 meV/Å for forces) are achieved, the errors for field-perturbed cases remain significantly higher than for field-free ones. This increased difficulty points to an inherent limitation in how well QEq-based methods can describe polarization.

As described in the Methods section, the inclusion of an external electric field in the QEq energy expression corresponds to an additive perturbation of the atomic electronegativities. This perturbation depends solely on the atomic positions and the direction and magnitude of the field, leading to a quadratic response of the energy and a linear response of the charges with respect to the field strength. This means that the field response is effectively ML-free in QEq-based MLIPs. Nonetheless, incorporating fields in the training is beneficial, since it leads to an optimal mean-field parameterization for the given range of applied fields.

Figure 5 illustrates the qualitative disagreement between DFT and kQEq for a water cluster subjected to external electric fields of varying magnitude but fixed direction. As shown, the QEq-based MLIP fails to reproduce the correct shape of the energy response to the field. Figure 5 also shows the difference in atomic charges obtained under −0.2 V/Å and 0.2 V/Å fields. The kQEq model predicts that the external field induces a dipole aligned with the field direction, resulting in a charge redistribution within the cluster. In contrast, changes in DFT-based Hirshfeld charges indicate a polarization of each individual water molecule, but no charge redistribution between the water molecules. This behavior highlights the intrinsic limitations of QEq-based methods in adequately capturing polarization effects. A further example demonstrating this linear charge redistribution in periodic water slabs is provided in Supplementary Fig. 2 and in Supplementary Note 3.

Fig. 5: Electric field response of QEq models.
figure 5

a Energetic response of DFT and machine learning (GAP+kQEq) for a neutral water cluster subjected to external electric fields of varying magnitudes along a fixed direction. Energies are shifted so that the DFT energy is zero at ∣ϵ = 0.0∣. b Difference in atomic charges obtained from Hirshfeld partitioning (DFT) and kQEq under external fields of −0.2 V/Å and 0.2 V/Å.

Full size image

More crucial than the quantitative disagreement between ML and DFT is the fact that the overpolarization tendency of QEq-based models can lead to pathological behavior under certain conditions. To illustrate this, we performed an MD simulation analogous to the work of Modine and co-workers38 (who used a classical QEq model). Specifically, we applied a constant external electric field of 0.2 V/Å in the z-direction to a water cluster consisting of 10 molecules. To confine the motion of the molecules in the z-direction, we imposed a harmonic constraint represented by planar boundaries at z = ± 30 Å.

As illustrated in Fig. 6, the water cluster begins to split into two distinct fragments around the 150 ps mark: one composed of two molecules moving in the direction of the applied field, and the other composed of eight molecules moving in the opposite direction. The larger subcluster accumulates a net negative charge and migrates against the field, while the smaller, positively charged subcluster moves along the field direction. The magnitudes of the net charges on both subclusters are approximately equal and opposite. Such charge separation is unphysical under realistic conditions, as it would require a potential difference approaching the ionization energy of water (12.6 eV)38, a threshold not reached under the simulated field strength. This behavior is a clear artifact of the QEq formalism, which enforces a linear and unconstrained charge response. The incorporation of environment-dependent ML electronegativities does not mitigate this limitation, indicating that the underlying QEq model remains fundamentally inadequate for accurately capturing polarization and charge transfer under strong external fields in non-metallic systems.

Fig. 6: Pathological overpolarization of a water cluster in a static field.
figure 6

Snapshots from a molecular dynamics simulation of a water cluster subjected to a static external electric field applied along the z-axis. Harmonic constraints with a force constant of 0.5 eV/A2 were applied in both positive and negative z-directions to confine the system.

Full size image

Discussion

Charge equilibration based on QEq-like ML-models is currently the state-of-the-art approach to introduce non-local charge transfer and electrostatic interactions into MLIPs. We find that such models can in principle accurately describe multiple total charge states and naturally incorporate a mechanism to describe the response to external fields. Despite their overall good performance, our results also showcase the limitations of ML-QEq models, however. While potential energy surfaces can be accurately reproduced, delocalization and overpolarization errors (that are known for classical QEq models) can lead to problematic behavior. This manifests in unphysical intermolecular charge transfer (particularly for fragmented systems) and a qualitatively incorrect response of both energies and charges to electric fields. A drastic consequence of this is pathological behavior in cases when a static electric field is applied in an MD simulation. Importantly, these issues are independent of the specific MLIP used herein, and can be traced to fundamental limitations of ML-QEq models.

Individual aspects of these problems can be addressed, e.g. by constraining the total charge of each subfragment or molecule. However, this strategy is not universally applicable. In particular, in reactive simulations (one of the main application areas of MLIPs), predefining individual fragments is not feasible. Nevertheless, QEq has some highly desirable properties, namely its variational nature and the capability to describe non-local effects. This points to a need to develop new ML charge equilibration approaches beyond the QEq paradigm. In the classical force-field domain, the Atom Condensed Kohn Sham (ACKS2) approach has proven to be the most promising successor for QEq, though it requires a complex atom pairwise parameterization54,55. Alternatively, a more complex (non-local) expression for the site energy potentially could also provide an avenue to overcoming the pathologies of QEq. The methods and datasets presented herein can provide a benchmark for such new developments.

Methods

Machine learning interatomic potentials

All ML models described herein are based on the sparse Gaussian Process Regression (GPR) methodology. Specifically, we approximate a target quantity y(x) as a linear combination of M basis functions \(\tilde{y}({\bf{x}})\)

$$\tilde{y}({\bf{x}})=\mathop{\sum }\limits_{m=1}^{M}{w}_{m}k({\bf{x}},{{\bf{x}}}_{m}),$$
(1)

where wm are regression weights that are fitted to match ab initio reference values, k is a kernel function, x is a representation vector (to be defined below) and M denotes the size of the representative set. Although this set can generally be chosen at random, in our case we select diverse points using CUR decomposition56, as is routinely done for Gaussian Approximation Potentials (GAP)1. In contrast to the representative set, N > M will denote the size of the total training set.

The GPR framework is used to create MLIPs that incorporate both short-range (SR) and long-range (LR) interactions. To this end, the total energy of the system is described via a SR part ESR (described by GAP) and a LR part EQEq described by (Kernel) Charge Equilibration (kQEq):

$${E}_{{\rm{tot}}}\approx {E}_{{\rm{SR}}}+{E}_{{\rm{LR}}}.$$
(2)

The SR energy of the system is expressed as a sum of atomic energy contributions ϵ(xi) that depend on local environments described by the descriptor xi.

$${E}_{{\rm{SR}}}=\mathop{\sum }\limits_{i=1}^{{N}_{{\rm{at}}}}\epsilon ({{\bf{x}}}_{i})$$
(3)

where the summation goes over all atoms in the system Nat.

This local atomic contribution ϵ(xi) is determined using a straigthforward GPR model as expressed in Eq. (1):

$$\epsilon ({{\bf{x}}}_{i})=\mathop{\sum }\limits_{m=1}^{M}{w}_{m}^{{\rm{SR}}}k({{\bf{x}}}_{i},{{\bf{x}}}_{m}),$$
(4)

The LR part of the energy is described by the QEq framework, where the total energy can be approximated as a second order Taylor expansion of on-site atomic charges qi combined with a screened pairwise Coulomb interaction (assuming Gaussian charge distributions with width αi):

$${E}_{{\rm{LR}}}=\mathop{\sum }\limits_{i=1}^{{N}_{{\rm{at}}}}\left[{\chi }_{i}{q}_{i}+\frac{1}{2}\left({J}_{i}+\frac{1}{{\alpha }_{i}\sqrt{\pi }}\right){q}_{i}^{2}\right]+\frac{1}{2}\mathop{\sum }\limits_{i,j}^{{N}_{{\rm{at}}}}{q}_{i}{q}_{j}\frac{{\rm{erf}}\left(\frac{{r}_{ij}}{\sqrt{2}{\gamma }_{ij}}\right)}{{r}_{ij}}.$$
(5)

Here, the screening parameter γij is computed from the width parameter, χi is the electronegativity of atom i and Ji is the non-classical contribution to the atomic hardness 37,57.

Self-consistent partial charges can be obtained by minimizing Eq. (5). As this expression is quadratic in the atomic charges qi, the ground-state charge distribution can be computed analytically. Specifically, setting the derivatives of the total energy with respect to the partial charges to zero yields a linear system of equations, which can be solved directly to obtain the self-consistent charges (under the constraint that total system charge, Qtot, is conserved):

$$\frac{\partial {E}_{{\rm{LR}}}}{\partial {q}_{i}}=\mathop{\sum }\limits_{j=1}^{N}{A}_{ij}{q}_{j}+{\chi }_{i}=0$$
(6)

with Aij being the element of the hardness matrix A defined as:

$${A}_{ij}=\left\{\begin{array}{ll}{J}_{i}+\frac{1}{{\alpha }_{i}\sqrt{\pi }}\quad &\,{\text{for}}\,i=j,\\ \frac{{\rm{erf}}\left(\frac{{r}_{ij}}{\sqrt{2}{\gamma }_{ij}}\right)}{{r}_{ij}}\quad &\,{\text{otherwise.}}\,\\ \quad \end{array}\right.$$
(7)

With this, ELR can be expressed in a matrix notation as

$${E}_{{\rm{LR}}}=\frac{1}{2}{{\bf{q}}}^{T}{\bf{A}}{\bf{q}}+{{\bf{q}}}^{T}{\boldsymbol{\chi }}.$$
(8)

For a description of the incorporation of periodic boundary conditions, see Supplementary Note 4. In contrast to classical QEq models, where χ is an elemental constant, ML-based QEq models introduce environment-dependent electronegativities30,31. The kQEq model used herein achieves this via GPR, analogously to how the atomic energies are expressed in the SR energy 37:

$${\chi }_{i}({{\bf{x}}}_{i})=\mathop{\sum }\limits_{m=1}^{M}{w}_{m}^{{\rm{LR}}}k({{\bf{x}}}_{i},{{\bf{x}}}_{m}).$$
(9)

These environment-dependent electronegativites are then used for the QEq scheme instead of constant element-dependent ones. For full details, please refer to our previous work 37.

The SR and LR models can in principle be trained separately. This is e.g. the strategy pursued for 4G-HDNNPs, where the QEq model is trained on Hirshfeld charges and kept fixed during the training of the short-ranged NN. However, in order to achieve a comprehensive description of various phenomena, such as polar interfaces, systems with varying total charge, or interactions with applied external fields, a joint training of both models is used herein.

External fields

One of the advantages of variational charge equilibration approaches like QEq is that they allow a straightforward description of the interactions of a system with an external electric field. This can be achieved using the method of finite fields, following the formalism of Chen and Martínez38,58. This leads to a modification of the QEq energy expression due to the field ϵ as

$$E{({\bf{q}};{\mathbf{\epsilon }})}_{{\rm{LR}}}=\frac{1}{2}{{\bf{q}}}^{T}{\bf{A}}{\bf{q}}+{{\bf{q}}}^{T}{\boldsymbol{\chi }}-{{\bf{q}}}^{T}\mathop{\sum }\limits_{\mu =1}^{3}{{\bf{R}}}_{\mu }{{\boldsymbol{\epsilon }}}_{\mu }=\frac{1}{2}{{\bf{q}}}^{T}{\bf{A}}{\bf{q}}+{{\bf{q}}}^{T}({\boldsymbol{\chi }}-\mathop{\sum }\limits_{\mu =1}^{3}{{\bf{R}}}_{\mu }{{\boldsymbol{\epsilon }}}_{\mu }),$$
(10)

where R is a matrix of atomic coordinates. The summation in this equation is over the cartesian directions μ = x, y, z. As can be seen, applying an external field thus perturbs the electronegativies by a scalar Rμϵμ. Minimizing Eq. (10) in the same way as Eq. (5), an analogous system of linear equations is obtained.

Computational settings

Reference data for neutral and charged water clusters was obtained using FHI-Aims59 with the hybrid PBE0 functional60 and tight basis set and integration settings. MD simulations for generating non-equilibrium configurations of charged clusters were performed with the xtb code, employing the semiempirical tight-binding method GFN2-xTB at 300 K43,44,45.

We use the Smooth Overlap of Atomic Positions (SOAP) descriptor61 as a representation of atomic environments, as implemented in QUIP via the quippy Python interface62,63. For the model describing varying total charge states, two SOAP descriptors with parameters \({l}_{\max }=5\), \({n}_{\max }=6\) and rcut = 3 Å or rcut = 5 Å, respectively, were used. Regularization parameters of 10−6 eV for energies and 10−3 eV/Å for forces were used. Non classical hardness for both elements were set to 0 Hartree. For clusters with applied fields, two SOAP descriptors with parameters \({l}_{\max }=6\), \({n}_{\max }=8\), rcut = 2.4 Å, and \({l}_{\max }=3\), \({n}_{\max }=8\), rcut = 5 Å were used. Non-classical hardness for both elements were set to 0.1 Hartree. Regularization parameters of 0.001 eV for energies and 0.01 eV/Å for forces were used.

MD of the water cluster under the influence of an external field was performed with the Langevin thermostat in the NVT ensemble, using a time step of 0.5 fs at 300 K. A Hookean constraint plane were placed at z = ± 30 Å with k = 0.5 eVÅ−2. The system was evolved in time using the Atomic Simulation Environment (ASE)64,65 calculator implemented in q-pac.