Introduction

With the development of space technology, more and more spacecraft are entering space. The normal operation of satellites and space stations is inseparable from liquid propellants, cryogens, thermal fluids, and wastes1. The flow characteristics of liquid in space are quite different from those on the ground. Due to the decrease of gravity, surface tension forces dominate the transport and management of free surface flow. Surface tension forces are negligible in most engineering problems. Whereas, the location and orientation of liquid within vessels, conduits, etc. in the low-gravity environment of orbiting vehicles are strongly influenced by surface tension forces2.

In space, the interior corner is often used to passively position and/or control large length scale capillary-dominated liquid inventories, i.e., fuel/cryogen storage tanks3. It is a common construct employed in liquid management systems aboard spacecraft. Without gravity, spontaneous capillary flow along interior corners dominates the liquid behavior in spacecraft4. A quick and precise prediction of capillary flow along interior corners is necessary for liquid management processes under microgravity to control liquid effectively5,6.

Capillary flow research dates back to the 1960s, when Concus and Finn7 proposed the Concus-Finn condition, a geometric wetting condition that corresponds to an underpressure in the liquid, resulting in capillary-driven flow into and along the interior corner8. Ayyaswamy et al.9 solved the two-dimensional equations of motion for steady laminar flow along interior corners by the Galerkin boundary method. They also indicated that the half angle of the interior corner and the contact angle are two independent parameters that characterize the flow configuration. Lenormand and Zarcone10 proposed an approximate solution for the nonlinear diffusion equation of the flow along the corners by analogy with a nonlinear thermal problem. Dong and Chatzis11 made improvements to the theory of Lenormand and Zarcone10 that predicts the imbibition rate of a wetting liquid in the corners by introducing the dimensionless flow resistance β12 and improved the model accuracy. Romero and Yost13 addressed the problem of capillary-driven flow in a V-shaped surface groove by solving a nonlinear diffusion equation for the liquid shape, which derived from mass conservation and Poiseuille flow conditions. A similarity transformation for this nonlinear equation was obtained, and the resulting ordinary differential equation was solved numerically for appropriate boundary conditions. Weislogel and Lichter5 considered the spontaneous redistribution of fluid along an interior corner of a container due to capillary forces. By using the lubrication approximation, they were able to simplify the Navier-Stokes equations and solve the governing equation via similarity solution. After that, Weislogel’s theory was applied to some complex containers4,14. Later, the problem of capillary flows along rounded interior corners was investigated theoretically and experimentally by Chen et al.15 and Kang et al.16. The gravity perpendicular and parallel to the channel axis were both taken into account in corner flows by Rame et al.17. The capillary flow in an asymmetric interior corner consisting of a straight vane and curved wall was investigated theoretically and experimentally by Jinghao Li18 and Yongqiang Li19. Weislogel and McCraney20 discovered a novel solution to the lubrication model for capillary liquid draining in straight and weakly curved channels.

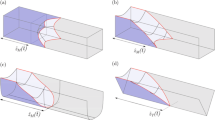
So far, the previous studies on capillary flow mainly focus on straight interior corners (see Fig. 1). However, the curved interior corner (see Fig. 2) provides a further generalization. By analysis, the channel curvature and corner angle are seen as two important factors that influence the capillary flow in curved interior corners. The influence of channel curvature on the capillary flow in curved interior corners was investigated theoretically and experimentally by Wu et al.6.

Fig. 1
figure 1

A liquid column in an isolated straight interior corner of angle 2α.

Full size image
Fig. 2
figure 2

A liquid column in an isolated curved interior corner of angle 2α.

Full size image

The present paper mainly discusses the influence of corner angle on capillary flow in a curved interior corner. An approach is presented for capillary flow along curved interior corners to predict the tip location. In this model, channel curvature effects have been taken into account. Furthermore, drop tower experiments are carried out to provide a microgravity environment. By setting a series of control experiments, the influence of corner angle on capillary flow in curved interior corners is investigated experimentally. Then, the experiments are compared with the theoretical calculations.

Results and discussion

Drop tower experimental results

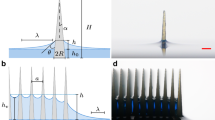
Several typical experimental frames of the drop tower tests are presented in Fig. 3. The free surface profiles are detected by the software GetData Graph Digitizer. GetData Graph Digitizer is a program to obtain original data from digitizing graphs and plots. In Fig. 4, free surface profiles for different time t are presented in the same figure. Due to the reflected light, the section of free surface profile close to the container’s bottom is difficult to figure out. Consequently, this section is not shown in Fig. 4. The resolution of all experimental frames is 1125 × 680. Following calibration, 1 cm equates to 74.438 pixels. Therefore, the side length of each pixel is 0.134 mm. The free surface profiles in the images are very clear and no more than three pixels in size. The error is less than 0.402 mm. In addition, Fig. 4 confirms that the assumption of constant height H is valid for t > 1s. The measured constant heights Hexp of model 1, model 2, model 3, model 4, and model 5 are 2.5130 cm, 1.6716 cm, 1.3480 cm, 1.2160 cm, and 0.6935 cm. According to the relationship between the constant height Hexp and the mean curvature radius \({R}_{{H}_{exp}}\)14,

$${R}_{{H}_{exp}}=f\cdot {H}_{exp}$$
(1)

the experimental mean curvature radius \({R}_{{H}_{exp}}\) can be obtained, where \({R}_{{H}_{exp1}}=0.88{\rm{cm}}\), \({R}_{{H}_{exp2}}=1.04{\rm{cm}}\), \({R}_{{H}_{exp3}}=1.35{\rm{cm}}\), \({R}_{{H}_{exp4}}=1.89{\rm{cm}}\), \({R}_{{H}_{exp5}}=1.67{\rm{cm}}\). The mean curvature radii for the test models should be fixed. However, different test models have different mean curvature radii \({R}_{{H}_{exp}}\) in our experiments. This fact is contrary to this hypothesis. As will be discussed later, it has a direct influence on the results.

Fig. 3: Typical capillary flow frames of the drop tower experiments at different microgravity time.
figure 3

a t = 0s, b t = 1s, c t = 2s and d t = 3s. From left to right are test model 1, 2, 3, 4, and 5. The arrow denotes the tip location of the meniscus in the corner.

Full size image
Fig. 4: The free surface profiles of different test models.
figure 4

The free surface profiles of (a) model 1, b model 2, c model 3, d model 4 and e model 5 for times t = 0s, 0.5s, 1 s, 1.5 s, 2 s, 2.5 s, 3 s, and 3.5 s. The dotted lines represent the free surface profiles and the solid lines represent the bottoms of the corners. The error of each free surface profiles is less than 0.4mm.

Full size image

Figure 5a shows the measured tip location Ltip changes with t. Figure 5b shows the measured tip location Ltip changes with \(\sqrt{t}\). At the start, the liquid’s response to the sudden decrease in gravity is complex, and inertia plays a significant role at this stage16. The liquid climbs rapidly, and what can be observed is the tip location Ltip grows linearly with t in this stage. About one second later, the effect of inertia disappears and that of viscous force becomes stronger. The liquid climbing speed decreases gradually.

Fig. 5: The comparison of experimental results with different corner angle α.
figure 5

a Tip location Ltip as a function of t. b Tip location Ltip as a function of t1/2.

Full size image

Comparison of experimental and theoretical results

The experimental results and the theoretical results are compared in Fig. 6. Herein the mean curvature radius RH is calculated by Eq. (10). Figure 6a shows the tip location Ltip changes with t. Figure 6b shows the tip location Ltip changes with \(\sqrt{t}\). The theoretical results have the same trend as the experimental results. However, for test models 1 and 2, the theoretical results are larger than the experimental results. For test models 3, 4, and 5, the theoretical results are smaller than the experimental results. It is noted that, for test models 1 to 5, the mean curvature radii calculated by Eq. (10) have the same value RH = 1.08 cm. However, \({R}_{{H}_{exp1}}\) and \({R}_{{H}_{exp2}}\) are smaller than RH. In addition, \({R}_{{H}_{exp3}}\), \({R}_{{H}_{exp4}}\) and \({R}_{{H}_{exp5}}\) are larger than RH.

Fig. 6: The comparison between measured tip location and theoretical tip location with different corner angle α.
figure 6

a Tip location Ltip as a function of t. b Tip location Ltip as a function of t1/2.

Full size image

Substituting RH by experimental \({R}_{{H}_{exp}}\), the modified tip location Ltip is presented in Fig. 7. The modified results have a good agreement with the experimental results. For different corner angles, the root mean square error between experimental and theoretical results is 2.1 mm (test model 1), 1.6 mm (test model 2), 2.4 mm (test model 3), 2.9 mm (test model 4), and 4.2 mm (test model 5). Therefore, the mean curvature radius RH has a direct influence on the tip location Ltip. By analysis, the precondition of Eq. (10) is that the bottom of the container should not have any dry spots21. In the experiment process, there is not a sufficient amount of liquid to cover the entire bottom because most of it flows into the corner. This is supposed to result in the error between RH and \({R}_{{H}_{exp}}\)6.

Fig. 7: The comparison between measured tip location and modified theoretical tip location with different corner angle α.
figure 7

a Tip location Ltip as a function of t. b Tip location Ltip as a function of t1/2.

Full size image

In addition, the machining error of the 3D printing, the residual acceleration, and the other disturbances can also affect the experimental results. Emphasizing that these potential causes are just hypotheses and require validation with additional data.

The tip location Ltip grows linearly with \(\sqrt{t}\) for t > 1s from Fig. 7b. grad(Ltip) is defined as,

$$grad({L}_{tip})=\frac{\Delta {L}_{tip}}{\Delta \sqrt{t}}$$
(2)

and it represents the gradient of \({L}_{tip} \sim \sqrt{t}\) curve. The relationship between the gradient grad(Ltip) and the corner angle α is shown in Fig. 8. The gradient grad(Ltip) decreases as the corner angle α increases. As a result, when the angle is infinitely close to 0, there should be a fast climb velocity, but the flow rate would be very small and therefore have no practical significance for engineering, as shown by others8,22. To apply the conclusion, further optimization research is required.

Fig. 8
figure 8

The influence of the corner angle α on the capillary flows along curved interior corners.

Full size image

Concluding remarks

The previous study6 has investigated the effect of channel curvature on capillary flow in curved interior corners theoretically and experimentally. In this paper, corner angle as another factor that has great influence on the capillary flow along curved interior corners is investigated. A series of microgravity drop tower experiments are operated at the National Microgravity Lab of Chinese Academy of Sciences. The experimental results are compared with the theoretical results that were obtained from the theoretical method introduced in ref. 6. The experimental results agree well with the theoretical results. Both experimental results and theoretical results show that the liquid rises faster as the corner angle decreases. This conclusion can be utilized to design and optimize the liquid management devices on board spacecraft. For example, when the liquid propellant in the fuel tank is disturbed and deviates from the outlet, we hope that the propellant can return to the outlet port as quickly as possible to provide a continuous flow of liquid propellant for the thrust chamber. Therefore, the climbing velocity of capillary flow along the curved interior corners should be fast, which means that the designers should choose interior corners with small corner angles.

Methods

Theoretical analysis

The gravity effects on the free surface flow become weak in space; instead, the surface tension plays an important role. An isolated curved interior corner under microgravity is considered in this section. As depicted in Fig. 2, the curved interior corner of angle 2α is partially filled with liquid, making contact angle θ with the solid surface and satisfying the Concus-Finn condition, θ ≤ (π/2 − α). The channel curvature radius Rm which refers to the curvature radius of the curved flow path, keeps constant. Due to the surface tension, the slender liquid column proceeds along the corner to an infinite distance. The flow in the interior corner is assumed to be viscous, incompressible, isothermal, and laminar. Due to the flow direction is nearly parallel to the contact line, the contact angle θ can be regarded as a constant without considering the hysteresis effect. In addition, there exists a constant height at z = 0 for all t, namely H = constant (see Fig. 2). Its validity is verified experimentally by Weislogel et al.5 and Wu et al.6.

In the curved interior corners, not only the surface tension but also the centrifugal force affect the free surface flow as introduced in ref. 20. The centrifugal force is caused by the curve motion of the flow, and conversely, it affects the capillary flow. Figure 9 shows the cross-section of the curved interior corner in Fig. 2. The free surface is a meniscus without gravity. Neglecting viscous normal stresses, there is a direct relationship between the free surface shape and the pressure difference across the free surface according to the Young-Laplace equation,

$${P}_{a}-P=\frac{2\sigma }{R}$$
(3)

where Pa is the ambient pressure, P is the liquid pressure, σ is the surface tension and R is the mean curvature radius of the free surface. If centrifugal force acts on the free surface, it will change the shape of the free surface. As a result, the free surface shape affects the capillary flow in the curved interior corner.

Fig. 9: Cross-section of an isolated interior corner.
figure 9

The centrifugal force acts on the liquid in the negative y-direction.

Full size image

At the lowest point of the free surface, a Cartesian coordinate is created. (see Fig. 9). The centrifugal force acts on the liquid in the negative y-direction. Due to H/Rm ≪ 1, the centrifugal acceleration g can be considered uniform in the x − y plane,

$$g=\frac{{\bar{w}}^{2}}{{R}_{m}}$$
(4)

herein \(\bar{w}\) is the average velocity of the cross-section which perpendicular to flow direction.

The free surface y(x) is determined by both surface tension and centrifugal force. The normalized differential equation of free surface can be expressed by(see6 for more details),

$$Bo\cdot Y+\cos (\theta +\alpha )-Bo\cdot \mathop{\int}\nolimits_{0}^{1}YdX=\frac{{Y}_{XX}}{{\left(1+{Y}_{X}^{2}\right)}^{\frac{3}{2}}}$$
(5)

subject to the Y(0) = 0 and YX(0) = 0, where X = x/r, Y = y/r, r is the half width of free surface, θ is the contact angle, Bo is Bond number defined by Bo = ρgr2/σ.

Eq. (5) is a second order integro-differential equation. The power-series method23, iterative method24, shooting method25 and Runge-Kutta method26 and so on were used to solve this equation. These methods share some drawbacks, such as poor convergence, dependence on initial values, and instability. The inevitable result of this is long calculation times and sudden calculation interruptions. Here an approximation modeling method based on an improved radial basis function27 is used to replace the free surface governing equation Eq. (5). Approximation model, also known as surrogate model or metamodel, provides a substitute for and is used in lieu of this real-world function f(t) with a small price. This approximation model is approximately equivalent to Eq. (5) through data training, but is much easier to solve.

Combining the approximation model, the tip location Ltip can be obtained (see6 for more details),

$${L}_{tip}=\mathop{\int}\nolimits_{0}^{t}0.8510\sqrt{\frac{(1+0.286B{o}_{{R}_{H}})\cdot G\cdot {R}_{H}}{f\cdot t}}{\rm{d}}t$$
(6)

where \(B{o}_{{R}_{H}}=\rho g{R}_{H}^{2}/f\sigma\) is the Bond number based on f and mean curvature radius RH. The parameter f can be denoted as,

$$f=\frac{\sin \alpha }{\cos \theta -\sin \alpha }$$
(7)

The parameter G can be denoted as,

$$G=\frac{\sigma {F}_{i}{\sin }^{2}\alpha }{\mu f}$$
(8)

where Fi is the friction factor defined by Weislogel and Lichter5.

Experimental setup and procedure

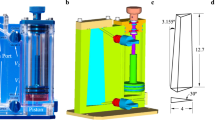
To investigate the influence of corner angle α on capillary flow along curved interior corners, a group of test models (see Fig. 10) with different corner angles α are fabricated by 3D printing technology. To get a better observation of the capillary flow, these models are made of transparent resin and polished.

Fig. 10
figure 10

Test models installed on the experimental platform of the drop capsule.

Full size image

Usually capillary phenomena can be observed only at a small scale under ground conditions. Capillary length l28 defined as,

$$l=\sqrt{\frac{\sigma }{\rho g}}$$
(9)

is an indication to judge whether the capillary phenomenon is obvious or not. It is a characteristic length scale for an interface between two fluids that is subject both to gravity and to surface tensions. For pure water and air at 20 °C, the capillary length takes the value 2.71mm. When the characteristic length is much less than the capillary length, the surface tension dominates the capillary flow, and the gravity can be neglected, and vice versa.

However, the capillary length under microgravity can be orders of magnitude larger than that on the ground. As a result, the test models of capillary flows under microgravity can be orders of magnitude larger than their normal-gravity counterparts. In addition, large-scale capillary flows are easier to visualize and can be tracked over long distances5. Within the limitations of the experimental installation platform, the test model sizes should be as large as possible.

A short-term microgravity experimental environment can be provided at a much lower cost by using the drop tower. The microgravity environment is accessed by using the drop tower facility at the National Microgravity Lab of Chinese Academy of Sciences for capillary flow experiments in this study. To minimize the effect of air resistance on the experiment, a dual-drop capsule system is employed, and a microgravity environment of 10−5g0 can be reached. Figure 11 shows the acceleration curve recorded by the accelerometer preset in the drop capsule. As can be seen from the curve, the entire microgravity time is about 3.5s.

Fig. 11
figure 11

The acceleration curve recorded by the accelerometer preset in the drop capsule.

Full size image

In this study, distilled water, ethanol, and silicone oil are selected as the alternative working fluids, and they are often used in microgravity experiments. Their surface tensions, viscosities, and densities are measured specifically for this research work using standard laboratory procedures (see Table 1).

Table 1 Liquid properties of the distilled water, ethanol and silicone oil
Full size table

The distilled water and ethanol can be better blended with the dye to facilitate observation. However, the distilled water climbs fast due to its large surface tension. It needs a high-speed camera to record the experiments; otherwise, it will bring great errors. In addition, the distilled water reaches the top of the test model too quickly, and it’s a waste of the precious microgravity time. In the compatibility test, it is found that cracking occurred on the surface of the resin after being immersed in ethanol. The silicone oil has the characteristics of safety, non-toxicity, good compatibility, and optional viscosity. Therefore, the 10 cSt silicone oil is chosen as the experimental fluid in this experiment.

The factors affecting the capillary flow in a curved interior corner are the geometry of the model and the properties of the liquid. It can be further subdivided into channel curvature \({R}_{m}^{-1}\), corner angle α, mean curvature radius RH, liquid viscosity ν and surface tension σ.

The channel curvature \({R}_{m}^{-1}\) and corner angle α are determined by the geometry of the test model. The viscosity ν, surface tension σ and contact angle α are determined by the properties of the liquid. The mean curvature radius RH is determined both by the geometry and contact angle α. In order to study the influence of corner angle α on the capillary flow, a set of test models with different corner angles are set up. In order to make the corner angle α the only variable affecting the capillary flow, the other factors should be fixed. Therefore, this set of test models has the same channel curvature \({R}_{m}^{-1}\), and the same working liquid is used. In addition, the mean curvature radius RH should also be fixed.

By using the method of de Lazzer et al.21, the mean curvature radius RH can be determined below14,

$${R}_{H}=\frac{{L}_{P}\cos \theta }{2\Sigma }\left(1-\sqrt{1-\frac{4{A}_{c}\Sigma }{{L}_{P}^{2}{\cos }^{2}\theta }}\right)$$
(10)

herein LP is the perimeter of cross-section, Ac is the cross-sectional area, \(\Sigma =0.5\mathop{\sum }\nolimits_{j=1}^{n}{k}_{j}{F}_{Anj}\), \({F}_{Anj}=\frac{\cos \theta \sin {\delta }_{j}}{\sin {\alpha }_{j}}-{\delta }_{j}\).

According to Eq. (10), we can choose appropriate geometrical parameters to make this set of test models have the same mean curvature radius RH. The geometrical parameters of the test models are listed in Table 2. The corner angle α increases from model 1 to model 5. Figure 12 shows the typical top view and front view of these models.

Table 2 Geometry parameters of the capillary flow test models
Full size table
Fig. 12: Different views of the capillary flow test model.
figure 12

a Front view. b Top view.

Full size image

Taking test model 1 as an example, it can be estimated that 10 cSt silicone oil can climb up to the top of the test model within 3.5 s according to Eq. (6). The purpose of fully utilizing the available microgravity time is achieved, which is also the reason for choosing 10 cSt silicone oil as the testing liquid.

A prescribed amount of silicone oil is injected into the bottom of the test models prior to the experiment. Before releasing the drop capsule, the test liquid stays at the bottom of the test models due to gravity. Upon release, the gravity effect disappears and surface tension becomes the dominant force. Meanwhile, the liquid begins to flow into the corner. These experiments are recorded by cameras with frame rates up to 50 frames per second.