Scalable noisy quantum circuits for biased-noise qubits

Abstract

In this work, we consider biased-noise qubits affected only by bit-flip errors, which is motivated by existing systems of stabilized cat qubits. This property allows us to design a class of noisy Hadamard tests involving entangling and certain non-Clifford gates, which can be conducted reliably with only a polynomial overhead in algorithm repetitions. On the flip side, we also found classical algorithms able to efficiently simulate both the noisy and noiseless versions of our specific variants of the Hadamard test. We propose to use these algorithms as a benchmark of the biasness of the noise at the scale of large circuits. The bias being checked on a full computational task makes our benchmark sensitive to crosstalk or time-correlated errors, which are usually invisible from individual gate tomography. For realistic noise models, phase-flip will not be negligible, but in the Pauli-Twirling approximation, we show that our benchmark could check the correctness of circuits containing up to 10⁶ gates, several orders of magnitude larger than circuits not exploiting a noise-bias. Our benchmark is applicable for an arbitrary noise-bias, beyond Pauli models.

Introduction

Quantum computers bring the hope of solving useful problems for society that would be out of reach for classical supercomputers. One can think of problems in optimization^1,2, cryptography^3,4, finance^5,6, quantum chemistry or material sciences^7,8,9,10,11. The main threats toward the realization of useful quantum computers are noise and decoherence¹², which cause errors and degrade the quality of the computation. In the long term, this problem will likely be addressed by quantum error correction and fault-tolerant quantum computing^{13,13,14,15,16,17,18}. Yet, the very high fidelity and considerable overhead this approach requires make it very challenging to implement.

In this context, the existence of quantum algorithms able to scale up to a large size, with low-fidelity hardware, would be highly desirable. Unfortunately, various studies showed that polynomial-time classical algorithms can efficiently simulate the algorithm outputs of specific circuits in the noisy case, such as random circuits^19,20 or general algorithms under some assumptions on the noise structure^21,22,23 (see also ref. ²⁴ and refs. ^25,26 for analogous results in the optical setting). All these studies indicate that without doing error-correction, for realistic noise models, it is not possible to preserve reliable algorithm outputs in a classically intractable regime (see, however, recent work²⁷, which showed that in certain oracular scenarios noisy quantum computers can offer an advantage over classical computers). One major difficulty to face is that, for most noise models, the fidelity of the output state drops exponentially with the number of gates involved in the computer²⁸, suggesting that a reliable estimation of any expectation value would require to run exponentially many times the algorithm, ruining any hope for an exponential speedup. Error mitigation techniques^{29,30,31,32,33,34,35,36} have been proposed, with the hope to solve this issue. However, various no-go results show that, for several noise models, error mitigation techniques are not scalable^33,37: the number of samples they require can grow exponentially with the algorithm’s depth or the number of qubits in the algorithm^34,38,39. Other approaches can be potentially more scalable, but they assume specific noise models⁴⁰, require knowledge of the entanglement spectrum of quantum states⁴¹ or have potentially high algorithmic complexity⁴².

In our work, motivated by the limitations of error-correction and error mitigation, we propose instances of the Hadamard test^43,44 that can be robustly implemented in systems of so-called biased-noise qubits^45,46,47, affected only by local stochastic bit flip (or phase-flip) errors. In technical terms, we show that, for suitably designed circuits tailored to a Pauli biased noise, the outcome of the ideal version of the Hadamard test can be estimated reliably by execution of its noisy versions with only a polynomial overhead in the number of repetitions of the algorithm. The model of biased-noise qubits is motivated by existing hardware realizing stabilized cat qubits^46,47,48. The key ingredient of our approach is that only specific gates are allowed, in order to preserve the noise bias along the computation^45,49. This allows us to design circuits in which the measurement will be isolated from most of the errors occurring (see Fig. 1). Importantly, the circuits themselves can be quite complicated: the allowed set of gates can generate large amounts of entanglement and contain certain non-Clifford gates, thus avoiding natural classical simulation techniques^50,51,52. Nonetheless, the restricted nature of these circuits allowed us to find an efficient classical algorithm that simulates realizations of our family of Hadamard tests, also in the presence of arbitrary local biased noise. We propose to use this algorithm as a simple benchmark of the biasness of the noise at the scale of large and complicated quantum circuits. The interest of our benchmark is that it is scalable and can detect some collective effects of the noise that cannot, by definition, be observed at the level of individual gates. For instance, it can detect some crosstalk and correlated errors. The overall principle of the benchmark, summarized at the end of the results section and detailed in the methods section, is to compare the experiment to the classical simulation, which assumes the noise model of each gate used inside the complete algorithm is identical to the one deduced from individual gate tomography. Hence, if the simulation and experiment differ, it would imply that collective effects are degrading the quality of the hardware when a complete algorithm is implemented, indicating a potential threat to the scalability of the hardware. For pedagogy, in the main text, we mainly focus on the case of Pauli noise, but our benchmark is applicable for the most general model of local biased model as explained in the methods section.

Fig. 1: The Hadamard test.

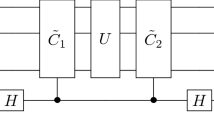
The Hadamard test represented on this figure allows to estimate $\left\langle \psi \right\vert U\left\vert \psi \right\rangle$ where $\left\vert \psi \right\rangle \equiv B{\otimes }_{i = 1}^{n}\left\vert {\phi }_{i}\right\rangle$, ($\left\vert {\phi }_{i}\right\rangle$ being a single-qubit state, B a unitary). This estimation is being done by initializing a measured register in $\left\vert 0\right\rangle$, and by implementing the unitary c_XU (see the paragraph “Notations and terminology” in the section Results to understand our notations). Finally, measuring the measured register in Pauli Y and Z bases gives access to the imaginary and real part of $\left\langle \psi \right\vert U\left\vert \psi \right\rangle$. We call L_n the number of gates applied on the measured register (including potential noisy identity gates), once c_XU has been decomposed on an experimentally feasible gateset. In this paper, we show that for a noise model only composed of bit-flips, and under some restrictions on the n-qubit unitaries U and B, the measurement will only be sensitive to bit-flips produced on the measured register, and entirely insensitive to the ones produced on the data register. Nonetheless, some `useful information” contained in the entangled state $\left\vert \psi \right\rangle$ will propagate toward the measurement. The intuitive principle we use is to encode the “useful” information in a “Pauli Z (or Y) channel” while making sure that any error is inside a “Pauli X channel”. If any Pauli X error (i.e., bit-flip) from the data register cannot propagate toward the measurement while the Pauli Z can, the information will reach the measurements but not the errors. Overall, if ${L}_{n}=O(\log (n))$, the noise will only introduce a polynomial overhead in the number of algorithm repetitions to guarantee a reliable outcome: the algorithm will be scalable despite the noise. Note that while ${L}_{n}=O(\log (n))$, the algorithm can nonetheless have a polynomial depth.

Results

Notations and terminology

Let (σ₀, σ₁, σ₂, σ₃) ≡ (I, X, Y, Z) denote single-qubit Pauli matrices. Let H denote the Hadamard gate. We call ${{\mathbb{P}}}_{n}^{X}$ the set of X-Pauli operators acting on n-qubits, ${{\mathbb{P}}}_{n}^{X}\equiv \{{\otimes }_{k = 1}^{n}{\sigma }_{{i}_{k}},| \forall k,{i}_{k}\in \{0,1\}\}$. We say that f_n ∈ poly(n) if there exist two reals C, a > 0 such that ${{\rm{lim}}}_{n\to \infty }\,{f}_{n}/(C{n}^{a})=1$. Moreover, when poly(n) appears in an equation, it means that the equation remains true by replacing poly(n) by any function f_n ∈ poly(n). Lastly, we say that f_n = O(g_n) if there exists C > 0 such that ${{\rm{lim}}}_{n\to \infty }| {f}_{n}/{g}_{n}| \le C$. For any unitary U, we define its coherently controlled operation in the X-basis as ${c}_{X}U\equiv \left\vert +\right\rangle \left\langle +\right\vert \otimes I+\left\vert -\right\rangle \left\langle -\right\vert \otimes U$. Let G be a single-qubit unitary. Unless stated otherwise, G_i indicates that G is applied on the i’th qubit in the tensor product (and I is applied elsewhere). Calling ${\mathcal{G}}$ the unitary map implementing a unitary quantum gate G, and ${{\mathcal{E}}}_{{\mathcal{G}}}$ the CPTP (Completely Positive Trace Preserving) operation describing the noisy implementation of the gate, we define the “noise map of G” (or the noise map associated with ${\mathcal{G}}$) the CPTP ${{\mathcal{N}}}_{{\mathcal{G}}}$ defined as ${{\mathcal{N}}}_{{\mathcal{G}}}\equiv {{\mathcal{E}}}_{{\mathcal{G}}}\circ {{\mathcal{G}}}^{\dagger }$. The noise map of a state preparation is the CPTP map that is applied after a noiseless state preparation, so that the overall process (noiseless preparation followed by CPTP map) describes the noisy state preparation. The noise map of a measurement is the CPTP map that must be applied before the noiseless measurement so that the overall process (CPTP map followed by noiseless measurement) describes the noisy measurement (noise maps for state preparation and noisy measurements are not uniquely defined). We call ${\rm{supp}}({\mathcal{G}})$ the set of qubits over which the CPTP ${\mathcal{G}}$ acts non-trivially. The notation ${\sum }_{\alpha \subset {\rm{supp}}({\mathcal{G}})}$ means that the summation is over every possible subset of ${\rm{supp}}({\mathcal{G}})$. For instance, if ${\mathcal{G}}$ is a two-qubit gate acting on qubits 1 and 2, we have ${\rm{supp}}({\mathcal{G}})=\{1,2\}$, and α will take every one the 4 values in the following set $\{\{{{\emptyset}}\},\{1\},\{2\},\{1,2\}\}$. These 4 values correspond to the 4 possible subsets of ${\rm{supp}}({\mathcal{G}})$. Finally, ${I}_{{\rm{supp}}({\mathcal{G}})}$ is the identity operator acting on the qubits where the CPTP map ${\mathcal{G}}$ acts non-trivially.

Introduction to the Hadamard test

The Hadamard test is the task over which all our examples are built. It allows for the estimation of the expectation value $\left\langle \psi \right\vert U\left\vert \psi \right\rangle$ of a unitary U on some prepared n-qubit state $\left\vert \psi \right\rangle =B{\otimes }_{i = 1}^{n}\left\vert {\phi }_{i}\right\rangle$ ($\left\vert {\phi }_{i}\right\rangle$ being a single-qubit state, B a unitary operation), leading to several applications^44,53,54. A way to implement it is represented in Fig. 1. It consists of a “measured” register initialized in $\left\vert 0\right\rangle$ combination with a “data” register, where the state $\left\vert \psi \right\rangle$ has been prepared. The reduced state of the measured register right before measurement takes the following form

$$\rho =\frac{1}{2}\left(I+{\alpha }_{n}\left(yY+zZ\right)\right),$$

(1)

where $y=-{\rm{Im}} (\left\langle \psi \right\vert U\left\vert \psi \right\rangle ),z={\rm{Re}} (\left\langle \psi \right\vert U\left\vert \psi \right\rangle )$ and α_n = 1 from now on. Hence, measuring the first register in the Y (resp. Z) basis allows to estimate the imaginary (resp. real) part of $\left\langle \psi \right\vert U\left\vert \psi \right\rangle$. Using Hoeffding’s inequality³³ we get that $N=2\log (2/\delta )/{\epsilon }^{2}$ experimental repetitions are sufficient to estimate y or z up to ϵ-precision with a probability 1−δ. It is well-known that estimating $\left\langle \psi \right\vert U\left\vert \psi \right\rangle$, for a general polynomial circuit U, to additive precision is a BQP-complete problem⁵³ and therefore, in general, we do not expect an efficient classical algorithm that would realize this task.

So far, we discussed what happens when the measured qubit is noiseless. Let us now assume that a bit-flip channel right before the measurement occurs in such a way that 0 < α_n < 1 in Eq. (1). Then, repeating the algorithm ${N}_{n}=2\log (2/\delta )/{({\alpha }_{n}\epsilon )}^{2}$ times would be sufficient to estimate y and z to ϵ precision with high probability (the scaling in $1/{({\alpha }_{n}\epsilon )}^{2}$ is also optimal⁵⁵). If α_n decreases exponentially with n, the total number of algorithm calls will necessarily grow exponentially with n and the algorithm wouldn’t be scalable. However, for α_n = 1/poly(n), only poly(n) overhead in experiment repetitions would be sufficient to reliably estimate $\left\langle \psi \right\vert U\left\vert \psi \right\rangle$. In this work, we will show that for biased-noise qubits, it is possible to design a class of non-trivial Hadamard tests for which α_n = 1/poly(n) in the presence of non-vanishing local biased noise.

Noise model

In general, both B, and c_XU have to be decomposed on a gateset implementable at the experimental level. Let ${\mathcal{G}}$ be a unitary channel describing a gate belonging to the accessible gateset, and ${{\mathcal{E}}}_{{\mathcal{G}}}$ be its noisy Completely Positive Trace Preserving (CPTP) implementation in the laboratory. We will assume a local biased noise model: ${{\mathcal{E}}}_{{\mathcal{G}}}={{\mathcal{N}}}_{{\mathcal{G}}}\circ {\mathcal{G}}$, where the CPTP “noise map” ${{\mathcal{N}}}_{{\mathcal{G}}}$ will only introduce (possibly correlated) bit-flip errors on the set of qubits over which ${\mathcal{G}}$ acts non-trivially. We call this set ${\rm{supp}}({\mathcal{G}})$. We have:

$${{\mathcal{N}}}_{{\mathcal{G}}}(\rho )=\sum _{\alpha \subset {\rm{supp}}({\mathcal{G}})}{p}_{\alpha }^{{\mathcal{G}}}{X}_{\alpha }\rho {X}_{\alpha },$$

(2)

where the summation is over every possible subsets α of ${\rm{supp}}({\mathcal{G}})$ (we clarify what it means with an example in a few lines). We also have X_α ≡ ∏_i∈αX_i for $\alpha \ne \{{{\emptyset}}\}$ and ${X}_{\{{{\emptyset}}\}}\equiv {I}_{{\rm{supp}}({\mathcal{G}})}$. Here, ${I}_{{\rm{supp}}({\mathcal{G}})}$ is the identity operator acting on the qubits where ${\mathcal{G}}$ acts non-trivially. Therefore, α denotes the set of qubits on which a bit-flip operator is applied in the summation in (2). Finally, $\{{p}_{\alpha }^{{\mathcal{G}}}\}$ is a probability distribution supported on the subsets of ${\rm{supp}}({\mathcal{G}})$. For instance, if ${\mathcal{G}}$ is a two-qubit gate acting on qubits 1 and 2, we have ${\rm{supp}}({\mathcal{G}})=\{\{1\},\{2\}\}$, and α will take each of the 4 values in the following set $\{\{{{\emptyset}}\},\{1\},\{2\},\{1,2\}\}$. These 4 values correspond to the 4 possible subsets of ${\rm{supp}}({\mathcal{G}})$. It means that ${{\mathcal{N}}}_{{\mathcal{G}}}$ will be a bit-flip noise model having the following 4 Kraus operators: $\sqrt{{p}_{\{{{\emptyset}}\}}}{I}_{1}\otimes {I}_{2},\sqrt{{p}_{\{1\}}}{X}_{1}\otimes {I}_{2},\sqrt{{p}_{\{2\}}}{I}_{1}\otimes {X}_{2}$ and $\sqrt{{p}_{\{1,2\}}}{X}_{1}\otimes {X}_{2}$. Noisy measurements are modeled by a perfect measurement followed by a probability p_meas to flip the outcome. Lastly, we assume that single-qubit noisy state preparation consists of a perfect state preparation followed by the application of a Pauli X-error with probability p_prep. Our noise model is based on an idealization of cat qubits that are able to exponentially suppress other noise channels than bit-flip, at the cost of a linear increase in bit-flip rate^46,47,48 (or the other way around). It is an idealization as (i) the Kraus operators are a linear combination of Pauli X and I operators only: this is what we call a perfect bias, (ii) we also neglect coherent errors, meaning that our noise model is a Pauli noise. The assumption (ii) is mainly used for pedagogical purposes in the main text. Indeed, our main result (the benchmarking protocol) is applicable for biased qubits which are designed in such a manner that their noise model is well approximated by the assumption (i) only (see Theorem 4 and Definition 4). We now provide the definition of “an error”.

Definition 1

(Error). Let $\left\vert \Psi \right\rangle$ be the state the qubits should be in at some timestep of the algorithm if all the gates were perfect. Because we consider a probabilistic noise model, the actual n-qubit quantum state will take the form $\rho ={\sum }_{i}{p}_{i}{E}_{i}\left\vert \Psi \right\rangle \left\langle \Psi \right\vert {E}_{i}^{\dagger }$, where E_i is a unitary operator and p_i some probability (p_i ≥ 0, ∑_ip_i = 1). The operator E_i is what we call the error that affected $\left\vert \Psi \right\rangle$.

Designing noise-resilient Hadamard test

The core idea behind our work is to exploit the fact that only bit-flips are produced, in order to design circuits guaranteeing that most of these errors will never reach the measurement in the Hadamard test. In order to explain our results we need to introduce first a number of auxiliary technical definitions.

Definition 2

(X-type unitary operators and errors). We call X-type unitary operators the set of unitaries that can be written as a linear combination of Pauli X matrices. For n-qubits, we formally define it as:

$${{\mathbb{U}}}_{n}^{X}\equiv \left\{U=\sum _{i}{c}_{i}{P}_{i},| {P}_{i}\in {{\mathbb{P}}}_{n}^{X},{c}_{i}\in {\mathbb{C}},{U}^{\dagger }={U}^{-1}\right\}.$$

(3)

Alternatively, ${{\mathbb{U}}}_{n}^{X}$ can be understood in terms of unitaries that are diagonal in the product basis $\left\vert {\bf{s}}\right\rangle =\left\vert {s}_{1}\right\rangle \left\vert {s}_{2}\right\rangle \ldots \left\vert {s}_{n}\right\rangle$, where s_i = ± and $\left\vert \pm \right\rangle$ are eigenstates of Pauli X matrix. We will call “X-error”, an error belonging to ${{\mathbb{U}}}_{n}^{X}$ (if the error is additionally Pauli, we will call it “Pauli X error”, or simply “bit-flip”).

What we need to do is to guarantee that any error occurring at any step of the computation is an X-error. It is possible with the use of “bias-preserving” gates: such gates map any initial X-error to another X-error. It motivates the following definition and property (all our results are derived in the Supplemental material).

Definition 3

(Bias-preserving gates). Let G be an n-qubit unitary operator. We say that G preserves the X-errors (or X-bias), if it satisfies the following property

$$\forall P\in {{\mathbb{P}}}_{n}^{X},\exists A\in {{\mathbb{U}}}_{n}^{X}\,\,{\text{such}}\, {\text{that}}\,\,GP=AG.$$

(4)

We denote ${{\mathbb{B}}}_{n}$ the set of such gates.

Property 1

(Preservation of the bias). If a quantum circuit is only composed of gates in ${{\mathbb{B}}}_{n}$, each subject to a local biased noise model from Eq. (2) (and the paragraph that follows for measurement and preparation), then any error affecting the state of the computation is an X-error.

As examples of bias-preserving gates, there are all the unitaries in ${{\mathbb{U}}}_{n}^{X}$, the cNOT, and what we call ${\text{Toffoli}}^{{\prime} }\equiv {H}_{1}{H}_{2}{H}_{3}\times \text{Toffoli}\,\times {({H}_{1}{H}_{2}{H}_{3})}^{\dagger }$ (We assume Toffoli’ can be implemented “natively” without having to actually apply the Hadamards (otherwise, because Hadamard would also be noisy, the full sequence wouldn’t be bias-preserving)). An example of a gate that does not preserve the bias is the Hadamard gate. The existence of gate preserving the bias also during the gate implementation is not straightforward, but cat-qubits are able to overcome this complication, at least for cNOT, Toffoli’ and gates in ${{\mathbb{U}}}_{n}^{X}$: see the section I C in the Supplemental Material. Finally, bias preserving gates have a nice interpretation: they correspond to permutations (up to a phase) in the Pauli X-eigenstates basis.

Property 2

(Characterization of bias-preserving gates). $V\in {{\mathbb{B}}}_{n}$ if and only if for any s ∈ {+, −}ⁿ, there exists a real phase φ_s,V such that: $V\left\vert {\bf{s}}\right\rangle ={e}^{i{\varphi }_{{\bf{s}},V}}\left\vert {\sigma }_{V}({\bf{s}})\right\rangle$ where σ_V is some permutation acting on {+, −}ⁿ.

We now sketch the sufficient ingredients guaranteeing the existence of noise-resilient Hadamard tests. First, (i) assume that individual gate errors, as well as individual measurement and state-preparation errors, occur with a probability smaller than p < 1/2. Furthermore, assume (ii) that only X-errors occur in the algorithm (it can be satisfied with the assumptions of Property 1), (iii) these errors cannot propagate from the data to the measured register, (iv) the number of interactions of the measured register with the data register satisfies ${L}_{n}=O(\log (n))$ (which implies the measured register will only be impacted by X-errors introduced at $O(\log (n))$ locations). Subject to conditions (i–iv) the reduced state ρ will satisfy Eq. (1) with α_n efficiently computable classically, and satisfying α_n ≥ 1/poly(n). As explained earlier, this would guarantee a scalable algorithm to estimate $\left\langle \psi \right\vert U\left\vert \psi \right\rangle$. In particular, the following Theorem holds.

Theorem 1

(Hadamard test resilient to biased noise). Let:

$$\begin{array}{lll}\left\vert \psi \right\rangle =B\mathop{\bigotimes }\limits_{i=1}^{{N}_{B}}\left\vert {\phi }_{i}\right\rangle ,U=W\cdot V,\\\, W\equiv \mathop{\prod }\limits_{i=1}^{{N}_{W}}{W}_{i},V\equiv \mathop{\prod }\limits_{i=1}^{{N}_{V}}{V}_{i},\end{array}$$

(5)

where B is a product of local bias preserving gates, gates V_i and W_i are local gates and belong to ${{\mathbb{U}}}_{n}^{X}$. In the context of this theorem, the index i on V_i and W_i refers to the i’th gate in the product (it does not necessarily mean the gate is applied on the i’th qubit). Additionally, the gates W_i are assumed to be Hermitian. We assume the circuit is implemented as indicated on Fig. 2. There, W is implemented thanks to the “parallelization register”, while V is implemented by making the measured and data register directly interact.

Furthermore, we assume the local bias noise model introduced in Eq. (2), and that state preparation, measurements, and each non-trivial gate applied on the measurement register have a probability at most p < 1/2 to introduce a bit-flip on the measured register.

Under these conditions, there exists a quantum circuit realizing a Hadamard test such that, in the presence of noise, the reduced state ρ satisfies Eq. (1) with ${\alpha }_{n}\ge {(1-2p)}^{O({N}_{V})}$.

Additionally, α_n is efficiently computable classically. Hence, if ${N}_{V}=O(\log (n))$, it is possible to implement the Hadamard test in such a way that running the algorithm poly(n) times is sufficient to estimate the real and imaginary parts of $\left\langle \psi \right\vert U\left\vert \psi \right\rangle$ to ϵ precision with high probability.

The Hadamard test is implemented with the circuit shown in Fig. 2. It uses a parallelization register. It is this parallelization register that allows for the implementation of a unitary acting on all the qubits of the data register (the unitary W mentioned in the theorem), while keeping a logarithmic number of interactions with the measured register (this is required to preserve noise-resilience). While Theorem 1 assumes the trivial identity gate to be noiseless, the results can be easily extended if they are noisy (in this case, W should have a depth in $O(\log (n))$, as discussed in the section III C of the Supplemental Material). Our approach is also scalable in the presence of noisy measurements (measuring the data register in the X basis to infer $\left\langle \psi \right\vert U\left\vert \psi \right\rangle$ would not be scalable in general in this case: see ref. ⁵⁶ and the section IV B of the Supplemental Material).

Fig. 2: Concrete implementation of the noise-resilient Hadamard test.

In this figure, we illustrate how $U=W\times V={\otimes }_{i = 1}^{{N}_{W}}{W}_{i}\times {\otimes }_{i = 1}^{{N}_{V}}{V}_{i}$ mentioned in Theorem 1 can be implemented in a noise-resilient manner. The coherently controlled unitaries with a blue contour implement the controlled Hermitian unitaries W_i, which overall implement the controlled W. The coherently controlled unitaries with a black contour implement the controlled V_i, which overall implement the controlled V. The central element in this construction is the parallelization register⁶⁸, which allows the implementation of the unitary W in such a way that it acts upon all the qubits in the data register while preserving the noise-resilience. Hence, it allows the implementation of a Hadamard test with U acting on all the qubits of the data register. Such unitaries are useful for our benchmarking protocol: see the third paragraph in the discussion section. The key point behind the parallelization register is that, while it introduces additional components that can introduce bit-flip errors, these bit-flips cannot, by construction, propagate to the measured register (in practice, they commute with the last c_XX gate drawn, (see the paragraph “Notations and terminology” in the section Results to understand our notations). It is an example where trading space (using more qubits) to gain time (guaranteeing that the measured register interacts with $O(\log (n))$ gates and not poly(n) gates) is worth doing. While the parallelization register does not propagate bit-flips toward the measured register, it will propagate phase-flip errors. We make use of this to easily detect an excessive production of phase-flip errors in the third paragraph of the discussion section.

Efficient simulation of noise-resilient Hadamard test

We just saw that restricted forms of Hadamard tests are resilient to bit-flip errors occurring throughout the circuit. The following result proves that the task realized by such a restricted Hadamard test can be efficiently simulated on a classical computer with polynomial effort.

Theorem 2

(Efficient classical simulation of restricted Hadamard test). Let $B\in {{\mathbb{B}}}_{n},U\in {{\mathbb{U}}}_{n}^{X}$ be n qubit unitaries specified by R_B and R_U local qubit gates (belonging to respective classes ${{\mathbb{B}}}_{n}$ and ${{\mathbb{U}}}_{n}^{X}$). Let $\left\vert {\psi }_{0}\right\rangle =\left\vert {\phi }_{1}\right\rangle \left\vert {\phi }_{2}\right\rangle \cdots \left\vert {\phi }_{n}\right\rangle$ be an initial product state. Then, there exists a randomized classical algorithm, taking as input classical specifications of circuits defining B, U, and the initial state $\left\vert {\psi }_{0}\right\rangle$, that efficiently and with a high probability computes an additive approximation to $\left\langle {\psi }_{0}\right\vert {B}^{\dagger }UB\left\vert {\psi }_{0}\right\rangle$. We call ${\mathcal{C}}$ this approximation. Specifically, we have

$$\Pr \left(| \left\langle {\psi }_{0}\right\vert {B}^{\dagger }UB\left\vert {\psi }_{0}\right\rangle -{\mathcal{C}}| \le \epsilon \right)\ge 1-\delta ,$$

(6)

while the running time is $T=O(\frac{{R}_{B}+{R}_{U}+n}{{\epsilon}^{2}}\log (1/\delta ))$.

The classical simulability of the restricted Hadamard test can be regarded as the limitation of our approach to constructing quantum circuits that are robust to biased noise. At the same time, it allows us to introduce an efficient and scalable benchmarking protocol that is tailored to validating the assumption of bias noise on the level of the whole (possibly complicated) circuit. It allows us to validate this assumption in a manner that individual gate tomography couldn’t, as we now explain.

Sketch of the benchmarking protocol

For pedagogy, in this section, we give an intuitive sketch of how the benchmarking would work for the Pauli bit-flip noise model considered so far. In the method section, we give the details behind the benchmarking protocol, which applies to the most general case of a biased noise model for qubits, beyond bit-flip (formally, a noise model satisfying Definition 4). In the methods section, we also provide the classical algorithms able to efficiently simulate the noisy implementation of the quantum circuit.

The issue with an individual benchmark of quantum gates is that it is blind to collective effects that can only build up when a full circuit, composed of many gates in sequence and in parallel, is implemented. One example is the presence of correlated errors, or more generally, non-local effects in the noise, that individual gate tomography cannot usually detect. Another example of collective effects is the presence of “scale-dependent noise”, i.e., a noise for which the intensity depends on the number of qubits or surrounding gates used in the algorithm^57,58,59. Note that scale-dependent noise can sometimes be implied by correlated noise models⁶⁰. Scale-dependent noise can be particularly damaging for biased qubits, as it could rule out the intrinsic interest of using such qubits in the case that the nearly suppressed error rate happens to grow when the circuits are scaled up. All these behaviors for the noise represent a major threat both in the near term, and to reach the large-scale^57,61,62. Our benchmarking protocol, which we now sketch, allows us to detect some of these effects. The intuitive idea is that we are able to classically predict the algorithm’s output under the assumption that the noise deduced from individual gate tomography is still realized for each gate, but now inside a whole algorithm. A mismatch between the classical algorithm and the quantum experiment would necessarily indicate a violation of the assumption behind the noise.

We emphasize here that while there exist scalable protocols able to benchmark the noise strength at the scale of entire circuits (for instance, randomized benchmarking⁶³), to our knowledge, there doesn’t exist any scalable protocol able to see whether or not the noise model is biased, at the scale of large circuits. Our benchmark is precisely able to do this, which is something crucial for cat qubit platforms. This is the main reason why our protocol differs from the existing approaches. Additionally, we are not aware of other classical simulation methods than the one we developed in Theorems 2, 3, for the class of circuits affected by biased noise considered by us. Specifically, none of the existing classical simulation techniques can efficiently simulate geometrically nonlocal circuits covered by our work, while such simulations are at the core of our benchmark.

For simplicity of the explanations, in all that follows we propose to implement our benchmark in the exact circuits we analyzed so far (i.e. the ones of Fig. 2). However, as mentioned at the end of the third paragraph of the discussion section, depending on which violation in the noise we aim to be sensitive to, simpler circuits could potentially be considered.

For a Pauli bit-flip noise, we first need to perform tomography on the gates that need to be applied on the measured register, in order to find the probability that each such gate introduces a bit-flip on the measured register. Other noise parameters p_meas and p_prep would also need to be estimated. Then, a Hadamard test satisfying the constraints of Theorem 1 is chosen. Subsequently, one needs to classically compute α_n, and estimate y, z up to ϵ-precision, with high probability (using Theorem 2). The estimates of the noiselessy, z are compared to values of Tr(ρY)/α_n, Tr(ρZ)/α_n estimated experimentally by running the quantum circuit polynomially many times. The experimental and theoretical predictions are then compared. If they don’t match (up to error resulting from a finite number of experiments), it would necessarily indicate a violation of the assumptions behind the assumed noise model (bit-flip) for the circuit participating in the Hadamard test. The precise implementation of the benchmarking protocol is provided in the methods section.

Discussion

In supplemental V B, we quantify the total number of quantum gates allowed in the circuit for which our benchmark could be practically useful. Based on available data in the literature, we show that, under the Pauli-Twirling approximation, our benchmark could be used for circuits containing 10⁶ gates. As it represents circuits three to four orders of magnitude bigger than in current experiments⁶⁴, it is a strong indication of the practical usefulness of our benchmark for the NISQ regime, and beyond, allowing us to check the hardware reliability for large circuits. Loosely speaking, our benchmark shall be used in the regime where the suppressed source of errors (phase-flip in our convention) is expected to be negligible. This is because it relies on the classical simulation, Theorem 3, which assumes a perfect bias, hence that no phase-flip are produced in the algorithm. This is precisely the regime where having a benchmark is interesting as there are propositions to use biased-qubits in large-scale algorithms where only the dominant source of errors is corrected, because the suppressed errors would have a negligible impact at the level of the algorithm (see supplemental E2 of ref. ⁶⁵ and references therein). Hence, our protocol is well-suited to analyze this regime of interest.

Our protocol can first detect some correlated errors or, more generally, non-local effects of the noise that are usually invisible from individual gate tomography. This is because our classical simulation algorithm assumes that individual gate tomography provides a fair description of the behavior of the noise, as it takes as inputs the noise maps of the gates extracted from tomography. Thus, if gate tomography does not fairly describe the noise, the results from simulation and experiment would disagree. To be concrete: if the noise model satisfies the general definition of perfect bias, beyond bit-flips, i.e., Definition 4, every gate applied on the measured register introduces noise that can impact the measurement outcomes. Furthermore, these are the only gates for which the noise can impact the measurement outcomes. This is because, with a perfect bias, no error produced outside of the measured register can propagate to the measured register (this is a consequence of how our circuits are built). Hence, we can first detect the presence of some correlated errors between the gates applied on the measured register, as they would violate the assumption that each gate can be described with a noise map independent from the others: this is a first example of a violation we can detect. We can also detect some violations of the locality assumption of the noise. If there are non-local effects in the noise, the noise maps of the gates applied on the measured register would, in general, not correctly describe the experimental outcomes. For instance, it could be that some operations done locally in the parallelization or data registers introduce unexpected errors in the measured one (because of crosstalk, for example). Our benchmarking will, in general, allow us to detect such effects. These are just some examples to help the reader understand what the benchmark can be useful for. Yet, we think that the most useful application of our protocol is its ability to detect the occurence of phase-flip errors produced at a higher rate than expected (we recall that having error-rates growing with the computer’s size is an effect experimentally observed in superconducting qubits^57,58,59). Indeed, such effects would in general lead to a mismatch between the classical simulation and the experiment for algorithms containing less gates than expected, i.e, a total number of gates, N, smaller than what (9) predicts ((9) quantifies the circuit’s size for which our benchmarking is applicable). To be concrete, an experimentalist should choose the largest N so that the bound (9) is saturated. If Δ ≥ 0 (Δ quantifies how much the expected noise model is violated experimentally: it is formally defined in the paragraph “Principle of the benchmarking” in Theorem 4), there is a violation of the assumption behind the noise model, indicating a potential threat to the scalability of the platform. For instance, for ϵ = 1/50, our quantitatives estimates of supplemental V B indicate that N = 10⁶ would work.

We can also provide a concrete example of a circuit that can be used to efficiently detect the production of phase-flip at a higher rate than expected. It would be the one implementing the controlled unitary c_XU, with $U={\otimes }_{i = 1}^{n}{X}_{i}$. This circuit matches the constraints of Theorem 1 (including its generalization to noisy identity gates mentioned in the paragraph that follows Theorem 1): we can thus implement it for the benchmarking. The reason why this circuit is useful is that it would, in general, make the measurement outcome sensitive to the introduction of phase-flip error on any of the qubits from the data register, after the preparation unitary B. This is because a phase-flip error occuring on any of the qubits from the data register would first propagate to the parallelization register (through the blue cNOTs implementing $W=U={\otimes }_{i = 1}^{n}{X}_{i}$ in Fig. 2), and finally to the measured register. Hence, phase-flip errors produced in B will, in general, modify the measurement outcome probability distribution, allowing to efficiently detect an excessive production of such errors. An experimentalist could then see if the circuit composed of bias-preserving gates of interest, encoded in the unitary B, does indeed produce more phase-flip errors than it should. Detecting such events is crucial for superconducting cat qubits given the fact their whole scalability strategy precisely relies on keeping negligible the phase-flip error rates also when used in large-scale circuits⁶⁵. Note that if the goal is only to detect the production of phase-flips at a higher rate than expected, and not to see if other non-local effects are occurring (we can detect some of these other non-local effects with our benchmarking, see the previous paragraph), simpler circuits than the ones based on Fig. 2 could very likely be used for benchmarking. Assuming noiseless measurements, one could for instance measure the observable X^⊗n on the prepared $\left\vert \psi \right\rangle$ by directly measuring all the data qubits in the Pauli-X basis (i.e., in this case, one would remove the parallelization and measured register of Fig. 2). In presence of a perfect bias, the errors will commute with the measurements. Hence, the implementation of the circuit would give the same outcome as the classical simulation algorithm Theorem 2 (for U = X^⊗n, $B\left\vert {\psi }_{0}\right\rangle =\left\vert \psi \right\rangle$). For this reason, we believe that a similar benchmarking protocol as Theorem 4 could be derived for this simpler circuit (a mismatch between the simulation and experiment would indicate a violation). However, we leave a rigorous proof of this guess for a future work (the proof should in particular acknowledge what happens if these measurements are noisy—something we acknowledged in Theorem 4 (See the paragraph preceeding Theorem 3 and the noise of Definition 4)). This noise model makes Pauli-Y and Pauli-Z measurements noisy, which are the only ones we use in our circuit of Fig. 2)—and precisely quantify the violation with similar equations as (9) and (10).

Overall, the important aspect of our benchmark is that it is scalable (even if measurements and state preparation are noisy), and allows to detect violation of the noise model in a manner that would not be visible from individual gate tomography, because some effects of the noise cannot be detected at this level, as we discussed at the beginning of section sketching the benchmarking protocol.

Finally, while our circuits are efficiently simulable, their strong noise-resilience, rigorously proven in presence of a Pauli bit-flip noise (i.e. the noise model described around (2), which is more restrictive than the one of Definition 4 for which the benchmark is applicable), makes natural to wonder if extensions of our work could lead to noise-resilient circuits also showing a computational interest: this work also shows what we analyzed on this question of fundamental interest. For this, we first notice that the set of bias-preserving gates, ${{\mathbb{B}}}_{n}$ can be composed of c_XX gates, which combined to initial states $\left\vert 0/1\right\rangle$ can generate arbitrary graph states (in the local X basis). It is known that a typical n-qubit stabilizer state exhibits strong multipartite entanglement⁶⁶. This, together with the fact that arbitrary graph states are locally equivalent to stabilizer states⁶⁷, implies that, in general bias-preserving circuits can generate a rich family of highly entangled states (these graphs states are however not computationally useful for the specific task adressed in our paper, see the section II B of the Supplemental Material). We can also implement certain non-Clifford gates, and for our task, $U\in {{\mathbb{U}}}_{n}^{X}$ can act non-trivially over all the qubits of the data register, there is no restriction on the number of gates in the preparation unitary B, and the circuit is scalable despite noisy measurements. The error rates of the gates could also grow with n, making our circuits noise-resilient against one of the main threats to the scalability⁶⁰ (see section IV A of the Supplemental Material).

Methods

Benchmarking protocol and simulation of the noisy circuits

In the last part of the results section, we gave a sketch of the benchmarking protocol for Pauli bit-flip biased noise. Here, we give the technical details behind the protocol while extending it beyond Pauli bit-flip noise. We also give the classical simulation algorithm, able to simulate the noisy circuit for this more general noise model. In general, the noise model describing biased qubits can have its Kraus operators describing the noise map of each gate, state preparation and measurements that do not exactly correspond to a Pauli bit-flip channel. We mean that the Kraus operators could be a linear combination of Pauli bit-flips (i.e., they would follow Definition 4: the bit-flip channel treated so far was a particular case of the expected noise model for such hardware). Additionally, there can be imperfections in the bias. It means that the Kraus operators describing the noise maps could have a non-zero Hilbert-Schmidt inner product with Pauli operators not belonging to ${{\mathbb{P}}}_{n}^{X}$. For instance, the Kraus operators could have a non-zero overlap with a multi-qubit Pauli P containing at least one Pauli Z, or one Pauli Y in the expression of its tensor product (such as P = X ⊗ Z for instance). If it occurs, we will say that the noise model also produces phase-flip errors. Our benchmarking protocol can detect violations of the assumed noise model in this more general case. The protocol is based on the fact that we can simulate the outcome of the Hadamard test in the noisy case, under the assumption that the bias is perfect but not necessarily Pauli (i.e., that it satisfies Definition 4). This classical simulation takes as input the noise model of each individual gate, approximated to that of a perfect bias. A deviation of this classical simulation from the experimental outcomes further than an error budget will imply that the noise model prescribed by individual gate tomography is not occurring experimentally, identifying a possible threat to the hardware scalability, due to collective effects occurring at the scale of the algorithm. This error budget is related to the quality of the approximation of the noise model taken from individual gate tomography with a perfect bias. The formal protocol is written in Theorem 4. We now state the definition and theorems we need.

Definition 4

(Perfect bias). Let ${\mathcal{G}}$ be a quantum channel describing either a noiseless unitary gate belonging to the accessible gateset, or a single-qubit state preparation, and ${{\mathcal{E}}}_{{\mathcal{G}}}$ be its noisy implementation in the laboratory. We say that the noisy implementation of the gate (or state preparation), ${{\mathcal{E}}}_{{\mathcal{G}}}$, follows a perfectly biased noise model if ${{\mathcal{E}}}_{{\mathcal{G}}}={{\mathcal{N}}}_{{\mathcal{G}}}\circ {\mathcal{G}}$, where the noise map ${{\mathcal{N}}}_{{\mathcal{G}}}$ is a CPTP (Completely Positive Trace Preserving) map that admits the following Kraus decomposition:

$$\begin{array}{rcl}{{\mathcal{N}}}_{{\mathcal{G}}}(\rho )&=&\mathop{\sum}\limits _{j}{K}_{j}^{{\mathcal{G}}}\rho {\left({K}_{j}^{{\mathcal{G}}}\right)}^{\dagger },\\ {K}_{j}^{{\mathcal{G}}}&=&\mathop{\sum}\limits_{\alpha \subset {\rm{supp}}({\mathcal{G}})}{c}_{\alpha }^{j}{X}_{\alpha },\end{array}$$

(7)

In (7), we follow the notations introduced around (2). We also have: $\forall j,{c}_{\alpha }^{j}\in {\mathbb{C}}$ and ${\sum }_{j}{({K}_{j}^{{\mathcal{G}}})}^{\dagger }{K}_{j}^{{\mathcal{G}}}={I}_{{\rm{supp}}({\mathcal{G}})}$. A quantum map satisfying (7) will be said to be perfectly biased.

A noisy single-qubit measurement will be modeled as a perfect measurement, preceded by the application of a perfectly biased single-qubit CPTP map on the qubit being measured. This CPTP channel, called the noise map of the measurement, represents the noise brought by the measurement.

To make the formulation of the following theorems simple, we will assume that state preparation and measurements are noiseless. In the case all gates are bias-preserving (which is what we consider in all this paper) and if the noise model satisfies Definition 4, this assumption doesn’t remove generality from our results. This is because the noise of the state preparation or measurement can be acknowledged by redefining the noise map of the following or preceding gate. The newly obtained noise map will still satisfy Definition 4.

Theorem 3

(Efficient classical simulation of a noisy Hadamard test under perfect bias). Let $B\in {{\mathbb{B}}}_{n}$, $U=W.V\in {{\mathbb{U}}}_{n}^{X}$, N_W, N_V satisfying the constraints of Theorem 1. Let $\left\vert {\psi }_{0}\right\rangle =\left\vert {\phi }_{1}\right\rangle \left\vert {\phi }_{2}\right\rangle \cdots \left\vert {\phi }_{n}\right\rangle$ be the initial product state for the data register. If ${N}_{V}=O(\log (n))$, if the noise model of each gate is perfectly biased according to Definition 4, if the total number of gates in the algorithm is in Poly(n), and if state preparation and measurements are noiseless (this is without loss of generality, see the comments before Theorem 3), there exists a randomized classical algorithm taking as input (I) classical specifications of the circuit implementing the Hadamard test for the chosen $(B,U,\left\vert {\psi }_{0}\right\rangle )$, (II) the quantum channel describing the noise model of each gate used in the computation, (III) the initial state $\left\vert {\psi }_{0}\right\rangle$ such that this algorithm efficiently and with a high probability computes an additive approximation to Tr(P₁ρ_X), where ρ_X is the reduced density matrix of the measured register at the end of the noisy implementation of the algorithm, and P₁ is a single-qubit Pauli matrix. We call ${\mathcal{C}}$ this classical approximation.

Specifically, we have:

$$\Pr \left(| Tr({P}_{1}{\rho }_{X})-{\mathcal{C}}| \le \epsilon \right)\ge 1-\delta ,$$

(8)

while the running time is $T=O((1/{\epsilon }^{2})\log (1/\delta )\times \,\text{poly}\,(n))$.

Theorem 4

(Benchmarking protocol). Consider a Hadamard test satisfying the constraints of Theorem 1. The circuit is implemented with N unitary gates represented by the unitary quantum channels ${\{{{\mathcal{G}}}_{i}\}}_{i = 1}^{N}$. We call ${{\mathcal{N}}}_{{{\mathcal{G}}}_{i}}$ the noise map associated with ${{\mathcal{G}}}_{i}$ (extracted from individual gate tomography) and we assume state preparation and measurements to be noiseless (this is without loss of generality up to a redefinition of the noise maps of the quantum gates, see comments before Theorem 3).

Let ${{\mathcal{N}}}_{X,{{\mathcal{G}}}_{i}}$ be an approximation to ${{\mathcal{N}}}_{{{\mathcal{G}}}_{i}}$, such that ${{\mathcal{N}}}_{X,{{\mathcal{G}}}_{i}}$ has a noise model satisfying Definition 4.

Let ρ be the density matrix of the measured register at the end of the algorithm if the noise map of each ${{\mathcal{G}}}_{i}$ was ${{\mathcal{N}}}_{{{\mathcal{G}}}_{i}}$. Let ρ_X be the reduced density matrix of the measured register at the end of the algorithm if the noise map of each ${{\mathcal{G}}}_{i}$ was ${{\mathcal{N}}}_{X,{{\mathcal{G}}}_{i}}$. Let ${\rho }_{\exp }$ be the reduced density matrix of the measured register that exactly predicts the experimental outcomes. More precisely, we mean that implementing the measurements used in the Hadamard test on ${\rho }_{\exp }$ would exactly reproduce the measurement outcomes experimentally observed.

Assume that there exist ϵ > 0 such that

$$\mathop{\max }\limits_{i}| | {{\mathcal{N}}}_{X,{{\mathcal{G}}}_{i}}-{{\mathcal{N}}}_{{{\mathcal{G}}}_{i}}| | \le \frac{\epsilon }{\sqrt{2}N}$$

(9)

is satisfied. Then, for any single-qubit Pauli P₁:

$$| Tr(\rho {P}_{1})-Tr({\rho }_{X}{P}_{1})| \le \epsilon .$$

(10)

Principle of the benchmarking

The benchmarking protocol works as follow. Tr(ρ_XP₁) corresponds to the outcome of the circuit with a noise model for each gate satisfying Definition 4. Hence, it can be classically estimated with Theorem 3. $Tr({\rho }_{\exp }{P}_{1})$ is accessed experimentally. If $| Tr({\rho }_{\exp }{P}_{1})-Tr({\rho }_{X}{P}_{1})| > \epsilon$, ${\rho }_{\exp }$ and ρ necessarily differ, indicating that the noise model predicted by individual gate tomography (the noise maps ${\{{{\mathcal{N}}}_{{{\mathcal{G}}}_{i}}\}}_{i = 1}^{N}$) is not occuring experimentally. It thus indicates the presence of collective effects in the noise, possibly threatening the scalability of the biased-noise qubits.

Noteworthy, $\Delta \equiv | Tr({\rho }_{\exp }{P}_{1})-Tr({\rho }_{X}{P}_{1})| -\epsilon$ can quantify how strong the noise violation is at the scale of the whole circuit (if Δ > 0). It is a consequence of the fact $| Tr({\rho }_{\exp }{P}_{1})-Tr(\rho {P}_{1})| \ge \Delta$ (the larger Δ, the larger the violation).