Quantum-data-driven dynamical transition in quantum learning

Abstract

Quantum neural networks, parameterized quantum circuits optimized under a specific cost function, provide a paradigm for achieving near-term quantum advantage in quantum information processing. Understanding QNN training dynamics is crucial for optimizing their performance. However, the role of quantum data in training for supervised learning such as classification and regression remains unclear. We reveal a quantum-data-driven dynamical transition where the target values and data determine the convergence of the training. Through analytical classification over the fixed points of the dynamical equation, we reveal a comprehensive ‘phase diagram’ featuring seven distinct dynamics originating from a bifurcation with multiple codimension. Perturbative analyses identify both exponential and polynomial convergence classes. We provide a non-perturbative theory to explain the transition via generalized restricted Haar ensemble. The analytical results are confirmed with numerical simulations and experimentation on IBM quantum devices. Our findings provide guidance on constructing the cost function to accelerate convergence in QNN training.

Introduction

Classical neural networks are the crucial paradigm of machine learning that drive the surge of artificial intelligence. Generalizing the classical notion to quantum, quantum neural networks (QNN) or variational quantum algorithms^{1,2,3,4,5,6,7,8}, have shown promise in solving complex problems involving different types of data. In variational quantum eigensolver (VQE)^1,9 and quantum optimization^2,10, the goal is to prepare a state that minimizes a cost function, without the need for training data. However, supervised quantum machine learning relies on sufficient training data—labeled quantum states encoding either quantum or classical information. Such learning tasks have been widely explored in identifying phases within many-body quantum systems¹¹, and classification of quantum sensing data^12,13,14,15 or classical data^{16,17,18,19,20}.

With the rise of QNN applications in supervised learning, the fundamental study of their convergence properties becomes an important task, especially in the overparametrization region²¹ where QNNs are empowered by a large number of layers. Recent progress in the theory of the Quantum Neural Tangent Kernel (QNTK)^{22,23,24,25,26} adopted the classical notion of neural tangent kernel to provide insight into the convergence dynamics. Furthermore, for QNNs with a quadratic loss function, a dynamical transition originating from the transcritical bifurcation has been revealed in the training dynamics of optimization tasks²⁷. However, the results do not apply to supervised quantum machine learning, where complex quantum data are involved.

In this work, we develop a quantum-data-driven theory of dynamical transition for supervised learning and reveal the complete multi-dimensional ‘phase diagram’ in QNN training dynamics (see Fig. 1b). Under the numerically supported assumption of the frozen relative quantum meta-kernel (dQNTK), we obtain a group of nonlinear dynamical equations of the training error and kernels that predict seven different types of dynamics via the corresponding fixed points. Around each physical fixed point, we can define a fixed-point charge, determined by the choice of target value. When the target value crosses the boundary, the minimum/maximum eigenvalue of the observable, the fixed-point charge changes its sign and induces a stability transition on the fixed point, which can be identified as a bifurcation with multi-codimension. Then, we perform a leading-order perturbative analysis and obtain the convergence speed of each of the seven dynamics, where an exponential convergence class and a polynomial convergence class are identified. All the analytical results are confirmed with numerical simulations of QNN training. Furthermore, we develop a non-perturbative unitary ensemble theory for the optimized quantum circuits to characterize the constrained randomness and to support the frozen relative dQNTK assumption. We also verify our results in examples of training dynamics with IBM quantum devices. As the QNN training dynamics is determined by the target value choice, our results provide guidance on constructing the cost function to maximize the speed of convergence.

Fig. 1: Illustration of the QNN for supervised learning and main results.

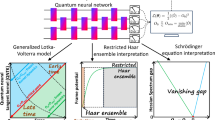
a We study the training dynamics of errors and kernels in minimizing the MSE loss function ${\mathcal{L}}=\frac{1}{2}\sum _{\alpha }{({\langle \hat{O}\rangle }_{\alpha }-{y}_{\alpha })}^{2}$, and develop a set of nonlinear dynamical equations (Eqs. (17)). b We identify a dynamical transition among two convergence classes involving seven different dynamics in total (six types are shown here), and perturbatively solve its convergence dynamics. c We also provide a non-perturbative interpretation via restricted Haar ensemble theory to characterize the optimized circuits under constraints from data.

Results

Overview of results

Given a QNN $\hat{U}({\boldsymbol{\theta }})$ with L variational parameters θ = (θ₁, …, θ_L), we consider a supervised learning task involving N quantum data ${\{\vert {\psi }_{\alpha }\rangle \}}_{\alpha = 1}^{N}$, each of which is associated with a real-valued target label y_α. As shown in Fig. 1a, the input data can be quantum states of a many-body systems¹¹, states output from quantum sensor networks¹⁴ or quantum states encoding classical data¹⁶.

For input quantum data $\left\vert {\psi }_{\alpha }\right\rangle$, the QNN applies the unitary $\hat{U}({\boldsymbol{\theta }})$ to produce the output $\hat{U}({\boldsymbol{\theta }})\left\vert {\psi }_{\alpha }\right\rangle$ and then performs the measurement $\hat{O}$, whose result is adopted as the estimated label. Note that the target label y_α can be assigned arbitrarily according to different tasks, although the measurement $\hat{O}$ typically has bounded maximum and minimum values ${O}_{{\rm{min/max}}}$. For example, while Pauli measurements always provide expectation ∈ [− 1, 1], in regression we may set the target values as ±0.5 and in binary classification we can also set the target values to be ±2. As indicated by the single data result in ref. ²⁷, the choice of the target values has an important role in the training dynamics.

The error—the average deviation of the estimated label to the target label—associated with a data-target pair $(\left\vert {\psi }_{\alpha }\right\rangle ,{y}_{\alpha })$ is therefore

$${\epsilon }_{\alpha }({\boldsymbol{\theta }})=\left\langle {\psi }_{\alpha }| {\hat{U}}^{\dagger }({\boldsymbol{\theta }})\hat{O}\hat{U}({\boldsymbol{\theta }})| {\psi }_{\alpha }\right\rangle -{y}_{\alpha }.$$

(1)

To take into account the overall error over N data, we define the mean squared error (MSE) loss as

$${\mathcal{L}}({\boldsymbol{\theta }})=\frac{1}{2N}\mathop{\sum }\limits_{\alpha =1}^{N}{\epsilon }_{\alpha }{({\boldsymbol{\theta }})}^{2}.$$

(2)

The training of QNN relies on gradient-descent update of the parameters θ, where each data’s gradient of the error ∇ ϵ_α(θ) (with respect to the parameters θ) plays an important role. Generalizing the kernel scalar in quantum optimization²⁷, we introduce the kernel matrix ${K}_{\alpha \beta }({\boldsymbol{\theta }})=\langle \nabla {\epsilon }_{\alpha },\nabla {\epsilon }_{\beta }\rangle$, an inner product of gradients over parameter space.

Our main result is that the target values ${\{{y}_{\alpha }\}}_{\alpha = 1}^{N}$ determine the QNN training dynamics. The overall training can exhibit exponential converge when none of the target values are chosen as the boundary values ${O}_{{\rm{min/max}}}$; on the other hand, any coincidence of the target value and the boundary values of observable will lead to polynomial convergence. More specifically, depending on the interplay of the target values, seven different types of training dynamics can be identified. As shown in Fig. 1b in a two data case, the target values y₁ and y₂ divide the parameter space into nine regions, with the lines ${y}_{1}={O}_{{\rm{min/max}}}$ and ${y}_{2}={O}_{{\rm{min/max}}}$. The four crossing points (red dots) are the critical point with polynomial convergence; the same polynomial convergence extends to the four lines, where critical-frozen-error (brown) and where critical-frozen-kernel (purple) dynamics are identified. The bulk regions enable exponential convergence and therefore are preferred. Furthermore, they are divided into three different dynamics, frozen-kernel (yellow), mixed-frozen (green) and frozen-error (blue). Besides the six dynamics depicted in Fig. 1b, an additional type of training dynamics, critical-mixed-frozen dynamics, uniquely appears when the number of data N > 2.

We provide analytical theory to derive and explain behaviors of the above seven types of dynamics. Our analyses combine the solution of fixed point, the perturbative analyses around the fixed points to derive the convergence speed. In particular, we interpret the transition among different dynamics via the stability transition of fixed points, corresponding to a bifurcation transition with multiple codimensions.

The dynamical transition is beyond the usual Haar random assumption of QNNs that only holds at initialization, as QNNs are under constraints from the convergence at late time. We develop the restricted Haar ensemble in a block-diagonal form

$${{\mathcal{U}}}_{{\rm{RH}}}=\left\{U\left| U=\left(\begin{array}{ll}Q&{\bf{0}}\\ {\bf{0}}&V\end{array}\right)\right.\right\},$$

(3)

where Q is a diagonal matrix with complex phases uniformly distributed to capture the convergence and V is a Haar random unitary. For any unitary ensemble, we can quantify its complexity via the frame potential²⁸ (see detailed definition in Eq. (41)), which is lower bounded by the value of the Haar measure. As sketched in Fig. 1c the ensemble has frame potential above the Haar value and increasing in a power-law with the number of data till saturation at close to the Hilbert space dimension. The frame potential is numerically verified in the QNN training.

At the end of this section, we provide the intuition on the different choices of target values. Although it seems uncommon to choose a target value ${y}_{\alpha } > {O}_{\max }$ (${y}_{\alpha } < {O}_{\min }$) to be nonphysical at the first glance, the minimization of loss function in Eq. (2) will force the QNN to output states with expectations of the bounded observable to be ${O}_{\max }$ (${O}_{\min }$), which is as close as possible to the targeted nonphysical value. Thus, indeed we will obtain an optimized QNN identical to the one when setting the target values to be ${O}_{\max }$ (${O}_{\min }$). Moreover, inspired by our previous work in optimization tasks²⁷, we find that setting nonphysical target values can also further provide speedup in the supervised learning task.

Fundamental dynamical equations for training a QNN

In this section, we aim to develop the fundamental dynamical equations to simultaneously characterize the training dynamics of errors and kernels from the first principle. During QNN training, we evaluate the cost function in Eq. (2) and minimize it using gradient descent to update each parameter,

$$\begin{array}{lll}\delta {\theta }_{\ell }(t)\,\equiv \,{\theta }_{\ell }(t+1)-{\theta }_{\ell }(t)=-\eta \frac{\partial {\mathcal{L}}({\boldsymbol{\theta }})}{\partial {\theta }_{\ell }}\\\qquad\quad =-\frac{\eta }{N}\mathop{\sum}\limits _{\alpha }{\epsilon }_{\alpha }({\boldsymbol{\theta }})\frac{\partial {\epsilon }_{\alpha }({\boldsymbol{\theta }})}{\partial {\theta }_{\ell }},\end{array}$$

(4)

where η ≪ 1 is the learning rate in gradient descent. Accordingly, quantities depending on θ also acquire new values in each training step, thus we only denote the time dependence explicitly for simplicity, e.g., ϵ_α(t) ≡ ϵ_α(θ(t)). From the first-order Taylor expansion, the total error ϵ_α(t) is updated using Eq. (4)

$$\delta {\epsilon }_{\alpha }(t)=\sum _{\ell }\frac{\partial {\epsilon }_{\alpha }({\boldsymbol{\theta }})}{\partial {\theta }_{\ell }}\delta {\theta }_{\ell }+{\mathcal{O}}({\eta }^{2})$$

(5)

$$=-\frac{\eta }{N}\sum _{\beta }{K}_{\alpha \beta }({\boldsymbol{\theta }}){\epsilon }_{\beta }({\boldsymbol{\theta }})+{\mathcal{O}}({\eta }^{2}).$$

(6)

Here, we have defined the QNTK matrix as

$${K}_{\alpha \beta }({\boldsymbol{\theta }})\equiv \sum _{\ell }\frac{\partial {\epsilon }_{\alpha }({\boldsymbol{\theta }})}{\partial {\theta }_{\ell }}\frac{\partial {\epsilon }_{\beta }({\boldsymbol{\theta }})}{\partial {\theta }_{\ell }}=\left\langle \nabla {\epsilon }_{\alpha },\nabla {\epsilon }_{\beta }\right\rangle ,$$

(7)

where $\nabla {\epsilon }_{\alpha }\equiv {\left(\frac{\partial {\epsilon }_{\alpha }}{\partial {\theta }_{1}},\ldots ,\frac{\partial {\epsilon }_{\alpha }}{\partial {\theta }_{L}}\right)}^{T}$ is the gradient vector of ϵ_α, and 〈 ⋅ , ⋅ 〉 represents the inner product over parameter space. By definition, the QNTK is a positive semidefinite symmetric matrix. The diagonal term ${K}_{\alpha \alpha }=\left\langle \nabla {\epsilon }_{\alpha },\nabla {\epsilon }_{\alpha }\right\rangle \equiv \parallel \nabla {\epsilon }_{\alpha }{\parallel }^{2}$ is the square of the norm of the gradient vector, while the off-diagonal term K_αβ provides information about the angle between different gradient vectors. Indeed, following the definition of angle between gradient vectors, $\cos \angle [\nabla {\epsilon }_{\alpha },\nabla {\epsilon }_{\beta }]=\langle \nabla {\epsilon }_{\alpha },\nabla {\epsilon }_{\beta }\rangle /\parallel \nabla {\epsilon }_{\alpha }\parallel \parallel \nabla {\epsilon }_{\beta }\parallel$, we can retrieve the geometric angle from the above defined QNTK as

$${\angle }_{\alpha \beta }({\boldsymbol{\theta }})\equiv \cos \angle \left[\nabla {\epsilon }_{\alpha },\nabla {\epsilon }_{\beta }\right]=\frac{{K}_{\alpha \beta }}{\sqrt{{K}_{\alpha \alpha }{K}_{\beta \beta }}}$$

(8)

where the matrix ${\angle }_{\alpha \beta }(\boldsymbol{\theta})$ is introduced to simplify the notation.

Our study focuses on the training dynamics of both errors and kernels of the QNNs. To study the convergence, we often separate the error into two parts: ϵ_α(t) ≡ ε_α(t) + ϵ_α(∞) consists of a constant remaining term ϵ_α(∞) and a vanishing residual error ε_α(t).

With similar techniques in obtaining Eq. (6), in Method we derive the dynamical equation of QNTK. Combining with Eq. (6), we have a set of coupled nonlinear dynamical equations for total error and QNTK

$$\left\{\begin{array}{l}\delta {\epsilon }_{\alpha }(t)=-\frac{\eta }{N}\sum _{\beta }{K}_{\alpha \beta }(t){\epsilon }_{\beta }(t);\\ \delta {K}_{\alpha \beta }(t)=-\frac{\eta }{N}\sum _{\gamma }{\epsilon }_{\gamma }(t)\left[{\mu }_{\gamma \beta \alpha }\left(t\right)+{\mu }_{\gamma \alpha \beta }\left(t\right)\right].\end{array}\right.$$

(9)

where the dQNTK μ_γαβ is defined as

$${\mu }_{\gamma \alpha \beta }({\boldsymbol{\theta }})=\sum _{{\ell }^{{\prime} },\ell }\frac{\partial {\epsilon }_{\gamma }({\boldsymbol{\theta }})}{\partial {\theta }_{\ell }}\frac{{\partial }^{2}{\epsilon }_{\alpha }({\boldsymbol{\theta }})}{\partial {\theta }_{\ell }\partial {\theta }_{\ell }^{{\prime} }}\frac{\partial {\epsilon }_{\beta }({\boldsymbol{\theta }})}{\partial {\theta }_{{\ell }^{{\prime} }}},$$

(10)

which is a bilinear form of total error’s gradient and Hessian. Since we utilize a quadratic loss function Eq. (2), there exists a gauge invariance under the orthogonal group O(N) on the data space for loss function, thus on the gradient descent update in Eq. (4) and dynamical equations in Eq. (9), as we show in Supplementary Note 3. However, quantities of inner products over parameter space, e.g., QNTK and dQNTK, are not gauge invariant.

Before moving on, we emphasize that the dynamical equations in this section actually apply to the gradient-descent training of any quadrature loss function in Eq. (2), regardless of whether it regards a QNN or classical systems.

Assumption of fixed relative dQNTK

In this section, we propose the key assumption (supported in ‘Ensemble average results’ section) in order to analytically study the training dynamics through reduction on the number of independent variables in Eq. (9). In a typical training process toward reaching a local minimum, the Hessian $\frac{{\partial }^{2}{\epsilon }_{\alpha }}{\partial {\theta }_{\ell }\partial {\theta }_{{\ell }^{{\prime} }}}$ converges to a constant during late-time training. Therefore, according to the definition of dQNTK in Eq. (10), we can expect that μ_γαβ ~ K_γβ has the same scaling. This intuition motivates us to define the relative dQNTK λ_γαβ(t) as

$${\lambda }_{\gamma \alpha \beta }(t)=\frac{{\mu }_{\gamma \alpha \beta }(t)}{\sqrt{{K}_{\gamma \gamma }(t){K}_{\beta \beta }(t)}},$$

(11)

which reduces to the scalar version in ref. ²⁷ for optimization when N = 1. Our major assumption in this work is that the relative dQNTK converges to a constant λ_γαβ(t) → λ_γαβ in the late time. We numerically verify the assumption in various cases, as we detail in Supplementary Note 6. In Fig. 2, we plot the sum of the absolute values, $\parallel {\lambda }_{\gamma \alpha \beta }{\parallel }_{1}\equiv \sum _{\gamma \alpha \beta }| {\lambda }_{\gamma \alpha \beta }|$, to show the convergence. This assumption is not only motivated by previous results of ref. ²⁷, but also supported by the unitary ensemble theory in ‘Ensemble average results’ section.

Fig. 2: Convergence of relative dQNTK.

We show the norm $\parallel {\lambda }_{\gamma \alpha \beta }(t){\parallel }_{1}\equiv \sum _{\gamma \alpha \beta }| {\lambda }_{\gamma \alpha \beta }(t)|$ for (a) exponential convergence class and (b) polynomial convergence class (detailed in ‘Classifying the dynamics’ section). The targets for orthogonal data states are y₁ = 0.3, y₂ = − 0.5 (blue), y₁ = 5, y₂ = − 6 (orange) and y₁ = 0.4, − 5 (green) in (a); y₁ = 1, y₂ = − 1 (blue), y₁ = 0.4, y₂ = − 1 (orange), y₁ = 1, y₂ = − 5 (green) and y₁ = 0.4, y₂ = 1, y₃ = − 5 (red) in (b). The corresponding dynamics are identified in Fig. 3 and Table. 1. Here random Pauli ansatz (RPA) consists of L = 48 variational parameters on n = 4 qubits with $\hat{O}={\hat{\sigma }}_{1}^{z}$, Pauli-Z operator on the first qubit.

Under the constant relative dQNTK assumption, the dynamical equations of Eq. (9) then become

$$\left\{\begin{array}{l}{\partial }_{t}{\epsilon }_{\alpha }(t)=-\frac{\eta }{N}\sum _{\beta }{K}_{\alpha \beta }(t){\epsilon }_{\beta }(t);\\ {\partial }_{t}{K}_{\alpha \beta }(t)=-\frac{\eta }{N}\left({f}_{\beta \alpha }(t)\sqrt{{K}_{\alpha \alpha }(t)}+{f}_{\alpha \beta }(t)\sqrt{{K}_{\beta \beta }(t)}\right).\end{array}\right.$$

(12)

where we have defined the functions

$${f}_{\alpha \beta }(t)=\sum _{\gamma }\sqrt{{K}_{\gamma \gamma }(t)}{\epsilon }_{\gamma }(t){\lambda }_{\gamma \alpha \beta }$$

(13)

for convenience and taken the continuous-time limit.

Our major result is the classification of the training dynamics of QNN in supervised learning based on Eq. (12). In the next section, we obtain the fixed points representing each dynamics under similar assumptions as in ref. ²⁷. In ‘Convergence towards fixed points’, we further provide perturbative analyses on the late-time training dynamics to obtain the convergence speed towards the fixed points. In ‘Ensemble average results’ section, we develop the unitary ensemble theory to support the assumption proposed above. In ‘Experiment’ section, we present experimental results on IBM quantum devices.

We point out that our main conclusions hold generally for gradient-descent training of bounded observables under quadratic loss function, assuming the fixed relative dQNTK assumption, regardless of the detailed dynamics—quantum or classical.

Solving the fixed points

From Eq. (12), we can obtain the fixed points below.

Result 1

(Frozen gradient angle and error-kernel duality) There exists a family of fixed points of the training dynamics of Eq. (12) satisfying

$${\epsilon }_{\alpha }{K}_{\alpha \alpha }=0,\forall \alpha ,$$

(14)

$${\angle }_{\alpha \beta }={\rm{const}}.$$

(15)

In other words, in late-time training, (1) the error ϵ_α and kernel K_αα satisfy a duality—either one of the two is zero or both are zero; (2) the relative orientation among gradient vectors associated with each data is fixed. We claim the above conclusion as a result instead of a theorem, as there is a weak assumption behind it: the functions f_αβ(t) have the same scaling versus t despite different α and β.

To show Result 1, we begin with the following lemma

Lemma 1

When the ratio

$${{\mathcal{A}}}_{\alpha \beta }=\mathop{\lim }\limits_{t\to \infty }\frac{\left(\frac{{f}_{\beta \alpha }(t)}{\sqrt{{K}_{\beta \beta }(t)}}+\frac{{f}_{\alpha \beta }(t)}{\sqrt{{K}_{\alpha \alpha }(t)}}\right)}{\left(\frac{{f}_{\beta \beta }(t)}{\sqrt{{K}_{\beta \beta }(t)}}+\frac{{f}_{\alpha \alpha }(t)}{\sqrt{{K}_{\alpha \alpha }(t)}}\right)}={\rm{const}},$$

(16)

is a finite constant in the interval [ − 1, 1]. Then ${\angle }_{\alpha \beta }(\infty )={{\mathcal{A}}}_{\alpha \beta }$ is a fixed point of Eq. (12).

We provide the proof in Supplementary Note 1 We expect the conditions in Lemma 1 to hold, as the functions f_αβ(t) defined in Eq. (13) have the same scaling with time t for different indices α, β at late time. Indeed, this is true unless the constants λ_γαβ’s are particularly chosen such that certain terms can exactly cancel out in the summation of Eq. (13). Under the assumption that the functions f_αβ(t) have the same scaling, we find that ${{\mathcal{A}}}_{\alpha \beta }$’s are indeed constants by symmetry of the expression. Furthermore, our numerical results (see Supplementary Note 6) indeed support that the constant is between [ − 1, 1].

From the definition in Eq. (8), with ${\angle }_{\alpha \beta }({t})$ = ${\angle }_{\alpha \beta }$ being a constant, ${K}_{\alpha \beta }(t)={\angle }_{\alpha \beta }\sqrt{{K}_{\alpha \alpha }(t){K}_{\beta \beta }(t)}$ is entirely determined by the diagonal kernels. Therefore, in the kernel-error dynamical Eq. (12), the only independent variables are ${\{{\epsilon }_{\alpha }(t),{K}_{\alpha \alpha }(t)\}}_{\alpha = 1}^{N}$ and the relevant dynamical equations among Eq. (12) can be simplified to

$$\left\{\begin{array}{l}{\partial }_{t}{\epsilon }_{\alpha }(t)=-\frac{\eta }{N}\sum _{\beta }{\angle }_{\alpha \beta }\sqrt{{K}_{\alpha \alpha }(t)}\sqrt{{K}_{\beta \beta }(t)}{\epsilon }_{\beta }(t);\\ {\partial }_{t}\sqrt{{K}_{\alpha \alpha }(t)}=-\frac{\eta }{N}\sum _{\beta }{\lambda }_{\alpha \alpha \beta }\sqrt{{K}_{\beta \beta }(t)}{\epsilon }_{\beta }(t).\end{array}\right.$$

(17)

From here, we can conclude that {K_ααϵ_α = 0, ∀ α} forms a family of fixed points, which arrives at Result 1.

Classification of the dynamics

As indicated in Result 1, {K_ααϵ_α = 0, ∀ α} defines a family of fixed points. Since K_ααϵ_α = 0 can be achieved by either K_αα = 0 or ϵ_α = 0 or both of them are zeros, we can have various different fixed points. Below we systematically classify the QNN dynamics based on the fixed points. Denote $\Omega ={\{\beta \}}_{\beta = 1}^{N}$ to be the whole set of data indices, we can define two sets of indices S_E, S_K conditioned on the convergence of errors and kernels as

$$\left\{\begin{array}{l}{S}_{E}\equiv \{\beta | \mathop{\lim }\limits_{t\to \infty }{\epsilon }_{\beta }(t)=0\};\\ {S}_{K}\equiv \{\beta | \mathop{\lim }\limits_{t\to \infty }{K}_{\beta \beta }(t)=0\},\end{array}\right.$$

(18)

where S_E ∪ S_K = Ω always holds. The fixed points can thus be classified in terms of the relation between the zero-error indices S_E and the zero-kernel indices S_K, as we list in the table below.

We also depict the Venn diagram of each type of dynamics to visually represent the table above in Fig. 3. All the names of the dynamics and the overall classification of exponential versus polynomial convergence (in the residual error) will be explained in ‘Convergence towards fixed points’ section. Compared with the case of optimization algorithms considered in ref. ²⁷, QNNs for supervised learning have four extra types of dynamics, mixed-frozen, critical-frozen-kernel, critical frozen-error and critical-mixed-frozen dynamics due to the interaction between data through convergence.

Fig. 3: Venn diagram of classes of dynamics.

In all cases, we have S_E ∪ S_K = Ω. Exponential convergence class consists of three types of dynamics in (a), (b), and (c). Polynomial convergence class consists of four types of dynamics depicted in (d), (e), (f), and (g). The corresponding dynamics are explained in ‘Convergence towards fixed points’ section. The bottom legend shows the connection of the set S_E and S_k to the target value configuration.

To determine which set a data state belongs to in Eq. (18), we need to identify for a particular data index β whether the kernel K_ββ(t) or the error ϵ_β(t) will decay to zero at late time. While the exact determination will require training the QNN to late time, we can obtain intuition from the relation between target value y_β and achievable values for the observable $\hat{O}$. When a target value y_β lies within the achievable region $({O}_{\min },{O}_{\max })$, the error ϵ_β(t) is expected to converge to zero when the circuit is deep, implying β ∈ S_E; When a target value is not in the achievable region, then we expect ϵ_β(t) to converge to nonzero constants. Thus, the fixed point condition in Result 1 requires K_ββ(t) vanishing to zero, and thus β ∈ S_K; when the target value is at the boundary ${y}_{\beta }={O}_{{\rm{min/max}}}$, then we expect the special case of critical phenomena with both error and kernel vanishing at late time thus β ∈ S_E ∩ S_K. The above intuition about target value and ‘phase diagram’ can be summarized as the following

$$\left\{\begin{array}{ll}\beta \in {S}_{E},\,\,{\text{if}}\,\,{y}_{\beta }\in [{O}_{\min },{O}_{\max }];\\ \beta \in {S}_{K},\,\,{\text{if}}\,\,{y}_{\beta }\in (-\infty ,{O}_{\min }]\cup [{O}_{\max },+\infty ).\end{array}\right.$$

(19)

When ${y}_{\beta }={O}_{\min }$ or ${O}_{\max }$, we have β ∈ S_E ∩ S_K. The Venn diagrams summarize the classification of fixed points and connection to target value configuration for each case, as shown in Fig. 3.

Numerical analysis confirms that this classification holds for the orthogonal data case, where $\left\langle {\psi }_{\alpha }| {\psi }_{\beta }\right\rangle ={\delta }_{\alpha \beta }$, as detailed in the following section. Although the orthogonality property does not hold always in machine learning tasks, we take the orthogonal data as a typical case to unveil the fruitful physical phenomena within the training dynamics. In practice, typical random states in high-dimensional space are expected to be exponentially close to orthogonal states. Important quantum machine learning tasks involving state discrimination and classification also benefit from orthogonal data encoding due to the Helstrom limit^29,30.

Since the dynamical equations in Eq. (9) are gauge invariant, the fixed point identified in Result 1 is also gauge invariant. However, the classification of the dynamics will be dependent on the choice of gauge—different ways of defining the error as combinations of the natural basis in Eq. (1). This is intuitive, as the dynamical transitions are driven by the data and the target values are naturally tuned according to each observable.

Stability transition of fixed points: bifurcation

We have identified the family of fixed points for the dynamical equations (Eq. (17)) in Result 1, and seen the classification of dynamics in ‘Classifying the dynamics’ section. In this part, we aim to study the stability of every possible fixed point, which provides theoretical support on the convergence of each dynamics discussed above, and reveals the nature of the transition among different dynamics.

Around any fixed point $({\epsilon }_{\alpha }^{* },{K}_{\alpha \alpha }^{* })$ of the dynamical equations in Eq. (17), we can define a group of constant fixed-point charges as

$${C}_{\alpha }={K}_{\alpha \alpha }^{* }-2{\lambda }_{\alpha \alpha \alpha }{\epsilon }_{\alpha }^{* },\forall \alpha .$$

(20)

Note that the above fixed-point charges are only well-defined around the fixed point. We introduce them to analyze the stability of fixed point as we will detail below. It is different from the conserved quantity identified in the optimization learning task²⁷ which holds for the entire late-time training supported by the corresponding dynamical equation. Thanks to the constants C_α, we can decouple the dynamical equation near the fixed point, and reduce it to a set of equations dependent only on K_αα(t),

$${\partial }_{t}\sqrt{{K}_{\alpha \alpha }(t)}=-\frac{\eta }{2N}\sum _{\beta }\frac{{\lambda }_{\alpha \alpha \beta }}{{\lambda }_{\beta \beta \beta }}\sqrt{{K}_{\beta \beta }(t)}\left({K}_{\beta \beta }(t)-{C}_{\beta }\right)$$

(21)

$$\equiv \frac{\eta }{2N}{G}_{\alpha }(\{{K}_{\beta \beta }\},\{{C}_{\beta }\}),$$

(22)

where we introduce the function G_α({K_ββ}, {C_β}) for convenience. Note that Eq. (22) only holds near the fixed point. Through the linearization at fixed point $\{{K}_{\alpha \alpha }^{* }\}$ (see details in Method), we have

$$\begin{array}{lll}{\partial }_{t}\sqrt{{K}_{\alpha \alpha }(t)}\\ =\frac{\eta }{2N}\mathop{\sum}\limits _{\beta }{M}_{\alpha \beta }(\{{K}_{\beta \beta }^{* }\},\{{C}_{\beta }\})\left(\sqrt{{K}_{\beta \beta }(t)}-\sqrt{{K}_{\beta \beta }^{* }}\right),\end{array}$$

(23)

where the matrix ${M}_{\alpha \beta }(\{{K}_{\beta \beta }^{* }\},\{{C}_{\beta }\})$ is the Jacobian of G_α w.r.t. each kernel element $\sqrt{{K}_{\beta \beta }}$ at the fixed point $\{{K}_{\beta \beta }^{* }\}$

$${M}_{\alpha \beta }(\{{K}_{\beta \beta }\},\{{C}_{\alpha }\})\equiv {\left.\frac{\partial {G}_{\alpha }(\{{K}_{\beta \beta }\},\{{C}_{\beta }\})}{\partial \sqrt{{K}_{\beta \beta }}}\right| }_{\{{K}_{\beta \beta }^{* }\}}.$$

(24)

The stability of the fixed point $\{{K}_{\beta \beta }^{* }\}$ can thus be determined from the spectrum of the matrix ${M}_{\alpha \beta }(\{{K}_{\beta \beta }^{* }\},\{{C}_{\beta }\})$. Once an eigenvalue with a positive real part appears, the fixed point becomes unstable. Combining the stable fixed point and {C_α}, we can directly derive the classification in Fig. 3, and therefore connect the each fixed point to the corresponding class of training dynamics.

We take the two-data case as an example to reveal the stability transition of the fixed points under the change of {C_β}. In this case, the eigenvalue of the 2-by-2 matrix M is a function of ${\rm{tr}}(M)$ and $\det (M)$ only. One can easily find the trace and determinant as

$$\left\{\begin{array}{l}{\rm{tr}}(M)={C}_{1}+{C}_{2}-3({K}_{11}^{* }+{K}_{22}^{* }),\\ \det (M)\propto \left({C}_{1}-3{K}_{11}^{* }\right)\left({C}_{2}-3{K}_{22}^{* }\right).\end{array}\right.$$

(25)

Recall that K_αα is defined to be the 2-norm of total error’s gradient w.r.t. variational parameters, the physically accessible fixed point can only be $({K}_{11}^{* },{K}_{22}^{* })=({C}_{1},{C}_{2}),({C}_{1},0),(0,{C}_{2})$ and (0, 0). Via tuning (C₁, C₂), the stability of each fixed point would undergo a transition, illustrated by the flow diagrams in Fig. 4. When C₁, C₂ > 0, all the four fixed points are physically accessible (Fig. 4c). However, only $({K}_{11}^{* },{K}_{22}^{* })=({C}_{1},{C}_{2})$ (red dot) is a stable fixed point with ${\rm{tr}}(M) < 0,\det (M) > 0$ where every flow points toward it, while the others (purple triangles) are all unstable to be either a saddle point or a source. As C₁, C₂ > 0 are both positive, its convergence toward (C₁, C₂) corresponds to the frozen-kernel dynamics. When we hold one of the charge to be positive while tuning the other one, for instance, decreasing C₂ from positive to negative with C₁ > 0 ((c)-(f)-(i)), due to the requirement that K_αα > 0, only the fixed points (C₁, 0) and (0, 0) are physically accessible, then we find that (C₁, 0) becomes a stable fixed point (red dots in (f), (i)), while (0, 0) (purple triangles in (f), (i)) is still unstable, corresponding to the critical-frozen-kernel dynamics and mixed-frozen dynamics separately. Similar analysis holds for tuning C₁ while holding C₂> 0 ((c)-(b)-(a)), resulting in the same dynamical transition. When we have C₂ < 0 while decreasing C₁ from positive to negative, we see the only physically accessible and stable fixed point is (0, 0) (red dots in (g)(h)), leading to the critical-frozen-error dynamics and frozen-error dynamics separately. Specifically, when we have both C₁ = C₂ = 0, all fixed points collide and leads to critical point. Therefore, we can identify the stability transition of the fixed point as a bifurcation transition with multiple codimensions. Although the linearized dynamics in Eq. (23) only hold close to the fixed point, the bifurcation transition in supervised learning we uncover holds generally. While the fixed point location changes under gauge transform O(N), its stability property persists since the spectrum of M_αβ is gauge invariant.

Fig. 4: Flow diagram for convergence toward fixed points.

The flow diagram is described by Eq. (22). Red dots in each subplot represent the only physically accessible stable fixed point, while purple triangles represent unstable fixed points. Here we choose C₁, C₂ to be ±2, 0.

Convergence towards fixed points: exponential convergence class

Now we assume the dynamical quantities—the errors and QNTKs—converge towards the fixed point given in Result 1 and study the convergence speed for different dynamics identified above in Table 1. To unveil the scaling of convergence for each dynamics, we solve the dynamical equations in Eqs. (17) close to the known stable fixed point identified above in ‘Stability transition of fixed points: bifurcation’ section, and present the corresponding solution in leading order, verify our theoretical predictions with numerical simulations.

Table 1 Summary of the relation between zero error and kernel index sets S_E, S_K and the corresponding different types of QNN training dynamics

In the numerical simulations to verify our solutions, without loss of generality, we consider the random Pauli ansatz (RPA)^23,27 constructed as $\hat{U}({\boldsymbol{\theta }})=\mathop{\prod }\nolimits_{\ell = 1}^{D}{\hat{W}}_{\ell }{\hat{V}}_{\ell }({\theta }_{\ell }),$ where θ = (θ₁, …, θ_L) are the variational parameters. Here ${\{{\hat{W}}_{\ell }\}}_{\ell = 1}^{L}\in {{\mathcal{U}}}_{{\rm{Haar}}}(d)$ is a set of unitaries with dimension d = 2ⁿ sampled from Haar ensemble, and ${\hat{V}}_{\ell }$ is a global n-qubit rotation gate defined to be ${\hat{V}}_{\ell }({\theta }_{\ell })={e}^{-i{\theta }_{\ell }{\hat{X}}_{\ell }/2},$ where ${\hat{X}}_{\ell }\in {\{{\hat{\sigma }}^{x},{\hat{\sigma }}^{y},{\hat{\sigma }}^{z}\}}^{\otimes n}$ is a randomly-sampled n-qubit Pauli operator nontrivially supported on every qubit. Note that ${\{{\hat{X}}_{\ell },{\hat{W}}_{\ell }\}}_{\ell = 1}^{L}$ remain unchanged through the training. The observable is chosen as Pauli-Z, which has the minimum and maximum achievable values ${O}_{{\rm{min/max}}}=\pm 1$. Without losing generality, the N orthogonal data states in the simulation are generated by applying a unitary sampled from Haar ensemble onto N different computational bases. The loss function of RPA in numerical simulations is minimized with learning rate η = 10⁻³, and all numerical simulations are implemented with TensorCircuit³¹.

We begin with the exponential convergence class of dynamics, which corresponds to the cases where each data can only have either zero error or zero kernel, ${S}_{E}\cap {S}_{K}={{\emptyset}}$, as we indicate in Fig. 3 and Table 1.

Frozen-kernel dynamics.— For frozen-kernel dynamics (Fig. 3a), we have an empty set of zero-kernel indices, ${S}_{K}={{\emptyset}}$, and a full set of zero-error indices, S_E = Ω, leading to the fixed point as ${\{({\epsilon }_{\beta }(\infty ) = 0,{K}_{\beta \beta }(\infty )\ > \ 0)\}}_{\beta \in \Omega }$. Around the fixed point, we can perform the leading-order perturbative analysis from Eq. (17) and obtain

$${\partial }_{t}{\epsilon }_{\alpha }(t)=-\frac{\eta }{N}\sum _{\beta \in \Omega }{K}_{\alpha \beta }(\infty ){\epsilon }_{\beta }(t),$$

(26)

for all indices α, where ${K}_{\alpha \beta }(\infty )\equiv {\angle }_{\alpha \beta }\sqrt{{K}_{\alpha \alpha }(\infty )}\sqrt{{K}_{\beta \beta }(\infty )}$ is the late-time QNTK matrix. As the QNTK matrix is symmetric and positive definite, the linearized equation leads to the exponential convergence of all errors {ϵ_α(t)} at the same rate and subsequently the exponential convergence of the kernels {K_αα(t)} towards the constant non-zero values as

$${\epsilon }_{\alpha }(t),{K}_{\alpha \alpha }(t)-{K}_{\alpha \alpha }(\infty )\propto {e}^{-\eta {w}^{* }t},\forall \alpha \in \Omega ,$$

(27)

where w* is the minimum eigenvalue of QNTK matrix K_αβ(∞). Since all errors vanish exponentially and ${S}_{K}={{\emptyset}}$, this is a generalization of the frozen-kernel dynamics in QNN-based optimization algorithms found in ref. ²⁷.

Now we compare the above theory results with the numerical simulations of QNN training. In Fig. 5 left panels (a1), (b1), and (c1), we provide the numerical results (solid curves) of N = 2 data states with y₁ = 0.3, y₂ = −0.5, and see alignment with our theoretical predictions (dashed curves), where the error exponentially vanishes (b1) while the kernels converge to a nonzero constant (c1). Note that in frozen-kernel dynamics the residual error equals the total error, ϵ_α(t) = ε_α(t), as the errors all converge to ϵ_α(∞) = 0 at late time.

Fig. 5: Exponential convergence class dynamics in QNN with orthogonal data.

From left to right we show the error and QNTK dynamics of frozen-kernel dynamics, frozen-error dynamics and mixed-frozen dynamics. From top to bottom we plot total error ϵ_α(t), residual error ε_α(t) = ϵ_α(t) − ϵ_α(∞), and QNTK K_αβ(t). Subplots in each row share the same legend. Light solid and dark dashed curves with same color represent numerical simulations and corresponding theoretical predictions for each data (see Supplementary Note 4). Subplots in each row share the same legend. Here random Pauli ansatz (RPA) consists of L = 48 variational parameters on n = 4 qubits with $\hat{O}={\hat{\sigma }}_{1}^{z}$, Pauli-Z operator on the first qubit. There are N = 2 orthogonal data states targeted at y₁ = 0.3, y₂ = −0.5 (left), y₁ = 5, y₂ = − 6 (middle) and y₁ = 0.4, y₂ = − 5 (right).

Frozen-error dynamics.— Similar to the frozen-kernel dynamics, in the frozen-error dynamics (Fig. 3b), we have ${S}_{E}={{\emptyset}}$ with the fixed point ${\{({\epsilon }_{\beta }(\infty )\,\ne\, 0,{K}_{\beta \beta }(\infty ) = 0)\}}_{\beta \in \Omega }$. Around the fixed point, leading-order perturbative analyses of Eq. (17) leads to

$${\partial }_{t}\sqrt{{K}_{\alpha \alpha }(t)}=-\frac{\eta }{N}\sum _{\beta \in \Omega }{F}_{\alpha \beta }\sqrt{{K}_{\beta \beta }(t)},$$

(28)

where F_αβ ≡ λ_ααβϵ_β(∞) is a constant matrix with positive eigenvalues at late time. Therefore, the convergence towards the fixed point is again exponential and all quantities have the same convergence rate as

$${\epsilon }_{\alpha }(t)-{\epsilon }_{\alpha }(\infty ),{K}_{\alpha \alpha }(t)\propto {e}^{-\eta {w}^{* }t},\forall \alpha \in \Omega ,$$

(29)

where w* is the minimum eigenvalue of F_αβ. As all kernels vanish exponentially while all errors converge to constant, this is a generalization of the frozen-error dynamics in QNN-based optimization algorithms in ref. ²⁷.

The numerical results are compared with the above theory in Fig. 5 middle panels (a2), (b2) and (c2). The total error ϵ_α(t) converges to a nonzero constant (a2) since the target y₁ = 5, y₂ = − 6 is out of reach from measurement; meanwhile, the residual error ε_α(t) and QNTK K_αβ(t) vanishes exponentially (b2-c2), as predicted by the theory.

Mixed-frozen dynamics.— When both the zero-error indices S_E and zero-kernel indices S_K are not empty (and have no overlap), the fixed point has only the error going to zero or only the kernel going to zero—${\{({\epsilon }_{\beta }(\infty ) = 0,{K}_{\beta \beta }(\infty )\ > \ 0)\}}_{\beta \in {S}_{E}}\cup {\{({\epsilon }_{\beta }(\infty )\,\ne\, 0,{K}_{\beta \beta }(\infty ) = 0)\}}_{\beta \in {S}_{K}}$. This is a combination of fixed points of the frozen-kernel dynamics and frozen-error dynamics, leading to a mixed-frozen dynamics (Fig. 3c). Similar to the previous two types of dynamics, we can perform perturbative analyses from Eq. (17), and obtain the leading-order solution

$${\epsilon }_{\alpha }(t),{K}_{\alpha \alpha }(t)-{K}_{\alpha \alpha }(\infty )\propto {e}^{-\eta {w}^{* }t/N},\forall \alpha \in {S}_{E}$$

(30)

and

$${\epsilon }_{\beta }(t)-{\epsilon }_{\beta }(\infty ),{K}_{\beta \beta }(t)\propto {e}^{-2\eta {w}^{* }t/N},\forall \beta \in {S}_{K}$$

(31)

where w* is a positive constant determined by a matrix in terms of frozen error and kernels, and the corresponding relative dQNTK and geometric angles.

From Fig. 5 right panels (a3), (b3) and (c3), since our measurement is $\hat{O}={\hat{\sigma }}_{1}^{z}$, for α ∈ S_E with ${y}_{\alpha }=0.4\in ({O}_{\min },{O}_{\max })$, we see the error decreases exponentially toward zero (blue in (a3)-(b3)) and its corresponding QNTK K_αα(t) converges to a positive constant (blue in (c3)). For β ∈ S_K with ${y}_{\beta }=-5 < {O}_{\min }$, the total error ends at a positive constant, while the residual error ε_β(t) and QNTK K_ββ(t) decay exponentially (red in (b3)-(c3)). For off-diagonal kernels K_αβ with α ≠ β that can be inferred from Eq. (8), it converges to a positive constant ∀ α, β ∈ S_E, or vanishes exponentially otherwise. An interesting phenomena induced by the interaction between data targeted within different types of dynamics is that the decay exponent of ε_β(t), K_ββ(t), ∀β ∈ S_K is about two times as large as the one from ε_α(t), ∀ α ∈ S_E and K_αβ(t), ∀α ∈ S_E, β ∈ S_K.

Convergence toward fixed points: polynomial convergence class

In this part, we address the cases of overlapping zero-error indices and zero-kernel indices, ${S}_{E}\cap {S}_{K}\ne {{\emptyset}}$, leading to the polynomial convergence class of dynamics, as we indicate in Fig. 3.

Critical point.— The simplest case is the critical point with both sets of indices full, S_E = S_K = Ω, as shown in Fig. 3d. In this case, the fixed point has all errors and kernels vanishing, ${\{({\epsilon }_{\alpha }(\infty ) = 0,{K}_{\alpha \alpha }(\infty ) = 0)\}}_{\alpha \in \Omega }$. From Eqs. (17), we can obtain the leading-order decay of all quantities as

$${\epsilon }_{\alpha }(t),{K}_{\alpha \alpha }(t)\propto 1/t,\forall \alpha \in \Omega .$$

(32)

In Fig. 6 left panels (a1), (b1) and (c1), indeed we see that both error and QNTK decay polynomially as ϵ_α(t), K_αβ(t) ~ 1/t, which can be regarded as a generalization of the critical point identified in QNN-based optimization algorithms from ref. ²⁷.

Fig. 6: Polynomial convergence class dynamics in QNN with orthogonal data.

From left to right we show the error and QNTK dynamics of critical point, critical-frozen-kernel dynamics and critical-frozen-error dynamics. From top to bottom we plot total error ϵ_α(t), residual error ε_α(t) = ϵ_α(t) − ϵ_α(∞), and QNTK K_αβ(t). Light solid and dark dashed curves with same color represent numerical simulations and corresponding theoretical predictions for each data (see Supplementary Note 4). Subplots in each row share the same legend. Here random Pauli ansatz (RPA) consists of L = 48 variational parameters on n = 4 qubits with $\hat{O}={\hat{\sigma }}_{1}^{z}$, the Pauli-Z operator on first qubit. There are N = 2 orthogonal data states targeted at y₁ = 1, y₂ = −1 (left), y₁ = 0.4, y₂ = −1 (middle) and y₁ = 1, y₂ = −5 (right).

Critical-frozen-kernel dynamics.— When the zero-kernel indices form a strict subset of zero-error indices, S_K ⊊ S_E = Ω, we have the critical-frozen-kernel dynamics (Fig. 3e), where the fixed point is a mixture of both quantities vanishing and only the error vanishing—${\{({\epsilon }_{\beta }(\infty ) = 0,{K}_{\beta \beta }(\infty ) = 0)\}}_{\beta \in {S}_{K}}\cup {\{({\epsilon }_{\beta }(\infty ) = 0,{K}_{\beta \beta }(\infty )\ > \ 0)\}}_{\beta \in {S}_{E}\setminus {S}_{K}}$. This is a combination of corresponding fixed points from critical point and frozen-kernel dynamics. Initially without noticeable interactions between data from S_K and S_E⧹S_K, we expect that error and QNTK from each set should vary with time nearly independently following the dynamics from critical point and frozen-kernel dynamics studied above, leading to the fact that $\sqrt{{K}_{\beta \beta }(t)}{\epsilon }_{\beta }(t),\forall \beta \in {S}_{K}$ decays much slower than that with indices ∀β ∈ S_E⧹S_K. Therefore, in late time, we approximate the dynamics of ϵ_α(t), K_αα(t), ∀ α ∈ S_K to be self-governed as a “free-field”, and maintains 1/t decay as in the critical point.

With the solution ∀ β ∈ S_K in hand, we can then perturbatively solve the rest and obtain the overall solution,

$${\epsilon }_{\alpha }(t),{K}_{\alpha \alpha }(t)\propto 1/t,\forall \alpha \in {S}_{K},$$

(33)

and

$${\epsilon }_{\beta }(t)\propto 1/{t}^{3/2},{K}_{\beta \beta }(t)-{K}_{\beta \beta }(\infty )\propto 1/t,\forall \beta \in {S}_{E}\setminus {S}_{K}.$$

(34)

Here S_E⧹S_K = {β∣β ∈ S_E, β ∉ S_K} is the set difference between sets S_E, S_K and K_ββ(∞)’s are the corresponding converged kernel values. The off-diagonal kernels K_αβ for α ≠ β can be determined from Eq. (8), and have the same scaling as corresponding diagonal counterparts if both indices α, β belongs to the same set, S_E⧹S_K or S_K, while $\sim 1/\sqrt{t}$ for α ∈ S_E⧹S_K, β ∈ S_K.

We verify our above theoretical predictions with numerical simulations in Fig. 6 middle panels (a2), (b2) and (c2). The “free-field theory” approach utilized above is valid as the corresponding error and QNTK decays ~1/t (see red curves (a2)-(c2)), just as the critical point. The interaction between data dynamics induces the higher-order polynomial decay of error ~t^−3/2 (blue in (b2)) on data α ∈ S_E⧹S_K at late time. Compared with the frozen-kernel dynamics dynamics, here the corresponding kernel K_ββ(t) for indices β ∈ S_E⧹S_K also converges to a positive constant though at a much slower speed $\sim 1/\sqrt{t}$ affected by the slowest decay from data targeted at the boundary.

Critical-frozen-error dynamics.— Similarly, when the zero-error indices form a strict subset of the zero-kernel indices, S_E ⊊ S_K = Ω, we have the critical-frozen-error dynamics (Fig. 3f) with the fixed point described by ${\{\left(\right.{\epsilon }_{\beta }(\infty ) = 0,{K}_{\beta \beta }(\infty ) = 0\}}_{\beta \in {S}_{E}}\cup {\{({\epsilon }_{\beta }(\infty )\,\ne\, 0,{K}_{\beta \beta }(\infty ) = 0)\}}_{\beta \in {S}_{K}\setminus {S}_{E}}$, just a combination of critical point and frozen-error dynamics. Due to the same reason as in critical-frozen-kernel dynamics discussed above, the late-time dynamics of ϵ_α(t), K_αα(t), ∀ α ∈ S_E are also self-governed as the “free field” and can be satisfied by the polynomial solution ∝ 1/t.

Then the rest of the variables can then be solved asymptotically and lead to the critical-frozen-error dynamics dynamics:

$${\epsilon }_{\alpha }(t),{K}_{\alpha \alpha }(t)\propto 1/t,\forall \alpha \in {S}_{E},$$

(35)

and

$${\epsilon }_{\beta }(t)-{\epsilon }_{\beta }(\infty )\propto 1/{t}^{2},{K}_{\beta \beta }(t)\propto 1/{t}^{3},\forall \beta \in {S}_{K}\setminus {S}_{E}.$$

(36)

The nontrivial off-diagonal terms of K_αβ for α ∈ S_E, β ∈ S_K⧹S_E are given by Eq. (8) and can have scaling of 1/t² at late time.

As shown in Fig. 6 right panels (a3), (b3) and (c3), the error and kernel of data targeted at boundary decays polynomially as ~ 1/t (blue in (a3)-(c3)), on the other hand, the total error of data targeted beyond accessible values still converges to a nonzero constants (red in (a3)), but the residual error ε_β(t), ∀ β ∈ S_K⧹S_E vanishes only at a higher-order polynomial speed of ~ 1/t² (red in (b3)), which is induced by the interaction with data targeted at the boundary, thus much slower compared to the mixed-frozen dynamics.

Critical-mixed-frozen dynamics.— Finally, we consider the most complex case where none of the sets contains the other, S_E ⊄ S_K and S_K ⊄ S_E, and two sets have nonempty overlap ${S}_{E}\cap {S}_{K}\,\ne\, {{\emptyset}}$, which corresponds to the critical-mixed-frozen dynamics (Fig. 3g). This dynamics only takes place for supervised learning with at least N ≥ 3 input quantum data. The fixed point is described by ${\{({\epsilon }_{\beta }(\infty ) = 0,{K}_{\beta \beta }(\infty ) = 0)\}}_{\beta \in {S}_{E}\cap {S}_{K}}\cup {\{({\epsilon }_{\beta }(\infty ) = 0,{K}_{\beta \beta }(\infty )\ > \ 0)\}}_{\beta \in {S}_{E}\setminus ({S}_{E}\cap {S}_{K})}\cup {\{({\epsilon }_{\beta }(\infty )\,\ne\, 0,{K}_{\beta \beta }(\infty ) = 0)\}}_{\beta \in {S}_{K}\setminus ({S}_{E}\cap {S}_{K})}$. Due to the existence of data targeted at the boundary for β ∈ S_E ∩ S_K, we can still solve its corresponding dynamics via the “free-field” approach which brings us the 1/t decay. Then, we can reduce the dynamical equations for the rest of quantities and obtain the leading-order result:

$${\epsilon }_{\alpha }(t),{K}_{\alpha \alpha }(t)\propto 1/t,$$

(37)

for all data ∀ α ∈ S_E ∩ S_K,

$${\epsilon }_{\alpha }(t)\propto 1/{t}^{3/2},{K}_{\alpha \alpha }(t)-{K}_{\alpha \alpha }(\infty )\propto 1/t,$$

(38)

for all data ∀ α ∈ S_E⧹(S_E ∩ S_K), and

$${\epsilon }_{\alpha }(t)-{\epsilon }_{\alpha }(\infty )\propto 1/{t}^{2},{K}_{\alpha \alpha }(t)\propto 1/{t}^{3},$$

(39)

for the rest data ∀ α ∈ S_K⧹(S_E ∩ S_K). The off-diagonal terms of K_αβ for α ≠ β can still be determined from Eq. (8) and for these with index crossing dynamics, it can have scaling of $\sim \!\!1/\sqrt{t}$ for all indices α ∈ S_E⧹(S_E ∩ S_K), β ∈ S_E ∩ S_K, ~1/t^3/2 for all indices α ∈ S_E⧹(S_E ∩ S_K), β ∈ S_K⧹(S_E ∩ S_K) and ~1/t² for all indices α ∈ S_E ∩ S_K, β ∈ S_K⧹(S_E ∩ S_K).

In Fig. 7, we verify our above theory predictions with numerical simulations. The error and kernel of data targeted at the boundary y_α = ±1 decays polynomially as ~1/t (orange in (a1), (a2), (b1)), well captured by the “free-field” approach. Meanwhile, for data targeted within the accessible region, the error decays polynomially with a faster speed at ~1/t^3/2 (green in (a1), (a2)) with kernel approaching a constant (green in (b1)). On the other hand, for data targeted outside the accessible region, the total error can only converge to a nonzero constant (blue in (a1)), however, the residual error ε_α(t) vanishes quadratically ~1/t² (blue in (a2)), and the kernel decays cubically ~1/t³ (blue in (b1)). In addition, the cross-dynamics off-diagonal terms of K_αβ also agree with the theory predictions—polynomial decay with $1/\sqrt{t},1/{t}^{3/2}$ and 1/t² scalings, as shown in (b2).

Fig. 7: Convergence of critical-mixed-frozen dynamics in QNN with orthogonal data.

We plot total error ϵ_α(t) in (a1), residual error ε_α(t) = ϵ_α(t) − ϵ_α(∞) in (a2), and diagonal K_αα(t) and off-diagonal QNTK K_αβ(t) in (b1) and (b2). Light solid and dark dashed curves with same color represent numerical simulations and corresponding theoretical predictions for each data. Here random Pauli ansatz (RPA) consists of L = 48 variational parameters (D = L for RPA) on n = 4 qubits with $\hat{O}={\hat{\sigma }}_{1}^{z}$, the Pauli-Z operator on first qubit. There are N = 3 orthogonal data states targeted at y₁ = 0.4, y₂ = 1, y₃ = − 5.

From the convergence of polynomial convergence class discussed above, we see that as long as there exists a data state targeted at the boundary, either ${O}_{\min }$ or ${O}_{\max }$, the convergence dynamics for all data will be suppressed to polynomial decay though with potential different orders, in contrast to the exponential convergence class. Therefore, our results imply that in quantum machine learning, a proper design of loss function is important to enable fast convergence towards the same QNN configuration.

Ensemble average results

In this section, we provide physical insight and analytical results to resolve the only assumption for deriving the dynamical equations Eq. (17) that the relative dQNTK λ_ααβ approaches a constant at late time. Our results rely on large depth D ≫ 1 (equivalently L ≫ 1), where the converged circuit unitaries optimized from random initialization can be modeled as a specific unitary ensemble, the restricted Haar ensemble.

Under random initialization, the circuit unitary can be represented as a typical sample from Haar random ensemble, as long as the circuit ansatz is universal^4,23,32. However, as the training starts, the circuit unitary quickly deviates from the Haar random unitary to map each of the input data state $\left\vert {\psi }_{\alpha }\right\rangle$ to the corresponding target state $\left\vert {\Phi }_{\alpha }\right\rangle$ due to the constraint imposed by the target value y_α; therefore, we model the converged circuit unitaries as the restricted Haar ensemble in a block-diagonal form

$${{\mathcal{U}}}_{{\rm{RH}}}=\left\{U\left| U=\left(\begin{array}{ll}Q&{\bf{0}}\\ {\bf{0}}&V\end{array}\right)\right.\right\},$$

(40)

where $Q={\oplus }_{\alpha = 1}^{N}{e}^{i{\phi }_{\alpha }}$ is a diagonal matrix with complex phases uniformly distributed ${\phi }_{\alpha } \sim {\mathbb{U}}\left[\left.0,2\pi \right)\right.$ (also known as random diagonal-unitary matrix in ref. ³³) and V is a Haar random unitary of dimension d − N. The rows and columns are represented in basis of input and target states. Specifically, for N ≥ d − 1, the unitary in the restricted Haar ensemble becomes a diagonal matrix with complex phases only; while for N = 1, the ensemble reduces to the restricted Haar unitary considered in QNN-based optimization algorithms²⁷.

We consider the multi-state preparation task as there are less degrees of freedom in the targets to provide insights into the ensemble-average results. As we discussed above, the input data states are orthogonal, $\langle {\psi }_{\alpha }| {\psi }_{\beta }\rangle ={\delta }_{\alpha \beta }$, which can be generated from a random unitary applied on the computational basis. The observable for each data state is a state projector to its corresponding target state ${\hat{O}}_{\alpha }=\left\vert {\Phi }_{\alpha }\right\rangle \left\langle {\Phi }_{\alpha }\right\vert$ with orthogonality $\langle {\Phi }_{\alpha }| {\Phi }_{\beta }\rangle ={\delta }_{\alpha \beta }$. To quantify the evolution of the QNN unitary ensemble, we study the frame potential, a widely utilized tool in quantum information science and quantum chaos²⁸. Here, we choose the second-order frame potential

$${{\mathcal{F}}}_{{\mathcal{U}}}^{(2)}={\int}_{{\mathcal{U}}}{\rm{d}}U\,{\rm{d}}{U}^{{\prime} }| {\rm{tr}}({U}^{\dagger }{U}^{{\prime} }){| }^{4},$$

(41)

as a typical nontrivial measure on the unitary ensemble ${\mathcal{U}}$, and results for higher-order frame potential are presented in Supplementary Note 5. A smaller value of the frame potential indicates a higher level of randomness for an unitary ensemble—the minimum value of the k-th-order frame potential, $\mathop{\min }\limits_{{\mathcal{U}}}{{\mathcal{F}}}_{{\mathcal{U}}}^{(k)}=k!$, is achieved by the Haar random ensemble (more generally the k-design²⁸).

For restricted Haar ensemble, we analytically obtain its frame potential as

$${{\mathcal{F}}}_{{\rm{RH}}}^{(2)}=\left\{\begin{array}{ll}2{N}^{2}+3N+2,\quad &N\le d-2,\\ 2{d}^{2}-d,\quad &N\ge d-1.\end{array}\right.$$

(42)

We see ${{\mathcal{F}}}_{{\rm{RH}}}^{(2)}$ grows quadratically with number of data until saturates at the squared Hilbert space dimension when N ≥ d − 1, which is in sharp contrast to the Haar random ensemble result ${{\mathcal{F}}}_{{\rm{Haar}}}^{(2)}=2$ independent of both system dimension and number of data (additional calculations can be found in Supplementary Note 5). As a sanity check, the N = 0 no data case agrees with the Haar random case. At large N, the frame potential saturates to 2d² − d, limited by the Hilbert space dimension due to orthogonal condition on input data. Such a phenomena can be understood from the reduction in the degree of freedom driven by the increasing number of data. The analytical formula is plot in Fig. 8a as the red dashed curve.

Fig. 8: Second-order frame potential of circuit unitaries of QNNs for multi-state preparation.

In (a) we plot the frame potential of circuit unitaries of QNNs versus number of data states. Red dashed curve and gray solid line show the frame potential of restricted Haar ensemble Eq. (42) and Haar unitary ensemble ${{\mathcal{F}}}_{{\rm{Haar}}}^{(2)}=2$. In (b) we plot the dynamics of ${{\mathcal{F}}}^{(2)}(t)$ in training with targets set in various types of dynamics represented by different colors. The black dashed line represents ${{\mathcal{F}}}_{{\rm{RH}}}^{(2)}=16$. Here in (a) random Pauli ansatz (RPA) consists of L = 128 parameters on n = 3 qubits, and the targets for N orthogonal data states are set within frozen-error dynamics y₁, y₂ > 1. In (b) the RPA consists of L = 64 parameters on n = 2 qubits with N = 2 input orthogonal data states. In both cases, the target states are chosen to be computational basis.

We expect when the converged state is unique, for example in the frozen-error dynamics, the frame potential will converge to the restricted Haar ensemble’s prediction. To provide a quantitative understanding, we show the frame potential from numerical simulation at late-time (blue dots) with various data states and see a good agreement with theory from restricted Haar ensemble (red dashed line) in Fig. 8a. Overall, similar convergence of frame potential can also be found in frozen-error, critical-point and critical-frozen-error, as we show in Fig. 8b. Their deviations from the exact theoretical result (black dashed) are due to finite samples in the ensemble, and slow convergence of unitary in dynamics belonging to polynomial convergence class. For non-unique converged states of dynamics with at least one target value chosen within accessible region ${y}_{\alpha }\in ({O}_{\min },{O}_{\max })$, the frame potential of unitary ensemble ${\mathcal{U}}$ can lie between the values of Haar and restricted Haar ensembles, ${{\mathcal{F}}}_{{\rm{Haar}}}^{(2)} < {{\mathcal{F}}}_{{\mathcal{U}}}^{(2)} < {{\mathcal{F}}}_{{\rm{RH}}}^{(2)}$, due to extra randomness allowed in the unitary, as shown by the green, purple and blue lines in Fig. 8b.

Given the sub-block unitary V forms a 4-design, we have the following results.

Theorem 1

For multi-state preparation task with observable ${\hat{O}}_{\alpha }=\left\vert {\Phi }_{\alpha }\right\rangle \left\langle {\Phi }_{\alpha }\right\vert$ satisfying $\langle {\Phi }_{\alpha }| {\Phi }_{\beta }\rangle ={\delta }_{\alpha \beta }$ with N < d − 1, when the circuit satisfies restricted Haar ensemble and the input data states are orthogonal, the ensemble average of QNTK and relative dQNTK for each data (unified indices) are

$$\overline{{K}_{\alpha \alpha }(\infty )}=\frac{L}{2d}{o}_{\alpha }(1-{o}_{\alpha }),$$

(43)

$$\overline{{\lambda }_{\alpha \alpha \alpha }(\infty )}=-\frac{1}{4d}\left[2(d{o}_{\alpha }-2)+L(2{o}_{\alpha }-1)\right],$$

(44)

at the L ≫ 1, d ≫ 1 limit, where o_α = ϵ_α(∞) + y_α.

Note that the average relative dQNTK are taken to be the ratio of corresponding average quantities, and we expect the change of order of average does not affect the result significantly due to self-averaging. In Fig. 9a, we see a clear dependence of the converged QNTK $\overline{{K}_{11}(\infty )}$ on different target values y₁ while $\overline{{K}_{22}(\infty )}$ remains the same as y₂ is fixed, and both are captured by the restricted Haar ensemble average result in Eq. (43). In Fig. 9b, the converged relative dQNTK $\overline{{\lambda }_{\alpha \alpha \alpha }(\infty )}$ scales linearly with the number of variational parameters in the ansatz, as predicted from Eq. (44). The accurate prediction on other components of interest $\overline{{K}_{\alpha \beta }(\infty )},\overline{{\lambda }_{\alpha \alpha \beta }(\infty )}$ requires more information such as the infidelity between output state and other target states, which we defer to future works.

Fig. 9: Average results under restricted Haar ensemble.

We plot (a) K_αα(∞) versus y₁ with y₂ = 0.5 and L = 256 fixed, (b) λ_ααα(∞) versus L with y₁ = 5, y₂ = 6 fixed. Blue and red dashed lines in (a) represent Eq. (43). Blue and red dashed lines (overlapped) in (b) represent Eq. (44). Here random Pauli ansatz (RPA) consists of L variational parameters on n = 4 qubits. There are N = 2 orthogonal data states and the corresponding target states are computational basis $\left\vert 0000\right\rangle ,\left\vert 0001\right\rangle$.

Experiment

In this section, we validate some of the unique training dynamics in the multi-data scenario on IBM quantum devices. Our experiments are implemented on the hardware IBM Kyiv, an IBM Eagle r3 hardware with 127 qubits, via Pennylane³⁴ and IBM Qiskit³⁵. The device has median T₁ ~ 251.87 us, median T₂ ~ 114.09us, median ECR error ~1.117 × 10⁻², median SX error ~3.097 × 10⁻⁴, and median readout error ~9.000 × 10⁻³. We adopt the QNN with the experimentally friendly hardware-efficient ansatz (HEA), where each layer consists of single-qubit rotations along Y and Z directions, followed by CNOT gates on nearest neighbors in a brickwall pattern⁹. As an example, we choose two different computational bases as the input data states, $\left\vert {\psi }_{1}\right\rangle =\left\vert 01\right\rangle ,\left\vert {\psi }_{2}\right\rangle =\left\vert 10\right\rangle$. Through complete state tomography (see Methods), the initial states are prepared with high fidelity at $\left\langle 01| {\rho }_{1}| 01\right\rangle =0.996\pm 0.0018$ and $\left\langle 10| {\rho }_{2}| 10\right\rangle =0.994\pm 0.0020$ for prepared states ρ₁, ρ₂ (mixed state in general due to hardware noise) averaged over 12 rounds. The high fidelity guarantees the condition of orthogonal data underlying our analyses. We randomly assign initial angles uniformly sampled from [0, 2π) to the parameterized gates in HEA, and maintain consistency across all experiments. For the observable, we consider the Pauli-Z operator of the first qubit, as a simple but sufficient demonstration of our theory.

In Fig. 10, we choose the target values to be (a) y₁ = − 0.3, y₂ = − 3 and (b) y₁ = − 1, y₂ = − 3, corresponding to the mixed-frozen dynamics and critical-frozen-error dynamics, both of which are unique for supervised learning compared to optimization algorithms studied in ref. ²⁷. In both cases, the experimental data (solid) agree well with the ideal simulation results (dashed), indicating the constant error within both dynamics for data targeted at ${y}_{\alpha } < {O}_{\min }$ (pink), the exponential convergence for data with target ${O}_{\min } < {y}_{\alpha } < {O}_{\max }$ (blue in (a)) and polynomial convergence for data with target at ${y}_{\alpha }={O}_{\min }$ (blue in (b)) up to some fluctuations due to shot and hardware noise. To suppress error, we repeat experiments two times for each case.

Fig. 10: Training dynamics of total error ϵ_α(t) on IBM quantum devices, Kyiv.

In (a, b), the target values are chosen to be y₁ = − 0.3, y₂ = − 3 and y₁ = − 1, y₂ = − 3 separately, corresponding to the mixed-frozen dynamics and critical-frozen-error dynamics. Solid light blue and purple curves represent experimental results for ϵ₁(t) and ϵ₂(t), dashed dark blue and pink curves represent corresponding ideal simulation results. An n = 2 qubit D = 6-layer hardware efficient ansatz (with L = 24 parameters) is utilized to minimize loss function with input states $\left\vert {\psi }_{1}\right\rangle =\left\vert 01\right\rangle$, $\left\vert {\psi }_{2}\right\rangle =\left\vert 10\right\rangle$, and the observable is $\hat{O}={\hat{\sigma }}_{1}^{z}$, Pauli-Z operator on the first qubit.

Discussion

Our results go beyond the data-induced barren plateau phenomenon from random initializations in the paradigm of quantum machine learning^36,37, and identify two distinct convergence classes including seven different dynamics in total via analytically solving the convergence of error and kernel of each data. The dynamical transition originating from bifurcation with multi codimensions is driven by the data in supervised learning, suggesting fruitful physics and a new source for dynamical transition in the framework of quantum machine learning. The effect of data is also revealed in the restricted Haar ensemble via its constrained randomness controlled by the number of data. In practical applications, our findings guide the design of the loss function to speedup the training of QNNs.

Our findings also connect to the observation in ref. ³⁸. When the target value is chosen to be ±1 in Pauli measurements, only a polynomial convergence is observed; while a rescaling of the observable, equivalent to shifting the target values within (−1, 1) leads to an exponential convergence though reaching to different solutions, which are fully explained by the critical point and frozen-kernel dynamics in our work. Reference ²² considered supervised learning only in the frozen-kernel dynamics, while the dynamical transition is not uncovered there.

The two convergence classes with seven different dynamics we identified are focused on the orthogonal input data states. For a more general case where input data are allowed to be non-orthogonal, one can expect that the accessible region of the measurement observable and thus the dynamical “phase” diagram will be changed induced by the overlaps among input data states, therefore we leave it as an open question for future study to understand the training dynamics with data correlations. In addition, it is an open problem whether a time-dependent tuning of target values can enhance the overall training of QNNs, given the different convergence dynamics in the time-independent cases considered in this work.

While comparisons between linear loss functions and quadratic loss functions are considered in previous work for optimization tasks²⁷, a linear loss function does not work for classification of more than two classes of data, since linear loss functions push the observable only to boundaries.

Methods

Experimental details

In this section, we provide additional details on our experiment on the IBM Quantum devices. In the experiment, we take 500 shots to estimate the expectation value of the measurement operator, and the learning rate in the experiment is chosen to be η = 0.01. Compared with the theory simulation choice of η = 0.001, we choose a relatively larger learning rate in the experiment to speed up the convergence and to mitigate the effect of noise from experimental imperfections.

We provide the detailed tomography results on the actual states prepared on the quantum devices, and compare it to ideal results. In Fig. 11, we show the deviations of tomography results $| \Delta {\rm{tr}}(\rho P)| =| {\rm{tr}}(\rho P)-\left\langle \psi | P| \psi \right\rangle |$ over all nontrivial Pauli operators P, with ρ being the actual state prepared on the device and $\left\vert \psi \right\rangle$ the ideal state. Each of the Pauli expectation values is measured repeatedly for 12 times. For all Pauli operators, the averaged deviation are less than 0.05 (blue bars) with fluctuations due to hardware drift noise. Overall, the input data states are prepared with high fidelity, thus the overlap between prepared states violating the orthogonal condition can be neglected.

Fig. 11: Deviation of prepared states ρ from corresponding ideal state $\left\vert {\mathbf{\psi}} \right\rangle$ in state tomography.

The deviation is defined as $| \Delta {\rm{tr}}(\rho P)| =| {\rm{tr}}(\rho P)-\left\langle \psi | P| \psi \right\rangle |$. Panels (a) and (b) show deviation for $\left\vert 01\right\rangle$ and $\left\vert 10\right\rangle$ separately. Blue bars show the average deviation over 12 rounds and error bars represent the standard deviation.

Dynamics of QNTK

In this section, we derive the dynamical equation for QNTK matrix. The dynamics of K_αβ(t) can be further evaluated as

$$\delta {K}_{\alpha \beta }(t)=\sum _{\ell }\delta \left(\frac{\partial {\epsilon }_{\alpha }(t)}{\partial {\theta }_{\ell }}\frac{\partial {\epsilon }_{\beta }(t)}{\partial {\theta }_{\ell }}\right)$$

(45)

$$\begin{array}{rcl}&=&\sum _{\ell }\left(\frac{\partial {\epsilon }_{\alpha }(t)}{\partial {\theta }_{\ell }}\delta \left(\frac{\partial {\epsilon }_{\beta }(t)}{\partial {\theta }_{\ell }}\right)+\delta \left(\frac{\partial {\epsilon }_{\alpha }(t)}{\partial {\theta }_{\ell }}\right)\frac{\partial {\epsilon }_{\beta }(t)}{\partial {\theta }_{\ell }}\right.\\ &&\left.+\delta \left(\frac{\partial {\epsilon }_{\alpha }(t)}{\partial {\theta }_{\ell }}\right)\delta \left(\frac{\partial {\epsilon }_{\beta }(t)}{\partial {\theta }_{\ell }}\right)\right).\end{array}$$

(46)

The last term is higher order in η ≪ 1, and we neglect it.

We can evaluate time difference of total error’s gradient via the first-order Taylor expansion

$$\delta \left(\frac{\partial {\epsilon }_{\alpha }(t)}{\partial {\theta }_{\ell }}\right)=\sum _{{\ell }^{{\prime} }}\frac{{\partial }^{2}{\epsilon }_{\alpha }(t)}{\partial {\theta }_{{\ell }^{{\prime} }}\partial {\theta }_{\ell }}\delta {\theta }_{{\ell }^{{\prime} }}(t)$$

(47)

$$=-\frac{\eta }{N}\sum _{\beta }{\epsilon }_{\beta }(t)\sum _{{\ell }^{{\prime} }}\frac{\partial {\epsilon }_{\beta }(t)}{\partial {\theta }_{{\ell }^{{\prime} }}}\frac{{\partial }^{2}{\epsilon }_{\alpha }(t)}{\partial {\theta }_{{\ell }^{{\prime} }}\partial {\theta }_{\ell }}$$

(48)

$$=-\frac{\eta }{N}\sum _{\beta }\sum _{{\ell }^{{\prime} }}{H}_{\alpha \ell {\ell }^{{\prime} }}(t){J}_{\beta {\ell }^{{\prime} }}(t){\epsilon }_{\beta }(t),$$

(49)

where we apply gradient descent rule Eq. (4) in the second line, and we introduce the Hessian of total error ${H}_{\alpha \ell {\ell }^{{\prime} }}(t)=\frac{{\partial }^{2}{\epsilon }_{\alpha }(t)}{\partial {\theta }_{\ell }\partial {\theta }_{\ell }^{{\prime} }}$. J_αℓ(t) = ∂ϵ_α/∂θ_ℓ is the gradient of total error as we introduced in the main text. Thus the time difference of K_αβ(t) in Eq. (46) becomes

$$\delta {K}_{\alpha \beta }(t)=\sum _{\ell }\left[\frac{\partial {\epsilon }_{\alpha }}{\partial {\theta }_{\ell }}\delta \left(\frac{\partial {\epsilon }_{\beta }}{\partial {\theta }_{\ell }}\right)+\delta \left(\frac{\partial {\epsilon }_{\alpha }}{\partial {\theta }_{\ell }}\right)\frac{\partial {\epsilon }_{\beta }}{\partial {\theta }_{\ell }}\right]+{\mathcal{O}}({\eta }^{2})$$

(50)

$$=-\frac{\eta }{N}\sum _{\gamma }\sum _{{\ell }^{{\prime} },\ell }\left[{J}_{\alpha \ell }{H}_{\beta \ell {\ell }^{{\prime} }}{J}_{\gamma {\ell }^{{\prime} }}{\epsilon }_{\gamma }+{\epsilon }_{\gamma }{J}_{\gamma {\ell }^{{\prime} }}{H}_{\alpha {\ell }^{{\prime} }\ell }{J}_{\beta \ell }\right]$$

(51)

$$=-\frac{\eta }{N}\sum _{\gamma }{\epsilon }_{\gamma }(t)\left({\mu }_{\gamma \beta \alpha }(t)+{\mu }_{\gamma \alpha \beta }(t)\right),$$

(52)

where ${\mu }_{\gamma \alpha \beta }\equiv \sum _{\ell ,{\ell }^{{\prime} }}{J}_{\gamma {\ell }^{{\prime} }}{H}_{\alpha {\ell }^{{\prime} }\ell }{J}_{\beta \ell }$ is the dQNTK we defined in Eq. (10). Therefore, the above equation is the exact dynamical equation presented in Eq. (9).

Stability transition of fixed points

In this section, we present additional details on the stability transition of fixed points by tuning the fixed-point charges ${\{{C}_{\beta }\}}_{\beta }$ defined in Eq. (20). Starting from the linearized equation Eq. (23) in the main text, the matrix Eq. (24) can be explicitly written out for the two data case as

$$M({\boldsymbol{g}},{\boldsymbol{C}})=\left(\begin{array}{ll}{C}_{1}-3{g}_{1}^{2}&{z}_{12}\left({C}_{2}-3{g}_{2}^{2}\right)\\ {z}_{21}\left({C}_{1}-3{g}_{1}^{2}\right)&{C}_{2}-3{g}_{2}^{2}\end{array}\right),$$

(53)

where for simplicity we define

$${g}_{\alpha }(t)\equiv \sqrt{{K}_{\alpha \alpha }(t)},$$

(54)

$${z}_{\alpha \beta }\equiv \frac{{\lambda }_{\alpha \alpha \beta }}{{\lambda }_{\beta \beta \beta }},$$

(55)

Its eigenvalue can be solved as

$${\nu }_{\pm }=\frac{{\rm{tr}}(M)\pm \sqrt{{\rm{tr}}{(M)}^{2}-4\det (M)}}{2}.$$

(56)

Therefore, the stability of any fixed point can be fully characterized by the trace and determinant of M as $({\rm{tr}}(M),\det (M))$. Both terms are functions of the fixed-point charges C₁, C₂ as

$$\left\{\begin{array}{l}{\rm{tr}}(M)={C}_{1}+{C}_{2}-3({g}_{1}^{2}+{g}_{2}^{2}),\\ \det (M)=\left({C}_{1}-3{g}_{1}^{2}\right)\left({C}_{2}-3{g}_{2}^{2}\right)\left(1-{z}_{12}{z}_{21}\right),\end{array}\right.$$

(57)

which is exactly what we see in Eq. (25) in the main text with typical z₁₂z₂₁ < 1. One can thus determine whether a fixed point is a stable one (‘sink’), unstable one (‘source’) or a saddle point from the signs of the ${\rm{tr}}(M)$ and $\det (M)$:

• When $\det (M) < 0$, we always have ν₋ < 0 and ν₊ > 0, indicating the fixed point to be a saddle point;

• If $\det (M)=0$ and ${\rm{tr}}(M) < 0$, the eigenvalues become ${\nu }_{-}={\rm{tr}}(M) < 0$ and ν₊ = 0, we have a line of stable fixed point as one of the degree of freedoms vanishes;

• When $\det (M) > 0$ and ${\rm{tr}}(M) < 0$, the real part of ν_± is negative and leads to the stable fixed point, identified as ‘sink’. Precisely speaking, for ${{\rm{tr}}}(M)^2 \gtreqless 0$ inducing either two different real eigenvalues, a single identical real eigenvalue, or two complex conjugate eigenvalues, the sink can be classified to be a regular sink, degenerate sink and spiral sink;

• For $\det (M)\ge 0$ and ${\rm{tr}}(M) > 0$, the fixed point can be classified in a similar way, leading to the ‘source’ and line of unstable fixed point.

Therefore, for any fixed point g*, we can identify its stability given arbitrary values of fixed-point charges C₁, C₂, as shown in Fig. 12. On the other hand, the shift of charges would induce a stability transition for every fixed point.

Fig. 12: Stability of each fixed point.

The fixed point can be classified as a sink (green), a saddle point (blue) or a source (red) depending on the values of C₁, C₂. The brown and pink colored axis represent the fixed point to be a line of unstable/stable fixed point. The gray-shaded regions indicate that the fixed point cannot be physically accessed under the current choice of C₁ and C₂.

At the end of this section, we connect the above stability analyses on the fixed point to QNN training. For a data with index α ∈ S_E⧹(S_E ∩ S_K), we can directly see that C_α > 0, on the other hand for α ∈ S_K⧹(S_E ∩ S_K), the quantity becomes C_α < 0. Specifically when α ∈ S_E ∩ S_K, C_α = 0. In Fig. 13, we plot the Poincaré diagram for different physically accessible fixed points within different dynamics. The only stable fixed points are those with ${\rm{tr}}(M)\le 0$ and $\det (M)\ge 0$ living in the second quadrant. The dashed curve in each figure represents the equation ${\rm{tr}}{(M)}^{2}-4\det (M)=0$ which determines the imaginary part of eigenvalues from Eq. (56) leading to the property of degeneracy and spiral. Here we see that from different initializations, the fine dynamical property of fixed points within each dynamics could be different, which leaves us an interesting open question beyond the scope of our work. Overall, the only stable fixed point within each dynamics aligns with our classification via S_E, S_K in the main text.

Fig. 13: Poincaré diagram of fixed points for QNN dynamics with two data.

The top and bottom panels show exponential and polynomial convergence classes with frozen-kernel, frozen-error, mixed-frozen (a–c) and critical point, critical-frozen-kernel, critical-frozen-error (d–f). Colored dots represent different physically accessible fixed points with different initialization of training parameters. Black horizontal and vertical dashed lines indicate $\det (M)=0$ and ${\rm{tr}}(M)=0$ for reference. Gray dashed curve shows ${\rm{tr}}{(M)}^{2}=4\det (M)$, a criteria to determine whether there exists a spiral surrounding the fixed point. All settings are the same as in Fig. 2.