Introduction

A major recent effort in the field of quantum materials is to engineer systems where topological fermion physics is realized in the regime of strong electron correlations. This effort has largely been explored in creating mini flat bands in twisted bilayer graphene1,2 and transition metal dichalcogenides3,4, topologically protected band crossings with correlation-driven narrow bandwidth in Weyl-Kondo systems5,6, and the coexistence of Dirac crossings and flat bands in geometrically frustrated systems7,8,9,10,11,12,13. Flat bands in momentum space correspond to localized states in real space, where the quenched kinetic energy of electrons is negligible in comparison to the Coulomb interactions. In such a regime, many-body effects can lead to emergent phases such as magnetism, density waves, nematicity, and superconductivity2,14,15,16,17,18,19,20. Arguably the system with the most abundant material platforms realized amongst these efforts so far are the kagome lattice compounds21,22,23,24,25,26,27. Consisting of corner-sharing triangles, the two-dimensional (2D) kagome lattice has been well-known as one of the most promising candidates for hosting quantum spin liquid states arising from the extensively degenerate magnetic ground states due to the lattice geometry-induced magnetic frustration28. Analogously, fermionic models on kagome lattices have also predicted the existence of electronic flat bands arising from a geometry-induced destructive interference of the electronic wavefunction7,8,9,10. In addition, Dirac fermions are expected to be found in the electronic structure, resembling the situation in graphene29. However, theoretical models for kagome lattices are largely 2D. In real material systems recently realized, kagome lattices are stacked in the bulk crystal structure where interlayer coupling is finite, giving rise to non-negligible dispersion along the kz direction, where the bandwidth of the flat bands could be on the order of hundreds of meV30,31.

Pyrochlore lattice, made of corner-sharing tetrahedrons, can be considered as a three dimensional (3D) analog of the kagome lattice, where geometric frustration is naturally realized in 3D (Fig. 1b). Similarly, pyrochlore crystals have been proposed and widely studied as candidates to host quantum spin liquid states from the 3D magnetic frustration in the past32,33,34,35,36,37. In the fermionic models, the same geometric frustration has been theoretically predicted to lead to bands that are flat along every direction in the 3D momentum space due to quantum destructive interference38,39. Meanwhile, previous theory studies have also predicted four-fold degenerated Dirac point at the high symmetry point of the Brillouin zone in the pyrochlore lattice, which, with further reduced symmetry, could evolve into Weyl points or gapped Dirac point40,41,42. The Dirac point is protected by the crystalline nonsymmorphic symmetry and fundamentally different from the previously observed Dirac cones induced by band inversions43,44,45. However, there exists no direct experimental observation of either the destructive interference-induced flat band or the nonsymmorphic symmetry-protected Dirac point in the pyrochlore lattice compound.

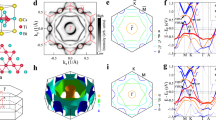
Fig. 1: Crystal structure, destructive interference and tight-binding model.
figure 1

a Crystal structure of CeRu2 shown in the conventional unit cell. b Ru atoms form the pyrochlore lattice, where ai are the lattice translation vectors within the faces of the cube. c Magnetization and d resistivity measurements showing superconductivity at 5.1 K. FC means field cooling and ZFC means zero field cooling. e Brillouin zone (BZ) with the high symmetry points labeled. We define kx, ky and kz here with respect to the (111) surface for the convenience of experimental description. f Four-band tight-binding model of the pyrochlore lattice without considering spin-orbit coupling (SOC), where the flat band is doubly-degenerate. g Tight-binding model including SOC. h Mechanism for 3D destructive interference on the pyrochlore lattice. The sites marked by magenta circles have zero Wannier amplitude and do not produce inter-kagome-plane hopping and hence do not detract from the flatness of the bands. i Density functional theory (DFT) calculations with projection onto different atoms. The black dashed rectangle marks out the Dirac points at the X point of the BZ. j Partial density of states (DOS) of the Ce-f and Ru-d orbitals.

Full size image

In this study, through a combination of angle-resolved photoemission spectroscopy (ARPES), theoretical modeling, and density functional theory (DFT) calculations, we report the electronic structure of a Laves phase superconductor, CeRu2, that possesses a Ru pyrochlore sublattice. In addition to dispersionless electronic states originating from strongly correlated Ce 4f states, we observe portions of flat bands of Ru 4d orbitals that are attributed to the 3D destructive interference inherent in the pyrochlore structure. The flat bands are actually partially flat in the momentum space due to strong hybridization with the Ce 4f orbitals, but still contribute to a large peak in the electronic density of states (DOS). In addition, we also observe 3D gapless Dirac crossing protected by the nonsymmorphic symmetry of the pyrochlore structure. Our results establish the metallic pyrochlore systems to be a new platform for hosting the rich phenomenology of correlated topology.

Results

While studies of insulating pyrochlores are abundant in the context of quantum spin liquids, limited ARPES studies of metallic pyrochlores are reported due to the challenge in cleaving the 3D crystals46,47,48. The recent improvement of beamspot focusing has enabled exploration of a wider range of 3D materials. Here we identify CeRu2 as an ideal candidate to explore the pyrochlore lattice as a platform for realizing correlated topology. The crystal structure of CeRu2 is that of the Laves phase in space group 227 (\({\rm{Fd}}\overline{3}{\rm{m}}\)) (Fig. 1a)49. The Ce atoms form a diamond sublattice (Wyckoff position 8 (a)) while the Ru atoms form the pyrochlore sublattice (Wyckoff position 16 (d)) as shown in Fig. 1b.

CeRu2 was first discovered in the search for magnetic superconductors over six decades ago50. It has a superconducting transition temperature around 5 K (Fig. 1c, d). Previous angle-integrated photoemission spectroscopy measurements have revealed an s-wave superconducting gap51. Recent high pressure work shows superconductivity to persist up to at least 168 GPa, with an appearance of a secondary superconducting transition onsetting at 30 GPa52. The superconducting state is unusual, marked by a secondary magnetic hysteresis loop, which originally led to interpretation of reentrant superconductivity but later understood to be due to a Fulde-Ferrell-Larkin-Ovchinnikov state52. Evidence for weak magnetism has also been suggested by Muon spin rotation (μSR) experiments in zero magnetic field53,54. There is, however, no corresponding magnetic transition in macroscopic magnetic susceptibility measurements (see Supplementary Note 1 and Supplementary Fig. 1). Polarized neutron scattering has found field-induced paramagnetic moment on the order of 10−4μBT−1 interpreted to be equally distributed on both the Ce and Ru sites55. Further clarification, however, is needed on the origin of magnetism in CeRu2. Interestingly, previous photoemission measurements of CeRu2 have identified two peak structures near the Fermi level in the integrated density of states, interpreted as originating from strongly correlated Ce 4f-electron states56,57,58. However, no momentum-resolved measurement of the electronic structure has been reported.

Tight-binding model

Before we present our ARPES experimental observation, to understand the salient features of the electronic structure of a pyrochlore lattice, we present calculations from a tight-binding model (see Methods for details), the results of which are consistent with previous studies59,60. First in the absence of spin-orbit coupling (SOC), the nearest-neighbor hopping yields four bands that include a pair of exactly flat degenerate bands, a Dirac nodal line between the X and W points in the Brillouin zone (BZ), and a triple point fermionic crossing at the Γ point (see Fig. 1f). Here we note that the pyrochlore lattice is the line-graph lattice of the diamond lattice. Hence the flat bands here are characteristics of the line-graph nature of the pyrochlore lattice61. To understand the origin of the flat bands more intuitively, we look at two cut planes of the pyrochlore lattice, each of which is a 2D kagome plane formed by the Ru atoms (Fig. 1h). These kagome planes can be thought of as the origin of the degenerate pair of flat bands. To see this clearly, we write the normalized eigenstates of the two degenerate flat bands projected onto the four sublattices as

$${{\bf{v}}}_{1}({k}_{x},{k}_{y},{k}_{z})=\frac{1}{\sqrt{{N}_{1}}}\left(\begin{array}{c}{s}_{{k}_{x}-{k}_{z}},{s}_{{k}_{y}+{k}_{z}},0,-{s}_{{k}_{x}+{k}_{y}}\end{array}\right)$$
(1)
$${{\bf{v}}}_{2}({k}_{x},{k}_{y},{k}_{z})=\frac{1}{\sqrt{{N}_{2}}}\left(\begin{array}{c}{s}_{{k}_{y}-{k}_{z}},{s}_{{k}_{x}+{k}_{z}},-{s}_{{k}_{x}+{k}_{y}},0\end{array}\right)$$
(2)

where the normalization factors are \({N}_{1}={s}_{{k}_{x}-{k}_{z}}^{2}+{s}_{{k}_{y}+{k}_{z}}^{2}+{s}_{{k}_{x}+{k}_{y}}^{2}\) and \({N}_{2}={s}_{{k}_{y}-{k}_{z}}^{2}+{s}_{{k}_{x}+{k}_{z}}^{2}+{s}_{{k}_{x}+{k}_{y}}^{2}\) with the definition \({s}_{{k}_{i}\pm {k}_{j}}\equiv \sin ({k}_{i}\pm {k}_{j})\). The Wannier orbitals associated with the two degenerate eigenstates (Eqs. 1, 2) are shown in Fig. 1h, obtained by Fourier transforming the two equations (unnormalized). In the chosen basis, it is clear from the structure of Eqs. 1, 2 how each of the two Wannier orbitals decomposes the pyrochlore lattice into decoupled parallel kagome planes – the eigenvector v1(v2) has zero Wannier amplitude in the third (fourth) sublattice component and v1 and v2 are linearly independent. This effectively ‘disconnects’ the pyrochlore lattice into 2D kagome planes along two distinct directions as the out-of-plane Wannier amplitudes at all sites connecting the parallel kagome planes are identically zero. Within each kagome plane, the flat band arises from a destructive interference of the remaining three sinusoidal Wannier amplitudes in Eqs. 1, 2, with phase factors alternating in sign on the 2D kagome hexagon (see Fig. 1h). Thus the mechanism for flat band formation in the 3D pyrochlore lattice can be mapped to that of (two copies of) the 2D kagome problem.

With the incorporation of SOC (Fig. 1g), the triply-degenerate point at Γ will be lowered to form a singly-degenerate point and a doubly-degenerate quadratic band touching node. Whether or not the latter involves the dispersive bands depends on the sign of the SOC, λ. For a negative value of λ, the doubly-degenerate subspace is formed entirely by the two flat bands, whereas for a positive value of λ, it involves one of each of the dispersive and flat bands. More interestingly, The double degeneracy along X–W will be lifted with only the degeneracy remaining at the X point to form a 3D Dirac point. This was the first proposed 3D Dirac point protected by nonsymmorphic symmetry but has never yet been observed experimentally40,41. In the following sections, we will present the unambiguous observation of the two signatures of the pyrochlore lattice that establishes it as a topological geometrically frustrated metal – the destructive interference-induced flat bands and the nonsymmorphic symmetry-protected Dirac cones.

Electronic structure and Ce 4f flat bands

We first present the overall measured band structure of CeRu2. In Fig. 2a, b we present the in-plane and out-of-plane Fermi surface mappings of the CeRu2 single crystal with respect to the (111) cleaved surface, respectively. The corresponding BZs are also overlaid for reference. The in-plane Fermi surface mapping (Fig. 2a) shows a mirror symmetry about the vertical axis. The three-fold rotational symmetry of the (111) surface can be seen in the three point-like spots within the BZ. The out-of-plane mapping is carried out via a photon-energy dependence measurement of the cut shown in the inset of Fig. 2b. To gain more insights into the band dispersions, we show the energy-momentum spectrum measured with 47 eV photons (Fig. 2c, d), which corresponds to the L – Γ – L direction as indicated in Fig. 2b. The band dispersions by DFT calculations along this high symmetry direction are overlaid in Fig. 2g, h for comparison. We note that we do not see any evidence for magnetic band splitting within our experimental resolutions at temperatures below 40 K (see Supplementary Note 3 and Supplementary Fig. 5) and therefore we compare our data with the results of nonmagnetic calculations exclusively (see Supplementary Figs. 3 and 4 for comparison of nonmagnetic and magnetic calculations). Several dispersive hole bands are observed near EF centered at the Γ point, which are reproduced by the DFT calculations. We note that the photoemission matrix elements along the cut shown here are not symmetric about the Γ point as the cut does not go through normal emission. The less dispersive bands near -2.5 eV in the data are also nicely captured by the calculations with a renormalization factor of 1.2. In general, the ARPES data and the DFT calculations exhibit a good consistency.

Fig. 2: Electronic structure and Ce 4f flat bands.
figure 2

a In-plane Fermi surface mapping of CeRu2 with respect to the (111) cleavage surface using 80 eV photons. b Out-of-plane Fermi surface mapping using photon energies from 40 eV to 200 eV. Inner potential is 22 V. c Spectral image measured with 47 eV photons along the momentum path indicated in (a). LH indicates linear horizontal polarization. d Spectral image for a zoomed-in energy range of (c) but with linear vertical (LV) light polarization. e Spectral image measured with 120 eV photons showing two flat bands close to EF, which correspond to the Ce 4\({f}_{5/2}^{1}\) and 4\({f}_{7/2}^{1}\) states. The momentum path is indicated in (a). f Energy distribution curve (EDC) stacks of spectral image (e). The blue EDCs correspond to the momentum positions indicated by the white dashed lines in (e). g, h Same as (c, d) but with the corresponding DFT calculations overlaid. The color and line thickness indicate the spectral weight of the different atoms. The DFT calculations are renormalized by a factor of 1.2.

Full size image

In the Ce-based materials, a common characteristic of the electronic structure is the presence of two flat features. One is the Kondo resonance state (4\({f}_{5/2}^{1}\)) located at the Fermi level62, and the other is its spin-orbit sideband (4\({f}_{7/2}^{1}\)) below EF, unresolved in the earliest studies62. DFT calculations have been shown to be unable to accurately reproduce these two flat bands63,64. In Fig. 2e, we plot the spectral image measured with 120 eV photons (Ce 4d → 4f resonance) under linear horizontal polarization. The corresponding momentum path is illustrated in Fig. 2b. Here, two flat bands are discernible, with one near the Fermi level and one at around −0.25 eV. These two flat bands are also evident in the peaks in the energy distribution curve (EDC) stacks (Fig. 2f). They correspond to the Ce 4\({f}_{5/2}^{1}\) and 4\({f}_{7/2}^{1}\) states (detailed photon energy-dependent measurements across the resonance energies of the Ce 4f states are shown in Supplementary Figs. 6 and 7), which were also observed as two peaks in the previous angle-integrated photoemission reports56,58. The spectra of Ce 4f flat bands observed here have a substantial surface component due to the short photoelectron mean free path associated with the utilized photon energy (120 eV)56,58. The presence of these Ce 4f states poses a challenge for observing flat bands induced by destructive interference of the Ru sublattice. In the following, to unambiguously reveal the flat bands originating from the pyrochlore lattice, we first identify the corresponding destructive-interference-induced flat bands from the calculations, and then demonstrate their existence via ARPES measurements using a photon energy where the Ce 4f spectral intensity is suppressed (see also Supplementary Note 4 and Supplementary Fig. 7)63,64.

Observation of flat bands induced by destructive interference

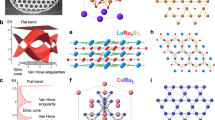
To identify the bands in CeRu2 originating from the destructive interference of the pyrochlore structure, we performed a series of systematic band structure calculations on Ru2, LaRu2, and finally CeRu2 (Fig. 3a–d). All the band calculations can be qualitatively traced back to the tight-binding calculation of the pyrochlore lattice, despite consisting of multiple orbitals, allowing us to track the flat bands originating from the 3D destructive interference (Supplementary Note 5 and Supplementary Fig. 8). First, we examine the band structure of the artificial bare Ru2 structure, which is obtained by removing all Ce atoms from CeRu2, resulting in a Ru2-only pyrochlore lattice (inset in Fig. 3a). The pyrochlore flat bands are most distinctly visible for the Ru2-only pyrochlore lattice (shaded region in Fig. 3a), positioned just above EF with Ru 4d orbital character. The 3D pyrochlore flat bands are observed to slightly deviate from the simple tight-binding model of an extremely flat band extending throughout the entire BZ due to strong hybridization with a dispersive band along Γ–X. To see how these flat bands evolve ultimately to those in CeRu2, we next calculate the band structure of LaRu2, which is isostructural to CeRu2 but with no f-electrons near EF(Fig. 3b). This is followed by CeRu2 without SOC (Fig. 3c), and then SOC is finally added (Fig. 3d). We track the evolution of the Ru d-originated flat bands by showing the side by side comparison of the band calculations projected on the Ru-d orbitals along this series of calculations. Two main effects are evident. First, a downward shift of the Ru-d orbital bands can be seen, which can be attributed to the La/Ce sites acting as electron donors to Ru sites. Second, the strong hybridization of the Ru electronic states and the La/Ce electronic states further widens the bandwidth of the flat bands and results in a more restricted k-space range of the flat bands. Consequently, with the inclusion of SOC, we identify the flat bands in the band calculations of CeRu2 to be mainly located around −0.6 eV with a much broadened band dispersion (shaded region in Fig. 3d). Despite the finite bandwidth, these bands can still exhibit significant flatness along specific directions in momentum space. We note that part of the flat band is segmented into a flat portion within a small k-region around the Γ point (blue arrow in Fig. 3d). A complementary view of the energy shift and broadening effect of the flat band dispersion is provided by a comparison plot of the Ru-d partial DOS in Fig. 3e. The presence of a similar Ce 4f DOS peak, also at -0.6 eV, provides evidence for the strong hybridization of the Ce 4f states with the Ru 4d flat band states.

Fig. 3: Flat bands by destructive interference.
figure 3

a–d Comparison of valence band electronic structure for the (a) Ru2 pyrochlore lattice only, (b) LaRu2, (c) CeRu2 and (d) CeRu2 including spin-orbit coupling (SOC). The CeRu2 lattice constant (a = 7.53 Å) is used for all structures. Symbol size reflects combined Ru \({d}_{{z}^{2}}\) + dxy + \({d}_{{x}^{2}-{y}^{2}}\) orbital character, and the shaded rectangles indicate the bands originating from the destructive-interference-induced flat bands. e Comparison of k-integrated Ru-d density of states illustrating the relative energy shift and dispersion broadening of the flat bands (FBs). The Ce 4f DOS, primarily above EF, also exhibits a similar hybridization peak at −0.6 eV coincident with Ru-d DOS peak. f Side view of the BZ, with cut positions marked. g Spectral image along L – Γ – L measured with 47 eV photons. The momentum path is indicated in (f). h EDC stacks of (g) showing the Ce 4\({f}_{7/2}^{1}\) state and flat band induced by destructive interference. i Spectral image and corresponding integrated EDC (−0.2 ~ 0.2 Å) measured with 21.2 eV photons. One sharp flat band is revealed. The corresponding momentum path is indicated in (f).

Full size image

Having theoretically identified the pyrochlore flat bands in CeRu2, we now present the ARPES data. To minimize spectral intensity from Ce 4f orbitals, we utilize photons with energy lower than the Ce 4d → 4f resonance of 120 eV. We present a spectral image along L–Γ–L in the near-EF region measured using a linear vertical polarization at 47 eV (Fig. 3g). Several hole-like dispersive bands are resolved, consistent with predictions from the DFT calculations (Figs. 3d,2g). In addition, we observe almost nondispersive features around −0.25 eV and −0.5 eV, which are also revealed distinctly by the corresponding EDC stacks (Fig. 3h). The flat band at -0.25 eV was identified as the Ce 4\({f}_{7/2}^{1}\) states, with the intensity strongly suppressed. The flat feature at around −0.5 eV has no other correspondence but aligns with the pyrochlore flat bands predicted by the DFT calculations at around −0.6 eV (Fig. 3d). We note that the DOS peak at around −0.5 eV in CeRu2 has been previously reported in angle-integrated photoemission measurements, correlated to the −0.5 eV peaks in experimental off-resonance (Ru-d) spectra57,65, and in Ce 3d → 4f resonance spectra65. Our results unequivocally establish that the pyrochlore flat bands are the underlying origin of the theoretical and experimental DOS peaks in CeRu2. Furthermore, the flat band segment at −0.16 eV in the calculation around the BZ center (Fig. 3d) is observed with a helium lamp using 21.2 eV photons (Fig. 3i), where the two Ce 4f states in the low energy are completely absent due to a low Ce 4f cross section that is known for this photon energy66. This flat band segment is observed at −0.11 eV and corresponds to a very sharp peak in the integrated EDC (Fig. 3i), which is reasonably consistent with the DFT calculations when considering a band renormalization factor of 1.2 (−0.133 eV). It can be brought even closer to the Fermi level with hole doping in CeRu2. However, we cannot exclude the possibility that this flat band segment is a surface state, which originates from the isolated Ru kagome surface layer out of its bulk pyrochlore lattice. Further studies, such as slab calculations, would help to clarify this. Taking all the measurements and band calculations together, we have successfully identified evidence of the flat bands originating from the destructive interference of the Ru pyrochlore sublattice in CeRu2.

Observation of 3D Dirac cones

Next, we explore the nontrivial band topology of CeRu2. The space group of CeRu2 is \({\rm{Fd}}\overline{3}{\rm{m}}\), from which the first Dirac semimetal and Weyl semimetal were theoretically proposed40,41,42. The crystal structures that belong to this space group include diamond lattice, pyrochlore lattice, β-cristobalite and spinel oxides. The same reasoning applies to the protection of the Dirac point at X for these compounds, in which the nonsymmorphic symmetries play an essential role. Specifically, for the pyrochlore lattice, the combination of two nonsymmorphic operations {I∣t0}, {C4x∣t0} and one symmorphic operation {C2z∣0} protects the Dirac point at X. Here I is the inversion operation, C4x is the four-fold rotation about the x-axis, C2z is the two-fold rotation about the z-axis, and the center of all the symmetry operations is the center of any tetrahedron. t0 is a non-Bravais translation along the diagonal direction (Fig. 4a)67. The pyrochlore lattice is in analogy to the well-studied diamond lattice. The diamond lattice can be simply viewed as formed by the centers of the tetrahedra of the pyrochlore lattice (Fig. 4b). One particular nonsymmorphic symmetry of the diamond lattice (Fig. 4c)68 is the screw axis {C4z∣tc/4}, where C4z is the four-fold rotation around axis z and tc/4 is a quarter translation along c. All the lattices that belong to space group \({\rm{Fd}}\overline{3}{\rm{m}}\) carry four dimensional irreducible representations at the X point of the BZ41,69. As a result, the four bands are degenerate at the X point and disperse linearly along all directions around X, forming a 3D Dirac cone. It is important to point out that, the nonsymmorphic symmetry here dictates that all band crossings at the X point, regardless of their energy or orbital character, are gapless 3D Dirac cones (see also Supplementary Note 6 and Supplementary Fig. 9 for DFT calculation projected unto different orbitals). We also note that comparing Fig. 3c, d the effect of the SOC is to split the Dirac nodal lines along X–W, as captured by the tight-binding model. When time-reversal symmetry is broken, the Dirac point will split into two Weyl points42. This Dirac point at the BZ high symmetry point protected by nonsymmorphic symmetry (Fig. 4c) is fundamentally different from the previously observed Dirac cones induced by band inversions43,44,45 and has never yet been observed.

Fig. 4: Three-dimensional Dirac cones.
figure 4

a Pyrochlore lattice and the nonsymmorphic symmetry operation {I∣t0}, where I is inversion with respect to the tetrahedron center (red circle), t0 is the fractional translation along the diagonal. The arrows connecting two atoms indicate the corresponding atom translation under the operation. b The centers of the tetrahedra in the pyrochlore lattice form a diamond lattice. c The diamond lattice with marked screw axis demonstrating the nonsymmorphic symmetry protecting the Dirac crossings at X. d Spectral image measured with 68 eV photons corresponding to the L–X direction as shown in (e). The overlaid blue dashed lines are guidelines for the Dirac point (DP). e Side view of the BZ, with cuts marked. f Left panel: spectral image measured with 90 eV photons along cut1. The overlaid blue dashed lines are guidelines for the Dirac crossing. Right panel: second energy derivative of the corresponding spectral image. g Second energy derivative of spectral image in (d). DP is labeled by the red arrow. h DFT calculations of the bands along L–X–L. The black dots indicate all band crossings at X are four-fold degenerate. The corresponding Dirac dispersions observed in experiments are indicated by the blue arrow, intersected by another Dirac point situated very close to it, formed by two weakly dispersive bands. i EDC stacks of (d) between the momentum range from kx = 1.7 Å−1 to kx = 2.3 Å−1. j Momentum distribution curve (MDC) stacks of (d) between the energy range from −2.1 eV to −1 eV. The green circles trace out the Dirac dispersions, which are obtained by fitting the peaks. The horizontal bars indicate the fitting errors.

Full size image

Here we present the evidence for the 3D Dirac cone structure through ARPES in CeRu2. In Fig. 4d we plot the band image measured with 68 eV photons which corresponds to the L – X momentum path as indicated in Fig. 4e. We can observe two bands that cross at the X point to form a Dirac point (DP) at −1.7 eV. The Dirac point can be better visualized through the second energy derivative spectral image shown in Fig. 4g, as well as by tracing the peaks in the EDC and momentum distribution curve (MDC) stacks (Fig. 4i, j). From the DFT calculations shown in Fig. 4h, we can also confirm that all band crossings at the X point, regardless of their energies, are indeed four-fold degenerate. Moreover, we can identify the Dirac crossing that corresponds to our measured observable Dirac crossing at similar energies after considering band renormalization (Fig. 4h). The existence of the 3D Dirac cone is further verified by our near-normal emission data and its second derivative with respect to energy (Fig. 4f, more details in Supplementary Fig. 9). We also note that from the spectral image taken in the first BZ, we observe an intensity asymmetry of the two bands giving rise to the crossing (Fig. 4d, f). This is an inherent property of the nonsymmorphic symmetry protection70, where the two bands across the BZ boundary exhibit different orbital characters due to the nonsymmorphic operation. Here we note that while we present one resolvable Dirac point in ARPES experiment, all band crossings at the X point must be Dirac crossings, including those near EF. Hence it would be interesting to further explore the tuning of these Dirac cones to EF via doping, as well as topological phase transitions with additional reduction of crystal symmetries.

Discussion

CeRu2 belongs to a large class of materials with the Laves phase that have the chemical composition AB2, where the B sublattice forms the pyrochlore structure. Superconductivity is commonly found in these compounds including SrIr2, Hf1−xZrxV2, and NbBe271,72,73. The 3D destructive interference originating from the B-site pyrochlore sublattice promotes flat bands in the electronic structure of those Laves phase materials, with the additional tuning of the flatness of the dispersions in the degree of hybridization of the B-site pyrochlore sublattice with the A-site sublattice. In particular, our ARPES experiments have identified portions of the electronic structure of CeRu2 consisting of the Ru 4d orbital that originate from the destructive interference associated with the pyrochlore sublattice. The potential connection between the pyrochlore flat bands and superconductivity in the Laves phase remains to be explored in future studies.

Both electronic features that we have observed here in CeRu2, namely the destructive interference-induced flat bands and the 3D Dirac cones are guaranteed signatures of the pyrochlore lattice structure, and should appear in a wide range of pyrochlore metals including the pyrochlore iridates46,47. CeRu2 as we demonstrated here, has its flat bands in very close proximity to EF, and therefore less challenging to observe. The 3D nature of the pyrochlore lattice makes it fundamentally distinct from the kagome lattice. As alluded to earlier, nonsymmorphic symmetries play a crucial role in determining its electronic structure. The Dirac point is hence robust to spin mixing from SOC effects. In contrast, the Dirac cones in a 2D kagome lattice are gapped out by SOC. Additionally, the direction of the SOC is irrelevant to the band structure in kagome systems, whereas, in the pyrochlore lattice, Fig. 1g shows how the 3D nature of the SOC makes the bands sensitive to the direction of the SOC. Moreover, the 3D nature of the pyrochlore lattice allows for strong topological insulating phases to be realized60. Such phases are not possible in a 2D kagome network. Furthermore, the pyrochlore electronic structure has features absent in a kagome lattice. These include triplet point crossings arising from the doubly-degenerate flat bands without SOC and the appearance of Dirac nodal lines in the limit of weak SOC. Finally, the three dimensionality of the pyrochlore lattice cuts-off any divergence in the density of states from the saddle points. This is unlike the case of kagome lattice where Van Hove singularities are expected to play a greater role in driving ordered phases74. Hence, the possibility of ordered phases resulting from weak coupling nesting effects is less likely; rather, the flat bands near the Fermi level serve as an ideal platform to explore correlated superconducting orders obtained from strong coupling approaches. Our results experimentally establish the potential for pyrochlores as a novel lattice platform with a wide range of material systems to realize and tune exotic correlated and topological phases that are to be discovered.

During the review process of our manuscript, we became aware of a similar work on the Laves phase75.

Methods

Sample growth and characterization

The single crystal of CeRu2 was grown using the Czochralski pulling method in a tetra-arc furnace. Firstly, a polycrystalline ingot of mass 10 g was prepared in an arc furnace as a precursor. The ingot was then placed on the water-cooled copper hearth of the tetra-arc furnace under Ar atmosphere with a Ti ingot adsorbing oxygen. An electric current of 16 A was applied into the ingot to melt it and the hearth rotated at a speed of 0.3 revolutions per minute. A columnar single crystal was successfully grown after several hours. Electrical transport and magnetization measurements were performed using a Quantum Design Physical Property Measurement System (PPMS) and Magnetic Property Measurement System (MPMS) under magnetic fields up to 7 T and at temperatures down to 1.8 K (Supplementary Fig. S1).

Angle-resolved photoemission spectroscopy (ARPES)

ARPES experiments were performed at beamline 5–2 of the Stanford Synchrotron Radiation Lightsource with a DA30 electron analyzer. The angular resolution was set to 0.1∘. The overall energy resolution was set to 15 meV. The energy resolution for the temperature dependent measurements was set to 11 meV. The samples were cleaved in-situ along the (111) crystalline plane below 15 K and the measurements were conducted in ultra-high vacuum with a base pressure of 3 × 10−11 Torr. The soft X-ray (500 ~ 880 eV) angle-integrated photoemission measurements were performed at the QMSC beamline of the Canadian Light Source with an R4000 electron analyzer with an energy resolution of around 100 meV. All the measurements were conducted at around 15 K unless otherwise noted. The ARPES measurements using helium lamp were performed at a lab-based system with a DA30 electron analyzer and the energy resolution was set to around 12 meV.

Density functional theory calculations

The first-principles calculations were performed by the Vienna Ab initio Simulation Package (VASP)76,77, within the projector augmented-wave method78. The generalized gradient approximation (GGA) with the Perdew-Burke-Ernzerhof (PBE)79 realization was adopted for the exchange-correlation functional. The 4f15d16s2 and 4p64d75s1 were treated as valence electrons for Ce and Ru atoms, respectively. A plane-wave cutoff energy of 500 eV and a MonkhorstPack k-point mesh80 with a size of 15 × 15 × 15 were used in the geometry optimization and the simulations of electronic properties. To account for the correlation effects for transition-metal elements, the DFT + U method with U = 1 eV for the 4d orbital of Ru atom was used for calculating the band structures, which shows magnetism consistent with the previous experiments55. Similar GGA-PBE WIEN2k81 calculations were performed for the comparison between Ru2, LaRu2 and CeRu2 band structures.

Tight-binding model

Symmetries of the Hamiltonian

The pyrochlore lattice belongs to space group 227 with Wyckoff positions at 16 (c) or 16 (d). We choose primitive vectors of the FCC lattice as a1 = (2, 2, 0), a2 = (2, 0, 2), a3 = (0, 2, 2). The unit cell contains four atoms that are translated along the diagonals of the faces of a cube to form corner sharing tetrahedra. The coordinates of the four atoms are A1 = (0, 0, 0), A2 = (1, 1, 0), A3 = (1, 0, 1), A4 = (0, 1, 1). The pyrochlore lattice contains corner sharing tetrahedra, and the point group of the lattice contains (i) a two fold rotation about an axis that passes through the midpoint of each edge of the tetrahedron and its center, (ii) a three fold rotation about an axis that passes through the vertex of the tetrahedron and its center, (iii) a four fold improper rotation about an axis that passes through the midpoint of each edge of the tetrahedron and its center, and (iv) a mirror reflection about a plane contain one edge of the tetrahedron and its center.

Total Hamiltonian

The total Hamiltonian in the absence of interactions takes the form

$$H={H}_{0}+{H}_{SO}$$
(3)

where we define the hopping and spin-orbit coupling terms in real space as

$$\begin{array}{l}{H}_{0}\,=\,-t\sum\limits_{\langle ij\rangle \sigma }{c}_{i\alpha \sigma }^{\dagger }{c}_{j\beta \sigma }\\ {H}_{SO}\,=\,\sqrt{2}i\lambda \sum\limits_{\begin{array}{c}\langle ij\rangle \\ \alpha \beta \end{array}}\left[{c}_{i\alpha \sigma }^{\dagger }\displaystyle\frac{{{\bf{b}}}_{ij}\times {{\bf{d}}}_{ij}}{| {{\bf{b}}}_{ij}\times {{\bf{d}}}_{ij}| }\cdot {\sigma }_{\sigma {\sigma }^{{\prime} }}{c}_{j\beta {\sigma }^{{\prime} }}+h.c.\right],\end{array}$$
(4)

respectively. Here the operator \({c}_{i\alpha \sigma }^{\dagger }\) creates an electron at site i, orbital α and spin σ, 〈. . 〉 denotes nearest neighbor hopping and t is the nearest neighbhor hopping parameter. Further λ is the strength of spin-orbit coupling, bij is a vector that connects the center of the tetrahedron to the mid-point of the bond connecting nearest neighbor sites i and j, and dij is a vector that connects nearest neighbor lattice sites i and j.

Hamiltonian matrix without SOC

Written in momentum space, the nearest neighbor hopping terms take the form

$${H}_{0}=\sum _{\begin{array}{c}{\bf{k}}\sigma \\ \alpha \beta \end{array}}{c}_{{\bf{k}}\alpha \sigma }^{\dagger }{h}_{\alpha \beta }({\bf{k}}){c}_{{\bf{k}}\beta \sigma }$$

where the Hamiltonian matrix hαβ(k) is given by

$${h}_{\alpha \beta }({\bf{k}})=-2t\left(\begin{array}{cccc}0&{c}_{{k}_{{\rm{x}}}+{k}_{{\rm{y}}}}&{c}_{{k}_{{\rm{x}}}+{k}_{{\rm{z}}}}&{c}_{{k}_{{\rm{y}}}+{k}_{{\rm{z}}}}\\ {c}_{{k}_{{\rm{x}}}+{k}_{{\rm{y}}}}&0&{c}_{{k}_{{\rm{y}}}-{k}_{{\rm{z}}}}&{c}_{{k}_{{\rm{x}}}-{k}_{{\rm{z}}}}\\ {c}_{{k}_{{\rm{x}}}+{k}_{{\rm{z}}}}&{c}_{{k}_{{\rm{y}}}-{k}_{{\rm{z}}}}&0&{c}_{{k}_{{\rm{x}}}-{k}_{{\rm{y}}}}\\ {c}_{{k}_{{\rm{y}}}+{k}_{{\rm{z}}}}&{c}_{{k}_{{\rm{x}}}-{k}_{{\rm{z}}}}&{c}_{{k}_{{\rm{x}}}-{k}_{{\rm{y}}}}&0\end{array}\right).$$
(5)

We have used the short hand \({c}_{{k}_{i}\pm {k}_{j}}\) to mean \(\cos ({k}_{i}\pm {k}_{j})\).

Hamiltonian matrix with SOC

The Hamiltonian in the presence of SOC is (12×2 is the identity matrix)

$$H=\sum _{\begin{array}{c}{\bf{k}}\sigma {\sigma }^{{\prime} }\\ \alpha \beta \end{array}}{c}_{{\bf{k}}\alpha \sigma }^{\dagger }\left[{h}_{\alpha \beta }({\bf{k}})+{h}_{\alpha \beta }^{SO}({\bf{k}})\right]{c}_{{\bf{k}}\beta {\sigma }^{{\prime} }},$$

where the matrices hαβ(k) and \({h}_{\alpha \beta }^{SO}({\bf{k}})\) are given as

$$\begin{array}{rcl}{h}_{\alpha \beta }({\bf{k}})\,\to \,{1}_{2\times 2}\otimes {h}_{\alpha \beta }({\bf{k}})\\ {h}_{\alpha \beta }^{SO}({\bf{k}})&=\,-\;2i\lambda ({\sigma }_{x}-{\sigma }_{y})\otimes \left(\begin{array}{cccc}0&-{c}_{{k}_{{\rm{x}}}+{k}_{{\rm{y}}}}&0&0\\ {c}_{{k}_{{\rm{x}}}+{k}_{{\rm{y}}}}&0&0&0\\ 0&0&0&0\\ 0&0&0&0\end{array}\right)\\&+\;2i\lambda ({\sigma }_{x}-{\sigma }_{z})\otimes \left(\begin{array}{cccc}0&0&-{c}_{{k}_{{\rm{x}}}+{k}_{{\rm{z}}}}&0\\ 0&0&0&0\\ {c}_{{k}_{{\rm{x}}}+{k}_{{\rm{z}}}}&0&0&0\\ 0&0&0&0\end{array}\right)\\ &-\;2i\lambda ({\sigma }_{y}-{\sigma }_{z})\otimes \left(\begin{array}{cccc}0&0&0&-{c}_{{k}_{{\rm{y}}}+{k}_{{\rm{z}}}}\\ 0&0&0&0\\ 0&0&0&0\\ {c}_{{k}_{{\rm{y}}}+{k}_{{\rm{z}}}}&0&0&0\end{array}\right)\\&+\;2i\lambda ({\sigma }_{y}+{\sigma }_{z})\otimes \left(\begin{array}{cccc}0&0&0&0\\ 0&0&-{c}_{{k}_{{\rm{y}}}-{k}_{{\rm{z}}}}&0\\ 0&{c}_{{k}_{{\rm{y}}}-{k}_{{\rm{z}}}}&0&0\\ 0&0&0&0\end{array}\right)\\ &-\;2i\lambda ({\sigma }_{x}+{\sigma }_{z})\otimes \left(\begin{array}{cccc}0&0&0&0\\ 0&0&0&-{c}_{{k}_{{\rm{x}}}-{k}_{{\rm{z}}}}\\ 0&0&0&0\\ 0&{c}_{{k}_{{\rm{x}}}-{k}_{{\rm{y}}}}&0&0\end{array}\right)\\&+\;2i\lambda ({\sigma }_{x}+{\sigma }_{y})\otimes \left(\begin{array}{cccc}0&0&0&0\\ 0&0&0&0\\ 0&0&0&-{c}_{{k}_{{\rm{x}}}-{k}_{{\rm{y}}}}\\ 0&0&{c}_{{k}_{{\rm{x}}}-{k}_{{\rm{y}}}}&0\end{array}\right),\end{array}$$
(6)

where σi are the Pauli matrices.