Introduction

In recent years, nonequilibrium states of condensed matter under external light irradiation have attracted significant attentions. When electrons are dynamically driven out of equilibrium, they exhibit behaviors distinct from their equilibrium counterparts, resulting in the emergence of exotic properties1,2,3. As an effective way, laser has been widely employed for ultrafast control of a variety of physical properties of quantum materials. For instance, light-induced superconductivity4, non-trivial topologies5,6, and high harmonic generation7 have been realized in experiments. Parallel to this, a growing number of theoretical predictions have been proposed, which might provide guidance for experiments8,9,10,11,12,13,14. In particular, Floquet theory stands out as a powerful theoretical framework to solve time-dependent problems subjected to periodic external fields, which averages the Hamiltonian over a time period to obtain quasistatic steady-state properties15,16,17. Therefore, it is convenient to predict properties of matter under light illumination using Floquet theory. Some phenomena in illuminated solids such as Floquet-Bloch bands6,18, optical Stark effect19, and anomalous Hall effect in time-reversal-symmetric systems5 have been demonstrated experimentally, greatly advancing the research frontier of Floquet engineering.

Over time, the conventional Hall effect20 has evolved into a large family of Hall effects including but not limited to anomalous Hall effect21,22,23, spin Hall effect24, valley Hall effect25, etc.26,27,28. These variations have sparked extensive research in their respective domains. Although these Hall variants under equilibrium states have been studied and well-established for long since their discovery, their nonequilibrium counterparts lack delicate experimental and theoretical investigations. Due to the exotic Dirac Fermions at the Fermi surface, graphene has been extensively employed in studying Hall effects under the illumination of light5,8,29,30,31. On the other hand, the monolayer transition metal dichalcogenide, taking MoS2 as a prototype, might give more tantalizing results when interacting with light, attributed to its unique spin and valley degrees of freedom32,33,34,35. Some previous works have shown the manipulation of these Hall conductivities in monolayer MoS2, which can be even quantized when the topological phase transition occurs36,37,38,39. However, most of these investigations have focused on off-resonant situations, requiring intense high-frequency lasers that are hard to be implemented in experiment37,38,39,40. Moreover, even when accounting for realistic resonant light, the equilibrium Fermi-Dirac distribution of electrons on electronic bands is often assumed36, and their effect on the spin degree of freedom in monolayer MoS2 is ignored41. Therefore, the modulation of these Hall effects in monolayer MoS2 under resonant light remains unclear, since the nonequilibrium electron occupations have to be taken into account. In addition, because of the spin splitting of electronic bands, laser of varying frequencies, each inducing different resonant conditions, can yield disparate outcomes.

Here, we employ Floquet theory to engineer the anomalous, valley, and spin Hall effects in monolayer MoS2 under periodic laser fields. The various Hall conductivities associated with intrinsic Berry curvature are calculated within the framework of linear response theory8,31,42, and the electronic occupation is simulated using a Green’s function approach29,43,44,45. Under the irradiation of linearly polarized light (LPL), the spin Hall conductivity exhibits different behaviors at two distinct frequencies. Specifically, with photon energy \({\rm{\hslash }}\omega\) = 1.7 eV, the spin Hall conductivity decreases almost to zero, whereas it remains nearly unchanged for \({\rm{\hslash }}\omega\) = 1.9 eV. This disparity arises from the distinct responses of spin-up and spin-down bands under resonant light. Under circularly polarized light (CPL), a large spin Hall effect emerges in the case of CPL with \({\rm{\hslash }}\omega\) = 1.7 eV. This phenomenon is mainly attributed to the distinct responses of bands at the \(K\) and \({K}^{{\prime} }\) valleys to CPL due to the optical selection rule. The primary effect originates from the \(K\) valley, where a topological phase transition occurs and the contribution of spin-up bands is substantially suppressed. Moreover, the quantum anomalous Hall effect emerges when assuming the Fermi-Dirac distribution of electrons. However, the anomalous Hall conductivity decreases considerably breaking the quantization condition, when taking into account the nonequilibrium occupation. Our work provides a novel avenue for engineering various Hall effects in two-dimensional materials via light-matter interactions.

Results

Lattice structure and electronic properties

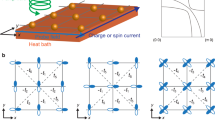
Monolayer MoS2 consists of two sulfur atoms and one molybdenum atom in each unit cell, forming a hexagonal quasi-two-dimensional lattice32,33,34,35, as shown in Fig. 1a. The absence of inversion symmetry in monolayer MoS2 results in the energy splitting of valence bands with opposite spins due to spin-orbit coupling (SOC), as illustrated in Fig. 1b. Notably, the spins at the \(K\) and \({K}^{{\prime} }\) valleys remain conserved and are related by the time-reversal symmetry, giving rise to the spin-valley locking. In such a material, when a charge current flows longitudinally through the sample, electrons with spins at different valleys move in opposite directions transversely, leading to the valley Hall effect. Furthermore, this movement results in spin accumulations on transverse sides of the sample, generating the spin Hall effect32, as depicted in Fig. 1c. In contrast to the bulk phase, monolayer MoS2 has a direct gap, allowing electrons to be directly excited from the top of valence bands to the bottom of conduction bands by incident light. Moreover, the band gaps between the conduction band bottom and the spin-up (|↑〉) and spin-down (|↓〉) valence band are 1.58 eV and 1.73 eV, respectively, as shown in Fig. 1b.

Fig. 1: Crystal structure and electronic properties in equilibrium.
figure 1

a The monolayer MoS2 in the quasi-two-dimensional plane. Purple and yellow balls represent the molybdenum and sulfur atoms, respectively. This figure is generated by the software VESTA. b The band structure near the K and K′ valleys. c Schematic illustration depicting the valley and spin Hall effects in the monolayer MoS2 without light. When a charge current flows though the sample, the electrons with spins at the K (skyblue) and K′ (pink) valleys move towards opposing transverse sides.

Full size image

The band structure of the monolayer MoS2 near the K/K′ valleys can be studied by the k ∙ p model Hamiltonian32,38,40,41:

$$\hat{H}=a{t}_{h}\left(\tau {k}_{x}{\hat{\sigma }}_{x}+{k}_{y}{\hat{\sigma }}_{y}\right)+\frac{\varDelta }{2}{\hat{\sigma }}_{z}-\frac{\lambda \tau }{2}\left({\hat{\sigma }}_{z}-1\right){\hat{s}}_{z},$$
(1)

where a = 3.193 Å is the lattice constant, th = 1.10 eV is the hopping parameter, Δ = 1.66 eV is the energy gap, and 2λ = 0.15 eV is the spin splitting at the the top of valence bands. τ = ±1 denotes the valley index for the K and K′ valley, and \(\hat{{\boldsymbol{\sigma }}}\) and \({\hat{s}}_{z}\) represent Pauli matrices for the pseudospin basis of orbitals and spin, respectively. To incorporate the effect of external light on the electronic structure of monolayer MoS2, the momentum k in above Bloch Hamiltonian is replaced by the Peierls substitution \({\boldsymbol{k}}\to {\boldsymbol{k}}+\frac{e}{{{\hslash }}}{\boldsymbol{A}}\left(t\right)\). Here, A(t) represents the vector potential of light with \({\boldsymbol{A}}\left({\boldsymbol{t}}\right)={A}_{0}\left(\cos \omega t,0\right)\) for LPL while \({\boldsymbol{A}}\left(t\right)={A}_{0}\left(\cos \omega t,-\sin \omega t\right)\) for CPL, where A0 is the amplitude and ω is the frequency. Then the Floquet Hamiltonian can be expanded in the Sambe space16. Within the framework of linear response theory8,31,32, the anomalous Hall conductivity σa, valley Hall conductivity σv, and spin Hall conductivity σs under Floquet theory can be obtained:

$${\sigma }_{a}=\mathop{\sum}\limits_{\alpha }\left({\sigma }_{\alpha }^{K}+{\sigma }_{\alpha }^{{K}^{{\prime} }}\right),$$
(2)
$${\sigma }_{v}=\frac{1}{e}\sum_{\alpha }\left({\sigma }_{\alpha }^{K}-{\sigma }_{\alpha }^{{K}^{{\prime} }}\right),$$
(3)
$${\sigma }_{s}=\frac{{{\hslash }}}{2e}\mathop{\sum}\limits_{\alpha }\left({\sigma }_{\alpha ,s}^{K}+{\sigma }_{\alpha ,s}^{{K}^{{\prime} }}\right),$$
(4)

where the valley and spin dependent Berry curvature and Hall conductivity can be further obtained by

$${\sigma }_{\alpha }^{\eta }=\frac{{e}^{2}}{2\pi h}\mathop{\sum}\limits_{i=v,c}{\int_{\eta}}d{\boldsymbol{k}}\left[{\rho }_{|{\alpha }_{i},\uparrow \rangle }\left({\boldsymbol{k}}\right){\Omega }_{|{\alpha }_{i},\uparrow \rangle }\left({\boldsymbol{k}}\right)+{\rho }_{|{\alpha }_{i},\downarrow \rangle }\left({\boldsymbol{k}}\right){\Omega }_{|{\alpha }_{i},\downarrow \rangle }\left({\boldsymbol{k}}\right)\right],\eta =K/{K}^{{\prime} },$$
(5)
$${\sigma }_{\alpha ,s}^{\eta }=\frac{{e}^{2}}{2\pi h}\mathop{\sum}\limits_{i=v,c}{\int_{\eta}}d{\boldsymbol{k}}\left[{\rho }_{|{\alpha }_{i},\uparrow \rangle }\left({\boldsymbol{k}}\right){\Omega }_{|{\alpha }_{i},\uparrow \rangle }\left({\boldsymbol{k}}\right)-{\rho }_{|{\alpha }_{i},\downarrow \rangle }\left({\boldsymbol{k}}\right){\Omega }_{|{\alpha }_{i},\downarrow \rangle }\left({\boldsymbol{k}}\right)\right],\eta =K/{K}^{{\prime} },$$
(6)
$${\Omega }_{|{\alpha }_{i},{s}_{z}\rangle }({\boldsymbol{k}})=\frac{1}{T}{\int_{0}^{T}}{dt}2{\rm{Im}}\left[\langle {\partial }_{{k}_{y}}{\phi }_{|{\alpha }_{i},{s}_{z}\rangle ,{\boldsymbol{k}}}(t)|{\partial }_{{k}_{x}}{\phi }_{|{\alpha }_{i},{s}_{z}\rangle ,{\boldsymbol{k}}}(t)\rangle \right],{s}_{z}=\uparrow /\downarrow,$$
(7)

\(|{\phi }_{|{\alpha }_{i},{s}_{z}\rangle ,{\boldsymbol{k}}}(t)\rangle =|{\phi }_{|{\alpha }_{i},{s}_{z}\rangle ,{\boldsymbol{k}}}(t+T)\rangle\) represents the Floquet modes associated with replica band index α, valence/conduction index i and period \(T=\frac{2\pi }{\omega }\), \({\Omega }_{|{\alpha }_{i},{s}_{z}\rangle }\left({\boldsymbol{k}}\right)\) is the time-averaged Berry curvature in momentum space, and \({\rho }_{|{\alpha }_{i},{s}_{z}\rangle }\left({\boldsymbol{k}}\right)\) is the nonequilibrium electron occupation which can be adapted from a Green’s function approach inspired by the simulation of time-resolved angle-resolved photoelectron spectroscopy (Tr-ARPES, see Methods)29,43,44,45. Notably, our approach is not confined solely to this model Hamiltonian, and it can also combine with the Wannier Hamiltonian obtained from the first-principles calculations12,43,46,47 to explore a broad range of realistic materials.

Valley and spin Hall effects under LPL

In the case of LPL, the effects of light on the band structure at the K and K′ valleys are identical since LPL does not carry angular momentum. Under Floquet theory, when electrons in the valence band (α = 0) absorb a photon, they form a replica band (α = 1), while another replica band (α = −1) is generated through the emission of a photon from the original band (α = 0). Besides, as the light field amplitude A0 increases from zero to 60 V/c (c is velocity of light), the original bands and the replica bands interact with each other, leading to the dressing of bands and redistribution of electrons, as shown in Fig. 2a, b. Here, we consider LPL with two different laser frequencies: ℏω = 1.7 eV and ℏω = 1.9 eV, corresponding to scenarios where the conduction bands (|0c,↑/↓〉) cross with only the spin-up valence replica band (|1v,↑〉) or both valence replica bands (|1v,↑/↓〉), respectively. Due to the conservation of time-reversal symmetry under LPL, the anomalous Hall effect is absent. However, the valley and spin Hall effects can be altered by LPL.

Fig. 2: The valley and spin Hall effects under the irradiation of LPL.
figure 2

a, b The original bands (α = 0) and Floquet replicas (α = ±1) near the K valley with amplitude A0 = 0 V/c and A0 = 60 V/c. The gray dashed lines represent the quasienergy bands, while the color shading denotes the electron count. c, d The valley Hall conductivity σv and spin Hall conductivity σs as a function of the laser amplitude A0 for different photon energy ℏω. The black triangles correspond to the conductivities assuming a Fermi-Dirac occupation of electronic bands, while the red circular (square) dots represent the values obtained when considering nonequilibrium occupation for ℏω = 1.7 eV (1.9 eV). The green diamond is the conductivity without light. The blue dashed lines are guide to the eye.

Full size image

Figure 2c depicts the results of the valley Hall conductivity as a function of light field amplitude A0. When considering the nonequilibrium occupation, the valley Hall conductivity gradually decreases with increasing A0 for ℏω = 1.7 eV and ℏω = 1.9 eV, but is lower than the values assuming that the electrons always reside in the α = 0 valence bands (i.e. assuming the Fermi-Dirac distribution). Interestingly, the spin Hall conductivities display distinct variations for different frequencies when the nonequilibrium occupation is taken into account. The spin Hall conductivity decreases rapidly and approaches zero for ℏω = 1.7 eV, while it remains nearly unchanged for ℏω = 1.9 eV, as depicted in Fig. 2d. The suppressed behavior observed at ℏω = 1.7 eV might be utilized as a switch: an “on” state without light and an “off” state with A0 ≥ 100 V/c.

To understand the variations in the spin Hall conductivity, we conducted a thorough analysis of the contributions from the Berry curvature \({\Omega }_{{|i},{s}_{z}\rangle }={\sum }_{\alpha }{\int_{K,{K}^{{\prime} }}}\frac{d{\boldsymbol{k}}}{2\pi }{\rho }_{|{\alpha }_{i},{s}_{z}\rangle }({\boldsymbol{k}}){\Omega }_{|{\alpha }_{i},{s}_{z}\rangle }({\boldsymbol{k}})(i=v/{c;}\,{s}_{z}=\,\uparrow /\downarrow )\) of individual bands in Fig. 2b. For ℏω = 1.7 eV, when comparing Fig. 3a with Fig. 3b, it is evident that the Berry curvature from the spin-up valence bands \({\Omega }_{{|v},\uparrow \rangle }\) is larger than that from the spin-down bands \({\Omega }_{|v,\downarrow \rangle }\) when the amplitude A0 is small. As the light intensity increases, more electrons are excited to the Floquet bands in higher energy, where the contributions \({\Omega }_{|c,\uparrow\rangle }\) and \({\Omega }_{|c,\downarrow \rangle }\) are opposite. Moreover, \({\Omega }_{|v,\uparrow \rangle }\) and \({\Omega }_{|c,\uparrow \rangle }\) decrease more rapidly than \({\Omega }_{|v,\downarrow \rangle }\) and \({\Omega }_{|c,\downarrow \rangle }\), respectively. This may be attributed to the fact that the excitations are resonant in the spin-up bands, whereas they are off-resonant in the spin-down bands, thus electrons are more easily excited in the former case.

Fig. 3: The spin-resolved Berry curvature irradiated by LPL.
figure 3

a, b The Berry curvature Ω|v,↑〉, Ω|c,↑〉, Ω|v,↓〉, and Ω|c,↓〉 contributed by the valence and conduction parts of the spin-up and spin-down bands with increasing laser amplitude A0 for photon energy ℏω = 1.7 eV. The black dots represent the values for the valence bands, while red dots correspond to the conduction bands, as indicated on the right axis. The blue dashed lines are guide to the eye. c, d The Berry curvature Ω|↑〉 and Ω|↓〉 of the total spin-up and spin-down bands for ℏω = 1.7 eV and ℏω = 1.9 eV. e, f Schematic illustration depicting the valley and spin Hall effects under LPL for ℏω = 1.7 eV and ℏω = 1.9 eV. The transparent balls represent the electrons that have disappeared under the influence of light.

Full size image

The total spin-resolved Berry curvature \({\Omega }_{|s_{z}\rangle }={\Omega }_{|v,{s}_{z}\rangle }+{\Omega }_{|c,{s}_{z}\rangle }\) \(({s}_{z}=\uparrow /\downarrow )\) is displayed in Fig. 3c. It is clear that \({\Omega }_{|\uparrow \rangle }\) is larger than \({\Omega }_{|\downarrow \rangle }\) initially and they gradually approach each other with increasing light intensity, leading to the disappearance of spin Hall conductivity. Figure 3e provides an intuitive illustration of this process, showing that the number of electrons on both sides of the sample decreases compared with Fig. 1c, while the electrons with opposite spins become almost equal on each side. As for ℏω = 1.9 eV, the excitations are resonant for both spin-up and spin-down bands under the radiation of light, and \({\Omega }_{|\uparrow \rangle }\) and \({\Omega }_{|\downarrow \rangle }\) decay in a similar way, as shown in Fig. 3d. Thus, the number difference between the electrons with opposite spins remains almost identical, as depicted in Fig. 3f.

Various Hall effects under CPL

When considering CPL, it is important to note that the optical selection rule of CPL results in different variations in the band structure at the K and K′ valleys, as shown in Fig. 4a. At the K valley, the valence band replica (|1v,↑/↓〉) interacts weakly with the conduction band (|0c,↑/↓〉), and only a small gap opens at the resonant energy. Conversely, at the K′ valley, there is a strong interaction between these bands. Thus, the bands undergo dramatic changes, akin to the scenario observed with LPL (Fig. 2b). Therefore, the Berry curvature cannot cancel each other completely at opposite momenta with remanent contribution, leading to the emergence of the anomalous Hall effect. When the light intensity is low, the newly opened gaps near the K valley are quite small and are susceptible to external disturbances. Thus, we choose a moderate amplitude A0 = 60 V/c to investigate the effect of CPL on monolayer MoS2.

Fig. 4: The anomalous, valley and spin Hall effects under the irradiation of CPL.
figure 4

a The α = 0 and α = ±1 Floquet replicas with amplitude A0 = 60 V/c near the K and K′ valleys. The gray dashed lines represent the quasienergy bands, while the color shading indicates the electron number. The inset zooms in the resonance region. b–d The anomalous Hall conductivity σh, valley Hall conductivity σv and spin Hall conductivity σs without and with light, while taking into account different electron occupation for photon energy ℏω = 1.7 eV and ℏω = 1.9 eV in the presence of light. The light blue box in (b) and the red box in (d) are designated for convenient comparison within their respective regimes.

Full size image

Figure 4b–d displays the anomalous, valley and spin Hall conductivities of monolayer MoS2 without and with light. With the Fermi-Dirac distribution, these conductivities display remarkable magnitudes, and the anomalous Hall conductivity exhibits quantization due to the topological phase transition near the K valley36. However, upon considering the nonequilibrium occupation, the anomalous Hall conductivity σa loses its quantized feature and decreases significantly, as shown in the light blue box of Fig. 4b. Then we shift our focus to the spin Hall conductivity. Compared to the case without light, CPL can dramatically enhance the spin Hall effects, even in the presence of nonequilibrium occupation. In particular, as depicted in the red box of Fig. 4b, the spin Hall conductivity at ℏω = 1.7 eV increases in the opposite direction reaching approximately three times of that in the absence of light.

To further clarify the origin of this phenomenon, an examination of the spin-resolved Berry curvature \({\Omega }_{|{s}_{z}\rangle }({s}_{z}=\uparrow /\downarrow )\) near the K or K′ valleys is conducted, as shown in Fig. 5a. The \({\Omega }_{|{s}_{z}\rangle }\) of the spin-up and spin-down bands near the K′ valley decreases simultaneously, and contributes little to the spin Hall conductivity. Concurrently, Ω|↓〉 near the K valley shows little variation, since the spin-down bands for |0c,↓〉 and |1v,↓〉 without resonance have very weak interactions. In contrast, Ω|↑〉 decreases down to a small value. To analyze Ω|↑〉 near the K valley more specifically, we show the k-resolved Berry curvature \({\Omega }_{|{\alpha }_{v},\uparrow \rangle }({\boldsymbol{k}})\) and \({\Omega }_{|{\alpha }_{c},\uparrow \rangle }({\boldsymbol{k}})\) in the two-dimensional plane, as illustrated in Fig. 5b. These quantities, with opposite values, mainly concentrate at points near the resonant ring, where the topological phase transition occurs. Considering the electron occupation, as shown in Fig. 5d, the main features of \({\sum }_{\alpha }{\rho }_{|{\alpha }_{v},\uparrow \rangle }({\boldsymbol{k}}){\Omega }_{|{\alpha }_{v},\uparrow \rangle }({\boldsymbol{k}})\) and \({\sum }_{\alpha }{\rho }_{|{\alpha }_{c},\uparrow \rangle }({\boldsymbol{k}}){\Omega }_{|{\alpha }_{c},\uparrow \rangle }({\boldsymbol{k}})\) resemble those ignoring the nonequilibrium occupation. However, the values are smaller because some electrons are excited. Consequently, the total \({\Omega }_{|\uparrow \rangle }\) becomes small due to the substantial cancellation between them. From an intuitive perspective, as depicted in the diagram of Fig. 5c, it is evident that the population of spin-up electrons on one side decreases significantly, resulting in a large spin Hall effect.

Fig. 5: The spin-resolved Berry curvature irradiated by CPL for photon energy ℏω = 1.7 eV.
figure 5

a The Berry curvature Ω|↑〉 and Ω|↓〉 contributed by the spin-up and down bands near the K or K′ valleys. b The k-resolved Berry curvature distribution \({\Omega }_{|{\alpha }_{v},\uparrow \rangle }({\boldsymbol{k}})\) and \({\Omega }_{|{\alpha }_{c},\uparrow \rangle }({\boldsymbol{k}})\) for the valence (left) and conduction (right) spin-up band near the K valley. c Schematic illustration depicting the various Hall effects under CPL. d is similar to (b), but considering the electron occupation \({\rho }_{|{\alpha }_{v},\uparrow \rangle }({\boldsymbol{k}})\) and \({\rho }_{|{\alpha }_{c},\uparrow \rangle }({\boldsymbol{k}})\).

Full size image

Dissipation effects

The dissipation effects are inherent in realistic systems. To account for dissipation including electron relaxation and decoherence processes, we adopt the relaxation-time approximation (see Methods). Here, we set the relaxion time T1 to 500 fs, and the decoherence time T2 to 40fs48,49. In general, including the effects of electron dissipation does not lead to significant changes of our major findings. We illustrate this point by taking the valley Hall effect under LPL and the spin Hall effect under CPL as examples, as shown in Fig. 6. Here Fig. 6a shows the valley Hall conductivity under LPL without and with dissipation. In both cases, the conductivities decrease with increasing light amplitude, although the decrease is more pronounced when dissipation effects are included. Similarly, in Fig. 6b, we depict the spin Hall conductivities under CPL, again without and with dissipation. Here, the behavior remains largely unchanged regardless of the presence of dissipation effects. Furthermore, Fig. 6b demonstrates the weak dependence of T1 and T2, indicating robustness of our conclusions irrespective of the specific choice of T1 and T2. In addition, the spin Hall effect for ℏω = 1.7 eV under LPL is also suppressed, and non-quantized anomalous Hall conductivities are generated under CPL when the electron dissipation is considered (not shown in the figure).

Fig. 6: The valley and spin Hall conductivities without and with dissipation.
figure 6

a The valley Hall conductivity σv as a function of laser amplitude A0 under the irradiation of LPL. The red (black) dots correspond to the conductivities without (with) dissipation, and circular (square) dots represents the values for ℏω = 1.7 eV (1.9 eV). b The spin Hall conductivity σs irradiated by CPL with different T1 at fixed T2 = 40 fs (left), and with different T2 at fixed T1 = 500 fs (right).

Full size image

Realistic pump pulse

In the calculations above, we adopt laser fields with hundreds of cycles to satisfy the conditions of Floquet theory. To verify our results with a more realistic pump pulse, we also use laser fields with only 25 cycles, which is feasible in the current experimental setups2. Figure 7 depicts the corresponding spin Hall conductivities under the irradiation of LPL and CPL. As shown in Fig. 7a, the spin Hall effect remains almost unchanged for ℏω = 1.9 eV, while is largely suppressed approaching zero values for ℏω = 1.7 eV under LPL. These results are similar to those obtained under pump light with many cycles. Under CPL, for ℏω = \(1.7\ \text{eV}\), the spin Hall effect is also enhanced, as shown in Fig. 7b, although the increase is smaller compared to results with a long-pulse-duration Floquet driving. This is because the gap at the K valley opened by CPL is small, and there is a larger energy bandwidth for a less cycled pump pulse. Consequently, the occupation between valence and conduction bands is redistributed, resulting in changes of spin Hall conductivities. Therefore, our conclusions are robust under realistic pump laser fields.

Fig. 7: The spin Hall conductivities under the irradiation of LPL and CPL with 25 cycles.
figure 7

a The spin Hall conductivity σs as a function of laser amplitude A0 irradiated by LPL. The black triangles represent the conductivities with FD distribution, while the red circular (square) dots correspond to values with nonequilibrium occupation for ℏω = 1.7 eV (1.9 eV). The green diamond is the conductivity without light. The blue dashed lines are guide to the eye. b The spin Hall conductivity σs irradiated by CPL with different electron occupation for photon energy ℏω = \(1.7\ \text{eV}\) and ℏω = \(1.9\ \text{eV}\). The red box is designated for convenient comparison.

Full size image

Discussion

Our work demonstrates the critical role of nonequilibrium occupation in the Floquet framework, and it can be adopted as an effective way to engineer the anomalous, valley, and spin Hall effects in monolayer MoS2 with linearly or circularly polarized light. When subjected to LPL, the spin Hall conductivity is effectively suppressed to nearly zero for ℏω = 1.7 eV, while it changes little for ℏω = 1.9 eV. Under the illumination of CPL, when the photon energy ℏω is 1.7 eV, the spin Hall effect experiences a substantial enhancement due to the suppression of the spin-up channel. Besides, the time-reversal symmetry of monolayer MoS2 is broken, resulting in the emergence of the anomalous Hall effect. However, the quantized anomalous Hall conductivity experiences a substantial reduction when considering the nonequilibrium electron occupation. Therefore, the manipulation of these Hall effects in monolayer MoS2 offers promising opportunities for future optoelectronic device applications. Our study provides insights into the behavior of electrons in the presence of light, which is beneficial to ongoing nonequilibrium engineering of quantum materials.

Methods

In the framework of Floquet theory, we can obtain the solution of the time-dependent Schrödinger equation \(|{\psi }_{\beta {\boldsymbol{k}}}(t)\rangle ={e}^{-i{\varepsilon }_{\beta {\boldsymbol{k}}}t/{{\hslash }}}|{\phi }_{\beta {\boldsymbol{k}}}(t)\rangle\), where \(\beta =|{\alpha }_{v/c},\uparrow /\downarrow \rangle\) and \({\varepsilon }_{\beta {\boldsymbol{k}}}\) is the quasienergy. Using the Fourier transform \(|{\phi }_{\beta {\boldsymbol{k}}}(t)\rangle =\sum _{m}{e}^{{im}\omega t}|{\phi }_{\beta {\boldsymbol{k}}}^{m}\rangle\), the Schrödinger equation becomes time-independent:

$$\sum _{m}\left[{H}_{{nm}}+m{{\hslash }}\omega {\delta }_{{nm}}\right]\left|{\phi }_{\beta {\boldsymbol{k}}}^{m}\right\rangle ={\epsilon }_{\beta {\boldsymbol{k}}}\left|{\phi }_{\beta {\boldsymbol{k}}}^{n}\right\rangle,$$
(8)
$${H}_{{nm}}=\frac{1}{T}{\int_{0}^{T}}{dt}{e}^{-i\left(n-m\right)\omega t}\hat{H}\left(t\right).$$
(9)

The above equations can be solved numerically to obtain the Floquet modes \(|{\phi }_{\beta {\boldsymbol{k}}}(t)\rangle\).

To simulate the electron occupation, we employ a Green’s function approach inspired by Tr-ARPES simulations29,43,44,45, which gives the probability distribution of electrons at different energy ε:

$$I\left({\boldsymbol{k}},\varepsilon \right)={\rm{I}}{\rm{m}}\sum_{a}\int d{t}_{1}\int d{t}_{2}{e}^{i\varepsilon \left({t}_{1}-{t}_{2}\right)/{{\hslash }}}{G}_{{aa}}^{ < }\left({\boldsymbol{k}},{t}_{1},{t}_{2}\right).$$
(10)

Here, the time integration spans 120 cycles of the pump pulse, ensuring the attainment of steady states and high resolution of energy. The lesser Green function \({G}^{ < }({\boldsymbol{k}},{t}_{1},{t}_{2})\) can be obtained by \(U({\boldsymbol{k}},{t}_{1},0){G}^{ < }({\boldsymbol{k}},0,0){U}^{\dagger }\left({\boldsymbol{k}},{t}_{2},0\right)\), where \({G}^{ < }({\boldsymbol{k}},0,0)\) is expressed as \(i\sum_{a}\left|{\varphi }_{a{\boldsymbol{k}}}\right\rangle \left\langle {\varphi }_{a{\boldsymbol{k}}}\right|f\left({E}_{a{\boldsymbol{k}}}\right)\) with the eigenstates \(\left|{\varphi }_{a{\boldsymbol{k}}}\right\rangle\) and Fermi-Dirac distribution \(f({E}_{a{\boldsymbol{k}}})\) in equilibrium. \(U({\boldsymbol{k}},{t}_{1},{t}_{2})=\hat{T}\exp (-i/{{\hslash }}{\int }_{{t}_{2}}^{{t}_{1}}H({\boldsymbol{k}},\,t){dt})\) represents the time evolution operator with the time-ordering operator \(\hat{T}\). Subsequently, the electron occupation at the quasienergy \({\varepsilon }_{\beta {\boldsymbol{k}}}\) can be calculated as29:

$${\rho }_{\beta }\left({\boldsymbol{k}}\right)={\int}_{\left({\varepsilon }_{\beta {\boldsymbol{k}}}+{\varepsilon }_{\beta -1,{\boldsymbol{k}}}\right)/2}^{\left({\varepsilon }_{\beta {\boldsymbol{k}}}+{\varepsilon }_{\beta +1,{\boldsymbol{k}}}\right)/2}I\left({\boldsymbol{k}},\varepsilon \right)d\varepsilon,$$
(11)

where the integration is performed from the center of the energy gap below \({\varepsilon }_{\beta {\boldsymbol{k}}}\) to the center of the gap above \({\varepsilon }_{\beta {\boldsymbol{k}}}\).

To simulate electron dynamics with dissipation3,50, we use a quantum Liouville equation to study the evolution of the density matrix \(P\left({\boldsymbol{k}},t\right)\):

$$\frac{{\rm{d}}}{{\rm{d}}t}P\left({\boldsymbol{k}},t\right)=\frac{\left[H\left({\boldsymbol{k}},t\right),P\left({\boldsymbol{k}},t\right)\right]}{{\rm{i}}{{\hslash }}}+D\left[P\left({\boldsymbol{k}},t\right)\right].$$
(12)

\(H({\boldsymbol{k}},t)\) is the time-dependent Hamiltonian incorporating the effect of light through Peierls substitution, and the relaxation operator \(D[P\left({\boldsymbol{k}},t\right)]\) under the relaxation-time approximation can be written as:

$${{\_}}\left(\begin{array}{cccc}\frac{{P}_{11}^{\uparrow }\left({\boldsymbol{k}},\,t\right)-{n}_{1}^{\uparrow }\left({\boldsymbol{k}},\,t\right)}{{T}_{1}} & \frac{{P}_{12}^{\uparrow }\left({\boldsymbol{k}},\,t\right)}{{T}_{2}} & 0 & 0\\ \frac{{P}_{21}^{\uparrow }\left({\boldsymbol{k}},\,t\right)}{{T}_{2}} & \frac{{P}_{22}^{\uparrow }\left({\boldsymbol{k}},\,t\right)-{n}_{2}^{\uparrow }\left({\boldsymbol{k}},\,t\right)}{{T}_{1}} & 0 & 0\\ 0 & 0 & \frac{{P}_{11}^{\downarrow }\left({\boldsymbol{k}},\,t\right)-{n}_{1}^{\downarrow }\left({\boldsymbol{k}},\,t\right)}{{T}_{1}} & \frac{{P}_{12}^{\downarrow }\left({\boldsymbol{k}},\,t\right)}{{T}_{2}}\\ 0 & 0 & \frac{{P}_{21}^{\downarrow }\left({\boldsymbol{k}},\,t\right)}{{T}_{2}} & \frac{{P}_{22}^{\downarrow }\left({\boldsymbol{k}},\,t\right)-{n}_{2}^{\downarrow }\left({\boldsymbol{k}},t\right)}{{T}_{1}}\end{array}\right)$$
(13)

Here, \({T}_{1}\) and \({T}_{2}\) represent electron relaxation and decoherence time, respectively. \({n}_{\mathrm{1,2}}^{\uparrow }({\boldsymbol{k}},t)/{n}_{\mathrm{1,2}}^{\downarrow }({\boldsymbol{k}},t)\) denotes the occupation for spin up/down electrons in thermal equilibrium concerning the instantaneous Hamiltonian \(H({\boldsymbol{k}},t)\). Then the lesser Green function \({G}^{ < }({\boldsymbol{k}},{t}_{1},{t}_{2})\) can be obtained by the generalized Kadanoff–Baym ansatz (GKBA)3,51:

$${G}^{ < }\left({\boldsymbol{k}},{t}_{1},{t}_{2}\right)={\rm{i}}U\left({\boldsymbol{k}},{t}_{1},{t}_{2}\right)P\left({\boldsymbol{k}},{t}_{2}\right).$$
(14)

Subsequently, the occupation with dissipation can be determined though equation (10) and (11).