A cell type and state specific gene regulation network inference method for immune regulatory analysis

Abstract

The gene regulatory network inference method based on bulk sequencing data not only confuses different types of cells, but also ignores the phenomenon of network dynamic changes with cell state. Single cell transcriptome sequencing technology provides data support for constructing cell type and state specific gene regulatory networks. This study proposes a method for inferring cell type and state specific gene regulatory networks based on scRNA-seq data, called inferCSN. Firstly, inferCSN infers pseudo temporal information from scRNA-seq data and reorders cells based on this information. Because of the uneven distribution of cells in pseudo temporal information, the regulatory relationship tends to lean towards the high-density areas of cells. Therefore, based on the cell state, we divide the cells into different windows to eliminate the temporal information differences caused by cell density. Then, a sparse regression model, combined with reference network information, is used to construct a cell type-specific regulatory network (CSN) for each window. The experimental results on both simulated and real scRNA-seq datasets show that inferCSN outperforms other methods in multiple performance metrics. In addition, experimental results on datasets of different types (such as steady-state and linear datasets) and scales (different cell and gene numbers) show that inferCSN is robust. To further demonstrate the effectiveness and application prospects of inferCSN, we analyzed the gene regulatory network of T cells in different states and different tumor subclons within the tumor microenvironment, and we found that comparing the regulatory networks in different states can reveal immune suppression related signaling pathways.

Introduction

Constructing and mining gene regulatory network are crucial for explaining biological phenomena such as cell differentiation and cell fate, and can even be used to discover the immune escape pathways adopted by tumor cells for evading immune system surveillance. For example, how tumor cells regulate the high expression of PD-L1 to inhibit cytotoxic T lymphocytes (CTL) cell killing. However, the expression level of the target gene in traditional bulk sequencing data is the average of its expression in different types and states of cells, which not only confuses different types of cells in gene regulatory network (GRN) construction methods, but also ignores the dynamic changes of the network with cell state, resulting in a large number of false positive or false negative edges in the regulatory network. Consequently, such defects will lead to confusion in understanding downstream biological phenomena.

Single-cell RNA sequencing (scRNA-seq) technology distinguishes different types of cells, and even different states of the same cell type, with unprecedented resolution, which is crucial for understanding dynamic and complex cellular processes^1,2. The use of scRNA-seq data can construct a GRN that is specific to cell type and even cell state. This is crucial for understanding the complex interactions between tumor cells and immune cells during tumor occurrence, development, and metastasis, and can guide researchers in identifying new drug targets and developing effective immunotherapy drugs. However, due to the high noise (low signal-to-noise ratio, SNR), high dimensionality, and a large number of dropouts of scRNA-seq data, constructing regulatory networks based on scRNA-seq data still faces challenges.

So far, many regulatory network methods have been proposed, and the datasets used for network inference can be divided into: methods based on bulk sequencing transcriptome data³, methods based on scRNA-seq data⁴, and methods based on multi-source and multi-omics data. The method based on bulk sequencing transcriptome data, such as GENIE3⁵ based on random forest model, combines the known relationships of TFs and target genes in the curated database, and uses the expression of TF-encoding gene to predict target gene expression to eliminate false positive edges. The main drawback of GENIE3 is its neglect of cellular heterogeneity and high false positive rate; Methods based on scRNA-seq data, such as SCENIC^6,7 using TF and target gene coexpression patterns to generate cell type specific GRNs, and then further pruning the edges of the network using the prior information. The regulatory relationship between TF and genes will change over time. However, due to the scarcity of temporal data in scRNA-seq, this kind of method ignores the highly dynamic nature of regulatory networks. Fortunately, studies have shown that cell differentiation processes can be modeled and inferred by calculating pseudo-time information of cells, which means that the pseudo-time information can be used to accurately construct GRN⁸. For example, LEAP⁹ and SINCERITIES¹⁰ both use pseudo-temporal sorting to infer the directionality between genes in GRN. The LEAP method defines a fixed size pseudo time window and assumes that genes expressed earlier within one time window may affect the expression of other genes. Then, the GRN is constructed by calculating the Pearson correlation coefficients (PCC). SINCERITIES¹⁰ uses Kolmogorov Smirnov (KS) distance to quantify the distance between two cumulative distribution functions of gene expression and subsequent time points, and infers the directional regulatory relationships between genes through ridge regression and partial correlation analysis. BiXGBoost¹¹ effectively utilizes temporal information and integrates XGBoost regression models to evaluate feature importance. Randomization and regularization are also applied in BiXGBoost to solve overfitting problems. Normi¹² employs a fixed size sliding window method throughout the entire trajectory to address these issues, and applies an average smoothing strategy to the gene expression of cells in each window to obtain representative cells. In addition, Normi determines the optimal time delay for each gene pair through distance correlation, resulting in good robustness. However, there is still significant room for improvement, such as not taking into account the distribution of cell density over time¹³, and simply treating the gene expression profiles of all cells as an expression matrix without considering cell types. Especially in some cases, their performance is not significantly better than that of random networks¹⁴; SCORPION uses a messagepassing algorithm to construct comparable GRNs which are suitable for population-level comparisons by leveraging the same baseline priors²; scMGATGRN is a kind of method based on deep learning model, which uses a multiview graph attention network to extract local feature information and high-order neighbor feature information of nodes in the GRN¹⁵. Transcriptome data cannot directly reflect TF protein abundance and DNA binding events, interactions between TFs and cofactors, etc. Therefore, methods based on multi-omics data integrate additional information during the construction of CSN to improve the accuracy of network construction. For example, Li et al. proposed a GRN construction method based on multi-omics data such as transcriptome and epigenomics data¹⁶; LINGER uses a neural network to infer GRN based multiome data data, whcih incorporates atlas-scale external bulk data across diverse cellular contexts and prior knowledge of transcription factor motifs¹⁷. Note that it is difficult to obtain other omics (such as scATAC-seq, snmC-seq, and lncRNA-data) that can be paired with scRNA-seq data, and there may be significant technical and biological noise between different omics of single-cell sequencing data. Therefore, the construction of GRN based on single-cell multi-omics data has encountered certain challenges.

In order to address such challenges, we proposed a cell type and cell state specific GRN inference method called inferCSN based on scRNA-seq data.

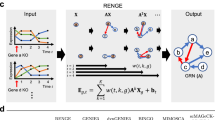
Figure 1 shows the main workflow of inferCSN, which includes: preprocessing scRNA-seq data (Fig. 1a), then combining pseudo time inference and GAMs to obtain the gene expression matrix containing cell annotation information and pseudo time information (Fig. 1b); Calculating the intersection point between two cell states based on the density of pseudo temporal information and then dividing all cells into multiple windows based on the intersection point; Constructing GRN in each window based on L0 and L2 regularization model (Fig. 1c, d); Building a reference network and using it to calibrate the cell type and state specific GRN (Fig. 1e–g). Experimental results on multiple simulated and real datasets show that: Firstly, the inferCSN has significant advantages in accuracy, efficiency, and robustness; Secondly, it can construct the GRN of T cells in different states within the tumor microenvironment at the single-cell level, and compare the regulatory networks in different states can reveal immune suppression related signaling pathways; Thirdly, it can construct the GRNs of different tumor subclons and comparing the regulatory networks to identify the immune escape pathways dominated by different subclons, which helps to achieve precise immunotherapy. Finally, inferCSN can help investigate the development trend of immunosuppressive molecules of immune cells and tumor cells and test their correlations as the tumor evolves.

Fig. 1: The workflow of inferCSN.

a Preprocessing of scRNA-seq data. b Pseudotime inference and generalized additive model are used to analyze the preprocessed gene expression data to obtain a gene expression matrix containing cell annotation information and pseudotime information. c, d The intersection of two different cell states is calculated based on the density of pseudo-time information, and all cells are divided into multiple windows based on these intersections. In each window, a sparse regression model with L0 and L2 regularization is used to construct a gene regulatory network (GRN). e–g Reference networks are constructed and used to calibrate cell type and state specific gene regulatory networks.

Results

To demonstrate the superiority of inferCSN, we conducted different experimental analyses from four perspectives: (1) comparing it with other methods to verify that our method is more accurate, efficient, and biologically interpretable in GRN construction; (2) we distinguished the different states of T cells and constructed GRNs corresponding to different states. Then, we compared GRNs of different states to explore whether inferCSN helps to discover signaling pathways related to immune suppression; (3) Subclonal differentiation was performed on tumor cells, and GRNs corresponding to different subclons were constructed. Then, the GRNs of different subclons were compared to explore whether inferCSN can help discover signaling pathways related to immune escape; (4) Simultaneously analyzing T cells and tumor cells in patients at the same clinical stage to observe whether there is a correlation between the two in suppressing the immune system.

Construction accuracy of inferCSN

First of all, we compared inferCNS with other popular methods, such as GENIE3⁵, SINCERITIES¹⁰, PPCOR¹⁸, LEAP⁹, and SCINET¹⁹, based on simulated and real datasets, respectively. Among these methods, GENIE3, SINCERITIES, PPCOR, and LEAP only need to provide gene expression matrix or both gene expression matrix and pseudo time information. Therefore, the inferCSN is set as a reference network free mode and compared with other methods on 200 simulated datasets. Note that SCINET relies on an external database and requires additional complex processing pipeline, so SCINET does not participate in computational complexity evaluation. In order to obtain the optimal AUROC and AUPRC on each dataset, all experiments were conducted on a server equipped with AMDRyzen9 5950 × 16 CPU, 128 G RAM, and Ubuntu 20.04.5 LTS system. The GENIE3 and inferCSN were set to run on 16 CPU cores, with other parameters defaulted; PPCOR and SCINET were tested according to default parameters; LEAP needs a parameter maxLag, which controls the maximum lag to be considered. According to the recommendation (do not use values greater than 1/3), 7 values were tested within the range of [0, 0.33]: 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, and 0.33, and the optimal parameters were selected; When inputting gene expression data with time information, SINCERITIES does not require any parameters. However, when using pseudo time information, according to the recommendation, the pseudo time values are discretely distributed to fixed windows, so the size of windows is set to be 5, 6, 7, 8, 9, 10, 15, and 20.

The results on simulated dataset: Table 1 shows the average AUROC of these five methods on different types of simulated datasets, such as Bifurcating (BF), Cycle (CY), Linear (LI) and long Linear (LL). On the BF dataset, the average AUROC of inferCSN is slightly lower than PPCOR, and higher than all other methods on other datasets. “ALL” in Table 1 represents the average AUROC on all 200 simulated datasets.

Table 1 The AUROC on different types of datasets

The AUROC results of five methods on four types of datasets were depicted in Fig. 2. Note that there is no significant difference in AUROC among inferCSN, GENIE3, and PPCOR on the BF dataset, while inferCSN performs significantly better than all other methods on other datasets. The box plot can reflect the distribution characteristics and degree of dispersion of results. In Fig. 2, the AUROC distribution of inferCSN is dense on different datasets, indicating that inferCSN has stable performance in constructing CSNs among different scales datasets.

Fig. 2: The AUROC results of five methods.

The AUROC results of 5 different methods are based on four different datasets: bifurcating (BF, a), cycle (CY, b), linear (LI, c) and long linear (LL, d). Use Wilcoxon test to evaluate the performance of these methods, with significance levels represented by “ns” and asterisks “*”. The “ns” represents P > 0.05, “*” represents P < 0.05, “**” represents P < 0.01, “* * *” represents P < 0.001, “***” represents P < 0.0001. P > 0.05 indicates that there is no significant difference between the two methods. The smaller the P value, the more significant difference between the two methods.

Table 2 and Fig. 3 show the AUPRC of these five methods on different types of datasets. Except for the BF dataset, the average AUPRC of inferCSN is higher than that of other methods. “ALL” in Table 2 represents the average AUPRC on all 200 simulated datasets.

Table 2 The Average AUPRC on different types of datasets

Fig. 3: The AUPRC results of five methods.

The results of 5 different methods are based on four different datasets: bifurcating (BF, a), cycle (CY, b), linear (LI, c) and long linear (LL, d). Use Wilcoxon test to evaluate the performance of these methods, with significance levels represented by “ns” and asterisks “*”. The “ns” represents P > 0.05, “*” represents P < 0.05, “**” represents P < 0.01, “* * *” represents P < 0.001, “***” represents P < 0.0001. P > 0.05 indicates that there is no significant difference between the two methods. The smaller the P value, the more significant difference between the two methods.

Figure 2 shows that there is no significant difference in AUROC between inferCSN and GENIE3 on the BF dataset, but their performance is significantly better than other methods on other datasets.

Experimental results on real datasets: inferCSN and other methods were run ten times on real datasets, and the average AUROC and AUPRC were calculated. The results in Fig. 4 show that inferCSN has significant performance advantages on real datasets.

Fig. 4: The AUROC and AUPRC results on real datasets.

The inferCSN, GENIE3 and other methods were run 10 times on the real datasets, and the average AUROC and AUPRC results were calculated. The AUROC results are shown in a, and the AUPRC results are shown in b.

Robustness evaluation of inferCSN

The number of cells may have certain impact on the GRN construction accuracy. To test the impact of cell number on accuracy, AUROC and AUPRC were compared for each method using simulated datasets containing 100, 200, 500, 2000, and 5000 cells. 40 benchmark datasets were tested for each cell count, and the average of AUROC and AUPRC were depicted. Figure 5 shows the average AUROC and AUPRC for all methods on these datasets. It can be observed that compared to other methods, inferCSN achieved the highest AUROC and AUPRC on all datasets, and was able to robustly construct CSNs on datasets of various scales.

Fig. 5: The AUROC and AUPRC of five methods on datasets with different numbers of cell.

The AUROC and AUPRC of each method were compared using simulated datasets containing 100, 200, 500, 2000, and 5000 cells. AUROC and AUPRC results are presented in panels a and b, respectively.

Computational complexity of inferCSN

The number of cells and the number of genes are the key factors affecting the computational efficiency of the GRN construction method. In order to analyze the effect of the number of cells on the running time, each dataset was fixed at 3,000 genes, and the number of cells was set to 2000, 4000, 6000, 8000, and 10,000, respectively. In order to analyze the effect of the number of genes on the running time, each dataset was fixed at 10,000 cells, and the number of genes was tested to be 600, 1200, 1800, 2400, and 3000 genes. The inferCSN and GENIE3 enable CPU multithreading acceleration on 24 CPU cores. Each method was run 10 times, resulting in an average running time as shown in Fig. 6. Compared to the GENIE3 method, inferCSN is more efficient as the number of cells and genes increases. Only some of the time points for the GENIE3 method are shown in the figure because the GENIE3 method takes too long to construct GRNs as the size of the dataset increases. Although both inferCSN and SINCERITIES construct CSNs based on regression models, there is a significant difference in the efficiency of these two methods. The reason why the running time of SINCERITIES is not shown is because the it takes too long to handle such large-scale datasets. These results further validate the effectiveness of adding the L2 regularization term to inferCSN model, which can effectively address the high-dimensionality and sparsity characteristics of scRNA-seq data. In addition, the inferCSN also supports specifying TFs lists, which greatly reduces the computational complexity. The PPCOR is a kind of univariate correlation method, and thus also has a great advantage in terms of running time, but it is less robust, especially when dealing with datasets of different types. To further demonstrate the applicability of inferCSN to large-scale datasets, we validated its accuracy and computational performance on datasets with 20,000 cells and 5000 genes, and the results are shown in Supplementary Table 1.

Fig. 6: Running time of five methods on datasets with different cell and gene numbers.

a each dataset is fixed to 3000 genes, and the number of cells is 2000, 4000, 6000, 8000, and 10,000. b each dataset is fixed to 10,000 cells, and the number of test genes is 600, 1200, 1800, 2400, and 3000. Each method was run 10 times, and the average running time was calculated to obtain the results.

In sum, inferCSN exhibits the best overall performance. Even without using a reference network, inferCSN still has satisfactory performance. It is worth noting that SINCERITIES performs poorly in terms of AUROC, AUPRC, and running time. The main reason may be that the accuracy of SINCERITIES heavily relies on the accuracy of pseudo time information. Although the inferCSN also utilizes pseudo time information when constructing CSN, the strategy of dividing time windows overcomes the information difference caused by pseudo time density on one hand. On the other hand, it also reduces the requirement for the quality of pseudo temporal information, thereby improving the robustness of inferCSN.

Interpretability of inferCSN

We selected a simulated dataset containing 18 genes and calculated the AUROC and AUPRC values for each method. Except for SINCERITIES, which had the lowest AUROC and AUPRC values, all other methods performed well, as shown in Table 3. However, indicators such as AUROC and AUPRC cannot fully reflect the advantages and disadvantages of the CSN inference method.

Table 3 The AUROC and AUPRC results on simulated datasets with 18 genes

Consequently, the networks obtained by different inference methods will be compared with the gold standard network. In Fig. 7, the results of PPCOR and LEAP differ significantly from the gold standard. GENIE3 and inferCSN perform similarly on AUROC and other indicators, but it can be seen from Fig. 7 that inferCSN constructs a better network. For example, inferCSN can recognize g1 → g18 as negative regulation, but GENIE3 mistakenly identifies it as positive regulation. In Fig. 7, it can be observed that the regulatory effect of g18 → g1 does not exist, but inferCSN identifies it as a negative regulatory effect. Although inferCSN identifies some incorrect regulatory relationships, it still has advantages over other methods overall.

Fig. 7: The heat maps of gold network and networks constructed by different methods.

The Gold is the heat map of the gold standard network. The networks obtained by other different inference methods (such as inferCSN, GENIE3, etc.) are compared with the gold standard network.

Both SINCERITIES and inferCSN use regression models, but their performance shows significant differences. The advantage of inferCSN is that it does not require complex parameter settings, while SINCERITIES requires a lot of parameter adjustments, and different parameter settings have a significant impact on performance. Moreover, SINCERITIES has very high requirements for the quality of pseudo time information, and as shown in Fig. 7, the network constructed by SINCERITIES differs significantly from the gold standard network.

Dynamic regulatory network inference and immune regulation analysis of T cells

Previous studies have shown heterogeneity in infiltrating CD8⁺T cells in the tumor microenvironment (TME), including immature T cells characterized by CCR7, LEF1, and TCF7, cytotoxic effector T cells characterized by CX3CR1, PRF1, and KLRG1, and dysfunctional T cells²⁰. The obvious feature of dysfunctional T cells is an increase in coinhibitory receptors, such as PD1, LAG3, TIM3, CTLA4, and TIGIT. Compared with effector CD8 + T cells, their effector function is limited. Dysfunctional T cells can be further divided into subgroups, such as pre dysfunctional, progenitor depleted, and ultimately depleted T cells.

The state transition of CD8⁺T cells in TME during dysfunction is jointly regulated by TFs and their related cofactors. In order to gain a deeper understanding of the regulatory mechanisms driving the transition of CD8⁺T cells from immature T cells to dysfunctional T cells, inferCSN was used to construct CSN on 2508 T cells in different states. Firstly, we inferred the pseudo temporal information and combined it with the cell state to divide these T cells into four windows, and then each window is mainly composed of cells between the intersection points of two time densities, as shown in Fig. 8. Among them, Window 1 (W1) is mainly composed of initial and intermediate state cells, W2 is mainly composed of intermediate state and GZMK marked prefunctional cells, W3 is mainly composed of GZMK characterized prefunctional cells and ZNF683 prefunctional cells, and W4 is mainly composed of ZNF683 prefunctional cells and dysfunction cells.

Fig. 8: The CD8 + T cell window divisions.

Window 1 (W1) was mainly composed of cells in the initial and intermediate states, W2 was mainly composed of intermediate states and GZMK-labeled prefunctional cells, W3 was mainly composed of GZMK marked prefunctional cells and ZNF683 prefunctional cells, and W4 was mainly composed of ZNF683 prefunctional cells and dysfunctional cells.

Then, we constructed CSNs for each window separately to analyze the regulatory relationship driving the transition of cell states. After constructing CSN for each window, a systematic comparison was conducted on the TFs and gene nodes of CSNs. The results show that there is a significant overlap of nodes between the CSNs of each window, as shown in Fig. 9. Figure 9a shows the overlap status of TFs nodes in each window, Fig. 9b shows the overlap status of gene nodes in each window, and the red bar chart shows the common nodes of CSN corresponding to these four windows.

Fig. 9: Overlapping status of TFs and gene nodes in each window.

a the overlap of TFs nodes in each window. b the overlap of gene nodes in each window.

The Jaccard coefficient (Jaccard ∈ [0,1]) is used to measure the similarity between two networks. A larger Jaccard coefficient indicates that the two CSNs are more similar, that is, there are more identical regulatory relationships in these two networks. We calculated the average Jaccard coefficient between the CSNs of each window, as shown in Table 4. The results indicate that although the CSNs of the four windows have a high proportion of duplicate nodes, the average Jaccard coefficient of all possible intersecting windows is only 0.165. It means that the regulation relationship in CSNs of different windows is significantly different, and a large number of reconnections have taken place in these same nodes, that is, TFs basically reconnect to different targets along the state transition process of T cells, and the same TFs dynamically regulate different genes, which further indicates that there is a complex interaction relationship between immune cells and tumor cells in TME.

Table 4 The Jaccard coefficients between different windows

Under different cellular states, reconnecting regulatory relationships may alter the network centrality of genes in CSN. Hub genes with high centrality interact with many other genes in specific cellular environment, therefore, it is assumed that they are more likely to play an important role in maintaining specific functions of specific cell types. Next, we used indicators such as degree, proximity, betweenness, eigenvalues, and PageRank to evaluate the centrality of nodes. Finally, the top 60 nodes with the highest ranking were selected as key TFs. The Mfuzz clustering algorithm is commonly used to identify the dynamic expression patterns of RNA-seq data with temporal characteristics, and link the dynamic expression pattern features with gene function²¹. In this study, the Mfuzz clustering algorithm was applied to cluster the expression patterns of these 60 key TFs using the default parameter settings. By default, Mfuzz outputs clusters with the same temporal features, where the temporal features are divided into four windows. Finally, these 60 TFs are divided into four clusters with different expression patterns (Fig. 10a), as detailed in Table 5.

Fig. 10: Expression patterns and enrichment analysis results of TFs.

a The result of Mfuzz clustering. b The expression pattern of TFs in Cluster 1 shows an overall upward trend as the cell state changes. c The pathways enriched by key TFs.

Table 5 The key transcription factors

According to the results of Mfuzz clustering, the expression patterns of TFs in Cluster1 showed an overall upward trend with cell state transition, as shown in Fig. 10a, b.

KEGG enrichment analysis was performed on these key TFs, as shown in Fig. 10c, where “n” represents the number of genes in this cluster. These TFs in Cluster1 mainly involve pathways related to tumor development, differentiation, and transcription, such as transcriptional dysregulation in cancer and Th1 and Th2 cell differentiation pathways, which suggests that the role of these TFs in T cell state transition may be related to tumor immune escape. Studies have shown that ZNF48 induces replication stress²², which is one of the characteristics of many invasive tumors. ID2 is an important TF involved in the formation of terminal differentiated T cells²³. In summary, these results indicate that these TFs play an important role in the state transition of T cells, and inferCSN effectively reveals the key TFs and their pathways in T cell state transition, which is of great significance for a deeper understanding of T cell function and the regulatory mechanisms of the immune system.

In order to further understand the regulatory mechanism in the process of T cell dysfunction and more clearly compare the possible regulatory role of regulatory factors in cell state transition. We visualized the CSNs derived by inferCSN for 20 key TFs in Cluster 1 across different windows (Fig. 11a–d, corresponding to Windows 1, 2, 3, and 4, respectively).

Fig. 11: CSNs of 20 key TFs.

“Activation” on the legend indicates that the TFs promote the expression level of the target gene, while “Repression” indicates that the TFs inhibit the expression level of the target gene. a–d correspond to windows W1, W2, W3 and W4 respectively. The expression of 20 key TFs in Cluster1 in different windows derived from CSN by inferCSN.

From Fig. 11, it can be clearly seen that as the cell state changes, the number of TFs and genes increases in different windows of CSN, resulting in more complex regulatory relationships.

Dynamic regulatory network inference and immune escape analysis of tumor cells

Similar to the T cell analysis, inferCSN was used to construct GRNs and analyze immune escape pathways on 7 tumor cell datasets. For example, 2243 tumor cells were screened from GSE127465, including 486 Alveolar cells, 48 CXCL1 Cancer cells, 640 Pathological Alveolar cells, 46 Proliferating Cancer cells, and 1023 SOX2 Cancer cells. Then, inferCSN divided these 2243 cells into 4 windows (Supplementary Fig. 1).

Finally, we constructed CSNs for each window to discover key changes in regulatory relationships between adjacent tumor cell states. By comparing the TFs and gene nodes of CSNs in various windows, we found that there is a significant overlap of nodes between the CSNs in each window, as shown in Supplementary Fig. 2.

The results in Supplementary Table 2 indicate that some of the CSNs in the four windows have a high proportion of duplicate nodes, and the edges between the same nodes undergo a significant amount of reconnection. This means that during tumor cell state transition, TFs reconnect to different targets, and the same group of TFs dynamically regulates different genes. However, starting from window 3, although the Jaccard coefficients of CSNs in different windows are relatively large, the P-value is also high, indicating that some false positive edges may have appeared from window 3. Therefore, it is necessary to add more additional information to filter the network edges.

Similarly, in order to identify the nodes that play a crucial role in CSNs, the importance of the nodes is evaluated through metrics such as PageRank value and node centrality. Finally, the top 10 nodes with higher rankings were selected as key TFs, and the expression of these TFs in different windows was depicted in Supplementary Fig. 3.

In order to further understand the regulatory mechanisms driving the development of tumor cells and the regulatory roles of TFs during tumor cell state transition, we conducted KEGG enrichment analysis on these 10 key TFs (Supplementary Fig. 3) and found that these TFs are involved in some signaling pathways of NSCLC, such as TNF signaling pathway, GnRH signaling pathway, IL-17 signaling pathway, and PD-L1 checkpoint signal, indicating that these TFs may be related to tumor immune response. For example, EGR1 plays a crucial role in regulating cell growth, differentiation, survival, and immune response²⁴; NBKBIA²⁵ regulates the NF kB signaling pathway, controlling cell apoptosis, inflammatory response, immune response, etc.; YBX1 is an RNA binding protein that participates in tumorigenesis, regulates a series of transcription factors, and promotes the tumorigenesis of NSCLC²⁶.

Then, some network edges were filtered based on parameters such as edge weights, and the network connectivity of these TFs was visualized using inferCSN (Supplementary Fig. 4). Stress protein ATF4²⁷ can promote tumor cell growth through fibroblasts, which may be a good target for cancer treatment. ATF4 can regulate the expression of Col1a1 and collagen biosynthesis in perivascular cancer related fibroblasts, thus supporting angiogenesis and progression of melanoma and pancreatic cancer. We found that the network edge weight of ATF4 and COL1A1 is getting less and less in four different windows; SFPQ²⁰ can bind to the TXNIP promoter, causing transcriptional inhibition of TXNIP. It can be observed that the network edge weights between SFPQ and TXNIP are decreasing in different windows of the network, indicating that SFPQ may inhibit the transcription of TXNIP.

Correlation analysis of immune regulation between T cells and tumor cells

In order to further understand the immune regulatory mechanism between T cells and tumor cells, the inferCSN was used to construct CSNs for tumor cells and immune cells in the same clinical stage. Patients in the GSE148071 dataset were all in clinical stage III/IV, so inferCSN was used to further analyze the GSE148071 dataset with a total of 51912 cells. Because it is difficult to distinguish normal epithelial cells from malignant tumor cells using gene markers, copy number variation (CNV) has been applied to identify tumor cells²⁸. Firstly, CNV analysis was performed on the dataset using the CopyKat²⁹ package. The advantage of using the CopyKat package is that it can calculate the genome copy variation of a single cell without setting up a normal cell control group, thereby predicting whether it is a normal cell (diploid) or a tumor cell (aneuploid). After that, a total of 4543 tumor cells were screened, including 245 CXCL1 cancer cells, 7 CDKN2A cancer cells, 6 LAMC2 cancer cells, 1083 Proliferating cancer cells, and 3202 SOX2 cancer cells. Next, inferCSN constructs CSNs of 4543 tumor cells. The inferCSN adopts Monocle3⁸ for pseudo time inference, and combines different types of tumor cell differentiation trajectories and pseudo time information to divide these tumor cells into four consecutive windows, as shown in Supplementary Fig. 5. Meanwhile, 470 CD8 + T cells were recognized from GSE148071.

The changes between the networks of the consecutive windows may help to identify the key pathway by which normal epithelial cells transform into cancer cells. In LUAD, the proportion of alveolar cells and pathological alveolar cells is much higher than in LUSC. LUAD samples also have a high proportion of LAMC2 and CXCL1 cells. The proportions of CDKN2A and SOX2 cancer cells in LUSC samples are higher³⁰. Compared with LUAD specific cell types (alveolar carcinoma, pathological alveolar carcinoma, CXCL1 carcinoma), the more abundant cell types (SOX2, CDKN2A, proliferative carcinoma) in LUSC lag behind in pseudo time, suggesting that LUAD promotes the stem cell like phenotype of LUSC cells, so that LUSC cells have stronger invasiveness.

Next, these CSNs are constructed for each window. Then, metrics such as PageRank and point centrality were used to evaluate the importance of nodes and identify TFs nodes that play a critical role in CSN. Finally, 13 key TFs were selected, and their expression of these key nodes in different windows over time was depicted in Supplementary Fig. 6.

For example, TFs such as ATF3, FOS, and HES1 are highly expressed in Window1, and their expression levels also decrease with the change of windows. However, TFs such as YBX1, SOX2, and SMARCA5 are the opposite^31,32.

In order to further understand the regulatory mechanisms involved in the evolution of tumor cells and to more clearly compare the regulatory roles that TFs may play during tumor cell state transitions, we examined the regulatory relationships between TFs and genes in each window, as shown in Supplementary Fig. 7.

Further KEGG pathway enrichment analysis was conducted on important genes in each window (Fig. 12), and it was found that some pathways enriched in different windows were common. For example, pathways such as cell apoptosis and chemical carcinogenesis indicate that these pathways are the infrastructure for tumor development and are involved in different stages of tumor cells. Other pathways, including TNF signaling pathway (w2, w3, w4), PD-L1 expression in tumors, PD-1 checkpoint pathway in cancer (w1, w4), and MAPK signaling pathway (w1, w3), are only enriched in specific windows. These pathways are all closely related to tumor development^25,33.

Fig. 12: The KEGG enrichment analysis results in different windows of tumor cells in GSE148071.

The horizontal axis is -LOG10 (FDR). The larger the value, the more significant the difference, indicating that there are more genes enriched in the pathway.

T cells are the main target of immunotherapy for NSCLC³⁴. Based on the current understanding of CD8⁺T cell differentiation, activated naïve T cells differentiate into different effector T cells and memory T cells. In tumors, chronic T cell stimulation leads to dysdifferentiation and functional exhaustion, characterized by loss of effector function and inhibition of receptor expression³⁵. Next, CD8⁺T cells were first screened, and the cell status of CD8⁺T was analyzed and calculated using the ProjecTILs³⁶ package, resulting in 470 CD8⁺T cells in different states. Finally, 35 central memory T cells (CD8. CM), 122 effector memory T cells (CD8. EM), 21 depleted precursor T cells (CD8. TPEX), and 288 depleted terminal T cells (CD8. TEX) were selected for CSN inference of T cells. Then, the pseudo time values of each CD8⁺T cell state were calculated using Monocle3 and divided into three windows as shown in Supplementary Fig. 8.

Use inferCSN to construct CSNs for T cells in each window. Due to the relatively small number of T cell datasets, only three TFs (JUN, NFKBIA, ID2) were derived, and their expression patterns in different windows with time variation were shown in Supplementary Fig. 9. The JUN gene is closely related to metabolism, cell proliferation, and apoptosis. ID2 plays an important role in regulating gene expression and response intensity in CD8 + T cells³⁷.

Supplementary Fig. 10 shows that as the window changes, the weight relationship between the CD69 gene and TFs in CSN gradually decreases, and the number of TFs that are regulated by CD69 also decreases with the change of the window. Only two TFs in Supplementary Fig. 10c are regulated by CD69. In addition, it can be seen from Supplementary Fig. 10 that as the pseudo time changes, the number of effector T cells and memory T cells gradually decreases, indirectly indicating a decrease in the expression level of CD69.

From Fig. 13, it can be observed that as pseudo time passes, the expression of DUSP1 gene in T cells is positively correlated with JUN and NFKBIA, but the expression level gradually decreases, while it is negatively correlated with the expression of ID2. DUSP1 is abnormally expressed in various human tumors and is associated with the prognosis of tumor patients. DUSP1 has also been found to play a role in tumor chemotherapy, immunotherapy, and biological therapy. However, the role of DUSP1 in different tumor carcinogenesis may be controversial^38,39. The relationship between the three TFs and DUSP1 revealed in this study may provide new perspectives for understanding the tumor immune escape of NSCLC.

Fig. 13: The changing correlations between DUSP1 and 3 TFs.

The vertical axis represents the weight, and the horizontal axis W1, W2, and W3 represent different windows, showing the weight changes of three different gene pairs (JUN-DUSP1, ID2-DUSP1, and NFKBIA-DUSP1) in three different windows.

Finally, enrichment analysis was performed on CSNs from different windows (Supplementary Fig. 11), and it was found that key pathways related to T cell differentiation and cancer evolution, such as Th1 and Th2 cell differentiation, T cell receptor signaling pathways, antigen processing and presentation, Th17 cell differentiation, and cancer pathways, varied in enrichment at different windows, indicating changes in T cell state transition.

More importantly, comparing the regulatory analysis results of T cells and tumor cells, it can be found that as the tumor progresses, there is a correlation in the immune regulation between T cells and tumor cells. For example, the two contain some similar signaling pathways, including the pathways in cancer, T cell differentiation pathway, B cell differentiation pathway, and cell apoptosis pathway. But the difference is that the enrichment levels of these pathways are not consistent between the two (Fig. 12, Supplementary Fig. 11). The enrichment degree of pathways in tumor cells in Fig. 12 is the most significant, but in T cells in Supplementary Fig. 11, the enrichment degree is not significant. However, the enrichment degree of them gradually increases in both T cells and tumor cells as the window changes.

The tumor cell enrichment analysis in Fig. 12 also includes some immune related signaling pathways such as T cell receptor signaling pathway and B cell receptor signaling pathway. For the T cell receptor signaling pathway, its enrichment degree gradually decreases with the change of window in T cells. The enrichment of T cell signaling pathways in w1 and w2 is decreasing in tumor cells, but it is increasing in w3 and w4. These pathways may play different and important roles in LUAD and LUSC. IL-17 is a key pro-inflammatory cytokine primarily produced by Th17 cells, highly expressed in patients with various autoimmune diseases. It is a major pathological cytokine and therapeutic target for many autoimmune diseases and cancers. In this study, as T cells developed in different states, the degree of IL-17 pathway enrichment gradually increased. At present, research has found that the IL-17 family genes play a promoting role in lung cancer, but the expression and function of IL-17A and IL-17B in lung cancer have not been fully elucidated, and larger sample size studies are needed⁴⁰. The enrichment analysis results of different windows of tumor cells in Fig. 12 show that the degree of IL-17 signaling pathway enrichment gradually increases from w2, indicating that it plays a promoting role in tumor differentiation. For w1, its signaling pathway has the highest significance, which means that the expression level of IL-17 family mRNA may be related to specific NSCLC histological types. For example, the upregulation frequency of IL-17, IL-17 b, and IL-17c mRNA in LUSC is lower than that in LUAD⁴⁰. Therefore, it is necessary to pay attention to the relationship between IL-17 and the progression of NSCLC.

In addition, based on the CSNs of tumor cell and T cell, we found that some TFs and genes play important roles together, and the presence of these genes is also found in some common signaling pathways. For example, the NFKBIA is not only a highly expressed immune checkpoint related gene in effector T cells, but also the NFKBIA signaling pathway may play an important role in the progression of tumor cells⁴¹.

Discussion

The inferCSN method proposed in this study outperforms current mainstream methods in multiple metrics. The comprehensive experimental results on simulated and real datasets show that inferCSN outperforms GENIE3 and other methods in accuracy metrics such as AUROC; The scRNA-seq data usually contains tens of thousands of cells, and traditional methods are either difficult to process directly or require a heavy computational burden. Our inferCSN shows significant improvement in computational efficiency. Compared with the gold standard network, inferCSN also has certain advantages in terms of network interpretability and stability. The main reasons why the inferCSN method can achieve the above advantages are:

• (1) The inferCSN uses the L0 regularization method to identify the correlation between target genes and TFs. Experiments have shown that the L0 regularization method can not only effectively identify high-order regulatory relationships between multiple TFs and target genes, but also avoid artificially setting thresholds, which helps to reduce false positives and significantly improve the accuracy and sparsity of network inference.

• (2) Pseudo time trajectories can simulate the dynamic differentiation process of cells, including temporal changes in gene expression. Fully utilizing such a dynamic differentiation process can improve the accuracy and biological significance of regulatory relationship recognition.

• (3) After distinguishing cells of different types and states, the Gaussian kernel density estimation method is used to combine cell state and pseudo time information, dividing cells into different windows to eliminate information differences caused by pseudo time density. The inferCSN is no longer a static model, but a dynamic CSN inference method, which helps to examine the changing trend of regulatory network as tumors occur and develop. In addition, the CSN is specific to cell type and state.

• (4) The regulatory relationship constructed solely based on the trend of changes in TFs and target genes may lack biological significance. Introducing prior information such as reference networks can help improve the interpretability of the network.

Therefore, the inferCSN method can be used to analyze the GRN of immune cells in different states within the tumor microenvironment at the single-cell level, compare the differences in regulatory networks under different T cell states, and discover immune suppression related signaling pathways. Moreover, this method can compare the GRNs of different tumor subclons to identify the immune escape pathways dominated by different subclons, which helps to achieve precise immunotherapy.

Although inferCSN has achieved certain advantages, it still needs improvement. For example, the edges between nodes in CSN are established based on statistical relationships, but in fact, even if the expression level of TFs remains unchanged, the expression level of target genes may also change. Although external reference information is embedded in inferCSN, the construction method of the reference network may still result in some false positive edges in the regulatory network. Therefore, it is still necessary to reasonably integrate other types of data (such as ATAC-seq data) for CSN inference methods.

Methods

Simulated and real datasets

We collected 24 NSCLC patients’ scRNA-seq dataset (The 10 NSCLC patients were downloaded from Philip et al.’s study⁴², and another 14 NSCLC patients’ were downloaded from the GEO database⁴³) and 200 benchmark scRNA-seq datasets to evaluate the performance of inferCSN¹⁴. The logarithmic transformation on fragments per kilobase million (FPKM) values were calculated, and genes expressed in less than 10% of cells were filtered out. 800 protein coding genes with the highest average expression value were selected for constructing CSNs. The preprocessed dataset contains 42,369 cells from 6 cell types, including 8288 tumor cells, 13,640 conventional T cells, 6086 natural killer cells (NK), 5738 CD8 + T cells, 2531 plasma cells, and 6068 B cells.

We used inferCSN to construct regulatory networks of T cells in different states, in order to demonstrate its practical application in discovering pathways related to T cell immune function inhibition. In this study, preprocessing techniques were performed on 14 NSCLC patients downloaded from the GEO database, such as extracting the count expression matrix of CD8 + T cells, removing genes with average counts less than 1, normalizing the counting matrix, and performing logarithmic transformation. Finally, 12,306 protein coding genes and 2508 CD8 + T cells were obtained, including 303 naive cells, 206 intermediate cells, 674 GZMK labeled pre-dysfunctional cells 832 ZNF683 labeled pre-dysfunctional cells and 439 dysfunctional cells spanning six different CD8 + T cell states.

Moreover, we also used inferCSN to construct regulatory networks of tumor cells in different subclones, in order to demonstrate its practical application in discovering pathways related to tumor immune escape. Here, we collected a total of 224,611 cells from 7 publicly available datasets: GSE13190728, GSE13624640, GSE14807142, GSE15393544, GSE127465, GSE11991149, and KU_ Loom (https://gbiomed.kuleuven.be/scrnaseq-nsclc). After preprocessing, there were 3385 alveolar cells, 1462 CXCL1 cancer cells, 345 LAMC2 cancer cells, 3017 pathological alveolar cells, 279 proliferating cancer cells, and 2169 SOX2 cancer cells.

The 200 benchmark scRNA-seq datasets was generated by the Boolean differential equation simulation¹⁴ proposed by Praapa et al., which includes four different types of time trajectory information, such as Bifurcating (BF), Cycle (CY), Linear (LI) and long Linear (LL). Each kind of time trajectory contains 50 datasets covering different cell counts (2000, 4000, 6000, 8000 and 10,000).

Experimental configuration and evaluation metrics

For performance evaluation with benchmark networks, simulated scRNA-seq datasets are generated by specifying regulatory relationships. The performance evaluation on the real scRNA-seq dataset used 260,962 gold standard positive gene pairs provided by the HumanNet database as the benchmark network⁴⁴.

We compare the inferred CSN with the reference benchmark network, and count the number of true positive (TP), true negative (TN), false positive (FP), and false negative (FN) edges to calculate metrics such as true positive rate (TPR, Formula 1), false positive rate (FPR, Formula 2), Precision (Formula 3), and Recall (Formula 4).

$${\text{TPR}}=\frac{{TP}}{{TP}+{FN}}$$

(1)

$${{FPR}}=\frac{{FP}}{{TN}+{FP}}$$

(2)

$${\text{Precision}}=\frac{{TP}}{{TP}+{FP}}$$

(3)

$${\text{Recall}}=\frac{{TP}}{{TP}+{FN}}$$

(4)

Calculate the area under receiver operating characteristic curve (AUROC) using FPR as the horizontal axis and TPR as the vertical axis, and calculate the area under precision recall curve (AUPRC) using Precision and Recall. When calculating AUROC and AUPRC, only the regulatory direction of the TF-gene regulatory relationship was considered, without considering whether the regulatory relationship was activated or inhibited. The higher the AUROC and AUPRC, the higher the accuracy of the method in constructing the CSN.

Combining pseudo time inference and generalized additive models

Monocle3⁸ aims to help researchers understand the biological processes at the single-cell level, including cell development, state transition, and cell type recognition. Monocle3 adopts uniform manifold approximation and projection (UMAP) for dimensionality reduction, then divides cells into discontinuous trajectories using the PAGA algorithm, and finally calculates the pseudo time. Slingshot is also a pseudo temporal inference method⁴⁵, which applies principal component analysis (PCA) by default, and then uses the minimum spanning tree method to infer the hierarchical structure of cell clusters and align cells in pseudo time. Because inferCSN requires temporal information reflecting the dynamic differentiation of cells (Fig. 1a), Slingshot and Monocle3 were integrated into inferCSN for inferring the pseudo time, and then cells were sorted based on the obtained pseudo time information⁴⁶. Meanwhile, we selected the branch with a higher number of cells for subsequent window partition from the pseudo time results.

The generalized additive model (GAM) is a regression model that can eliminate the non-linear relationship between the dependent variable and the independent variable by smoothing the independent variable. It uses a smooth spline function to capture the relationship between gene expression and time, in order to identify dynamic genes related to temporal changes. The GAM is formulated as ${{\rm{y}}}_{{\rm{i}}}={{\rm{\beta }}}_{0}+{\rm{f}}({{\rm{t}}}_{{\rm{i}}})+{{\rm{\epsilon }}}_{{\rm{i}}}$, where ${{\rm{y}}}_{{\rm{i}}}$ is the expression value of the gene, ${{\rm{t}}}_{{\rm{i}}}$ is its corresponding pseudo time, ${\rm{f}}({{\rm{t}}}_{{\rm{i}}})$ is the nonlinear smoothing function, and ${{\rm{\epsilon }}}_{{\rm{i}}}$ is the error term following a normal distribution. The gam package implements the GAM, and the smoothness of the model is automatically determined by Generalized Cross Validation, and default parameters are used in this study. The gam package can simultaneously calculate the residual variance of the GAM model and use F-test to evaluate the statistical significance of the model, thereby obtaining the P value of each gene. To control for false positives introduced by multiple hypothesis testing, we used the Bonferroni method to correct for P values and ultimately selected genes with adjusted P values less than 0.0001 as dynamic genes.

Sliding windows

It is necessary to use sliding windows for processing temporal data, otherwise critical time points may be missed. Meanwhile, since the distribution of cells in pseudo temporal information is not uniform, the regulatory relationship tends to lean towards the high-density regions of cells. To address such an issue, assuming that there are different cell states in each cell type, Gaussian kernel density estimation method is used to calculate the density of different cell states based on the pseudo time information. The basic idea of kernel density estimation is to apply a kernel function to fit each data point, and then estimate the probability density function by weighted averaging these kernel functions. The Gaussian kernel density estimation (Formula 5) uses a Gaussian kernel function (Formula 6) for each data point.

$$f\left(x\right)=\frac{1}{n}\mathop{\sum }\limits_{i=1}^{n}{K}_{h}(x-{x}_{i})$$

(5)

where n is the size of the dataset, ${x}_{i}$ is the i-th data point, and K_h(x-x_i) is a Gaussian kernel function centered on x_i with a bandwidth of h.

$$K\left(x\right)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{{x}^{2}}{2{\sigma }^{2}}}$$

(6)

where x is the distance between the data point and a given center point, and $\sigma$ is the bandwidth parameter of the kernel function, which determines the width of the kernel function and thus affects the smoothness of the estimated probability density.

Then, we calculate the intersection point between the density curves of two adjacent cell states. If there are multiple intersection points between the two cell states, use the intersection point at the highest density point as the benchmark to redraw the boundary and set sliding windows with variable width (Fig. 1c). Consequently, the interval between the two consecutive intersection points is considered as a time window. Finally, all cells are divided into multiple windows, each consisting of cells with continuous states. The density function implemented in R package stats achieves the Gaussian kernel density calculation, and default parameters are used.

Construction of gene regulatory network based on L0 regularization

Hazimeh et al. proposed a combination optimization algorithm using local combinatorial optimization and cyclic coordinate descent⁴⁷, which effectively solved the L0 regularization problem. In this study, the combination of L0 and L2 regularization term, known as the L0L2 sparse regression model (Formula 7), can be applied to overcome the characteristics of high dimensionality, high sparsity, and low signal-to-noise ratio of scRNA-seq data.

$${{\arg }}\mathop{\min }\limits_{\beta \in {{\mathbb{R}}}^{p}}\frac{1}{2}{\left\Vert {\boldsymbol{y}}-{\boldsymbol{X}}\beta \right\Vert }_{2}^{2}+{\gamma }_{1}{\left\Vert {\boldsymbol{\beta }}\right\Vert }_{0}+{\gamma }_{2}{\left\Vert {\boldsymbol{\beta }}\right\Vert }_{2}^{2}$$

(7)

where$\,{\bf{y}}$ represents the expression level vector of the $i$-th target gene in the matrix (${\boldsymbol{Y}}\in {{\mathbb{R}}}^{g\times m}$, ${\boldsymbol{Y}}$ is a matrix of m samples and g target genes), ${\boldsymbol{X}}$ is a matrix of m samples and p TFs, ${\boldsymbol{\beta }}$ is a regression coefficient vector, ${\gamma }_{1}$ controls the number of non-zero coefficients of TFs, and ${\gamma }_{2}$ controls the amount of shrinkage caused by L2 regularization.

The L0L2 model is used to construct the CSN for each window (Fig. 1d), in which the weight of the TF-gene regulation is defined as Formula 8. Note that the n-1 cell specific regulatory network corresponds to n-1 windows, where n represents the number of cell types or cell states.

$${w}_{i}=\frac{1}{n-1}\mathop{\sum }\limits_{1}^{n-1}\left|\frac{{\beta }_{i}}{{\sum }_{1}^{p}|{\beta }_{j}|}\right|$$

(8)

where p represents the number of TFs and $\left|{{\boldsymbol{\beta }}}_{i}\right|$ is the absolute value of the regression coefficient of TF-gene pairs in each window. Next, each CSN is merged with the adjacency matrix of the reference network (Fig. 1e) and normalize the matrix to obtain the CSN for each cell type (Fig. 1f).

Construction of reference network

The protein coding genes defined by the consensus coding sequence database (CCDS)⁴⁸ are used for constructing a reference network. In this study, building a reference network involves the following four steps:

Step 1: Use the Bayesian method provided in the R package SAVER⁴⁹ to calculate the missing values in the scRNA-seq count matrix, and then exclude genes with zero values greater than 99% in each cell.

Step 2: Use the NormalizeData function of the R package Seurat to logarithmically normalize the matrix derived, then calculate the Pearson correlation coefficients (PCC) between gene pairs, and only retain edges with PCC > 0.8.

Step 3: Use the R package MetaCell to denoise the matrix⁵⁰, and then use the mcell_ MC_ From_ Coclust_ Balanced function with the parameters K = 30 and alpha=2 to generate a metacell matrix, and then remove cells with UMIs less than 500. After that, we calculate the PCC network between gene pairs based on the metacell matrix.

Step 4: Use R package bigSCale2 to perform Z-score transformation on the processed matrix⁵¹, and use the transformed Z-score matrix to calculate the PCC network.

The PCC networks obtained in steps 2, 3, and 4 were merged to obtain a reference network with 1,125,494 edges. And Bayesian models and log likelihood score (LLS) are used to evaluate the accuracy of the reference networ⁵². The LLS is calculated for the reference network sorted by weight, as shown in Formula 9.

$${LLS}=\log \left(\frac{\frac{P\left(L|D\right)}{P\left({{\neg }}L|D\right)}}{\frac{P\left(L\right)}{P\left({{\neg }}L\right)}}\right)$$

(9)

where L is the gold standard positive gene pair in reference network D, $P(L| D)$ and $P({{\neg }}L| D)$ represent the positive and negative probabilities of gold standard gene pairs in the given dataset, $P(L)$ and $P({{\neg }}L)$ represent the probabilities of gold standard positive gene pairs and negative gene pairs, respectively.

In sum, a threshold is set to filter out low signal or noise interactions. Only when the weight value of a gene pair exceeds this threshold, the interaction between the gene pair is considered significant in the corresponding cell type or state. Next, these significant interactions are compared with the reference network. If a gene pair exists in the reference network and its weight value passes the threshold, the interaction is considered cell type specific and ultimately retained in the generated CSN.