Introduction

Generation and improper disposal of wastewater pose a significant threat to the environment and the availability of clean water, hindering sustainable human development1. Currently, the global annual production of wastewater ranges from 360 to 380 billion m3 2,3, with projections indicating a 24% increase by 2030 and a substantial 51% rise by 20502,3. Alarmingly, nearly half (48%) of this wastewater is directly released into the environment without proper treatment, especially in developing nations3. Contaminated water sources contain complex pollutant mixtures, whose complexity is intensified by human resource exploitation4,5,6. This complexity challenges the achievement of the UN’s Sustainable Development Goal 6.3 that aims to reduce untreated wastewater by half and enhance global recycling and safe reuse by 20307. To address these challenges, a long-term, nature-based solution is crucial, which is capable of simultaneously addressing multiple pollutants in a cost-effective way and with high efficiency and low energy consumption, and which is particularly suitable for deployment in developing regions3,7,8,9.

Globally recognized for their effectiveness and cost efficiency, constructed wetlands (CWs) is a nature-based solution for wastewater treatment8,10,11,12,13. Comparative financial analyses highlight the advantage of CWs, with capital, energy consumption, and maintenance costs collectively amounting to only 50, 28, and 20% of those associated with conventional wastewater treatment plants (CWTPs)14. The primary objective of CWs is universal contaminant removal effectiveness15,16. Over recent decades, extensive scholarly efforts have delved into various aspects of CWs, such as pollutant removal, influencing factors, operational mechanisms, engineering design, managerial practices, and maintenance protocols11,15,17,18,19.

Despite the recognized advantages and advancements of CWs for pollution control, a contentious issue surrounds their feasibility and long-term effectiveness in concurrently addressing multiple pollutants8. While some short-term studies report collaborative pollutant removal through physicochemical and biological interactions within CWs, others suggest antagonistic microorganism interactions20,21,22,23. Studies have observed asynchrony in pollutant removal and found no significant differences in nitrogen and phosphorus removal efficiency24,25. Collectively, the obtained results indicate synergistic, antagonistic, or neutral relationships in pollutant removal processes26,27. Moreover, pollutant removal in CWs exhibits temporal variations, prompting a global inquiry into the sustainability of wetland performance over operational durations8,13,28,29,30,31,32,33,34,35,36,37. A systematical quantification of the relationships among pollutant removal processes in CW systems holds significant importance for global sustainable wastewater management37.

The pollutant removal mechanisms of wetlands are a topic of significant focus in environmental science, involving physical, chemical, and biological processes15,18,38. Although many studies concentrate/are conducted on wetland areas, temperature, and hydraulic conditions, a global understanding of the relative importance of these factors in pollutant removal is lacking8,15,34,39,40,41. Moreover, factors influencing pollutant removal may have specific thresholds, potentially causing abrupt ecosystem transformations42. Recognizing these thresholds is crucial for developing sustainable water governance policies as they determine ecosystem functionality and the nature of relationships, transitioning from synergistic to antagonistic43,44. A comprehensive global assessment of these factors is therefore essential for effective wastewater management42,43,45,46.

Despite the global expansion of CWs, their substantial land area requirement poses a challenge, particularly in developing regions8,47. The quest is to achieve high-quality effluents with reduced land area needs27,47,48. Recently, interest has surged in understanding the landscape-scale significance of small wetlands, driven partly by the adoption of the “Resolution on Protection and Management of Small and Micro Wetlands”27,48,49,50,51,52,53. In this context, small CWs are defined as CWs with an area of less than eight hectares48,53. To enhance restoration accuracy, it is crucial to comprehend how the characteristics of these small wetlands influence pollutant processing54,55,56. Currently, such knowledge is lacking globally, and urgent efforts are therefore needed to quantify the global contribution of small CWs to multiple pollutant processing27.

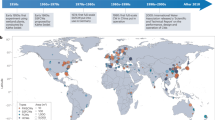
To address the existing knowledge gaps, we collected data from 364 global sites utilizing small CWs of up to eight hectares for wastewater restoration (Fig. 1a). These sites were distributed across Europe, Asia, America, Africa, and Oceania. Focusing on key pollution variables (COD, NH4+-N, TN, TP) that are closely regulated in wastewater management and impact factors (wetland operating time, wetland area, HLR, HRT, air temperature), our study aimed to answer three primary questions: (i) Can small CWs globally and effectively remove multiple pollutants, and what is the nature of their removal relationships (synergy, antagonism, or neutrality)? (ii) Can these removal relationships operate sustainably, and are they influenced by temporal thresholds? (iii) What is the key factor among design parameters, hydraulic conditions, and environmental factors in multiple pollutant removal, and are there corresponding significance thresholds? The answers to these questions will contribute to determining the long-term viability of small-scale CWs as solutions for global water pollution challenges.

Fig. 1: LMEM analysis showing positive bivariate relationships among the removal efficiency (%) of total nitrogen (TNRE), total phosphorus (TPRE), chemical oxygen demand (CODRE), and ammonium nitrogen (NH4+-NRE).
figure 1

a The research sites were geographically distributed across five continents: Asia, America, Africa, Europe, and Oceania. b, c Pairwise relationships between pollutant removals in LMEM. A standardized coefficient >0 indicates a positive effect between the two pollutant removals, and a standardized coefficient <0 indicates a negative effect. Error bars are 95% CIs. d, e The interrelationship of the four pollutant removals. Slope_PRE >0 indicates a synergistic relationship between the pairwise pollutant removals, and slope_PRE <0 denotes an antagonistic relationship.

Full size image

Results

Effectiveness of small CWs in removing pollutants

Over the past decades, the average removal efficiencies for TN, TP, COD, and NH4+-N in small CWs were 50.2% (n = 269, 95% confidence interval (CI) [47.2–53.2]), 50.5% (n = 276, 95% CI [47.4–53.7]), 65.2% (n = 214, 95% CI [62.1–68.4]), and 57.1% (n = 201, 95% CI [53.5–60.8]), respectively (Supplementary Figs. 1, 2). Small CWs present a potential solution for global control of organic matter and nutrients, achieving a 75th percentile removal efficiency for COD, TN, TP, and NH4+-N of 84.0, 68.8, 72.7, and 78.6%, respectively (Supplementary Fig. 2). More importantly, the outflow pollutant loading rates were significantly smaller than the inflow rates (Supplementary Fig. 2). This underscores the noteworthy capability of small CWs to effectively remove organic matter and nutrients (Supplementary Fig. 2). Furthermore, we identified significant variations in pollutant removal efficacy among different types of CW ecosystems8,57 and across various continents (Supplementary Fig. 3).

Interrelationships between pollutant removal processes

Our analysis suggests synergistic relationships between the pairwise pollutant removals as reflected by significant positive effects in the LMEMs (Fig. 1b, c, standardized coefficient = 0.27–0.64, p < 0.001, Supplementary Table 2). While the magnitude of these standardized coefficients varied among the twelve pairwise relationships, an overarching trend emerged: Thus, there was a positive interactive effect within the dataset of four organic matter and nutrient pollutants, where the removal efficiency of one pollutant was enhanced when also removing another pollutant.

To further characterize the synergies between pairwise pollutant removals, we calculated the slope coefficient between the two pollutant removals (hereafter expressed as slope_PRE) in the LMEMs (Fig. 1d, e), the removal of TN displayed an ascending trend with increasing removal of TP, COD, and NH4+-N (slope_PRE = 0.24–0.72, p < 0.001). Concurrently, TP removal was directly associated with increased removal of COD and NH4+-N (slope_PRE = 0.28–0.71, p < 0.001). Additionally, the proficiency in COD removal correlated positively with NH4+-N removal (slope_PRE = 0.24–0.39, p < 0.001). Consistently, structural equation modeling (SEM) analysis showed positive interactions of pairwise pollutant removals (Supplementary Fig. 5 and Supplementary Table 8, standardized path coefficient, b = 0.31–0.59, p < 0.001). These findings underscore the strong synergistic relationships between the removal of organic matter and nutrients in small CWs on a global scale.

Furthermore, to assess the consistency of this trend at a finer-scale level, we examined the correlation between pairwise pollutant removals in four distinct types of CWs. A total of 43 out of 48 examined pairwise interactions were characterized by significant positive effects, consistently spanning all four distinct CW types (Supplementary Fig. 6, p < 0.05). Additionally, we extended our analysis to encompass 56 pairwise relationships involving the removal of the four pollutants across five continents, namely Asia, America, Africa, Europe, and Oceania. Remarkably, a total of 48 of these relationships exhibited statistically significant positive effects across the five continents (Supplementary Fig. 6, p < 0.05). These findings provide compelling evidence of pronounced synergy at a global scale in the simultaneous removal of organic matter and nutrients within small CWs, independent of otherwise major differences in climate among the regions. This synergistic phenomenon has consistently and comprehensively manifested itself across all types of wetlands, including FCWs, FWSCWs, SSFCWs, and HCWs, and has transcended geographical boundaries to encompass five continents: Asia, America, Africa, Europe, and Oceania. Therefore, in the subsequent sections, we primarily focus on synergistic relationships.

Sustainability of the synergy of pollutant removals

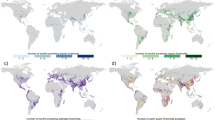
Among the 36 predicted pairwise relationships, the synergistic relationships among the four pollutant removals changed significantly over the operational duration since the slope_PREs varied between the three durations (Supplementary Fig. 7). These slope_PREs were further assessed by an ordinary least squares (OLS) test and were found to be significantly correlated with duration (Fig. 2, marked in peacock blue, p < 0.001). Specifically, there were two temporal trends for the alterations of slope_PRE, a positive temporal trend (Fig. 2a, b, d, g, i, j, marked in peacock blue, slope_OLS >0, p < 0.001) and a negative temporal trend (Fig. 2c, e, f, h, k, l, marked in peacock blue, slope_OLS <0, p < 0.001). This underpins the influence of operating time on the effectiveness of CW systems for pollutant control.

Fig. 2: Predicting changes in the synergy between pairwise pollutant removals with observation duration.
figure 2

a, g Synergy between TNRE and TPRE. b, h Synergy between TNRE and CODRE. c, i Synergy between TNRE and NH4+-NRE. d, j Synergy between TPRE and CODRE. e, k Synergy between TPRE and NH4+-NRE. f, l Synergy between CODRE and NH4+-NRE. Slope_PRE >0 and p < 0.05 indicate a significant synergistic relationship between pairwise pollutant removals (red marks), and Slope_PRE <0 reflects an antagonistic relationship. Slope_OLS >0 indicates an increasing trend of slope_PRE with enhanced duration, and slope_OLS <0 denotes a decreasing trend. TNRE, TPRE, CODRE, and NH4+-NRE reflect the removal efficiency of total nitrogen, total phosphorus, chemical oxygen demand, and ammonium nitrogen, respectively. ***p < 0.01.

Full size image

Among the 12 pairwise relationships of the four pollutant removals, our inquiry using the Johnson-Neyman technique identified 11 distinct temporal thresholds delineating synergistic associations (Fig. 2, red marks, slope_PRE >0, p < 0.05). These duration thresholds ranged from 34.3 months (~3 years) to 142 months (~12 years) and varied across the four types of CWs (Supplementary Fig. 8). This means that the synergistic associations of small CWs begin to erode when the CW system has been in operation for 3 years when some of the 12 synergistic relationships for pollutant removals began to disintegrate (slope_PRE >0, p > 0.05). The synergistic performance of CWs collapses when they had run for more than 12 years when all the 12 synergistic relationships for pollutant removals had disintegrated (slope_PRE >0, p > 0.05) or even been replaced by antagonistic relationships (slope_PRE <0). These results highlight that the synergy of pollutant removals changed greatly during the operating period, and the sustainability (i.e., 3–12 years) of the synergistic performance of organic matter and nutrient pollutants was determined in these small CW systems.

Mechanisms underlying the synergistic relationships

The area sizes, HRL, HRT, and air temperature not only significantly affected the removal efficiency of the four pollutants (Supplementary Fig. 9) but also influenced the synergistic relationships between pairwise pollutant removals (Supplementary Fig. 10). We anticipated two potential trends in the synergistic relationship with changes in these influencing factors: (1) strengthening since the positive interactions of pairwise pollutant removals increased with an increase of influencing factors (Fig. 3, slope_OLS >0, p < 0.001) and weakening (slope_OLS <0, p < 0.001), possibly shifting towards antagonism since the positive interactions decreased with an increase of influencing factors. Similar phenomena were found in different types of CWs (Supplementary Figs 11–14).

Fig. 3: Predicting changes in the synergy between pairwise pollutant removals with environmental changes.
figure 3

Predicting changes in the synergy between pairwise pollutant removals with wetland area (a), HLR (b), HRT (c), and air temperature (d). Slope_PRE >0 indicates a synergistic relationship between pairwise pollutant removals. Slope_PRE <0 indicates an antagonistic relationship between pairwise pollutant removals, and slope_PRE = 0 denotes a neutral relationship between pairwise pollutant removals. The relationships between slope_PRE and area, HLR, HRT, and air temperature were assessed using OLS (blue marks). Slope_OLS >0 denotes a positive connection between slope_PRE with the factor, whereas slope_OLS <0 reflects a negative correlation between slope_PRE and the factor. *** indicates p < 0.001. Thresholds of area, HLR, HRT, and air temperature for significant (p < 0.05, red marks) and non-significant (p > 0.05, gray marks) slope_PRE values were calculated by using Johnson_Neyman. TNRE, TPRE, CODRE, and NH4+-NRE indicate the removal of total nitrogen, total phosphorus, chemical oxygen demand, and ammonium nitrogen, respectively.

Full size image

Furthermore, substantial threshold effects were found regarding the influence of wetland area, HLR, HRT, and air temperature on the synergistic interdependencies of pollutant removal. Specifically, a total of five, ten, ten, and 12 threshold values related to area size, HLR, HRT, and air temperature were identified for the 12 pollutant relationships under investigation, respectively (Fig. 3). Among the five thresholds for wetland area, the minimum value was 17,587 m2 (about 1.7 ha), and the maximum value was 43,349 m2 (about 4.3 ha) (Fig. 3a). The threshold values for HLR ranged from 0.45 m/d to 3.56 m/d (Fig. 3b) based on the ten thresholds of HLR. Similarly, the ranges of the HRT threshold and temperature were 8.2 days–96.6 days (Fig. 3c) and 20.2–30.2 °C (Fig. 3d), respectively. However, these thresholds varied across CW types (Supplementary Figs. 11–14). The 12 synergistic relationships governing the removal of the four pollutants were observed to be robust when area, HLR, HRT, and temperature remained below the designated minimum thresholds (optimal threshold) (red marks, slope_PRE <0, p < 0.05). However, as these factors surpassed the minimum thresholds, certain synergistic relationships began to exhibit signs of deterioration (gray marks, slope_PRE >0, p > 0.05). Notably, when these factors exceeded the maximum thresholds, the integrity of all 12 synergistic pairs associated with the removal of the four pollutants underwent complete disintegration (gray marks, slope_PRE >0, p > 0.05) or were even substituted by an antagonistic relationship (gray marks, slope_PRE <0). Therefore, appropriate critical thresholds should be established to assess the influences of wetland design parameters and hydrological and environmental conditions on the intricate interplay of pollutants.

To further disentangle the direct and main effects of these drivers on the synergistic relationships of pollutant removals, SEM analyses were performed with the presumed relationships among the interaction of pollutant removals and the four considered factors (Supplementary Table 8). The wetland area played a negative role (Fig. 4a and Supplementary Table 8, standard path coefficient (b) = −0.18–−0.3, p < 0.05) in directly shaping the interactions of pollutant removal. A similar finding was observed regarding the effects of HLR and air temperature, while HRT had a positive direct influence on the interactions of pollutant removals (Fig. 4a and Supplementary Table 9, b = 0.17–0.35, p < 0.05). We further found significant differences in the effects of these factors on the interactions of pollutant removal (Fig. 4b, One-way ANOVA, p < 0.001), with wetland area having the greatest effect (Fig. 4b, mean b = −0.23), followed by HRT (Fig. 4b, mean b = 0.22), which was consistent with the conducted Random Forest (RF) analysis (Supplementary Fig. 15). This means that small areas, rather than large wetlands, favor the maintenance of synergistic relationships in the pollutant removal process. Our analysis provided insight into the hierarchy of significance among wetland design areas, hydraulic characteristics, and environmental conditions, but it also underscored the critical imperative of identifying and comprehensively characterizing the principal determinants influencing the studied phenomena.

Fig. 4: Structural equation models (SEMs) showing the relationships between the interaction of the pairwise pollutant removals and wetland area, HLR, HRT, and air temperature and their average standardized effects.
figure 4

a Only significant pathways are shown (p < 0.05). Positive and negative associations are denoted by violet and brown arrows, respectively. The numerical values in proximity to the pathway arrows correspond to the standard path coefficients. Additionally, R2 signifies the proportion of variance elucidated for each dependent variable. The Comparative Fit Index (CFI) equals 1, RMSEA = 0, and the sample size is composed of 364 independent plots. b: Average standard path coefficients of wetland area, HLR, HRT, and air temperature. TNRE, TPRE, CODRE, and NH4+-NRE indicate the removal efficiency of total nitrogen, total phosphorus, chemical oxygen demand, and ammonium nitrogen, respectively.

Full size image

Discussion

We found (first question) that despite their limited area size, small-scale CWs had a high capacity to retain organic matter and nutrients from wastewater, even at high latitudes and high altitudes with cold climates (Supplementary Fig. 16). One possible reason for this relatively high capacity is that small-scale CWs, compared with large ones, have a large biochemical reaction area ratio (the ratio between the area occupied by biochemical reactions per unit of area), which enhances the biological, physical, and chemical reactions of pollutant removal processes (Supplementary Fig. 17)58,59. Small-scale CWs also seem to be well-adapted to relatively low temperatures (Supplementary Fig. 18) as judged from experimental studies60, and they provide conditions for synergistic interactions for the removal of different pollutants, as demonstrated in our study. Previous review studies have also pointed to synergistic effects of pollutant removal by small-scale CWs; however, these studies did not quantitatively assess the pollutant removal processes but were mostly narrative syntheses of individual case studies from different parts of the world8,10,11. The synergistic effects may be attributed to the integrated reaction system involving multiple processes (e.g., diversity and synergy of microbial communities, biological uptake, sorption and adsorption of substrates, and nutrient cycling) that can simultaneously remove multiple pollutants such as nutrients and organics8,57. We found that the synergy between organic matter and nutrient removal was weaker than that between nitrogen and phosphorus removal (Supplementary Fig. 19), reflecting the fact that the strength of the synergy between the different removal processes in CWs can vary. Although the strength of the synergy between the different removal processes in CWs can vary based on several factors, including the design of the wetland, environmental conditions, and the specific interactions between organic matter, nutrient removal (nitrogen and phosphorus), and microbial activity, proper management of the balance between organic matter and nutrient concentrations (e.g., COD:TN and COD:TP) is crucial to maximize the synergy of these removal processes in the wetland8,11,16,48,57,61. In theory, a stoichiometric COD/N ratio of 4.20 is deemed necessary for the denitrification process62. However, in practice, studies have confirmed that a COD/TN ratio >7 is necessary to achieve satisfactorily high denitrification62. An inflow COD/TP ratio >40 is generally desirable for inhibiting phosphorus release and promoting effective biological phosphorus uptake63. Moreover, we found that the synergistic interactions in HCWs were the greatest among the four CW types, followed by FWSCWs, SSFCWs, and FCWs in that order (Supplementary Fig. 6). In FWSCWs, wastewater can directly interact with wetland surface, promoting the dynamics of physical, chemical, and biological processes64. Increased hydraulic mixing in the surface of FWSCWs can transport pollutants to removal areas with plant uptake and microbial activity65. The dense surface vegetation in FWSCWs supports nutrient removal and microbial activity, facilitating the transformation and exchange of pollutants66. The open water surface of FWSCWs provides continuous aeration, sedimentation, and vegetation growth for pollutant removal65. In contrast, SSFCWs and FCWs offer more closed interactions with wastewater during treatment. SSFCWs rely on subsurface denitrification and microbial degradation, while FCWs mainly rely on the uptake of pollutants by floating vegetation13,31,67. In addition, HCWs are constructed by integration of the three other types of CWs, which maximizes the benefits offered by each system17. A recent review study also found that HCWs had the greatest pollutant treatment performance of the four types of CWs8.

The second question that we raised concerned the sustainability of synergistic relationships. Based on a systematic assessment of the sustainability of pollutant control by small CWs at a global scale8,19,28,37, we found that the threshold for maintaining synergistic relationships in the removal of various pollutants spans from three to 12 years. We emphasize the differences occurring in the direction (e.g., Fig. 2a, g) of synergistic relationships between different pollutant removals and highlight the variability in thresholds (e.g., Fig. 2a, b) as shown by the variations of the duration of synergistic interactions among the different pairwise contaminant removals (Fig. 2). For instance, the thresholds for the synergistic relationship of TN and TP removal were 113–122 months (Fig. 2a, g), while for the synergy of COD and NH4+-N removal it was only 34–43 months (Fig. 2f, i). Therefore, the assessment of CW sustainability should consider the type of pollutant rather than simply the removal performance of one pollutant, as this acknowledges the diversity of pollutants and the complexity of pollutant interactions, ultimately leading to more effective and holistic environmental management8,37. Previous assessments of the persistence of CWs have generally been based on the removal performance of a single or a few pollutants28,37, while only a few studies have considered the synergistic interactions of pollutant removal processes for evaluating the sustainability of CWs31,37. We also found that the duration thresholds for maintaining synergistic interactions varied among the four CW types (Supplementary Fig. 8), which may reflect differences in the design and operating characteristics of the CWs. For instance, FWSCWs and FCWs generally have areas of open water that can adapt to changing water levels, reducing the likelihood of hydraulic failure, whereas SSFCWs are prone to substrate clogging8. Our results thus emphasize the critical role that design and functionality play in achieving the treatment goals and their long-term viability under evolving environmental and societal conditions36. Overall, our study provides valuable insights for assessing the sustainability of CWs globally.

Our data collection exercise also revealed that monitoring data were rare on CWs that have been in operation for more than a decade. Therefore, strengthening long-term monitoring of CW performance would be a promising development. Moreover, for systems that only show short-term synergistic effects compared with the expectations based on our analyses (Fig. 2), additional management measures are needed. These could include aeration, adding electron donor substrates, or dredging8,68,69,70, as demonstrated by studies undertaken in the Czech Republic, Poland, and Brazil68,71,72. Similarly, most research on CWs has been conducted on data from only the first few years following their establishment, with a median duration of only three years36, making it difficult to elucidate long-term effects. Our study, however, enhances the confidence in the long-term viability of small-scale CWs as a solution for simultaneously controlling multiple pollutants and promoting water sustainability (Supplementary Figs. 23, 24)9,73.

Finally, our results also answered the third question. Thus, our study not only revealed significant effects of wetland area, HRT, HLR, and temperature on the synergistic relationship between nutrient and organic matter removal (Figs. 3, 4), but it also determined area size as the most influential factor (Fig. 4b). During the design phase, wetland area sizes are typically calculated based on hydraulic characteristics. However, in actual operation, the size of a wetland affects its hydraulic characteristics, including flow velocity, residence time, and flow pathways74. These characteristics, in turn, influence the contact time between pollutants and treatment media, such as the plant root zone and substrate, ultimately affecting pollutant removal10. The heterogeneity of wetland environments, including the density and diversity of plant species and microbial communities, is influenced by wetland area size, which is linked to pollutant removal efficiency74. Diverse biological communities often possess a broader range of pollutant uptake capacities, leading to a more comprehensive treatment40. Additionally, wetland area size is associated with their buffering capacity, including buffering and regulating environmental conditions, which can help to maintain stable environmental conditions, for instance, the pH level31,74. Stable environmental conditions are critical for the activity of microbes and for plant physiology10. Therefore, wetland area size influences the synergistic pollutant removal by affecting many aspects of CWs, such as microbial activity, plant density and diversity, hydraulic characteristics, environmental stability (e.g., pH), and pollutant load and mixing47,66,67. The optimal threshold of area size for maintaining the synergistic relationships was about 1.7 ha at a global scale, i.e., CWs below <1.7 ha may be able to meet the control of both organic matter and nutrients in polluted water synergistically. It is important to note, though, that the suitability of CW size for wastewater treatment is context-dependent8. The choice of CW size should be based on a detailed assessment of local conditions, pollution levels, available land resources, and treatment objectives. Smaller CWs may be effective in some situations, but larger ones may be necessary in others, particularly when dealing with high pollution loads of contaminants13,75. We found that the threshold of HRT and HLR to maintain the synergistic relationships of pollutant removals was, respectively, 8 days and 0.45 m/d or below. These values represent a balance between ensuring effective treatment and avoiding system overload. HLR represents the rate at which wastewater is applied to the treatment system, while HRT is the average time that pollutants spend in the system76,77. Generally, low HRT and high HLR reduce the effective contact between pollutants and the various treatment zones (i.e., plant, microbial, and substrates) within the CWs, which in turn reduces the pollutant removal performance76. Earlier empirical studies have shown that the most effective HRT ranges from 4 to 15 days77. According to technical manuals from the US, Europe, and China, the HLR of CWs is typically below 0.5 m/d78. Likewise, temperature fluctuations can impact the pollutant removal processes and their interactions in the CWs. For instance, the optimal temperature range for efficient nitrification and denitrification is 20–25 °C78. Temperature changes can also affect the phosphorus adsorption capacity of substrates by altering water viscosity60. We found the global optimal temperature threshold to be 20.2 °C. Therefore, we emphasize the importance of the presence of overarching thresholds pertaining to these mechanisms that influence the pollutant control capabilities of CWs42.

Additionally, the thresholds for maintaining the synergistic relationships of pollutant removal varied across the four types of CWs (Supplementary Figs. 11–14). This may be related to their characteristics, i.e., differences in the water flow path through the system8 and different sensitivities to temperature changes and different areas sizes; SSFCWs are, for example, as stated above, generally smaller in area size and less sensitive to low temperatures, while FWSCWs and FCWs generally are larger in area size and sensitive to temperature changes57.

The need for a reduced land area is particularly significant in regions with mountainous terrain and high population density where land resources are scarce and costly47,79. The availability and cost of land can restrict the feasibility and sustainability of CW implementation, rendering it economically viable primarily in areas with readily available and affordable land47,80. As the area size of CWs continues to expand globally8, the global challenge lies in exploring the possibilities to diminish land area requirements while simultaneously achieving high-quality effluents27,47. Therefore, small-scale CWs have the potential to be an effective wastewater treatment tool, particularly in developing countries and regions27,48. Nevertheless, it is also crucial to acknowledge and consider the significance of other mechanisms such as climatic conditions, plant and substrate selection, wastewater characteristics, water depth, and feeding modes31,37.

Limitations and potential caveats

Although our analysis encompassed an extensive dataset derived from over 364 CW sites worldwide, it is noteworthy that the availability of observations from pivotal regions, including Africa and Oceania, was comparatively limited even though CWs are widely used for pollutant control here8,81,82. The poor data availability can be attributed, at least in part, to the absence of comprehensive data on certain CW sites where essential attributes such as area size and multiple pollutant removal were notably absent from the available records. More data on such areas are needed to mitigate the uncertainty associated with global extrapolations.

CWs play a crucial role in the regulation of microplastics, antibiotics, and heavy metals8 beyond their primary function of managing nutrients and organic matter, and it is therefore imperative to conduct further in-depth studies to assess the sustainability of the synergistic removal processes for these pollutants and the factors that affect them. It should also be recognized that consideration of area size, HLR, HRT, and air temperature constraints inherent to CWs is only part of the evaluation of the viability expanse for the pollution control of CWs8; other points to contemplate are a range of supplementary factors, including the pollutant concentration ratio, sociopolitical policies, economic deliberations, properties of wastewater, nutrient quality and availability, substrate composition, rainfall and climate extremes, and the assemblage of plant species67,83,84. These factors collectively have the potential to influence the intricate dynamics governing the interplay of pollutant elimination processes8. For instance, wastewater policies and engineering practices differ considerably across continents due to variations in economic development, environmental priorities, regulatory frameworks, and cultural factors. In North America, notably in the United States and Canada, there are robust and strict environmental regulations overseeing wastewater management. The Clean Water Act in the United States and comparable regulations in Canada establish benchmarks for water quality and pollution control. European Union (EU) member countries adhere to EU directives for water quality and environmental protection. In contrast, Asia and Africa have a varied regulatory panorama marked by differences in environmental policies and enforcement capacities among nations.

By analyzing the interactions of different pollutant removal processes, in this global analysis we demonstrated that small-sized CWs provide pronounced co-benefits, persistence, threshold effects, and principal mechanistic factor effects regarding the treatment of multiple pollutants (Fig. 5). Our findings carry significant importance in shaping practical and adaptable frameworks for guiding the design, construction, operation, and maintenance of small CWs as a long-term solution to global water environmental challenges. The focal point of global development endeavors is implementing nature-based solutions to treat wastewater and restore contaminated water bodies. The overall goal of this strategic approach is to achieve water security and sustainability in line with the requirements of the United Nations’ Decade of Ecosystem Restoration and the SDGs. In this context, we advocate for the establishment of small-scale CWs as a nature-based solution to address the escalating challenges of wastewater treatment and to remedy polluted water bodies at a global scale.

Fig. 5: Conceptual model showing synergies between organisms and nutrient removals in global small CWs and their sustainability and threshold influencing factor.
figure 5

The numerical values in proximity to the pathway arrows correspond to the standard path coefficients of SEM and LMEM (Fig. 1 and Supplementary Fig. 5), indicating the magnitude of synergies. TNRE, TPRE, CODRE, and NH4+-NRE display the removal efficiency of total nitrogen, total phosphorus, chemical oxygen demand, and ammonium nitrogen, respectively. The optimal threshold indicates the maximum value of the influencing factor for maintaining 12 pairs of synergies. The threshold for relationship transition indicates that all 12 synergistic effects collapsed or were replaced by antagonistic relationships.

Full size image

Methods

Global data collection

The data used in this study were extracted from articles published in the Web of Science Core Collections from 2000 to 2022. A total of 13,792 publications were collected according to the search strings “TS = (“constructed wetland*” or “treatment wetland*” or “reed bed*” or “floating wetland*” or “artificial wetland*” or “manmade wetland*”)” after excluding non-English publications. Additionally, two global datasets were used in our study: the ‘Water Quality Parameters’ dataset on CWs8 and the CWs dataset on global small water bodies27. We screened all these datasets based on the following criteria: (1) the study was conducted outdoors; (2) the CWs treated real wastewaters; (3) the CWs were constructed for engineering applications rather than for experimental purposes; (4) data on basic parameters on the CWs, such as location and area, were available; (5) the area of the CWs was less than eight hectares (<80,000 m2)48,53; (6) the efficacy of pollutant removal for minimum two contaminants was examined; (7) data on the duration of operation or investigation were available. Finally, 196 qualified publications involving 364 CW sites were used to extract information on water quality parameters for further exploration.

We extracted the following information from each original paper: (1) location, including latitude, longitude, country, and continent; (2) CW type, free water surface flow CWs (FWSCWs), subsurface flow CWs (SSFCWs), floating CWs (FCWs) and hybrid CWs (HCWs)8,57; (3) area (m2); (4) removal efficiency (%) and loading rate (g m−2 d−1) of TN, TP, COD, and NH4+-N. When data on the removal efficiency of a pollutant were not available, we used the following equation:

$${RE}=\frac{{C}_{{in}}-{C}_{{out}}}{{C}_{{in}}}\times 100 \%$$

where RE indicates the removal efficiency of the pollutant, Cin and Cout are the measured mass fluxes at the inlet and outlet of the system in units of mass per time27; (5) HLR (m/day), HRT (days), and air temperature (°C); (6) operational or investigated duration of the CWs (months). When data on the operational duration of the CWs were not available, we extracted the investigation duration; (7) elevation (m).

Relationship between pairwise pollutant removals

To test whether there were publication biases in our meta-database, we initially created funnel plots for individual effectsize metrics, followed by assessing funnel plot asymmetry through visual inspection and Egger’s test (Supplementary Fig. 22). The presence of a symmetrical distribution of effect sizes in a funnel plot (Egger’s test p > 0.05) suggests the absence of publication bias. As the data were collected from existing studies, they were not completely independent, and values were missing. Therefore, LMEMs85 was executed to discern the associations pertaining to pairwise efficacy in pollutant removal. This model sought to delineate the interinfluence stemming from the efficacious elimination of any two among the four distinct pollutants, this being concomitant with the study site being treated as a random effect (e.g., pollutant A removal – pollutant B removal + (1|study site), Supplementary Table 1). To comprehensively elucidate the inherent interdependence of the two variables under consideration (i.e., pollutant A removal – pollutant B removal + (1|study site) vs. pollutant B removal – pollutant A removal + (1|study site)), we contemplated a scenario wherein these two variables reciprocally assumed roles as response variables within the framework of our model formulation (Supplementary Table 1). Ultimately, a total of 12 bivariate correspondence models were meticulously developed, each corresponding to a distinct pairing among the aforementioned quartet of pollutants.

To ascertain the fidelity and resilience of the formulated LMEM, an assessment of bias was undertaken. This involved the generation of two-dimensional regression plots juxtaposing the actual observed values and the model-predicted values of the dependent variables utilizing an OLS analysis86 (Supplementary Fig. 3). Within this evaluative framework, slope = 1 indicates a null baseline that signifies complete congruence between the model’s fitted values and the empirical observations, denoting absence of deviation (Supplementary Fig. 3). Conversely, greater divergence of the fitted line from the null baseline signifies heightened instability inherent to the constructed mixed-effects model. In tandem with this analysis, the determination of explanatory efficacy was pursued through the utilization of the R-squared (R2) coefficient in the context of OLS. The magnitude of the R2 value corresponds to the extent of elucidation offered by the predicted values in relation to the observations. As such, a higher R2 value denotes a substantial alignment between the predicted values and the empirical observations within the LMEM, thereby bolstering its robustness. We found that the R2 in the OLS regression ranged from 0.76 to 0.88 (Supplementary Fig. 4, p < 0.001), indicating that about 76–88% of the observed variances were explained by the LMEM. This indicates a goodness of fit for LMEM based on these 12 correspondences.

Subsequent to establishing the fidelity and resilience of the LMEM, we proceeded to compute the standardized effects associated with the fixed effects encompassed by the LMEM. This endeavor aimed to elucidate the interrelation existing between the removal dynamics of the paired pollutants. In instances where the magnitude of the standardized effects attains a value of 0, it signifies the absence of statistically significant concurrence between the two pollutants. Conversely, a standardized effect exceeding 0 and p < 0.05 signifies a positive association between the two pollutant removal processes, manifesting itself as a synergistic effect. Conversely, a standardized effect less than 0 and p < 0.05 signify a negative association between the two pollutant removal processes, which is indicative of an antagonistic effect. To further characterize the relationship between pollutant removals, we calculated the slope value of pairwise pollutant removals (hereafter termed slope_PRE) in the LMEM. A slope_PRE >0 indicates a positive relationship between the two pollutant removals, while a slope_PRE <0 indicates a negative relationship. A slope_PRE = 0 indicates a neutral relationship between the two pollutant removals. Furthermore, the absolute magnitude of the slope_PRE provides insight into the vigor of the interaction characterizing the two pollutant removal processes.

Persistence of pollutant removal relationships

Despite notable advancements, the evaluation of pollutant removal efficacy within CWs and the enduring nature of their associations has received limited scholarly attention30. Therefore, we collated the investigated duration (months) spanning the 364 locations worldwide and integrated these as moderating variables within the 12 LMEMs encompassing the 12 previously established interrelations of pollutant removal (e.g., pollutant A removal–pollutant B removal × duration + (1|study site), Supplementary Table 3). The primary objective was to scrutinize the potential influence of the temporal dimension on these 12 associations. To explore whether the relationship between pollutants changes under different duration scenarios when employing the mixed-effects modeling framework, we embarked on predicting the correlations inherent to these 12 associations across three distinct duration contexts by using the Johnson_Neyman technology: minimum observation duration, mean observation duration, and maximum observation duration. The assessment of pollutant removal interactions across the three scenarios was conducted through the examination of slope_PRE.

To detect whether and how the relationships of pollutant removals change over the operating time, an OLS analysis was utilized to test the relatedness between slope_PRE and duration. In the event that the slope of OLS (hereafter termed slope_OLS) surpasses 0 and attains a significance level (p value) of less than 0.05, it signifies a constructive enduring influence within the pollutant removal relationship. Conversely, if the slope_OLS <0 and p < 0.05, it denotes an adverse lasting impact in the correlation governing pollutant elimination.

Ultimately, in the pursuit of identifying potential duration thresholds underpinning the pollutant removal associations, a Johnson_Neyman interval was harnessed87. This analytical technique was employed to compute distinct duration thresholds corresponding to each of the 12 established correspondences pertaining individually to the quartet of pollutants. The Johnson-Neyman interval provides the threshold values of the moderator (duration) at which the slope_PRE goes from non-significant (p > 0.05) to significant (p < 0.05). To detect the sustainability of the operation of different CW types, we applied the above analyses to a sub-dataset of different wetland types.

Factors influencing the pollutant removal relationships

To discern the influences arising from wetland design parameters, hydraulic conditions, and local environment on the interrelations governing pollutant removal dynamics, an assessment was undertaken to examine the moderating influence exerted by wetland area, HLR, HRT, and air temperature dimensions on the aforementioned 12 interrelationships. The assessment was executed within the framework of LMEM encapsulating these 12 paired associations (e.g., pollutant A removal–pollutant B removal × HLR + (1| study site), Supplementary Tables 4–7). Subsequently, projections were made concerning the configuration of these dozen pairs of pollutant removal relationships, individually tailored to each of the three distinct level scenarios (i.e., minimum, mean, and maximum) by using the Johnson_Neyman analysis. Consequently, for each factor, a prognostication encompassing a comprehensive aggregate of 36 pairs of pollutant removal relationships was executed. These projections were intended to offer an initial characterization of how the factor is a moderator within the intricate framework of pollutant removal relationships. Finally, a total of 144 pairwise relationships of pollutant removal were evaluated across the four factors considered in this study.

To quantify how the wetland design parameters, hydraulic conditions, and local environment affect the pollutant removal relationship, we established the relatedness between slope_PRE and wetland area, HLR, HRT, and air temperature by using an OLS analysis. A slope_OLS >0 and p value <0.05 signify a positive influence of the factor on the interplay between the two pollutant removals. Conversely, when the slope_OLS falls below 0, it denotes a notable adverse impact of the factor on the correlation between the two pollutant removals.

Ultimately, to ascertain the presence of a substantive threshold effect attributed to these factors within the pollutant relationships, the Johnson_Neyman threshold was calculated as a reference. This threshold enables elucidation of the alterations within pollutant removal associations, transitioning from meaningful and statistically significant (p < 0.05) connections to insignificant ones (p > 0.05). Furthermore, this threshold holds the potential to uncover shifts between synergistic (slope_PRE >0) and antagonistic (slope_PRE <0) affiliations among these pollutant relationships. To detect the influencing factors of different CW types, we applied the above analyses to a sub-dataset of different wetland types.

Prior to undertaking comparisons, the normality and homogeneity of residuals within the model were subjected to scrutiny by the Shapiro-Wilk and Levene tests, respectively. Due to the fact that certain groups did not adhere to the assumptions, the evaluation of disparities was pursued using non-parametric methodologies. Specifically, Wilcoxon two-sided tests were employed to estimate differences in pollutant removal efficiency across diverse categories of CWs and continents. All divergences were regarded as being statistically significant at a threshold level of p ≤ 0.05.

Structural equation modeling analysis

To further unravel the direct interaction of pollutant removals, SEM analyses were performed to examine the relationship between pairwise pollutant removals by calculating their covariance matrix. Initially, we examined a hypothesized conceptual framework encompassing all plausible routes (Supplementary Fig. 21). To discern the direct and main effects of these drivers on the interaction of pollutant removals, SEM analyses were run to detect the relationships between the interaction of pollutant removals and wetland area, HRL, HRT, and temperature. Initially, we examined a hypothesized conceptual framework encompassing all plausible routes (Supplementary Fig. 17). Subsequently, we iteratively removed pathways lacking statistical significance, unless these pathways offered significant biological and environmental insights, or we incorporated pathways based on residual correlations. This process was reiterated until the model achieved a satisfactory fit, as indicated by a root mean square error of approximation (RMSEA) <0.0888. In the SEM, a standard path coefficient (b) > 0 indicates a positive effect of the factor on the interaction of pollutant removals, while b < 0 reflects a negative influence of the factor on the interaction of pollutant removals. The magnitude of the absolute value of b indicates the magnitude of the effect, which can infer the main influencing factor. Additionally, to detect the relative importance of these factors for the interactions of pollutant removal processes, a Random Forest analysis was performed (Supplementary Methods).

The process of model fitting, comparison, confidence interval estimation, bootstrapping, and integration was executed employing several software packages including nlme (version 3.1.162), lmerTest (version 3.1-3), randomForest (version: 4.7-1.1), frPermute (version 2.5.1), lavaan (version 0.6-15), nlstools (version 2.0.0), car (version 3.1-2), stats (version 4.2.3), effectsize (version 0.8.3), and interactions (version 1.8.5). Visualization techniques were employed through the utilization of the ggplot2 package (version 3.4.2) within the R v4.2.3.