Introduction

The Activated Sludge Model (ASM) has been widely applied for simulating the biological wastewater treatment process since its introduction in the 1980s, serving as the theoretical foundation for process design, operation optimisation, and digital twin applications in modern wastewater treatment plants. Challenges have remained in complex parameter calibration and uncertainties in parameter selection, which pose significant difficulties during model validation and implementation1.

TT for ASM typically involves manual optimisation of stoichiometric and kinetic parameters to ensure that the predicted values of the ASM closely match the observed data2. In this process, all parameters (e.g., 7 in ASM13 and 40 in ASM2d4) are adjusted manually and individually, requiring extensive and repetitive operations. This approach is not only labor-intensive but also heavily reliant on personal experience, which significantly limits its scalability and practicality in full-scale wastewater treatment plants, especially under stricter discharge regulations and growing demand for automation and energy efficiency, making it challenging to address the nonlinear interactions between parameters and the high-dimensional parameter spaces, which are commonly encountered in the ASM5. Additionally, parameter optimisation for ASM usually targets a single objective, such as effluent COD, total nitrogen, or total phosphate6,7,8, while the practical demand would be a model that fits all effluent indices well. This warrants the necessity of multi-objective optimisation. The traditional parameter optimisation relying excessively on personal judgment would suffer from poor reproducibility and limited transferability in this multi-objective optimisation9. These limitations highlight the critical need for automated and intelligent tuning methods that can efficiently handle the complexity and high dimensionality of ASMs10, while improving reproducibility and optimisation outcomes.

Various automated calibration methods for ASM have been developed, with Genetic Algorithm (GA)6 and Monte Carlo methods7 being widely applied to achieve automation and systematisation of the calibration process. GA, with its global optimisation capabilities, can effectively explore the parameter space, avoiding the issue of local optima commonly encountered in TT, thereby improving calibration efficiency and accuracy. However, when dealing with complex nonlinear systems, GA may still face challenges such as high computational costs and difficulties in parameter identifiability. On the other hand, the Monte Carlo method transforms traditional manual trial-and-error calibration into a systematic process through automated parameter space sampling and large-scale simulations. While this approach reduces manual intervention and enhances efficiency, it also faces challenges, including high computational demands, parameter non-uniqueness, and insufficient handling of uncertainties.

Automatic calibration of ASM typically requires the realisation of ASM and parameter optimisation on a programming platform, such as C + + or MATLAB, which demands extensive expertise in algorithms and programming. Thus, studies and publications on this topic are pretty limited, since the relevant skill requirement is considerably challenging for researchers in water and wastewater treatment11.

However, existing studies still have obvious deficiencies in several key aspects: First, most of them are limited to single-objective optimization and cannot meet the optimization requirements of multiple effluent indicators; second, there is a lack of systematic consideration of the interaction between parameters, and the analysis is often conducted in a single dependent variable parameter adjustment manner, ignoring the influence of high-dimensional nonlinear relationships; third, there is a lack of flexible, efficient, and scalable automatic parameter adjustment frameworks, and no study has systematically introduced modern machine learning’s hyperparameter optimization tools into the calibration of ASM models.

This study innovatively introduces the Optuna framework under the Python platform, combining TPE and NSGA-II optimisation algorithms to construct an automatic multi-objective parameter adjustment system suitable for ASM2d. This system can not only achieve complete parameter optimisation but also dynamically capture the nonlinear interaction between parameters, effectively improving the parameter adjustment efficiency and model prediction accuracy, filling the gap in traditional methods’ ability to handle high-dimensional parameter spaces and multi-objective trade-offs.

Massive open-source libraries are available on the Python platform nowadays. Quantitative Sustainable Design sanitation (QSDsan) and PeePyPoo are two professional Python libraries for ASM12, and Optuna is a comprehensive Python framework for hyperparameter optimisation and multi-objective optimisation.

QSDsan enables modular construction of ASM, allowing for the flexible definition of wastewater compositions, reactor structures, and system processes13. Additionally, its dynamic simulation capabilities capture the changes in complex wastewater treatment processes, providing realistic and reliable model outputs for optimisation. Meanwhile, the rapid dynamic simulation and predefined ASM design concepts from PeePyPoo enhance the efficiency and simplicity of the modelling process, making it particularly suitable for efficiently constructing complex wastewater treatment systems.

Once the ASM is established on the Python platform, parameter optimisation can be easily realised with specialised libraries, like Optuna, which are widely used in machine learning and deep learning. Optuna offers the Tree-structured Parzen Estimator (TPE)14 and the Non-dominated Sorting Genetic Algorithm II (NSGA-II)15, which can quickly and automatically search for the best combination of hyperparameters while supporting multi-objective optimisation. The TPE effectively explores the parameter space using probabilistic models, achieving higher search efficiency in high-dimensional and complex problems. NSGA-II, on the other hand, is particularly suited for multi-objective scenarios, such as balancing different effluent indexes in wastewater treatment processes. For ASM calibration, TPE may offer an efficient and adaptive approach for single-objective optimisation by focusing on promising regions of the search space through probabilistic modelling. At the same time, NSGA-II may excel at multi-objective optimisation by providing diverse and robust Pareto-optimal solutions. In contrast, Monte Carlo is computationally expensive and lacks focus, and traditional GA are prone to premature convergence and struggle with multi-objective trade-offs in ASM calibration. Therefore, it is believed that TPE coupling with NSGA-II would outcompete the GA and Monte Carlo methods in addressing the challenges of ASM optimisation.

It is anticipated that TPE and NSGA-II may enable automated and efficient parameter tuning for ASM to provide comprehensive support for wastewater treatment modelling and optimisation. This would be quite realisable with the mature programming language ecosystem of Python. To the best of the authors’ knowledge, this approach has not been explored yet.

Therefore, this study aims to develop an automated and efficient calibration framework for ASM by integrating Optuna-based optimisation with TT methods. In this work, the ASM2d model was constructed on the Python platform using the QSDsan package and calibrated using operational data from a full-scale municipal wastewater treatment plant in Shenzhen, China. The model was then coupled with Optuna’s TPE for single-objective optimisation and NSGA-II for multi-objective optimisation, enabling dynamic parameter interaction modelling and full-parameter tuning. By comparing the results obtained from Optuna-based and traditional trial-and-error strategies, this study evaluates the accuracy, efficiency, and robustness of both approaches. The proposed framework not only improves calibration performance but also contributes to scalable, intelligent, and automated modelling strategies for real-world wastewater treatment system optimisation and control.

Results and discussion

Parameter sensitivity analysis

Sensitivity analysis is always conducted to alleviate the burden of parameter optimisation, so that the optimisation can be focused on the parameters with high sensitivity. The Traditional sensitivity analysis and the optuna sensitivity analysis were compared. The sensitivity coefficients of the top 7 parameters identified by each method were normalised and shown in Fig. 1. It can be observed that in the TSA, the sensitivity coefficients were relatively evenly distributed, with no significantly dominant parameter. However, in the OSA method, the sensitivity coefficient of YH was substantially higher than other parameters in both single- and multi-objective optimisations, demonstrating its strong dominance.

Fig. 1: The sensitivity analysis results for TN and COD using different methods.
figure 1

The first row a and b represent the relative sensitivity coefficients for the seven different parameters of TN and COD, respectively, using TSA. The second row c and d show the relative sensitivity coefficients for TN and COD, respectively, using OSA, with e representing the results of MO-OT and f representing the results of MO-TT. The sensitivity analysis compares the impact of different methods on parameter selection, providing insights for choosing the optimisation method.

Full size image

This phenomenon can be attributed to the fact that TSA evaluates parameters by individually adjusting them without considering interactions between parameters. As a result, the influence of each parameter on the model outcome is treated separately, leading to a relatively even distribution of sensitivity coefficients. In contrast, the OSA adopted a global optimisation approach, which simultaneously considered the interactions and competitive relationships between parameters.

In the ASM, YH plays a crucial role in COD degradation and TN removal processes16. Heterotrophic bacteria, whose growth efficiency is determined by YH, are the primary microorganisms responsible for COD degradation. Moreover, in nitrogen removal, heterotrophic bacteria consume carbon sources during denitrification, and changes in YH directly affect carbon source utilisation efficiency and denitrification performance. Consequently, in the global optimisation process, the sensitivity of YH is significantly amplified, resulting in a much higher sensitivity coefficient17. This highlighted that the Optuna method was more effective in identifying the key parameters that have the most significant impact on the objective function. In contrast, TT, which overlooks complex parameter interactions, tends to produce more evenly distributed results.

Single-objective optimisation

In this study, OSA and TSA were employed as two different RSF methods, along with OT and TT as two distinct parameter tuning methods. These different sensitivity analysis methods and tuning methods were paired in a two-by-two combination, and the relative error between the simulated values and actual values was recorded daily for each combination. The data collected over 50 days were then aggregated and analysed using box plots for comparative analysis. The parameters identified in the sensitivity analyses were optimised through TT and TPE. With the optimised parameters, the relative errors between the model predictions and the observations are shown in Fig. 2.

Fig. 2: Relative errors in the single-objective optimisation using different RSF (TSA and OSA) and tuning methods (TT and OT).
figure 2

a Relative error of TN and b telative error of COD.

Full size image

In single-objective parameter tuning, when TN is set as the optimisation target, the average relative errors for TSA-TT, TSA-OT, OSA-TT, OSA-OT are 4.587, 8.079, 0.550, 0.798%, respectively. When COD is set as the optimisation target, the average relative errors for TSA-TT, TSA-OT, OSA-TT, OSA-OT are 24.846, 25.793, 14.491, 15.291%, respectively. A t-test analysis showed that there is no significant difference between TSA-TT and TSA-OT, as well as between OSA-TT and OSA-OT, indicating that under the same RSF method, TT and OT yield similar optimisation results. By performing a t-test analysis, it was found that there was no significant difference between TSA-TT and TSA-OT, as well as between OSA-TT and OSA-OT. This indicates that under the same RSF method, the optimisation results for TT and OT performed similarly. The reason for this phenomenon lies in the activated sludge model, where the TPE, as an optimisation method for tuning multiple parameters, typically requires a larger number of parameters to participate in the optimisation process. In contrast, TT tends to highlight the importance of individual parameters more effectively when the number of parameters is limited18. This characteristic suggests that when fewer parameters are involved, the performance of the TPE may be similar to that of TT, or it may not exhibit a significant advantage.

As shown in Fig. 2, there is a significant difference between OSA and TSA (p-value < 0.05), indicating that the sensitivity analysis results of the TPE algorithm in ASM2d tuning are significantly better than those of traditional methods. The main advantage lies in TPE’s use of Bayesian optimisation and Gaussian processes to handle uncertainty. By iteratively updating the surrogate model and selecting parameter combinations based on the “Expected Improvement (EI)” criterion, TPE can quickly identify parameter sets that are close to the global optimum, thereby accelerating convergence. In ASM, this approach efficiently identifies the best parameter sets, minimising TN and COD, and avoids the local optima that traditional methods may encounter. The Bayesian optimisation in TPE is particularly suited for handling complex systems involving multiple biological processes and reaction rates, enabling effective parameter adjustment under uncertain conditions. Therefore, TPE can capture complex nonlinear relationships between parameters more deeply, significantly improving the accuracy and efficiency of sensitivity analysis compared to TSA.

Although TT and OT showed insignificant difference in the optimisation, TT usually relies on expert experience, introducing considerable uncertainty, and it is time-consuming even if it was programmed for automation here5. Due to the limitation of human resources and its low efficiency, TT often focuses on limited parameters with higher sensitivity coefficients, restricting its scope. OT leveraging the TPE could support full parameter tuning.

Multi-objective optimisation

The single-objective optimisation above, focused on either TN or COD, could hardly predict the other one, as indicated in Fig. S1 in the Supplementary Information. This warranted the necessity of multi-objective optimisation, which was expected to track both effluent TN and COD well.

According to the supplementary data, in single-objective tuning with TN as the target, the average relative error of COD under OSA-MO-TT was 20.674%. Similarly, in single-objective tuning with COD as the target, the average relative error of TN under OSA-MO-TT was 14.299%. However, by using the multi-objective tuning method, the overall relative errors of TN and COD were significantly reduced. Compared to the single-objective TN and COD methods, the multi-objective tuning approach significantly lowered the overall relative errors of TN and COD. As shown in Fig. 3, in MO-OT, the average values of COD and TN were 15.17 and 4.72%, respectively, which are better than the TN results reported in19. As shown in Fig. 5, OSA-MO-OT and OSA-FP-MO-OT performed better in TN than OSA-MO-TT and OSA-FP-MO-TT (p value < 0.05), indicating that the OSA-MO-OT method is significantly better than the OSA-MO-TT tuning method. The obtained COD value is lower than that of single-objective tuning, further validating the superiority of the multi-objective tuning method in optimisation performance.

Fig. 3: Relative error in the models using different multi-objective optimisation different methods (OSA-MO-OT, OSA-FP-MO-OT, OSA-MO-TT, OSA-FP-MO-TT).
figure 3

a Relative error of TN and b relative error of COD.

Full size image

The reason for Optuna superiority over traditional methods lies in the complex interactions between TN and COD in the ASM system. Optuna multi-objective tuning method uses the NSGA-II algorithm, which performs global searches via a GA, allowing for better parameter adjustment and more balanced optimisation solutions. In contrast, TPE is more suitable for single-objective optimisation, as it is based on Bayesian optimisation, which converges faster on smaller datasets. However, in multi-objective optimisation, it may lead to imbalanced optimisation, making it difficult to improve the removal rates of TN and COD simultaneously. Therefore, NSGA-II is more suitable for multi-objective optimisation.

OSA-FP-MO-OT measured the average relative errors for COD and TN at 8.43% and 0.01%, respectively. Compared to MO-OT, OSA-FP-MO-OT exhibited lower medians, smaller maximum differences, and fewer overall outliers. By comparing MO-OT and OSA-FP-MO-OT with OSA-MO-TT and OSA-FP-MO-TT, it is evident that the strength of the OT method lies not in locally adjusting individual parameters but in considering all parameters comprehensively. This demonstrates that, when using Optuna for multi-objective tuning, the main reason why Optuna outperforms traditional methods in full parameter tuning is its ability to consider the synergistic effects and nonlinear relationships between multiple parameters, avoiding the potential oversight of interactions that occur when adjusting each parameter individually. Traditional methods often rely on empirical rules, making it difficult to effectively address parameter interactions in complex systems and face challenges in setting appropriate weights. On the other hand, Optuna, using Bayesian optimisation and adaptive techniques, dynamically adjusts the search process and automatically optimises multiple parameter combinations, avoiding bias from manually set weights, thereby improving optimisation efficiency and accuracy. In complete parameter optimisation, Optuna not only avoids local optima but also significantly increases computational efficiency, offering more comprehensive and precise optimisation results, outperforming single-parameter tuning.

The number of iterations to achieve the target result

From Fig. 4, it was observed that under the same RSF method, the TT approach required more iterations to reach the target value (p < 0.05). This indicated that OT had a higher tuning efficiency than TT and was more effective in searching the parameter space. The results showed that, compared to the TT method, the OT method obtained the optimal parameter set required for simulation more quickly. This was because, unlike the TT algorithm, which computed the optimal solution one by one, the TPE algorithm constructed a probabilistic model, classified the evaluated parameters, and intelligently selected hyperparameters with high potential benefits, thereby reducing unnecessary searches. Compared to traditional optimisation methods, TPE converged to the optimal solution more quickly, resulting in fewer optimisation iterations.

Fig. 4: Comparison of Iteration Counts Across Different Methods for TN and COD.
figure 4

a The number of iterations in the single-objective optimisation for TN, b the number of iterations for single objective optimisation for COD, and c the number of iterations for multi-objective optimisation.

Full size image

In MO-TT, as shown in Fig. 4c, compared to the TT approach (OSA-MO-TT and OSA-FP-MO-TT), the OT approach (OSA-MO-OT and OSA-FP-MO-OT) required significantly fewer iterations (p < 0.05). This suggested that the OT method achieved faster convergence during optimisation, thereby reducing the computational cost required for parameter tuning. Additionally, most of the iteration counts in the TT method were close to the maximum value, indicating that its optimisation process was relatively slow and might have suffered from convergence difficulties or inefficient searching. Compared to the OT tuning approach, the TT method required more iterations to complete the optimisation process, implying that it might have failed to find a superior solution within a limited computational budget. Moreover, hyperparameter tuning based on Optuna, utilising the TPE algorithm and the NSGA-II genetic algorithm, achieved target values more efficiently during the tuning process. Therefore, it was concluded that the number of iterations required for tuning primarily depended on the optimisation method used.

Compared with the TT adjustment method, the OT method requires fewer iterations to complete the optimisation process, indicating that it can find a better solution more effectively within a limited computational budget. Additionally, the hyperparameter tuning based on Optuna further optimises the adjustment process by using an SQLite database to store trial information. Multiple servers can work collaboratively to accelerate the optimisation process and allow for interruption during execution, with the ability to resume from the interruption point later. This mechanism ensures the stability and reproducibility of the tuning process, thereby enhancing the flexibility and reliability of the entire optimisation flow.

The time required for parameters to converge

As shown in Fig. 5a, the computation time for most methods ranged between 10 and 30 seconds, indicating that, at the single optimisation level, all methods maintained an acceptable computational cost, with efficiency primarily depending on the algorithm itself. As shown in Fig. 5a, the computation time of the OT methods (TSA-OT, OSA-OT) was shorter than that of the TT methods (TSA-TT, OSA-TT) (p < 0.5), demonstrating that OT methods achieved faster convergence in each optimisation step, resulting in lower computational costs. In contrast, multi-objective optimisation methods (OSA-FP-MO-OT, OSA-FP-MO-TT) generally required slightly longer single optimisation times than single-objective methods but remained within a reasonable range.

Fig. 5: The elapsed time for single time adjustment and total adjustment in the optimisations using different parameter tuning methods.
figure 5

a Single adjustment time and b total adjustment time.

Full size image

Figure 5b shows that multi-objective full-parameter optimisation methods typically required longer total computation times, reaching approximately 15,000 s. However, the total tuning time for OSA-FP-MO-OT was relatively shorter, indicating higher optimisation efficiency. As illustrated in Fig. 5a, the single tuning time generally remained within an acceptable range (10–30 s), suggesting that most methods maintained a controlled computational cost at the single computation level. Furthermore, Fig. 5b highlights that the OT methods consistently outperformed the TT methods in both single and total tuning times (p < 0.5), making them a more favourable choice. This is because, compared to TT, multi-objective optimisation approaches such as OSA-FP-MO-OT demonstrated shorter computation times and higher efficiency than conventional multi-objective methods (e.g., OSA-FP-MO-TT), making them more computationally acceptable20.

This improvement can be attributed to Optuna’s diverse optimisation capabilities, especially its application in single-objective and multi-objective optimisation, as well as its unique parallel optimisation, pruning algorithm, and dynamic search space adjustment mechanism. Compared to traditional optimisation methods, Optuna significantly reduces the computational time during the optimisation process. Firstly, Optuna can conduct multiple trial tasks simultaneously through parallel optimisation, significantly enhancing computational efficiency, particularly in high-dimensional parameter spaces. The NSGA-II algorithm adopted by Optuna in multi-objective optimisation outperforms traditional multi-objective optimisation methods19, enabling more efficient exploration of the search space. Additionally, Optuna’s pruning algorithm automatically terminates underperforming trials in real-time by monitoring their performance, thereby reducing redundant computations. This approach avoids the need for complete calculations of all parameters in each iteration, as in traditional tuning methods, significantly improving efficiency. Traditional methods such as TSA and TT typically rely on expert experience for manual adjustments. At the same time, Optuna uses Bayesian optimisation and the TPE algorithm to dynamically update the search space based on acquired data, gradually narrowing the optimisation range and avoiding the risk of getting trapped in local optima21. Particularly in multi-objective optimisation, Optuna can perform global search and consider the interaction of multiple objectives through Pareto optimal solutions.

In contrast, traditional methods often combine multiple objectives into a single objective for adjustment, which limits the optimisation effect22. Compared to the sequential parameter tuning of conventional methods, Optuna’s pruning algorithm and multi-threading significantly improve the speed. These features enable Optuna not only to converge to the optimal solution quickly but also to enhance computational efficiency significantly, especially when dealing with complex multi-objective problems, demonstrating more substantial advantages over traditional methods.

Interrelatedness of single target parameters

Parallel coordinate plots intuitively display relationships between variables and the distribution patterns of samples in multidimensional data, as shown in Fig. 6. Each vertical axis represents the range of a parameter, and each line corresponds to a tuning process. The trajectory of the lines reflects relationships between parameters, while the colour intensity indicates the magnitude of the objective value. From the distribution of lines, the influence of key variables, trends in objective value changes, and potential outliers can be directly observed.

Fig. 6: Relationship between the model parameters in the single-objective optimisation showed by parallel coordinate plots.
figure 6

a Correlation between TN removal efficiency and key parameters under the TSA-TT optimization method; b Correlation between COD removal efficiency and key parameters under the TSA-TT optimization method; c Correlation between TN removal efficiency and key parameters under the OSA-OT optimization method; d Correlation between COD removal efficiency and key parameters under the TSA-OT optimization method.

Full size image

As shown in Fig. 6a, each vertical axis represents the tuning range and value of a parameter. For example, when the value of the parameter eta_NO3_H is 1.2, ten lines extend from this point to the other parameter axes, indicating that during the tuning process, the optimal tuning value of eta_NO3_H was selected as 1.2, and this value was fixed for subsequent tuning of the remaining parameters. Similarly, Fig. 6b displays a similar tuning pattern, and the line distribution reveals the optimal values of the different parameters.

The interactions between these parameters reflect the varying degrees of influence each parameter has on the optimisation of TN or COD. In Fig. 6c, the values of Y_H are concentrated between 0.35 and 0.6, indicating that when b_H is lower, the optimisation of TN removal is more effective. Therefore, lower values of b_H help improve optimisation efficiency. The distribution of eta_NO3 and K_O2_H is broader, suggesting that these two parameters have a more scattered influence on the optimisation target, and their varying values produce only minor changes. This implies their weaker contribution to the optimisation, allowing them to be considered as secondary optimisation factors.

In Fig. 6d, the values of Y_H are concentrated between 0.7 and 0.85, K_h values range from 1.5 to 2.4, and K_IPP values are concentrated between 0.024 and 0.003. The concentration of these parameters within specific ranges indicates that the optimal values of these parameters are crucial to achieve better optimisation results. For example, the concentration of K_h values in the lower range suggests that lower K_h values may lead to better TN removal23. The concentrated range of K_IPP likely indicates that this parameter has a strong influence on the optimisation target and plays a key role in the removal efficiency.

Overall, the interactions between these parameters ensured the balance, efficiency, and stability of the TN and COD removal processes. Optimising and adjusting each parameter within a specific range guaranteed the stable operation of the entire process, preventing any single parameter from overly influencing the results or causing instability in the optimisation outcomes.

Overall, OSA effectively captured the nonlinear relationships and interactions between parameters through coordinated adjustments, significantly enhancing the optimisation results. For example, by analysing the concentration ranges of parameters in (c) and (d), it became clearer how different parameters influenced each other and collectively affected the optimisation results. In the TN tuning process, higher K_h values contributed to faster PHA hydrolysis and nitrate reduction, which, when combined with lower Y_H and b_H values, helped balance aerobic and anaerobic reactions and optimised nitrogen removal efficiency24. This interaction and coordinated adjustment of parameters demonstrated their nonlinear relationships, and OSA effectively captured and optimised these relationships and interactions.

OSA not only coordinated the adjustment of multiple parameters but also captured the interactions between them, significantly improving optimisation results. In contrast, although TSA assessed the sensitivity of individual parameters, it could not consider the interactions between parameters in complex systems, limiting its optimisation potential, especially in multidimensional optimisation problems. Therefore, OSA provided a more comprehensive and precise approach to solving complex multidimensional optimisation challenges.

The interrelation of parameters in multi-objective optimisation

As shown in Fig. 7, in panel (c), under the OSA-MO-OT optimisation method, a strong correlation exists between Y_H and K_NO3_PAO, which may be closely related to reaction rates or mechanisms in the wastewater treatment process. Additionally, the significant correlation between f_XI_H and K_NO3_PAO indicates that the concentration of NO3 or its reaction rate has a considerable impact on TN removal efficiency. In panel (a), under the OSA-MO-TT optimisation method, a strong correlation is observed between Y_H and K_NO3_PAO, suggesting that these parameters are closely related to organic matter degradation rates and microbial metabolic processes.

Fig. 7: Relationship between the model parameters in the multi-objective optimisation showed by parallel coordinate plots.
figure 7

a Correlation between TN removal efficiency and key parameters under the OSA-MO-TT optimisation method. b Association between COD removal efficiency and key parameters under the OSA-MO-TT optimisation method. c Correlation between TN removal efficiency and key parameters under the OSA-MO-OT optimisation method. d Association between COD removal efficiency and key parameters under the OSA-MO-OT optimisation method.

Full size image

For COD removal efficiency, panels (d) and (b) illustrate the associations between key parameters under the OSA-MO-OT and OSA-MO-TT optimisation methods, respectively. In panel (d), under the OSA-MO-OT optimisation method, the relationship between eta_fe and K_NO3_PAO further emphasises the impact of NO3 concentration on COD removal efficiency. In panel (b), under the OSA-MO-TT optimisation method, the significant correlation between f_XI_H and b_H suggests that these two parameters may play a key role in COD removal, involving reaction rates and dissolved oxygen levels.

The difference between the OSA-MO-OT and OSA-MO-TT methods lies in their optimisation approaches. Optuna NSGA-II algorithm can simultaneously consider multiple objectives and flexibly adjust parameters, exploring more possible solutions to help find the optimal one. In contrast, the traditional method combines various objectives into a single one. It adjusts parameters step by step, often being confined to a specific range and unable to find the best solution. Therefore, NSGA-II provides more comprehensive optimisation, while the traditional method has limited effectiveness.

In summary, Optuna demonstrates remarkable optimisation capabilities in TN and COD tuning by capturing parameter sensitivity and correlations, significantly enhancing optimisation results and expanding the range of objective values. In contrast, the traditional method relies more on single-parameter adjustments, making it less effective at capturing complex parameter relationships and weaker in handling complex systems for multi-objective optimisation problems with high complexity. Optuna is undoubtedly the better choice, with its advantages in applicability and efficiency in high-dimensional nonlinear systems standing out prominently.

Research on the application of the Optuna framework in parameter optimization for intelligent sewage treatment

The proposed Optuna-based calibration framework demonstrates strong potential for practical application in wastewater treatment plant (WWTP) modelling and optimisation. By integrating TPE and the NSGA-II algorithm, the method enables full-parameter, multi-objective optimisation with improved convergence efficiency. Built entirely on an open-source Python platform, the framework supports modular integration with process simulators such as QSDsan, making it flexible for use in diverse operational scenarios. It is particularly suitable for automated model calibration, multi-objective process control, and intelligent optimisation in data-rich WWTP environments.

Although the Optuna-based automatic calibration framework proposed in this study achieved high accuracy and efficiency in optimising parameters of the ASM, several limitations remain that should be acknowledged for future improvements. First, the dataset used was obtained from a single full-scale WWTP located in Shenzhen, China. This limited spatial and process coverage restricts the model’s generalizability to other WWTPs with different treatment technologies, influent characteristics, or operational strategies. Additionally, the proposed framework was developed specifically for the ASM2d model and has not yet been validated for other emerging process models, such as anaerobic ammonium oxidation (Anammox) or membrane-aerated biofilm reactors (MABR), which may exhibit different kinetic behaviours and optimisation requirements.

Moreover, like most data-driven modelling approaches, the performance of the proposed method heavily depends on the quality and availability of input data. Incomplete, noisy, or inconsistent influent and effluent measurements may disrupt the optimisation process and lead to biased parameter estimates. While the framework significantly reduces the manual effort associated with traditional trial-and-error calibration, it still imposes substantial computational demands under full-parameter optimisation and long-term simulation scenarios, particularly in real-time or low-resource environments. Finally, the current model is trained exclusively on static historical datasets without incorporating real-time monitoring or feedback mechanisms. This limits its adaptive capability in dynamic operating environments and reduces its suitability for intelligent wastewater treatment systems that require continuous learning and real-time control.

The parameter optimisation method for the ASM model, based on Optuna, proposed in this study, provides a new idea for improving the performance of wastewater treatment plants, especially in terms of adjusting operating parameters. Although this paper does not directly address the improvement of energy consumption, in actual wastewater treatment plants, precisely adjusting operating parameters (such as aeration volume, reaction time, etc.) is crucial for enhancing treatment efficiency and reducing energy consumption. In the operation of actual wastewater treatment plants, precisely regulating operating parameters plays a key role in improving treatment efficiency and optimising energy efficiency, especially in dynamic adjustment and energy optimisation25,26. These studies emphasise the use of adjusting wastewater treatment operating parameters to reduce energy consumption and improve treatment quality, especially in regulation strategies under different climatic conditions. By optimising operation modes and adopting more effective control strategies, energy use efficiency can be significantly improved, and environmental impacts can be reduced. Combining the application of Optuna and an SQL database, multi-threaded distributed operation can be achieved under dynamic simulation, which not only improves computational efficiency but also ensures the security and stability of data, promoting the practical application of data-driven optimisation adjustment methods in wastewater treatment plants. This suggests that Optuna will play a crucial role in adjusting operating parameters in future wastewater treatment plants, thereby enhancing energy efficiency and treatment processes.

These results indicate that the proposed optimisation framework is not only applicable to offline model calibration, but also has promising prospects in practical applications of intelligent wastewater treatment. In the future, if this method is further integrated into real-time monitoring systems, adaptive control strategies, reinforcement learning, and other intelligent algorithms, it is expected to achieve an automatic update and parameter adjustment mechanism for dynamic operating conditions. At the same time, extending this method to emerging models other than ASM2d (such as Anammox, IFAS, MABR, etc.) will also be a key step in achieving universal applicability for various processes.

Methods

WWTP and data overview

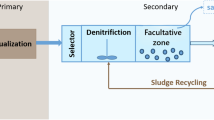
The data used in this study were collected from a WWTP in Shenzhen, which adopts the treatment process as shown in Fig. 8. First, coarse screens and fine screens are used to remove large debris and fine suspended solids. The aerated grit chamber removes settling particles, while the Anaerobic–Anoxic–Aerobic (AAO) process eliminates pollutants such as chemical oxygen demand (COD), nitrogen, and phosphorus. The secondary sedimentation tank separates suspended solids from supernatant, and magnetic coagulation helps in removing colloidal substances. Finally, ultraviolet (UV) disinfection and sodium hypochlorite ensure the complete elimination of pathogenic microorganisms, meeting discharge standards.

Fig. 8
figure 8

Schematic diagram of the wastewater treatment process in the WWTP.

Full size image

The data from this WWTP covers various water quality and operational parameters, including inflow and outflow volumes, pH, COD, BOD, SS, TP, ammonia nitrogen, TN, NO3-N, TKN, daily sludge cake production, sludge cake moisture content, sludge concentration, external reflux volume, average DO, and PAC and PAM usage in the high sedimentation tank. The data was collected over a period from November 20, 2018, to January 8, 2019. A statistical summary of the data used for modelling in this study is shown in Table 1.

Table 1 Statistical Summary of data collected from WWTP
Full size table

ASM on Python

This study uses the QSDsan Python package to model and analyse wastewater treatment processes based on the WWTP model, and conducts simulation processing analysis using the ASM2d. The ASM2d is developed based on ASM1 (1987) and ASM2 (early 1990s) models, and it comprehensively integrates the processes of organic matter removal, denitrification, and phosphorus removal27. It is widely applied in the design and optimisation of WWTP. The process configuration includes five interconnected reactors and a final sedimentation tank, as shown in Fig. 1. The treatment system consists of anoxic and aerobic sections to optimise biological nitrogen removal and organic matter degradation.

The QSDsan model is used to simulate the WWTP system. Key data, including influent flow, residual sludge flow, external reflux flow, COD, and TN concentrations, were first input into the model, with the temperature set to 20 °C (293.15 K). Reactors were set up on the model according to the process in the WWTP, as shown in Fig. 1. More details on the process configuration in the ASM could be found in the Supplementary Information.

The dynamic simulation of the system is created using the System class in QSDsan, with a simulation time of 50 days. The Backwards Differentiation Formula (BDF) integration method is used for solving the system, with a mass conservation error tolerance of 10-5 to ensure high-precision numerical calculations. During the simulation, the system tracks the concentration changes of key components, such as dissolved oxygen, ammonia nitrogen, nitrate nitrogen, and organic matter, while also tracking the dynamics of biological components, including heterotrophic bacteria, phosphorus-accumulating bacteria, and nitrifying bacteria. Finally, the simulation results are exported as an Excel file for further analysis, providing data support for optimising the wastewater treatment system.

Parameter optimisation through the traditional method

TT, relying on empirical adjustments, was also automated in Python. In this study, a 50-day tuning period (November 20, 2018, to January 8, 2019) was used, with January 2, 2019, selected for sensitivity coefficient analysis. The goal was to minimise the difference between simulated and actual TN and COD values in the ASM2d.

The sensitivity analysis, conducted using the Traditional Sensitivity Analysis (TSA)3method, involved increasing each of the 55 parameters by 10% and calculating the sensitivity coefficient for TN and COD. The sensitivity coefficient was calculated using the formula:

$$\begin{array}{c}{RSF}=\frac{\varDelta y}{y}\times \frac{\varDelta p}{p}\end{array}$$
(1)

where y is the simulated value, \(\frac{\Delta {\rm{y}}}{{\rm{y}}}\) is the difference from the actual value, p is the default value, and \(\frac{\Delta {\rm{p}}}{{\rm{p}}}\) is the change in the parameter value.RSF represents the sensitivity coefficient of the parameter.

After calculating the relative sensitivity coefficients for all parameters, select the top seven parameters3 with the highest relative sensitivity coefficients2. To reduce the fluctuations caused by TT methods, the parameters should be adjusted in descending order of their relative sensitivity coefficients. The optimisation steps for traditional parameter tuning are as follows: First, reduce the value of the parameter with the highest relative sensitivity coefficient to 50% of its default value, while keeping the other parameters unchanged. Then, increase the parameter’s value in 10% increments, recording the relative error between the simulated values and the actual values at each adjustment, until the parameter reaches 150% of its default value. From these ten simulation results, select the parameter value that corresponds to the lowest relative error as the optimal value for that parameter. Next, repeat the same procedure for the next parameter, until all seven selected parameters have been adjusted. For each adjustment, the relative error was calculated9:

$$\begin{array}{c}{\text{Relative}}\,{\text{Error}}=\frac{{\text{Measured}}\,{\text{Value}}\,-{\text{True}}\,{\text{Value}}}{{\text{True}}\,{\text{Value}}}\times 100\end{array}$$
(2)

The adjustment with the smallest relative error was selected as the optimal value. This process was repeated for all key parameters to find the optimal set for the model.

Hyperparameter optimisation

The approach of relative Optuna sensitivity analysis (OSA) was as follows: During parameter tuning, Optuna executed a full parameter single-objective optimisation process for each of the 50 days, dynamically adjusting all parameters within a range of 50% to 150% of their default values28. This process was repeated 70 times daily. For each day, the relative sensitivity coefficients of all parameters were calculated. The relative sensitivity coefficients obtained for all parameters over the 50 days were then summed and averaged to determine the relative sensitivity coefficients for all parameters. The top seven parameters with the highest relative sensitivity coefficients were selected as the parameter set for Optuna Tuning (OT).

The OT approach was conducted as follows: The seven selected parameters were used as the parameter set, and these parameters were dynamically adjusted within a range of 50% to 150% of their default values. For each day, the tuning process was executed 70 times. From these 70 iterations, the minimum relative error between the TN obtained by tuning with TN as the objective and the actual TN, and the minimum relative error between the COD obtained by tuning with COD as the objective and the actual COD, were extracted. The optimal parameter sets for TN and COD were subsequently determined based on these results.

Throughout these processes, Optuna served as an auxiliary tool to identify and select the most influential and critical parameters, guiding and controlling the optimisation process. The TPE implemented in Optuna enhanced the search efficiency within the high-dimensional and complex search space of the ASM2d. TPE constructed two probability models, l(x) and g(x), representing the distributions of hyperparameters for better (lower) and worse (higher) objective values, respectively. By defining a threshold y∗(the current best objective value) and a quantile γ, TPE categorised the hyperparameters and utilised Parzen kernel density estimation (KDE) to build the probability models. The algorithm also incorporated a Truncated Gaussian Mixture Model (TGMM), which excluded poorly performing regions and focused the search on more promising areas. Ultimately, this approach achieved precise convergence toward the optimal parameter configuration.

Multi-objective optimisation

WWTP always involves multi-objective optimisation, such as COD and TN in effluent; therefore, it is necessary to explain the situation of multi-objective tuning further. In TT, it is challenging to compute the relationship between tuning TN and COD parameters, as well as to control the effluent concentrations of TN and COD simultaneously. Expert judgment and experience often play a decisive role.

The data used in the multi-object parameter adjustment process is the same as that used in the single-object parameter adjustment process. If the TT of RSF were used, it would be challenging to accurately determine the appropriate weights for each objective, resulting in significant instability. In contrast, the TPE can simultaneously account for the impact of two objective values on the parameters, thereby deriving a unified relative sensitivity coefficient. Consequently, the optimisation process continued to utilise the TPE for RSF. MO-TT.

In the optimisation of the ASM2d, the multi-objective traditional tuning method (MO-TT) approach typically involves aggregating all objective values into a single objective value. This aggregation allows for a unified measure of model performance, making it easier to optimise multiple objectives(obj) simultaneously29.

$$\begin{array}{c}{obj}={\alpha }_{1}{{obj}}_{1}+{\alpha }_{2}{{obj}}_{2}+{\alpha }_{3}{{obj}}_{3}+\ldots .\end{array}$$
(3)

MO-TT typically relies on expert judgment to assign weights, denoted as α. In this optimisation process, the focus is primarily on TN and COD values, where TN and COD are defined as obj1 and obj2, respectively, with both α1 and α2 initially assigned a value of 1 for calculation. Subsequently, the overall objective is defined as the sum of all individual objectives.

Since Optuna provides the NSGA-II multi-objective optimisation algorithm, which utilises Pareto frontiers to guide the search process, this study adopted multi-objective Optuna-based optimisation (MO-OT) to optimise the ASM2d30. The method for performing multi-objective parameter tuning in Optuna was primarily based on the implementation of the NSGA-II algorithm. First, the objectives were defined as the relative errors of TN and COD, to minimize these two relative error values simultaneously. Next, the search space was defined to include the parameters to be optimised (e.g., Y_H, K_A_PAO, eta_NO3), with each parameter’s range set between 50% and 150% of its default value. Based on this setup, a multi-objective optimisation function was constructed, which returned the error values for the two objectives during each evaluation. For instance, the relative errors of TN and COD were calculated by comparing the simulated values of the optimised parameters to their actual values. The optimisation direction was then set to minimisation, enabling Optuna to explore the parameter space during trials to find parameter combinations that minimised both objective errors as much as possible.

Using the NSGA-II algorithm, Optuna was able to handle the complex relationships between multiple objectives simultaneously. In each generation of the population, the algorithm selected a set of Pareto front solutions that were not dominated by any other solutions using non-dominated sorting. It further evaluated the diversity and uniformity of the solution set through crowding distance. With successive iterations, the algorithm gradually converged to a set of Pareto-optimal solutions, containing multiple parameter combinations that balanced TN and COD optimally. Finally, the Pareto front solutions were further filtered to select the parameter configuration that best met specific optimisation requirements31, ensuring practical applications of the ASM2d multi-objective optimisation model.

Evaluation of tuning process efficiency

The efficiency of the tuning process is evaluated as follows13. For each tuning session, the total time required for each tuning iteration is calculated, along with the time for each tuning step within a day. These times are then recorded. Additionally, the number of iterations required to reach the minimum objective value for each tuning session is tracked. By comparing the total tuning time, the time per individual tuning step, and the number of iterations needed to reach the minimum objective value, the elapsed time of different tuning methods and strategies was assessed.

Computational environment

All simulations and optimisation tasks in this study were performed on a computer. The system was equipped with an Intel(R) Core(TM) i9-12900K processor (16 cores, 24 threads), 32 GB of RAM, and an NVIDIA GeForce RTX 4060 Ti discrete graphics card. During model training and optimisation, the GPU remained largely idle, indicating that computations were primarily executed on the CPU and GPU acceleration was not utilised. The operating system was 64-bit Windows 10 Professional (version 22H2). The machine included a 477 GB Samsung NVMe solid-state drive (SSD) as the system disk and a 1.8 TB WDC mechanical hard disk (HDD) for data storage. The SSD ensured fast system response and high read/write efficiency, while the HDD was used for long-term storage of raw data and simulation outputs. This configuration provided stable and efficient performance for medium- to large-scale machine learning modelling and simulation tasks.