Abstract
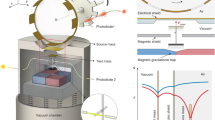
Dark energy, a mysterious form of energy that pervades the entire Universe, is believed to be responsible for the Universe’s accelerated expansion. Various theoretical attempts have been made to explain the elusive nature of dark energy. One of the compelling theories is the so-called symmetron dark energy, which predicts a fifth force that interacts with matter. However, the screening of the fifth force in high-density environments poses a challenge for laboratory experiments. Although several experiments have constrained certain aspects of the model’s parameter space, there is still a vast and unexplored region. Here we have constructed an experimental platform based on a magnetically levitated force sensor with a specially designed structure to search for the symmetron fifth force at the submillimetre scale and minimize screening effects. We have improved the limits of the model by over six orders of magnitude within the three-dimensional parameter space. Our findings demonstrate the substantial potential of this system in probing forces beyond the Standard Model.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
The raw numerical simulation data used to produce Fig. 3 are available from the corresponding authors upon reasonable request. Source data are provided with this paper.
Code availability
The numerical code supporting the figures presented in this paper is available from the corresponding authors upon reasonable request.
References
Perlmutter, S. et al. Discovery of a supernova explosion at half the age of the Universe. Nature 391, 51–54 (1998).
Riess, A. G. et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 116, 1009–1038 (1998).
Joyce, A., Jain, B., Khoury, J. & Trodden, M. Beyond the cosmological standard model. Phys. Rep. 568, 1–98 (2015).
Khoury, J. & Weltman, A. Chameleon fields: awaiting surprises for tests of gravity in space. Phys. Rev. Lett. 93, 171104 (2004).
Upadhye, A. Dark energy fifth forces in torsion pendulum experiments. Phys. Rev. D 86, 102003 (2012).
Hamilton, P. et al. Atom-interferometry constraints on dark energy. Science 349, 849–851 (2015).
Jaffe, M. et al. Testing sub-gravitational forces on atoms from a miniature in-vacuum source mass. Nat. Phys. 13, 938–942 (2017).
Yin, P. et al. Experiments with levitated force sensor challenge theories of dark energy. Nat. Phys. 18, 1181–1185 (2022).
Pietroni, M. Dark energy condensation. Phys. Rev. D 72, 043535 (2005).
Olive, K. A. & Pospelov, M. Environmental dependence of masses and coupling constants. Phys. Rev. D 77, 043524 (2008).
Hinterbichler, K. & Khoury, J. Screening long-range forces through local symmetry restoration. Phys. Rev. Lett. 104, 231301 (2010).
Hinterbichler, K., Khoury, J., Levy, A. & Matas, A. Symmetron cosmology. Phys. Rev. D 84, 103521 (2011).
Sabulsky, D. et al. Experiment to detect dark energy forces using atom interferometry. Phys. Rev. Lett. 123, 061102 (2019).
Brax, P. & Burrage, C. Atomic precision tests and light scalar couplings. Phys. Rev. D 83, 035020 (2011).
Kapner, D. J. et al. Tests of the gravitational inverse-square law below the dark-energy length scale. Phys. Rev. Lett. 98, 021101 (2007).
Sushkov, A. O., Kim, W. J., Dalvit, D. A. R. & Lamoreaux, S. K. New experimental limits on non-newtonian forces in the micrometer range. Phys. Rev. Lett. 107, 171101 (2011).
Upadhye, A. Symmetron dark energy in laboratory experiments. Phys. Rev. Lett. 110, 031301 (2013).
Tan, W.-H. et al. Improvement for testing the gravitational inverse-square law at the submillimeter range. Phys. Rev. Lett. 124, 051301 (2020).
Zhao, Y.-L., Tan, Y.-J., Wu, W.-H., Luo, J. & Shao, C.-G. Constraining the symmetron model with the HUST-2020 torsion pendulum experiment. Phys. Rev. Lett. 129, 141101 (2022).
Cronenberg, G. et al. Acoustic Rabi oscillations between gravitational quantum states and impact on symmetron dark energy. Nat. Phys. 14, 1022–1026 (2018).
Xiong, F. et al. Lens-free optical detection of thermal motion of a submillimeter sphere diamagnetically levitated in high vacuum. Phys. Rev. Appl. 16, l011003 (2021).
Lewandowski, C. W., Knowles, T. D., Etienne, Z. B. & D’Urso, B. High-sensitivity accelerometry with a feedback-cooled magnetically levitated microsphere. Phys. Rev. Appl. 15, 014050 (2021).
Leng, Y. et al. Mechanical dissipation below 1 μHz with a cryogenic diamagnetic levitated micro-oscillator. Phys. Rev. Appl. 15, 024061 (2021).
Tebbenjohanns, F., Mattana, M. L., Rossi, M., Frimmer, M. & Novotny, L. Quantum control of a nanoparticle optically levitated in cryogenic free space. Nature 595, 378–382 (2021).
Hofer, J. et al. High-Q magnetic levitation and control of superconducting microspheres at millikelvin temperatures. Phys. Rev. Lett. 131, 043603 (2023).
Fuchs, T. M. et al. Measuring gravity with milligram levitated masses. Sci. Adv. 10, eadk2949 (2024).
Kaltenbaek, R. et al. Research campaign: Macroscopic quantum resonators (MAQRO). Quantum Sci. Technol. 8, 014006 (2023).
Geraci, A. A., Papp, S. B. & Kitching, J. Short-range force detection using optically cooled levitated microspheres. Phys. Rev. Lett. 105, 101101 (2010).
Bassi, A., Lochan, K., Satin, S., Singh, T. P. & Ulbricht, H. Models of wave-function collapse, underlying theories, and experimental tests. Rev. Mod. Phys. 85, 471–527 (2013).
Bose, S. et al. Spin entanglement witness for quantum gravity. Phys. Rev. Lett. 119, 240401 (2017).
Long, J. C. et al. Upper limits to submillimetre-range forces from extra space-time dimensions. Nature 421, 922–925 (2003).
Zheng, D. et al. Room temperature test of the continuous spontaneous localization model using a levitated micro-oscillator. Phys. Rev. Res. 2, 013057 (2020).
Acknowledgements
The numerical calculations were performed on the computing facilities at the High Performance Computing Center of Nanjing University. J.D. and P.H. acknowledge support from the National Natural Science Foundation of China (grant T2388102). P.H. acknowledges support from the National Natural Science Foundation of China (grants 62071118, 12075115 and 12150011), the Primary Research & Development Plan of Jiangsu Province (grant BE2021004-2) and the Fundamental Research Funds for the Central Universities (grant 2024300343). J.-H.H. acknowledges support from the National Natural Science Foundation of China (grants 12075116 and 12150011), the National Key R&D Program of China (grant 2021YFC2203002), the science research grants from the China Manned Space Project (grant CMS-CSST-2021-A03) and the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (grant 22KJB630006). S.L. acknowledges support from the National Natural Science Foundation of China (grant 12205291). P.Y. acknowledges support from the Natural Science Foundation of Jiangsu Province (grant BK20241255).
Author information
Authors and Affiliations
Contributions
P.H., J.-H.H. and J.D. conceived the general idea. S.L., P.H., P.Y. and J.D. designed and built the experimental set-up. P.Y., K.T., Y.S. and D.L. performed the measurements. X.X., J.-H.H. and C.Y. performed the theoretical calculations. J.-H.H., P.H., J.D., P.Y., X.X. and C.-K.D. wrote the paper. P.H., J.-H.H. and J.D. supervised the research.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Astronomy thanks Steven Lamoreaux and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 The distribution of the ratio ∣ϕ − ϕ0∣/ϕ0 within and surrounding the nuclei for different values of Ms.
The left panel is for gold, the heaviest element used in our experiments. Pink shaded areas represent the regions inside the nuclei, whereas light blue areas denote the external regions. Within the parameter space explored in this study, the nuclei exhibit negligible impacts on the background field with the variation of the field less than 1%. The right panel shows similar results for nitrogen. Compared with gold, lighter elements exert a lesser effect on the background field.
Extended Data Fig. 2 The measured PSDs at different pressures.
The PSDs of the voltage of photodiode at pressures 5 × 10−4 mbar a and 5 × 10−5 mbar b. At pressure 5 × 10−4 mbar, each measurement loop lasts 800 seconds, being averaged 35 times; and at pressure 5 × 10−5 mbar, each measurement loop lasts 2000 seconds, being averaged 12 times. The dots represent the averaged PSD, and the error bars show the standard deviation. The red line is a Lorentz fitting to the dots. At pressure 5 × 10−4 mbar, the fitted mechanical dissipation is γhi/2π = 5.8 mHz with an s.d. of fitting 0.9 mHz; and at pressure 5 × 10−5 mbar, it is γlo/2π = 1.6 mHz with an s.d. of fitting 0.1 mHz.
Extended Data Fig. 3 Measurement of the gravitational drive force.
a. The PSD of the force sensor’s motion, with the tungsten disk at rest, is shown by the blue line labeled “thermal noise”. Each measurement has a duration of 1000 s, and the results are averaged over 10 runs. The noise baseline, averaging 1.06 × 10−6 V2/Hz, is represented by the blue dashed line. The area under the peak, highlighted by the blue-shaded region, is obtained by integrating the PSD within the 15.35 to 15.36 Hz frequency range. b. The PSD of the force sensor’s motion, with the tungsten disk rotating above the force sensor, is depicted by the red line labeled as “Gravity drive". The noise baseline, averaging 1.24 × 10−6 V2/Hz, is represented by the red dashed line. The area under the peak, represented by the red-shaded region, is also obtained by integrating the PSD within the 15.35 to 15.36 Hz frequency range. c. Photograph of the tungsten source mass disk used in the Newtonian gravity measurement. d. The red point represents the average measured force, calculated from the 10 results shown in panels a and b, with error bars indicating the standard deviation. The grey band with grid lines represents the theoretical Newtonian gravity value, with uncertainty arising from geometric errors.
Extended Data Fig. 4 A schematic of our computational grid on the O-xz plane.
The central part of the diagram shows the primary structures. Three distinct red boxes highlight enlarged specific areas. The top-left subplot shows the arrangement of the source mass, electrical shield, and test mass along the z-axis. The bottom-left one shows the most refined grids surrounding the electrical shield. Meanwhile, the top-right sub-figure illustrates the mesh structure on the source mass, as seen from the O-xy plane. A colorbar below indicates the varying densities of the different materials employed in our experimental setup. Overall, high-level refinement is employed to capture the detailed nuances of our experimental apparatus. High-level refinement is also employed to areas proximate to material boundaries for enhanced numerical accuracy.
Extended Data Fig. 5 Normalized phase functions f(θ) as a function of θ for Ms ranging between 100.5 GeV < Ms < 104.0 GeV.
The markers are the numerical results obtained at various phases. Specifically, θ = 0 corresponds to the scenario where the source mass film is directly aligned above the test mass (phase 1). Notably, these phase functions are close to each other and the differences between their PSD magnitude at the resonance frequency of the force sensor are ≤0.5%.
Extended Data Fig. 6 The calculated fifth force for different distance parameters.
a. The differential fifth force signal ΔF as a function of the distance between the test mass and the source masses d1 + d2 for Ms > 102.0 GeV where the shielding effect of the electrical shield is negligible. In this case, reducing the distance between the test mass and the source masses tends to increase the signals of the fifth force. b. The symmetron fifth force as a function of both d1 and d2 for Ms = 10 GeV (left panel) and Ms = 101.5 GeV (right panel), respectively. In these cases, the shielding effect of the electrical shield becomes evident. The color bar to the right indicates the normalized value of the signal ΔF to its maximum value. In this analysis, we restrict the parameters d1 and d2 as d1 > 0.09 mm and d2 > 0.2 mm. The peak signals can be obtained at d2 ≈ 0.3 mm.
Extended Data Fig. 7 Frequency stability of the force sensor and the linewidth of the source masses.
a. The frequency drift of the magnetic levitated mechanical oscillator over an entire measurement loop lasting 105 s. The grey dashed line represents the average resonant frequency. b. The measured I(ω) as a function of the frequency. The red dots represent the measured laser intensity I(ω) at intervals of every 1μHz. The red line shows the calculated I(ω) for an ideal square wave signal with the same amplitude and period. They agree with each other very well, with errors less than the line width in the figure. The peak of I(ω) corresponds to the measured drive frequency.
Extended Data Fig. 8 The constraints on (Ms, λ) plane.
The constraints on (Ms, λ) for μ at different values μ = 1.2, 2.4, 4.8 meV. The solid lines show the results obtained from our experiments with d2 = 0.2 mm and the dashed lines are for d2 = 0.3 mm. The blue horizontal line corresponds to λ = 10−2. The intersections of the blue line with the (Ms, λ) contours lines give the constraints on Ms for different μ as shown Fig. 3b.
Supplementary information
Supplementary Information
Supplementary Discussion and Figs. 1–7.
Source data
Source Data Extended Data Fig. 1
The distribution of the ratio ∣ϕ − ϕ0∣/ϕ0 for gold and nitrogen at different values of Ms.
Source Data Extended Data Fig. 2
The PSDs at pressures of 5 × 10−4 mbar (Extended Data Fig. 2a) and 5 × 10−5 mbar (Extended Data Fig. 2b).
Source Data Extended Data Fig. 3
The PSDs of the force sensor’s motion without (Extended Data Fig. 3a) and with (Extended Data Fig. 3b) drive generated by a tungsten disc. Source data for Extended Data Fig. 3d give the values of gravity drive obtained from measurements and theoretical calculation.
Source Data Extended Data Fig. 4
Material density corresponding to each grid point in coordinate system.
Source Data Extended Data Fig. 5
f(θ) for different values of Ms.
Source Data Extended Data Fig. 6
ΔF as a function of d1 + d2 (Extended Data Fig. 6a) and as functions of d1 and d2 (Extended Data Fig. 6b).
Source Data Extended Data Fig. 7
The measured frequency of the force sensor (Extended Data Fig. 7a), and the measured I(ω) (Extended Data Fig. 7b).
Source Data Extended Data Fig. 8
Constraints on (Ms, λ) plane for different values of μ.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Yin, P., Xu, X., Tian, K. et al. Experimental constraints on the symmetron field with a magnetically levitated force sensor. Nat Astron 9, 598–607 (2025). https://doi.org/10.1038/s41550-024-02465-8
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/s41550-024-02465-8