A small core in Vesta inferred from Dawn’s observations

Abstract

Vesta’s large-scale interior structure had previously been constrained primarily using the gravity and shape data from the Dawn mission. However, these data alone still allow a wide range of possibilities for the differentiation state of the body. The moment of inertia is arguably the most diagnostic parameter related to the radial density distribution of a planetary body, making it crucial for assessing the body’s state of internal differentiation. Determining the moment of inertia requires additional measurements of the amplitudes of small rotational motions, such as precession and nutation. Here we report an updated estimate of the moment of inertia of Vesta inferred from Dawn’s Doppler tracking via the Deep Space Network and onboard imaging data. The recovered value for Vesta’s normalized polar moment of inertia is $\bar{C}/M{R}^{2}=0.4208\pm 0.0047$ (where M is the mass of Vesta and R is the reference radius), which is only 6.6% lower than the homogeneous value of 0.4505. This value, combined with the gravity field and global shape, suggests that Vesta’s interior has limited density stratification beneath its howardite–eucrite–diogenite-dominated crust. We propose two possible origin scenarios that are consistent with the observed constraints. In the first scenario, Vesta’s interior did not undergo full differentiation due to late accretion. In the second scenario, Vesta originated as an impact remnant of a larger differentiated body re-accreted with non-chondritic bulk composition produced from a catastrophic impact. Vesta did not experience complete differentiation in either scenario, suggesting that its current state reflects a complex interplay between its accretion timing, thermal evolution, redistribution of ²⁶Al bearing melt and/or impact processes.

Main

The mean moment of inertia (MOI), which measures the radial density variations^1,2, is a crucial parameter for understanding the interior structure of a planetary body. Once the mean MOI is obtained, different interior structure models can be tested for consistency through a forward modelling process. This inverse problem of inferring interior structure from MOI is generally underconstrained and leads to non-unique solutions; however, when combined with other information, such as a shape model, a high-degree gravity field, geochemical modelling or composition data and a model of topographic support³, more robust constraints on the internal structure can be derived^2,4.

For a planetary body, there is no simple, practical way of measuring the mean MOI directly. This is the reason why many studies simplify the problem by assuming hydrostatic equilibrium. In the case of Vesta, this is not possible because of the asteroid’s very irregular shape. One conventional procedure for computing the MOI is to estimate the six independent components of the full 3 × 3 symmetric inertia tensor and compute the mean MOI from the trace. If a spacecraft is in orbit around the body, or performs multiple flybys, the degree-2 gravity field can be recovered by accurately tracking the motion of the spacecraft⁵. The degree-2 gravity field provides five independent parameters related to the full inertia tensor⁶. An additional independent observation usually comes from measuring small rotational effects, such as precession or nutation⁷. These rotational variations are generally very small for planetary bodies, and measuring them requires precise data acquired over a long period of time⁸. This also means that the accuracy of the mean MOI is usually limited by the accuracy of the measured rotational variations (Extended Data Table 1).

The Dawn spacecraft orbited Vesta for about 1 year, sampling more than one-quarter of its 3.6-year orbital period around the Sun. The motion of the Dawn spacecraft is perturbed by Vesta’s non-spherical gravity field, which is tied to Vesta’s body-fixed coordinate frame. Thus, accurately tracking the motion of the Dawn spacecraft provides a unique opportunity to recover both Vesta’s gravity field and its slowly precessing and nutating spin axis. The two primary data types used to determine Vesta’s gravity field and rotational motion are the Deep Space Network Doppler tracking data⁹ and onboard imaging data¹⁰. The Doppler data measure the Earth-relative line-of-sight speed of the spacecraft, while the optical data measure the Vesta-relative position of the spacecraft¹¹.

This study employed a calibration approach improved from that used by Konopliv et al.¹² to estimate control network points (Extended Data Fig. 6) and consistent landmark locations to compute a stereophotoclinometry-based Vesta topography model with a map resolution of 50 m (Methods and Extended Data Fig. 1). For Vesta’s body-fixed coordinate system, the Claudia Double-Prime system was adopted to ensure consistency with the International Astronomical Union’s definition (Extended Data Fig. 5). Previous studies have argued for a differentiated structure within Vesta based on comparisons of the recovered value of the degree-2 zonal gravity coefficient J₂ = 0.07106 and homogenous J₂ = 0.07867 (ref. ¹³). When assuming hydrostatic equilibrium, the Radau–Darwin relationship can be used to describe an approximate relationship between J₂ and the MOI². Thus, J₂ is often used as a constraint on the interior structure of planetary bodies. However, the Radau–Darwin relationship is not valid if the body has a substantial level of non-hydrostaticity or if the rotation rate is high, both of which are true for Vesta. Measurements of the MOI of Vesta therefore provide non-degenerate internal structure information with respect to gravity coefficients.

In this study, we estimated a degree-26 gravity field called VESTA26J, which shows a global sensitivity of up to degree and order of approximately 20 and is mostly consistent with the previous gravity results VESTA20H¹². Together with the gravity field, the normalized polar MOI of Vesta was also estimated as a parameter that scales inversely with the precession and nutation amplitudes (Methods and Extended Data Tables 1–3). The recovered value is $\bar{C}=0.4208\pm 0.0047$, which is 6.6% lower than the homogenous value of 0.4505. By combining this with the recovered degree-2 gravity field, Vesta’s normalized mean MOI is $\bar{I}=0.3734\pm 0.0027$, which is 6.2% lower than the homogenous value of 0.3980.

The mean MOI is related to the internal density distribution via:

$$I=\frac{2}{3}{\int }_{\!V}\rho (r){r}^{2}{\mathrm{d}}V,$$

(1)

where ρ is the density distribution, r is the distance from the centre of mass and V is the volume. The mean MOI is an integral of the product of density and radius squared over the entire volume, directly measuring the radial mass distribution. The normalized mean MOI, $\bar{I}$, is computed by dividing I by MR², where M is the mass of Vesta and R is the reference radius (265 km) used to scale the spherical harmonic coefficients. Thus, comparing the estimated $\bar{I}$ of 0.3734 to the homogenous $\bar{I}$ of 0.3980 indicates that Vesta’s interior has a higher density than its near-surface material. For comparison, fully differentiated Earth’s $\bar{I}$ is 0.3308 (ref. ¹⁴), Mars’s $\bar{I}$ is 0.364 (ref. ⁸) and partially differentiated Ceres’s $\bar{I}$ is 0.37 (ref. ²).

In addition, we observed that the correlation between the measured gravity and the gravity from shape is close to unity. In fact, the correlation is greater than 0.95 up to degree 17 and decreases afterwards (Fig. 1a) due to the increased error in the high-degree harmonic coefficients. Such high correlation values allow the effective density spectrum (Methods) to be used to independently constrain the radial density structure based on the higher-degree harmonics that are sensitive to shallower structures. The effective density spectrum (Fig. 1b) is defined as the spectral ratio of the gravity and gravity-from-shape spectral amplitudes scaled by the mean body density^15,16,17.

Fig. 1: The correlation between gravity and gravity from shape, and effective density.

a. The correlation between gravity and gravity from shape is shown as a function of spherical harmonic degree (n). The black line is the central value and the orange shading corresponds to 1σ of the correlation. b. The effective density spectrum of Vesta as a function of the spherical harmonic degree is shown. The black line is the central value and the orange shading corresponds to 1σ of the effective density (see equation (24)). The purple curve indicates the best-fit model calculated using equation (22). The shape model is assumed to be errorless, as its accuracy is known to be substantially better than that of the gravity field. The dashed blue curves show the modelled effective crustal density (ρ_crust) spectra for a crustal thickness of 50 km, mantle density of 4,000 kg m⁻³ and a range of crustal densities.

Internal structure model

We developed an internal structure model that consists of three constant-density layers (crust, mantle and core). The bulk volume (7.49 × 10⁷ km³) and mass (2.59028 × 10²⁰ kg) of the model were fixed to the observed values of Vesta (Methods). The model has five free parameters: the radii and densities of the core and mantle and the palaeorotation period (Extended Data Table 4). The density of the crust was computed from the input parameters to satisfy the observed mass. First, we computed the hydrostatic shape for the three-layer model using a numerical method for the chosen rotation period¹⁸. This approach provided the hydrostatic flattening factor of the shape. It was previously found that the northern terrains of Vesta probably represent its shape before large impacts¹⁵, and it was concluded that Vesta acquired a hydrostatic shape early in its thermal history¹⁹. The northern terrains unperturbed by the impacts thus probably represent the hydrostatic shape frozen at a palaeorotation rate, and we matched the hydrostatic flattening to the ellipsoidal fit to the northern terrains derived by Ermakov et al.¹⁵. To compute the MOI, we replaced the outer hydrostatic shape with the observed shape of Vesta (Methods). The flattening of the mantle was also computed to satisfy J₂. The shape of the core was kept hydrostatic. Thus, the model yielded the full MOI tensor, as well as the flattening of the northern hemisphere. Given the densities of the crust and mantle, we could also compute the effective density spectrum, assuming uncompensated topography (Methods).

We used Markov-chain Monte Carlo (MCMC) to infer the posterior distribution of the internal structure parameters. For this, we used the affine invariant ensemble sampler²⁰ implemented in the publicly available emcee Python library²¹. The final product of the MCMC is a converged chain sampling the posterior distribution of the model parameters. To analyse the MCMC results, we mapped the posterior distributions of the model parameters using corner plots (Fig. 2)²². We constrained the density to monotonically increase with depth and limited the maximum size of the core to 150 km.

Fig. 2: Corner plot showing the posterior distributions of the parameters of the internal structure model based on the new MOI estimate.

Median values and 5–95% quantile intervals (dashed vertical lines) are given for layer thicknesses (h_i) and densities (ρ_i). The indices 1, 2 and 3 refer to the crust, mantle and core, respectively. The grey shades represent the posterior distribution of MCMC samples. The inset shows the probability density distribution of the density as a function of radius. The different shades of blue correspond to the probability intervals stated in the legend. The probability density was computed by stacking the three-layer model density profiles from the converged Markov chain.

Vesta’s interior

Our results show that Vesta’s mantle density is higher than previously determined on the basis of geochemical evolution models²³. We also found a more uniform density profile below the vestan crust with a limited mantle–core density contrast. The MCMC inversion results based on the new MOI estimate are shown in Fig. 2. We report the median values and 5–95% confidence intervals. The MCMC inversion yielded a crustal thickness of ${47}_{-13}^{+12}\,{\mathrm{km}}$ with a density of ${2.70}_{-0.10}^{+0.07}\,{\mathrm{g}}\,{{\mathrm{cm}}^{-3}}$, a mantle density of ${4.1}_{-0.3}^{+0.2}\,{\mathrm{g}}\,{{\mathrm{cm}}^{-3}}$ for a mantle thickness of ${169}_{-80}^{+32}\,{\mathrm{km}}$ and a core density of ${5.6}_{-1.4}^{+3.0}\,{\mathrm{g}}\,{{\mathrm{cm}}^{-3}}$ for a core radius of ${45}_{-32}^{+87}\,{\mathrm{km}}$. The palaeorotation period was constrained to be ${4.98}_{-0.04}^{+0.04}\,{\mathrm{h}}$, consistent with the results of Ermakov et al.¹⁵.

A comparison of Fig. 2 with Extended Data Fig. 2, which does not include the observed MOI as a constraint, clearly shows that the MOI constraint makes the density distribution resemble a two-layer model. The effective density spectrum (Fig. 1b) constrains the crustal density to be lower than the mean density, which means that the MOI is lower than in a homogeneous model. If a high-density core is introduced in addition to a low-density crust, the MOI is reduced even further below the observed value. The permitted core–mantle density contrast is more limited for large core radii. Without including the MOI as a constraint (Extended Data Fig. 2) for cores with radii greater than 50 km and 100 km, 90% of the models from the converged MCMC run had core–mantle density contrasts of less than 3.83 g cm⁻³ and 2.96 g cm⁻³, respectively. Once we included the MOI constraint, these density contrasts were reduced to 3.20 g cm⁻³ and 1.29 g cm⁻³, respectively.

We also ran an MCMC inversion that assumed an ellipsoidal mantle that does not contribute to gravity beyond degree 2 using the effective density from equation (23). As the crustal density is less constrained with this approach, we obtained a broader posterior distribution (Extended Data Fig. 3), with core–mantle density contrasts of 3.92 g cm⁻³ and 1.48 g cm⁻³ for 50 and 100 km cores, respectively. We therefore could not exclude a completely coreless Vesta, but determined that the core–mantle density contrast is better constrained by the MOI and gravity observations.

It was suggested that Vesta’s crust is thick on the basis of hydrocode simulations of the impacts that formed Rheasilvia and Veneneia²⁴. A thick crust is required to avoid excavation of olivine-rich mantle, as olivine-rich ejecta were not found on the surface²⁵. As the effective density spectrum constrains the crustal density, a crust of greater thickness would lead to a further reduction of the MOI compared with a homogeneous model. This requirement for a thicker crust is thus difficult to reconcile with the presence of a high-density core, as it would yield MOI values smaller than that observed. If we constrained the crust to be thicker than 80 km, the core radius was constrained to be ${33}_{-21}^{+100}\,{\mathrm{km}}$. To satisfy the total mass, the mantle and core densities were increased to ${4.73}_{-0.12}^{+0.13}\,{\mathrm{g}}\,{\mathrm{cm}}^{-3}$ and ${6.0}_{-1.2}^{+2.6}\,{\mathrm{g}}\,{\mathrm{cm}}^{-3}$, respectively (see Extended Data Fig. 4). The result of this constrained case shows that 90% of the models have the core–mantle density contrasts of less than 1.70 g cm⁻³ and 0.49 g cm⁻³ for cores with radii greater than 50 km and 100 km, respectively.

Discussion

The Dawn payload confirmed that Vesta’s crust is dominated by howardite–eucrite–diogenite (HED)-like material¹³, indicating that Vesta went through a phase of partial or global melting^26,27. Indeed, geochemical and geochronological evidence of HEDs indicates extensive melting of chondrite-related material very early in Solar System history.

This has led to the paradigm of Vesta as a highly differentiated body with a metal/sulfide core, a mafic mantle and a basaltic crust. This scenario is consistent with previous assessments of Vesta’s geophysical properties²⁷, as well as with indirect evidence, such as the high remanent magnetization in eucrite ALHA81001, which records a crustal magnetic field generated by a crust that may have been magnetized by a dynamo-drive magnetic field on early Vesta²⁸. However, the analysis presented here clearly challenges this simple view of a three-layer structure. To explain our new findings, we propose two alternative scenarios that may explain Vesta’s current interior structure.

Incomplete differentiation

Differentiation in the early Solar System was principally driven by short-lived radioelements, particularly aluminium-26 (²⁶Al). In general terms, an earlier accretion time (relative to the condensation of calcium aluminium inclusions) leads to higher initial concentrations of ²⁶Al and more potential for global differentiation. As aluminium is a lithophile and incompatible, in the case of melting, this element preferentially concentrates in the silicate liquid, the subsequent distribution being controlled by relative rates of heating on the one hand and melt extraction on the other²⁹. For very early accretion (<1.15 Myr after calcium aluminium inclusions condense, as estimated by Monnereau et al.²⁹), heating is faster than melt extraction and global melting is inevitable. For accretion in the time window 1.15–1.5 Myr after calcium aluminium inclusions condense, melt extraction is predicted to occur, with silicate melt being compacted towards the surface, transporting active ²⁶Al to shallow depths while arresting deep melting³⁰. In the time window 1.5–1.7 Myr, melt is expelled upwards but ²⁶Al has lost its capacity to generate additional melting of the crustal region. For accretion after 1.7 Myr, melt extraction is too slow, and any liquids generated will recrystallize where they formed.

Primitive achondrites, such as the acapulcoite-lodranite clan, have been studied extensively to understand the efficiency of Fe, Ni–S, and Al-rich plagioclase melt migration^31,32,33, demonstrating the possibility of silicate melt being extracted while a high-density, Fe–Ni metal-rich bearing residue is preserved. Numerical models of melt migration in the acapulcoite-lodranite parent body suggest the development of a region of compacted, approximately chondritic composition with a density close to 4 g cm⁻³, as we infer for the bulk of the vestan interior³⁴, consistent with accretion around the 1.7 Myr limit of Monnereau et al.²⁹.

However, the application of such a ‘late’ accretion to the case of Vesta would not seem possible in light of the abundant geochemical and geochronological evidence of HEDs that clearly argues for abundant melt extraction and differentiation that was complete within a couple of million years after Solar System accretion (for example, the crystallization ages of basaltic eucrites at 2.66 Myr; ref. ³⁵) and metal–silicate separation within the first 2 Myr (ref. ³⁶), in addition to evidence for a highly complex thermal history of the vestan crust^37,38 that implies active heat sources in the crustal region. Indeed, many geochemical studies argue for accretion within the first million years of Solar System history.

Alternatively, it is interesting to consider a scenario of accretion in the time window 1.15–1.5 Myr. In this case, silicate melting occurs and the liquids produced are extracted towards the crustal region (driving complex crustal magmatism), while depriving the internal region of additional melting, which could result in a lower region dominated by olivine–metal mixtures. This timing may be sufficiently old for the preservation of magnetic fields related to the solar nebula without requiring an internal dynamo^39,40.

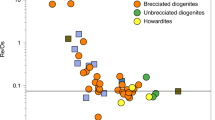
To explore this idea further, the geochemical models presented by Toplis et al.²⁷ have been used to predict density–depth profiles for differentiated chondrite-like bodies²⁷. In contrast to the original work (which considered differentiation into a three-layer structure with a metal/sulfide core, an olivine–orthopyroxene mantle and a basaltic eucrite crust), in this study the same geochemical constraints were used to predict the density and thickness of a two-layer structure with a lower metal/sulfide/olivine layer and an upper porous layer of orthopyroxene (diogenite) and eucrite. Remarkably, the H-chondrite and H-CM mixture compositions that provide the best fits to a wide range of geochemical constraints (for example, the capacity to form Juvinas-like eucrite, Mn/Fe ratios and the oxygen isotopic composition) are also those that provide excellent agreement with the new interpretation of the MOI and gravity data presented here (Fig. 3). The total porosity of the upper layer for such a composition is 18.5%. In other words, the densities and thicknesses found here are geochemically plausible but require an accretion time window that effectively leaves an olivine-melt residue. In this respect, we note that Neri et al.⁴¹ have shown that surface tension effects lead to the intimate association of olivine and metal during partial melting and that these phases are difficult to separate unless the percolation threshold of metallic melt is met and/or convective movements occur. This may be the case at the base of the lower layer, and would explain the potential increase in density inferred in the central region of Vesta (Fig. 2). We note that the predicted density of the pure metallic phase of the closest geochemical match is 6.3 g cm⁻³, which is also consistent with gravity modelling and that with the size inferred here. Thus, this scenario has several advantages but implies accretion that is later than currently thought, and a second alternative is proposed.

Fig. 3: Confidence regions for the crustal density, mantle density and crustal thickness.

The 1σ, 2σ and 3σ confidence regions (contours) for various bulk chondritic compositions are shown for the same Markov chain used for Fig. 2 (blue dots) following the analysis of ref. ²⁷ with a two-layer structure (a lower metal/sulfide/olivine layer and an upper porous layer of orthopyroxene (diogenite) and eucrite). The yellow curves on the top and right sides of each plot represent the histograms of the confidence regions shown on the corresponding axes. CM, CO, CV, CK, CR, CH, L, H, EL and EH are chondrite types.

Vesta as a second-generation object

Vesta could be the ejecta product of a catastrophic impact event on a differentiated precursor body. Many energetic catastrophic impact geometries are expected to produce copious amounts of debris⁴². In published works, these energetic catastrophic impacts were simulated to occur on target protoplanets ranging in size from Mars to Earth masses, and projectiles that were typically assumed to be lunar mass or larger—even of similar sizes to the target. For instance, Vesta could be a re-accreted body in the tidal tail of material that stretches out from a catastrophic impact site^43,44, mixing the iron-rich core and mantle material. Depending on the parameters of the catastrophic impact, these objects can be bound or escape into heliocentric orbits. While the ejected material is moving at escape speeds relative to the target, the relative speed between ejected components is low and the ejected material is quickly incorporated into new bodies due to gravity^42,43.

The ejecta is likely to have a non-chondritic composition and be a mixture of projectile mantle, projectile core and target mantle. Some simulated ejecta seems to have little to no projectile core^43,45,46. Those bodies could therefore be made entirely of silicate. The ejecta is coming from substantial depth within the projectile, and target bodies and may be molten before impact. Shocks will pass through the ejecta during the impact process, depositing substantial entropy⁴⁷. Furthermore, the overburden pressure will be relieved immediately when the material is ejected during the impact, and as it will take time to transport internal heat out of the body, the ejected material could undergo decompression melting. Thus, Vesta-sized masses of ejecta could be mostly molten post-impact. The observed MOI and the proposed impact scenario could also help to explain the composition of HED meteorites, particularly the observed depletion in volatiles (for example, alkalis), which in turn favours orthopyroxene relative to olivine, consistent with HED lithologies⁴⁸.

Although the petrology of the HED meteorites implies a complex magmatic history^{23,37,38,49,50}, models almost invariably make the assumption of a chondritic bulk composition. A post-impact formation hypothesis has the potential to deviate significantly from this assumption, as Vesta could be a mixture of the pre-impact mantles (and possibly cores) of probably already molten and differentiated bodies. Given that escaping ejecta is mostly target mantle material^42,43,44, this could naturally explain the small (~0.8 wt%) core inferred above.

However, the major challenge to such an impact disruption model is the bulk density of Vesta, which, at 3.4 g cm⁻³, is more consistent with a bulk chondritic composition than that of an Fe-depleted mantle. More specifically, the density of ${4.1}_{-0.3}^{+0.2}\,{\mathrm{g}}\,{\mathrm{cm}}^{-3}$ of the volumetrically dominant layer inferred from our MCMC inversion is difficult to reconcile with that of a mixture of silicates alone, unless olivine and orthopyroxenes were close to their Fe-rich endmembers (a hypothesis that is not consistent with the composition of observed eucrites and diogenites).

This could be explained if the vestan mantle resembles mesosiderites, which are a mixture of Fe–Ni metal and silicate clasts, some of which are similar to basaltic eucrites and have a density of ~4.2–4.8 g cm⁻³. Thus, the volumetrically dominant mantle layer of Vesta may consist of a mechanical mixture of native Fe–Ni and silicates in similar proportion to mesosiderites⁵¹. Finally, as mesosiderite material is more spectrally similar to HED meteorites^52,53,54, it would more easily blend in with the rest of Vesta, explaining the lack of exposed olivine in the Rheasilvia and Veneneia basins.

Conclusion

The value recovered for Vesta’s MOI from Dawn’s monitoring of Vesta’s rotational dynamics and gravity data, along with the inferred constraints, suggests that Vesta has not experienced full differentiation into a metallic core, silicate mantle and basaltic crust. This incomplete differentiation could be due to the timing of accretion or to accretion from non-chondritic debris. Our results highlight the power of measuring the rotational dynamics of small, non-hydrostatic bodies to complement gravity investigations. Similar measurements are planned for the Psyche mission to determine the state of differentiation of (16) Psyche⁵⁵, as well as for NASA’s OSIRIS-APEX mission to Apophis⁵⁶ and ESA’s Hera mission to the Didymos–Dimorphos system⁵⁷.

Methods

Vesta dataset from the Dawn mission

During the 1-year science phase at Vesta, the Dawn spacecraft acquired X-band (7.2 GHz uplink and 8.4 GHz downlink) Deep Space Network (DSN) tracking data and onboard framing camera images. The DSN tracking provides the time of flight and Doppler shift of the radio signal transmitted from a DSN station to the spacecraft and back to a DSN station. The time-of-flight data measure the distance (<2 m one-way accuracy) and the Doppler data measure the line-of-sight component of the velocity (<0.1 mm s⁻¹ one-way accuracy at 60 s count time) of the spacecraft relative to a DSN station. The gravity field of Vesta is primarily determined from the Doppler data, whereas the ranging data are used to determine the heliocentric orbit of Vesta. The onboard images provide surface-relative positional information on the spacecraft orbit, which is important for improving the long-wavelength gravitational signal and determining the rotational motion of Vesta.

Dawn’s entire science phase at Vesta consisted of the Approach (15 days, 25,000–5,214 km altitude), Survey (30 days, 2,725–2,737 km altitude), High-Altitude Mapping Orbit (HAMO) (35 days, 663–701 km altitude), Low-Altitude Mapping Orbit (LAMO) (166 days, 169–324 km altitude) and HAMO-2 (49 days, 650–714 km altitude) phases¹². Except for the Approach phase, the spacecraft was on a circular polar orbit, but with a different orbital radius for each phase. The lowest altitude was ~169 km relative to a 265 km reference sphere during the LAMO phase. The data collected during the Survey, HAMO, LAMO, and HAMO-2 phases were distributed around the globe, allowing a global recovery of the gravity field and shape. Additional data were collected during the transfers between each phase, but due to strong non-gravitational forces from transfer manoeuvres, these were not considered in our data analysis.

Determination of Vesta’s shape

The Dawn spacecraft was equipped with two framing cameras: the primary (FC2) and backup (FC1). Each camera had an instantaneous field of view of 93.7 μrad per pixel and field of view of 5.5° × 5.5° (ref. ⁵⁸). The FC2 camera was used throughout the Dawn mission to Vesta and provided the data used in this study.

An accurate shape model is essential to understand the geophysical nature of Vesta. In this study, a high-resolution global shape model of Vesta was determined using a stereophotoclinometry (SPC) technique by processing Dawn’s framing camera data acquired during all phases of the mission. A total of about 16,500 images were processed with image resolutions ranging from 600 m to 20 m. The Approach and Survey data were mainly used to compute an a priori shape model and were not used to compute the final global topography model, as their contributions were essentially negligible. The final topography model delivered in this study was produced with 50 m spatial resolution using images with 65 m and 20 m pixel resolutions acquired during the HAMO, LAMO and HAMO-2 phases of the mission. This process required approximately 75,000 individual maps to completely cover the entire body, including the partial overlap between maps that is essential to tie neighbouring maps together.

Using framing camera images, a high-resolution, SPC-based 3D shape model of Vesta was computed^59,60,61. By matching images to the model through iterations, the same SPC process provides the data needed for the orbit determination to estimate landmark positions, which are crucial for determining Vesta’s global parameters (for example, spin-pole axis, rotation rate and so on). The SPC shape model was computed relative to the centre of mass and in this coordinate system, the centre of figure is located at (0.99, 1.05, −0.05) ± 0.1 km (that is, the centre of the homogeneous Vesta relative to the centre of mass). The resulting best-fit ellipsoid is (284.62, 277.24, 226.33) km and the resulting best-fit spheroid is (280.89, 226.32) km. The topography relative to the best-fit ellipsoid is shown in Extended Data Fig. 1.

The SPC-derived global shape models of Vesta have been archived in the Planetary Data System. Specifically, we archived ICQ global shape models and gridded shape models with a map scale of 50 m through the PDS NAIF node⁶², along with ancillary files such as the spacecraft ephemeris, camera pointing, Vesta spin-pole axis, prime meridian and rotation rate (that is, the Planetary Constants Kernel) and so on.

Determination of Vesta’s gravity field and rotation

The external gravitational potential of Vesta can be modelled using a spherical harmonic expansion^2,63:

$$U(r,\lambda ,\phi )=\frac{GM}{r}\mathop{\sum }\limits_{n=0}^{\infty }\mathop{\sum }\limits_{m=0}^{n}{\left(\frac{R}{r}\right)}^{n}{P}_{nm}(\sin \phi )\,[{C}_{nm}\,\cos (m\lambda )+{S}_{nm}\,\sin (m\lambda )],$$

(2)

Here, G is the universal gravitational constant, M is the mass of Vesta, R is the reference radius of Vesta (265 km), n is the degree, m is the order, P_nm are the associated Legendre functions and C_nm and S_nm are the unnormalized spherical harmonic coefficients (the corresponding unnormalized zonal harmonics are J_n = −C_n0). The unnormalized spherical harmonic coefficients are related to the fully normalized spherical harmonic coefficients as $\left({\bar{C}}_{{nm}},{\bar{S}}_{{nm}}\right){N}_{{nm}}=\left({C}_{{nm}},{S}_{{nm}}\right)$, where the normalization factor is defined as:

$${N}_{{nm}}=\sqrt{\frac{\left(n-m\right)!\left(2-{\delta }_{0m}\right)\left(2n+1\right)}{\left(n+m\right)!},}$$

(3)

where δ_0m represents the Kronecker delta function. At each body-fixed point defined by the latitude (ɸ), longitude (λ) and radius (r), the gravitational acceleration of an external point source (for example, the Dawn spacecraft) is given by the gradient of this potential. As the spacecraft dynamics is influenced by Vesta’s gravity field, which is tied to its body-fixed coordinate frame, accurately tracking the spacecraft motion allows the recovery of gravity field and rotational parameters. Given a degree-n gravity field, the half-wavelength resolution is defined as πR/n. For example, degree 26 would yield a spatial resolution of 32 km.

Previous studies have reported a degree- and order-20 gravity field^12,64 for Vesta. Our study shows that some regions have a global sensitivity of up to degree and order of approximately 20. Thus, to avoid any signal tapering at high degrees, we estimated VESTA26J.

The Vesta gravity field was modelled in a Vesta body-fixed frame, and its inertial orientation in the International Celestial Reference Frame was modelled with (α,δ,W), where α represents the spin-pole right ascension, δ represents the spin-pole declination and W represents the rotation around the spin-pole axis. Specifically, the time series of (α,δ,W) are defined as:

$$\begin{array}{rcl}\alpha (t) & = & {\alpha }_{0}+(1-\chi)\left[{\dot{\alpha }}_{0}t+{\ddot{\alpha }}_{0}{t}^{2}+\mathop{\sum }\limits_{j=1}^{q}{A}_{\!j}\,\sin ({\dot{\varOmega }}_{j}t+{\varOmega }_{j})\right],\\ \delta (t) & = & {\delta }_{0}+(1-\chi)\left[{\dot{\delta }}_{0}t+{\ddot{\delta }}_{0}{t}^{2}+\mathop{\sum }\limits_{j=1}^{q}{B}_{\!j}\,\cos ({\dot{\varOmega }}_{j}t+{\varOmega }_{j})\right],\\ W(t) & = & {W}_{0}+{\dot{W}}_{0}d+(1-\chi)\left[\mathop{\sum }\limits_{j=1}^{q}{C}_{\!j}\,\sin ({\dot{\varOmega }}_{j}t+{\varOmega }_{j})\right],\end{array}$$

(4)

where (α₀,δ₀,W₀) are constant terms, $\left({\dot{\alpha }}_{0},{\dot{\delta }}_{0},{\dot{W}}_{0}\right)$ are rate terms, $\left({\ddot{\alpha }}_{0},{\ddot{\delta }}_{0}\right)$ are acceleration terms, χ is the fractional change in the polar MOI ($\bar{C}$), q is the number of terms in the nutation series, (A_j,B_j,C_j) are nutation amplitudes, ${\dot{\varOmega }}_{j}$ is the nutation frequency, ${\varOmega }_{j}$ is the nutation phase, t is the time in seconds since J2000 and d is the time in days since J2000. J2000 is defined as 2000 January 1 12:00:00. The rate terms ${\dot{\alpha }}_{0}$ and ${\dot{\delta }}_{0}$ represent the spin-pole’s precession and the terms in the summation represent the nutation series.

For Vesta, the prime meridian, W₀, was chosen such that it is consistent with the International Astronomical Union’s definition of Vesta’s body-fixed frame, called the Claudia Double-Prime system. In this coordinate system, a small crater called Claudia defines the meridian at 146° longitude, and the gravity field is defined relative to the Claudia Double-Prime system, which is not aligned with the principal-axis frame. Extended Data Fig. 5 shows the location of the body-fixed location of the Claudia crater.

The precession rate, acceleration terms and nutation parameters were initialized by integrating the Euler equation for rotational dynamics for a constant-density Vesta with $\bar{C}=0.4505$ and by fitting the amplitude, frequency and phase to the integrated series. The amplitudes scale with the inverse of $\bar{C}$; thus, estimating the scale factor, χ, directly measures the normalized polar MOI.

The radio and optical data were then processed using the Jet Propulsion Laboratory’s Mission Analysis, Operations, and Navigation Toolkit Environment (MONTE) software suite⁶⁵. For data processing, the year-long Vesta science phase was divided into multiple small arcs, ranging from ~2 days to ~10 days. For each arc, the parameters estimated were the spacecraft state, angular momentum desaturation burns, stochastic accelerations, camera pointing and a few measurement calibration parameters. Globally estimated parameters were the degree-26 gravity field, constant spin-pole axis, χ, landmark positions and heliocentric Vesta ephemeris. The local and global solutions were both iterated until they fully converged using a batch least-squares filter^66,67, where the correction to the MOI scale factor is much smaller than the formal uncertainty.

A previous study attempted to recover Vesta’s MOI¹², but the result was not conclusive due to an observed conflict between the DSN Doppler tracking data and the onboard imaging data. This inconsistency was clearly shown as a systematic trend in the difference between estimated landmark positions from orbit determination and SPC (see fig. 12 of Konopliv et al.¹²). The source of this conflict was identified and resolved during Ceres operations when the Dawn Gravity Science Team had to process radio tracking and imaging data simultaneously for the Ceres Gravity Science Investigation². This was related to data calibration, and the problem was apparent only when the radio tracking and imaging datasets were combined. Once Doppler and imaging data were calibrated with consistent techniques, reanalysis of the Vesta data showed excellent agreement between the two methods. Extended Data Fig. 6 shows the differences between the estimated landmark positions from the global gravity solution and the a priori landmark locations given by the SPC shape model for the Cartesian coordinates. When compared with fig. 12 of Konopliv et al.¹², the mean zero differences shown here indicate that the global gravity solution and SPC solution are consistent; thus, the systematic errors have been resolved by the calibration.

Extended Data Table 1 shows the recovered GM, degree-2 gravity field and normalized MOI parameters. Using the universal gravitational constant value of (6.67430 ± 0.00015) × 10⁻²⁰ km³ kg⁻¹ s⁻² from Tiesinga et al.⁶⁸, the mass of Vesta is found to be 2.59028 ± 0.00006) × 10²⁰ kg. When combined with the volume of (7.49 ± 0.01) × 10⁷ km³ from the SPC shape, Vesta’s bulk density is determined to be 3.458 ± 0.005 g cm⁻³. For the purposes of comparison, corresponding constant-density values are also provided. Extended Data Tables 1 and 2 show fully converged rotational parameters. The reconstructed Vesta-relative spacecraft orbit accuracy was better than 1 m in all three directions during the HAMO, LAMO and HAMO-2 phases. Extended Data Table 3 shows the estimate of the normalized polar MOI based on variations in subset solutions, showing robustness in the recovered MOI estimate. Comparisons of subset solutions are often conducted to assess potential systematic errors in the estimated parameters⁶⁹.

Internal structure model

We modelled Vesta as a three-layer body in which the layers have uniform densities. The ranges of model parameters are given in Extended Data Table 4. Gravity coefficients for a model of Vesta were computed from the gravity coefficients of the individual layers:

$$\{{C}_{nm},{S}_{nm}\}=\frac{1}{M}\mathop{\sum }\limits_{i=0}^{N-1}\left\{{C}_{nm}^{(i)},{S}_{nm}^{(i)}\right\}\left[\frac{4}{3}\uppi {R}_{\mathrm{vol,i}}^{3}(\;{\rho }_{i+1}-{\rho }_{i})\right],$$

(5)

where M is the total mass of Vesta and R_vol,i are the volume-equivalent radii of the interfaces. For the mantle and core, we assumed ellipsoidal shapes. For an ellipsoid of evolution, the unnormalized degree-2 zonal gravity coefficient can be found by:

$${C}_{20}=\frac{1}{{5R}^{2}}\left({c}^{2}-{a}^{2}\right),$$

(6)

where a and c are the ellipsoidal semi-major and semi-minor axes, respectively. The volume-equivalent radius is found from the ellipsoidal axes:

$${a}^{2}c={R}_{{\mathrm{vol}}}^{3}.$$

(7)

To satisfy the observed value of C₂₀, we found the required ${C}_{20}^{\;(1)}$ (that is, the mantle contribution) using equation (5). The outer shape was assumed to be the observed shape of Vesta and the shape of the core was assumed to be a hydrostatic ellipsoid. In other words, the shape of the core was found by solving for hydrostatic equilibrium of a three-layer body with defined volume-equivalent radii of each layer and a rotation rate. We then found the dimensions of the mantle ellipsoid by combining equations (6) and (7), which led to the following cubic equation for the polar (semi-minor) axis of the mantle ellipsoid:

$$\frac{1}{5}{R}^{2}{\left({c}_{{\mathrm{mantle}}}\right)}^{3}-{C}_{20}^{\;\left(1\right)}{c}_{{\mathrm{mantle}}}-{R}_{{\mathrm{vol}},{\mathrm{mantle}}}^{3}=0.$$

(8)

Solving this cubic equation, and using the mantle volumetric radius as an input, allowed us to find the equatorial axis of the mantle ellipsoid. Thus, our modelled Vesta reproduced the observed mass, volume and J₂ gravity coefficient of Vesta.

MCMC inversion of model parameters

We used the affine invariant ensemble sampler implemented in the emcee Python library²¹. This sampler updates the position of an individual Markov chain depending on the previous position of an ensemble of Markov chains, called walkers. The ensemble sampler requires an initial ensemble of plausible internal structure models to initiate the sampling of the model parameter space. To choose the initial positions of walkers, we randomly created 10 times more initial positions and chose those that had the highest likelihood. This reduced the burn-in parts of the chains.

The key step in MCMC is defining the likelihood function. As our observables were degree-2 gravity and shape, the log-likelihood function took the following form:

$$\mathrm{ln}L=-\frac{1}{2}\left({\bf{X}}-{\bf{Y}}\right){{{\varSigma }}}^{-1}{\left({\bf{X}}-{\bf{Y}}\right)}^{T},$$

(9)

where ${\bf{X}}=(\;{f}_{p},{I}_{1},{I}_{2},{I}_{3},{\widetilde{\rho }}_{3},{\widetilde{\rho }}_{4},\ldots ,{\widetilde{\rho }}_{16})$ is the vector of observations that contains the northern flattening factor, observed principal MOI and effective density spectrum values, Y is the vector of model predictions and Σ is the covariance matrix that contains contributions from the observational and model covariances:

$$\displaystyle{\varSigma}={{\varSigma}}_{{\mathrm{model}}}+{{\varSigma}}_{{\mathrm{obs}}}.$$

(10)

To guarantee MCMC convergence, we computed integrated autocorrelation times τ_int for the Markov chains and ensured that we produced chains longer than $50{\tau }_{\mathrm{int}}$.

Effective density spectrum

Similar to the gravity field, the shape of a planetary body can be expressed in spherical harmonics:

$$r(\lambda ,\phi )=\mathop{\sum }\limits_{n=0}^{\infty }\mathop{\sum }\limits_{m=0}^{n}{P}_{nm}(\sin \phi )\,[{A}_{nm}\,\cos (m\lambda )+{B}_{nm}\,\sin (m\lambda )],$$

(11)

Having the gravitational potential and shape in spherical harmonic expansions, we can express the gravity variance spectra (V_n^gg) and the topography variance spectra (V_n^tt) as:

$$\begin{array}{rcl}{V}_{n}^{\,gg} & = & \mathop{\sum }\limits_{m=0}^{n}{C}_{nm}^{2}+{S}_{nm}^{2},\\ {V}_{n}^{\,tt} & = & \mathop{\sum }\limits_{m=0}^{n}{A}_{nm}^{2}+{B}_{nm}^{2}.\end{array}$$

(12)

In addition, we can expand the gravity computed from the shape assuming a homogenous interior in a spherical harmonic series¹⁷. We can define the variance spectrum of the gravity from shape as:

$${V}_{n}^{\;g{\prime} g{\prime} }=\mathop{\sum }\limits_{m=0}^{n}{\left({C}_{{nm}}^{{\prime} }\right)}^{2}+{\left({S}_{{nm}}^{{\prime} }\right)}^{2},$$

(13)

where ${C}_{{nm}}^{{\prime} }$ and ${S}_{{nm}}^{{\prime} }$ are the spherical harmonic coefficients of the gravitational potential induced by the uniform density shape. The effective density is defined as the ratio of the gravitational potential spherical harmonic coefficients to the gravity-from-shape spherical harmonic coefficients multiplied by the mean density of the body:

$${\widetilde{\rho }}_{n}=\sqrt{\frac{{V}_{n}^{\;{gg}}}{{V}_{n}^{\;{g}^{{\prime} }{g}^{{\prime} }}}}{\rho }_{{\mathrm{mean}}}.$$

(14)

As higher-degree spherical harmonic coefficients sample shallower structures and density typically increases with depth, the effective density spectrum usually decreases with n.

To derive the effective density spectrum from the density distribution, we first defined a short notation for the normalized spherical harmonic gravity coefficients:

$${\bar{C}}_{{nm}}={\sigma }_{1{nm}};{\bar{S}}_{{nm}}={\sigma }_{2{nm}}.$$

(15)

We assumed that the body consists of multiple layers, each of which has a constant density⁷⁰. We also assumed that the shape of these layers is the downscaled version of the outer shape of the body. This assumption effectively limits our analysis to the parts of the effective density spectrum that are not affected by isostatic compensation, since the bottom boundary of the isostatically compensated layer is a mirror image of its top boundary (that is, outer surface).

The gravity coefficients of the outer shape are ${\sigma }_{{inm}}^{\,{\rm{const}}}$ and they are referenced to R. The gravity coefficients of the inner layers are also ${\sigma }_{{inm}}^{\,{\rm{const}}}$ if they are referenced to the corresponding volumetric radii, but their contributions to the total gravity σ_inm need to be weighted by the upward propagation factor $\scriptstyle{(\frac{{r}_{i}}{R})}^{n}$. In addition, ${\sigma }_{{inm}}^{\,{\rm{const}}}$ needs to be weighted by the fractional mass of the layers. In summary, σ_inm took the following form:

$$\begin{array}{l}{\sigma }_{{inm}}=\frac{1}{M}\left({\sigma }_{{inm}}^{\,{\rm{const}}}\frac{4}{3}\uppi {r}_{1}^{3}{\rho }_{1}{\left(\frac{{r}_{1}}{R}\right)}^{n}+{\sigma }_{{inm}}^{\,{\rm{const}}}\frac{4}{3}\uppi {r}_{2}^{3}\left(\,{\rho }_{2}-{\rho }_{1}\right){\left(\frac{{r}_{2}}{R}\right)}^{n}+\ldots\right.\\\qquad\;\;\left.+{\sigma }_{{inm}}^{\,{\rm{const}}}\frac{4}{3}\uppi {r}_{k}^{3}\left(\,{\rho }_{k}-{\rho }_{k-1}\right){\left(\frac{{r}_{k}}{R}\right)}^{n}\right),\end{array}$$

(16)

where r_i are the volumetric radii of layers (r_i = R; that is, the volumetric radius of the outermost layer) and ρ_i are the densities of the layers. Taking $M=\frac{4}{3}\uppi {R}^{3}\bar{\rho }$, where $\bar{\rho }$ is the mean density, we obtained (after simplification):

$${\sigma }_{{inm}}=\frac{{\sigma }_{{inm}}^{\,{\rm{const}}}}{\bar{\rho }{R}^{n+3}}\left({r}_{1}^{n+3}{\rho }_{1}+{r}_{2}^{n+3}\left(\,{\rho }_{2}-{\rho }_{1}\right)+\ldots +{r}_{k}^{n+3}\left(\,{\rho }_{k}-{\rho }_{k-1}\right)\right).$$

(17)

Next, we replaced the sum with an integral. The density difference between layers was, therefore, also replaced by a differential expression $\left(\,{\rho }_{k}-{\rho }_{k-1}\right)\to -\frac{{\mathrm{d}}\rho \left(r\right)}{{{\mathrm{d}}r}}\cdot {{\mathrm{d}}r}$. We obtained the following integral for the gravity coefficients:

$${\sigma }_{{inm}}=\frac{{\sigma }_{{inm}}^{\,{\rm{const}}}}{\bar{\rho }{R}^{n+3}}{\int }_{\!\!\!{R}^{+}}^{0}{r}^{n+3} \frac{{\mathrm{d}}\rho \left(r\right)}{{{\mathrm{d}}r}} {{\mathrm{d}}r},$$

(18)

where R⁺ signifies that integration needs to go past the outer interface. The effective density spectrum is defined as:

$${\widetilde{\rho }}_{n}=\frac{{\sigma }_{{inm}}}{{\sigma }_{{inm}}^{\,{\rm{const}}}}\bar{\rho }.$$

(19)

Therefore, we obtained an integral expression for ${\widetilde{\rho }}_{n}$:

$${\widetilde{\rho }}_{n}=\frac{1}{{R}^{n+3}}{\int }_{{\!\!\!R}^{+}}^{0}{r}^{n+3} \frac{{\mathrm{d}}\rho \left(r\right)}{{{\mathrm{d}}r}} {{\mathrm{d}}r}.$$

(20)

At the outer interface r = R, the density goes instantaneously from surface density ρ_surf to zero. The derivative of the density with respect to volumetric radius therefore has a singularity at r = R. Replacing the value of the derivative at r = R by a Dirac delta function times the amplitude of the density jump, ρ_surf ⋅ δ(r − R, we can integrate through r = R and get:

$${\widetilde{\rho }}_{n}={\rho }_{{\rm{surf}}}+\frac{1}{{R}^{n+3}}{\int }_{\!\!\!{R}^{-}}^{0}{r}^{n+3} \frac{{\mathrm{d}}\rho \left(r\right)}{{{\mathrm{d}}r}} {{\mathrm{d}}r}.$$

(21)

${\widetilde{\rho }}_{n}$ has the following two interesting properties:

• 1. At n = 0, ${\widetilde{\rho }}_{0}=\bar{\rho }$. Therefore, when fitting the modelled effective density spectrum to the observed one, we could add an extra observation for n = 0.

• 2. For $n\to \infty ,{\widetilde{\rho }}_{\infty }={\rho }_{{\rm{surf}}}$. Therefore, the high-degree effective density spectrum approaches the surface density of the body.

The derived equation (21) can be used with simple density profiles. The three-layer density with a spherical core model results in the following effective density spectrum:

$${\widetilde{\rho }}_{n}={\rho }_{{\mathrm{crust}}}-{\left(\frac{{r}_{{\mathrm{mantle}}}}{R}\right)}^{n+3}\left(\,{\rho }_{{\mathrm{crust}}}-{\rho }_{{\mathrm{mantle}}}\right).$$

(22)

As in our model we assumed a hydrostatic core, which is not spherical, we could not use the degree 2, order 0 of the effective density spectrum, which is excluded before computing ${\widetilde{\rho }}_{n}$. We note that unlike Besserer et al.⁷⁰, we did not use the mass-sheet approximation in deriving the effective density spectra. The derived formulas can therefore be used to constrain the density profiles of irregularly shaped asteroids, given their observed effective density spectra. Finally, if the crust–mantle interface does not contribute to the gravity anomaly (that is, perfectly hydrostatic), the effective density spectrum simplified to:

$${\widetilde{\rho }}_{n}={\rho }_{{\mathrm{crust}}}.$$

(23)

Effective density error

We took two sources of error in the effective density spectrum into account. First, we sampled the covariance matrix of the gravity coefficients to produce an ensemble of gravity clones. For each gravity clone, we computed the effective density spectrum. We then computed the standard deviation of the effective density spectra ${\sigma }_{{\widetilde{\rho }}_{n},{\rm{clones}}}$. Given that gravity is known to a much higher signal-to-noise ratio at low degrees, ${\sigma }_{{\widetilde{\rho }}_{n},{\rm{clones}}}$ is effectively zero for n < 10 and increases to 226 kg m⁻³ at n < 19. Second, we observed the jagged behaviour of the observed ${\widetilde{\rho }}_{n}$ (Fig. 1), which probably arises from superposition of internal density anomalies. We found the best fit of the effective density spectrum using equation (16) (shown as magenta curve in Fig. 1) and found residuals of the best fit with respect to the observed values. We then found the r.m.s. of those residuals ${\sigma }_{\widetilde{\rho },{\rm{residuals}}}$. To determine the total error, we computed:

$${\sigma }_{{\widetilde{\rho }}_{n},{\rm{total}}}=\sqrt{{\left({\sigma }_{\widetilde{\rho },{\rm{residuals}}}\right)}^{2}+{\left({\sigma }_{{\widetilde{\rho }}_{n},{\rm{clones}}}\right)}^{2}}.$$

(24)