Estimated human-induced warming from a linear temperature and atmospheric CO₂ relationship

Abstract

Assessing compliance with the human-induced warming goal in the Paris Agreement requires transparent, robust and timely metrics. Linearity between increases in atmospheric CO₂ and temperature offers a framework that appears to satisfy these criteria, producing human-induced warming estimates that are at least 30% more certain than alternative methods. Here, for 2023, we estimate humans have caused a global increase of 1.49 ± 0.11 °C relative to a pre-1700 baseline.

Main

Given the importance of being able to assess compliance with the temperature objectives set out in the Paris Agreement¹, suitable methods for specifying human-induced warming (HIW) in near real time are urgently needed². However, the magnitude of HIW is not directly observed but is, instead, estimated from global mean surface temperature anomaly data. There are two elements to this estimation. The first involves specifying a suitable pre-industrial baseline for the temperature anomaly data to produce estimates of global mean surface temperature (GMST) change. The second involves removing the effects of natural variability from the GMST change data to leave just HIW. The Intergovernmental Panel on Climate Change (IPCC) have made the pragmatic choice to use the mean of the 1850–1900 global temperature anomaly data as the pre-industrial baseline condition³, although it is known that both emissions⁴ and the atmospheric burden⁵ (Fig. 1b) were rising well before this period. Furthermore, the 1850–1900 data are the most uncertain in the global temperature anomaly series⁶ (Fig. 1a), and this uncertainty is currently not accounted for when applying baseline adjustments. A range of methods have emerged for filtering out natural variability; however, the associated HIW estimates either incur lag as a byproduct of the filtering of GMST data⁷ or require model forecasts to make HIW estimates independent of natural variability^2,8,9,10. Clearly, lag is unwelcome when evaluating climate policy as it introduces delay in policy responses to observed change, something that is particularly problematic in the context of the risks presented by, for example, climate tipping points. Although employing climate modelling approaches to avoid lag effects appears sensible, this introduces significant and often difficult-to-quantify uncertainties.

Fig. 1: HIW estimates.

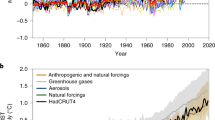
a, HadCRUT5 global temperature anomalies relative to their 1961–1990 mean⁶, estimated GMST change and HIW (Methods). b, Law Dome ice core⁵ and Mauna Loa¹⁸ atmospheric CO₂ concentrations. c, The relationship between increases in atmospheric CO₂ concentration above its pre-1700 baseline and the HadCRUT5 global temperature anomaly, WLS regression fit and HIW estimates (Methods). d, Median HIW estimates for 2023 from ref. ¹⁶ along with the regression-based estimates from this study. Here the regression-based estimates are also shown baselined to 1850–1900 and without the CO₂ baseline uncertainty to be comparable to those in ref. ¹⁶. All uncertainties are expressed as 95th percentile ranges. Regression uncertainties are estimated from N = 10⁴ samples (Methods).

There is an extensive literature highlighting how temperature change has responded linearly to cumulative carbon emissions throughout the industrial era (fig. 5.3.1 in ref. ¹¹), and this relationship, referred to as the transient response to cumulative carbon emissions (TCRE), is now central to specifying remaining carbon budgets to keep within the 1.5 and 2.0 °C levels set out in Article 2 of the Paris Agreement^11,12. Because the airborne fraction appears to have been stationary to date¹¹, variations in cumulative emissions should also be proportional to variations in the atmospheric CO₂ concentration, implying linearity between global temperature changes and atmospheric CO₂ concentrations (Fig. 1c). This has been somewhat overlooked given many studies have emphasized the nonlinear relationship between atmospheric CO₂ and the radiative forcing it imposes¹³, yet recent research shows the spatial pattern of forcing induced by CO₂ leads to a far more linear temperature response than previously appreciated¹⁴. HIW is not driven by CO₂ alone, but also by a range of non-CO₂ forcing agents, the relative contributions of which have varied throughout the industrial era^3,13. Therefore, any linearity we observe between changes in atmospheric CO₂ and global temperatures suggests the effects of non-CO₂ forcings have been subsumed within, and may even have contributed to, any CO₂–temperature linearity observed to date.

Figure 1b shows a reconstruction of the atmospheric CO₂ record from 13 ce to present. From this we estimate a stationary pre-1700 baseline of 280 ± 7 ppm. Figure 1c shows the relationship between the observed increase in atmospheric CO₂ above this baseline (x) and the HadCRUT5 global temperature anomaly data (y). This appears linear, lending itself to regression methods. Weighted least squares (WLS) regression on the full 1850–2023 paired data gives y = mx + c + e; m = 1.06 ± 0.11 °C per 100 ppm; c = −0.54 ± 0.09 °C (Methods), and once decorrelated, the regression residuals, e, pass tests for stationary zero mean normality (P < 0.01).

The regression result suggests the HadCRUT5 data require rescaling by −0.54 ± 0.09 °C from their 1961–1990 average to estimate temperature change since our pre-1700 baseline period (Fig. 1c). By comparison, the 1850–1900 mean value of the HadCRUT5 data is −0.36 ± 0.21 °C, suggesting ~0.2 °C of HIW is embedded in the current IPCC pre-industrial baseline. However, our regression-based estimate for HIW 1850–1900 is 0.11 ± 0.07 °C (Fig. 1a), associated with a mean CO₂ increase of 10 ± 8 ppm relative to the pre-1700 baseline (Fig. 1b), which is essentially the same as the 1750 to 1850–1900 warming estimated from radiative forcing modelling studies³.

The IPCC Sixth Assessment Report (AR6) provides a pooled estimate for the TCRE of 1.65 (1.0–2.3) °C (TtC)^–1 (table 5.7 of ref. ¹¹). If, on average, non-CO₂ forcings comprise 20% of the anthropogenic total¹³ and the airborne fraction is 0.44 (ref. ¹¹), Fig. 1c suggests a TCRE of 1.75 ± 0.18 °C (TtC)^–1, which is indistinguishable from the current median expected value. Again, the observed co-linearities between the global temperature anomaly and atmospheric CO₂ concentration (Fig. 1c), and the corresponding TCRE linearity¹¹ can be observed only if the airborne fraction has been statistically stationary to date.

The IPCC AR6 employed three statistical methods to estimate HIW on the basis of climate models, radiative forcing and temperature change data baselined to 1850–1900¹⁵, and these three approaches have been updated to provide estimates for 2023 with a median of 1.31 °C (1.1–1.7 °C; ref. ¹⁶) (Fig. 1d). By comparison, our regression-based method gives a 2023 HIW of 1.49 ± 0.11 °C (Fig. 1d) associated with atmospheric CO₂ having risen by 142 ± 7 ppm above its pre-1700 baseline. Approximately 0.1 °C of this difference is again attributed to having accounted for the HIW embedded in the 1850–1900 baseline. If we instead use 1850–1900 as the baseline period and exclude its uncertainty, we estimate a 2023 HIW of 1.31 ± 0.07 °C (Fig. 1d). Our contemporary HIW estimates are ~30% more certain than their published equivalents (Fig. 1d). We attribute this improvement to the efficiency of the regression framework leveraging all paired data 1850–2023 set against the uncertainty entrained through using climate models.

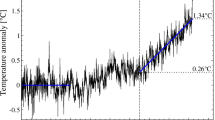
Although the observed relationship between CO₂ and temperature change appears to have been statistically linear to date, this cannot be guaranteed going forwards, hence the need to avoid extrapolating beyond the domain of the paired CO₂–temperature observations. However, providing the pre-industrial baselines for both CO₂ and temperature have been accurately specified, the CO₂–temperature sensitivity can be estimated in near real time directly from the CO₂ and temperature anomaly data, and this can be used to indicate significant departures from the linear regime (Fig. 2 and Methods). Not only could this provide early warning for the onset of nonlinearities, including tipping points, if the regression framework was to adopt a recursive form, HIW could continue to be estimated in near real time.

Fig. 2: Recursive evaluation.

Recursive WLS estimates of the sensitivity, m, and temperature anomaly baseline, c, made by sequentially adding paired CO₂ increase and temperature anomaly data, 1900–2003. Post-2003 sensitivity is estimated as (y – c)/x where x and y are drawn from their corresponding observational distributions shown in Fig. 1 and c is the 2003 baseline estimate (Methods). Error bars show the estimated range for the 2023 WLS estimates for the sensitivity m and baseline c. All uncertainties are expressed as 95th percentile ranges estimated from N = 10⁴ samples (Methods).

Linearization is ubiquitous in the sciences, engineering and decision making because of the robustness, reduced uncertainty and transparency it offers. This explains why the TCRE framework has been so readily embraced by the climate science and policy community, even though it appears to overlook much of the multivariate and nonlinear thinking that underpins more-detailed climate model evaluations. The attractiveness of the framework is further supported by the ability to generate HIW estimates in near real time given the timeliness of both temperature anomaly and atmospheric CO₂ concentration data releases and the simplicity of the analysis, which through being performed in the CO₂–temperature state space is largely lag-free.

Although the regression developed here provides a more accurate pre-industrial baseline, because the 1850–1900 baseline appears to have become embedded within the climate science and policy community, it is important to evaluate the likelihood the community would embrace changing to a pre-1700 baseline. The fact that climate policy is yet to define how its central decision metric is measured speaks of an emerging policy framework necessarily still open to change, and the pool of methods from which it is selecting presents a range of HIW estimates similar to the baseline adjustment we are calling for (Fig. 1d). The transition from AR5 to AR6 also saw the climate science community switch from using the 1961–1990 baseline to the 1850–1900 baseline in their evaluations^3,17, and the temperature anomaly data themselves have been subject to recent revision on the order of 0.1 °C (ref. ⁶). Note, however, because the 1.5 °C level for HIW has now in effect been reached if HIW is estimated using the CO₂–temperature linearity, this would end any further discussion of keeping below 1.5 °C unless within the context of transient overshoot scenarios.

As with the TCRE framework, we make no claim that the observed temperature–CO₂ linearity is down to more than happenstance and the linearizing effects of local perturbations, or will hold going forwards. In addition, as with the TCRE framework, we must remain mindful of the future effects of non-CO₂ forcing and any reorganization of the climate system. However, as we have shown, the regression framework articulated here could prove extremely useful for statistically detecting any such change, while continuing to supply robust GMST change and HIW estimates. The pre-1700 baseline we have established for both remains valid in these conditions through the analysis of the linear regime that appears to have persisted for at least the past 174 years.

Methods

We exploit observed linearity between atmospheric CO₂ and temperature change using linear regression methods to derive a pre-industrial baseline for both GMST change and HIW, as well as near real time, lag and climate model free estimates of HIW. Assuming that pre-industrial non-CO₂ anthropogenic warming is negligible, when cumulative anthropogenic CO₂ emissions are effectively zero the atmospheric CO₂ concentration will be at its pre-industrial level and HIW is, by definition, zero. All subsequent persistent increases above this level are then assumed to be caused directly or indirectly by human activity.

The atmospheric CO₂ concentration is well observed in ice-core data, and this allows us to look back well before the beginning of the industrial era to establish a pre-industrial baseline for atmospheric CO₂ not reliant on somewhat uncertain CO₂ emissions inventory data. A further advantage of exploiting the atmospheric CO₂ concentration data over the cumulative emissions data traditionally used in TCRE analysis is that the former are a direct observation of the cumulative effects of anthropogenic emissions on atmospheric composition and hence forcing, while the later are the sum of rather uncertain annual energy use inventories and hence are vulnerable to compound errors. Cumulative emissions estimates also often exclude the effects of land-use change, which, by contrast, are necessarily included in the atmospheric CO₂ record.

We take the compiled Law Dome ice-core data⁵ covering 13–1700 ce as our baseline condition since we find no statistically significant increase in atmospheric CO₂ over this interval (Fig. 1b), and this time frame probably reflects a genuinely pre-industrial state given estimates of primary energy use and anthropogenic CO₂ emissions start growing significantly only after this time⁴. We subtract this baseline from the concatenated Law Dome–Mauna Loa¹⁸ atmospheric CO₂ concentration series (Fig. 1b) to produce the 1850–2023 increase in atmospheric CO₂ concentration shown in Fig. 1c. The ice-core data offer 60% coverage 1850–1958, with the remaining 40% supplemented following the interpolation method used in ref. ⁵.

We then relate the 1850–2023 increase in atmospheric CO₂ concentrations (x) to the 1850–2023 HadCRUT5 global temperature anomaly data (y; ref. ⁶; Fig. 1a) in the linear regression model y = mx + c + e (Fig. 1c). Here the offset c is our linear regression estimate of the pre-1700 baseline condition for the global temperature anomaly data that are specified relative to their 1961–1990 mean; e is the stochastic variation about this linear trend attributable in part to the stochastic elements of non-CO₂ forcing, nonlinearity, nonstationarity, natural variability and measurement error. Providing they correlate with variations in atmospheric CO₂ or are statistically insignificant, the systematic net effects of non-CO₂ forcing become embedded in the estimate for the CO₂–temperature sensitivity, m. Any significant systematic change in non-CO₂ forcing that is not correlated with observed CO₂ increases, for example, through the recent decoupling of aerosol from CO₂ forcing¹⁰, should degrade any CO₂–temperature change linearity leading to significant changes in m and c and their associated uncertainties. We evaluate this through the recursive regression shown in Fig. 2.

Given the heteroskedasticity of the temperature anomaly data (Fig. 1a), we employ a WLS regression. In this regression, we take the 5th to 95th percentile range for the HadCRUT5 temperature anomalies (Fig. 1a) as a measure of the 4σ uncertainty in these data. From this, we then construct 1/σ² weights. Although the CO₂ data are also heteroskedastic (Fig. 1b), their measurement uncertainties are far smaller than those of the temperature anomaly data, and we find error-in-variable effects on the regression are not significant. We do, however, find e to be significantly autocorrelated and so accommodate this following the Cochrane–Orcutt iterative regression procedure. We find e to be close to AR(1), and full convergence of the regression occurs within four iterations, with the decorrelated regression residuals passing an Anderson–Darling test for stationary zero mean normality (P < 0.01). We find the second difference of the CO₂ data and the first difference of the temperature data to be stationary, in line with our understanding of the effects of near-exponential emissions growth on the accumulation of CO₂ in the atmosphere¹¹ and its effects on the global energy balance^13,15. Using synthetic data, we tested our regression framework and found this form of nonstationarity in our regression data had little impact on our regression results other than to further weight the most recent, largest observed increases in CO₂ and temperature. Given these are also the most certain data, we view this as advantageous.

We subtract the regression-estimated pre-1700 temperature anomaly baseline, c, from the HadCRUT5 global temperature anomaly data, y, to produce estimates of GMST change, y – c. We construct the uncertainty in this GMST change estimate by sampling the uncertainties associated with the pre-1700 CO₂ baseline estimate, the regression parameter covariance matrix, the AR(1) regression errors and the HadCRUT5 temperature anomaly uncertainties (Fig. 1a; N = 10⁴). Finally, our estimate for HIW in any year 1850–2023 is given simply by mx. To reflect the fact HIW is a trend estimate, uncertainties in this estimate are constructed from sampling the regression parameter covariance matrix along with the uncertainty in the CO₂ increase estimate, x (N = 10⁴). This includes both the uncertainty associated with the pre-1700 CO₂ baseline estimate and measurement uncertainty in the CO₂ data themselves. Given the timely release of both temperature anomaly and atmospheric CO₂ concentration data and the simplicity of the analysis, year-end updates of the regression and hence the HIW estimate can be made as soon as the paired CO₂ and temperature data are published.

Estimating both GMST change and HIW in this way is not saying that we see temperature change as being uniquely dependent on changes in atmospheric CO₂ concentration, even though CO₂ accounts for approaching 80% of current net radiative forcing¹⁶. Our framework is simply exploiting the observed linear covariation between increases in CO₂ and temperature to constrain within-sample estimates of GMST change and HIW. Furthermore, our method does not require the relationship between CO₂ and temperature to be unaffected by non-CO₂ factors, just that these factors do not compromise the linearity, although we relax this constraint when thinking about how to accommodate future nonlinear effects. We also do not attempt any extrapolation in this framework other than through the assumption that HIW is zero when atmospheric CO₂ concentration is statistically stationary about its pre-1700 mean, which we take as the definition of the pre-industrial state. Although this might represent 150 years or more extrapolation in time, this represents only a 4% extrapolation in the CO₂–temperature anomaly state space (Fig. 1c).

We stress that, because of the linearity in the paired CO₂–temperature anomaly data to date, the regression-based estimate for re-baselining the HadCRUT5 data, c, utilizes the entire 1850–2023 paired data, not simply the most uncertain 1850–1900 temperature anomaly data. For example, if we use only the more certain post-1958 paired data, we obtain similar regression results to those from using all 1850–2023 paired data. The same is true if we use only the more uncertain pre-1959 paired data closer to the baseline state. We take this as evidence that the linearity shown in Fig. 1c has largely persisted throughout the industrial era, even if the relative contributions of the different forcing agents to warming has changed marginally over this time¹⁶. If we approach the regression recursively, we find the regression converges from ~1900 onwards and produces stable estimates for both m and c post-1940 (Fig. 2), with the only significant change thereafter being increasing confidence in the regression parameters, and in particular that for the CO₂–temperature sensitivity, m.

We compare our results with those from the three HIW methods investigated in the IPCC AR6¹⁵ updated and unified for 2023 by ref. ¹⁶. For this, we run the regression on the 1850–2023 paired data before constructing our HIW estimates. Because the three methods we are comparing with use the 1850–1900 baseline, we construct HIW estimates using either the pre-1700 CO₂ baseline or, for comparison, the 1850–1900 baseline (Fig. 1d). In addition, because the three methods we are comparing with do not include the baseline uncertainty in the GMST change data they exploit, we produce HIW estimates that exclude that uncertainty again to aid comparison (Fig. 1d). We find our like-for-like 2023 HIW estimate is ~30% more certain than its counterparts (Fig. 1d), and that including the CO₂ baseline uncertainty increases the 2023 HIW uncertainty by a further ~30%.

There is an expectation that higher levels of warming will induce nonlinear effects in the climate system and these nonlinearities could be expressed either through the reorganization of elements of the climate system altering climate sensitivity or warming-induced enhanced levels of non-CO₂ forcing, such as through methane, substantially altering the relative contribution of CO₂ to warming^11,13. Furthermore, the relative contributions of CO₂ and non-CO₂ forcing could change in the future through changes in patterns of anthropogenic emissions. Given the importance of detecting changes in climate sensitivity because of the risks a change could present, a possibly useful ongoing test for linearity would be out-of-sample evaluation of the stationarity of m. Having estimated c on a subset of the paired CO₂–temperature data, we can produce ensemble out-of-sample annual estimates for m through (y – c)/x (Fig. 2). These capture both the observation uncertainty in x and y, and the parametric uncertainty in c. We can then test whether the regression estimate for m differs significantly from the out-of-sample forecast. Figure 2 shows one such evaluation where the regression is calibrated on the 1850–2003 paired data and the regression estimate for m is evaluated 2003–2023 against (y – c)/x. If we had detected any significant change, the adjustments we would make to the regression framework to continue to estimate HIW would depend on what form this nonlinearity took, exploiting the array of available recursive regression methods.