Main

Subduction zones are critical features of our planet, providing the forces needed to move tectonic plates and deform margins, develop volcanic arcs and sedimentary basins, and unleashing the most devastating megathrust earthquakes1. In recent years, researchers have observed that these geodynamic settings can be substantially altered by the emergence of a nearby subduction zone, usually forming so-called double subduction systems. These impacts include dramatic changes in plate kinematics, trench motions, slab dips and the associated mantle flow2,3,4,5,6,7,8,9.

Double subduction zones occur in three discernible geometries: divergent double subduction10, evident in active settings such as the Molucca Sea subduction zones9 and the Mediterranean region4; convergent double subduction, typified by areas hosting oppositely dipping subduction zones, such as those surrounding the Caribbean plate11 and Southeast Asia12; and same-dip double subduction (SDDS), which features both ancient and active examples like the Mesozoic Neothetyan arc system3,6 and the late Cenozoic Ryukyu/Izu–Bonin–Marianas SDDS2,5,13 (Fig. 1a). Notably, recent investigations have highlighted the geodynamic impact of SDDS initiation, elucidating its role in driving major changes in direction and/or plate velocity3,6,14. Studies focused on the Ryukyu/Izu–Bonin–Marianas SDDS, involving the subduction of the Pacific plate beneath the Philippine Sea plate, which in turn subducts beneath the Eurasian plate along the Ryukyu–Nankai trench, indicate that this system leads to Pacific slab steepening and trench advance2,5,13,15 (Fig. 1a–c). Taken together, these findings suggest that the geodynamics of many subduction zones is best understood when considering these plate boundaries as components within larger-scale subduction networks. This opens up exciting avenues for understanding active margin dynamics and, more specifically, the magnitudes and length scales at which double subduction is relevant. In this regard, while most studies on SDDS have focused on the effects confined to the area of double plate convergence, the broader influence of SDDS on nearby plate margin tectonics remains unknown.

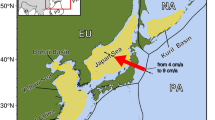
Fig. 1: Present-day plate kinematic setting and mantle structure of the western Pacific subduction zone.
figure 1

a, Map indicating the major tectonic plates in the study area, subduction isodepths57, absolute trench and upper plate kinematics40, the location of northeast Japan and the Japan Sea, and the Ryukyu–Nankai/Izu–Bonin–Marianas SDDS system. Negative and positive trench velocity values corresponds to trench advance and retreat, respectively. b, A composite structural cross-section from the northeast Japan arc29 to the back-arc region up to the eastern Korean margin28 (location shown in a). c Seismic tomography sections59 showing the mantle structure and slab seismicity associated with the northeastern Japan subduction and the Ryukyu/Izu–Bonin–Marianas SDDS system. EUR, Eurasian plate; AP, Amurian plate; PSP, Philippine Sea plate; PAC, Pacific plate; OP, Okhotsk plate; HI, Hokkaido Island; SI, Sakhalin Island; NEJ, northeastern Japan; SW, southwest Japan; JS, Japan Sea; R, Ryukyu trench; N, Nankai trench; IB, Izu–Bonin subduction segment; M, Marianas subduction segment; SVPB, extinct Shikoku–Parece–Vela back-arc basin; δVp (%), percent perturbation (or deviation) of P-wave velocity relative to a reference Earth model.

Full size image

Here we assess this issue by analysing the geological evolution of northeast Japan and the neighbouring Ryukyu/Izu–Bonin–Marianas SDDS, presenting evidence for what we define as double subduction-induced orogeny. We hypothesize that the initiation of the Ryukyu/Izu–Bonin–Marianas SDDS modifies trench kinematics along the Pacific subduction, triggering non-collisional compression in northeast Japan and inducing the active subduction initiation process in the eastern Japan Sea. We test this hypothesis through geologically constrained three-dimensional (3D) geodynamic numerical experiments on double subduction, illustrating how SDDS impacts tectonic stress within the overriding plates of adjacent active margins. The tectonic consequences of SDDS onset illustrate a mechanism whereby complex plate tectonic interactions create optimal plate kinematic conditions for non-collisional orogeny16.

Late Cenozoic tectonic evolution of northeast Japan

During the Oligocene–Miocene epoch (~25–20 Myr ago; Ma), several marginal basins, including the Japan Sea back-arc basin, and the Shikoku and Parece–Vela basins of the Philippine Sea plate, underwent simultaneous opening caused by the eastward Pacific trench retreat and major strike slip tectonics17,18,19,20 (Figs. 1a and 2a,b). This process caused the Japanese Island arc to separate from the Asian continental margin through accelerated back-arc rifting during the early to middle Miocene17,20,21,22. This culminated ~16–15 Ma, resulting in the formation of a 3–3.7-km-deep basin with rifted continental crust and local oceanic floor (for example, refs. 17,18,23,24; Figs. 1a and 2b). In northeast Japan, neutral stress conditions during thermal subsidence progressively changed from mild east–west compression since ~10–8 Ma to highly compressional since ~5.6–3.5 Ma17,18,19,20,25,26 (Fig. 2b). Pliocene–Quaternary east–west compression led to 10–15 km of shortening within northeast Japan25, propagating westwards to the Japan Sea25,27 and the east Korean margin28. Currently, the shortening is distributed across several east- and west-dipping thrusts and basin inversion structures19,20,25,26,27,29, with rates reaching up to 15 mm yr−1 off central Japan30 (Fig. 1b). A compilation map of active faulting shows that compression affects a ~1,200-km-long deformed belt extending into the back-arc region west of Hokkaido Island (see Fig. 5 in ref. 20). The structural observations, coupled with the documentation of thrust earthquakes occurring in this area over the past century, with magnitudes ranging from Mw 6.9 to 7.8, have prompted several authors to propose incipient subduction initiation in the eastern Japan Sea (for example, refs. 27,31,32; Fig. 1a,b). Active back-arc faulting in this region was responsible for the recent Noto Hanto earthquake (2024, Mw 7.6) that generated strong ground motion, large crustal deformation and tsunamis that caused major damage in the region33. Recent studies also reported geological and geophysical evidence for diffuse subduction initiation along the eastern Korean margin active since ~5 Ma28 (Fig. 1a,b). To the south, tectonics are locally dominated by the interaction of the Izu–Bonin arc (Fig. 1a). This area is characterized by a main phase of arc subduction and deformation occurring since ~6–5 Ma and crustal motion within the active fault system controlled by the indented configuration of the plate boundary (for example, refs. 20,34).

Fig. 2: Cenozoic kinematics of the Izu–Bonin–Marianas trench and its relationship to deformation events in the arc and back-arc regions of northeast Japan.
figure 2

a, Evolution of the Izu–Bonin–Marianas trench migration in the late Cenozoic from ref. 5 that considers a moving Indian/Atlantic hotspot reference frame41. b, Time correlation of tectonic and kinematic changes in the study area. Note that the progressive shift in the motion of the Izu–Bonin–Marianas trench, following Philippine Sea plate fusion and the reactivation of subduction along the Ryukyu–Nankai trench, slightly precedes and overlaps with the onset of strong compressional conditions in northeast Japan and the Japan Sea back-arc basin. IBM, Izu–Bonin–Marianas trench; EUR, Eurasian plate; PSP, Philippine Sea plate; PAC, Pacific plate; MOR, mid-ocean ridge. Panel a reproduced with permission from ref. 5, Elsevier.

Full size image

Hypotheses for the origin of northeast Japan compression

The origin of the Pliocene–Quaternary compressional tectonic regime across the northeastern Japanese active margin and the back-arc Japan Sea remains highly contentious. One hypothesis suggests a predominant role for the lower plate35, proposing that the Pacific plate accelerated since ~5 Ma, introducing a significant compression component normal to the Japan trench36. However, in this mechanism, it is unclear why compression localized only in northeast Japan and not along the entire high-convergence western Pacific subduction37. Moreover, in global surveys of all major subduction zones, high plate convergence does not correlate with upper plate compression38. An alternative, classic hypothesis highlights the impact of eastward upper plate motion, which is attributed to the clockwise rotation of the Amurian plate in response to the distant effects of the India–Eurasia collision19,22,27. This rotation would have triggered slow convergence between the Amurian plate and the Okhotsk plate along the eastern margin of the Japan Sea. Nevertheless, Amurian plate extrusion has been an ongoing process since at least the late Oligocene–early Miocene39, complicating a direct link with the Pliocene onset of compression in northeast Japan and its back-arc region. Furthermore, while the motion of the upper plate towards the trench is significant, it alone does not suffice to initiate compression because upper plate deformation is driven by the relative difference between upper plate and trench motion16. It is therefore crucial to examine how the movement of the upper plate interacts with trench dynamics to fully understand the triggering of compression.

Both global parametric analyses and simple conceptual/kinematic models indicate that plate margin compression is favoured when the trench retreat velocity is less than the upper plate velocity37. In the study area, the Japan trench east of northeast Japan is advancing at rates of 0.7–0.6 cm yr−1 in a seafloor-spreading aligned absolute reference frame40, resulting in an overall convergence with the near-stationary upper plate (in the same reference frame), and thus meeting the plate kinematic conditions for upper plate compression (Fig. 1a). These kinematic conditions are still met even when analysing other widely used absolute plate motion reference frames41,42,43. Based on this, it has been suggested that the presence of a wide Pacific slab, preventing rapid slab rollback and trench retreat combined with a trenchward-moving upper plate, created this plate kinematic condition in northeast Japan37 (Fig. 1a,b). However, this conflicts with robust plate reconstructions including mantle slab records suggesting the subduction of a wide Pacific plate since 50–40 Ma (for example, ref. 44), well before the onset of regional compression in the study area. The Pacific kinematic conditions driving compression in the study area have also been associated with the clockwise rotation and northwestward movement of the Philippine Sea plate45. However, major rotation of this plate occurred since at least ~30–40 Ma44,46, again significantly before the onset of compression in northeast Japan (Fig. 2a,b).

Alternatively, recent numerical experiments on Pacific subduction47 suggest that the plate kinematics leading to compression may result from a combination of an imposed eastward asthenospheric flow and slab folding processes at depth, resulting in several trench retreat–advance cycles since 50 Ma. The issue with the applicability of this model to northeast Japan is that these experiments predict an extensional phase from 6 to 3 Ma, whereas geological data indicate strong and continuous compression since then17,18,19,20,25,26 (Fig. 2b). Moreover, the many alternations of compression and extension since ~35 Ma, as shown in their modelling results, do not correlate well with geological data and the overall tectonic evolution of this specific region (see previous section; Fig. 2b).

Lastly, alternatives such as compression triggered by subduction or accretion of bathymetric highs are unlikely due to the localized nature of the associated compression37,38. More importantly, the absence of a major aseismic ridge or oceanic plateaus interacting with the northeastern Japan trench—features necessary to induce eastward-directed compression—further diminishes the plausibility of this hypothesis. The only bathymetric high that may influence compression is the Izu–Bonin arc (Fig. 1a). However, as previously shown34, it is considered more of a local factor, with its main deformational effects not extending more than approximately 150–200 km north of the accretion zone. Therefore, it cannot account for the documented ~1,200-km-long region under compression, as evidenced by both active and ancient thrust faults, as well as thrust-related intraplate earthquakes observed over the past few decades (see Fig. 5 in ref. 20).

In summary, over the past ~5–6 Ma, the northeast Japan arc-to-back-arc region has experienced increasing compression due to the onset of a plate kinematic context associated with an advancing trench. Existing explanations for this phenomenon are either unfeasible35,36,47 or appear incomplete19,22,27,37,38,45. More importantly, numerical geodynamic models specifically designed to test conceptual frameworks in this region are still lacking.

Double subduction-induced orogeny in northeast Japan

To investigate the geodynamic mechanisms driving effective plate kinematic conditions for non-collisional orogeny in northeast Japan over the past ~5.6–3 Myr, it is essential to consider trench kinematics and the Cenozoic evolution of Pacific subduction. Present-day trench kinematics40, spanning from northeast Japan to the Izu–Bonin–Marianas subduction segments (that is, Pacific trench in this study), depict a southward increase in westward trench advance (Fig. 1a). This southward shift in trench motion, towards increased advance, is also observed in various trench motion catalogues and is independent of the chosen absolute reference frame41,42,43,48. A potential explanation for the induced compression in Japan is then that forces associated with this Izu–Bonin–Marianas trench advance are transmitted northwards to this region. In this scenario, the slowly moving upper plate resists the west-directed force associated with trench advance, as transmitted from the south, and that this results in compression in the northeastern Japan arc and back-arc region (Fig. 1a,b). If this is correct, we would expect a temporal correlation between the initiation of trench advance in the Izu–Bonin–Marianas subduction zone and compression in northeastern Japan and the Japan Sea.

The onset of trench advance along the Izu–Bonin–Marianas subduction zone has been linked to a reorganization of major tectonic boundaries associated with the evolution of the Ryukyu/Izu–Bonin–Marianas SDDS2,5,13,15. Between ~40 and 15 Ma, the Izu–Bonin–Marianas trench predominantly underwent rapid, intermittent retreat17,18,19,20, shifting progressively to trench advance since ~10–5 Ma2,5,13,15,49,50 (Fig. 2a,b). Numerical models support the hypothesis that subduction reactivation of the Philippine Sea plate since 15–10 Ma in the Ryukyu–Nankai trench, following a slab detachment caused by ridge subduction5,51, exerted a pronounced northwestward pull on the Philippine Sea plate, consequently driving Pacific trench advance and facilitating the steepening of the Pacific slab (Fig. 2a). Recent numerical studies indicate that the initial stage of Ryukyu subduction (~30–15 Ma) did not significantly affect the Izu–Bonin–Marianas trench motion, most probably due to ineffective stress transmission caused by a thermally weakened upper plate at the Shikoku–Parece–Vela basins back-arc spreading centre15. However, after this system cooled and strengthened/fused since ~15–10 Ma, the reactivated Ryukyu subduction exerted a strong pull, driving the trench advance observed today5,52 (Fig. 2b).

We note that the progressive shift in trench motion for the Izu–Bonin–Marianas trench since ~10–5 Ma5,49,50,52 slightly precedes and coincides with the onset of strong compressional conditions in northeast Japan and the Japan Sea back-arc basin since ~5.6–3 Ma17,18,19,20,25,26,27,28,32 (Fig. 2b). These observations indicate a potential causal relationship between the reactivation of the Ryukyu/Izu–Bonin–Marianas SDDS after Philippine Sea plate fusion/strengthening, trench advance, and the onset of the compressional regime in northeast Japan and the incipient subduction in the Japan Sea.

Geodynamic models of double subduction-induced orogeny

To evaluate the viability of double subduction-induced orogeny in northeast Japan, we set up 3D numerical subduction models (Methods, Fig. 3a–g and Extended Data Figs. 1–6). Our aim was to examine whether the insertion of an additional (Ryukyu–Nankai) subduction zone enhances compression within the northeast Japan upper plate region relative to a single subduction model containing only Pacific plate subduction along the Japan–Izu–Bonin–Mariana trenches. We therefore modelled two subduction scenarios—with and without subduction along the Ryukyu–Nankai trench (that is, single versus double subduction)—using the Advanced Solver for Planetary Evolution, Convection and Tectonics (ASPECT) finite element code53,54,55,56 (Fig. 3a,b).

Fig. 3: Three-dimensional numerical subduction models testing the influence of the Ryukyu/Izu–Bonin–Marianas SDDS on driving upper plate compression in the northeastern arc-to-back-arc regions of Japan.
figure 3

a–f, Set up for single (a) and double (b) subduction experiments, with the viscosity and velocity fields in cross-sections (c,d) and the computed trench-perpendicular (x-direction) normal stress field (σxx) and plate velocity (e,f) for the reference single and double subduction models, respectively. Stress and velocity are extracted within the lithospheric plates at 30 km depth. g, The normal stress difference between the models indicating significantly enhanced compression in the area corresponding to the location of northeast Japan. For simplicity, the Okhotsk plate is not included, and only an equivalent to the Eurasian plate is considered. EUR, Eurasian plate; PSP, Philippine Sea plate; PAC, Pacific plate.

Full size image

In our models, we solve for the velocity and stress fields associated with imposed slab and tectonic plate geometries. The plan-view margin shapes are an idealized representation of the present-day plate geometry. The Pacific and Philippine Sea subduction geometries are based on the present-day slabs, as delineated by earthquake hypocentres and seismic tomography57,58,59 (Fig. 1c). We do not model the transition from single to double subduction; rather, we intend to represent the change in stress state from before ( ~10 Ma) to significantly after Ryukyu–Nankai subduction reinitiation5,51 (present day). We therefore run our ‘pseudo-instantaneous’ single and double subduction models for only 10 kyr; this is sufficiently short that the plate and slab geometry undergoes minimal evolution from the geometries imposed. In both models, we considered a single, mechanically continuous (that is, no weak back-arc area15) upper plate, and identical Pacific plate/slab geometries. We adopt a linear viscous rheology for the lithosphere and crust, and we use a simplified power-law viscous rheology for the underlying flowing mantle. This enables us to hone in on the as yet unexplored first-order impact of double subduction on the upper plate stress state, while avoiding complexities associated with a large number of rheological parameters. Here we focus on two models (single and double subduction) with equivalent crustal viscosities (ηcrust = 5 × 1019 Pa s) and lithospheric strengths relative to the underlying mantle (ηlith./ηmantle = 500). We chose the viscosity values to be intermediate within the ranges inferred from various geophysical, geodynamic and experimental constraints (for example, refs. 60,61,62,63,64,65), and to produce tectonic plate velocities compatible with those observed in the western Pacific, but we have also run additional tests to verify our first-order conclusions are unchanged if we vary these values (Extended Data Figs. 1 and 2).

In the single subduction model, the Pacific trench advances slowly to the left/west at ~2 cm yr−1 and far-field Eurasia is near-stationary (Fig. 3e and Extended Data Fig. 3). Pacific plate motion is trench-perpendicular and at ~8–10 cm yr−1 with respect to far-field Eurasia. These modelled velocities exhibit first-order agreement with observed plate velocities in seafloor-spreading aligned40,48 or fixed Pacific hotspot reference frames43. Adding the Ryukyu–Nankai subduction zone induces a westward Pacific trench advance of 3–4 cm yr−1 adjacent to the Philippine Sea plate (that is, Izu–Bonin–Mariana; Fig. 3f and Extended Data Figs. 1 and 4). This is consistent with observed trench motions48 and previous subduction modelling13,52,66 (Fig. 1a). These agreements suggest that our models capture the relevant large-scale geodynamic processes and are, in turn, suitable for investigating changes in the large-scale lithospheric stress state induced by double subduction.

Our numerical models show that the establishment of a double subduction system influences notably the upper plate stress state in the Japan triple junction and immediately north of this region (Fig. 3e–g and Extended Data Figs. 4 and 5). Without double subduction, the lithosphere in the Japan triple junction region is under relatively moderate trench-perpendicular compression of ~10–20 MPa (Fig. 3e and Extended Data Fig. 4a). In such geodynamic models, this absolute upper plate stress state is largely controlled by the imposed upper plate size, thickness, density and strength (for example, refs. 67,68). Here, we therefore focus on the relative change in stress state induced by double subduction, as opposed to absolute stress values. Throughout the upper plate, double subduction induces a notable increase in the magnitude of trench-perpendicular compressive stress (Fig. 3f and Extended Data Fig. 4b). Approximately 350 km onboard of the modelled Japan trench, that is, in the vicinity of thrusting in northeast Japan, the average trench-perpendicular compressive normal stress in the lithosphere doubles from ~20 MPa to ~40 MPa (Fig. 3g and Extended Data Fig. 5). The other normal stress components (vertical and trench-parallel) are only minimally affected by double subduction (Extended Data Fig. 4). This increase in trench-perpendicular compression is due to the along-strike transmission of the Philippine Sea plate slab pull at the Pacific margin15,52, which causes the Pacific slab to indent into the Eurasian upper plate at the northeast Japan trench, thereby inducing enhanced upper plate compression. The region experiencing increases in horizontal compressive stress extends significantly, covering an area ~1,000–1,200 km northwards along the Pacific trench and an additional ~1,300–1,500 km inland (Fig. 3g). This observation aligns with geological and geophysical evidence of compression, not only within the Japan arc but also in the back-arc domain, which includes a deformed belt approximately ~1,200 km in length17,18,19,20,25,26,27,28,30,31,32 (Figs. 3g and 1a). The model results also highlight subtle compression extending north of northeast Japan, consistent with structural geomorphological, seismological and GPS data, all of which indicate mild compression/transpression along Sakhalin Island18,69 (Fig. 1a). The observation that the increased compressional lithospheric stress in the models does not extend beyond approximately ~1,500 km aligns with newly derived strain maps of eastern Eurasia, which indicate negligible active deformation west of the analysed area70 (Figs. 3g and 1a).

Additional tests also demonstrate that, irrespective of the chosen crustal and lithospheric strengths, an increase in trench-perpendicular horizontal compressive stress is a robust feature in transitioning from single to double subduction (Extended Data Figs. 1 and 2). The magnitude of the increase in horizontal compression varies with these properties—increasing for higher lithosphere viscosity or lower crustal viscosity—but the single-to-double stress increase is always prevalent. Hence, these results support the double subduction-induced orogeny hypothesis and provide an integrative geodynamic framework that links the evolution of the Ryukyu/Izu–Bonin–Marianas SDDS system2,5,13, the motion of the Philippine Sea plate, the associated westward drag of the Pacific trench45,49,50 and the onset of arc–back-arc compression in northeast Japan17,18,19,20,25,26,27,28,32. We suggest that this process accounts for the transition from soft to hard deformation during Izu arc subduction between 8 and 6 Ma20.

Double subduction-induced orogeny in the geological record

Despite the substantial variability in scale and geometrical configuration inherent to highly dynamic double subduction systems, the documentation of active double subduction-induced orogeny in northeast Japan has major implications for the orogenic evolution of plate margins proximal to other ancient SDDS systems.

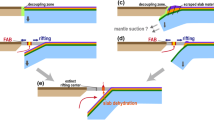
We propose that double subduction-induced orogeny, generalized in Fig. 4a, offers a plausible explanation for the widespread Cretaceous compression documented west of the contemporaneous Neotethys subduction system71,72 (Fig. 4b). Here, a major change in absolute plate motion direction and the rapid northward drift of the African plate have been invoked to explain Late Cretaceous compression in northern Africa71 ( ~86–84 Ma, Ayyubid Orogen73), subduction initiation along the western Mediterranean region14 and far-field deformation in central Europe (~84–75 Ma, Subhercinian basin intraplate deformation74; Fig. 4b). Recent studies suggest that the onset of a ~12,000-km-long SDDS approximately 105 Ma72, along with the initiation of effective slab pull around ~95 Ma, coincided with the directional shift and acceleration in the drift of the African plate14. Updated plate kinematic data indicate that Africa–Eurasia relative plate motion along the western Mediterranean active margin transitioned from very slow motion (<5 mm yr−1) in a south–southeast direction between ~125 and 90 Ma to a northeast direction with a velocity of 30–20 mm yr−1 from ~95 to 70 Ma14 (Fig. 4b). Although differing in dimensions, exact configuration and partially in the nature of the orogenic processes it involves—such as the collision of Iberia—we propose that, within the framework of the double subduction-induced orogeny concept introduced here (Fig. 4a), a potential genetic connection exists (Fig. 4b). Specifically, this connection links the lifespan (105–75 Ma) of the large neighbouring SDDS zone in the Neotethys Ocean with the associated plate kinematic change and the plate-wide compression (~90–75 Ma14,72) observed to the west of this system (Fig. 4b).

Fig. 4: Generalized conceptual model of double subduction-induced orogeny and a proposed Mesozoic case associated with the Neotethys SDDS system.
figure 4

a, A conceptual model illustrating the impact on trench dynamics, transitioning from trench retreat to trench advance, triggered by the onset of an SDSS on a plate capable of transmitting slab pull between trenches. This model illustrates the tectonic effects of this process, highlighting plate margin compression occurring away from the SDSS. For simplicity, the upper-right panel depicts a fixed upper plate. The conceptual framework builds on the established understanding of SDSS dynamics2,3,5,6,13,14,15 and our own results on the tectonic effects on nearby plate margins. b, Proposal of a double subduction-induced orogenic event based on the documentation of Late Cretaceous plate margin and intraplate compression71,73,74 west of the contemporaneous Neotethys SDDS system14. Global and regional plate kinematic reconstructions for the late Early to Late Cretaceous are from ref.14 and ref. 39, respectively. Panel b adapted with permission from: main maps, ref. 14, Springer Nature Limited; inset, ref. 39 under a Creative Commons licence CC BY-NC-ND 4.0.

Full size image

Although more speculative owing to the limited precision of early Palaeozoic plate margin reconstructions for southwest Gondwana, another potential candidate for ancient double subduction-induced orogeny is the Palaeozoic southern South American margin. Notably, the Chaitenia SDDS ( ~380–340 Ma) to the west of Patagonia75 partially overlaps in time with the Chanic orogeny ( ~385–350 Ma) immediately to the north of this ancient SDDS76. If active subduction characterized the entire margin at this time, as recently suggested77, and there was a north–south mechanical connection between the Chaitenia subduction and that to the north, it is possible that the onset of the Chaitenia SDDS may have contributed to sustaining, if not driving, the protracted Chanic orogeny north of Patagonia. Although this hypothesis provides an elegant explanation for the required trench advance to drive back-arc closure of the Cuyano proto-ocean basin, it warrants further investigation in light of more precise information on the nature and configuration of plate margins during the early Palaeozoic era.

The case of double subduction-induced orogeny in Japan illustrates how subduction interactions, linked to the emergence of a nearby subduction zone, can trigger far-field effects that cascade onto neighbouring plate margins. This perspective offers valuable insight into the interpretation of the seismotectonic setting of northeast Japan, a region renowned for its devastating seismic events, including the Tohoku megathrust earthquake (2011, Mw = 9.0)35 and the recent Noto Peninsula intraplate earthquake (2024, Mw = 7.6)33 in the back-arc area. With this understanding of the tectonic impact of SDDS zones, we anticipate that a more thorough examination of ancient plate margin geological records will uncover additional cases of double subduction zone-induced orogeny.

Methods

Numerical subduction modelling

Our 3D subduction models were constructed using the ASPECT finite element code (version 2.5.0)53,54,55,56. ASPECT was used to solve the conservation of momentum (Stokes equation) and mass (continuity equation) for an incompressible viscous fluid (Boussinesq approximation). Our models are purely compositional. That is, we neglect temperature/thermal diffusion and density and viscosity are purely dependent on compositional fields. Our models contain four compositional fields that have distinct material properties: the crust, upper plate (Eurasia) lithosphere, subducting plate (Philippine Sea plate and Pacific plate) lithosphere, and stiffer material placed at the lateral edges of the Pacific and Eurasian plates (for example, see Extended Data Fig. 3a,c). The background material corresponds to the sub-lithospheric mantle and has another set of mechanical properties (see later paragraphs of this section). The lateral plate edges are imposed to be stiffer (higher viscosity) to retard subduction initiation in these locations. Our models are ‘pseudo-instantaneous’ in that we solve for the velocity and stress fields associated with the imposed slab and plate tectonic geometries, as opposed to allowing the structure/slabs to advect for millions of years. In practice, we extract the solution after 10 kyr of model evolution. Given modelled plate velocities of ≤10 cm yr−1, we do not observe noticeable advection of the mantle/tectonic plates over this duration.

We use ASPECT’s adaptive mesh refinement functionality to highly refine the finite element mesh within the lithospheric plates—including the crustal layer that makes up the plate boundary shear zone—and within other regions containing large viscosity gradients (for example, the upper-to-lower mantle transition). In these regions, we have a maximum resolution corresponding to ~4-km-wide cubic finite elements. The lowest resolution occurs far away from the tectonic plates and corresponds to ~60-km-wide cubic finite elements. This approach results in ~5,500,000 cells unequally distributed throughout the model domains. Simulations were run on the Skylake (SKX) nodes of the Texas Advanced Computing Center’s Stampede3 cluster.

Our subduction models have a Cartesian domain spanning 8,000 km (trench-perpendicular) × 5,000 km (trench-parallel) × 1,000 km (depth). There are no external forces or velocities applied to the subduction system and all model boundaries are mechanically free slip. In our single subduction case, we model Pacific subduction beneath a homogeneous Eurasian plate (Fig. 3a). In the double subduction case, we add the Philippine Sea plate and Ryukyu–Nankai subduction, but leave the Pacific plate/slab geometry completely unchanged (Fig. 3b and Extended Data Fig. 6). At the northern edge of the subduction system (y = 5,000 km), we impose a ‘free’ plate boundary (that is, tectonic plates are not attached to the model boundary; Extended Data Fig. 3a,c). This enables the Pacific plate to have a north–south velocity component in this northerly model region. At the other side of the subduction system (y = 0), the plates are ‘fixed’ to the model boundary. This boundary acts as a plane of symmetry, thereby enabling us to model the diamond-shaped Philippine Sea plate as a triangle (Fig. 3a,b and Extended Data Fig. 3).

We constructed the input plate and slab geometries using the Geodynamic World Builder tool78,79. We included only the tectonic complexities that are of first-order importance for our proposed mechanism. Our plate boundaries are linear, aside from the protruding cusp of the Pacific trench in northern Japan. This north–south segment is 1,000 km long and at an angle of 27° relative to the 1,600-km-long northern (Kuril–Kamchatka) and southern (Izu–Bonin) Pacific sections (Fig. 1a). In the double subduction case, the Philippine Sea plate was added by including the Ryukyu–Nankai trenches (Fig. 1a). This Philippine Sea plate–Eurasia plate boundary is 1,700 km long and at 29° to the Japan trench. We adopt a constant Pacific slab geometry from north to south, with the base of the slab extending to 625 km depth. Of the 1,700-km-long Philippine Sea plate–Eurasia plate boundary—in the double subduction system—the southern 1,250 km corresponds to deeper Ryukyu subduction (400 km slab depth) and the northern 450 km corresponds to shallower Nankai subduction (210 km slab depth)44,57,58. Detailed slab geometries are displayed in Extended Data Fig. 3 (cross-sections) and Extended Data Fig. 6 (3D visualization). Both the Pacific and Philippine Sea plate slabs have a slab-top radii of curvature of 185 km and, below this curved portion, dips of 60°. To approximate the interaction of the Pacific slabs with the higher-viscosity lower mantle, we linearly reduce the dip to zero as a function of along-slab distance along the deepest 200 km of the slab. We impose lithospheric thicknesses of 90 km and 60 km for the older and younger Pacific and Philippine Sea plates, respectively, and a 60 km thickness for the idealized Eurasian plate. A weak, 10-km-thick crustal layer is place on top of all plates and along the upper surface of slabs to 70 km depth. This facilitates plate boundary decoupling, thereby enabling us to reproduce the main features of observed plate and trench velocities (for example, refs. 40,43,48; Fig. 1a). To ensure the Philippine Sea plate (and Nankai slab) and Eurasian plate are also decoupled, a ~150-km-long and 50-km-wide weak zone, with the same properties as the background mantle, is placed at the northern edge of the Philippine Sea plate and Nankai slab. This weak zone extends through the entire plate and has two components: an east–west (x-directed) component that delineates the northern/top edge of the Philippine Sea plate, and a southeast–northwest component that is parallel to the lateral edge of the northwest-dipping Nankai slab (see Extended Data Fig. 6 for a 3D view of the weak zone). The latter is needed to stop the Nankai slab from intersecting/coupling with the overriding Eurasian plate. To check that the specific geometry of this weak zone does not impact first-order model behaviour, we ran an additional double subduction model with a wider weak region in the triple junction region. In this case, weak material fills the entire region (triangle) between the northern edge of the Nankai slab and its projection onto the Japan trench. Neither the stress pattern nor stress magnitudes are significantly affected (Extended Data Fig. 4b,c).

The Pacific and Philippine Sea lithospheric plates have constant densities of 3,350 kg m−3; 50 kg m−3 denser than the sub-lithospheric mantle. The Eurasian plate and crustal layers are neutrally buoyant with respect to the mantle, with densities of 3,300 kg m−3. This is to approximate the lower densities of continental lithosphere and basaltic crust relative to oceanic lithosphere. The lithospheric and crustal layers are isoviscous and the underlying sub-lithospheric mantle has a composite Newtonian and power-law rheology (for example, ref. 80) to mimic the first-order effects of diffusion and dislocation creep, respectively. Lithospheric plates are set to be 500 times more viscous (5 × 1022 Pa s) than the reference mantle viscosity (1020 Pa s). This is within the 10–1,000 range of slab–mantle viscosity contrasts generally suggested by geoid constraints61,62, slab shapes and trench motions60,81,82, and plate bending considerations63,83,84. We consider isoviscous plates, that is, without plastic yielding, to both simplify our model setups and minimize nonlinearity (and hence speed up model convergence). While this limits lithospheric deformation to diffuse viscous deformation distributed over hundreds to thousands of kilometres, as opposed to more ‘Earth-like’ localized shear zones, it enables us to examine which regions experience high viscous stress and hence would ultimately be prone to yielding. We increase the lithosphere viscosity by an order of magnitude within 1,000-km-wide (trench-perpendicular) edges of the Eurasian and Pacific plates; this is to ensure that subduction does not initiate at the edges. This higher plate edge viscosity causes the stress discontinuities noticeable at x = 1,000 km and 6,000 km (Fig. 3e,f). The crustal layer has a viscosity of 5 × 1019 Pa s. Considering a deep plate interface temperature of, for example, 500–600 °C, and strain rate of 10−12 s−1, this viscosity overlaps with that recorded for blueschists, and resides between that of stronger meta-basalts and weaker metasediments and serpentinite64,85,86,87,88. It is also within the 1018–1020 Pa s range estimated using numerical shear experiments for the global range of exhumed shear zones lithological distributions65. However, given that our simplified shear zone implementation (a single isoviscous layer), the most appropriate effective shear zone viscosity, is uncertain, we therefore test a range of values (Extended Data Fig. 1).

Power-law flow in the sub-lithospheric mantle is included due to its large effect on plate and trench motions (for example, refs. 89,90). Owing to the compositional nature of our models, we neglect the temperature dependence of mantle viscosity, and additionally omit the pressure dependence. The Newtonian viscosity component of the mantle, ηN, is set to 2 × 1020 Pa s. The power-law component, ηP, is calculated following:

$${\eta }_{{\rm{P}}}={\eta }_{{\rm{N}}}{(\dot{\epsilon }/{\dot{\epsilon }}_{{\rm{T}}})}^{\frac{1-n}{n}}$$
(1)

where \(\dot{\epsilon }\) is the square root of the second invariant of the strain rate tensor, n is the power-law exponent (= 3.5) and \({\dot{\epsilon }}_{{\rm{T}}}\) is the transition strain rate. Following ref. 90, we set \({\dot{\epsilon }}_{{\rm{T}}}\) = 5 × 10−15 s−1. For strain rates at this value, ηP = ηN = 2 × 1020 Pa s. The effective model viscosity is then calculated as:

$${\eta }_{{\rm{eff}}}={\left(\frac{1}{{\eta }_{{\rm{N}}}}+\frac{1}{{\eta }_{{\rm{P}}}}\right)}^{-1}$$
(2)

which produces the reference mantle viscosity of ηeff = 1020 Pa s at \(\dot{\epsilon }\) = 5 × 10−15 s−1. Given that significant uncertainty remains regarding the appropriate creep law parameters (for example, ref. 91), even for the dominant upper mantle mineral olivine, we consider our simplified mantle rheology to be appropriately complex. Beyond 660 km depth, the lower mantle is set to a viscosity of 5 × 1021 Pa s (that is, a factor 50 increase relative to the reference upper mantle viscosity). This follows geoid and slab sinking rate studies that indicate the lower mantle has a higher viscosity than the upper mantle (for example, refs. 92,93).

To verify that the first-order behaviour of our models does not depend on the assigned crustal and lithospheric viscosities, we have run additional models with different values. Relative to the reference crustal viscosity (5 × 1019 Pa s), we test a lower value of 1019 Pa s and higher values of 2.5 × 1020 Pa s and 1020 Pa s (Extended Data Fig. 2). Relative to the reference slab–mantle viscosity ratio (500), we test higher and lower values of 2,000 and 125 (Extended Data Fig. 3). For each of these additional parameter tests, we turn off power-law flow (that is, equation (1)) within the sub-lithospheric mantle and instead use a constant (Newtonian) mantle viscosity of 1020 Pa s. Removing this complexity does not substantially affect the modelled stress fields (Fig. 3e–g and Extended Data Figs. 2 and 3), but reduces model run times to ~30% of the equivalent power-law models. Overall, increasing the slab–mantle viscosity ratio and/or decreasing the crustal viscosity increases the magnitude of the double subduction-induced stress increase. However, there is always an increase in horizontal compression due to double subduction.