Main

Throughout the Quaternary period (the past 2.58 Myr), glaciation has acted as a dominant control in sculpting landscapes on Earth1,2. Understanding of the variability in rates and distribution of glacial erosion is needed to assess its influence on many current interdisciplinary societal questions regarding ocean and riverine sedimentation and alkalinity3, the evolution of mountain topography1, and the long-term management of used nuclear fuel in geological repositories4. Despite the importance of glacial erosion, the physical processes of quarrying, abrasion and subglacial meltwater incision that govern its magnitude and distribution are understudied5,6,7,8. Furthermore, owing to the difficulty of sampling in subglacial systems, observations of these processes are limited7,8. In recent decades, numerous indirect measurements have supplemented these in situ observations under active glaciers to understand material removal better. These methods commonly comprise sediment discharge estimates from meltwater streams, the volume of bulk sediment stored proglacially and the depth of bedrock removal constrained by geochronological approaches5,7,8,9,10,11,12,13. Collectively, estimates of glacial erosion using these methodologies record rates that span multiple orders of magnitude2,7,9,12,14.

Physical reasoning indicates that glacial erosion rates are influenced by many ice, substrate and climate characteristics, but ice-flow velocity is likely to exert notable control (for example, refs. 6,8). Pioneering efforts to derive erosion models from measurements spanning the past ~10,000 years have found dependence on glacial velocity expressed as linear or exponential ‘velocity–erosion rules’5,7,8,11,15. Since the introduction of the first velocity–erosion rule, which was primarily based upon observations of an Alaskan surge-type glacier15, similar velocity–erosion rules have been independently produced from marine-terminating glaciers covering a transect from Patagonia to the Antarctic Peninsula5, New Zealand’s Franz Josef Glacier11, and global datasets that include land, marine and surge-type glaciers7,8, lending support for a relationship between glacial velocity and erosion. While velocity–erosion rules do not directly reveal subglacial processes6,8, landscape-evolution models have effectively implemented them to duplicate long-term topographic evolution under glaciers (for example, refs. 1,16,17,18,19,20,21,22).

Despite wide implementation of velocity–erosion rules, multiple observations support continuing efforts to expand these rules to include other glaciological, topoclimatic and geological controls6. For example, in environments with almost identical glacial sliding velocities, erosion rates have been shown to differ hugely5,7,10, with strong positive relationships between glacial erosion and latitude (acting as a proxy for temperature)5 and precipitation7. More complex thermomechanical ice-sheet and landscape-evolution models support multivariable control of glacial erosion predictions by providing mechanistic links between glacial erosion, lithology, tectonics and climate on geological timescales13,23,24. Additionally, earlier velocity–erosion rules often focused on relatively high-velocity glaciers in surging15 or marine-terminating5 environments likely to be especially geomorphically active7; however, recent work has noted limited correlations between velocity and erosion rates, especially in regions that yield minimal rates of erosion5,7, suggesting other controls, in addition to velocity, may be important.

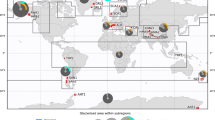
Here we assemble a global synthesis of 181 published glacial erosion rates (previous velocity–erosion rules used n = 3–38) estimated using both in situ and indirect measurements derived from subglacial material removal and sediment export rates. We also compile a broad range of possible glaciological, topoclimatic and geological controlling variables to explore the dependency of glacial erosion rates using machine learning techniques. In line with previous erosion syntheses7, we compile erosion measurements from topographically constrained extant glaciers and ice caps (separated into glacier basins25) characterized by dominantly warm basal thermal regimes (164 erosion rates are averaged over the past ~350 years or less and 17 span the early to late Holocene; Fig. 1 and Supplementary Table 1). Our full dataset shows no strong method-based biases related to measurement technique (Supplementary Figs. 1 and 2) or significant ‘timescale dependence’14 (coefficient of determination R2 = 0.0097; see Methods and Supplementary Fig. 3).

Fig. 1: Distribution of contemporary glacial erosion rates.
figure 1

a, Spatial distribution of synthesized glacial erosion rates (see Supplementary Table 1 for referenced datapoints). Regions and their numbers correspond to the RGI25 regions. The total number (no.) of glacial erosion rate measurements and RGI region mean (µ) are displayed. In cases where a circle represents more than one erosion rate and a majority exists, colour coding represents the mode b, Latitudinal distribution of synthesized glacial erosion rates. Each point corresponds to an individual measurement of glacial erosion. Basemap in a from Natural Earth (https://www.naturalearthdata.com).

Full size image

Using this synthesis, we first test predictions of previous velocity–erosion rules. We then produce a stratified statistical model that best predicts an erosion rate for each glacier. We use elastic net regression26, a linear-regression approach that reduces variance by combining two regularization techniques (L1 and L2 penalties) to shrink coefficients, select variables and cope with collinearity (Fig. 2). This way, we provide multivariable empirical equations integrating glacier surface and sliding velocity27 absolute latitude25, geothermal heat flux (GHF)28, mean annual precipitation (MAP)29,30, mean annual air temperature (MAAT)29,30, seismicity (as peak ground acceleration (PGA); Methods)31, ice thickness27, glacier length25, area25, surface slope25 and elevation25. Where available, measurements for these variables were taken from direct observations or from global datasets that broadly temporally correspond with the collection interval of an erosion rate (Methods); however, we acknowledge that when temporal discrepancies between erosion rate measurements and explanatory variables occur, spuriously low apparent predictor influence could result. Using these new equations, we provide a near-global estimate of contemporary glacial erosion rates.

Fig. 2: Correlation matrix (Pearson correlation coefficient, r) of continuous explanatory variables in different glacier environments.
figure 2

a, Surge-type environment. b, Land-terminating environment. c, Marine-terminating environment. d, All datapoints regardless of the glacier environment. Cells with insignificant P values (the probability of obtaining a correlation coefficient as large or larger than we observed by chance if the true correlation was zero (the null hypothesis)) are marked with X at a significance threshold of 0.05. Variables are ordered based on similarity following hierarchical cluster analysis with the complete linkage method. Max., maximum; med., median; precip., precipitation; slid., sliding; surf., surface; temp., temperature; vel., velocity.

Full size image

Importance of glacial velocity in predicting glacial erosion

We test previous velocity–erosion rules using our global synthesis of 181 glacial erosion rates, between 0.01 and 370 mm yr−1 (Fig. 1 and Supplementary Table 1). These velocity–erosion rules, estimated from a non-random subset of glaciers included in our dataset, are not especially effective in predicting erosion rates from velocity across the whole dataset, with R2 (coefficient of determination) values ≤0.19 and mean absolute error (MAE, the average absolute difference between observed and predicted values) values higher for all datasets than for our preferred models (Fig. 3). Note, here and throughout, when we refer to R2 or the root mean squared error (RMSE, square root of the average of the squared differences between observed and predicted values), we refer to the statistic calculated on the scale of model fitting (that is, the natural logarithm of erosion rate). In contrast, MAE is in linear erosion rate units (mm yr−1) to ensure the result is interpretable. Not surprisingly, multiple-variable equations developed here from the whole dataset generally perform much better (Fig. 3). The elastic net regression employed is partly analogous to exponential or power law regression by including both logged and linear versions of our velocity variables, so we are implicitly testing the same formulation as previously published erosion rules. The individual linear trends between the natural log of erosion rate and the predictors, including velocity, are visualized in Supplementary Fig. 4. The leave-one-out cross-validation (LOOCV) performance of our full variable elastic net models against comparable metrics for models trained on only velocity-based explanatory variables reveals that our selected models perform better than the velocity-only counterparts (Supplementary Tables 3 and 4). None of the velocity-only synthesis models yield LOOCV R2 higher than 0.39, while our land-terminating glacier model shows higher coefficients of determination. In land-terminating glaciers we observe LOOCV R2 = 0.55 (RMSE = 1.20; compared with R2 = 0.27 and RMSE = 1.51 for the velocity-only synthesis dataset). LOOCV performance is challenging to evaluate for surge-type and marine-terminating glaciers, given the relatively low predictive skill of all models of these types and the wide range of erosion rates in these subsets. We do not see improvements in R2 in the complete surge and marine models; however, our preferred elastic net regression models exhibit lower MAE (34.19 mm yr−1 (surge); 9.21 mm yr−1 (marine)) than the velocity-only synthesis model (MAE = 40.23 mm yr−1 (surge); 213.08 mm yr−1 (marine)). This difference for surge-type and marine-terminating glaciers indicates these glacier types are better predicted on average using our full elastic net regression model (Supplementary Tables 3 and 4).

Fig. 3: Glaciological, topoclimatic and geological controls on glacial erosion rates.
figure 3

a–c, Predicted versus measured glacial erosion rate in surge-type (a), land-terminating (b) and marine-terminating (c) environments based on equations presented in this study. These data are compared with previously proposed velocity–erosion rules, based only on previously published datasets5,7,11,15. MAE values are the mean absolute error of predictions relative to observations, while R2 is the coefficient of determination for the natural logarithm of erosion rate measurements and predictions. d, Variable importance in surge-type, marine- and land-terminating environments. Cross-hatched variables are excluded owing to insufficient data. Scores are the scaled coefficient of each explanatory variable, such that the most important (that is, largest coefficient) is 100 for each bootstrap resample (n = 1,000); bars represent the mean variable importance across all resamples. Thick and thin error bars show the approximate ±1 standard deviation (15.87th–84.13th percentile) and ±2 standard deviation (2.28th–97.72nd percentile) ranges of the bootstrapped distributions, respectively. X markers indicate the median importance from the resampling, while hollow circles indicate variable importances from the final trained model. Each continuous variable is presented as both ‘linear’ and ‘log-transformed’.

Full size image

Variables controlling glacial erosion rates

We measure collective variable importance for predictors as the sum of final model effects (combining log and linear versions) of variables (dots in Fig. 3d). Our full-predictor elastic net regression analysis finds the strongest predictors of glacial erosion rates in surge-type settings are MAP and glacier length (comprising 46% and 54% of the total variable importance, respectively; Fig. 3d). In contrast, 85% of the erosion signal in land-terminating environments is explained by glacier elevation, median sliding velocity, glacier length, absolute latitude, median surface velocity, MAP, glacier area and seismicity. Interestingly, glacier velocity (maximum and median, sliding and surface velocity) imparts reduced predictive influence in our analysis of surge-type and land-terminating environments (velocity accounts for 27% of the modelled effect in land-terminating and negligible effect in surge-type environments; Fig. 3d). This contrasts with marine-terminating environments, where 83% of the erosion signal results from MAP, GHF and absolute latitude.

Glaciological controls

Past work has often started with glacial velocity as a predictor of erosion5,7,11,15 based on physical reasoning, as noted above. In our analysis, velocity is not the dominant predictor of erosion rate for any environment, although it seems more important for erosion in land-terminating glaciers. Interestingly, our dataset’s median sliding velocity is substantially (240%) higher than the global median of median velocities27. Similarly, previous studies that presented glacial erosion as explained by glacial velocity were composed of or included multiple marine-terminating glaciers exhibiting high velocities5,7 or have focused on high-velocity glaciers11,15 that, in some cases, were also undergoing short periodic surge events15. Based on these observations, we suggest that while non-velocity predictors appear to strongly influence erosion, given the significant positive correlations between velocity variables and the natural logarithm of erosion rate (Fig. 2), high-velocity environments are also most likely to exhibit high erosion rates, although other variables seem to be more consistent predictors in our analysis.

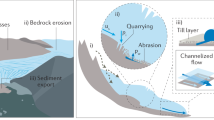
Including glaciological, geological and topoclimatic variables improves our erosion rate predictions relative to velocity-only erosion rules in all three glacial environments (Fig. 3a–c), echoing results from process-based landscape-evolution modelling13. Field data and process understanding document how velocity and erosion rate can be decoupled6. In particular, a subglacial till layer between ice and bedrock smooths the bed and protects underlying bedrock from further glacial erosion6,22,32,33 while allowing glacial movement by subglacial deformation6,22. While we are not modelling this explicitly, by including other glaciological, topoclimatic and geological variables, the effects of a subglacial till layer may be partly incorporated by proxy, improving predictions of glacial erosion rate. For example, research has demonstrated that increases in MAP, glacial melt or MAAT may increase the rate of sediment removal by subglacial meltwater34,35,36, which in turn could remove the subglacial till layer, thus enabling incision into previously protected bedrock6. However, to validate this conclusion, direct measurements of glacial erosion rates derived exclusively from bedrock erosion beneath a glacier rather than sediment volumes removed from the glacier, in addition to measurements of the thickness of the subglacial till layer, would be needed.

Topoclimatic controls

In all three glacial environments, MAP displays a positive correlation with glacial erosion rate (Fig. 2), supporting a connection between glacial erosion and climate7,10,11,37. This relationship has been previously highlighted in sedimentary10 and contemporary records37, and recently empirically linked to glacial erosion7. If MAP effects are separated into linear and log versions of explanatory variables, the share of variable importance for marine-terminating glaciers is strongly weighted towards MAP over log MAP, lending support to previous observations made on a global scale7 (Supplementary Fig. 4). However, log MAP is favoured in land-terminating and surge-type environments, suggesting a power law relationship over the exponential relationship previously proposed7. We thus support the view that higher MAP values may result in an increased surface slope due to snow accumulation and/or a greater subglacial meltwater flux7, both of which would increase the rate of basal sliding and, in turn, abrasion and quarrying5,7,11,23,37. Owing to the strong relationship between MAP and erosion, we suggest that in addition to affecting glacial sliding velocity, MAP must also modulate the subglacial erosion rate by other mechanisms. For example, as previously highlighted5,6,11, high MAP may increase the sediment removal and transport rate by increasing subglacial water flows, which otherwise would inhibit abrasion and quarrying, and may also facilitate bedrock erosion by carving subglacial channels.

Previous studies have shown that, like MAP, changes in MAAT (and its effects, proxied indirectly through elevation and latitude) can affect a glacier’s dynamics and basal thermal conditions and, therefore, its ability to erode5,23. On a global scale, we find that MAAT and, to a greater extent, elevation and latitude strongly predict glacial erosion. However, it appears that these topoclimatic variables exert a secondary control compared with MAP. In line with previous studies5,7, we speculate that their lesser influence is because we examine erosion in dominantly warm basal thermal regimes. In the majority of cases, these glaciers exceed the thermal boundary conditions needed to facilitate basal ice movement, and thus, an increase in temperature (surface or geothermal) is far less important than a proportional increase in precipitation5,7,23.

Geological controls

The lithology, bedrock structure and seismicity of a catchment together exert influence on erosion rates in all three glacial environments (Fig. 3). In land-terminating environments (and in some bootstrap resamples of marine and surge-type environments), seismicity (active regions defined as those with PGA values >1.7 m s−2; Methods) is a useful predictor of erosion, a result for glaciers that mirrors results in fluvial settings38. In the fluvial context, it has been proposed that seismically active regions may display weakened bedrock conditions and, therefore, enhanced erosion associated with these fractured surfaces38,39,40. Within a glacial context, studies have linked increased fracture density and favourable orientation to increased erosion by quarrying9,41,42,43, highlighting these as controls on valley formation (for example, refs. 9,44). In line with this work, if PGA is related to fracture density, regions with higher PGA may exhibit higher erosion rates through quarrying. Additionally, we observe that variation in lithology also imparts a control in our largest and most lithologically balanced subset, land-terminating environments. We did not assess the influence of lithology on marine-terminating or surge-type glacier erosion, owing to the unequal distribution of these subsets’ lithologies. However, this does not exclude lithology as an erosion control, and we hypothesize that a similar effect may be observed in surge-type and marine-terminating environments if comprehensive lithology data could be examined. In addition to the roles exerted by lithology and bedrock structure, globally we observe a positive relationship between glacial erosion and GHF using contemporary glacial erosion data. Our results, therefore, support a recently proposed association among these variables documented using artificial erosion surfaces in a landscape-evolution model24 and are consistent with observations in geothermally active regions (for example, ref. 45), which document increased subglacial meltwater production and basal temperatures, which can, in turn, affect ice-flow dynamics24.

Global distribution of glacial erosion

Using our multiple-variable equations determined from 181 contemporary glacial erosion rates in combination with available glaciological, topoclimatic and geological variables, we estimate erosion rates for 185,081 contemporary glaciers (85% of Randolph Glacier Inventory version 6 (RGI)25; Supplementary Table 2.) On this near-global scale, we estimate that 99% of these glaciers display predicted erosion rates between 0.02 mm yr−1 (95% confidence interval (CI): 0.020–0.021) and 2.68 mm yr−1 (95% CI: 2.619–2.747). Our best estimate suggests that these glaciers collectively erode approximately 23 Gt of bedrock material each year (Supplementary Fig. 5) if all material is evacuated from beneath each glacier. By comparison, fluvial sediment flux from exorheic drainage areas has been estimated to generate ~18.5–20 Gt yr−1 (refs. 46,47,48).

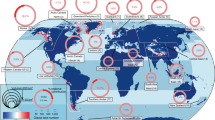
In total volume terms, the majority of glacial erosion occurs above 50°N/S in regions with widespread modern ice cover in Alaska, the Canadian Arctic, Greenland, Scandinavia and the southern Andes (Fig. 4 and Supplementary Figs. 6 and 7). The highest collective rates of glacial erosion are observed in areas of Alaska, Central and South Asia (RGI regions 13–15 (ref. 25)), Caucasus and the Middle East, and New Zealand (regional medians of ~0.5–1.5 mm yr−1; Supplementary Table 5). This global distribution is predominantly driven by the noteworthy effects of precipitation, glacial elevation, length, latitude and the underlying geology, in addition to glacial velocity.

Fig. 4: Predicted contemporary glacial erosion rates displayed on a near-global scale.
figure 4

a, Global variability in predicted glacial erosion rates for RGI25 regions. Owing to incomplete surface velocity and ice thickness data necessary to predict glacial erosion rates, all glaciers in Antarctica (part of RGI region 19) are excluded. b–d, Regional variability in predicted glacial erosion rates in the southern Andes (RGI region 17; b), Alaska, western Canada and northwestern USA (RGI zones 1 and 2; c), and South and Central Asia (RGI zones 13, 14 and 15; d). Grid cells are assigned based on the most-frequent erosion rate value, as classified in the key, within each cell (100-km pixels for a; 50-km pixels for b–d). Basemaps from Natural Earth (https://www.naturalearthdata.com).

Full size image

Challenges in predicting glacial erosion

We acknowledge that the new insights and improved understanding of glacial erosion we develop here are derived from a small population and thus have limitations. First, our erosion rates are derived using a variety of methodologies, many of which reconstruct erosion indirectly from subglacial sediment export rates. While we detect no strong method-based biases in our dataset (Supplementary Figs. 1 and 2), we caution that these methodological differences may influence measured erosion rates. Second, as highlighted by previous studies, erosion rates used to derive our equations have been collected during contemporary accelerated glacial retreat conditions2,5,14,49,50, which almost certainly increases sediment fluxes6,49. Therefore, consistent with other studies (for example, refs. 14,49), our equations should not be used to estimate erosion rates on longer timescales or under past or future glaciological or climatic conditions; however, the equations may be pertinent, especially when modelling past and future periods of rapid deglaciation. Lastly, because, to our knowledge, only ref. 51 has measured glacial erosion where sliding velocity is minimal (< 0.01 m yr−1), we excluded this datapoint and focused our analysis on predominantly warm-based environments. However, as no global database of cold-based glaciers is available, we cannot remove them from our predictions, and in these cases we recommend treating our predicted glacial erosion rates as maximum values only (Methods).

Despite these limitations, our multiple-variable equations indicate that glacial erosion is predicted better using a collection of glaciological, topoclimatic and geological variables, rather than by glacial velocity alone. We provide further evidence to support the idea that MAP influences erosion rates in all glacial environments and that MAAT (and its effect observed through glacial elevation and latitude) is also influential, although to a lesser extent. Moreover, our results highlight the importance of seismicity, lithology and GHF in controlling glacial erosion. In summary, our study emphasizes the need for a holistic assessment of the controls on glacial erosion that includes glaciological, topoclimatic and geological influences.

Methods

Synthesis of data

Glacial erosion rates (that is, data that aim to estimate the removal of material from the glacier bed) were synthesized from glacial studies published before January 2021 (Fig. 1 and Supplementary Table 1). Erosion rates from clearly defined glacial catchments for which glaciological, geological and topoclimatic variables are available were collated. We include a considerable number of datapoints, previously synthesized in erosion rate datasets and review studies (for example, refs. 7,9,12,52), which are cited in Supplementary Table 1. Like previous compilations, we synthesized erosion data from studies that utilized four different methods to measure glacial erosion rate, including sediment discharge estimates from meltwater streams, bulk sediment in proglacial environments, the depth of overlying bedrock removal measured using geochronological techniques (terrestrial cosmogenic nuclide dating) and instrumental measurements from extant glaciers (for example, ref. 12). In cases where several studies measured glacier erosion rates for the same glacier, we included all measurements. In line with previous syntheses of glacial erosion rates used to derive erosion rules7, we synthesized short-term erosion rates (164 contemporary erosion rates and 17 spanning the early to late Holocene) derived only from topographically constrained extant glaciers and ice caps (separated into glacier basins as per ref. 25) characterized by dominantly warm basal thermal regimes. Holocene rates included are those used in previous erosion rules or erosion rate compilations.

Glaciological variables

Where not measured by the original erosion rate study, key glaciological variables including ‘maximum length of an ice mass, ‘area of an ice mass’, ‘median elevation of an ice mass’, ‘ice surface slope’, ‘termination type’, ‘form’ and ‘surge/non surge behaviour’, were obtained from the RGI25. Where the original author and the RGI had missing variables, data were sourced from the Shuttle Radar Topography Mission digital elevation model (DEM) between 56° S and 60° N (~80% of the globe; https://www2.jpl.nasa.gov/srtm/) and the Advanced Spaceborne Thermal Emission and Reflection Radiometer Global DEM version 2 (https://asterweb.jpl.nasa.gov/gdem.asp) for all other areas. In cases where the maximum length of an ice mass (longest surface flowline) was not recorded by the RGI25, we used the same algorithm to calculate this variable53. Likewise, ‘median elevation of an ice mass’ was derived for all glaciated DEM cells within their area polygon as in the RGI25.

Following the practices used by previous ‘velocity–erosion rule’ studies5,7,11,15, when available, we use measurements of maximum and median sliding and surface velocities and median ice thicknesses (94 of 181 cases for velocity and 20 of 181 cases for ice thickness) that have been measured over multiple years and broadly correspond to the timespan over which erosion rate measurements were made. These were either collected by the authors of the original erosion rate study or another study that took measurements that temporally correspond with measurements taken by the original erosion rate study. For some glaciers, the same value is used for median and maximum surface velocity due to a lack of available measurements. Consistent with ref. 7, we tried to avoid very short-term measurements of glacial velocity, such as those recorded over a few days, because these have been shown to vary greatly54; however, in some cases, short-term measurements were included as these were the only velocity measurements available. In some land- and marine-terminating cases, a slight offset exists between glacial velocity and an erosion rate measurement. Additionally, where studies average erosion over longer timescales (for example, >100 years), no velocity measurements span this entire erosion rate interval. Although we have used, to our knowledge, velocity data that are the best available temporal match to erosion rates, we acknowledge these limitations and highlight that mismatches in the interval over which erosion rates and velocities were measured still occur. We also note that surging activity is not well documented for all erosion rates, and we acknowledge that some surge-type erosion rate periods and velocity measurement periods encompass quiescence and active surge conditions.

In cases where no direct measurement of surface or sliding velocity was recorded, these data were derived from ref. 27. This dataset has a resolution of 50 m, and surface velocity is derived using cross-correlation55 between consecutive images taken in 2017 and 2018. Ice thickness was estimated from previously established ice motion and surface slope data27 using the shallow ice approximation and calibrating parameters using field-based measurements56. We extracted median and maximum values of surface velocity and median ice thickness for each glacier in the RGI25. These values are summarized in Supplementary Table 1 and used to estimate the near-global distribution of glacial erosion rates (Supplementary Table 2 and Fig. 4). In cases for which ice thickness and surface velocity variables were not documented corresponding with the period of erosion rate data collection or by ref. 27, we used surface velocities from regional ice velocity datasets57,58,59 and a global modelled ice thickness dataset60.

In all cases where sliding velocity (Usliding) is not directly measured, we estimated sliding velocities based on surface speed (Usurface) and slope (β)27: Usliding = βUsurface. In this parameterization, we first computed the ratio between surface slopes and surface speed. This ratio was then constrained within the interval (0.001, 0.1). The sliding speeds in regions where this ratio is 0.001 were assumed to be Usliding = 0.9 × Usurface, and sliding speeds were set to Usliding = 0.1 × Usurface in regions where this ratio is 0.01. We use a linear interpolation for β in between these two regimes.

Geological variables

We extracted lithologic information from the Global Lithological Map (GLiM)61 to describe the bed of each glacier from its centroid (glacier area from ref. 25) using the ‘Calculate geometry (centroid)’ tool in ArcGIS 10.7. GLiM data were rasterized at a resolution of 50 m. Within the GLiM polygons labelled as ‘ice and glaciers’, ‘no data’ and ‘water bodies’ (probably proglacial lakes in the context of this study), a lithology value was set based on a nearest neighbour value using the ‘Nibble (spatial analyst)’ tool in ArcGIS 10.7. The lithology specified by the original study was used (if recorded) when erosion rates were recorded from terrestrial cosmogenic nuclide or in situ instrumental studies. Lithologies were then further grouped into three categories: ‘crystalline’ (inclusive of intrusive igneous and metamorphic), ‘sedimentary’ (inclusive of carbonates, sandstones and shales) and ‘volcanics’ (inclusive of volcanics and basalts).

Following investigations focused on fluvial erosion38 we used PGA (described as the maximum instantaneous ground movement during an earthquake, based on the amplitude of the largest absolute acceleration with a 10% likelihood of exceeding in 50 years31,38) as an alternative means to estimate seismicity. We extracted PGA values from the Global Seismic Hazard Assessment Program map31. This dataset has a resolution of 10 km. Using this dataset, we assigned locations in Svalbard, Antarctica (omitted from ref. 31) and PGA values <1.7 m s−2 (a natural break in the global PGA dataset) as seismically inactive. In contrast, all other sites (that is, PGA ≥ 1.7 m s−2) were considered active (Fig. 3d).

We assigned an average GHF value to each glacier using a global map of solid earth surface heat flow28. This map has a resolution of 2°, which may limit the differentiation of GHF under neighbouring glaciers where GHF is spatially highly variable, such as in volcanic regions. We extracted median values from glacier centroids (glacier area from ref. 25) using the ‘Calculate geometry (centroid)’ tool in ArcGIS 10.7 and collating the ‘Final_HF_median’ attribute of ref. 28.

Topoclimatic variables

Glaciers were divided into climate zones according to the Köppen–Geiger classification map62. However, these values were excluded from predictor analysis because they were very unequal (>80% were polar). MAAT and MAP values, which broadly correspond with glacial erosion rates that were on contemporary timescales, were obtained for each glacial erosion rate site from the CHELSA V1.2 climate dataset (http://chelsa-climate.org). These data span the period 1979–201329 and have a resolution of ~1 km (30 arcsec). MAAT and MAP values for erosion rates that occurred during the late Holocene (4.2–0.3 kyr ago), mid-Holocene (8.326–4.2 kyr ago) and early Holocene (11.7–8.326 kyr ago) were obtained for each erosion rate site from the PaleoClim dataset (http://www.paleoclim.org)30. These datasets have a resolution of ~5 km (2.5 arcsec). For each of these datasets, variables were obtained from glacier centroids (glacier area from ref. 25) using the ‘Calculate geometry (centroid)’ tool in ArcGIS 10.7.

Dataset and analysis limitations

Glacial erosion rates in our synthesis were collected using four different measurement techniques, and as such, biases may be present due to how each technique constrains an erosion rate (see also refs. 8,12,63). For example, erosion rates calculated using instrumental measurements often only record glacial erosion resulting from abrasion and do not consider the effects of quarrying or subglacial meltwater incision12. Furthermore, erosion rates derived from bulk sediment in proglacial environments can be affected by short-term sediment storage in proglacial lakes or subglacial deposits9,10,12,64,65. Likewise, meltwater stream flux-derived erosion rates are often solely calculated based on suspended sediment loads and do not take into account or measure solute and bedload12. To minimize method-based biases, we collate all rates where more than one erosion rate measurement exists (collected via different techniques), to reflect the spectrum of potential erosion rates of one glacier.

The distribution of collated erosion rates separated by measurement technique is shown in Supplementary Fig. 1. Although the distribution of erosion rates shown in Supplementary Fig. 1 are from various regions and glacial systems, the median erosion rates separated by measurement technique are within a single order of magnitude. This broad agreement is suggestive that no single measurement technique exerts a strong systematic bias. We explored the measurement technique-specific relationships for each explanatory variable in each of three glacier types investigated (Supplementary Fig. 2). While only a few measurements were collected via instrumental means and terrestrial cosmogenic nuclide dating, making comparison difficult, the trends they exhibit are broadly consistent and variability between methods is comparable to the natural or measurement variability between observations.

The duration over which a glacial erosion rate is recorded has been shown to affect the rate calculated, with erosion rates measured over longer durations often showing lower average values2,7,12,14,49,50,63,66,67. To minimize this timescale dependence14 (also observed in a range of geomorphic systems, for example, the Sadler effect63,68) we limit our erosion rate synthesis to shorter-term measurements of glacial erosion (164 erosion rates that are averaged over the past ~350 years or less and a further 17 that span the early to late Holocene), rather than including erosion rates that span multiple glaciations. A comparison between our synthesized glacial erosion measurements and the timespan over which they were measured indicates an insignificant correlation (y = 0.87 × x−0.056, R2 = 0.0097; Supplementary Fig. 3), suggesting the timespan over which measurements were recorded imparts a negligible influence on the erosion rates in our dataset.

Temporal discrepancies between when variables are measured and when an erosion rate is measured could affect our results. This is especially important in the case of velocity, which has been shown to vary dramatically on short timescales69. This effect may thus affect the relationship observed between a glacier’s velocity and the erosion rate measurement7,14,67 in this study. To minimize this effect, when available, we utilized measurements of velocity that temporally overlapped with when an erosion rate measurement was made. In addition, to explore the potential impact of including velocity data from various sources and temporal scopes, we conducted a sensitivity analysis of three data synthesis strategies: (1) favouring remotely sensed data (which often do not temporally overlap with an erosion rate measurement); (2) favouring velocity measurements that temporally overlap with erosion rate measurements; and (3) an approach that uses all available data, but with a preference towards temporally matched author-reported velocities where available. We compared the LOOCV performance of elastic net models given only velocity data as predictors but including all its permutations (that is, median, maximum, surface, sliding, linear velocity (m yr−1) and their natural logarithms; Supplementary Table 4). We observed that using the full suite of available velocity data sources, with preference to originally reported velocities, provides generally lower RMSE and MAE estimates than other methods, particularly in land-terminating and surge-type environments (Supplementary Tables 3 and 4), supporting our adoption of this data treatment approach.

Less than 15% of erosion rates in our synthesis have been recorded from surge-type glaciers (in comparison with <0.6% of the RGI25,70). Erosion rates measured during periods of surging have been suggested to be higher than those under more quiescent conditions15,71. This heterogeneity is the motivation behind our stratification of surge-type glaciers in our analyses. We note that in our analysis we attribute RGI categories of ‘possible, probable and observed surge-type glaciers’ as ‘surge-type’, but acknowledge that these glaciers will not always be actively surging.

As stated in the main text, to our knowledge, constraints on erosion from beneath cold-based glaciers that exhibit a minimal sliding velocity have only been recorded by ref. 51 (sliding velocity <0.01 m yr−1). As a result, we cannot statistically assess the controls of glacial erosion in such environments, and we choose to remove this single datapoint and instead focus on glaciers with predominantly warm basal thermal regimes. Our predictive equations are, therefore, not built or tested using data from such extreme cold-based environments and are not suitable for use in these environments. Any predictions made using these equations for cold-based environments are maximum limiting only.

We would have preferred to assess bed roughness and fracture density when developing predictive equations between glaciological, topoclimatic and geological variables and glacial erosion rates. However, we do not include this variable, as, to our knowledge, it has not been estimated globally or empirically determined in enough extant glacial environments to include in our study.

Statistical analysis

We employed elastic net regression26, a regularized form of linear regression that combines L1 and L2 penalties (as in, Lasso regression72 and Ridge regression73, respectively) to predict erosion rate across all cases with complete explanatory covariates. To study environment-specific controls on erosion, we subdivided glaciers into three categories: surge-type, land-terminating (non-surging) and marine-terminating (non-surging). Tuning parameters for the various models were optimized by grid search and exhaustive LOOCV. LOOCV was also used to evaluate predictive model performance once tuned. We use the same metrics to compare both our primary (all-predictor) models and those that explored surface- and sliding-velocity-only predictors (R2 and RMSE for goodness of fit to the natural logarithm of erosion rate, and MAE to assess average residuals in linear erosion rates).

All continuous covariates were input as candidate explanatory variables in two forms: their conventional (that is, linear) representation and the natural logarithm of these values (that is, log-transformed). Erosion rate, the dependent variable, was represented by the natural logarithm of erosion rate. This follows previous studies5,7,10 and addresses the skewed nature of global erosion rate data over many orders of magnitude, while simultaneously promoting linearity, a requirement of elastic net regression. The categorical variables, lithology and PGA class, were encoded to preserve each level (that is, non-full-rank parameterization).

Within our synthesis, several datapoints were excluded from statistical analysis based on collection and calculation techniques or glaciological context (for reference). A description outlining the reasoning for the exclusion of an erosion rate is included in Supplementary Table 1. From a statistical perspective, these data were flagged as high-residual points when included in an initial linear model or were otherwise problematic.

We present variable importance as an indication of variable effect in our predictive models (that is, the magnitude of the absolute value of regression coefficients after values for each covariate are converted to z-scores). Variable importance calculation was bootstrapped with 1,000 resamples to assess the stability of effect strength. Variable importance is portrayed as the percent of the maximum resample (as in Fig. 3) or the proportion of total predictive influence (that is, one variable type relative to the sum of all variable importance). The coefficients of non-z-scored variables are relayed in formulas (Supplementary Text 2) and in tabular form (Supplementary Table 6).

Many of the explanatory variables used in this study were highly correlated (Fig. 2). These dependencies include fundamental correlations between linear and log-transformed versions of the same variables. Although our approach is strictly empirical in its perspective, the effects of interrelated and correlated variables must still be evaluated from a mechanistic view. Likewise, those potential drivers with a well-founded physical basis should not be discounted based on their exclusion from, or substantial shrinkage in, our models.

Erosion rate predictions

Prediction intervals accompanying each glacier’s erosion rate were calculated through bootstrap resampling with 2,000 resamples. We employ the 0.632+ approach74 to estimate and account for sample noise and bias in our predictions. Within this framework, each bootstrapped prediction is the sum of the model’s base prediction and a residual term (which is a weighted combination of training data and out-of-bag residuals, where the weight depends on the relative overfitting rate and the proportion of held-out data for each bootstrap).

Owing to incomplete surface velocity and ice thickness data necessary to predict glacial erosion rates, all glaciers in Antarctica (part of RGI region 19) are excluded from our predictions. We restrict our reported predictions to the range of erosion rates of our training dataset (0–500 mm yr−1). In cases where erosion rates are higher than this range, we do not report erosion rates, but instead, we assign a value of >500 mm yr−1. The total estimated volumetric erosion for the RGI glaciers is the estimated erosion rate for each glacier multiplied by the glacier’s area, while censoring exceptionally high erosion rates to 500 mm yr−1. Considering the spatial heterogeneity implicit in glacierized catchment erosion rates (that is, the central point estimate could be meaningfully higher or lower than the across-the-glacier average), including confidence intervals on this value would imply unfounded precision in the global sum. However, we explore the full distribution of bootstrap-derived mass flux (after censoring) in Supplementary Fig. 5.