Main

Dicke superradiance5 refers to the enhanced radiation of correlated emitters. Unlike ordinary spontaneous emission of individual emitters, the correlation among emitters effectively makes them behave as a single giant dipole and thus the radiation intensity scales nonlinearly with the number of emitters. In conventional superradiance, the correlation slowly builds up via spontaneously emerging entanglement of close-spaced emitters through radiative decay initiated by vacuum fluctuations6,7. The correlation build-up should be faster than its dephasing to achieve superradiance, as demonstrated in the latest experiments performed with Bose–Einstein condensates12, trapped atoms13 and nitrogen-vacancy centres in diamond14.

The recent technical advances in precision control of emitters make it possible to prepare a superradiant state by actively imposing quantum correlation without relying on the spontaneous emergence of correlation3,9,10. In experiments with superconducting circuits9, trapped ions8 and atoms15 with high degree of control over individual qubits, internal states of individual emitters were manipulated to observe subradiance as well as superradiance, although the maximum number of emitters was limited to two. In macroscopic ensembles of quantum dots16 and cold atoms17, direct correlation imprinting was achieved by adopting a single-photon superradiance scheme18 with a moderate state-preparation efficiency. A superradiant state made of a large number of emitters with imposed correlation can generate the enhanced radiation at high efficiency without a correlation build-up delay. This feature is advantageous in superradiant light sources3 as well as in robust quantum communication with efficient retrieval of stored photons19.

One can envisage superabsorption (enhanced absorption by correlated emitters) as the opposite of superradiance. Many studies suggest it is possible to increase absorption efficiency by utilizing collective behaviour of emitters in light-harvesting4,20, but most of them focus on enhancing excitation energy transfer with a single-photon superradiant state4 or through superradiance transition21, rather than seeking correlated absorption. As absorption and emission of light are related by time-reversal symmetry, the absorption rate of the so-called bright state responsible for superradiance also nonlinearly scales with the number of emitters. The bright state can be accessed in the superradiance ringing process22,23, but the atoms and the emitted field are highly entangled without a preferred phase and thus superabsorption of an externally introduced field does not occur. The recent theoretical studies suggest suppressing the vacuum density of states for the downwards transition of superradiant states and thereby allowing only the upwards transition for superabsorption11, but its experimental realization is yet to be achieved.

Here we experimentally demonstrate superabsorption by implementing a time-reversal process of superradiance with phase control of a superradiant state in a cavity. We reverse the whole system in time—not only the atomic state but also the photonic state. In our scheme, in the absence of an input field, the superradiant state of correlated atoms would generate a coherent-state superradiant field10 with its phase determined by that of the atomic superradiant state. By controlling the phase of the prospective superradiant field opposite to that of an input field in a cavity, we can make the superradiant state undergo an upwards transition in the Dicke ladder, resulting in a time reversal of the superradiance, that is, the realization of superabsorption. We observed greatly enhanced absorption, with the number of absorbed photons scaling with the square of the number of atoms, while its rate was much greater than that of the ordinary ground-state absorption.

The superradiant state that we consider is an N-atom symmetric state analogous to a spin-coherent state, which is localized within the equator in the N-atom Bloch sphere (see Fig. 1a) and is defined in terms of the collective spin operator \(\hat{{J}_{\mu }}=\frac{1}{2}\mathop{\sum }\nolimits_{i = 1}^{N}{\hat{{\sigma }}}_{i}^{\mu }\), where \({\hat{\sigma }}_{i}^{\mu }\) represents the Pauli matrices for the ith atom and μ = x,y,z. In the absence of an input field, the emission process of superradiant state \({\left|{{\Psi }}\right\rangle }_{{\rm{a}}}\) in a cavity can be approximately described by

$$\hat{U}(t){\left|{{\Psi }}\right\rangle }_{{\rm{a}}}{\left|0\right\rangle }_{{\rm{f}}}={\left|{{\Psi }}^{\prime} \right\rangle }_{{\rm{a}}}{\left|\alpha \right\rangle }_{{\rm{f}}},$$
(1)

where \(\hat{U}(t)\) ≡ \({\mathrm{e}}^{-i\hat{H}t/\hslash }\) denotes the time-evolution operator of the Tavis–Cummings Hamiltonian \(\hat{H}\) = \(\hslash g\mathop{\sum }\nolimits_{i = 1}^{N}\left({\hat{a}}^{\dagger }\hat{{\sigma }_{i}}+\hat{a}{\hat{{\sigma }_{i}}}^{\dagger }\right)\), in which ℏ is Planck’s constant, g is the atom-cavity coupling constant, \(\hat{a}({\hat{a}}^{\dagger })\) is the annihilation (creation) operator for the cavity field, \(\hat{{\sigma }_{i}}({\hat{{\sigma }_{i}}}^{\dagger })\) is the lowering (raising) operator for the ith atom, \({\left|0\right\rangle }_{{\rm{f}}}\) denotes a photonic vacuum state, \({\left|\alpha \right\rangle }_{{\rm{f}}}\) represents a photonic coherent state with an amplitude α, and \({\left|{{\Psi }}^{\prime} \right\rangle }_{{\rm{a}}}\) is the resulting atomic state by the time evolution. Equation (1) describes a superradiance process10, where the average photon number of \({\left|\alpha \right\rangle }_{{\rm{f}}}\) is proportional to N2. The approximation used in equation (1) is valid at gτ ≪ 1, where τ is the atom-field interaction time for the atoms traversing the cavity. The final state \({\left|{{\Psi }}^{\prime} \right\rangle }_{{\rm{a}}}\) is a state rotated downwards by an angle in the order of (gτ)2 from the initial state \({\left|{{\Psi }}\right\rangle }_{{\rm{a}}}\) in the N-atom Bloch sphere (see Supplementary Notes 6 and 7 for derivations). By introducing a field-phase-flipping operator \({\hat{R}}_{\pi }\) (corresponding to π-rotation in the field phase space) and by utilizing the relation \({\hat{R}}_{\pi }\hat{U}(t){\hat{R}}_{\pi }^{\dagger }=\hat{U}(-t)\), one can then show (see the Methods for details)

$$\hat{U}(t){\left|{{\Psi }}^{\prime} \right\rangle }_{{\rm{a}}}{\left|-\alpha \right\rangle }_{{\rm{f}}}\simeq {\left|{{\Psi }}\right\rangle }_{{\rm{a}}}{\left|0\right\rangle }_{{\rm{f}}}.$$
(2)

We next describe what equation (2) means. By preparing the cavity with an initial state \({\left|-\alpha \right\rangle }_{{\rm{f}}}\), we can achieve the time reversal of the superradiance process of equation (1). The atomic state returns to the initial state and the cavity field is completely absorbed to become the vacuum state with the absorbed number of photons proportional to N2. As \({\left|{{\Psi }}^{\prime} \right\rangle }_{{\rm{a}}}\) is very close to \({\left|{{\Psi }}\right\rangle }_{{\rm{a}}}\) as discussed above, we can employ the superradiant state \({\left|{{\Psi }}\right\rangle }_{{\rm{a}}}\) instead of \({\left|{{\Psi }}^{\prime} \right\rangle }_{{\rm{a}}}\) in the experiment described below. Incidentally, the time-reversal idea was employed in coherent perfect (ordinary) absorption as time reversal of lasing24; time-reversed photon pulse shaping was also used in efficient absorption of optical as well as microwave photons25.

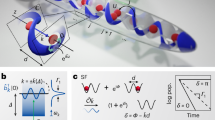
Fig. 1: Experimental scheme and state preparation with a nanohole array.
figure 1

a, Dicke states \(\left|J,M\right\rangle\) are represented as latitudinal rings (corresponding to the maxima of their Q functions mapped on the Bloch sphere) in the N-atom Bloch sphere. Similar to a spin-coherent state, our superradiant state is localized in the equator. b, Images of the nanohole-array aperture captured with a scanning electron microscope. Two-level atoms travelling in the y direction are excited by a pump laser propagating in the x direction to a superposition state after being filtered by the nanohole-array aperture. The state-prepared atoms interact with the cavity mode, whose axis lies in the z direction. The period of the nanohole array matches the transition wavelength of the two-level atom (λ = 791 nm of barium-138). The total array size is 50λ × 50λ. The single (double)-headed arrow indicates the travelling (standing) wave nature of the pump (cavity) field, with the sinusoidal oscillation depicting the phase variation. c, The Bloch vector of the atoms passing through the red (blue)-marked hole is associated with a pump-laser phase of 0 (π). As the atom-cavity coupling of the atoms going through the red-marked hole is opposite in sign to that of the blue-marked hole, these two groups of atoms experience the same atom-cavity relative phase. d, The experimentally observed radiation intensity as a function of Δz is shown in a normalized average photon number \(\langle \hat{n}\rangle /{n}_{\max }\), where \({n}_{\max }\) is the maximum number of photons generated by fully excited atoms. The atoms in the same superposition state radiate much more than those in the fully excited state due to the correlation among the atoms. The mean number of atoms in the cavity is N = 2.7 for both cases. The error bars indicate standard deviations from repeated measurements (see Supplementary Note 10 for details).

Source data

Full size image

In our experiment, a beam of two-level atoms (barium-138 with a 1S0 ↔ 3P1 transition at λ = 791 nm) travelling in the y direction in Fig. 1b passes through a nanohole-array aperture26 in a draughts-board pattern with a period of λ. Just behind the nanohole array, the atoms are excited by a pump laser propagating in the x direction with a pulse area of Θ and then enter a high-finesse Fabry–Pérot cavity. By the nanohole array, the atomic vertical (x) position is localized at π-different equiphase planes of the pump laser and its horizontal (z) position is localized at one of the cavity anti-nodes (Fig. 1c). With both the atom-cavity coupling and the pump laser phase alternating their signs at a period of λ/2, every atom is then excited to a superposition state of the ground and excited states with the same atom-cavity relative phase10. Under this condition, the atomic state can be written as \({\left|{{\Psi }}\right\rangle }_{a}=\mathop{\prod }\nolimits_{k = 1}^{N}\left[\cos ({{\Theta }}/2){\left|{\rm{g}}\right\rangle }_{k}+\exp (-i{\phi }_{0})\sin ({{\Theta }}/2){\left|{\rm{e}}\right\rangle }_{k}\right]\), which, for Θ = π/2, corresponds to a superradiant state localized in the equator of the N-atom Bloch sphere. Here, g (e) represents the ground (excited) state of the atom and ϕ0 is a common atom-cavity relative phase. Our experiment belongs to the strong coupling regime for single atoms with \(({\gamma }_{{\rm{a}}},{\gamma }_{{\rm{c}}},\bar{g})\) = 2π × (25,131,256) kHz, where \({\gamma }_{{\rm{a}}}\) (\({\gamma }_{{\rm{c}}}\)) is the atomic (cavity-field) half linewidth and \(\bar{g}\) is the spatially averaged (over the nanohole opening) atom-cavity coupling constant. Due to strong coupling and a short atom-cavity interaction time of τ ≈ 100 ns, the spontaneous emission into the free space and thus the decoherence of the atomic state can be neglected during the interaction time.

By contrast to randomly distributed atomic dipoles, every dipole moment p of our atomic superposition state is the same with an identical phase, and thus the total dipole moment in the cavity behaves like a macro dipole, Np. Although each dipole resides in the cavity only for the short interaction time τ, as the dipole moment of a newly entering atom is perfectly in phase with the preceding ones, coherence is maintained among the dipoles with different entering times. The sustained coherence among entering and exiting dipoles allows us to simplify our system as a macro dipole Np that is stationary in the cavity, and thus the description by equations (1) and (2) can be applied to our experiment. Supporting data show enhanced radiation or superradiance by such N atoms in a superradiant state is observed in the steady state (Fig. 1d) without any input field. Due to the correlation among the dipoles, the superposition state (Θ = π/2) emits more photons than the fully excited state (Θ = π) when the holes of the aperture are centred at the cavity anti-nodes (Δz = 0).

To investigate the aforementioned time-reversal relation between superradiance and superabsorption, we observed both phenomena in a time-dependent manner (Fig. 2a). With the cavity initially empty, we let the superradiant-state atoms pass through the cavity and emit photons into the cavity mode. The photon number increases quadratically in time during the photon build-up (blue curve in Fig. 2a) because the amplitude of the electric field generated by the constant macro dipole increases linearly in time in the slowly varying envelope approximation. Specifically, the mean number of photons is given by \(\langle \hat{n}(t)\rangle \simeq | {\rho }_{{\rm{eg}}}Ngt{| }^{2}\) (see Supplementary Note 2 for derivation), where ρeg is the off-diagonal element of the atomic density matrix; however, if we initially prepare the cavity with the coherent state, \({\left|-\alpha \right\rangle }_{{\rm{f}}}\), the superradiant-state atoms absorb the photons in the cavity instead of emitting photons, undergoing a time-reversed process of superradiance (dotted red curve in Fig. 2a). After fully absorbing photons in the cavity, the superradiant state starts to radiate (see the grey-shaded region in Fig. 2a as well as equation (5)). The temporal profile of the radiation and that of the absorption are nearly symmetric, with a mild imbalance due to the cavity decay. The ratio of the signals at a fixed time interval (t0) from the minimum point is approximately given by \({\mathrm{e}}^{-2{\gamma }_{c}{t}_{0}}\) (see Supplementary Note 9).

Fig. 2: Time-dependent intracavity photon numbers by superradiance, superabsorption and ordinary absorption.
figure 2

a, Starting from zero, the mean photon number grows quadratically in superradiance with time (blue squares). With an opposite-phase field (green-shaded region) prepared in the cavity initially, the superradiant state exhibits superabsorption (red dots in the unshaded area) instead. After fully absorbing the photons, the superradiant state starts to radiate (grey-shaded region). Mild asymmetry in the dotted red curve is due to the cavity decay (maroon dashed line). b, The superabsorption of the superradiant state gives much faster absorption than the ordinary absorption (blue squares) of the ground-state of atoms. The mean number of atoms in the cavity is the same for both cases (N ≈ 6.8). The thick, shaded blue and red curves in a and b represent the theoretically calculated mean photon numbers with no adjustable parameters. The error bars indicate the standard deviations from repeated measurements.

Source data

Full size image

For enhanced absorption by superradiant-state atoms to be called superabsorption, the absorption rate of the superradiant state should be much faster than that of the ground state. In Fig. 2b, the superradiant state atoms clearly give faster absorption than the ground-state atoms. As a part of photons leaks out due to the cavity decay, for a fair comparison we define the absorption ratio (rab) as a ratio between the number of absorbed photons for a given time interval (tab) and the total number of photons initially prepared in the cavity. We can calculate the number of cavity-decayed photons by numerically integrating the expression \(2{\gamma }_{{\rm{c}}}\mathop{\int}\nolimits_{0}^{{t}_{{\rm{ab}}}}\langle \hat{n}(t)\rangle dt\). When taking the numbers of cavity-decayed photons into account (the integral corresponds to the grey shaded areas in Fig. 2b), we obtain the absorption ratios rSA = 0.85 ± 0.07 for superabsorption (SA) and rOA = 0.37 ± 0.07 for ordinary absorption (OA). Simple algebra (see Supplementary Note 3) shows that we need 5.2-times more atoms for ordinary absorption to achieve the same absorption ratio as the superabsorption in Fig. 2b.

It can be shown that the superabsorption rate is always larger than the ordinary absorption rate. This inequality can be easily understood by considering Δn/N (the number of absorbed photons per atom) in both cases for a short time interval of Δt. The quantity is approximately given by \({({{\Delta }}n/N)}_{{\rm{SA}}}=\sqrt{{n}_{0}}g{{\Delta }}t\) and (Δn/N)OA = n0g2τΔt, where n0 is the initial mean number of photons (see Supplementary Note 5 for derivations). We therefore have the ratio \(\frac{{({{\Delta }}n/N)}_{{\rm{OA}}}}{{({{\Delta }}n/N)}_{{\rm{SA}}}}=\sqrt{{n}_{0}}g\tau ={({{\Delta }}n/N)}_{{\rm{SA}}}{| }_{{{\Delta }}t = \tau }\). This ratio is always less than unity as at most one photon can be absorbed by a two-level atom without re-emitting photons. In the regime of usual absorption with a dephasing rate (~1/τ in our case) that is much larger than the radiative decay rate (~\(2\gamma_{\mathrm{a}}\)), we get \(\sqrt{{n}_{0}}g\tau \ll 1\) (see Supplementary Note 5) and thus the superabsorption rate becomes much greater than the ordinary absorption rate. This consideration is supported by the data shown in Fig. 3a, where observed (Δn/N)SA and (Δn/N)OA are compared. The maximum number of absorbed photons per atom was as large as 0.4 for superabsorption, approaching the theoretical upper bound of 0.5 of the present scheme. One can also notice that the superabsorption would excel for a small number of initial photons, implying usefulness in faint-light sensing27.

Fig. 3: Comparison of superabsorption and ordinary absorption.
figure 3

a, The number of the absorbed photons per atom for a time interval Δt = τ in superabsorption (red) and ordinary absorption (blue). Solid symbols represent experimental data at gτ = 0.16, whereas hollow symbols correspond to those at gτ = 0.10. Solid lines are theoretical expectations given by Supplementary Equation 20a,b. b, The ratio of the effective optical depths as a function of N. The squares represent experimental data, whereas the solid line represents the approximation by Supplementary Equation 19. The approximation is valid for N ≫ 1; n0 = 1.0. The effective optical depth for superabsorption is much larger than that of the ordinary absorption and the ratio scales with N. The error bars indicate standard deviations from repeated measurements.

Source data

Full size image

In superabsorption, a coherent input field can be completely absorbed by the atoms within a finite time, given by \({t}_{0}\simeq \frac{\sqrt{{n}_{0}}}{| {\rho }_{{\rm{eg}}}| Ng}\) for a given n0. By contrast, such complete absorption cannot be achieved within a finite time in ordinary absorption, which exhibits exponential decay of the input field. In the superabsorption data of Fig. 2, a small number of photons (\(\langle \hat{n}\rangle \sim 0.2\)) remained unabsorbed. These photons are in part incoherent photons generated by atomic spontaneous emission due to the non-zero excited-state population, ρee. Experimental imperfections such as incomplete phase matching between the input field and the atomic dipoles—as well as the phase variation among the dipoles due to the finite nanohole size—also contribute to the residual photons. Excluding such experimental imperfections, the degree of absorption for superabsorption as well as ordinary absorption can be characterized by considering the effective optical depth (EOD)28, an equivalent free-space optical depth, which in our case is given by \({\rm{EOD}}=\frac{{r}_{{\rm{ab}}}}{1-{r}_{{\rm{ab}}}}\) (see Supplementary Note 4). It equals the ratio of the number of absorbed photons to that of unabsorbed photons (including cavity-decayed photons). It can be shown analytically (see Supplementary Note 4) that the EOD for superabsorption is much larger than that of the ordinary absorption by a factor proportional to the mean number of atoms. This feature is experimentally confirmed in Fig. 3b, where the EOD for superabsorption is measured to be at most 40-times larger than that of the ordinary absorption.

One of the most distinctive features of superradiance is its nonlinear scaling of radiation intensity on the number of atoms, that is, the maximum number of emitted photons in a fixed time interval is proportional to N2. Likewise, we can consider nonlinear scaling of the absorbed photons in superabsorption (Fig. 4). We measured the maximum number of photons that can be completely absorbed in a fixed time interval as a function of the mean number of atoms (Fig. 4a). Note that in the actual experiment the photon number is reduced by both the cavity decay and the absorption by the correlated atoms but increased by the atomic spontaneous emission. Their individual contributions calculated from the theory are indicated in Fig. 4b. The number of purely absorbed photons by the correlated atoms are plotted in the log–log scale in Fig. 4c. The result can be well fit by the expression \(\langle \hat{n}\rangle \propto {N}^{q}\), where q = 1.86 ± 0.03. The small deviation from N2 can be explained by the aforementioned experimental imperfections.

Fig. 4: Quadratic dependence of superabsorption on atom number.
figure 4

a, For a given number of atoms in the cavity, the maximum number of photons that can be completely absorbed is evaluated at t0. b, The reduced number of photons from t = 0 to t0 (280 ns) in a versus N. The upper grey-shaded area indicates the theoretically expected photon number reduction from the cavity decay, whereas the lower red-shaded area indicates the increase by the spontaneous emission. The absorption by the correlated dipoles then corresponds to the sum of the blue- and the red-shaded areas. c, The absorbed number of photons obtained in b versus N. The N-dependence is well fit by Nq (red curve) with q = 1.86 ± 0.03. The inset shows a linear fit in the log–log plot. The error bars indicate the standard deviations from repeated measurements.

Source data

Full size image

In summary, we have experimentally realized superabsorption by implementing a time-reversed process of coherent superradiance with correlated atoms in a high-Q cavity. It is observed that the rate of superabsorption is much higher than that of ordinary ground-state absorption. The number of absorbed photons scales with the square of the number of atoms as a result of atomic cooperative interaction with the input field. By noting that our scheme described by equations (1) and (2) does not mandate a cavity, we expect that superabsorption could also be possible by employing atoms in a superposition state interacting with a tightly focused laser field in free space. It might be possible to employ two-level systems with much faster transition rates along with frequency- and time-division multiplexing of continuous-wave input light to make our scheme more relevant to practical application. As the quantum state of absorbed photon is coherently mapped to the atomic internal states, our superabsorption can also be utilized in coherence-critical applications such as quantum memory29 and light–matter quantum interfaces2.

Methods

Superabsorption by reversing superradiance in time

The atom-field interaction in our system is described by the Tavis–Cummings Hamiltonian,

$$\hat{H}=\hslash g\mathop{\sum }\nolimits_{i}^{N}\left({\hat{a}}^{\dagger }\hat{{\sigma }_{i}}+\hat{a}{\hat{{\sigma }_{i}}}^{\dagger }\right).$$
(3)

Superradiance process of a superradiant state \({\left|{{\Psi }}\right\rangle }_{{\rm{a}}}\) is then approximately described by the following time evolution operation.

$$\hat{U}(t){\left|{{\Psi }}\right\rangle }_{{\rm{a}}}{\left|0\right\rangle }_{{\rm{f}}}={\left|{{\Psi }}^{\prime} \right\rangle }_{{\rm{a}}}{\left|\alpha \right\rangle }_{{\rm{f}}},$$
(4)

where \(\hat{U}(t)\equiv {\mathrm{e}}^{-i\hat{H}t/\hslash }\). We introduce a field-phase flip operator \({\hat{R}}_{\pi }={e}^{-i\pi {\hat{a}}^{\dagger }\hat{a}}\) that corresponds to π-rotation in the field phase space30. The operator \({\hat{R}}_{\pi }\) only acts on the photonic state and satisfies the property \({\hat{R}}_{\pi }\hat{a}{\hat{R}}_{\pi }^{\dagger }=-\hat{a}\) and similarly \({\hat{R}}_{\pi }{\hat{a}}^{\dagger }{\hat{R}}_{\pi }^{\dagger }=-{\hat{a}}^{\dagger }\), and thus \({\hat{R}}_{\pi }^{\dagger }\hat{U}(t){\hat{R}}_{\pi }=\hat{U}(-t)\).

The result from simply applying \(\hat{U}(-t)\) to both sides of equation (4) is the time-reversed process of superradiance, \(\hat{U}(-t){\left|{{\Psi }}^{\prime} \right\rangle }_{{\rm{a}}}{\left|\alpha \right\rangle }_{{\rm{f}}}={\left|{{\Psi }}\right\rangle }_{{\rm{a}}}{\left|0\right\rangle }_{{\rm{f}}}\), which is superabsorption. As direct time reversal is not experimentally possible, we utilize a phase-flip operation. Let us consider

$$\begin{array}{lll}&\hat{U}(t^{\prime} )&{\left|{{\Psi }}^{\prime} \right\rangle }_{{\rm{a}}}{\left|-\alpha \right\rangle }_{{\rm{f}}}=\hat{U}(t^{\prime} ){\hat{R}}_{\pi }^{\dagger }{\hat{R}}_{\pi }{\left|{{\Psi }}^{\prime} \right\rangle }_{{\rm{a}}}{\left|-\alpha \right\rangle }_{{\rm{f}}}\\ &=&\hat{U}(t^{\prime} ){\hat{R}}_{\pi }^{\dagger }{\left|{{\Psi }}^{\prime} \right\rangle }_{{\rm{a}}}{\left|\alpha \right\rangle }_{{\rm{f}}}={\hat{R}}_{\pi }^{\dagger }\hat{U}(-t^{\prime} ){\left|{{\Psi }}^{\prime} \right\rangle }_{{\rm{a}}}{\left|\alpha \right\rangle }_{{\rm{f}}}\\ &=&{\hat{R}}_{\pi }^{\dagger }\hat{U}(-t^{\prime} +t)\hat{U}(-t){\left|{{\Psi }}^{\prime} \right\rangle }_{{\rm{a}}}{\left|\alpha \right\rangle }_{{\rm{f}}}\\ &=&{\hat{R}}_{\pi }^{\dagger }\hat{U}(-t^{\prime} +t){\left|{{\Psi }}\right\rangle }_{{\rm{a}}}{\left|0\right\rangle }_{{\rm{f}}}=\hat{U}(t^{\prime} -t){\hat{R}}_{\pi }^{\dagger }{\left|{{\Psi }}\right\rangle }_{{\rm{a}}}{\left|0\right\rangle }_{{\rm{f}}}\\ &=&\hat{U}(t^{\prime} -t){\left|{{\Psi }}\right\rangle }_{{\rm{a}}}{\left|0\right\rangle }_{{\rm{f}}}\ .\end{array}$$
(5)

If \(t^{\prime} =t\), we completely reverse the superradiance to recover the initial vacuum state. This is superabsorption. If t’ < t, the reversal is not complete. If \(t^{\prime} >t\) > t, we then get a normal superradiance process progressing for a time period of \(t^{\prime} -t\). We can therefore realize time-reversal process of superradiance by preparing the field state as \({\left|-\alpha \right\rangle }_{{\rm{f}}}\) and by letting the system evolve in an appropriate time.

Nanohole-array aperture

The nanohole-array aperture was fabricated by using the focused ion beam technique on a 10-nm-thick silicon nitride membrane mounted on a 200-μm-thick silicon frame. The individual hole size measured with a scanning-electron microscope is 0.35λ × 0.24λ (λ = 791 nm). The horizontal spread of the atomic distribution by the finite hole size has an effect of averaging the atom-cavity coupling. The resulting variation in g is Δg/g = 0.20. The vertical spread of the atomic distribution decreases atomic phase purity due to the position dependence of the pump laser phase. The height of the hole was thus intentionally made smaller than the width to minimize atomic phase variation while maintaining a sufficient atomic flux. The aperture is mounted on a six-axis stage with an additional piezoelectric transducer for precise alignment along the cavity axis. The aperture is coarsely placed at the centre of the waist of the cavity mode (vertically and horizontally) by the six-axis stage and then a feedback loop places the centre of each hole at cavity anti-nodes by using the piezoelectric transducer. The average atom-cavity coupling is decreased further because the vertical size (40 μm) of the nanohole-array aperture is comparable to the cavity mode waist (43 μm), resulting in Δg/g = 0.06.

Atom number measurement

To measure the mean number of atoms in the cavity, the 1S0 ↔ 1P1 transition is used. The wavelength of the transition is 553 nm with a radiative decay rate of 18.9 MHz. While the atoms in the cavity were illuminated with a resonant probe laser propagating along the cavity mode, the fluorescence photons were collected from the side. The mean number of atoms in the cavity N and the mean number of photons in the cavity \(\langle \hat{n}\rangle\) are simultaneously calibrated by measuring both quantities in the nonlinear \(\langle \hat{n}\rangle\) versus N regime of the conventional microlaser lasing and by comparing the data with the well-known master equation theory10. The number of atoms is controlled by a mechanical blocker, which partially blocks the atomic beam flux well in front of the nanohole array aperture as well as the cavity. Although the blocker is supposed to change the mean atom number with a step size smaller than 0.1, the precision of atomic fluorescence measurement is not high enough to resolve such stepwise changes.