Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Resource-efficient photonic quantum computation with high-dimensional cluster states

Nature Photonics volume 18, pages 1218–1224 (2024)Cite this article

Subjects

Abstract

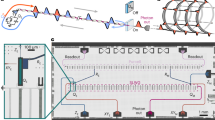
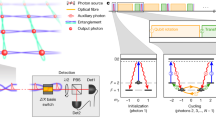
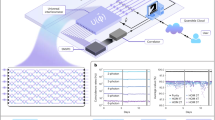
Quantum computers can revolutionize science and technology, but their realization remains challenging across all platforms. A promising route to scalability is photonic-measurement-based quantum computation, where single-qubit measurements on large cluster states, together with feedforward steps, enable fault-tolerant quantum computation; however, generating large cluster states at high rates is notoriously difficult as detection probabilities drop exponentially with the number of photons comprising the state. We tackle this challenge by encoding multiple qubits on each photon through high-dimensional spatial encoding, generating cluster states with over nine qubits at a rate of 100 Hz. We also demonstrate that high-dimensional encoding substantially reduces the computation duration by enabling instantaneous feedforward between qubits encoded in the same photon. Our findings pave the way for resource-efficient measurement-based quantum computation using high-dimensional entanglement.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: High-dimensional spatially encoded cluster states.
Fig. 2: Generation and certification of an eight-qubit cluster state.
Fig. 3: Single-qubit rotation using instantaneous intra-feedforward.
Fig. 4: Qudit cluster state d = 5.

Similar content being viewed by others

Data availability

All data are available in the main text and Supplementary Information, or at https://doi.org/10.5281/zenodo.8358012 (ref. 63).

References

  1. Daley, A. J. et al. Practical quantum advantage in quantum simulation. Nature 607, 667–676 (2022).

    Article  ADS  Google Scholar 

  2. Shor, P. W. Algorithms for quantum computation: discrete logarithms and factoring. In Proc. 35th Annual Symposium on Foundations of Computer Science 124–134 (ACM, 1994).

  3. Preskill, J. Quantum computing in the NISQ era and beyond. Quantum 2, 79 (2018).

    Article  Google Scholar 

  4. Knill, E., Laflamme, R. & Milburn, G. J. A scheme for efficient quantum computation with linear optics. Nature 409, 46–52 (2001).

    Article  ADS  Google Scholar 

  5. Raussendorf, R., Browne, D. E. & Briegel, H. J. Measurement-based quantum computation on cluster states. Phys. Rev. A 68, 022312 (2003).

    Article  ADS  Google Scholar 

  6. Browne, D. E. & Rudolph, T. Resource-efficient linear optical quantum computation. Phys. Rev. Lett. 95, 010501 (2005).

    Article  ADS  Google Scholar 

  7. Tóth, G. & Gühne, O. Detecting genuine multipartite entanglement with two local measurements. Phys. Rev. Lett. 94, 060501 (2005).

    Article  ADS  Google Scholar 

  8. Walther, P. et al. Experimental one-way quantum computing. Nature 434, 169–176 (2005).

    Article  ADS  Google Scholar 

  9. Yao, X.-C. et al. Experimental demonstration of topological error correction. Nature 482, 489–494 (2012).

    Article  ADS  Google Scholar 

  10. Thomas, P., Ruscio, L., Morin, O. & Rempe, G. Efficient generation of entangled multiphoton graph states from a single atom. Nature 608, 677–681 (2022).

    Article  ADS  Google Scholar 

  11. Freedman, S. J. & Clauser, J. F. Experimental test of local hidden-variable theories. Phys. Rev. Lett. 28, 938 (1972).

    Article  ADS  Google Scholar 

  12. Cogan, D., Su, Z.-E., Kenneth, O. & Gershoni, D. Deterministic generation of indistinguishable photons in a cluster state. Nat. Photon. 17, 324–329 (2023).

    ADS  Google Scholar 

  13. Erhard, M., Krenn, M. & Zeilinger, A. Advances in high-dimensional quantum entanglement. Nat. Rev. Phys. 2, 365–381 (2020).

    Article  Google Scholar 

  14. Vallone, G., Pomarico, E., Mataloni, P., De Martini, F. & Berardi, V. Realization and characterization of a two-photon four-qubit linear cluster state. Phys. Rev. Lett. 98, 180502 (2007).

    Article  ADS  Google Scholar 

  15. Chen, K. et al. Experimental realization of one-way quantum computing with two-photon four-qubit cluster states. Phys. Rev. Lett. 99, 120503 (2007).

    Article  ADS  Google Scholar 

  16. Ceccarelli, R., Vallone, G., De Martini, F., Mataloni, P. & Cabello, A. Experimental entanglement and nonlocality of a two-photon six-qubit cluster state. Phys. Rev. Lett. 103, 160401 (2009).

    Article  ADS  Google Scholar 

  17. Vallone, G., Pomarico, E., De Martini, F. & Mataloni, P. Active one-way quantum computation with two-photon four-qubit cluster states. Phys. Rev. Lett. 100, 160502 (2008).

    Article  ADS  Google Scholar 

  18. Reimer, C. et al. High-dimensional one-way quantum processing implemented on d-level cluster states. Nat. Phys. 15, 148–153 (2019).

    Article  Google Scholar 

  19. Vigliar, C. et al. Error-protected qubits in a silicon photonic chip. Nat. Phys. 17, 1137–1143 (2021).

    Article  Google Scholar 

  20. Zhang, H. et al. Encoding error correction in an integrated photonic chip. PRX Quantum 4, 030340 (2023).

    Article  ADS  Google Scholar 

  21. Mirhosseini, M. et al. High-dimensional quantum cryptography with twisted light. New J. Phys. 17, 033033 (2015).

    Article  ADS  MathSciNet  Google Scholar 

  22. Leedumrongwatthanakun, S. et al. Programmable linear quantum networks with a multimode fibre. Nat. Photon. 14, 139–142 (2020).

    Article  ADS  Google Scholar 

  23. Goel, S. et al. Inverse-design of high-dimensional quantum optical circuits in a complex medium. Nat. Phys. 20, 232–239 (2024).

  24. Zheng, Y. et al. Multichip multidimensional quantum networks with entanglement retrievability. Science 381, 221–226 (2023).

    Article  ADS  Google Scholar 

  25. Ecker, S. et al. Overcoming noise in entanglement distribution. Phys. Rev. X 9, 041042 (2019).

    Google Scholar 

  26. Istrati, D. et al. Sequential generation of linear cluster states from a single photon emitter. Nat. Commun. 11, 5501 (2020).

    Article  ADS  Google Scholar 

  27. Walborn, S. P., Monken, C., Pádua, S. & Ribeiro, P. S. Spatial correlations in parametric down-conversion. Phys. Rep. 495, 87–139 (2010).

    Article  ADS  Google Scholar 

  28. Calsamiglia, J. Generalized measurements by linear elements. Phys. Rev. A 65, 030301 (2002).

    Article  ADS  Google Scholar 

  29. Paesani, S., Bulmer, J. F., Jones, A. E., Santagati, R. & Laing, A. Scheme for universal high-dimensional quantum computation with linear optics. Phys. Rev. Lett. 126, 230504 (2021).

    Article  ADS  Google Scholar 

  30. Wang, J. et al. Multidimensional quantum entanglement with large-scale integrated optics. Science 360, 285–291 (2018).

    Article  ADS  MathSciNet  Google Scholar 

  31. Morizur, J.-F. et al. Programmable unitary spatial mode manipulation. J. Opt. Soc. Am. A 27, 2524–2531 (2010).

    Article  ADS  Google Scholar 

  32. Labroille, G. et al. Efficient and mode selective spatial mode multiplexer based on multi-plane light conversion. Optics Exp. 22, 15599–15607 (2014).

    Article  ADS  Google Scholar 

  33. Lin, X. et al. All-optical machine learning using diffractive deep neural networks. Science 361, 1004–1008 (2018).

    Article  ADS  MathSciNet  Google Scholar 

  34. Fontaine, N. K. et al. Laguerre–Gaussian mode sorter. Nat. Commun. 10, 1865 (2019).

    Article  ADS  Google Scholar 

  35. Kupianskyi, H., Horsley, S. A. R. & Phillips, D. B. All-optically untangling light propagation through multimode fibres. Optica 11, 101–112 (2023).

  36. Brandt, F., Hiekkamäki, M., Bouchard, F., Huber, M. & Fickler, R. High-dimensional quantum gates using full-field spatial modes of photons. Optica 7, 98–107 (2020).

    Article  ADS  Google Scholar 

  37. Hiekkamäki, M. & Fickler, R. High-dimensional two-photon interference effects in spatial modes. Phys. Rev. Lett. 126, 123601 (2021).

    Article  ADS  Google Scholar 

  38. Lib, O., Sulimany, K. & Bromberg, Y. Processing entangled photons in high dimensions with a programmable light converter. Phys. Rev. Appl. 18, 014063 (2022).

    Article  ADS  Google Scholar 

  39. Gühne, O. & Tóth, G. Entanglement detection. Phys. Rep. 474, 1–75 (2009).

    Article  ADS  MathSciNet  Google Scholar 

  40. Prevedel, R. et al. High-speed linear optics quantum computing using active feed-forward. Nature 445, 65–69 (2007).

    Article  ADS  Google Scholar 

  41. Danos, V. & Kashefi, E. Determinism in the one-way model. Phys. Rev. A 74, 052310 (2006).

    Article  ADS  Google Scholar 

  42. Zhou, D., Zeng, B., Xu, Z. & Sun, C. Quantum computation based on d-level cluster state. Phys. Rev. A 68, 062303 (2003).

    Article  ADS  Google Scholar 

  43. Gokhale, P. et al. Asymptotic improvements to quantum circuits via qutrits. Proc. 46th International Symposium on Computer Architecture 554–566 (ACM, 2019).

  44. Wang, Y., Hu, Z., Sanders, B. C. & Kais, S. Qudits and high-dimensional quantum computing. Front. Phys. 8, 589504 (2020).

    Article  Google Scholar 

  45. Karácsony, M., Oroszlány, L. & Zimborás, Z. Efficient qudit-based scheme for photonic quantum computing. SciPost Phys. Core 7, 032 (2024).

    Article  Google Scholar 

  46. Campbell, E. T., Anwar, H. & Browne, D. E. Magic-state distillation in all prime dimensions using quantum reed-muller codes. Phys. Rev. X 2, 041021 (2012).

    Google Scholar 

  47. Booth, R. I., Kissinger, A., Markham, D., Meignant, C. & Perdrix, S. Outcome determinism in measurement-based quantum computation with qudits. J. Phys. A 56, 115303 (2023).

    Article  ADS  MathSciNet  Google Scholar 

  48. Sciara, S. et al. Universal N-partite d-level pure-state entanglement witness based on realistic measurement settings. Phys. Rev. Lett. 122, 120501 (2019).

    Article  ADS  Google Scholar 

  49. Raussendorf, R., Harrington, J. & Goyal, K. Topological fault-tolerance in cluster state quantum computation. New J. Phys. 9, 199 (2007).

    Article  ADS  MathSciNet  Google Scholar 

  50. Chen, S. et al. Heralded three-photon entanglement from a single-photon source on a photonic chip. Phys. Rev. Lett. 132, 130603 (2024).

  51. Cao, H. et al. Photonic source of heralded Greenberger–Horne–Zeilinger states. Phys. Rev. Lett. 132, 130604 (2023).

  52. Joo, J., Knight, P. L., O’Brien, J. L. & Rudolph, T. One-way quantum computation with four-dimensional photonic qudits. Phys. Rev. A 76, 052326 (2007).

    Article  ADS  MathSciNet  Google Scholar 

  53. Luo, Y.-H. et al. Quantum teleportation in high dimensions. Phys. Rev. Lett. 123, 070505 (2019).

    Article  ADS  Google Scholar 

  54. Hu, X.-M. et al. Experimental high-dimensional quantum teleportation. Phys. Rev. Let. 125, 230501 (2020).

    Article  ADS  Google Scholar 

  55. Okoth, C., Cavanna, A., Santiago-Cruz, T. & Chekhova, M. Microscale generation of entangled photons without momentum conservation. Phys. Rev. Lett. 123, 263602 (2019).

    Article  ADS  Google Scholar 

  56. Santiago-Cruz, T. et al. Resonant metasurfaces for generating complex quantum states. Science 377, 991–995 (2022).

    Article  ADS  Google Scholar 

  57. Carolan, J. et al. Universal linear optics. Science 349, 711–716 (2015).

    Article  MathSciNet  Google Scholar 

  58. Morimoto, K. et al. Megapixel time-gated SPAD image sensor for 2D and 3D imaging applications. Optica 7, 346–354 (2020).

    Article  ADS  Google Scholar 

  59. Cao, H. et al. Photonic source of heralded Greenberger–Horne–Zeilinger states. Phys. Rev. Lett. 132, 130604 (2024).

    Article  ADS  Google Scholar 

  60. Azuma, K., Tamaki, K. & Lo, H.-K. All-photonic quantum repeaters. Nat. Commun. 6, 6787 (2015).

    Article  ADS  Google Scholar 

  61. Dong, M.-X. et al. Highly efficient storage of 25-dimensional photonic qudit in a cold-atom-based quantum memory. Phys. Rev. Lett. 131, 240801 (2023).

    Article  ADS  Google Scholar 

  62. Wehner, S., Elkouss, D. & Hanson, R. Quantum internet: a vision for the road ahead. Science 362, eaam9288 (2018).

    Article  ADS  MathSciNet  Google Scholar 

  63. Lib, O. & Bromberg, Y. Supplementary data for "Resource-efficient photonic quantum computation with high-dimensional cluster states". Zenodo https://doi.org/10.5281/zenodo.8358012 (2023).

Download references

Acknowledgements

We thank O. Katz, B. Dayan and Z. Aqua for helpful discussions. This project was supported by the Zuckerman STEM Leadership Program and the Israel Science Foundation (grant no. 2497/21). O.L. acknowledges the support of the Clore Scholars Programme of the Clore Israel Foundation. This research project was financially supported by the State of Lower Saxony, Hannover, Germany.

Author information

Authors and Affiliations

  1. Racah Institute of Physics, The Hebrew University of Jerusalem, Jerusalem, Israel

    Ohad Lib & Yaron Bromberg

Authors
  1. Ohad Lib
    View author publications

    Search author on:PubMed Google Scholar

  2. Yaron Bromberg
    View author publications

    Search author on:PubMed Google Scholar

Contributions

O.L. and Y.B. conceived and conceptualized the project. O.L. designed and built the experimental set-up, performed the experiment, and performed the data analysis under the supervision of Y.B. All authors contributed to the writing of the manuscript.

Corresponding author

Correspondence to Ohad Lib.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Photonics thanks Che-Ming Li, Peter van Loock and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Figs. 1–9 and Supplementary Text.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lib, O., Bromberg, Y. Resource-efficient photonic quantum computation with high-dimensional cluster states. Nat. Photon. 18, 1218–1224 (2024). https://doi.org/10.1038/s41566-024-01524-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41566-024-01524-w

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing