Abstract
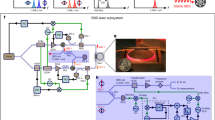
Optical atomic clocks have demonstrated revolutionary advances in precision timekeeping, but their applicability to the real world is critically dependent on whether such clocks can operate outside the laboratory. Photonic integration offers one compelling solution to address the miniaturization and ruggedization needed to enable clock portability, but brings with it a new set of challenges in recreating the functionality of an optical clock using chip-scale building blocks. The clock laser used for atom interrogation is one particular point of uncertainty, as the performance of the meticulously engineered bulk-cavity-stabilized lasers would be exceptionally difficult to transfer to chip. Here we demonstrate that an integrated ultrahigh-quality-factor spiral cavity, when interfaced with a 1,348 nm seed laser, is able to reach a fractional frequency instability of 7.5 × 10−14 on chip. On frequency doubling the light to 674 nm, we use this laser to interrogate the narrow-linewidth transition of 88Sr+ and showcase the operation of a Sr-ion clock with short-term instability averaging down as \(3.9\times 1{0}^{-14}/\sqrt{\tau }\) (τ, averaging time). Our demonstration of a high-performance optical atomic clock interrogated by an integrated spiral cavity laser opens the door for future advanced clock systems to be entirely constructed using lightweight, portable and mass-manufacturable integrated optics and electronics.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The datasets that support this study are available from the corresponding authors on reasonable request. Source data are provided with this paper.
Code availability
The code used for analysis and simulations are available from the corresponding authors on reasonable request.
Change history
17 February 2025
A Correction to this paper has been published: https://doi.org/10.1038/s41566-025-01643-y
References
Hinkley, N. et al. An atomic clock with 10−18 instability. Science 341, 1215–1218 (2013).
Bloom, B. J. et al. An optical lattice clock with accuracy and stability at the 10−18 level. Nature 506, 71–75 (2014).
Ludlow, A. D., Boyd, M. M., Ye, J., Peik, E. & Schmidt, P. O. Optical atomic clocks. Rev. Mod. Phys. 87, 637 (2015).
Brewer, S. M. et al. 27Al+ quantum-logic clock with a systematic uncertainty below 10−18. Phys. Rev. Lett. 123, 033201 (2019).
Koller, S. B. et al. Transportable optical lattice clock with 7 × 10−17 uncertainty. Phys. Rev. Lett. 118, 073601 (2017).
Godun, R. M. et al. Frequency ratio of two optical clock transitions in 171Yb+ and constraints on the time variation of fundamental constants. Phys. Rev. Lett. 113, 210801 (2014).
Huntemann, N., Sanner, C., Lipphardt, B., Tamm, Chr & Peik, E. Single-ion atomic clock with 3 ×10−18 systematic uncertainty. Phys. Rev. Lett. 116, 063001 (2016).
Maleki, L. & Prestage, J. Applications of clocks and frequency standards: from the routine to tests of fundamental models. Metrologia 42, S145–S153 (2005).
McGrew, W. F. et al. Atomic clock performance enabling geodesy below the centimetre level. Nature 564, 87–90 (2018).
Leibrandt, D. R., Thorpe, M. J., Bergquist, J. C. & Rosenband, T. Field-test of a robust, portable, frequency-stable laser. Opt. Express 19, 10278–10286 (2011).
Liu, L. et al. In-orbit operation of an atomic clock based on laser-cooled 87Rb. Nat. Commun. 9, 22760 (2018).
Grotti, J. et al. Geodesy and metrology with a transportable optical clock. Nat. Phys. 14, 437–441 (2018).
Stuhler, J. et al. Opticlock: transportable and easy-to-operate optical single-ion clock. Meas. Sens. 18, 100264 (2021).
Cao, J. et al. A compact, transportable optical clock with 1 × 10−17 uncertainty and its absolute frequency measurement. Appl. Phys. Lett. 120, 054003 (2022).
Takamoto, M. et al. Test of general relativity by a pair of transportable optical lattice clocks. Nat. Photon. 14, 411–415 (2020).
Mehta, K. K., Zhang, C., Malinowski, M., T. Nguyen, M. S. & Home, J. P. Integrated optical multi-ion quantum logic. Nature 586, 533–537 (2020).
Niffenegger, R. et al. Integrated multi-wavelength control of an ion qubit. Nature 586, 538–542 (2020).
Young, B. C., Cruz, F. C., Itano, W. M. & Bergquist, J. C. Visible lasers with subhertz linewidths. Phys. Rev. Lett. 82, 3799–3802 (1999).
Jiang, Y. Y. et al. Making optical atomic clocks more stable with 10−16-level laser stabilization. Nat. Photon. 5, 158–161 (2011).
Kessler, T. et al. A sub-40-mHz-linewidth laser based on a silicon single-crystal optical cavity. Nat. Photon. 6, 687–692 (2012).
Robinson, J. M. et al. Crystalline optical cavity at 4 K with thermal-noise-limited instability and ultralow drift. Optica 6, 240–243 (2019).
Numata, K., Kemery, A. & Camp, J. Thermal-noise limit in the frequency stabilization of lasers with rigid cavities. Phys. Rev. Lett. 93, 250602 (2004).
Kessler, T., Legero, T. & Sterr, U. Thermal noise in optical cavities revisited. J. Opt. Soc. Am. B 29, 178–184 (2012).
Davila-Rodriguez, J. et al. Compact, thermal-noise-limited reference cavity for ultra-low-noise microwave generation. Opt. Lett. 42, 1277–1280 (2017).
Didier, A. et al. Ultracompact reference ultralow expansion glass cavity. Appl. Opt. 57, 6470–6473 (2018).
Jin, N. et al. Micro-fabricated mirrors with finesse exceeding one million. Optica 9, 965–970 (2022).
Liu, Y. et al. Thermal-noise-limited, compact optical reference cavity operated without a vacuum enclosure. In 2023 IEEE Photonics Conference (IPC) 1–2 (IEEE, 2023).
Gorodetsky, M. L. & Grudinin, I. S. Fundamental thermal fluctuations in microspheres. J. Opt. Soc. Am. B 21, 697–705 (2004).
Matsko, A. B., Savchenkov, A. A., Yu, N. & Maleki, L. Whispering-gallery-mode resonators as frequency references. I. Fundamental limitations. J. Opt. Soc. Am. B 24, 1324–1335 (2007).
Huang, G. et al. Thermorefractive noise in silicon-nitride microresonators. Phys. Rev. A 99, 061801 (2019).
Panuski, C., Englund, D. & Hamerly, R. Fundamental thermal noise limits for optical microcavities. Phys. Rev. X 10, 041046 (2020).
Lee, H. et al. Chemically etched ultrahigh-Q wedge-resonator on a silicon chip. Nat. Photon. 6, 369–373 (2012).
Loh, W. et al. Dual-microcavity narrow-linewidth Brillouin laser. Optica 2, 225–232 (2015).
Gundavarapu, S. et al. Sub-hertz fundamental linewidth photonic integrated Brillouin laser. Nat. Photon. 13, 60–67 (2019).
Xiang, C. et al. 3D integration enables ultralow-noise isolator-free lasers in silicon photonics. Nature 620, 78–85 (2023).
Lee, H. et al. Spiral resonators for on-chip laser frequency stabilization. Nat. Commun. 4, 2468 (2013).
Guo, J. et al. Chip-based laser with 1-Hertz integrated linewidth. Sci. Adv. 8, 43 (2022).
Liu, K. et al. 36 Hz integral linewidth laser based on a photonic integrated 4.0 m coil resonator. Optica 9, 770–775 (2022).
Newman, Z. L. et al. Architecture for the photonic integration of an optical atomic clock. Optica 6, 680–685 (2019).
Barwood, G. P., Huang, G., Klein, H. A., Gill, P. & Clarke, R. B. M. Subkilohertz comparison of the single-ion optical-clock 2S1/2−2D5/2 transition in two 88Sr+ traps. Phys. Rev. A 59, R3178–R3181 (1999).
Dubé, P., Madej, A. A., Zhou, Z. & Bernard, J. E. Evaluation of systematic shifts of the 88Sr+ single-ion optical frequency standard at the 10−17 level. Phys. Rev. A 87, 023806 (2013).
Steinel, M. et al. Evaluation of a 88Sr+ optical clock with a direct measurement of the blackbody radiation shift and determination of the clock frequency. Phys. Rev. Lett. 131, 083002 (2023).
Nichol, B. C. et al. An elementary quantum network of entangled optical atomic clocks. Nature 609, 689–694 (2022).
Loh, W., Yegnanarayanan, S., O’Donnell, F. & Juodawlkis, P. W. Ultra-narrow linewidth Brillouin laser with nanokelvin temperature self-referencing. Optica 6, 152–159 (2019).
Loh, W. et al. Operation of an optical atomic clock with a Brillouin laser subsystem. Nature 588, 244–249 (2020).
Jefferts, S. R., Meekhof, D. M., Shirley, J. H., Stepanovic, M. & Parker, T. E. Accuracy results from NIST-F1 laser-cooled cesium primary frequency standard. In Proc. IEEE/EIA International Frequency Control Symposium and Exhibition 714–717 (IEEE, 2000).
Bauters, J. F. et al. Ultra-low-loss high-aspect-ratio Si3N4 waveguides. Opt. Express 19, 3163–3174 (2011).
Stein, S. R. Frequency and time—their measurement and characterization. Precision Freq. Control 2, 191–232 (1985).
Bruzewicz, C. D., McConnell, R., Stuart, J., Chiaverini, J. & Sage, J. M. Dual-species, multi-qubit logic primitives for Ca+/Sr+ trapped-ion crystals. npj Quantum Inf. 5, 102 (2019).
Ma, L. S., Junger, P., Ye, J. & Hall, J. L. Delivering the same optical frequency at two places: accurate cancellation of phase noise introduced by an otical fiber or other time-varying path. Opt. Lett. 19, 1777–1779 (2019).
Nicholson, T. L. et al. Comparison of two independent Sr optical clocks with 1 × 10−17 stability at 103s. Phys. Rev. Lett. 109, 230801 (2012).
Nicholson, T. L. et al. Systematic evaluation of an atomic clock at 2 × 10−18 uncertainty. Nat. Commun. 6, 6896 (2015).
Biedermann, G. W. et al. Zero-dead-time operation of interleaved atomic clocks. Phys. Rev. Lett. 111, 170802 (2013).
Chauhan, N. et al. Trapped ion qubit and clock operations with a visible wavelength photonic coil resonator stabilized integrated Brillouin laser. Preprint at https://arxiv.org/abs/2402.16742 (2024).
Drever, R. W. P. et al. Laser phase and frequency stabilization using an optical resonator. Appl. Phys. B 31, 97–105 (1983).
Howe, D. A. The total deviation approach to long-term characterization of frequency stability. IEEE Trans. Ultrason., Ferroelectr., Freq. Control 47, 1102–1110 (2000).
Acknowledgements
This work was sponsored by the Under Secretary of Defense for Research and Engineering under Air Force contract no. FA8721-05-C-0002 and by the Defense Advanced Research Projects Agency (DARPA) under contract number FA8702-15-D-0001. The views, opinions and/or findings expressed are those of the authors and should not be interpreted as representing the official views or policies of the Department of Defense or the US Government. Distribution Statement “A” (Approved for Public Release, Distribution Unlimited).
Author information
Authors and Affiliations
Contributions
W.L., D.R., R.M. and D.G. conceived, designed and carried out the experiments with the ISCL. D.R., R.M., W.L. and W.S. conceived, designed and carried out the experiments with the clock protocol. D.K. and A.S. fabricated the spiral resonators. C.B., R.T.M. and A.M. prepared the fibre-attached spiral resonator. C.D.B. and D.R. developed the fibre and vibration noise cancellation for the clock system. All authors discussed the results and contributed to the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Photonics thanks Junqiu Liu, Myoung-Gyun Suh and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Spiral Resonator Component Sections.
Plot of the spiral resonator with its different component sections highlighted. The number of revolutions is reduced from 25 to 2 for clarity. The spiral resonator comprises the following sections: pure circles, central cubics, inward going racetrack, outward going racetrack, a rotated clone of all the preceding, racetrack interconnects, and bus waveguide.
Extended Data Fig. 2 Integrated Spiral Cavity Laser Optical System.
Simplified system diagram showcasing the optical components of the ISCL. Photographs of the corresponding optical devices in the setup are also displayed.
Extended Data Fig. 3 Optimization of ISCL Operation.
a, Frequency noise spectra measured at a variety of chip-coupled optical powers. The line noise at 180 Hz and 300 Hz reduces with optical power. However, at 5.1 mW, the broadband noise level increases sharply. b, Noise at the power line frequencies of 60 Hz, 180 Hz, and 300 Hz plotted versus the on-chip optical power. The measured power line noise at all three frequencies decreases with increasing power. c, Fractional frequency noise of the ISCL across the same range of optical powers previously tested. Changes in optical power lead to competing effects in the stability of the laser at both short and longer averaging times. d, Fractional frequency noise versus optical power for averaging times of 1 ms and 30 ms. The optimum chip-coupled power is near 4.1 mW.
Extended Data Fig. 4 ISCL Fiber Link Noise.
a, Phase noise of ISCL measured at the output of the ISCL at 1348 nm and across the fiber link to the Sr-ion laboratory after frequency doubling to 674 nm (scaled to 1348 nm for comparison). The noise increases slightly around 10 Hz-1 kHz offset frequencies. b, Fractional frequency instability measured for the 1348 nm ISCL before and after the fiber link. The fiber noise is most prominent near 10 ms averaging time.
Extended Data Fig. 5 Experimental Tests of Atom Locking With Integration.
Tests of the atom lock with τint = 1 ms and an intentionally applied 0.1 Hz sinusoidal modulation having an amplitude that increases over time. The trial where integration is included in the locking protocol (α = 0.13, β = 0.0035, and γ = 0.995) outperforms the case with no integration (α = 0.2).
Extended Data Fig. 6 Atom Measurements Using the ISCL.
a, Narrow spectroscopy using Rabi pulses was performed with the atom and the ISCL. A 2.5 ms probe pulse is used, increasing the dead time of the clock and requiring greater performance. The observed linewidth of 380 Hz is Fourier limited by the interrogation time. The scan is performed with 400 trials per point and was obtained in ∼2 minutes. b, Rabi oscillation spectroscopy performed with the ISCL. The fit demonstrates π-pulse time of 11 μs, with the observed decoherence due to the thermal state of the ion corresponding to mean axial mode occupation \(\bar{n}\approx 19.5\).
Source data
Source Data Fig. 1
Spiral resonator curvature.
Source Data Fig. 2
ISCL noise.
Source Data Fig. 3
Spiral resonator curvature.
Source Data Fig. 4
Sr-ion clock measurements.
Source Data Extended Data Fig. 3
ISCL power comparison measurements.
Source Data Extended Data Fig. 4
Fibre link noise.
Source Data Extended Data Fig. 5
Integration tests for atom locking.
Source Data Extended Data Fig. 6
Atom measurements.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Loh, W., Reens, D., Kharas, D. et al. Optical atomic clock interrogation using an integrated spiral cavity laser. Nat. Photon. 19, 277–283 (2025). https://doi.org/10.1038/s41566-024-01588-8
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/s41566-024-01588-8
This article is cited by
-
A hyperfine-transition-referenced vector spectrum analyzer for visible-light integrated photonics
Nature Communications (2025)
-
Building atomic clock lasers with integrated photonics
Nature Photonics (2025)
-
Magic cancellation point for vibration resilient ultrastable microwave signal synthesis
Nature Communications (2025)