Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Generation of three-dimensional cluster entangled state

Nature Photonics volume 19, pages 526–532 (2025)Cite this article

Subjects

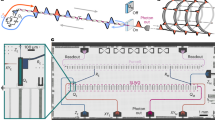
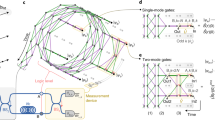
Abstract

Measurement-based quantum computing is a promising paradigm of quantum computation, in which universal computing is achieved through a sequence of local measurements. The backbone of this approach is the preparation of multipartite entanglement, known as cluster states. Although a cluster state with two-dimensional connectivity is required for universality, a three-dimensional cluster state is necessary for additionally achieving fault tolerance. However, the challenge of making three-dimensional connectivity has limited cluster state generation capability up to two dimensions. Here we demonstrate the deterministic generation of a three-dimensional cluster state based on the photonic continuous-variable platform. To realize three-dimensional connectivity, we harness a crucial advantage of time–frequency modes of ultrafast quantum light: an arbitrary complex mode basis can be accessed directly, enabling connectivity as desired. We demonstrate the versatility of our method by generating cluster states with one-, two- and three-dimensional connectivities. For their complete characterization, we develop a quantum state tomography method for multimode Gaussian states. Moreover, we verify the cluster state generation by nullifier measurements as well as full inseparability tests. Our work paves the way towards fault-tolerant and universal-measurement-based quantum computing.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Experimental scheme.
Fig. 2: Full characterization of cluster states.
Fig. 3: Verification of cluster state generation.
Fig. 4: Ancilla-assisted cluster state generation.

Similar content being viewed by others

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Code availability

The code used to produce the results are available from the corresponding author upon reasonable request.

References

  1. Bourassa, J. E. et al. Blueprint for a scalable photonic fault-tolerant quantum computer. Quantum 5, 392 (2021).

    Article  Google Scholar 

  2. Yokoyama, S. et al. Ultra-large-scale continuous-variable cluster states multiplexed in the time domain. Nat. Photon. 7, 982–986 (2013).

    Article  ADS  Google Scholar 

  3. Chen, M., Menicucci, N. C. & Pfister, O. Experimental realization of multipartite entanglement of 60 modes of a quantum optical frequency comb. Phys. Rev. Lett. 112, 120505 (2014).

    Article  ADS  Google Scholar 

  4. Larsen, M. V., Guo, X., Breum, C. R., Neergaard-Nielsen, J. S. & Andersen, U. L. Deterministic generation of a two-dimensional cluster state. Science 366, 369–372 (2019).

    Article  ADS  MathSciNet  Google Scholar 

  5. Asavanant, W. et al. Generation of time-domain-multiplexed two-dimensional cluster state. Science 366, 373–376 (2019).

    Article  ADS  MathSciNet  Google Scholar 

  6. Hamilton, C. S. et al. Gaussian boson sampling. Phys. Rev. Lett. 119, 170501 (2017).

    Article  ADS  Google Scholar 

  7. Deshpande, A. et al. Quantum computational advantage via high-dimensional Gaussian boson sampling. Sci. Adv. 8, eabi7894 (2022).

    Article  ADS  Google Scholar 

  8. Zhong, H.-S. et al. Quantum computational advantage using photons. Science 370, 1460–1463 (2020).

    Article  ADS  Google Scholar 

  9. Madsen, L. S. et al. Quantum computational advantage with a programmable photonic processor. Nature 606, 75–81 (2022).

    Article  ADS  Google Scholar 

  10. Aaronson, S. & Arkhipov, A. The computational complexity of linear optics. In Proc. Forty-Third Annual ACM Symposium on Theory of Computing 143–252 (Association for Computing Machinery, 2013).

  11. Raussendorf, R. & Briegel, H. J. A one-way quantum computer. Phys. Rev. Lett. 86, 5188–5191 (2001).

    Article  ADS  Google Scholar 

  12. Menicucci, N. C. et al. Universal quantum computation with continuous-variable cluster states. Phys. Rev. Lett. 97, 110501 (2006).

    Article  ADS  Google Scholar 

  13. van Loock, P., Weedbrook, C. & Gu, M. Building Gaussian cluster states by linear optics. Phys. Rev. A 76, 032321 (2007).

    Article  ADS  Google Scholar 

  14. Menicucci, N. C., Flammia, S. T. & van Loock, P. Graphical calculus for Gaussian pure states. Phys. Rev. A 83, 042335 (2011).

    Article  ADS  Google Scholar 

  15. Enomoto, Y., Yonezu, K., Mitsuhashi, Y., Takase, K. & Takeda, S. Programmable and sequential Gaussian gates in a loop-based single-mode photonic quantum processor. Sci. Adv. 7, eabj6624 (2021).

    Article  ADS  Google Scholar 

  16. Larsen, M. V., Guo, X., Breum, C. R., Neergaard-Nielsen, J. S. & Andersen, U. L. Deterministic multi-mode gates on a scalable photonic quantum computing platform. Nat. Phys. 17, 1018–1023 (2021).

    Article  Google Scholar 

  17. Raussendorf, R., Harington, J. & Goyal, K. A fault-tolerant one-way quantum computer. Ann. Phys. 321, 2242–2270 (2006).

    Article  ADS  MathSciNet  Google Scholar 

  18. Raussendorf, R., Harrington, J. & Goyal, K. Topological fault-tolerance in cluster state quantum computation. New J. Phys. 9, 199 (2007).

    Article  ADS  MathSciNet  Google Scholar 

  19. Kitaev, A. Fault-tolerant one-way quantum computer. Ann. Phys. 303, 2242–2270 (2006).

    MathSciNet  Google Scholar 

  20. Fowler, A. G., Mariantoni, M., Martinis, J. M. & Cleland, A. N. Surface code: towards parctical large-scale quantum computation. Phys. Rev. A 86, 032324 (2012).

    Article  ADS  Google Scholar 

  21. Bolt, A., Duclos-Cianci, G., Poulin, D. & Stace, T. M. Foliated quantum error-correcting codes. Phys. Rev. Lett 117, 070501 (2016).

    Article  ADS  MathSciNet  Google Scholar 

  22. Zhang, J., Xie, C., Peng, K. & van Loock, P. Anyon statistics with continuous variables. Phys. Rev. A 78, 052121 (2008).

    Article  ADS  MathSciNet  Google Scholar 

  23. Aoki, T. et al. Quantum error correction beyond qubits. Nat. Phys. 5, 541–546 (2009).

    Article  Google Scholar 

  24. van Loock, P. A note on quantum error correction with continuous variables. J. Mod. Opt. 57, 1965–1971 (2010).

    Article  ADS  Google Scholar 

  25. Gottesman, D., Kitaev, A. & Preskill, J. Encoding a qubit in an oscillator. Phys. Rev. A 64, 012310 (2001).

    Article  ADS  Google Scholar 

  26. Fukui, K., Tomita, A., Okamoto, A. & Fujii, K. High-threshold fault-tolerant quantum computation with analog quantum error correction. Phys. Rev. X 8, 021054 (2018).

    Google Scholar 

  27. Fukui, K., Asavanant, W. & Furusawa, A. Temporal-mode continuous-variable three-dimensioinal cluster state for topologically protected measurement-based quantum computation. Phys. Rev. A 102, 032614 (2020).

    Article  ADS  Google Scholar 

  28. Larsen, M. V., Chamberland, C., Noh, K., Neergaard-Nielsen, J. S. & Andersen, U. L. Fault-tolerant continuous-variable measurement-based quantum computation architecture. PRX Quantum 2, 030325 (2021).

    Article  ADS  Google Scholar 

  29. Wu, B. H., Alexander, R. N., Liu, S. & Zhang, Z. Quantum computing with multidimensional continuous-variable cluster states in a scalable photonic platform. Phys. Rev. Res. 2, 023138 (2020).

    Article  Google Scholar 

  30. Du, P., Wang, Y., Liu, K., Yang, R. & Zhang, J. Generation of large-scale continuous-variable cluster states multiplexed both in time and frequency domains. Opt. Express 31, 7535–7544 (2023).

    Article  Google Scholar 

  31. Roslund, J., Araújo, R. M., Jiang, S., Fabre, C. & Treps, N. Wavelength-multiplexed quantum networks with ultrafast frequency combs. Nat. Photon. 8, 109–112 (2014).

    Article  ADS  Google Scholar 

  32. Roman-Rodriguez, V. et al. Multimode squeezed state for reconfigurable quantum networks at telecommunication wavelengths. Phys. Rev. Res. 6, 043113 (2024).

    Article  Google Scholar 

  33. Roh, C., Yoon, Y.-D., Park, J. & Ra, Y.-S. Continuous-variable nonclassicality certification under coarse-grained measurement. Phys. Rev. Res. 5, 043057 (2023).

    Article  Google Scholar 

  34. Cai, Y. et al. Multimode entanglement in reconfigurable graph states using optical frequency combs. Nat. Commun. 8, 15645 (2017).

    Article  ADS  Google Scholar 

  35. Ansari, V., Donohue, J. M., Brecht, B. & Silberhorn, C. Tailoring nonlinear processes for quantum optics with pulsed temporal-mode encodings. Optica 5, 534–550 (2018).

    Article  ADS  Google Scholar 

  36. Ra, Y.-S. et al. Non-Gaussian quantum states of a multimode light field. Nat. Phys. 16, 114–147 (2020).

    Article  Google Scholar 

  37. Sørensen, A. S. & Mølmer, K. Entanglement and extreme spin squeezing. Phys. Rev. Lett. 86, 4431–4434 (2001).

    Article  ADS  Google Scholar 

  38. Sośnicki, F., Mikołajczyk, M., Golestani, A. & Karpiński, M. Interface between picosecond and nanosecond quantum light pulses. Nat. Photon. 17, 761–766 (2023).

    Article  ADS  Google Scholar 

  39. Serino, L. et al. Realization of a multi-output quantum pulse gate for deconding high-dimensional temporal modes of single-photon states. PRX Quantum 4, 020306 (2023).

    Article  ADS  Google Scholar 

  40. Duan, L.-M., Giedke, G., Cirac, J. I. & Zoller, P. Inseparability criterion for continuous variable systems. Phys. Rev. Lett. 84, 2722–2725 (2000).

    Article  ADS  Google Scholar 

  41. Bowen, W. P., Schnabel, R., Lam, P. K. & Ralph, T. C. Experimental investigation of criteria for continuous variable entanglement. Phys. Rev. Lett. 90, 043601 (2003).

    Article  ADS  Google Scholar 

  42. Patera, G., Treps, N., Fabre, C. & De Valcárcel, G. J. Quantum theory of synchronously pumped type I optical parametric oscillators: characterization of the squeezed supermodes. Eur. Phys. J. D 56, 123–140 (2009).

    Article  ADS  Google Scholar 

  43. Braunstein, S. L. Squeezing as an irreducible resource. Phys. Rev. A 71, 055801 (2005).

    Article  ADS  Google Scholar 

  44. van Loock, P. & Furusawa, A. Detecting genuine multipartite continuous-variable entanglement. Phys. Rev. A 67, 052315 (2003).

    Article  ADS  Google Scholar 

  45. Simon, R. Peres-Horodecki separability criterion for continuous variable systems. Phys. Rev. Lett. 84, 2726–2729 (2000).

    Article  ADS  Google Scholar 

  46. Wiseman, H., Jones, S. & Doherty, A. Steering, entanglement, nonlocality, and the Einstein-Podolsky-Rosen paradox. Phys. Rev. Lett. 98, 140402 (2007).

    Article  ADS  MathSciNet  Google Scholar 

  47. Kim, H.-J., Jung, J.-H., Lee, K.-J. & Ra, Y.-S. Recovering quantum entanglement after its certification. Sci. Adv. 9, eadi5261 (2023).

    Article  Google Scholar 

  48. Kogias, I., Lee, A. R., Ragy, S. & Adesso, G. Quantification of Gaussian quantum steering. Phys. Rev. Lett. 114, 060403 (2015).

    Article  ADS  Google Scholar 

  49. González-Arciniegas, C., Nussenzveig, P., Martinelli, M. & Pfister, O. Cluster states from Gaussian states: essential diagnotic tools for continuous-variable one-way quantum computing. PRX Quantum 2, 030343 (2021).

    Article  ADS  Google Scholar 

  50. Eisert, J., Scheel, S. & Plenio, M. B. Distilling Gaussian states with Gaussian operations is impossible. Phys. Rev. Lett. 89, 137903 (2002).

    Article  ADS  MathSciNet  Google Scholar 

  51. Miwa, Y. et al. Demonstration of cluster-state shaping and quantum erasure for continuous variables. Phys. Rev. A 82, 032305 (2010).

    Article  ADS  Google Scholar 

  52. Clements, W. R., Humphreys, P. C., Metcalf, B. J., Kolthammer, W. S. & Walsmley, I. A. Optimal design for universal multiport interferometers. Optica 3, 1460–1465 (2016).

    Article  Google Scholar 

  53. Presutti, F. et al. Highly multimode visible squeezed light with programmable spectral correlations through broadband up-conversion. Preprint at https://arxiv.org/abs/2401.06119 (2024).

  54. Menicucci, N. C. Fault-tolerant measurement-based quantum computing with continuous-variable cluster states. Phys. Rev. Lett. 112, 120504 (2014).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We thank M. S. Kim and J. Park for fruitful discussions. This work was supported by the Ministry of Science and ICT (MSIT) of Korea (NRF-2020M3E4A1080028, NRF-2022R1A2C2006179 and RS-2023-NR119925) under the Information Technology Research Center (ITRC) support program (IITP-2025-2020-0-01606) and the Institute of Information & Communications Technology Planning & Evaluation (IITP) grant (no. 2022-0-01029, Atomic ensemble based quantum memory) and by the Air Force Office of Scientific Research award (nos. FA2386-21-1-4020 and FA2386-22-1-4083).

Author information

Authors and Affiliations

  1. Department of Physics, Korea Advanced Institute of Science and Technology, Daejeon, Korea

    Chan Roh, Geunhee Gwak, Young-Do Yoon & Young-Sik Ra

Authors
  1. Chan Roh
    View author publications

    Search author on:PubMed Google Scholar

  2. Geunhee Gwak
    View author publications

    Search author on:PubMed Google Scholar

  3. Young-Do Yoon
    View author publications

    Search author on:PubMed Google Scholar

  4. Young-Sik Ra
    View author publications

    Search author on:PubMed Google Scholar

Contributions

C.R. conducted the experiment with contributions from G.G. and Y.-D.Y. C.R. analysed the data and developed the theory. Y.-S.R. conceived and supervised the project. C.R. and Y.-S.R. wrote the manuscript with inputs from all authors.

Corresponding author

Correspondence to Young-Sik Ra.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Photonics thanks Jiangrui Gao and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Ancilla-assisted generation of a cluster state with negative weights.

The same method as Fig. 4 is used to generate a 3D cluster state with negative weights. a, Four edges (6-7, 6-13, 9-10, and 10-11) in Gbasic have negative weights. b, Experimentally generated 3D cluster state after local phase correction in the range of (− 0.18, 0.18) rad. c, Nullifier measurements on the generated 3D cluster state. d, Conditional covariance matrix in the target modes. e, Inseparability test for the cluster state in (d), exhibiting negative minimum eigenvalues for all bipartitions. f, Nullifier variances of the target cluster state after removing the ancilla. In c and f, data are presented as scatter plots (from four repeated experiments), with mean values as bar charts and ± 1 s.d. as error bars.

Supplementary information

Supplementary Information

Supplementary Figs. 1–5, Sections 1–4 and References.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Roh, C., Gwak, G., Yoon, YD. et al. Generation of three-dimensional cluster entangled state. Nat. Photon. 19, 526–532 (2025). https://doi.org/10.1038/s41566-025-01631-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41566-025-01631-2

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing