Main

Ultrafast magnetic field steps are unipolar, time-varying magnetic field pulses with short rise times and long decay times, which are promising as a universal means to control magnetization1,2,3,4,5,6. Microcoils have been used to generate magnetic field steps with amplitudes of tens of milliteslas and rise times of hundreds of picoseconds or longer7,8,9. Auston switches can generate faster steps and are used to produce magnetic pulses with picosecond rise times and sub-nanosecond decay times10,11. In this case, the amplitude of the generated magnetic field is limited by Joule heating in the resistive coplanar waveguides carrying the pulse. Moreover, the spatial profile of the generated magnetic field is generally confined to micrometre-sized regions (tens of micrometres) with strong spatial gradients. Alternatively, picosecond magnetic field pulses with Tesla-level amplitudes are generated with relativistic electron bunches12,13.

Intense ultrafast magnetic transients have also been produced starting from circularly polarized light pulses. In materials with a large Verdet constant, the inverse Faraday effect generates a transient magnetic field induction that follows the envelope of the driving pulse14,15,16,17. Similarly, circularly polarized terahertz and mid-infrared pulses can excite circular phonons, where the atomic motions generate effective magnetic fields as high as ~36 mT (ref. 18) and ~20 mT (ref. 19), a value four orders of magnitude larger than the theoretically predicted value20. Despite the importance of these findings, the nature of these magnetic transients remains poorly understood. It is particularly unclear whether these are analogous to conventional fields governed by Maxwell’s equations or synthetic fields confined to the material, unable to propagate outside the sample21.

Here we present a new tabletop method to overcome many of these shortcomings and demonstrate the generation of magnetic field steps that retain the fastest rise times, long decay times and sizeable amplitudes, and offer new opportunities for tailoring the spatial and temporal profiles of the induced magnetic fields.

The physical principle that enables the generation of magnetic steps with picosecond rise times and ‘on’ times far over a nanosecond (and potentially as long as milliseconds) is based on a superconducting material with large diamagnetism, quenched with an ultrafast optical pulse. Applying a magnetic field to a zero-field cooled superconductor generates persistent currents22,23 to exclude the magnetic flux from the sample volume. We use sub-picosecond high-frequency laser pulses to disrupt superconductivity24,25,26,27,28,29, and prompt a sudden change in the magnetic field near the material. In this way, we generate near-field, ultrafast magnetic steps. These pulses are extremely broadband, with frequency content spanning several octaves, from sub-gigahertz to terahertz frequencies.

Here we used a thin film of optimally doped YBa2Cu3O7, cooled below Tc and excited with a 100-fs-long, 400-nm-wavelength optical pulse, which disrupts superconductivity24,25,26,27,28,29. To track the temperature and time evolution of the magnetic field surrounding the superconductor after optical excitation, we used a time-resolved magneto-optical imaging technique30,31,32. We placed a diamagnetic GaP(100) crystal above the superconductor, and the fast Faraday response to the local magnetic field was probed with a time-delayed optical pulse with 50-μm spatial resolution. Previous realizations of this field detection technique used ferrimagnetic detectors33,34,35, limiting the time resolution to ~100 ps. Here we use diamagnetic GaP as a magneto-optic detector, allowing for a time resolution better than ~1 ps at the expense of a smaller signal and longer measurement times (Supplementary Section 1).

Thermally driven magnetic field step

A 1-mm-diameter disc with a well-defined edge was prepared using optical lithography, starting from a 150-nm-thick film of superconducting YBa2Cu3O7 grown on Al2O3. We placed a 75-µm-thick (100)-oriented GaP crystal in close contact with the YBa2Cu3O7 film (Supplementary Sections 2 and 3). The two formed a stack with the magneto-optic detector on top and the superconducting device right beneath it (Fig. 1a).

Fig. 1: Thermally driven magnetic field step.
figure 1

a, Sketch of the experimental geometry. A 150-nm-thick, 1-mm-diameter YBa2Cu3O7 (YBCO7) disc was grown on an Al2O3 substrate. The local magnetic field surrounding the YBa2Cu3O7 disc is measured by tracking the Faraday polarization rotation of a linearly polarized 800-nm probe pulse, reflected after propagation through a 75-µm-thick GaP(100) crystal placed on top of the sample. A 2-mT magnetic field (Bapp) is applied in the z direction. Its polarity is periodically cycled to isolate the magnetic contributions to the polarization rotation. The colour plot (zoomed-in view) illustrates the simulated (Supplementary Section 7) changes in the z component of the local magnetic field (Bz) induced by the superconductor below Tc. Blue (red) indicates areas with reduced (enhanced) magnetic field, following the colour scale shown in b. b, Temperature dependence of Bz measured above the centre of the YBa2Cu3O7 disc. Each data point represents the mean value ± s.e.m. (smaller than the size of the data points) extracted from a sample of 100 acquisitions (Supplementary Section 5). A clear transition at Tc = 85 K is observed. The measured field exclusion is not complete due to the finite thickness of the GaP detector, which leads to averaging in the z direction (see the main text and Supplementary Section 8). The left inset shows a two-dimensional map of Bz, measured as a function of the x and y positions at T = 30 K < Tc. An increase in the magnetic field is measured near the sample edge (red), and a reduction above its centre (blue). The dashed black line indicates the outline of the superconducting disc. The right inset shows the same measurement at T = 300 K > Tc. No spatial dependence is observed throughout the field of view.

Source data

Full size image

The YBa2Cu3O7 sample and GaP detector were subjected to a 2-mT uniform magnetic field applied along the z direction using a Helmholtz coil pair (Fig. 1a). A linearly polarized 800-nm ultrashort probe pulse was focused to a spot size of ~50-µm full-width at half-maximum, impinging at near-normal incidence on a wedged GaP crystal. The Faraday effect induced a polarization rotation on the beam transmitted through the GaP and reflected from its second surface, yielding a measurement of the vertical component of the local magnetic field, averaged over the volume traversed by the probe in the magneto-optic detector. The external applied magnetic field Happ was sinusoidally modulated in time, synchronously to the laser probe pulse train. In this way, signals acquired with −Happ were subtracted from those acquired with +Happ (Supplementary Sections 4 and 5). This measurement protocol isolated contributions to the polarization rotation having a magnetic origin and suppressed potential non-magnetic contributions such as static and pump-induced birefringence.

Because Happ was varying in time as YBa2Cu3O7 was held in its superconducting state, the magnetization in the superconductor originated from the exclusion of a time-varying magnetic field rather than the expulsion of a static magnetic field as in the Meissner effect. Compared with applying static magnetic fields, this protocol is advantageous because it minimizes the effect of trapped flux22 and leads to the largest possible magnetic field steps (Supplementary Sections 6 and 7).

Figure 1a displays a finite-element simulation of the z component of the magnetic field surrounding the sample. We simulate the magnetic field exclusion in YBa2Cu3O7 by modelling it as a medium with virtually infinite conductivity and applying a time-dependent external magnetic field (Supplementary Section 7). The magnetic field is reduced above the sample (blue regions) and increased near its edges (red regions) as the magnetic flux is kept from the sample.

Figure 1b (left inset) shows a two-dimensional map of the z component of the magnetic field measured when the YBa2Cu3O7 disc is cooled to T = 30 K < Tc. As predicted from the simulations, we observed a reduction in the local magnetic field when measuring above the disc (blue area) and a corresponding enhancement near the edge (red area). The amplitude of the measured changes is determined by the geometry of the experiment and by the thickness of the detection crystal (Supplementary Section 8). The same measurement was repeated at T = 300 K > Tc. The results are displayed in Fig. 1b (right inset), showing that when the YBa2Cu3O7 disc is in its normal state, no spatial dependence of the local magnetic field is detected.

The temperature was then varied between 40 K and 120 K to track the evolution of the magnetic field above the centre of the YBa2Cu3O7 disc (Fig. 1b). As the temperature was swept across Tc ≈ 85 K, a sharp change in the magnetic field was observed, resembling a magnetic field step. The speed at which this magnetic field change can be induced by varying the temperature is limited by how fast the material is heated or cooled through the transition (~0.3 K s–1), limiting the highest frequency content to less than a few hertz.

Ultrafast magnetic field step

Picosecond rise times were achieved by irradiating YBa2Cu3O7 with ultrashort optical pulses, which disrupt superconductivity depleting the condensate on ultrafast timescales24,25,26,27,28,29 (Supplementary Section 9 provides a more in-depth review on the disruption mechanisms). After disruption, we expect the supercurrents shielding the applied magnetic field to disappear on a timescale probably determined by the L/R time constant of the resistive disc (L is the total inductance of the disc and R is the resistance in the photoexcited state). As a result, we expect the magnetic field to penetrate back into the sample volume on the same timescales (Supplementary Section 10).

The geometry of the experiment (Fig. 2a) was the same as that used in the temperature-dependent measurements, with the only addition of a quench pulse (centre wavelength, 400 nm; duration, ~100 fs; fluence, ~0.3 mJ cm–2), which struck the sample from the side opposite to the GaP detector. Note that the YBa2Cu3O7 thin film was opaque to 400-nm radiation, and the quench beam was shaped like a disc with a flat intensity profile imaged onto the sample to match its size (Supplementary Section 11). These precautions prevented a direct interaction of the ultraviolet pump with the magneto-optic detector that could give rise to nonlinear interactions leading to spurious responses (Supplementary Section 12 shows that no magnetic pump–probe signal was detected when the device was kept at 100 K, above Tc of the superconductor). Furthermore, the measurements were performed using the differential magnetic field scheme described above, isolating signals only connected to the applied magnetic field Happ.

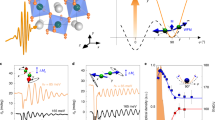
Fig. 2: Ultrafast magnetic field step.
figure 2

a, Sketch of the experimental geometry. The sample–detector assembly is the same as that in Fig. 1a. The YBa2Cu3O7 disc is kept at a base temperature T = 55 K < Tc and photoexcited with an ultraviolet laser pulse (λ = 400 nm) to disrupt superconductivity. This quench pulse is shaped into a flat-top disc by a shadow mask and imaged by a 4f imaging system onto the YBa2Cu3O7 disc (Supplementary Section 11). The pump-induced changes in the local magnetic field were quantified using Faraday magnetometry in a GaP(100) detector as a function of the time delay between the probe and quench pulses. A 2-mT magnetic field (Bapp) is applied in the z direction. Its polarity is periodically cycled to isolate the magnetic contributions to the polarization rotation. b, Quench-induced changes in the z component of the local magnetic field ΔBz, measured above the centre of the disc as a function of the pump–probe delay. Each data point represents the mean value ± s.e.m. extracted from a sample of 1,100 acquisitions (Supplementary Section 5), and the solid line is a fit with a single-time-constant exponential model (Supplementary Section 10). The inset shows a zoomed-in view at short time delays around time zero. The value of the measured magnetic field at negative time delays is equal to 0.45 mT due to the dynamics of the trapped flux in the superconductor between consecutive pump pulses (Supplementary Section 14).

Source data

Full size image

Figure 2b displays the time dependence of the changes in the local magnetic field induced by the quench pulse and measured above the centre of the YBa2Cu3O7 film at a base temperature T = 55 K < Tc. As shown in Fig. 1b, the YBa2Cu3O7 shields the applied magnetic field effectively at this temperature. As the quench pulse hit the sample, an increase in the magnetic field was detected. This change produced an ultrafast magnetic field step of ~0.2-mT amplitude with a rise time of ~1 ps (Fig. 2b, inset), corresponding to a slew rate of ~200 MT s–1 (further details about this measurement and the fitting procedure are reported in Supplementary Sections 10, 12 and 13).

An equivalent L/R circuit describes the system’s dynamics well when assuming a conductivity of the excited state of 0.1 MS m–1, which is lower than, but comparable to, the normal-state conductivity of YBa2Cu3O7 (refs. 36,37). The validity of this model is confirmed by finite-element simulations, which predict a time constant that scales linearly with the diameter of the disc (more details are described in Supplementary Section 10).

Importantly, after the transient, the magnetic field remained constant for several hundreds of picoseconds even if the superconductivity in YBa2Cu3O7 thin films is expected to recover within a few picoseconds after photoexcitation27 (Supplementary Section 9). That is the case since the superconductor’s equilibrium and photoexcited magnetic responses originate entirely from shielding currents, screening the time-dependent applied magnetic field (Supplementary Sections 6 and 14). When the superconductor recovers after the quench in an applied magnetic field, only a weak Meissner expulsion appears, which gives rise to a response that is below our experimental field resolution (Supplementary Section 7). Note that in alternative realizations of magnetic field steps, based on Auston switches or by free-space terahertz pulses, the low-frequency cut-off is generally limited to tens10,11,38 and hundreds39,40,41,42,43,44 of gigahertz, respectively. In the present case, the lowest frequency achievable is well below 1 GHz, limited only by the time dependence of the externally applied magnetic field (Supplementary Section 14).

Coherent magnetization control in a ferrimagnet

The broad frequency content of the ultrafast magnetic field steps shown above makes them suitable for controlling magnetization in various magnetic materials that feature magnons and spin-lattice relaxation rates in the sub-gigahertz to terahertz frequency range. As a proof of principle, we apply these magnetic field steps to control the orientation of magnetization in a ferrimagnetic Lu3−xBixFe5−yGayO12 garnet45 (Bi:LIGG). A commercial Bi:LIGG sample with bismuth substitution x ≈ 1 and gallium substitution y ≈ 1 (Supplementary Section 2) was used in place of the GaP detector. The geometry of the experiment is shown in Fig. 3a. The in-plane magnetized Bi:LIGG film was ~3 µm thick and grown on a Gd3Ga5O12 substrate (not shown; Supplementary Sections 2 and 3). Unlike in the measurements shown in Figs. 1 and 2, now we measure the Faraday rotation accumulated by a linearly polarized 800-nm probe pulse traversing the Bi:LIGG layer. In this configuration, the polarization rotation becomes a highly sensitive probe of the magnetization dynamics triggered in the Bi:LIGG43,46,47. Similar to the experiment shown in Fig. 2, a 400-nm quench pulse is used to disrupt superconductivity in the YBa2Cu3O7 disc and trigger a magnetic field step that excites the Bi:LIGG sample.

Fig. 3: Ultrafast control of magnetization.
figure 3

a, Sketch of the experimental geometry. A film of Bi:LIGG is placed on top of the same YBa2Cu3O7 disc shown in Fig. 2a. The disc is photoexcited with an ultraviolet laser pulse (λ = 400 nm) at T = 55 K < Tc to disrupt superconductivity. The magnetic field step generated (Fig. 2) triggers coherent magnon oscillations in the neighbouring Bi:LIGG sample. b, The data points show the time evolution of the changes in the z component of the Bi:LIGG magnetization ΔMz, quantified by measuring the Faraday rotation above the centre of the superconducting disc versus quench-probe delay. Each data point represents the mean value ± s.e.m. (smaller than the size of the data points) extracted from a sample of 360 acquisitions (Supplementary Section 5). The fluence of the quench pulse is ~0.3 mJ cm–2. At negative time delays, Mz equals –1.4 mT due to negative trapped flux before the pump pulse hits the YBa2Cu3O7 disc (Supplementary Section 14). The solid line shows a simulation of ΔMz above the centre of the YBa2Cu3O7 disc using a Landau–Lifshitz–Gilbert model and the magnetic field step shown in Fig. 2b as the input bias (Supplementary Section 15). c, Representation of the effective magnetic field (Heff) dynamics inside Bi:LIGG. Heff is given by the sum of a constant field accounting for shape anisotropy (HA) and the time-varying magnetic field step (Hstep) generated by photoexciting the adjacent superconducting disc. Hstep is negative at negative delays due to the trapped magnetic flux in the superconductor (Supplementary Section 14). d, Representation of the magnetization (M) dynamics in Bi:LIGG. Initially, M is aligned with Heff. The sudden change in Heff induces a precessional motion of M around the new direction of the effective field. At longer timescales, the magnetization aligns with the effective field.

Source data

Full size image

Figure 3b shows the time-dependent changes in the z component of the magnetization triggered by the magnetic field step, measured in correspondence with the centre of the disc, with the same pump fluence used in Fig. 2b (~0.3 mJ cm–2). As the magnetic field step excited the Bi:LIGG sample, we observed a pronounced, damped oscillation superimposed with a sudden change in magnetization direction. The frequency of the oscillations (~6 GHz) is in good agreement with the ferromagnetic resonance frequency of similar Bi-substituted rare-earth iron garnets46,47.

Figure 3c shows a schematic of the time dependence of the magnetic field applied to the Bi:LIGG. Hstep is the local field generated by the superconducting thin film. At negative time delays, it is antiparallel to the externally applied field Happ due to magnetic flux trapped in the superconductor (Supplementary Section 14). After the quench pulse hits YBa2Cu3O7, it becomes parallel to Happ. HA lies in the plane of the Bi:LIGG film to account for shape anisotropy. Due to a demagnetizing factor close to unity in our geometry48, we set HA equal to the saturation magnetization (~175 kA m–1; see below and Supplementary Section 15). Although Hstep varies in time, the anisotropy field HA is constant. The combination of HA and Hstep gives rise to an effective magnetic field Heff, along which the magnetization points in equilibrium conditions and whose changes determine the magnetization dynamics (note that the angles shown in Fig. 3c,d are exaggerated for clarity).

Figure 3d describes the dynamics of the net magnetization in Bi:LIGG. At negative pump–probe time delays, the system is in equilibrium, and the magnetization is parallel to the effective field Heff. When Hstep suddenly changes after the disruption of superconductivity in YBa2Cu3O7, the magnetization starts precessing around the new direction of Heff. The z component of the magnetization oscillates in time at a frequency given by47,48 ω = γ(Hstep – HA), with γ representing the gyromagnetic ratio. Neglecting Hstep (which is much smaller than the anisotropy field) and taking γ/2π = 28 GHz T–1 (ref. 49), we extract a saturation magnetization of 175 kA m–1 for the measured oscillation frequency of ~6 GHz (Fig. 3b). This value is in good agreement with the literature data46 for similar Bi-substituted rare-earth iron garnets and justifies the assumptions made above. The magnetization rotation achieved is of the order of ~1° (Supplementary Section 15). For comparison, Fig. 3b (solid line) displays the result of a Landau–Lifshitz–Gilbert model calculation of the magnetization dynamics following the ultrafast magnetic field step. We set the saturation magnetization of Bi:LIGG to 175 kA m–1, assume the presence of in-plane shape anisotropy only (as discussed above) and vary the damping constant to match our experimental data (Supplementary Section 15). The results of this calculation are in good agreement with the data shown in the same figure.

Discussion

The disruption of superconductivity in YBa2Cu3O7 discs using ultraviolet laser pulses was used to perturb the magnetic field profile surrounding them and enabled the generation of magnetic field steps with ultrafast rise times and super-nanosecond-long decay times.

As shown in a proof-of-principle experiment, ultrafast magnetic field steps open up a new path towards efficient magnetization control. With the unique properties of our magnetic transient, one could switch the magnetization of a magnetic material with a coercive magnetic field of a millitesla or less. The size of our device, and therefore the region in which the ultrafast magnetic step is applied, is tailorable. For instance, faster rise times could be achieved by reducing the size of the superconducting disc down to the micrometre scale to lower the geometrical inductance of the superconducting disc (Supplementary Section 10).

We also foresee possible applications of our technique as a probing tool for quantum materials. For example, a step function with long decay times represents a suitable tool to study persistent currents in (photoexcited) superconductors. Due to its perfect conductivity, a superconductor responds to a step-like magnetic field excitation by creating superconducting currents shielding the magnetic transience for infinitely long timescales. Because our magnetic field can be switched on at timescales shorter than the lifetime of the transient state, inducing magnetic shielding currents, this time-domain technique could be used to study transient superconductors50,51,52,53,54.

Furthermore, our technique can be applied as a complementary tool to terahertz time-domain spectroscopy to study low-lying excitations in a large variety of quantum materials given its broadband frequency content, ranging from sub-gigahertz to 1 THz (Fig. 4). Because the generated fields are effectively in the near field, our technique may be particularly suitable to study—using a purely magnetic excitation—samples with small lateral dimensions, inaccessible to sub-terahertz radiation. That is, for example, the case of novel two-dimensional (anti)ferromagnetic materials55, which are available only in micrometre-scale sizes. Paired with impulsive stimulated Raman scattering, our technique could be beneficial in exploring new collective modes in these materials by enabling the estimation of the out-of-plane transient magnetization associated with low-energy spin waves.

Fig. 4: A complete set of tools for low-frequency magnetic spectroscopy.
figure 4

a, Experimental data (blue squares) and fit (blue solid line) for a magnetic step generated with our technique and the amplitude of the measured electric field of a single-cycle terahertz pulse44 (red solid line). The two signals are normalized to have the same peak value. b, Fast Fourier transform of the time domain traces in a. The experimental data relative to the magnetic step (blue squares) are shown up to 0.3 THz—above which the signal falls below the noise threshold.

Source data

Full size image

Finally, we also envision how the amplitude of these magnetic field steps could be made larger using ultrafast demagnetization in ferromagnetic materials56 or by quenching superconductivity in a superconductor with higher purity and first critical field. Such improvements would pave the way towards a universal tool for magnetization control.

Methods

All methods can be found in the Supplementary Information.