Main

Low-threshold laser sources realized in ultracompact cavities enabled by extremely tight mode confinement, exhibiting energy-efficient and monolithic integrated characteristics, are highly desired in modern optoelectronic applications, such as on-chip communication1, biological sensing2 and quantum information3,4. Photonic bound states in the continuum (BIC) are peculiar non-radiative localized modes that theoretically have infinite lifetime within the radiation continuum5,6,7,8, rendering them favourable candidates for pursuing single-mode, low-threshold and surface-emitting lasers9,10,11,12,13,14,15. In large-scale photonic cavities, the symmetry-protected BIC mode resides at the centre of the Brillouin zone (Γ point), making it also function as a traditional band edge mode16,17 with a small group velocity that can simultaneously provide exceptional in-plane and out-of-plane field localization. However, in miniaturized devices, the continuous photonic band splits into a series of discrete modes due to momentum-space quantization18. Furthermore, the fundamental mode deviates from the Γ point, resulting in the degeneration of its non-radiative and dispersionless feature. Consequently, both group index and quality (Q) factor suffer notable reductions, accompanied by particularly increased side leakages and radiation losses (Fig. 1a).

Fig. 1: Principle of construction of the compact flat-band multi-BIC laser.
figure 1

a, Comparison of group indices and Q factors between cavity modes in a normal BIC device with infinite and finite sizes (top). The continuous band (grey curve) in an infinite-sized cavity transforms into a series of discrete modes (black dots) in a finite-sized cavity, with the corresponding group indices (red dots) and Q factors (blue dots) deviating from the values at the Γ point. Here the group index ng = c/vg, where vg = dωk/dk (v, group velocity; ω, angular frequency; k, wave vector), can reflect the in-plane feedback and localization capabilities in a photonic-crystal slab. A higher group index means a stronger in-plane feedback and localization. For a normal BIC mode in a finite-sized device, substantial radiation losses, scattering losses and side leakages exist in the cavity (bottom). b, Three-dimensional photonic band diagram of the hexagonal supercell in d with a flat-band BIC design (top). The side leakages can be well suppressed in this case enabled by the flat-band design (bottom). Inset: a schematic of the polarization singularity of the flat band with a topological charge of q = +2 at the Γ point. kx and ky represent the in-plane components of the wave vector along the x and y directions in the Brillouin zone, respectively. c, Schematic of the flat-band multi-BIC design in momentum space. The plus and minus signs represent a topological charge of +1 and −1, respectively. Both radiation and side-leakage losses are well suppressed when a multi-BIC is introduced into the flat-band cavity (bottom). d, A typical double-metal QCL configuration is used here. The air-hole photonic-crystal structure is constructed by drilling through the top Au/QCL layers. The top and bottom Au layers act as electrodes for current injection, as well as vertical confinement of the cavity mode. f, frequency.

Full size image

A straightforward and commonly used approach to mitigate side leakages is to introduce photonic-heterostructure confinement, such as the implementation of topological band inversion19,20 or photonic-bandgap boundaries21,22. However, the symmetry-mismatch-induced mode confinement in these typical designs occurs only around the band edge. The Q factor still faces substantial compromise when a finite-sized cavity is constructed with its mode deviating from the Γ point. Furthermore, the imposition of external boundaries inevitably introduces mode scatterings and increases the overall cavity footprint23,24,25,26.

In this work, we report a highly compact cavity design based on a flat band combined with multiple bound states above the light cone, denoted as ‘flat-band multi-BIC’ below. By localizing the photonic state in the in-plane (out-of-plane) directions by using the flat-band (multi-BIC) feature (Fig. 1b,c), a high Q factor of ~1,440 (considered as high Q in the platform of terahertz quantum cascade lasers (QCLs)27,28,29) in an ultracompact photonic cavity (side length, L = 5a; Fig. 1d) can be achieved. This value exceeds the normal BIC modes by approximately 40-fold and is also significantly higher than other optimized cavity designs (Supplementary Table 1). Experimentally, we demonstrate a high-performance terahertz laser exhibiting stable single-mode operation with a side-mode suppression ratio (SMSR) of ~20 dB and an ultralow lasing threshold of ~0.19 kA cm–2. In particular, the lateral dimension of the cavity is just ~3λ, rendering it one of the most compact devices within the realm of photonic-crystal-based lasers9,19,28. Moreover, benefiting from the favourable mode selectivity associated with the Dirac-cone-like photonic band feature, the device exhibits scalability without compromising on its excellent single-mode performance.

Results

Design of a flat-band multi-BIC cavity

Our laser cavity design is constructed by etching periodic air holes through the active medium of a three-well resonant-phonon GaAs/Al0.15Ga0.85As designed terahertz QCL wafer to form a triangular photonic-lattice structure (Fig. 1d and Supplementary Figs. 1 and 2). The air holes feature a daisy-like shape, which facilitates the manipulation of the photonic band structure30,31. The shape can be written as r(ϕ) = r0 – rdcos(6ϕ). By forcing an accidental degeneracy between the isolated B mode and the doubly degenerated E1 and E2 modes (Supplementary Fig. 3), a distinct flat band intersecting with two linear dispersion bands (Dirac cone) at their apex can be achieved (Fig. 1b). The slow light effect, arising from the dispersionless nature of the flat band, provides excellent in-plane field confinement and considerably reduces side-leakage losses, even as the mode shifts away from the Γ point in finite-sized cavities. All three selected bands belong to different irreducible representations at the Γ point (B, E1 and E2) and decoupled from free space30, that is, typical symmetry-protected BIC modes32, which effectively mitigate radiation losses that may occur due to mode coupling when they come into proximity to each other33 (Supplementary Figs. 4 and 5). These non-radiative modes (with a theoretically infinite Q factor) are characterized by a polarization singularity (for example, the flat band) at the centre of the Brillouin zone. By tuning the lattice parameters, we further engineer a series of accidental BICs around the Γ point, giving rise to a unique feature denoted as ‘multi-BIC’ (Fig. 1c). The multi-BIC with a broad, high-Q region enable the cavity mode to stand robust against photonic finite-size effects, systematic disorders and structural imperfection, significantly suppressing radiation and scattering losses34,35,36,37,38.

Flat-band-enhanced in-plane mode confinement

We emphasize the advantages of the flat-band BIC mode (E1 mode; Fig. 2a (top)) by comparing it with the conventional BIC, that is, the B′ mode with C6v symmetry at the bottom of Fig. 2a (referred to as the ‘normal C6v-BIC’ hereafter). The full band structures and electric-field distributions within a unit cell for these photonic lattices are shown in Supplementary Fig. 6. As illustrated, the E1-irreducible photonic mode displays a remarkable flat-band feature in the entire region above the light cone, whereas the B′ mode features a quadratic band dispersion. To investigate their disparities on mode localization within a miniaturized photonic cavity (L = 5a), we calculated the fundamental modes of these two bands with distinct dispersion behaviours (Fig. 2b). Our simulations (Methods) are modelled strictly according to the actual device structure with a finite size, incorporating a typical absorption boundary (the outer unpatterned region), which also serves as wire bonding for pumping current injection39. The electric field (|Ez|) associated with the E1 mode is tightly confined to the centre of the cavity, in stark contrast to the B′ mode, which substantially leaks out of the patterned region, forming a near-plane wavefront away from the interfaces. The effective in-plane field confinement in the flat-band cavity arises from the ultralow group velocity with enhanced mode feedback. Figure 2c illustrates the group indices for bands featuring different dispersion characteristics. In particular, the group index of the E1 band exceeds that of the B′ band by approximately ten times as they deviate from the Γ point. Both cases exhibit negligible mode extension above the photonic-crystal slab, attributed to the non-radiative nature of the BICs. Further simulations based on a normal BIC in commonly used C4v-symmetric lattice structure are also performed (Supplementary Fig. 7). The consistent results collectively support the conclusion that a flat band with minimal dispersion indeed ensures effective in-plane confinement in miniaturized cavities.

Fig. 2: Comparison between the flat-band BIC mode and other normal BIC modes.
figure 2

a, Calculated band diagrams of the daisy-like air-hole photonic crystal with flat-band BIC (top) and conventional circular air-hole structure with normal C6v-BIC. b, Near-field profiles in finite-sized cavities (L = 5a) corresponding to the fundamental mode of the E1 band (top; flat-band) and B′ band (bottom) in the corresponding data in a. c, Group indices for the representative modes computed from the corresponding Bloch-band structures. d,e, Near-field profiles of the fundamental modes belong to the two adjacent bands (B (d) and E2 (e) bands) with linear dispersion, for the cavity with L = 13a (top). Bottom, extracted electric-field intensity along the dashed line within the cavities. f, Calculated Q factors of the B, E1 and E2 modes with distinct band dispersion features, treating the pumped region as a lossless dielectric with absorbing boundaries (Methods). Here a flat-band BIC cavity with lattice parameters of a = 37.2 μm and r0 = 14.5 μm is adopted to exclude the influence of the multi-BIC, which will be discussed later in Fig. 3.

Source data

Full size image

We also observed that the B and E2 bands, characterized by linear dispersion, exhibit an exceedingly low group index of ~5.2 near the Γ point, which suggests weak in-plane feedback and a limited localization effect. Direct examination of the effective index (Supplementary Fig. 8) based on the band structure reveals a characteristic ‘zero-index’ behaviour30,40,41. These effective zero-index structures are renowned for their lossless propagating nature and the flat-envelop field distribution in previous research33. To provide a more intuitive understanding of the electric-field distribution arising from this distinctive dispersion behaviour, we examined the fundamental modes within a larger cavity (L = 13a) than that (L = 5a) used in Fig. 2b. The results reveal that the electric fields associated with the B and E2 modes exhibit uniform distributions and extend beyond the cavity boundary (Fig. 2d,e and Supplementary Fig. 9). The substantial side-leakage losses lead to significantly lower Q factors of approximately ~39 and ~51, respectively (Fig. 2f). By contrast, these two bands in the normal C6v-BIC cavity featuring quadratic band dispersion exhibit typical Gaussian-shaped field distributions, with the modes tightly confined within the cavity core, resulting in much higher (approximately 15-fold) Q factors (Supplementary Fig. 10). It is worth noting that the substantial side leakages of the neighbouring B and E2 modes significantly enhance the mode selectivity (notable Q contrast) between these two modes and the flat-band mode (E1 mode, with a Q factor of approximately ~2,840), facilitating the attainment of stable single-mode flat-band lasers, despite the fact that they are also non-radiative BIC modes. The exceptional mode selectivity afforded by the Dirac-cone-like band design exhibits notable robustness against fabrication errors (Supplementary Fig. 11).

Multi-BIC-enabled Q-factor enhancement

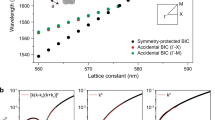
We emphasize the significance of multi-BIC in the pursuit of ultracompact lasers. Normally, two main issues introduce additional radiation losses in a finite-sized BIC cavity. First, the splitting of the modes into discrete points away from the Γ point is due to band quantization, where the Q factor is dramatically decreased18. Second, the mixing of the BIC mode with off-Γ low-Q modes because of the out-of-plane scattering losses arise from fabrication imperfections and lattice disorders34,35. Regarding these issues, we constructed a series of accidental BICs around the Γ point (Fig. 3a and Supplementary Fig. 12). We performed Q-factor calculations for flat-band cavities with and without the multi-BIC feature. To control the variables, both cavities share basically identical band features and group indices (Supplementary Fig. 13). The only distinction lies in the intentional construction of unremarkable points featuring divergent Q factors at k = ±0.36(2π/√3/a) accompanied by a larger polarization singularity core within the flat-band multi-BIC cavity. These modifications establish a broad high-Q region in the Brillouin zone (Fig. 3b), endowing the cavity with greater tolerance to systematic disorders (Supplementary Fig. 14), structural imperfections (Supplementary Fig. 15) and photonic finite-sized layouts. As a result, the Q factors of the flat-band multi-BIC cavities exhibit remarkable enhancement. Taking the example of a cavity with a side length of L = 5a, the Q factor can be as high as ~1,440 (considering absorption losses in unpatterned regions, see Methods). By contrast, the Q factor for the flat-band cavity without the multi-BIC and the ‘normal C6v-BIC cavity’ (B′ mode) only reach values of ~368 and ~37, respectively, and are submerged within the bulk modes (Fig. 3c). It should be noticed that the Q factor of the flat-band cavity without the multi-BIC remains approximately ten times higher than that of the normal BIC mode (B′), benefiting from the enhanced group index, despite the fact that all of them possess theoretically infinite Q values in an infinitely large cavity. We highlight that our flat-band multi-BIC design also outperforms previously optimized cavity designs based on the same double-metal QCL configuration (Supplementary Table 1).

Fig. 3: Q factors of the BIC modes with and without the flat-band multi-BIC design.
figure 3

a, Two-dimensional map of the Q-factor and polarization distributions of the flat-band with multi-BIC states in momentum space. The colour map represents the Q factor and the white dashed line represents the polarization vector. The topological charge was determined to be q = +2 by selecting a circle centred around the Γ point with |k| = 0.1(2π/√3/a) (Methods). b, Q-factor comparison of the flat-band cavities with and without the multi-BIC. The simulations here are conducted with periodic boundary conditions along the x–y axis (that is, infinite cavity sizes). c, Calculated Q factors for the fundamental mode of the flat-band cavities with and without the multi-BIC, along with the cavity with normal C6v-BIC. Here the calculations are based on realistic cavity structures with finite sizes, incorporating a double-metal device configuration with the consideration of the corresponding cavity losses. The solid lines are guides for the eyes.

Source data

Full size image

Measurements of flat-band multi-BIC lasers

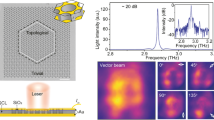
Benefiting from the exceptional in-plane and out-of-plane field confinements offered by the flat-band multi-BIC mode as discussed, we successfully fabricated compact QCL devices with high performance. As presented in Fig. 4a,b, the lateral size of the L = 5a cavity is just 294 μm (~3λ), with the daisy-like air-hole patterns imprinted onto the QCL slab. The surrounding absorption boundary (unpatterned) is experimentally realized by inserting a thin SiO2 insulation layer between the metal and QCL medium layers (Supplementary Fig. 2). The laser was characterized by using a customized setup (Methods). The light–current–voltage (L–I–V) curves (Fig. 4c) demonstrate a distinct lasing threshold of approximately 0.19 kA cm–2, attributed to the enhanced Q factor that stems from the collective effect of the flat band with a high group index and the multi-BIC with a broad high-Q region. The ultracompact device footprint as well as the low lasing threshold leads to a small pumping current (Supplementary Fig. 17), which is essential for pursuing low-power-consumption, low-thermal-generation THz QCLs. Moreover, distinct single-mode lasing emission can be identified across the entire dynamic range (Fig. 4d,e). The single-mode performance is evaluated by calculating the SMSR of the device at a pumping current density of 0.27 kA cm–2, where the SMSR can reach up to ~20 dB (Fig. 4f). It is worth highlighting that, to the best of our knowledge, this flat-band multi-BIC QCL represents the most compact single-mode photonic-crystal laser. Additionally, the substantial group-index contrast between the E1 band and the adjacent B (E2) band effectively increases the imaginary free spectral range, thereby facilitating single-mode operation in larger cavities. We conducted full-wave simulations to assess the mode distribution and Q factor for cavities with side lengths of L = 9a and L = 17a. In both cases, the electric fields are tightly confined within the cavities with Q factors of approximately 1.0 × 104 and 5.7 × 104, respectively (Supplementary Fig. 18). Experimentally, stable single-mode lasing emission is maintained when continuously increasing the pumping current densities (Fig. 4h,k), with a measured SMSR of ~23 dB and ~25 dB, respectively (Fig. 4i,l).

Fig. 4: Experimental demonstration of the flat-band multi-BIC lasers.
figure 4

a, Zoomed-in scanning electron microscopy image of the daisy-like air-hole photonic cavity. b, Scanning electron microscopy image of the fully fabricated laser device, incorporating the cavity structure displayed in a. c, L–I–V curves of the fabricated lasers. d, Laser spectra of the L = 5a device at various pumping current densities. e, Two-dimensional spectral mapping of the L = 5a laser as a function of the frequency and pumping current density. f, Laser spectrum of the L = 5a device at 0.27 kA cm–2 with a measured SMSR of ~20 dB. g–i, Scanning electron microscopy image (g), two-dimensional spectral mapping (h) and SMSR calculation (i) of the L = 9a device. j–l, Scanning electron microscopy image (j), two-dimensional spectral mapping (k) and SMSR calculation (l) of the L = 17a device.

Source data

Full size image

The far-field pattern of the designed flat-band multi-BIC laser was collected using a customized intensity scanner equipped with a THz Golay cell detector. Due to the sensitivity limitations of the detector, the L = 9a device with a peak power of 1.02 mW was characterized here (Supplementary Fig. 19). Numerical calculations indicate that the cavity mode features a cylindrical vector beam profile with good directionality and a doughnut-shaped far-field pattern (Supplementary Fig. 20a). The experimentally obtained near-C6-symmetric intensity profiles (Supplementary Fig. 20b,c) are in good agreement with the simulation results, and the beam divergence is approximately 15°.

We also fabricated control devices using an optimized photonic-bandgap-confined ‘normal C4v-BIC’ design (B″ mode) based on the same QCL wafer (Supplementary Fig. 22a–f). In particular, the observed Q factor is significantly lower (~265) than the flat-band multi-BIC mode, resulting in an enhanced lasing threshold of ~0.28 kA cm–2, despite the fact that the overall side length is larger (~5λ). Moreover, the device based on the ‘normal C4v-BIC’ design, without any optimization, can only operate with multiple modes (Supplementary Fig. 22g–i). Therefore, we emphasize that the multi-BIC-assisted flat-band cavity undoubtedly provides threshold reduction and well-preserved single-mode performance, which is not limited to THz QCLs but can be extended to any other photonic-cavity-based laser devices.

Discussion

We propose and demonstrate a designed flat-band multi-BIC cavity that can effectively suppress side-leakage and radiation losses originating from finite-size effects, as well as the out-of-plane scattering due to fabrication imperfections. The remarkable electric-field confinement leads to a highly compact (~3λ) electrical pumping QCL device with an ultralow lasing threshold (~0.19 kA cm–2) and excellent single-mode performance (~20 dB). Considering the fact that the laser cavity solely relies on dielectric-constant modulations, our design is readily extended to other wavelength regimes, for example, the near-infrared and visible regions. Our work represents an effective approach in pursuing energy-efficient and monolithically integrated ultracompact laser sources with low laser thresholds, which are highly desired for on-chip applications in advanced optoelectronics and integrated photonics. Our design is not limited to laser applications but can also be extended to other realms such as sensing, modulation and harmonic-signal generation.

Methods

Numerical calculation

A commercial finite-element solver, COMSOL Multiphysics 6.0, was used to perform the simulations in this work. The photonic cavity consists of a hexagonal lattice of daisy-like shaped holes drilled through the 18.3-μm-thick active medium of a THz QCL wafer. The three-dimensional band structures, eigenmodes and Q factors of the photonic-crystal structures were calculated using the ‘eigenfrequency’ module in the frequency domain with the periodic condition imposed in the x–y plane. The QCL active layer was modelled as a lossless dielectric with a refractive index of 3.6; the top and bottom boundaries of the dielectric medium were set as perfect electric conductor layers to extract the transverse-magnetic mode. For the full-structure simulations with a finite cavity size, scattering boundary conditions were used to make a boundary transparent and avoid back-reflection for the outgoing waves. Furthermore, the surrounding unpumped region was realized by setting an imaginary refractive index of 0.016 (corresponding to an absorption loss of ~20 cm−1) in the simulations39.

The topological charges (q) of the symmetry-protected BIC mode (Fig. 3a) is calculated to be +2. As determined by the winding number of the polarization vectors,

$$q=\frac{1}{2\uppi }{\oint }_{C}{\rm{d}}{\bf{k}}{\rm{\cdot }}{\nabla }_{{\bf{k}}}\phi \left({\bf{k}}\right),$$

where C is the closed path with a counterclockwise direction surrounding a BIC. ϕ(k) = arg[cx(k) + icy(k)] represents the polarization angle at each k, and cx and cy are the coefficients of far-field radiation with electric fields along the x and y directions, respectively.

Device fabrication

The flat-band multi-BIC lasers were designed on a broadband three-well resonant-phonon GaAs/Al0.15Ga0.85As THz QCL wafer with a metal–semiconductor–metal device configuration. The thickness of the QCL active region was measured to be around 18.3 μm. The calculated gain bandwidth of the wafer is around 2.8–3.3 THz, with a refractive index of n ≈ 3.6.

The details of the laser fabrication are provided in Supplementary Fig. 2.

Device characterization

The fabricated devices were placed in a helium-gap-steam cryostat system with a temperature of ~8.6 K. For the spectral measurements, the lasers were pumped by an electrical pulse generator (repetition rate, 10 kHz; pulse width, 500 ns). The laser spectra were collected using a Bruker Vertex 80 Fourier-transform infrared spectrometer with a room-temperature deuterated triglycine sulfate detector. The spectral resolution is 0.08 cm−1. The far-field image was obtained by collecting the beam intensity with a THz Golay cell detector (TYDEX GC-1T). The Golay cell was mounted on a mechanical arm with a scan step of 1 mm. The detector was approximately 5 cm away from the QCL devices and has an aperture diameter of ~5 mm.