Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Noise-immune quantum correlations of intense light

Nature Photonics volume 19, pages 751–757 (2025)Cite this article

Subjects

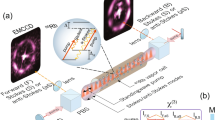
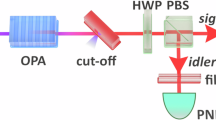
Abstract

Lasers with high intensity generally exhibit strong intensity fluctuations far above the shot-noise level. Taming this noise is pivotal to a wide range of applications, both classical and quantum. Here we demonstrate the creation of intense light with quantum levels of noise even when starting from inputs with large amounts of excess noise. In particular, we demonstrate how intense squeezed light with intensities approaching 0.1 TW cm−2, but noise at or below the shot-noise level, can be produced from noisy inputs associated with high-power amplified laser sources (an overall noise reduction of 30-fold). On the basis of a new theory of quantum noise in multimode systems, we show that the ability to generate quantum light from noisy inputs results from multimode quantum correlations, which maximally decouple the output light from the dominant noise channels in the input light. As an example, we demonstrate this effect for femtosecond pulses in nonlinear fibres, but the noise-immune correlations that enable our results are generic to many other nonlinear systems in optics and beyond.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: High-intensity sources of light with quantum levels of noise.
Fig. 2: Generating intense squeezed light from noisy amplified sources.
Fig. 3: Noise statistics of nonlinear filtering.
Fig. 4: Noise immunity owing to multimode quantum correlations.
Fig. 5: Noise immunity for pairs of colours induced by quantum correlations.

Similar content being viewed by others

Data availability

The data used to generate the plots in Figs. 2, 3 and 5 are available via figshare at https://doi.org/10.6084/m9.figshare.28664672. All data that support the other findings of this study are available from the corresponding author upon reasonable request. Source data are provided with this paper.

Code availability

The scripts used to implement the model used in this study are available from the corresponding author upon reasonable request.

References

  1. The LIGO Scientific Collaboration. A gravitational wave observatory operating beyond the quantum shot-noise limit. Nat. Phys. 7, 962–965 (2011).

  2. Taylor, M. A. et al. Biological measurement beyond the quantum limit. Nat. Photon. 7, 229–233 (2013).

    Article  ADS  Google Scholar 

  3. Casacio, C. A. et al. Quantum-enhanced nonlinear microscopy. Nature 594, 201–206 (2021).

    Article  ADS  Google Scholar 

  4. Kaufman, A. M. & Ni, K.-K. Quantum science with optical tweezer arrays of ultracold atoms and molecules. Nat. Phys. 17, 1324–1333 (2021).

    Article  Google Scholar 

  5. Rao DS, S. et al. Shot-noise limited, supercontinuum-based optical coherence tomography. Light Sci. Appl. 10, 133 (2021).

    Article  ADS  Google Scholar 

  6. Mourou, G. A., Tajima, T. & Bulanov, S. V. Optics in the relativistic regime. Rev. Mod. Phys. 78, 309 (2006).

    Article  ADS  Google Scholar 

  7. Loudon, R. The Quantum Theory of Light (Oxford Univ. Press, 2000).

  8. Caves, C. M. Quantum limits on noise in linear amplifiers. Phys. Rev. D 26, 1817 (1982).

    Article  ADS  Google Scholar 

  9. Haus, H. A. Electromagnetic Noise and Quantum Optical Measurements (Springer, 2000).

  10. Bachor, Hans-A & Ralph, T. C. A Guide to Experiments in Quantum Optics (Wiley, 2019).

  11. Slusher, R. E., Hollberg, L. W., Yurke, B., Mertz, J. C. & Valley, J. F. Observation of squeezed states generated by four-wave mixing in an optical cavity. Phys. Rev. Lett. 55, 2409 (1985).

    Article  ADS  Google Scholar 

  12. Bergman, K. & Haus, H. A. Squeezing in fibers with optical pulses. Opt. Lett. 16, 663–665 (1991).

    Article  ADS  Google Scholar 

  13. Andersen, U. L., Gehring, T., Marquardt, C. & Leuchs, G. 30 years of squeezed light generation. Phys. Scr. 91, 053001 (2016).

    Article  ADS  Google Scholar 

  14. Spasibko, K. Y. et al. Multiphoton effects enhanced due to ultrafast photon-number fluctuations. Phys. Rev. Lett. 119, 223603 (2017).

    Article  ADS  Google Scholar 

  15. Heimerl, J. et al. Multiphoton electron emission with non-classical light. Nat. Phys. 20, 945–950 (2024).

    Article  Google Scholar 

  16. Gorlach, A. et al. High-harmonic generation driven by quantum light. Nat. Phys. 19, 1689–1696 (2023).

    Article  Google Scholar 

  17. Mitrano, M. et al. Possible light-induced superconductivity in K3C60 at high temperature. Nature 530, 461–464 (2016).

    Article  ADS  Google Scholar 

  18. Kennes, D. M., Wilner, E. Y., Reichman, D. R. & Millis, A. J. Transient superconductivity from electronic squeezing of optically pumped phonons. Nat. Phys. 13, 479–483 (2017).

    Article  Google Scholar 

  19. Garrett, G. A., Rojo, A. G., Sood, A. K., Whitaker, J. F. & Merlin, R. Vacuum squeezing of solids: macroscopic quantum states driven by light pulses. Science 275, 1638–1640 (1997).

    Article  Google Scholar 

  20. Cartella, A., Nova, T. F., Fechner, M., Merlin, R. & Cavalleri, A. Parametric amplification of optical phonons. Proc. Natl Acad. Sci. USA 115, 12148–12151 (2018).

    Article  ADS  Google Scholar 

  21. Friberg, S. R., Machida, S., Werner, M. J., Levanon, A. & Mukai, T. Observation of optical soliton photon-number squeezing. Phys. Rev. Lett. 77, 3775 (1996).

    Article  ADS  Google Scholar 

  22. Hirosawa, K. et al. Photon number squeezing of ultrabroadband laser pulses generated by microstructure fibers. Phys. Rev. Lett. 94, 203601 (2005).

    Article  ADS  Google Scholar 

  23. Rosenbluh, M. & Shelby, R. M. Squeezed optical solitons. Phys. Rev. Lett. 66, 153 (1991).

    Article  ADS  Google Scholar 

  24. Yamamoto, Y., Machida, S. & Richardson, W. H. Photon number squeezed states in semiconductor lasers. Science 255, 1219–1224 (1992).

    Article  ADS  Google Scholar 

  25. Sizmann, A. & Leuchs, G. V the optical Kerr effect and quantum optics in fibers. Prog. Opt. 39, 373–469 (1999).

    Article  ADS  MathSciNet  Google Scholar 

  26. Lumer, Y., Plotnik, Y., Rechtsman, M. C. & Segev, M. Self-localized states in photonic topological insulators. Phys. Rev. Lett. 111, 243905 (2013).

    Article  ADS  Google Scholar 

  27. Mukherjee, S. & Rechtsman, M. C. Observation of Floquet solitons in a topological bandgap. Science 368, 856–859 (2020).

    Article  ADS  Google Scholar 

  28. Fermann, M. E., Kruglov, V. I., Thomsen, B. C., Dudley, J. M. & Harvey, J. D. Self-similar propagation and amplification of parabolic pulses in optical fibers. Phys. Rev. Lett. 84, 6010 (2000).

    Article  ADS  Google Scholar 

  29. Dudley, J. M., Finot, C., Richardson, D. J. & Millot, G. Self-similarity in ultrafast nonlinear optics. Nat. Phys. 3, 597–603 (2007).

    Article  Google Scholar 

  30. Wright, L. G., Christodoulides, D. N. & Wise, F. W. Spatiotemporal mode-locking in multimode fiber lasers. Science 358, 94–97 (2017).

    Article  ADS  Google Scholar 

  31. Wu, F. O., Hassan, A. U. & Christodoulides, D. N. Thermodynamic theory of highly multimoded nonlinear optical systems. Nat. Photon. 13, 776–782 (2019).

    Article  ADS  Google Scholar 

  32. Wright, L. G., Wu, F. O., Christodoulides, D. N. & Wise, F. W. Physics of highly multimode nonlinear optical systems. Nat. Phys. 18, 1018–1030 (2022).

    Article  Google Scholar 

  33. Pourbeyram, H. et al. Direct observations of thermalization to a Rayleigh–Jeans distribution in multimode optical fibres. Nat. Phys. 18, 685–690 (2022).

    Article  Google Scholar 

  34. McMahon, P. L. et al. A fully programmable 100-spin coherent Ising machine with all-to-all connections. Science 354, 614–617 (2016).

    Article  ADS  MathSciNet  Google Scholar 

  35. Leefmans, C. et al. Topological dissipation in a time-multiplexed photonic resonator network. Nat. Phys. 18, 442–449 (2022).

    Article  Google Scholar 

  36. Roques-Carmes, C. et al. Biasing the quantum vacuum to control macroscopic probability distributions. Science 381, 205–209 (2023).

    Article  ADS  Google Scholar 

  37. Nehra, R. et al. Few-cycle vacuum squeezing in nanophotonics. Science 377, 1333–1337 (2022).

    Article  ADS  Google Scholar 

  38. Guidry, M. A., Lukin, D. M., Yang, K. Y. & Vučković, J. Multimode squeezing in soliton crystal microcombs. Optica 10, 694–701 (2023).

    Article  ADS  Google Scholar 

  39. Ng, E., Yanagimoto, R., Jankowski, M., Fejer, M. M. & Mabuchi, H. Quantum noise dynamics in nonlinear pulse propagation. Preprint at https://arxiv.org/abs/2307.05464 (2023).

  40. Rivera, N., Sloan, J., Salamin, Y., Joannopoulos, J. D. & Soljačić, M. Creating large Fock states and massively squeezed states in optics using systems with nonlinear bound states in the continuum. Proc. Natl Acad. Sci. USA 120, e2219208120 (2023).

    Article  MathSciNet  Google Scholar 

  41. Sloan, J., Rivera, N. & Soljačić, M. Driven-dissipative phases and dynamics in non-Markovian nonlinear photonics. Optica 11, 1437–1444 (2024).

    Article  Google Scholar 

  42. Lahini, Y. et al. Anderson localization and nonlinearity in one-dimensional disordered photonic lattices. Phys. Rev. Lett. 100, 013906 (2008).

    Article  ADS  Google Scholar 

  43. Lib, O. & Bromberg, Y. Quantum light in complex media and its applications. Nat. Phys. 18, 986–993 (2022).

    Article  Google Scholar 

  44. Kippenberg, T. J., Gaeta, A. L., Lipson, M. & Gorodetsky, M. L. Dissipative Kerr solitons in optical microresonators. Science 361, eaan8083 (2018).

    Article  Google Scholar 

  45. Guidry, M. A., Lukin, D. M., Yang, K. Y., Trivedi, R. & Vučković, J. Quantum optics of soliton microcombs. Nat. Photon. 16, 52–58 (2022).

    Article  ADS  Google Scholar 

  46. Kues, M. et al. Quantum optical microcombs. Nat. Photon. 13, 170–179 (2019).

    Article  ADS  Google Scholar 

  47. Konotop, V. V., Yang, J. & Zezyulin, D. A. Nonlinear waves in PT-symmetric systems. Rev. Mod. Phys. 88, 035002 (2016).

    Article  ADS  Google Scholar 

  48. Harari, G. et al. Topological insulator laser: theory. Science 359, eaar4003 (2018).

    Article  Google Scholar 

  49. Bandres, M. A. et al. Topological insulator laser: experiments. Science 359, eaar4005 (2018).

    Article  Google Scholar 

  50. Jürgensen, M., Mukherjee, S. & Rechtsman, M. C. Quantized nonlinear Thouless pumping. Nature 596, 63–67 (2021).

    Article  ADS  Google Scholar 

  51. Gorlach, A., Neufeld, O., Rivera, N., Cohen, O. & Kaminer, I. The quantum-optical nature of high harmonic generation. Nat. Commun. 11, 4598 (2020).

    Article  ADS  Google Scholar 

  52. Lewenstein, M. et al. Generation of optical Schrödinger cat states in intense laser–matter interactions. Nat. Phys. 17, 1104–1108 (2021).

    Article  Google Scholar 

Download references

Acknowledgements

We acknowledge useful discussions with E. Ippen, L. Wright, R. Yanagimoto, T. Onodera and F. Wise. N.R. acknowledges the support of a Junior Fellowship from the Harvard Society of Fellows as well as funding from the School of Applied and Engineering Physics at Cornell University. Y.S. acknowledges the support from the Swiss National Science Foundation (SNSF) through the Early Postdoc Mobility Fellowship number P2EZP2-188091. J.S. acknowledges the previous support of a Mathworks Fellowship, as well as previous support from a National Defense Science and Engineering Graduate (NDSEG) Fellowship (F-1730184536). This material is based on work also supported in part by the US Army Research Office through the Institute for Soldier Nanotechnologies at MIT, under Collaborative Agreement Number W911NF-23-2-0121. We also acknowledge the support of P. Tayebati. This publication was also supported in part by the DARPA Agreement number HO0011249049.

Author information

Author notes

  1. These authors contributed equally: Shiekh Zia Uddin, Nicholas Rivera.

Authors and Affiliations

  1. Department of Physics, Massachusetts Institute of Technology, Cambridge, MA, USA

    Shiekh Zia Uddin, Nicholas Rivera, Yannick Salamin & Marin Soljačić

  2. Research Laboratory of Electronics, Massachusetts Institute of Technology, Cambridge, MA, USA

    Shiekh Zia Uddin, Devin Seyler, Jamison Sloan, Yannick Salamin, Charles Roques-Carmes & Marin Soljačić

  3. Department of Physics, Harvard University, Cambridge, MA, USA

    Nicholas Rivera

  4. School of Applied and Engineering Physics, Cornell University, Ithaca, NY, USA

    Nicholas Rivera

  5. CREOL, The College of Optics and Photonics, University of Central Florida, Orlando, FL, USA

    Yannick Salamin

  6. E. L. Ginzton Laboratory, Stanford University, Stanford, CA, USA

    Charles Roques-Carmes

  7. Department of Electrical and Computer Engineering and BU Photonics Center, Boston University, Boston, MA, USA

    Shutao Xu & Michelle Y. Sander

  8. Division of Materials Science and Engineering, Boston University, Brookline, MA, USA

    Michelle Y. Sander

  9. Department of Biomedical Engineering, Boston University, Boston, MA, USA

    Michelle Y. Sander

  10. Department of Electrical and Computer Engineering, Technion-Israel Institute of Technology, Haifa, Israel

    Ido Kaminer

Authors
  1. Shiekh Zia Uddin
    View author publications

    Search author on:PubMed Google Scholar

  2. Nicholas Rivera
    View author publications

    Search author on:PubMed Google Scholar

  3. Devin Seyler
    View author publications

    Search author on:PubMed Google Scholar

  4. Jamison Sloan
    View author publications

    Search author on:PubMed Google Scholar

  5. Yannick Salamin
    View author publications

    Search author on:PubMed Google Scholar

  6. Charles Roques-Carmes
    View author publications

    Search author on:PubMed Google Scholar

  7. Shutao Xu
    View author publications

    Search author on:PubMed Google Scholar

  8. Michelle Y. Sander
    View author publications

    Search author on:PubMed Google Scholar

  9. Ido Kaminer
    View author publications

    Search author on:PubMed Google Scholar

  10. Marin Soljačić
    View author publications

    Search author on:PubMed Google Scholar

Contributions

N.R. developed the theoretical framework and models used to analyse the data, with contributions from S.Z.U. and J.S. N.R. and S.Z.U. analysed the data. S.Z.U. led the construction of the experimental set-up and the data collection with contributions from D.S., Y.S., J.S., S.X. and N.R. The concept of noise immunity was conceived by N.R. and developed in discussions with S.Z.U., I.K. and M.S. The paper was written by N.R. with input from S.Z.U., D.S., J.S., Y.S., S.X., C.R.-C., M.Y.S., I.K. and M.S. All authors contributed to the reading and revision of the paper.

Corresponding author

Correspondence to Nicholas Rivera.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Photonics thanks the anonymous reviewers for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Figs. 1–5 and Discussion Sections 1–3.

Source data

Source Data Fig. 2

Contains workbook with csv files for all x and y data for all lines and scatter plots in the figure representing measured or computed data.

Source Data Fig. 3

Contains workbook with csv files for all x and y data for all lines and scatter plots in the figure representing measured or computed data. Also contains colour data for relevant colour maps.

Source Data Fig. 5

Contains workbook with csv files for all x and y data for all lines and scatter plots in the figure representing measured or computed data. Also contains colour data for relevant colour maps.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zia Uddin, S., Rivera, N., Seyler, D. et al. Noise-immune quantum correlations of intense light. Nat. Photon. 19, 751–757 (2025). https://doi.org/10.1038/s41566-025-01677-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41566-025-01677-2

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing