Abstract
Compact photonic systems that offer high frequency stability and low noise are of increasing importance to applications in precision metrology, quantum computing, communication and advanced sensing technologies. However, on-chip resonators comprising dielectrics cannot match the frequency stability and noise characteristics of Fabry–Pérot cavities, whose electromagnetic modes live almost entirely in vacuum. Here we present a novel strategy to interface microfabricated Fabry–Pérot cavities with photonic integrated circuits to realize compact, high-performance integrated systems. Using this new integration approach, we demonstrate the self-injection locking of an on-chip laser to a millimetre-scale vacuum-gap Fabry–Pérot cavity using a circuit interface that transforms the reflected cavity response to enable efficient feedback to the laser. This system achieves a phase noise of –97 dBc Hz–1 at 10-kHz offset frequency, a fractional frequency stability of 5 × 10−13 at 10 ms, a 150-Hz 1/π integral linewidth and a 35-mHz fundamental linewidth. We also present a complementary integration strategy that utilizes a vertical-emission grating coupler and a back-reflection cancellation circuit to realize a fully co-integrated module that effectively redirects the reflected signals and isolates back-reflections with a 10-dB suppression ratio, serving as a key for on-chip Pound–Drever–Hall locking. Together, these results highlight how vacuum-gap Fabry–Pérot reference cavities can be harnessed for ultrastable, low-noise photonic systems.
Similar content being viewed by others
Main
Fabry–Pérot (FP) resonators have many unique properties that make them indispensable for applications ranging from ultrastable lasers1,2, optical clocks3 and microwave signal generators4,5 to quantum networks6. Since they host electromagnetic modes that live almost entirely in vacuum, vacuum-gap FP cavities exhibit greatly reduced frequency instabilities relative to dielectric resonators1,7,8. To enable next-generation quantum communications, computation and timekeeping technologies, it will be necessary to bring the performance advantages of FP resonators to compact, integrated platforms5 (Fig. 1a). As the basis for integrated technologies, new techniques for the wafer-scale fabrication of vacuum-gap micro-FP (μFP) cavities have produced compact reference cavities with ultrahigh quality (Q) factors (>109) and excellent frequency stability9,10. However, before we can harness these performance advantages in next-generation integrated photonic systems, new strategies are needed to interface μFP reference cavities with photonic integrated circuits (PICs).
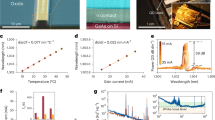
a, Survey of the resonator thermal noise limit at 10 kHz and Q factor for on-chip ring cavity, whispering-gallery-mode (WGM) cavity and vacuum FP cavity. Ring resonator data are obtained from refs. 13,24,30,31,32; WGM resonator data, from refs. 7,33,34; and vacuum FP resonator data, from this work and refs. 1,2. Note that our cavity has more than 104 times smaller form factor than that in other work1 and does not require a vacuum enclosure. b, Schematic of the in-vacuum-bonded μFP cavity (i). ROC, radius of curvature. Photograph of the μFP cavity (ii). c, Optical ring-down measurement of the μFP cavity, yielding a Q factor of 4.26 billion. d, Schematic of the integration architecture. An RTC is required to transform mirror-like reflection to the response desired by the application. For SIL, a resonant optical feedback is required. For other applications, like PDH locking, a complete reflection suppression is required. e, Schematic of the mode-matching approach from PIC to μFP with an end-fire (i) and a grating (ii) coupler.
The most challenging obstacle to the integration of such μFP cavities with PICs is the near-unity reflectivity produced by FP cavities in the off-resonance condition. Due to the lack of on-chip circulators, such a strong reflection will destabilize and even damage on-chip lasers and amplifiers. Moreover, the efficient utilization of μFP cavities as on-chip frequency references requires efficient access to the resonator modes and methods to transform the cavity reflection response for various applications. For instance, electrical feedback can be used to actively stabilize a laser to the modes of an FP cavity by detecting its reflection response using Pound–Drever–Hall (PDH)-based feedback control. However, such schemes require strategies to protect the on-chip laser from unwanted back-reflections as well as the efficient redirection of the reflected laser light to a detector. To address this challenge, a novel reflection cancellation circuit has been developed that adapts conventional schemes for a poor man’s isolator into the circuit architecture11. However, the fully co-integrated module proposed in another work5 has not been demonstrated.
Alternatively, the frequency stability of a μFP reference cavity can be transferred to a laser oscillator using optical feedback through self-injection locking (SIL)12. This method eliminates complex feedback control and producing noise suppression at higher bandwidths using a simpler system architecture. However, unlike dielectric ring resonators that utilize Rayleigh backscattering to generate the necessary resonant feedback2,13,14,15, the mirror-like, broadband reflection of an FP cavity poses challenges for SIL. Conventional remedies have relied on free-space circulators16 or on the partial excitation of higher-order modes by tilting the cavity17,18,19,20, but these solutions are hard to implement in integrated photonic platforms. Consequently, new strategies to reshape and control the FP cavity’s reflection response are required to achieve efficient and stable SIL with integrated lasers.
In this paper, we introduce novel reflection transformation circuits (RTC) that enables compact and ultrahigh-performance lasers and oscillators through the co-integration of vacuum-gap μFP reference cavities with PICs. To harness μFP cavities for SIL, we demonstrate a new RTC that transforms the reflection response of the μFP to produce the requisite resonant feedback; using this system, we demonstrate the SIL of a waveguide-integrated laser to an in-vacuum-bonded μFP reference cavity that was fabricated using a wafer-scale process. Through self-injection locking of the distributed-feedback (DFB) laser to the μFP reference cavity, we achieve a single side-band phase noise of –97 dBc Hz–1 at a 10-kHz offset frequency, 5 × 10−13 fractional frequency stability at 10 ms, with a 150-Hz 1/π integral linewidth and a 35-mHz fundamental linewidth, corresponding to an ultralow-noise operation of a self-injection-locked laser within a waveguide-integrated system. To harness the frequency stability of μFP reference cavities using PDH locking schemes, we demonstrate a fully co-integrated μFP cavity through a complementary RTC11. This co-integrated μFP is used to demonstrate an isolator-free circuit interface for PDH locking, consisting of a circuit-based two-port interferometer that cancels unwanted back-reflections and mapping the cavity’s reflection response to a separate optical port. Looking ahead, these approaches to harness reference cavities within integrated circuits open new avenues for ultrahigh-performance portable photonic microwave systems5, integrated optical gyroscopes21 and enhanced quantum systems22, with the continued advancement of such μFP reference cavity technologies.
Results
Photonic interface for SIL
To realize the SIL of waveguide-integrated semiconductor lasers through co-integration with vacuum-gap μFP reference cavities, we present a novel circuit interface that reshapes the cavity’s reflection spectrum, producing the resonant response necessary for self-injection-based feedback and laser control. In general, the reflection response of the FP cavity appears as antiresonances (dips) atop a high-reflectivity background, which are unsuitable for SIL. Note that such antiresonances result from interference between light that is resonantly scattered by the cavity modes and a broadband background reflection produced by the mirrors. To utilize the μFP for SIL, it is crucial to eliminate the high-reflectivity background, leaving only resonant scattering (or cavity leakage field) to produce feedback; this is because broadband mirror reflections can produce parasitic resonances that destabilize the laser23. If the wideband mirror reflection can be eliminated, leaving only resonant backscatter from the cavity modes, efficient resonant feedback can be achieved. When resonant feedback is realized, the sudden phase shift produced by resonant backscattering about the cavity resonance provides the optimal feedback mechanism for SIL.
The circuit interface that we use to produce resonant feedback into a waveguide-based DFB laser is shown in Fig. 2a. An on-chip directional coupler divides the incoming light, directing a portion of light into an on-chip loop mirror that introduces an additional broadband mirror reflection. The remaining light travels to the chip facet, where it is collimated by a gradient refractive index (GRIN) lens to match the mode of the co-integrated μFP cavity. These two reflections interfere on recombination at the directional coupler. With the correct phase ϕ2, the loop-mirror reflection destructively interferes with the μFP cavity reflection, cancelling the broadband mirror reflections and preserving only the resonant backscattered light. This results in a resonant (Lorenzian) feedback spectrum, facilitating SIL by adjusting the feedback phase ϕ1.
a, Schematic of the on-chip circuit design enabling SIL to the co-integrated μFP cavity. b, Photograph of the DFB laser self-injection locked to the μFP cavity through an interface chip. c, Schematic of the experimental setup for noise measurement. The black lines indicate electrical control, and the red lines indicate optical circuits. PD, photodetector; ESA, electrical spectrum analyser; AOM, acousto-optical modulator. The output of the self-injection-locked laser either beats with another stable laser or performs self-heterodyne with an 800-m delay line for the ESA to measure the phase noise. d, Phase noise spectra for the self-injection-locked and free-running lasers. The phase noise of the free-running laser is measured using self-heterodyne. The faded curve indicates that the noise is limited by the measurement noise floor. e, RF beat-note spectrum of the self-injection-locked laser and a stable laser revels linewidth compression when locked. A zoomed-in view of (i) is shown in (ii). Free-running beat note is taken with 91-kHz RBW, and the locked beat note is taken with 3-kHz RBW. f, Allan deviation of the self-injection-locked laser measured from the frequency counter (FC) with and without linear drift removal.
The vacuum-gap μFP reference cavity used in this study (Fig. 1b(i),(ii)) is created from ultralow-expansion (ULE) glass using a wafer-scale microfabrication process. To produce these cavities, an array of concave micromirrors (35-cm radius of curvature) are patterned on a super-polished 2-inch ULE glass wafer using a reflow-based fabrication process8. A ULE spacer is then used to bond a flat mirror with the microfabricated mirror array together in a vacuum, creating an array of vacuum-gap cavities that can be diced into individual units. The fabricated vacuum-gap μFP cavity measures 9 × 9 × 7 mm3 (<0.6-ml volume) and supports a fundamental Gaussian mode with a 240-μm mode field diameter and a Q factor of 4.26 × 109 (45-kHz linewidth) as measured through optical ring-down spectroscopy. The vacuum-gap cavity design virtually eliminates thermorefractive noise and the ULE cavity material greatly reduces frequency drift, producing unrivalled phase noise and frequency stability within a millimetre-scale device, as validated through independent measurements10.
A GRIN lens is used to expand and collimate the beam of light emitted from the waveguide end-facet to match the μFP cavity mode. To accomplish this mode transformation using our circuit interface, we use an inverse taper at the output facet of a Si3N4 waveguide, producing a mode diameter of approximately 3 μm. A GRIN lens with an effective focal length of 0.46 mm is then used to expand this from 3 μm to 240 μm, matching the mode field diameter of the μFP cavity, permitting a mode-matching efficiency as high as 95%. Hence, this simple and compact photonic interfacing technique (Fig. 2b) offers a practical means of co-integrating the μFP cavity with PICs, to enable high-performance oscillators and lasers for next-generation photonic systems.
The circuit interface shown in Fig. 2c is used to control the optical feedback parameters of this system, as necessary to obtain a stable SIL. The interface circuit includes integrated heaters that allow for adjusting the coupler splitting ratio, feedback phase ϕ1 and interferometer phase ϕ2. Piezo actuators on both DFB laser and μFP cavity are also used for fine-tuning ϕ1 and ϕ2 by modulating their separation from the photonic circuit. When ϕ1 and ϕ2 are adjusted to produce a self-injection-locked state, the frequency of the laser emission becomes resonant with the μFP cavity, producing an increase in the light intensity within the μFP cavity. Light transmitted from the μFP cavity is collected through free space and monitored using a photodetector to observe the onset of the SIL process. The output from the self-injection-locked laser is then coupled into the fibre-based apparatus of Fig. 2c for phase noise measurements.
Two complementary techniques are used to quantify the phase noise of the self-injection-locked laser. To measure the phase noise at low offset frequencies, we analyse the beat note between the integrated self-injection-locked laser and another frequency-stabilized reference laser using a phase noise analyser (Fig. 2c(i)). The stable laser comprises a fibre laser that is PDH-locked to a 10-cm-long table-top FP reference cavity housed in a vacuum chamber; this stabilized reference laser has low phase noise at a low offset frequency (0 dBc Hz–1 at a 1-Hz offset frequency). However, since the PDH feedback loop introduces excess noise, seen as a servo bump at offset frequencies above 10 kHz, a complementary measurement method is required to analyse the phase noise of the self-injection-locked laser at higher offset frequencies. Here we use the fibre interferometer with an 800-m delay (Fig. 2c(ii)) to perform self-heterodyne measurements. This complementary approach is ideal for phase noise measurements at high offset frequencies since the fibre interferometer is essentially free of technical noise for frequencies above 5 kHz. Combining these two techniques, we obtain a complete picture of the phase noise spectrum of the self-injection-locked laser from 1 Hz to 1 MHz (Fig. 2d).
The measurements shown in Fig. 2d reveal a dramatic reduction in the phase noise of the DFB laser when it is injection locked to the μFP cavity. SIL is shown to reduce the phase noise of the DFB laser by eight, seven and six orders of magnitude at offset frequencies of 1 kHz, 10 kHz and 100 kHz, corresponding to phase noise levels of –65 dBc Hz–1, –97 dBc Hz–1 and –122 dBc Hz–1, respectively. Further analysis of the phase noise spectrum reveals a fundamental linewidth of 35 mHz and a 1/π integral linewidth of 150 Hz. The reduction in laser linewidth produced by SIL is further demonstrated in the direct RF beat-note spectrum between the self-injection-locked laser and a stable reference laser (Fig. 2e). It is important to note that the linewidth shown in Fig. 2e(ii) is constrained by the resolution bandwidth (RBW) of the electronic spectrum analyser. Note that these measurements were performed with a relatively large resolution bandwidth (>3 kHz) to ensure a stable beat-note spectrum within the acquisition time. The Allan deviation, which is indicative of fractional frequency stability for different averaging times (Fig. 2f), is 5 × 10−13 at 10-ms averaging time. After removing a linear drift of 109 Hz s–1, the system exhibits a fractional frequency stability better than 5 × 10−12 from 1-ms to 50-s averaging times.
Note that these measurements correspond to an ultralow phase noise performance among state-of-the-art chip-integrated systems24 and were obtained without tight environmental controls. The measurements described above were obtained without active temperature stabilization of the cavity, illustrating the temperature insensitivity and robustness of such in-vacuum-bonded μFP reference cavities. Deviations from the thermal noise limit at low offset frequencies are attributed to mechanical noise from the translation stages used to position the cavity and DFB laser. Hence, the low offset phase noise and frequency drift are likely to greatly improve when this system is fully co-integrated.
We also analyse the dynamics of the SIL by slowly modulating the DFB laser current to observe shifts in the RF beat-note spectrum with a stable reference laser (Fig. 3a). This system enters and exits the self-injection locked state at points b to b′ and f to f′ (Fig. 3a,b), respectively, demonstrating a locking range of 265 MHz. Comparison with a theoretical model (Supplementary Section II) of the SIL process suggests that the onset of SIL occurs earlier than expected (point b in Fig. 3b rather than the end of the curve); this is probably due to laser relaxation oscillations produced by the semiconductor gain medium15. The asymmetric feature for two directions of SIL is due to the fact that ϕ1 is not ideal (Supplementary Fig. 2c). It is also notable that away from the μFP resonance, the relationship between the output frequency and DFB laser frequency diverges from the identity line, indicating that mirror reflections are not entirely cancelled, leaving a small amount of residual broadband feedback (Supplementary Fig. 2e). Nevertheless, provided that this feedback remains sufficiently weak to avoid destabilizing the laser, it appears to have little impact on the performance of the self-injection-locked laser.
a, RF beat-note spectrum of the self-injection-locked laser and a stable laser with a sweeping current on the DFB laser yields a 265-MHz locking range. b, Theoretical locking curve. The self-injection-locked laser entering and exiting the locked state are due to the relaxation oscillation of the DFB laser. The off-resonance curve deviates from free running due to the residual broadband mirror reflection.
Photonic interface to enable electrical control
Beyond SIL, new circuit interfaces for the efficient interrogation of μFP cavity modes can enable complementary applications involving on-chip frequency metrology and microwave photonic signal processing. For example, PDH locking provides a very versatile means of harnessing reference cavities with many practical advantages. Since PDH locking can be implemented with low incident optical powers (~10 μW) relative to the SIL (>1 mW), photothermal noise is greatly reduced, permitting us to more readily reach the thermal noise limit (Fig. 2d). Additionally, PDH locking enables frequency tunability and lower phase noise at low offset frequencies, making it indispensable for the most demanding applications requiring precise frequency control5,10 (for a more detailed comparison with SIL, see Supplementary Section III). Alternatively, such ultrahigh-Q-factor μFP cavities can be used for microwave photonic filtering and signal processing25. Applications such as PDH locking and microwave photonic signal processing require a photonic interface for the efficient interrogation of μFP cavities and protecting on-chip lasers from strong feedback and reflections. Optical circulators are often used for redirecting reflected light for such applications26,27, but circulators and isolators are not yet widely available in integrated photonics due to the incompatibility of magnetic media with complementary metal–oxide–semiconductor fabrication processes.
To address this challenge, we implement a distinct reflection cancellation circuit based on the concept of a ‘poor man’s isolator’11, thereby demonstrating a fully co-integrated μFP cavity with PICs. This second strategy for interfacing and integrating the μFP cavity uses a silicon photonic circuit fabricated from a silicon-on-insulator platform, which is favourable for an efficient grating coupler. This circuit comprises a two-port interferometer that connects to an inverse-designed two-port polarization-splitting grating coupler (PSGC), as described in ref. 11. By fine-tuning the on-chip phase shifter, this vertical-emission PSGC efficiently couples circularly polarized light into the μFP cavity, permitting the interrogation of the reflection response of the cavity. Making use of the fact that the chirality of circularly polarized light is reversed on reflection from the μFP cavity, this circuit achieves a function very similar to that of a circulator11.
Efficient coupling into the μFP is achieved by using a GRIN lens to expand the beam produced by the PSGC. The PSGC is designed to produce vertical emission of a 10.4-μm mode field diameter. This beam is expanded using an off-the-shelf GRIN lens with an effective focal length of 0.94 mm. The collimated beam couples to the fundamental mode of the μFP cavity with a 91% mode overlap. The GRIN lens and μFP cavity are then co-integrated with the PIC using a custom spacer that provides mechanical stability for the bonded assembly (Fig. 4b; Methods provides the mode details). Using this integration method, light can be coupled from the silicon circuit into the μFP cavity with an efficiency of –2.8 dB, corresponding to an insertion loss of –5.6 dB. Further optimization can be achieved using a back-side mirror to achieve near-unity efficiency28. Alternatively, such an interface circuit can also be achieved through an edge coupler with transverse-electric and transverse-magnetic modes for circularly polarized light, which is widely used in industry for low-loss (<1.5-dB) coupling29.
a, Schematic of the approach for co-integrating the μFP cavity with signal redirection and back-reflection isolation. b, Cross-section of the co-integrated μFP cavity (i) and optical picture of a co-integrated module (ii). c, Experimental data validating signal redirection and characterizing back-reflection isolation ratio. d, Outlook for the on-chip PDH locking system. PM, phase modulator; LD, laser diode; EIC, electric integrated circuit.
Figure 4c shows the optical reflection from port A and the transmission to port B as a function of laser detuning from the cavity resonance. As shown in Fig. 4c, this circuit maps the μFP cavity reflection response with a visibility of 35% at the output port and simultaneously suppressing back-reflections from the input port. The relative magnitudes of transmission and reflection reveal a 10-dB back-reflection suppression, to aid in protecting an on-chip laser from unwanted feedback. This fully integrated μFP is readily suitable for an on-chip PDH locking system (Fig. 4d), as proposed in ref. 5. Together with many other applications such as photonic RF filtering25 and microwave signal generators5, the co-integration of vacuum-gap μFP cavities paves the way for the next generation of compact, high-performance RF photonic systems.
Discussion and conclusion
We have demonstrated complementary approaches for the integration of high-performance vacuum-gap μFP reference cavities with PICs, to enable both electrical and optical feedback for next-generation lasers, oscillators and sensors. We achieve table-top-level stability in an integrated platform, miniaturized to a millilitre-scale form factor. Using a new circuit interface to transform the response of the μFP resonator, we have created resonant optical feedback necessary for self-injection locking a waveguide-based laser with the reference cavity. This strategy produces an integrated laser with a fundamental linewidth of 35 mHz and an integrated 1/π linewidth of 150 Hz, corresponding to an ultralow-noise performance. Phase noise measurements represent a 19-dB (17-dB) improvement in phase noise at a 1-kHz (10-kHz) offset frequency relative to prior studies that have utilized 1.4-m spiral waveguide resonators24. As shown by the comparison plot (Fig. 5), the co-integration of such μFP vacuum-gap cavities produces a system with an unrivalled combination of size and performance.
In ref. 2, free-space optics are used for PDH locking to a vacuum-housed 8-ml FP cavity. In ref. 10, free-space optics are used for PDH locking to a vacuum-gap 9.6-ml FP cavity. In ref. 35, fibre optics are used for PDH locking to a vacuum-gap 2-ml FP cavity. In ref. 16, free-space optics are used for SIL to an air-gap 0.5-ml FP cavity. Here we demonstrate SIL to a vacuum-gap 0.56-ml FP cavity on an integrated platform (solid green). Additionally5,11, we propose PDH locking to a vacuum-gap 0.56-ml FP cavity on an integrated platform. A fully co-integrated μFP is presented in this work. The dashed green circle indicates the envisioned noise performance of on-chip PDH locking in this platform.
Since the electromagnetic energy is stored almost entirely in vacuum, this vacuum-gap μFP cavity overcomes numerous limitations imposed by dielectric-induced thermorefractive noise. Moving from stage-controlled pieces to a fully packaged and on-chip electro-optically controlled system, we anticipate that the low offset frequency noise will be further improved and long-term locking robustness will be extended from several hours to longer durations. Such low phase noise levels make this system highly suitable for photonic microwave signal generators through the use of optical frequency division, potentially eliminating the need for more complex PDH locking schemes5.
Through a complementary approach, we have shown that the reflection response of such vacuum-gap μFP cavities can be interrogated using a circuit interface, to enable on-chip PDH locking and microwave photonic signal processing. Co-integration of the cavity with a silicon photonic circuit is achieved by attaching the cavity to a multiport vertical-emission grating coupler. Using this grating interface, the cavity is placed within an optical interferometer that cancels unwanted back-reflections, eliminating the need for on-chip circulators and isolators. This same interferometer maps the reflection response to a separate optical port, permitting an efficient interrogation of the reflection response required for PDH locking and microwave photonic signal processing. Hence, this complementary interfacing method provides access to an ultranarrow-linewidth, stable reference cavity that becomes a versatile resource for advanced microwave photonic filtering, on-chip PDH locking and sensing applications.
Looking beyond these specific demonstrations, the co-integration of such high-performance vacuum-gap reference cavities with photonic circuits presents numerous advantages. By storing electromagnetic field mostly in vacuum, it mitigates the limitations associated with thermorefractive noise and enables high performance across various photonic integrated systems. Additionally, with sealed vacuum and athermal material, these cavities greatly reduce environmental constraints, thereby broadening the operating conditions. Furthermore, such reference cavities can achieve substantially higher performance with larger mode volumes, increased cavity lengths and improved packaging. Hence, these innovative techniques provide crucial capabilities that are essential for the development of next-generation integrated lasers, oscillators and sensors.
Methods
Process of co-packaging
For the SIL demonstration with the end-fire-based coupling scheme, the inverse taper in the PIC expands the waveguide mode to a 3-μm mode field diameter. For a single-lens collimator, the collimated beam diameter D can be calculated as
where λ is the optical wavelength, f is the focal length of the lens and ϕf is the mode field diameter at the focal point. To achieve a 240-μm mode field diameter, the focal length should be 0.36 mm. Here we used an off-the-shelf GRIN lens with a 0.46-mm focal length to collimate the beam, giving 95% mode matching. To minimize parasitic etalon, we used an antireflection-coated GRIN lens.
For the potential electrical feedback interface with the grating-coupler-based scheme, we used a GRIN lens with a focal length of 0.94 mm. Using the equation above with a 10.4-μm mode field diameter from the PSGC, we can calculate that the mode overlap is approximately 91%. It is noteworthy that this overlap efficiency will only impact the visibility of the cavity. After the coupling in and coupling out to the circuit, we can still preserve 35% of visibility, which is enough for PDH locking. To co-package the parts with PIC, first we glued the GRIN lens with a three-dimensionally printed spacer. Then, we align the GRIN lens to the PSGC, and observe the collimated beam using a beam profiler. After alignment, the GRIN lens–spacer assembly is glued to the PIC. Then, the μFP cavity is aligned and glued to the spacer.
Data availability
Source data are provided with this paper. Further data are available from the corresponding authors upon reasonable request.
References
Kessler, T. et al. A sub-40-mHz-linewidth laser based on a silicon single-crystal optical cavity. Nat. Photon. 6, 687–692 (2012).
Guo, J. et al. Chip-based laser with 1-hertz integrated linewidth. Sci. Adv. 8, eabp9006 (2022).
Ludlow, A. D., Boyd, M. M., Ye, J., Peik, E. & Schmidt, P. O. Optical atomic clocks. Rev. Mod. Phys. 87, 637 (2015).
Liu, Y. et al. Low-noise microwave generation with an air-gap optical reference cavity. APL Photon. 9, 010806 (2024).
Kudelin, I. et al. Photonic chip-based low-noise microwave oscillator. Nature 627, 534–539 (2024).
Kuhn, A., Hennrich, M. & Rempe, G. Deterministic single-photon source for distributed quantum networking. Phys. Rev. Lett. 89, 067901 (2002).
Liang, W. et al. Whispering-gallery-mode-resonator-based ultranarrow linewidth external-cavity semiconductor laser. Opt. Lett. 35, 2822–2824 (2010).
Jin, N. et al. Microfabrication of dielectric resonators with Q-factor exceeding 5 billion. In Frontiers in Optics FM4C–1 (Optica Publishing Group, 2022).
Jin, N. et al. Micro-fabricated mirrors with finesse exceeding one million. Optica 9, 965–970 (2022).
Liu, Y. et al. Ultrastable vacuum-gap Fabry–Pérot cavities operated in air. Optica 11, 1205–1211 (2024).
Cheng, H. et al. A novel approach to interface high-Q Fabry–Pérot resonators with photonic circuits. APL Photon. 8, 116105 (2023).
Kondratiev, N. et al. Self-injection locking of a laser diode to a high-Q WGM microresonator. Opt. Express 25, 28167–28178 (2017).
Jin, W. et al. Hertz-linewidth semiconductor lasers using CMOS-ready ultra-high-Q microresonators. Nat. Photon. 15, 346–353 (2021).
Lihachev, G. et al. Platicon microcomb generation using laser self-injection locking. Nat. Commun. 13, 1771 (2022).
Xiang, C. et al. 3D integration enables ultralow-noise isolator-free lasers in silicon photonics. Nature 620, 78–85 (2023).
Liang, W. & Liu, Y. Compact sub-hertz linewidth laser enabled by self-injection lock to a sub-milliliter FP cavity. Opt. Lett. 48, 1323–1326 (2023).
Dahmani, B., Hollberg, L. & Drullinger, R. Frequency stabilization of semiconductor lasers by resonant optical feedback. Opt. Lett. 12, 876–878 (1987).
Laurent, P., Clairon, A. & Breant, C. Frequency noise analysis of optically self-locked diode lasers. IEEE J. Quantum Electron. 25, 1131–1142 (1989).
Hjelme, D. R., Mickelson, A. R. & Beausoleil, R. G. Semiconductor laser stabilization by external optical feedback. IEEE J. Quantum Electron. 27, 352–372 (1991).
Savchenkov, A., Zhang, W., Iltchenko, V. & Matsko, A. Robust self-injection locking to a non-confocal monolithic Fabry–Pérot cavity. Opt. Lett. 49, 1520–1523 (2024).
Gundavarapu, S. et al. Sub-hertz fundamental linewidth photonic integrated Brillouin laser. Nat. Photon. 13, 60–67 (2019).
Lai, Y.-H. et al. Ultra-narrow-linewidth lasers for quantum applications. In 2022 Conference on Lasers and Electro-Optics (CLEO) 1–2 (IEEE, 2022).
Tkach, R. & Chraplyvy, A. Regimes of feedback effects in 1.5-μm distributed feedback lasers. J. Lightwave Technol. 4, 1655–1661 (1986).
He, Y. et al. Chip-scale high-performance photonic microwave oscillator. Sci. Adv. 10, eado9570 (2024).
Marpaung, D. et al. Si3N4 ring resonator-based microwave photonic notch filter with an ultrahigh peak rejection. Opt. Express 21, 23286–23294 (2013).
Herrmann, J. F. et al. Mirror symmetric on-chip frequency circulation of light. Nat. Photon. 16, 603–608 (2022).
Cheng, H. et al. A terahertz-bandwidth non-magnetic isolator. Nat. Photon. 19, 533–539 (2025).
Cheng, L., Mao, S., Li, Z., Han, Y. & Fu, H. Grating couplers on silicon photonics: design principles, emerging trends and practical issues. Micromachines 11, 666 (2020).
Siew, S. Y. et al. Review of silicon photonics technology and platform development. J. Lightwave Technol. 39, 4374–4389 (2021).
Li, B. et al. Reaching fiber-laser coherence in integrated photonics. Opt. Lett. 46, 5201–5204 (2021).
Sun, S. et al. Integrated optical frequency division for microwave and mmWave generation. Nature 627, 540–545 (2024).
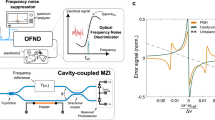
Idjadi, M. H., Kim, K. & Fontaine, N. K. Modulation-free laser stabilization technique using integrated cavity-coupled Mach-Zehnder interferometer. Nat. Commun. 15, 1922 (2024).
Wu, L. et al. Greater than one billion Q factor for on-chip microresonators. Opt. Lett. 45, 5129–5131 (2020).
Jin, X. et al. Microresonator-referenced soliton microcombs with zeptosecond-level timing noise. Preprint at https://arxiv.org/abs/2401.12760 (2024).
McLemore, C. A. et al. Fiber-coupled 2 ml vacuum-gap Fabry–Pérot reference cavity for portable laser stabilization. Opt. Lett. 49, 4737–4740 (2024).
Acknowledgements
We thank C. McLemore, T. Nakamura and W. Groman for useful technical discussion and feedback. This work was supported by Defense Advanced Research Projects Agency (DARPA) under award no. HR0011-22-2-0009 (H.C., C.X., N.J., I.K., J.G., M.H., Y.L., J.P., Q.-X.J., K.J.V., F.Q., S.A.D., J.E.B. and P.T.R.) as well as the US Department of Energy (DoE) under award no. DE-SC0019406 (N.J. and P.T.R.) and the National Science Foundation (NSF) under award no. 2137740 (H.C., Y.Z. and P.T.R.). Any opinions, findings and conclusions or recommendations expressed in this publication are those of the authors and do not necessarily reflect the views of DARPA, DoE and NSF.
Author information
Authors and Affiliations
Contributions
H.C., C.X., K.J.V., F.Q., S.A.D., J.E.B. and P.T.R. led the project and conceived the physics and experiment. H.C. and C.X. designed the SIL/PDH interface circuits. N.J. and H.C. fabricated and packaged the μFP cavity. H.C., I.K., N.J. and M.H. measured the self-injection-locked laser. J.G. and J.P. fabricated the self-injection-locked interface circuit. H.C. fabricated and measured the PDH interface circuits. H.C., C.X., N.J. and P.T.R. wrote the paper with input from all authors. All authors contributed to the design and discussion of the results.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Photonics thanks Lute Maleki, David Marpaung and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Sections I–III, Figs. 1 and 2, Table 1 and discussion.
Source data
Source Data Fig. 1
Statistical source data.
Source Data Fig. 2
Statistical source data.
Source Data Fig. 3
Statistical source data.
Source Data Fig. 4
Statistical source data.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Cheng, H., Xiang, C., Jin, N. et al. Harnessing micro-Fabry–Pérot reference cavities in photonic integrated circuits. Nat. Photon. 19, 992–998 (2025). https://doi.org/10.1038/s41566-025-01701-5
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/s41566-025-01701-5