Main

Mixed reality (MR) aims to seamlessly connect people in hybrid physical–digital spaces, offering experiences beyond the limits of our physical world. These immersive platforms provide transformative capabilities to applications including training, communication, entertainment and education1,2, among others. To achieve a seamless and comfortable interface between a user and a virtual environment, the near-eye display must fit into a wearable form factor that ensures style and all-day usage while delivering a perceptually realistic and accessible experience comparable to the real world. Current near-eye displays, however, fail to meet these requirements3. To project the image produced by a microdisplay onto a user’s retina, existing designs require optical bulk that is noticeably heavier and larger than conventional eyeglasses. Moreover, existing displays support only two-dimensional images, with limited capability to accurately reproducing the full light field of the real world, resulting in visual discomfort caused by the vergence–accommodation conflict4,5.

Emerging waveguide-based holographic displays are among the most promising technologies to address the challenge of designing compact near-eye displays that produce perceptually realistic imagery. These displays are based on holographic principles6,7,8,9,10, which have been demonstrated to encode a static three-dimensional (3D) scene with a quality indistinguishable from reality in a thin film11 or to compress the functionality of an optical stack into a thin, lightweight holographic optical design12,13. Holographic displays also promise unique capabilities for near-eye displays, including per-pixel depth control, high brightness, low power and optical aberration correction capabilities, which have been explored using benchtop prototypes providing limited visual experiences14,15,16,17,18. Most recently, holographic near-eye displays based on thin optical waveguides have shown promise in enabling very compact form factors for near-eye displays19,20,21, although the image quality, the ability to produce 3D colour images or the étendue achieved by these proposals have been severely limited.

A fundamental problem of all digital holographic displays is the limited space–bandwidth product, or étendue, offered by current spatial light modulators (SLMs)22,23. In practice, a small étendue fundamentally limits how large of a field of view and range of possible pupil positions, that is, eyebox, can be achieved simultaneously. While the field of view is crucial for providing a visually effective and immersive experience, the eyebox size is important to make this technology accessible to a diversity of users, covering a wide range of facial anatomies as well as making the visual experience robust to eye movement and device slippage on the user’s head. A plethora of approaches for étendue expansion of holographic displays has been explored, including pupil replication as well as the use of static phase or amplitude masks20,24,25,26,27,28. By duplicating or randomly mixing the optical signal, however, these approaches do not increase the effective degrees of freedom of the (correlated) optical signals, which is represented by the rank of the mutual intensity (MI)29,30,31 (Supplementary Note 2). Hence, the image quality achieved by these approaches is typically poor, and perceptually important ocular parallax cues are not provided to a user32.

One of the key challenges for achieving high image quality with holographic waveguide displays is to model the propagation of light through the system with high accuracy20. Non-idealities of the SLM, optical aberrations, coherence properties of the source, and many other aspects of a specific holographic display are difficult to model precisely, and minor deviations between simulated model and physical optical system severely degrade the achieved image quality. This challenge is drastically exacerbated for holographic displays using compact waveguides in large-étendue settings. A practical solution to this challenge requires a twofold approach. First, the propagation of light has to be modelled with very high accuracy. Second, such a model needs to be efficient and scalable to our large-étendue settings. Recent advances in computational optics have demonstrated that artificial intelligence (AI) methods can be used to learn accurate propagation models of coherent waves through a holographic display, substantially improving the achieved image quality33,34. These learned wave propagation models typically use convolutional neural networks (CNNs), trained from experimentally captured phase–intensity image pairs, to model the opto-electronic characteristics of a specific display more accurately than purely simulated models35. However, as we demonstrate in this Article, conventional CNN-based AI models fail to accurately predict complex light propagation in large-étendue waveguides, partly because of the incorrect assumption of the light source being fully coherent. Other important problems include the efficiency of a model, such that it can be trained within a reasonable time from a limited set of captured phase–intensity pairs and run quickly at inference time, and scalability to large-étendue settings while ensuring accuracy and efficiency.

Here, we reformulate the wave propagation learning problem as coherence retrieval based on the theory of partial coherence31,36. For this purpose, we derive a physics-based wave propagation model that parameterizes a low-rank approximation of the MI of the wave propagation operator inside a waveguide accounting for partial coherence, which models holographic displays more accurately than existing coherent models. Moreover, our approach parameterizes the wave propagation through waveguides with emerging continuous implicit neural representations37, enabling us to efficiently learn a model for partially coherent wavefront propagation at arbitrary spatial and frequency coordinates over a large étendue. Our implicit model achieves superior quality compared with existing methods; it requires an order of magnitude less training data and time than existing CNN model architectures, and its continuous nature generalizes better to unseen spatial frequencies, improving accuracy for unobserved parts of a wavefront. Along with our unique model, we design and implement a holographic display system, incorporating a holographic waveguide, holographic lens and micro-electromechanical system (MEMS) mirror. Our optical architecture provides a large effective étendue via steered illumination with an ultra-compact form factor and solves limitations of similar designs by removing unwanted diffraction noise and chromatic dispersion using a volume-holographic waveguide and holographic lens, respectively. Our architecture is inspired by synthetic aperture imaging38, where a large synthetic aperture is formed by digitally interfering multiple smaller, mutually coherent apertures. Our goal is to form a large display eyebox—the synthetic aperture built up from multiple scanned and mutually incoherent apertures, each limited in size by the instantaneous étendue of the system. This idea is inspired by classic synthetic aperture holography39, but we adapt this idea to modern waveguide holography systems driven by AI algorithms.

After a wave propagation model is trained in a one-time preprocessing stage, a CGH algorithm converts the target content into one or multiple phase patterns that are displayed on the SLM. Large-étendue settings require the target content to contain perceptually important visual cues that change with the pupil position, including parallax and occlusion. Traditional 3D content representations used for CGH algorithms, such as point clouds, multilayer images, polygons or Gaussians40,41,42, however, are inadequate for this purpose. Light field representations, or holographic stereograms43,44, meanwhile, contain the desired characteristics. Motivated by this insight, we develop a light-field-based CGH framework that uniquely models our setting where a large synthetic aperture is composed of a set of smaller, mutually incoherent apertures that are, however, partially coherent within themselves. Our approach uniquely enables seamless, full-resolution holographic light field rendering for steered-illumination-type holographic displays.

In summary, we present synthetic aperture waveguide holography as a system that combines a new and compact large-étendue waveguide architecture with AI-driven holographic algorithms. Through our prototypes, we demonstrate high 3D image quality within a 3D eyebox that is two orders of magnitude larger, marking a pivotal milestone towards practical holographic near-eye display systems.

Results

Ultra-thin full-colour 3D holographic waveguide display

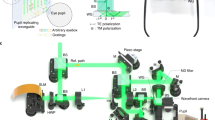
Our architecture is designed to produce high-quality full-colour 3D images with large étendue in a compact device form factor to support synthetic aperture holography based on steered waveguide illumination, as shown in Fig. 1. Our waveguide can effectively increase the size of the beam without scrambling the wavefront, unlike diffusers or lens arrays27,45. Moreover, it allows a minimum footprint for beam steering using a MEMS mirror at the input side. For these reasons, waveguide-based steered illumination has been suggested for holographic displays19,46. Existing architectures, however, suffer from two problems: world-side light leakage from the waveguide and chromatic dispersion of the eyepiece lens. Here, we overcome conventional limitations with two state-of-the-art optical components to overcome conventional limitations: the angle-encoded holographic waveguide and the apochromatic holographic eyepiece lens.

Fig. 1: Holographic MR display system.
figure 1

a, An illustration of the synthetic aperture waveguide holography principle. The illumination module consists of a collimated fibre-coupled laser, a MEMS mirror that steers the input light angle, and a holographic waveguide. Together, these components serve as a partially coherent backlight of the SLM. The SLM is synchronized with the MEMS mirror and creates a holographic light field, which is focused towards the user’s eye using an eyepiece lens. Our design achieves an ultra-thin form factor as it consists only of flat optical elements and it does not require optical path length to form an image. The steered illumination mechanism produces a synthetic aperture, which supports a two-orders-of-magnitude larger étendue than that intrinsic to the SLM. Our angle-encoded holographic waveguide and apochromatic holographic lens design solve bidirectional diffraction noise and chromatic dispersion issues, respectively. b, An exploded view of the schematic image and captured photos of the holographic MR display prototype. The use of thin holographic optics achieves a total optical stack thickness of less than 3 mm (panel to lens). Top- and side-view photographs of the prototype are shown.

Full size image

Our holographic waveguide shares many characteristics with conventional surface relief grating (SRG)-type waveguides. Specifically, our design uses a similar pupil replication principle and layout, which consists of an in-coupler, an exit-pupil expanding grating and an out-coupler grating. By contrast, our couplers are constructed of uniquely designed volume Bragg gratings (VBGs) instead of SRGs. SRGs used in conventional waveguides47 have a degeneracy that supports multiple modes of diffraction. This causes a light leakage issue as the light is out-coupled bidirectionally, to both the world side and viewer’s eye side. When the waveguide is used for illumination, the leakage enters the eyepiece without being modulated by the SLM, resulting in d.c. noise throughout the entire field of view. This d.c. noise significantly degrades the contrast of the displayed image19, and it is challenging to filter out this noise as it shares the optical path with the signal. On the contrary, VBGs exhibit a type of diffraction known as Bragg diffraction48,49, where only light that satisfies a specific incident angle and a narrow spectral bandwidth is diffracted to a single diffraction order with high efficiency. This single-direction diffraction greatly suppresses stray light and ghost images compared with conventional waveguides. In addition, we use the angle-encoded multiplexing method to cover the larger steering angle, where each grating supports only a portion of the target angular bandwidth with a specific narrow band wavelength with high efficiency. The multiplexing is performed by overlapping volume gratings with the same surface pitch but with different slant angles (see Supplementary Note 1 for additional details). This allows us to collectively cover the target angular bandwidth with high efficiency, while supporting three wavelengths of red (638 nm), green (520 nm) and blue (460 nm) without crosstalk.

Our display architecture achieves an ultra-thin form factor of only 3 mm thickness from the SLM to the eyepiece lens, including a 0.6-mm waveguide and 2-mm holographic lens. The MEMS mirror in our display steers the illumination angles incident on our SLM, which creates a synthetic aperture (that is, eyebox) of size 9 × 8 mm2, supporting an eyebox volume that is two orders of magnitude larger than that intrinsic to the SLM. The diagonal field of view of our display is 38° (34.2° horizontal and 20.2° vertical). An in-depth discussion of the full system and additional components is found in the Methods and Supplementary Note 1.

Partially coherent implicit neural waveguide model

Our synthetic aperture waveguide holographic display is partially coherent because its synthetic aperture consists of a scanned set of mutually incoherent apertures. In addition, the instantaneous eyebox exhibits partial coherence due to factors such as millimetre-scale optical path length differences generated by the pupil replication process in the waveguide, mode instability of diode lasers and imperfect polarization management. Neither existing AI-based wave propagation models for coherent wavefronts21,33,34 nor recent waveguide propagation models20 are sufficient in adequately describing the complex behaviour of partially coherent light50,51. In this section, we first develop a partially coherent waveguide model to accurately characterize physical optical systems based on implicit neural representations52. Then, we adapt this model to our synthetic aperture waveguide holography setting. Our model can be trained automatically using camera feedback, it generalizes well to unseen spatial frequencies and it is used to produce the high-quality experimental results demonstrated in later sections.

A partially coherent wavefront can be represented by its MI or its Fourier transform—the Wigner distribution function53,54. With our waveguide model, we aim to model the MI of the waveguide, \(J\left({{\bf{r}}}_{1},{{\bf{r}}}_{2}\right)\), where r1 and r2 are spatial coordinates on the SLM plane. This MI depends on the steered illumination angle, so it needs to be characterized for each of them separately. Representing such a high-resolution, four-dimensional function for many apertures within the synthetic aperture, however, is computationally intractable. Consider a discretized MI for 1,920 × 1,080 spatial SLM coordinates for each of 10 × 10 steering angles—the corresponding ensemble of MIs would require more than 100 terabytes of memory to be stored. Moreover, it is unclear how to smoothly interpolate these MIs between aperture positions as they are characterized at discrete positions.

To address these challenges, we introduce a low-rank implicit neural representation for the ensemble of steering-angle-dependent MIs of the waveguide. Specifically, for each steering angle um, m = 1, …, M, the MI is approximated by K coherent spatial modes that are incoherently summed55 as \(J({{\bf{r}}}_{1},{{\bf{r}}}_{2},{\bf{u}})\approx \mathop{\sum }\nolimits_{k = 1}^{K}{f}_{{\rm{WG}}}^{\;k}({{\bf{r}}}_{1},{\bf{u}}){f}_{{\rm{WG}}}^{\;k}{({{\bf{r}}}_{2},{\bf{u}})}^{{\rm{H}}}\), where \({f}_{{\rm{WG}}}^{\;k}({{\bf{r}}}_{1},{\bf{u}})\) is a single coherent mode at spatial frequency u, k = 1, …, K indicates the mode index and H denotes the Hermitian transpose. Note that coherent waveguide models are a special case of this partially coherent model, namely, those of rank 1. This low-rank MI representation is inspired by coherence retrieval methods31. Rather than representing the ensemble of low-rank MIs explicitly, however, we introduce a novel waveguide representation based on emerging neural implicit representations37. This neural-network-parameterized representation is more memory efficient than a discretized representation and it is continuous, so it can be queried at any spatial or spatial frequency (that is, aperture) coordinate. Specifically, our implicit neural representation is a multilayer perceptron (MLP) network architecture, \({f}_{{\rm{WG}}}\left({\bf{r}},{\bf{u}};{\varPsi} \right):{{\mathbb{R}}}^{4}\to {{\mathbb{C}}}^{K}\), that represents the MI ensemble of the waveguide using network parameters Ψ. Once trained, the MLP can be queried with the input of spatial (r) and frequency (u) coordinates and it outputs the K modes of the corresponding MI. The primary benefits of this implicit neural representation over a conventional discrete representation are its memory efficiency (a few tens of megabytes versus terabytes) and, as we demonstrate in the following experiments, the fact that our representation generalizes better to aperture positions that were not part of the training data. Remarkably, even in a low-étendue setting, our implicit model achieves faster convergence and better accuracy than state-of-the-art CNN-based models based on explicit representations (Fig. 2d), so the implicit model can serve as a drop-in replacement for existing holographic displays. In a large-étendue setting, our implicit neural model is the only one achieving high-quality results.

Fig. 2: Partially coherent implicit neural waveguide model.
figure 2

a, Using our prototype, we capture training and validation datasets consisting of sets of an SLM phase pattern as well as the corresponding aperture position and intensity image. The aperture positions are uniformly distributed across the synthetic aperture, enabling model training with large étendue. b, The captured dataset is used to train our implicit neural waveguide model. The parameters of our model are learned using backpropagation (dashed grey line) to predict the experimentally captured intensity images. c, A visualization of two waveguide modes of the trained model, including amplitude and phase, at two different aperture positions. Our model faithfully reconstructs the wavefront emerging out of the waveguide, exhibiting the patch-wise wavefront shapes expected from its pupil-replicating nature. d, Evaluation of wave propagation models with varying training dataset sizes for a single aperture (that is, low-étendue setting). Our model achieves a better quality using a dataset size that is one magnitude lower than state-of-the-art models34. e, Experimentally captured image quality for different wave propagation models in the low-étendue setting. Our model outperforms the baselines, including the ASM60 and the time-multiplexed neural holography model (TMNH)34, by a large margin.

Full size image

Our implicit waveguide models the MI of input light arriving at the SLM plane. Then, the phase of each coherent mode of the MI is modulated by the corresponding SLM phase pattern ϕm. Each of the modes continues to propagate in free space, by distance z, to the image plane in the scene. We use an off-axis angular spectrum method (ASM)35,56 to implement this free-space wave propagation operator for each coherent mode, migrating the bandwidth over a large étendue. Finally, all propagated modes are incoherently summed over the full synthetic aperture to form the desired intensity, Iz, at distance z.

$${f}^{\;k}({\bf{x}},{{\bf{u}}}^{m},{\phi }^{m})={{\mathcal{P}}}_{z}\left({f}_{{\rm{WG}}}^{\;k}\left({\bf{r}},{{\bf{u}}}^{m}\right){e}^{i{\phi }^{m}};{{\bf{u}}}^{m}\right),$$
(1)
$${I}_{z}({\bf{x}})={\left\langle {\left\vert\; {f}^{\;k}\left({\bf{x}},{{\bf{u}}}^{m},{\phi }^{m}\right)\right\vert }^{2}\right\rangle }_{k,m},$$
(2)

where \({{\mathcal{P}}}_{z}(\cdot ;{\bf{u}})\) is the coherent wave propagation operator with propagation distance z through the aperture centred at u, and \(\left\langle \cdot \right\rangle\) is the mean operator denoting the incoherent sum of modes. As detailed in the Methods, to optimize experimental image quality, the wave propagation operator \({{\mathcal{P}}}_{z}\) also includes several learned components, including pupil aberrations and diffraction efficiency of the SLM.

Using these equations, we can map phase patterns shown on the SLM ϕm with steering angle um to the image that a user would observe. To assess our partially coherent waveguide model with respect to state-of-the-art holographic wave propagation models, we capture a dataset from our display prototype consisting of triplets, each containing an SLM phase pattern, an aperture position and the corresponding intensity at the image plane (Fig. 2a). We then train models to predict the experimentally captured intensity images, given the known input phase patterns and aperture positions.

To evaluate and compare waveguide models in a large-étendue setting, we train ours along with baseline models on a dataset captured at 72 aperture positions with our prototype. We evaluate the generalization capabilities of these models on a test set containing nine aperture positions that were not part of the training set. Quantitative results are presented in Table 1. Previously proposed explicit CNN models generalize poorly to the unseen aperture positions. Importantly, it takes more than 2 days of training for them to converge, which is somewhat impractical. Our implicit waveguide model is smaller in size and shows better generalization capabilities than explicit models, while also converging much faster. Moreover, when used in a partially coherent configuration, the accuracy of our model is drastically improved over all coherent models, as seen by the high quality achieved on both training and test sets when used with three or six modes.

Table 1 Comparison of different waveguide and wave propagation models
Full size table

Figure 2a illustrates the data collection aspect of our approach: we show a sequence of phase patterns, ϕm, on the SLM and capture corresponding intensity images, Im, with a camera focused on the image plane. The implicit neural model is trained on these data, as shown in Fig. 2b. For this purpose, we simulate the forward image formation given the phase patterns ϕm and a random set of initialized model parameters. A loss function \({\mathcal{L}}\) measures the mean-squared error between simulated and captured intensity images. The backpropagation algorithm is applied to learn all model parameters, including the partially coherent waveguide model. This model comprises a set of coherent modes \({f}_{{\rm{WG}}}^{\;k}\), each being a complex-valued image on the SLM plane with amplitude and phase, that can be queried at the spatial frequencies corresponding to the MEMS steering angles um (Fig. 2c). In a low-étendue setting, that is, when operating with a fixed steering angle um, this implicit neural model achieves a higher quality with significantly less training data compared with state-of-the-art explicit CNN models34 (Fig. 2d). Therefore, our model serves as a drop-in replacement for existing wave propagation models with strictly better performance. Even though the gain in peak signal-to-noise ratio for explicit and implicit models on the validation set at convergence is only a few decibel (Fig. 2d), the generalization capabilities of our implicit model are far superior to those of the explicit model. This is observed in Fig. 2e, where we show experimental results comparing a model-free free-space wave propagation operator35, the results achieved by the coherent explicit model34 and our partially coherent implicit model. The images used here are representative of a test set of images unseen during training and show that our model outperforms both baselines by a large margin.

The 3D eyebox describes the volume within which a hologram is visible to the observer’s eye. A large eyebox is crucial for guaranteeing high image quality when the eye moves and for making any display accessible to a diverse set of users with different binocular characteristics. Figure 3a illustrates the supported eyebox volume of our system (green volume), which is two orders of magnitude larger than that intrinsic to the SLM without steered illumination (orange volume). Moreover, our CGH framework fully utilizes the bandwidth corresponding to an eyebox size of 9 × 8 mm, unlike conventional holographic displays16,44,57, which use only a small fraction of the available bandwidth supported by the SLM (red volume). Figure 3b visualizes images of the phase aberrations of the waveguide system learned by our model at various positions within the supported eyebox. These aberrations vary drastically over the eyebox, making it challenging to be learned using approximately shift-invariant CNN-based models. We further validate our model’s ability to produce high-quality imagery across an extended étendue and compare its performance with that of conventional holography in Fig. 3c,d. Figure 3c shows experimentally captured light fields of a two-dimensional resolution chart image located at optical infinity over the extended eyebox in the top row, while the insets in the bottom present the results at specific positions, indicated by corresponding colours. As expected, conventional holography provides a very small eyebox, which restricts the image to be seen only from the centre position. Our approach supports a significantly larger eyebox with high uniformity for transversely shifting eye positions. Figure 3d demonstrates longitudinal eyebox expansion. Conventional holography suffers from vignetting, and naive pupil-steered holography25 does not account for the axial shift of the eye, resulting in inconsistent image overlap. In addition, variations in the waveguide output and aberrations across different steering states significantly degrade image quality, even when the issue of inconsistent image overlap is addressed, as shown in the third row of Fig. 3d. Our method generates robust, high-quality imagery as the eye moves along the optical axis. Note that the pupil position denoted with a blue marker is not used during model training, yet our model achieves comparable image quality and consistent interpolation of parameters, demonstrating its generalization capabilities.

Fig. 3: Experimental validation of the waveguide holography system in a large-étendue setting.
figure 3

a, Visualizations of the supported étendue (3D eyebox). Conventional holography, such as smooth phase techniques (red volume at the origin), supports only a portion of the eyebox that the SLM can produce (intrinsic étendue, orange volume). Our system supports a two-orders-of-magnitude larger eyebox than conventional holographic display systems (green volume). b, Visualization of our learned model across the expanded étendue. For better visualization and interpolation capabilities, refer to the Supplementary Video. c, Experimentally captured resolution chart images with expanded eyebox. Our system supports an eyebox size of 9 × 8 mm, which is significantly larger than the display-limited eyebox of conventional holographic displays. Using our implicit model, we can efficiently calibrate the system, achieving high image quality uniformly across the extended eyebox, as shown in the inset. d, Longitudinal eyebox expansion results. Markers show the corresponding pupil positions in the octahedron shown in a.

Full size image

CGH framework for synthetic aperture waveguide holography

At runtime, a phase-retrieval-like CGH algorithm computes one or multiple phase patterns that are displayed on the SLM to create a desired intensity image, volume or light field. In the large-étendue setting, conventional 3D content representations, such as point clouds, multilayer images or polygons40,41, are infeasible because the large synthetic aperture requires view-dependent effects to be modelled. For this reason, a light field L is a natural way to represent the target content in this setting. Existing light-field-based CGH algorithms aim to minimize the error between each ray of the target light field and the hologram converted into a light field representation34,43,44, typically using variants of the short-time Fourier transform. Supervising the optimized SLM phase on light rays, however, is not physically meaningful because the notion of a ray does not exist in physical optics at the scale of the wavelength of visible light.

To address this issue, we propose a new light-field-based CGH framework. Unlike existing algorithms that rely on ray-based representations for light-field holograms or use random pupils in the Fourier domain58, we supervise our optimization reflecting the wave nature of light more accurately, by incorporating partial coherence and phase continuity at the target field. For this purpose, we formulate the physically correct partially coherent image formation of our hologram to simulate an image passing through the user’s pupil, Iholo, and compare it with the corresponding image simulated incoherently from the light field, Ilf, as

$${I}_{{\rm{lf}}}^{\mu }\left({\bf{x}}\right)={\int}_{\!{\bf{u}}}L\left({\bf{x}},{\bf{u}}\right)\,{{\bf{1}}}_{\mu }\left({\bf{u}}\right)d{\bf{u}},$$
(3)
$${I}_{{\rm{holo}}}^{\mu }\left({\bf{x}}\right)={\left\langle {\left\vert {{\mathcal{F}}}^{-1}\left(\;{\mathcal{F}}\left({f}^{\;k}({\bf{x}},{{\bf{u}}}^{m},{\phi }^{m})\right){{\bf{1}}}_{\mu }\left({\bf{u}}\right)\right)\right\vert }^{2}\right\rangle }_{k,m},$$
(4)
$$\mathop{\min }\limits_{\{{\phi }^{m = 1\ldots M}\}}\sum _{\forall \mu \subset {\bf{U}}}{\mathcal{L}}\left({I}_{{\rm{lf}}}^{\mu }\left({\bf{x}}\right),{I}_{{\rm{holo}}}^{\mu }\left({\bf{x}}\right)\right),$$
(5)

where 1μ is the indicator function for a set of subapertures μ (a subaperture is a small aperture state spanning the pupil positions closest to the corresponding light field view), and U is the set of all possible subaperture combinations within our synthetic aperture. We thus aim to optimize phase patterns for any possible pupil position, diameter and shape of the user simultaneously. For this purpose, we randomly sample a batch of subaperture configurations in each iteration of our optimization routine, with the loss function \({\mathcal{L}}\) measuring the mean-squared error for each subset of the apertures within the batch (see the Methods and Supplementary Note 5 for additional details).

In Fig. 4, we show experimentally captured 3D holograms. Figure 4a shows photographs captured at various focal distances—0 D (∞ m), 1.5 D (0.67 m) and 2.5 D (0.4 m)—for two different camera positions within the eyebox (that is, shifted laterally by 4.5 mm). Moreover, we compare a conventional 3D CGH algorithm57, the state-of-the-art light-field-based CGH algorithm34, and our CGH framework for all of these settings. Our results achieve the highest quality, exhibiting the best contrast and sharpness, and they demonstrate clear 3D refocusing capabilities as well as view-dependent parallax. In Fig. 4b, we capture a scene from a single camera position and a fixed focus with a varying camera pupil diameter. As is expected, the in-focus part of the 3D scene remains sharply focused without the conventional resolution degradation while the out-of-focus blur, that is, the depth-of-field effect, gets stronger with an increasing pupil diameter. The phase SLM patterns do not need to be recomputed for varying pupil positions, diameters or shapes, as all possible configurations are intrinsically accounted for by our unique CGH framework. All diffraction orders created by the SLM are jointly optimized to reduce artefacts59.

Fig. 4: Experimentally captured results in a large-étendue setting.
figure 4

a, Comparison of holographic rendering techniques using experimentally captured results with different focus states (far: 0 D, middle: 1.5 D, near: 2.5 D) and pupil positions. b, Experimental results with various pupil sizes demonstrate robust image quality in the focused object (left insets), with correctly represented depth of field (right insets) according to the pupil size. RGB channel images were captured separately at the same wavelength and merged to enhance the visual perception of the 3D effect and image quality (pseudo-colour).

Full size image

Discussion

The co-design of our synthetic aperture waveguide holography hardware and AI-based holography algorithms enables a compact full-colour 3D MR system with large étendue, demonstrating a high-quality holographic light field across a large 3D eyebox within a compact display device form factor. Partial coherence is the key to achieving the high-quality results we demonstrate with a large étendue, because it enables the creation of light-field holograms with high-rank MI, thus offering more degrees of freedom than purely coherent image formations.

Our prototype supports a 9 × 8 mm eyebox size. In Supplementary Note 8, we derive the relationship between the transverse eyebox size e, SLM size LSLM, eyepiece focal length f and the maximum steering angle θscan as

$$e=\min \left(\frac{{L}_{{\mathtt{SLM}}\;}f}{| z| },\frac{f\lambda }{p}+2f\sin {\theta }_{{\rm{scan}}}\right)\le {L}_{{\mathtt{SLM}}},$$
(6)

where the equality holds when the gap between the eyepiece and the SLM approaches zero (that is, zero thickness waveguide and polarizers).

Indeed, equation (6) shows that the eyebox size of our prototype approaches the theoretical upper bound we could achieve with any holographic display system, as our eyebox size is close to that of the SLM. This is particularly exciting because Fresnel holography configurations, such as ours, typically support only very small eyebox sizes.

The proposed co-design of compact large-étendue waveguide architecture and AI-driven algorithms enables compact 3D MR display modes with high image quality across a large eyebox, offering a path towards true 3D holographic MR glasses.

Methods

Experimental set-up

Our architecture is shown in Fig. 1. The total field of view of the compact prototype is 38° diagonal, with a supported eyebox size of 9 × 8 mm and an eye-relief distance range of 23–33 mm (Fig. 3). The diffraction-limited resolution of this system is 1.2 arcmin of visual angle, which is close to the human visual acuity of 20/20 vision, that is, 1 arcmin. The fibre-coupled laser is collimated using a small lens, and the MEMS mirror is tilted 45° to steer the beam directly into the waveguide.

The layout of the waveguide is similar to typical pupil-replicating waveguides47, with three diffractive elements, an in-coupler, a pupil-expansion coupler and an out-coupler. In our compact prototype, each coupler is an angle-encoded multiplexed VBG hologram to cover the target steering angle of 20°, for three wavelengths of 460 nm, 520 nm and 638 nm. The grating is optically fabricated by recording interference pattern of two laser beams on photo-refractive polymer using custom-designed prisms61. The substrate thickness is 0.6 mm, and anti-reflective coating is applied for visible light. The output light is filtered using a polarizer before illuminating the SLM. The achievable frame rates of our prototype are limited by the refresh rate of the SLM (60 Hz). Yet, it is possible to achieve the full bandwidth of the MEMS mirror (400 Hz) with the use of high-frame-rate SLMs that are commercially available62. We do not filter higher-order copies, which contribute to the images by reducing contrast (for example, in Fig. 4, the 8-mm pupil exhibits slightly lower contrast than the 2.5-mm pupil). We note that the effect of higher diffraction orders decreases as the pixel pitch size of the SLM decreases. While our SLM has an 8-μm pixel pitch, a pixel pitch below 4.8 μm can effectively separate higher diffraction orders for pupil sizes of 3 mm.

In addition to a compact prototype, we also built a benchtop prototype as a testbed for our algorithms. The main purpose of the benchtop set-up is to test our waveguide and wave propagation models. For this prototype, we use a conventional eyepiece and SRG waveguide and expand the beam path using multiple 4-f systems to ablate the effect of undiffracted light by optically separating it from the waveguide, while keeping the specifications of wavelengths, SLM, MEMS mirror and geometric parameters similar to those of the compact prototype set-up, which uses the holographic waveguide and eyepiece. We captured Figs. 1 and 2 with our compact prototype and Figs. 3 and 4 with our benchtop prototype.

Coherent wave propagation model with bandwidth migration

In a large-étendue setting, we need to simulate a coherent wave propagation operator for a wide range of spatial frequencies. This is computationally challenging for conventional wave propagation algorithms, because a very large number of spatial positions or, similarly, spatial frequencies must be processed simultaneously. We derive a computationally efficient implementation of this wave propagation in synthetic aperture waveguide holography displays based on bandwidth migration.

The naive approach to modelling the propagation of a coherent input field fin with a steering angle um, for example, guided by steered illumination, is to apply a phase ramp function to the input as \({f}_{{\rm{in}}}{e}^{j2\uppi ({{\bf{u}}}^{m}\cdot {\bf{r}})}\). As mentioned above, however, adequately sampling this function would require a prohibitively large number of spatial frequencies to be considered. Instead, we migrate the bandwidth in the Fourier plane and use an off-axis wave propagation to sample the output field at the shifted coordinates56. This off-axis wave propagation with bandwidth migration \({{\mathcal{P}}}_{z}\) can be represented as

$${{\mathcal{P}}}_{z}\left(\;{f}_{{\rm{in}}};{{\bf{u}}}^{m}\right)\left({\bf{x}}\right)={{\mathcal{F}}}^{-1}\left({\mathcal{F}}(\;{f}_{{\rm{in}}})({\bf{u}}-{{\bf{u}}}^{m})\times {{\mathcal{H}}}_{z}({\bf{u}})\times {e}^{i{{\bf{x}}}^{m}\cdot {\bf{u}}}\right)\left({\bf{x}}+{{\bf{x}}}^{m}\right),$$
(7)
$${{\mathcal{H}}}_{z}({\bf{u}})={e}^{j\frac{2\pi z}{\lambda }\sqrt{1-{\lambda }^{2}| {\bf{u}}{| }^{2}}},$$
(8)

where x is the spatial coordinate at the propagated plane and \({{\bf{x}}}^{m}=z\tan \left(\arcsin \left(\lambda {{\bf{u}}}^{m}\right)\right)\) is the shift in the spatial domain during the propagation. Note that this calculation can be performed at the same cost as the original wave propagation, without steering. The inverse Fourier transform along the shifted frequency coordinate does not affect the incoherent sum of each propagate mode, while avoiding aliasing in the transfer function \({{\mathcal{H}}}_{z}({\bf{u}}) {e}^{i{{\bf{x}}}^{m}\cdot {\bf{u}}}\) (see Supplementary Note 4 for details).

In our implementation of equations (1) and (7), we additionally parameterize and learn non-idealities of the physical optical setup, including nonlinear voltage-to-phase mapping and imperfect diffraction efficiency of the SLM. Thus, in our partially coherent propagation model, each coherent mode is propagated to the target plane at z as

$${f}^{\;k}\left({\bf{x}};{{\bf{u}}}^{m},{\phi }^{m}\right)={{\mathcal{P}}}_{z,{\mathcal{A}}}\left({f}_{{\rm{WG}}}^{\;k}\left({\bf{r}};{{\bf{u}}}^{m}\right){e}^{j{\phi }_{{\rm{SLM}}}}+{c}_{{\rm{WG}}}^{k}\left({\bf{r}};{{\bf{u}}}^{m}\right);{{\bf{u}}}^{m}\right),$$
(9)

where k and m are the index for coherent modes and the synthetic aperture, respectively, \({f}_{{\rm{WG}}}^{\;k}\left(\cdot \right),{c}_{{\rm{WG}}}^{k}\left(\cdot \right)\) are the kth mode of the waveguide output and the corresponding undiffracted component from the SLM, \({\phi }_{{\rm{SLM}}}(\cdot ;m)={\rm{LUT}}\left({\phi }^{m}\right)\) is the nonlinear phase response of the SLM represented as a small MLP33, and \({{\mathcal{P}}}_{z,{\mathcal{A}}}\) is propagation operator with learned aberrations \({\mathcal{A}}\): \({{\mathcal{P}}}_{z,{\mathcal{A}}}(\;f\;)={{\mathcal{F}}}^{-1}\left({\mathcal{F}}({{\mathcal{P}}}_{z}(\;f\;))\times {e}^{i{\mathcal{A}}}\right)\). These modes are added up incoherently and, optionally, an incoherent term to model additional stray light can be added as a separate mode. We note that modelling high diffraction orders and off-axis propagation are essential to capturing the accurate physics of this wave propagation, as presented in Table 1.

Implicit neural waveguide model

The waveguide output can be understood as an ensemble of beam patches shaped by multiple total internal reflections and interactions with the gratings. These interactions are governed by the diffraction efficiency of the gratings, which varies spatially owing to non-uniformities, such as fabrication-induced defects, and angularly in response to changing input angles. In addition, propagation within the waveguide necessitates bandwidth migration, as described in equation (7), which reveals predictable wavefront shifts with varying input angles. This understanding motivates our use of a learned coordinate mapping (coordinate transform MLP) that flexibly learns these shifts with angle changes, enabling scalable modelling over a large étendue.

Our model is general enough to model steered or non-steered illumination through a waveguide or for a free-space optical set-up. In all cases, we first input the spatial coordinates and steered angles into a coordinate transformation MLP with three layers, 32 features and rectified linear unit nonlinearity. This MLP outputs transformed spatial coordinates, which are then passed through a hyperbolic tangent layer to ensure a valid range. Finally, these transformed coordinates are used to query features using multi-resolution hash encoding37. The features from the hash table are subsequently fed into the main waveguide MLP with 3 layers, 64 features and rectified linear unit nonlinearity, as illustrated in Fig. 2a, and outputs K complex field values at given spatial coordinates. We use K = 4 for the benchtop set-up and K = 16 for the thin benchtop set-up. As discussed in the primary text, this model significantly reduces the number of parameters that need to be optimized and, thus, provides a much more compact representation that can be optimized faster and with less training data than comparable explicit CNN-based models. Moreover, this model is continuous and naturally interpolates the low-rank MI it represents to any spatial frequency on the synthetic aperture.

We note that implicit neural representations offer a flexible design trade-off for modelling large-étendue optical systems, as memory scales with signal complexity rather than resolution. These representations have been shown to efficiently recover 3D refractive index maps and volumetric fluorescence images, outperforming classical methods in optical microscopy63,64. Unlike these approaches, which map 3D coordinates to a refractive index or image volume, our model maps 4D spatio-angular coordinates to the complex-valued wavefront or pupil aberrations, making it well suited for modelling large-étendue optical systems.