Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Universal routing of light via optical thermodynamics

Nature Photonics volume 19, pages 1116–1121 (2025)Cite this article

Subjects

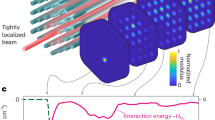
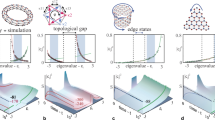
Abstract

Understanding and exploiting the dynamics of complex nonlinear systems is nowadays at the core of a broad range of scientific and technological endeavours. Within the optical domain, light evolution in a nonlinear multimode environment presents a formidable problem, as its chaotic evolution often hinders predictive insights. Recently, an optical thermodynamic framework has been put forward that, in a systematic manner, can not only predict but also harness the intricate behaviour of these systems. By deploying entropic principles, here we demonstrate a counter-intuitive optical process in which light, launched into any input port of a judiciously designed nonlinear array, universally channels into a tightly localized ground state, a response that is completely unattainable in linear conservative arrangements. This phenomenon arises from the interplay between lattice structure and the way the kinetic and nonlinear Hamiltonian components unfold, leading to two optical thermal processes: Joule–Thomson-like expansion followed by mode thermalization. Experimentally, this effect is demonstrated in properly configured nonlinear time-synthetic mesh lattices, where the optical temperature approaches near zero, causing light to condense at a single spot, regardless of the initial excitation position. The effect demonstrated here opens new avenues for applying the principles of optical thermodynamics in realizing new optical functionalities, such as all-optical beam-steering, multiplexing and nonlinear beam-shaping in high-power regimes, while also offering a greater understanding of the notable physics of light–matter interactions in multimode nonlinear systems.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Nonlinear funnelling of light.
Fig. 2: Thermodynamic principle of light-funnelling.
Fig. 3: Experimental observation of universal light-funnelling.
Fig. 4: Regime of optical funnelling.

Similar content being viewed by others

Data availability

Source data are provided with this paper. All other data supporting the plots and findings within this paper are available from the corresponding authors upon request.

Code availability

The numerical codes used in this study (MATLAB) are available upon request from the corresponding authors.

References

  1. Wit, X. M., Fruchart, M., Khain, T., Toschi, F. & Vitelli, V. Pattern formation by turbulent cascades. Nature 627, 515–521 (2024).

    Article  ADS  Google Scholar 

  2. Manneville, P. Instabilities, Chaos and Turbulence, Vol. 1 (World Scientific, 2010).

  3. Pelissetto, A. & Vicari, E. Critical phenomena and renormalization-group theory. Phys. Rep. 368, 549–727 (2002).

    Article  ADS  MathSciNet  Google Scholar 

  4. Wigen, P. E. Nonlinear Phenomena and Chaos in Magnetic Materials 1–12 (World Scientific, 1994).

  5. Deng, S. et al. Phase transitions associated with magnetic-field induced topological orbital momenta in a non-collinear antiferromagnet. Nat. Commun. 15, 822 (2024).

    Article  ADS  Google Scholar 

  6. Uversky, V. N. Dancing protein clouds: the strange biology and chaotic physics of intrinsically disordered proteins. J. Biol. Chem. 291, 6681–6688 (2016).

    Article  Google Scholar 

  7. Jumper, J. et al. Highly accurate protein structure prediction with AlphaFold. Nature 596, 583–589 (2021).

    Article  ADS  Google Scholar 

  8. Boyd, R. W. & Gaeta, A. L. in Laser Optics of Condensed Matter, Vol. 2, The Physics of Optical Phenomena and Their Use as Probes of Matter (eds Garmire, E. et al.) 99–105 (Springer, 1991).

  9. Zakharov, V. E., L’vov, V. S. & Falkovich, G. Kolmogorov Spectra of Turbulence I: Wave Turbulence (Springer, 2012).

  10. Mangini, F., Ferraro, M., Tonello, A., Couderc, V. & Wabnitz, S. High-temperature wave thermalization spoils beam self-cleaning in nonlinear multimode GRIN fibers. Opt. Lett. 48, 4741–4744 (2023).

    Article  ADS  Google Scholar 

  11. Longhi, S. Modulational instability and space time dynamics in nonlinear parabolic-index optical fibers. Opt. Lett. 28, 2363–2365 (2003).

    Article  ADS  Google Scholar 

  12. Mangini, F. et al. Statistical mechanics of beam self-cleaning in GRIN multimode optical fibers. Opt. Express 30, 10850–10865 (2022).

    Article  ADS  Google Scholar 

  13. Wu, F. O., Hassan, A. U. & Christodoulides, D. N. Thermodynamic theory of highly multimoded nonlinear optical systems. Nat. Photonics 13, 776–782 (2019).

    Article  ADS  Google Scholar 

  14. Parto, M. et al. Thermodynamic conditions governing the optical temperature and chemical potential in nonlinear highly multimoded photonic systems. Opt. Lett. 44, 3936–3939 (2019).

    Article  ADS  Google Scholar 

  15. Makris, K. G. et al. Statistical mechanics of weakly nonlinear optical multimode gases. Opt. Lett. 45, 1651–1654 (2020).

    Article  ADS  Google Scholar 

  16. Pathria, R. K. & Beale, P. D. in Statistical Mechanics 1–23 (Elsevier, 2011).

  17. Martynov, G. A. The problem of phase transitions in statistical mechanics. Phys.-Uspekhi 42, 517 (1999).

    Article  ADS  Google Scholar 

  18. Bekenstein, J. D. Generalized second law of thermodynamics in black-hole physics. Phys. Rev. D 9, 3292 (1974).

    Article  ADS  Google Scholar 

  19. Marques Muniz, A. L. et al. Observation of photon-photon thermodynamic processes under negative optical temperature conditions. Science 379, 1019–1023 (2023).

    Article  ADS  Google Scholar 

  20. Pourbeyram, H. et al. Direct observations of thermalization to a Rayleigh-Jeans distribution in multimode optical fibres. Nat. Phys. 18, 685–690 (2022).

    Article  Google Scholar 

  21. Mangini, F. et al. On the maximization of entropy in the process of thermalization of highly multimode nonlinear beams. Opt. Lett. 49, 3340–3343 (2024).

    Article  ADS  Google Scholar 

  22. Fusaro, A., Garnier, J., Krupa, K., Millot, G. & Picozzi, A. Dramatic acceleration of wave condensation mediated by disorder in multimode fibers. Phys. Rev. Lett. 122, 123902 (2019).

    Article  ADS  Google Scholar 

  23. Pyrialakos, G. G., Ren, H., Jung, P. S., Khajavikhan, M. & Christodoulides, D. N. Thermalization dynamics of nonlinear non-Hermitian optical lattices. Phys. Rev. Lett. 128, 213901 (2022).

    Article  ADS  Google Scholar 

  24. Baudin, K. et al. Observation of light thermalization to negative-temperature Rayleigh-Jeans equilibrium states in multimode optical fibers. Phys. Rev. Lett. 130, 063801 (2023).

    Article  ADS  Google Scholar 

  25. Ren, H. et al. Nature of optical thermodynamic pressure exerted in highly multimoded nonlinear systems. Phys. Rev. Lett. 131, 193802 (2023).

    Article  ADS  Google Scholar 

  26. Shi, C., Kottos, T. & Shapiro, B. Controlling optical beam thermalization via band-gap engineering. Phys. Rev. Res. 3, 033219 (2021).

    Article  Google Scholar 

  27. Ferraro, M., Mangini, F., Zitelli, M. & Wabnitz, S. On spatial beam self-cleaning from the perspective of optical wave thermalization in multimode graded-index fibers. Adv. Phys.: X 8, 2228018 (2023).

    Google Scholar 

  28. Picozzi, A. Towards a nonequilibrium thermodynamic description of incoherent nonlinear optics. Opt. Express 15, 9063–9083 (2007).

    Article  ADS  Google Scholar 

  29. Kirsch, M. S. et al. Observation of Joule–Thomson photon-gas expansion. Nat. Phys. 21, 214–220 (2025).

    Article  Google Scholar 

  30. Podivilov, E. et al. Thermalization of orbital angular momentum beams in multimode optical fibers. Phys. Rev. Lett. 128, 243901 (2022).

    Article  ADS  Google Scholar 

  31. Ramos, A., Fernández-Alcázar, L., Kottos, T. & Shapiro, B. Optical phase transitions in photonic networks: a spin-system formulation. Phys. Rev. X 10, 031024 (2020).

    Google Scholar 

  32. Weidemann, S. et al. Topological funneling of light. Science 368, 311–314 (2020).

    Article  ADS  MathSciNet  Google Scholar 

  33. Haus, H. A. Waves and fields in optoelectronics. Opt. Acta: Int. J. Opt. 32, 748 (1984).

    Google Scholar 

  34. Lu, L., Joannopoulos, J. D. & Soljačić, M. Topological photonics. Nat. Photonics 8, 821–829 (2014).

    Article  ADS  Google Scholar 

  35. Vakil, A. & Engheta, N. Transformation optics using graphene. Science 332, 1291–1294 (2011).

    Article  ADS  Google Scholar 

  36. Plotnik, Y. et al. Experimental observation of optical bound states in the continuum. Phys. Rev. Lett. 107, 183901 (2011).

    Article  ADS  Google Scholar 

  37. Kildishev, A. V., Boltasseva, A. & Shalaev, V. M. Planar photonics with metasurfaces. Science 339, 1232009 (2013).

    Article  Google Scholar 

  38. Hsu, C. W. et al. Observation of trapped light within the radiation continuum. Nature 499, 188–191 (2013).

    Article  ADS  Google Scholar 

  39. Yu, Z. & Fan, S. Complete optical isolation created by indirect interband photonic transitions. Nat. Photonics 3, 91–94 (2009).

    Article  ADS  Google Scholar 

  40. Alù, A. & Engheta, N. Achieving transparency with plasmonic and metamaterial coatings. Phys. Rev. E 72, 016623 (2005).

    Article  ADS  Google Scholar 

  41. Bar-Hillel, L. et al. Time refraction and time reflection above critical angle for total internal reflection. Phys. Rev. Lett. 132, 263802 (2024).

    Article  ADS  MathSciNet  Google Scholar 

  42. Brongersma, M. L. & Shalaev, V. M. The case for plasmonics. Science 328, 440–441 (2010).

    Article  ADS  Google Scholar 

  43. Lederer, F. et al. Discrete solitons in optics. Phys. Rep. 463, 1–126 (2008).

    Article  ADS  Google Scholar 

  44. Kivshar, Y. S. & Campbell, D. K. Peierls–Nabarro potential barrier for highly localized nonlinear modes. Phys. Rev. E 48, 3077 (1993).

    Article  ADS  Google Scholar 

  45. Stegeman, G. I. & Segev, M. Optical spatial solitons and their interactions: universality and diversity. Science 286, 1518–1523 (1999).

    Article  Google Scholar 

  46. Chen, H.-H. & Liu, C.-S. Solitons in nonuniform media. Phys. Rev. Lett. 37, 693 (1976).

    Article  ADS  MathSciNet  Google Scholar 

  47. Peschel, U., Pertsch, T. & Lederer, F. Optical Bloch oscillations in waveguide arrays. Opt. Lett. 23, 1701–1703 (1998).

    Article  ADS  Google Scholar 

  48. Morandotti, R., Peschel, U., Aitchison, J., Eisenberg, H. & Silberberg, Y. Experimental observation of linear and nonlinear optical Bloch oscillations. Phys. Rev. Lett. 83, 4756 (1999).

    Article  ADS  Google Scholar 

  49. Agrawal, G. P. in Nonlinear Science at the Dawn of the 21st Century (eds Christiansen, P. L. et al.) 195–211 (Springer, 2000).

Download references

Acknowledgements

This research was partially supported by the US Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering (Award No. DE-SC0025224 for developing the theory and building the experimental set-up to H.M.D., A.M.B.B., M.A.S., H.R., G.G.P., D.N.C. and M.K.), Army Research Office (Grant No. W911NF-23-1-0312 to H.M.D., A.M.B.B., M.A.S., H.R., G.G.P., D.N.C. and M.K.), the Air Force Office of Scientific Research (AFOSR) Multidisciplinary University Research Initiative (MURI) (Award No. FA9550-20-1-0322 for novel light–matter interactions in topologically non-trivial Weyl semimetal structures and systems to H.M.D., A.M.B.B., M.A.S., H.R., G.G.P., D.N.C. and M.K.), ONR MURI (Award No. N00014-20-1-2789 for the classical entanglement of light to H.M.D., A.M.B.B., M.A.S., H.R., G.G.P., D.N.C. and M.K.), AFOSR MURI (Award No. FA9550-21-1-0202 for programmable systems with non-Hermitian quantum dynamics to H.M.D., A.M.B.B., M.A.S., H.R., G.G.P., D.N.C. and M.K.), Department of Energy (Grant No. DESC0022282 to M.A.S., H.R., G.G.P. and D.N.C.), W. M. Keck Foundation (M.A.S., H.R., G.G.P. and D.N.C.), the MPS Simons collaboration (Simons Grant No. 733682 to M.A.S., H.R., G.G.P. and D.N.C.), US Air Force Research Laboratory (Grant No. FA86511820019 to M.A.S., H.R., G.G.P. and D.N.C.), and fellowships from the University of Southern California (H.M.D. and A.M.B.B.).

Author information

Author notes

  1. These authors contributed equally: Hediyeh M. Dinani, Georgios G. Pyrialakos.

Authors and Affiliations

  1. Ming Hsieh Department of Electrical and Computer Engineering, University of Southern California, Los Angeles, CA, USA

    Hediyeh M. Dinani, Georgios G. Pyrialakos, Abraham M. Berman Bradley, Huizhong Ren, Mahmoud A. Selim, Demetrios N. Christodoulides & Mercedeh Khajavikhan

  2. Abbe Center of Photonics, Friedrich Schiller University Jena, Jena, Germany

    Monika Monika & Ulf Peschel

  3. Department of Physics and Astronomy, University of Southern California, Los Angeles, CA, USA

    Demetrios N. Christodoulides & Mercedeh Khajavikhan

Authors
  1. Hediyeh M. Dinani
    View author publications

    Search author on:PubMed Google Scholar

  2. Georgios G. Pyrialakos
    View author publications

    Search author on:PubMed Google Scholar

  3. Abraham M. Berman Bradley
    View author publications

    Search author on:PubMed Google Scholar

  4. Monika Monika
    View author publications

    Search author on:PubMed Google Scholar

  5. Huizhong Ren
    View author publications

    Search author on:PubMed Google Scholar

  6. Mahmoud A. Selim
    View author publications

    Search author on:PubMed Google Scholar

  7. Ulf Peschel
    View author publications

    Search author on:PubMed Google Scholar

  8. Demetrios N. Christodoulides
    View author publications

    Search author on:PubMed Google Scholar

  9. Mercedeh Khajavikhan
    View author publications

    Search author on:PubMed Google Scholar

Contributions

G.G.P., H.M.D., D.N.C. and M.K. developed the idea. H.M.D. and G.G.P. performed the simulations. H.M.D. and A.M.B.B. built the set-up, and H.M.D. performed the experiments. All authors contributed to the analysis of the results and preparation of the paper.

Corresponding authors

Correspondence to Demetrios N. Christodoulides or Mercedeh Khajavikhan.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Photonics thanks Tsampikos Kottos, Maxim Shcherbakov and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Figs. 1–13 and Discussion Sections 1–13.

Source data

Source Data Figs. 3 and 4

Source data for all experimental figures presented in the main text.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dinani, H.M., Pyrialakos, G.G., Berman Bradley, A.M. et al. Universal routing of light via optical thermodynamics. Nat. Photon. 19, 1116–1121 (2025). https://doi.org/10.1038/s41566-025-01756-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41566-025-01756-4

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing