Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Topological bands and correlated states in helical trilayer graphene

Nature Physics volume 21, pages 239–244 (2025)Cite this article

Subjects

Abstract

The intrinsic anomalous Hall effect (AHE) is driven by non-zero Berry curvature and spontaneous time-reversal symmetry breaking. This effect can be realized in two-dimensional moiré systems hosting flat electronic bands but is not usually seen in inversion-symmetric materials. Here, we show that this physics is manifested in helical trilayer graphene—three graphene layers, each twisted in sequence by the same angle—although the system retains global in-plane inversion symmetry. We uncover a phase diagram of correlated and magnetic states at a magic twist angle of 1.8∘, which is explained by a lattice relaxation that leads to the formation of large periodic domains where in-plane inversion symmetry is broken on the moiré scale. Each domain harbours flat topological bands with opposite Chern numbers in the two valleys. We find correlated states at multiple integer and fractional electron fillings per moiré unit cell and an AHE at a subset of them. The AHE disappears above a critical electric displacement field at one electron per unit cell, indicating a topological phase transition. We establish helical trilayer graphene as a platform that presents an opportunity to engineer topology due to its emergent moiré-scale symmetries.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: HTG.
Fig. 2: Strong electronic interactions.
Fig. 3: AHE.
Fig. 4: Density-induced switching near ν = 3.

Similar content being viewed by others

Data availability

All the experimental data used in this work are available via Harvard Dataverse at https://doi.org/10.7910/DVN/TVYXOI (ref. 67). Source data are provided with this paper. All other data that support the findings of this study are available from the corresponding authors upon reasonable request.

References

  1. Xiao, D., Chang, M.-C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959–2007 (2010).

    ADS  MathSciNet  MATH  Google Scholar 

  2. Sharpe, A. L. et al. Emergent ferromagnetism near three-quarters filling in twisted bilayer graphene. Science 365, 605–608 (2019).

    ADS  MATH  Google Scholar 

  3. Serlin, M. et al. Intrinsic quantized anomalous Hall effect in a moiré heterostructure. Science 367, 900–903 (2020).

    ADS  MATH  Google Scholar 

  4. Chen, G. et al. Tunable correlated Chern insulator and ferromagnetism in a moiré superlattice. Nature 579, 56–61 (2020).

    ADS  MATH  Google Scholar 

  5. Polshyn, H. et al. Electrical switching of magnetic order in an orbital Chern insulator. Nature 588, 66–70 (2020).

    ADS  Google Scholar 

  6. Chen, S. et al. Electrically tunable correlated and topological states in twisted monolayer–bilayer graphene. Nat. Phys. 17, 374–380 (2021).

    MATH  Google Scholar 

  7. Stepanov, P. et al. Competing zero-field Chern insulators in superconducting twisted bilayer graphene. Phys. Rev. Lett. 127, 197701 (2021).

    ADS  Google Scholar 

  8. Tschirhart, C. L. et al. Imaging orbital ferromagnetism in a moiré Chern insulator. Science 372, 1323–1327 (2021).

    ADS  MATH  Google Scholar 

  9. He, M. et al. Competing correlated states and abundant orbital magnetism in twisted monolayer-bilayer graphene. Nat. Commun. 12, 4727 (2021).

    ADS  MATH  Google Scholar 

  10. Polshyn, H. et al. Topological charge density waves at half-integer filling of a moiré superlattice. Nat. Phys. 18, 42–47 (2022).

    MATH  Google Scholar 

  11. Tseng, C.-C. et al. Anomalous Hall effect at half filling in twisted bilayer graphene. Nat. Phys. 18, 1038–1042 (2022).

    MATH  Google Scholar 

  12. Kuiri, M. et al. Spontaneous time-reversal symmetry breaking in twisted double bilayer graphene. Nat. Commun. 13, 6468 (2022).

    ADS  MATH  Google Scholar 

  13. Chen, G. et al. Tunable orbital ferromagnetism at noninteger filling of a moiré superlattice. Nano Lett 22, 238–245 (2022).

    ADS  MATH  Google Scholar 

  14. Lin, J.-X. et al. Spin-orbit-driven ferromagnetism at half moiré filling in magic-angle twisted bilayer graphene. Science 375, 437–441 (2022).

    ADS  MATH  Google Scholar 

  15. Polski, R. et al. Hierarchy of symmetry breaking correlated phases in twisted bilayer graphene. Preprint at https://arxiv.org/abs/2205.05225 (2022).

  16. Zhang, C. et al. Local spectroscopy of a gate-switchable moiré quantum anomalous Hall insulator. Nat. Commun. 14, 3595 (2023).

    ADS  MATH  Google Scholar 

  17. Zhang, N. J. et al. Angle-resolved transport non-reciprocity and spontaneous symmetry breaking in twisted trilayer graphene. Nat. Mater. 23, 356–362 (2024).

    ADS  MATH  Google Scholar 

  18. He, M. et al. Symmetry-broken Chern insulators in twisted double bilayer graphene. Nano Lett 23, 11066–11072 (2023).

    ADS  MATH  Google Scholar 

  19. Li, T. et al. Quantum anomalous Hall effect from intertwined moiré bands. Nature 600, 641–646 (2021).

    ADS  MATH  Google Scholar 

  20. Anderson, E. et al. Programming correlated magnetic states with gate-controlled moiré geometry. Science 381, 325–330 (2023).

    ADS  MATH  Google Scholar 

  21. Cai, J. et al. Signatures of fractional quantum anomalous Hall states in twisted MoTe2. Nature 622, 63–68 (2023).

    ADS  MATH  Google Scholar 

  22. Zeng, Y. et al. Thermodynamic evidence of fractional Chern insulator in moiré MoTe2. Nature 622, 69–73 (2023).

    ADS  MATH  Google Scholar 

  23. Foutty, B. A. et al. Mapping twist-tuned multiband topology in bilayer WSe2. Science 384, 343–347 (2024).

    ADS  Google Scholar 

  24. Park, H. et al. Observation of fractionally quantized anomalous Hall effect. Nature 622, 74–79 (2023).

    ADS  MATH  Google Scholar 

  25. Xu, F. et al. Observation of integer and fractional quantum anomalous Hall effects in twisted bilayer MoTe2. Phys. Rev. X 13, 031037 (2023).

    Google Scholar 

  26. Uri, A. et al. Superconductivity and strong interactions in a tunable moiré quasicrystal. Nature 620, 762–767 (2023).

    ADS  MATH  Google Scholar 

  27. Yang, C., May-Mann, J., Zhu, Z. & Devakul, T. Multi-moiré trilayer graphene: Lattice relaxation, electronic structure, and magic angles. Phys. Rev. B 110, 115434 (2024).

    MATH  Google Scholar 

  28. Mora, C., Regnault, N. & Bernevig, B. A. Flatbands and perfect metal in trilayer moiré graphene. Phys. Rev. Lett. 123, 026402 (2019).

    ADS  Google Scholar 

  29. Foo, D. C. W. et al. Extended magic phase in twisted graphene multilayers. Phys. Rev. Res. 6, 013165 (2024).

    MATH  Google Scholar 

  30. Popov, F. K. & Tarnopolsky, G. Magic angle butterfly in twisted trilayer graphene. Phys. Rev. Res. 5, 043079 (2023).

    Google Scholar 

  31. Mao, Y., Guerci, D. & Mora, C. Supermoiré low-energy effective theory of twisted trilayer graphene. Phys. Rev. B 107, 125423 (2023).

    ADS  Google Scholar 

  32. Popov, F. K. & Tarnopolsky, G. Magic angles in equal-twist trilayer graphene. Phys. Rev. B 108, L081124 (2023).

    ADS  Google Scholar 

  33. Devakul, T. et al. Magic-angle helical trilayer graphene. Sci. Adv. 9, eadi6063 (2023).

    Google Scholar 

  34. Guerci, D., Mao, Y. & Mora, C. Chern mosaic and ideal flat bands in equal-twist trilayer graphene. Phys. Rev. Res. 6, L022025 (2024).

    Google Scholar 

  35. Nakatsuji, N., Kawakami, T. & Koshino, M. Multiscale lattice relaxation in general twisted trilayer graphenes. Phys. Rev. X 13, 041007 (2023).

    MATH  Google Scholar 

  36. Yoo, H. et al. Atomic and electronic reconstruction at the van der Waals interface in twisted bilayer graphene. Nat. Mater. 18, 448–453 (2019).

    ADS  MATH  Google Scholar 

  37. Guerci, D., Mao, Y. & Mora, C. Nature of even and odd magic angles in helical twisted trilayer graphene. Phys. Rev. B 109, 205411 (2024).

    ADS  Google Scholar 

  38. Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).

    ADS  MATH  Google Scholar 

  39. Zondiner, U. et al. Cascade of phase transitions and dirac revivals in magic-angle graphene. Nature 582, 203–208 (2020).

    ADS  MATH  Google Scholar 

  40. Wong, D. et al. Cascade of electronic transitions in magic-angle twisted bilayer graphene. Nature 582, 198–202 (2020).

    ADS  MATH  Google Scholar 

  41. Kwan, Y. H., Ledwith, P. J., Lo, C. F. B. & Devakul, T. Strong-coupling topological states and phase transitions in helical trilayer graphene. Phys. Rev. B 109, 125141 (2024).

    ADS  Google Scholar 

  42. Park, J. M., Cao, Y., Watanabe, K., Taniguchi, T. & Jarillo-Herrero, P. Tunable strongly coupled superconductivity in magic-angle twisted trilayer graphene. Nature 590, 249–255 (2021).

    ADS  MATH  Google Scholar 

  43. Huang, C., Wei, N. & MacDonald, A. H. Current-driven magnetization reversal in orbital Chern insulators. Phys. Rev. Lett. 126, 056801 (2021).

    ADS  MathSciNet  Google Scholar 

  44. Sharpe, A. L. et al. Evidence of orbital ferromagnetism in twisted bilayer graphene aligned to hexagonal boron nitride. Nano Lett 21, 4299–4304 (2021).

    ADS  MATH  Google Scholar 

  45. Grover, S. et al. Chern mosaic and berry-curvature magnetism in magic-angle graphene. Nat. Phys. 18, 885–892 (2022).

    MATH  Google Scholar 

  46. Lau, C. N., Bockrath, M. W., Mak, K. F. & Zhang, F. Reproducibility in the fabrication and physics of moiré materials. Nature 602, 41–50 (2022).

    ADS  Google Scholar 

  47. Dong, J., Ledwith, P. J., Khalaf, E., Lee, J. Y. & Vishwanath, A. Many-body ground states from decomposition of ideal higher Chern bands: applications to chirally twisted graphene multilayers. Phys. Rev. Res. 5, 023166 (2023).

    MATH  Google Scholar 

  48. Zhu, J., Su, J.-J. & MacDonald, A. H. Voltage-controlled magnetic reversal in orbital Chern insulators. Phys. Rev. Lett. 125, 227702 (2020).

    ADS  Google Scholar 

  49. Zhang, C. et al. Manipulation of chiral interface states in a moiré quantum anomalous hall insulator. Nat. Phys. 20, 951–956 (2024).

    MATH  Google Scholar 

  50. Long, M., Jimeno-Pozo, A., Sainz-Cruz, H., Pantaleón, P. A. & Guinea, F. Evolution of superconductivity in twisted graphene multilayers. Proc. Natl Acad. Sci. USA 121, e2405259121 (2024).

    Google Scholar 

  51. Wang, L. et al. One-dimensional electrical contact to a two-dimensional material. Science 342, 614–617 (2013).

    ADS  MATH  Google Scholar 

  52. Spietz, L., Teufel, J. & Schoelkopf, R. J. A twisted pair cryogenic filter. Preprint at https://arxiv.org/abs/cond-mat/0601316 (2006).

  53. Chiba, D. et al. Electrical control of the ferromagnetic phase transition in cobalt at room temperature. Nat. Mater. 10, 853–856 (2011).

    ADS  MATH  Google Scholar 

  54. Arrott, A. Criterion for ferromagnetism from observations of magnetic isotherms. Phys. Rev. 108, 1394–1396 (1957).

    ADS  MATH  Google Scholar 

  55. Slater, J. C. & Koster, G. F. Simplified LCAO method for the periodic potential problem. Phys. Rev. 94, 1498–1524 (1954).

    ADS  MATH  Google Scholar 

  56. Koshino, M. Interlayer interaction in general incommensurate atomic layers. New J. Phys. 17, 015014 (2015).

    ADS  MATH  Google Scholar 

  57. Wilhelm, P. H., Lang, T. C., Scheurer, M. S. & Läuchli, A. M. Non-coplanar magnetism, topological density wave order and emergent symmetry at half-integer filling of moiré Chern bands. SciPost Phys 14, 040 (2023).

    ADS  Google Scholar 

  58. Zhu, Z., Cazeaux, P., Luskin, M. & Kaxiras, E. Modeling mechanical relaxation in incommensurate trilayer van der Waals heterostructures. Phys. Rev. B 101, 224107 (2020).

    ADS  MATH  Google Scholar 

  59. Cazeaux, P., Luskin, M. & Massatt, D. Energy minimization of two dimensional incommensurate heterostructures. Arch. Ration. Mech. Anal. 235, 1289–1325 (2019).

    MathSciNet  MATH  Google Scholar 

  60. Carr, S. et al. Relaxation and domain formation in incommensurate two-dimensional heterostructures. Phys. Rev. B 98, 224102 (2018).

    ADS  MATH  Google Scholar 

  61. Kaxiras, E. & Duesbery, M. S. Free energies of generalized stacking faults in Si and implications for the brittle-ductile transition. Phys. Rev. Lett. 70, 3752–3755 (1993).

    ADS  Google Scholar 

  62. Zhou, S., Han, J., Dai, S., Sun, J. & Srolovitz, D. J. Van der Waals bilayer energetics: generalized stacking-fault energy of graphene, boron nitride, and graphene/boron nitride bilayers. Phys. Rev. B 92, 155438 (2015).

    ADS  Google Scholar 

  63. Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558–561 (1993).

    ADS  MATH  Google Scholar 

  64. Kresse, G. & Furthmüller, J. Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).

    MATH  Google Scholar 

  65. Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).

    ADS  MATH  Google Scholar 

  66. Peng, H., Yang, Z.-H., Perdew, J. P. & Sun, J. Versatile van der Waals density functional based on a meta-generalized gradient approximation. Phys. Rev. X 6, 041005 (2016).

    MATH  Google Scholar 

  67. Xia, L. Replication data for ‘Topological bands and correlated states in helical trilayer graphene’. Harvard Dataverse https://doi.org/10.7910/DVN/TVYXOI (2024).

Download references

Acknowledgements

We thank M. Kastner, P. Ledwith and E. Berg for helpful discussions, A. Bangura, G. Jones, R. Nowell, A. Woods and S. Hannahs for technical support and X. Wang for assistance with device fabrication. This work was partially supported by the Army Research Office MURI (grant no. W911NF2120147), the 2DMAGIC MURI (grant no. FA9550-19-1-0390), the National Science Foundation (grant no. DMR-1809802), the STC Center for Integrated Quantum Materials (NSF grant no. DMR-1231319), the Ramón Areces Foundation and the Gordon and Betty Moore Foundation’s EPiQS Initiative through grant no. GBMF9463 to P.J.H. This work was supported by the Air Force Office of Scientific Research (AFOSR) under grant no. FA9550-22-1-0432. Measurement infrastructure was funded in part by the Gordon and Betty Moore Foundation’s EPiQS initiative through grant nos. GBMF3429 and GBMF9460. D.G.-G. gratefully acknowledges support from the Ross M. Brown Family Foundation. D.G.-G.’s involvement in measurements at Stanford and data analysis was supported by the US Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division, under contract DE-AC02-76SF00515. K.W. and T.T. acknowledge support from the JSPS KAKENHI (grant nos. 21H05233 and 23H02052) and World Premier International Research Center Initiative (WPI), MEXT, Japan. A portion of this work was performed at the National High Magnetic Field Laboratory, which is supported by National Science Foundation cooperative agreement no. DMR-2128556 and the State of Florida. This work was performed in part at the Harvard University Center for Nanoscale Systems (CNS); a member of the National Nanotechnology Coordinated Infrastructure Network (NNCI), which is supported by the National Science Foundation under NSF grant no. ECCS-2025158. This work was carried out in part through the use of MIT.nano’s facilities. This work made use of the MRSEC Shared Experimental Facilities at MIT, supported by the National Science Foundation under grant no. DMR-1419807. A.U. acknowledges support from the MIT Pappalardo Fellowship and from the VATAT Outstanding Postdoctoral Fellowship in Quantum Science and Technology. Z.Z. is supported by a Stanford Science fellowship. Sandia National Laboratories is a multimission laboratory managed and operated by National Technology & Engineering Solutions of Sandia, LLC, a wholly owned subsidiary of Honeywell International Inc., for the US Department of Energy’s National Nuclear Security Administration under contract no. DE-NA000352.

Author information

Author notes

  1. These authors contributed equally: Li-Qiao Xia, Sergio C. de la Barrera, Aviram Uri.

Authors and Affiliations

  1. Department of Physics, Massachusetts Institute of Technology, Cambridge, MA, USA

    Li-Qiao Xia, Sergio C. de la Barrera, Aviram Uri, Aaron Sharpe, Liang Fu, Trithep Devakul & Pablo Jarillo-Herrero

  2. Department of Physics, University of Toronto, Toronto, Ontario, Canada

    Sergio C. de la Barrera

  3. Materials Physics Department, Sandia National Laboratories, Livermore, CA, USA

    Aaron Sharpe

  4. Princeton Center for Theoretical Science, Princeton University, Princeton, NJ, USA

    Yves H. Kwan

  5. Stanford Institute for Materials and Energy Sciences, SLAC National Accelerator Laboratory, Menlo Park, CA, USA

    Ziyan Zhu & David Goldhaber-Gordon

  6. Research Center for Electronic and Optical Materials, National Institute for Materials Science, Tsukuba, Japan

    Kenji Watanabe

  7. Research Center for Materials Nanoarchitectonics, National Institute for Materials Science, Tsukuba, Japan

    Takashi Taniguchi

  8. Department of Physics, Stanford University, Stanford, CA, USA

    David Goldhaber-Gordon & Trithep Devakul

Authors
  1. Li-Qiao Xia
    View author publications

    Search author on:PubMed Google Scholar

  2. Sergio C. de la Barrera
    View author publications

    Search author on:PubMed Google Scholar

  3. Aviram Uri
    View author publications

    Search author on:PubMed Google Scholar

  4. Aaron Sharpe
    View author publications

    Search author on:PubMed Google Scholar

  5. Yves H. Kwan
    View author publications

    Search author on:PubMed Google Scholar

  6. Ziyan Zhu
    View author publications

    Search author on:PubMed Google Scholar

  7. Kenji Watanabe
    View author publications

    Search author on:PubMed Google Scholar

  8. Takashi Taniguchi
    View author publications

    Search author on:PubMed Google Scholar

  9. David Goldhaber-Gordon
    View author publications

    Search author on:PubMed Google Scholar

  10. Liang Fu
    View author publications

    Search author on:PubMed Google Scholar

  11. Trithep Devakul
    View author publications

    Search author on:PubMed Google Scholar

  12. Pablo Jarillo-Herrero
    View author publications

    Search author on:PubMed Google Scholar

Contributions

S.C.d.l.B. and A.U. conceived the project. L.-Q.X. fabricated the devices with the help of A.U. L.-Q.X., A.U. and S.C.d.l.B. carried out the helium-3 transport measurements. A.S. and L.-Q.X. carried out the dilution refrigerator transport measurements under the supervision of D.G.-G. T.D. and Y.H.K. performed band structure, magnetization and Hartree–Fock calculations. T.D. and Z.Z. performed lattice-relaxation calculations. K.W. and T.T. supplied the boron nitride crystals. A.U., S.C.d.l.B., L.-Q.X., A.S., T.D., L.F. and P.J.-H. analysed the data and discussed the interpretation. A.U., S.C.d.l.B. and L.-Q.X. wrote the manuscript with input from all authors. P.J.-H. supervised the project.

Corresponding authors

Correspondence to Li-Qiao Xia, Sergio C. de la Barrera, Aviram Uri or Pablo Jarillo-Herrero.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks Ipsita Das and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

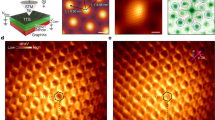
Extended Data Fig. 1 Optical micrographs of HTG devices.

a, Device 1 - a secondary device with θ = 1.77∘. b, Device 2 - our main device with θ = 1.79∘. c, Device 3. This device shares the van der Waals heterostructure with Device 2. Rxx and Ryx contacts are indicated by black dots for all devices. d, Contrast-enhanced optical micrograph of Device 2 after stacking. The crystallographic edges of the top hBN, bottom hBN, and top monolayer graphene are highlighted, showing no accidental alignment between hBN and HTG. All scale bars are 2 μm.

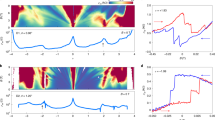
Extended Data Fig. 2 Twist angle determination.

a, Rxx Landau fan from Device 2, measured at D = 0 and T = 300 mK. Electron-side (right) and hole-side (left) are plotted with different color scales to improve contrast. Dashed lines correspond to the best-fit series shown in b. b, Map of the best-fit slopes from a emerging from a consistent set of integer fillings, ν. Red lines emerge from nν=±4 and ν = ± 4 (off-scale due to measurement limitations) in a and b, respectively.

Extended Data Fig. 3 Device 1 characterization.

a, Rxx versus n and D, showing resistance peaks at charge neutrality (ν = 0), at the moiré band gaps (ν = ± 4), and at the correlated states at ν=1,2,3. b, Field-trained ΔRyx measured at T = 300 mK and B = ± 60 mT versus ν and D. Hot spots near ν=1,3 indicate AHE. c,d, Field-antisymmetrized Ryx and field-symmetrized Rxx taken at ν=2.9 (cyan circle in b) and D/ϵ0 = − 0.15 V/nm while sweeping B up (solid) and down (dashed) at different temperatures as indicated. Temperature colorcode in d is identical to c. e,f, Same as c,d, taken at ν=0.8 and D/ϵ0 = 0.1 V/nm (pink triangle in b).

Extended Data Fig. 4 Device 3 characterization.

a, Rxx versus n and D, showing resistance peaks at charge neutrality (ν=0), at the moiré band gaps (ν = ± 4), and at the correlated states at ν=1,2,3. The contact resistance becomes very large when ν ≳ 3.2, leading to artifacts in the data. b, Field-trained ΔRyx measured at T = 300 mK and B = ± 60 mT versus ν and D. Hot spots near ν=1,3 indicate AHE. c,d, Field-antisymmetrized Ryx and field-symmetrized Rxx taken at ν=3.1 (cyan circle in b) and D/ϵ0 = 0 while sweeping B up (solid) and down (dashed) at different temperatures as indicated. The temperature color code in d is identical to c. e,f, Same as c,d, taken at ν=0.8 and D/ϵ0 = − 0.09 V/nm (pink triangle in b).

Extended Data Fig. 5 Single-particle density of states and Van Hove singularity.

(left) The single particle DOS with momentum-dependent tunneling as a function of filling factor and layer potential. The Van Hove singularity at which the Hall density switches sign is indicated by the dashed lines. (right) Extended Fermi surfaces at the Van Hove singularity are shown for the four points indicated by stars in the DOS plot.

Extended Data Fig. 6 Extraction of the Curie temperature using an Arrott plot.

\({R}_{yx}^{2}\) versus ∣B/Ryx∣. Positive (negative) extrapolated intercept of the linear part at high B indicates a ferromagnetic (paramagnetic) state. The curve taken at T = 10.5 K has approximately zero intercept, indicating a Curie temperature TC ≈ 10.5 K.

Extended Data Fig. 7 Temperature dependence and gap sizes estimation.

a, Rxx (raw data, not field-symmetrized) versus ν and T of Device 2 at D = 0 and B = 0. The jumps in resistance near ν=3 reflect the AHE of different magnetic states combined with Ryx mixing. A pronounced electron-hole asymmetry is demonstrated. b, line cuts of a versus 1/T at different ν as indicated. Some curves show non-monotonic temperature dependence due to the parallel conduction of the insulating domains and the metallic network of domain walls. The total resistance can be modelled by \({R}_{{{\rm{tot}}}}={({R}_{{{\rm{M}}}}^{-1}+{R}_{{{\rm{I}}}}^{-1})}^{-1}\), where RM and RI are the resistance of the metallic walls and insulating domains, respectively. When one of the resistances is much smaller than the other, we have \({R}_{{{\rm{tot}}}}\approx \min ({R}_{{{\rm{M}}}},{R}_{{{\rm{I}}}})\). At low temperatures, 1/T ≳ 0.2 K−1, the insulating bulk is shunted by the metal, saturating the increased resistance of the insulating domains. As T is increased to intermediate values, 1/T ~ 0.1 K−1, the domains become less resistive and Rtot ≈ RI. We use this regime to estimate the gap sizes for ν=0,2,3 (indicated) by fitting the data to \(R={R}_{0}\exp \{-{\Delta }_{\nu }/2{k}_{B}T\}\), where Δν is the gap at filling ν and kB is Boltzmann’s constant. At higher temperatures, 1/T ≲ 0.05 K−1 for ν=2,3, the correlated states give way to a metallic phase, accounting for the increasing resistance with T at those filling factors. At ν=1, evidence for thermal activation is absent, indicating a semimetallic state without a fully developed correlated gap.

Extended Data Fig. 8 Correlated state at ν=7/2.

a, Rxx versus ν, measured on Device 2 at D = 0, B = 0, and T = 300 mK. At ν=7/2, we find a resistance peak distinct from the one at ν=3. b, Waterfall plot of antisymmetrized Ryx taken by sweeping B up (solid) and down (dashed) as the fast axis at D = 0 and different ν, as indicated on the right of every other curve. The AHE persists beyond ν=7/2.

Extended Data Fig. 9 Hartree-Fock calculations at ν=7/2 and 2/3.

a, Charge density n(r) (measured relative to that at full flat band filling nν=+4(r)) of the tetrahedral antiferromagnet (TAF) at ν=7/2. Grey dots indicate ABA-stacking regions. b, Local spin orientation in the TAF. Arrows denote spin direction in sx − sy plane, while red (blue) coloring indicates out-of-plane polarization along \(+{\hat{s}}_{z}(-{\hat{s}}_{z})\). Grey parallelogram indicates the new quadrupled moiré unit cell. c,d Same as a except for the \({\hat{C}}_{3z}\) charge density wave and stripe charge density wave respectively. e, ΔE of the different translation symmetry breaking solutions at ν=7/2 as a function of interlayer potential U. ΔE is measured relative to that of the best translation- symmetric solution. f, Charge gap of the translation symmetry breaking solutions at ν=7/2. g,h, Same as e,f except for the best translation symmetry breaking solution at ν=2/3. All calculations performed on a 18 × 18 system using θ = 1.80∘, wAA = 75 meV.

Supplementary information

Supplementary Information

Supplementary Figs.1–10, discussion and Tables 1 and 2.

Source data

Source Data Fig. 3

See headers for a description of the data structure.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xia, LQ., de la Barrera, S.C., Uri, A. et al. Topological bands and correlated states in helical trilayer graphene. Nat. Phys. 21, 239–244 (2025). https://doi.org/10.1038/s41567-024-02731-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41567-024-02731-6

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing