Abstract
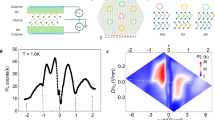
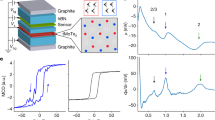
Topological flat bands formed in two-dimensional lattice systems offer an opportunity to study fractional phases of matter in the absence of an external magnetic field. Examples include fractional quantum anomalous Hall effects and fractional topological insulators. Recently, fractional quantum anomalous Hall effects have been experimentally realized in both twisted bilayer MoTe2 and rhombohedral-stacked multilayer graphene on hexagonal boron nitride. These studies focus mainly on the first moiré flat band, but there is a possibility that non-Abelian states could occur in the second moiré band. Here we present a systematic transport study of twisted bilayer MoTe2 devices, focusing on the second moiré band. We observe ferromagnetism in the second moiré band, and a Chern insulator state driven by out-of-plane magnetic fields at a filling factor of three holes per moiré unit cell. Between fillings of 2.2 and 2.7 holes per moiré unit cell, we observe a finite temperature resistivity minimum with a 1/T scaling law at low temperatures and a large out-of-plane negative magnetoresistance. Applying an out-of-plane electric field can induce quantum phase transitions at both integer and fractional filling factors. Our studies lay the groundwork for realizing tunable topological states and other unexpected magnetic phases beyond the first moiré flat band based in twisted MoTe2.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data shown in the main figures are provided with this paper. All other data are available from the corresponding authors upon request. Source data are provided with this paper.
Code availability
The codes related to the findings of this study are available from the corresponding authors upon request.
References
Regnault, N. & Bernevig, B. A. Fractional Chern insulator. Phys. Rev. X 1, 021014 (2011).
Sheng, D. N., Gu, Z. C., Sun, K. & Sheng, L. Fractional quantum Hall effect in the absence of Landau levels. Nat. Commun. 2, 389 (2011).
Tang, E., Mei, J. W. & Wen, X. G. High-temperature fractional quantum Hall states. Phys. Rev. Lett. 106, 236802 (2011).
Sun, K., Gu, Z., Katsura, H. & Das Sarma, S. Nearly flatbands with nontrivial topology. Phys. Rev. Lett. 106, 236803 (2011).
Neupert, T., Santos, L., Chamon, C. & Mudry, C. Fractional quantum Hall states at zero magnetic field. Phys. Rev. Lett. 106, 236804 (2011).
Stern, A. Fractional topological insulators: a pedagogical review. Annu. Rev. Condens. Matter Phys. 7, 349–368 (2016).
Wu, F., Lovorn, T., Tutuc, E., Martin, I. & MacDonald, A. H. Topological insulators in twisted transition metal dichalcogenide homobilayers. Phys. Rev. Lett. 122, 086402 (2019).
Yu, H., Chen, M. & Yao, W. Giant magnetic field from moiré induced Berry phase in homobilayer semiconductors. Natl Sci. Rev. 7, 12–20 (2020).
Devakul, T., Crépel, V., Zhang, Y. & Fu, L. Magic in twisted transition metal dichalcogenide bilayers. Nat. Commun. 12, 6730 (2021).
Li, H., Kumar, U., Sun, K. & Lin, S. Z. Spontaneous fractional Chern insulators in transition metal dichalcogenide moiré superlattices. Phys. Rev. Res. 3, L032070 (2021).
Crépel, V. & Fu, L. Anomalous Hall metal and fractional Chern insulator in twisted transition metal dichalcogenides. Phys. Rev. B 107, L201109 (2023).
Li, T. et al. Quantum anomalous Hall effect from intertwined moiré bands. Nature 600, 641–646 (2021).
Zhao, W. et al. Realization of the Haldane Chern insulator in a moiré lattice. Nat. Phys. 20, 275–280 (2024).
Tao, Z. et al. Valley-coherent quantum anomalous Hall state in AB-stacked MoTe2/WSe2 bilayers. Phys. Rev. X 14, 011004 (2024).
Anderson, E. et al. Programming correlated magnetic states with gate-controlled moiré geometry. Science 381, 325–330 (2023).
Foutty, B. A. et al. Mapping twist-tuned multiband topology in bilayer WSe2. Science 384, 343–347 (2024).
Cai, J. et al. Signatures of fractional quantum anomalous Hall states in twisted MoTe2. Nature 622, 63–68 (2023).
Zeng, Y. et al. Thermodynamic evidence of fractional Chern insulator in moiré MoTe2. Nature 622, 69–73 (2023).
Park, H. et al. Observation of fractionally quantized anomalous Hall effect. Nature 622, 74–79 (2023).
Xu, F. et al. Observation of integer and fractional quantum anomalous Hall effects in twisted bilayer MoTe2. Phys. Rev. X 13, 031037 (2023).
Kang, K. et al. Evidence of the fractional quantum spin Hall effect in moiré MoTe2. Nature 628, 522–526 (2024).
Kang, K. et al. Double quantum spin hall phase in moiré WSe2. Nano Lett. 24, 14901–14907 (2024).
Ji, Z. et al. Local probe of bulk and edge states in a fractional Chern insulator. Nature 635, 578–583 (2024).
Redekop, E. et al. Direct magnetic imaging of fractional Chern insulators in twisted MoTe2. Nature 635, 584–589 (2024).
Lu, Z. et al. Fractional quantum anomalous Hall effect in multilayer graphene. Nature 626, 759–764 (2024).
Xie, J. et al. Tunable fractional Chern insulators in rhombohedral graphene superlattices. Preprint at https://arxiv.org/abs/2405.16944 (2024).
Xu, C., Mao, N., Zeng, T., & Zhang, Y. Multiple Chern bands in twisted MoTe2 and possible non-Abelian states. Phys. Rev. Lett. 134, 066601 (2025).
Reddy, A. P., Paul, N., Abouelkomsan, A. & Fu, L. Non-Abelian fractionalization in topological minibands. Phys. Rev. Lett. 133, 166503 (2024).
Wang, C. et al. Higher Landau-level analogues and signatures of non-Abelian states in twisted bilayer MoTe2. Preprint at https://arxiv.org/abs/2404.05697 (2024).
Ahn, C. E., Lee, W., Yananose, K., Kim, Y., & Cho, G. Y. Non-abelian fractional quantum anomalous Hall states and first Landau level physics in second moiré band of twisted bilayer MoTe2. Preprint at https://arxiv.org/abs/2403.19155 (2024).
Zhang, Y. H. Non-Abelian and Abelian descendants of vortex spin liquid: fractional quantum spin Hall effect in twisted MoTe2. Phys. Rev. B 110, 155102 (2024).
Villadiego, I. S. Halperin states of particles and holes in ideal time reversal invariant pairs of Chern bands and the fractional quantum spin Hall effect in moiré MoTe2. Phys. Rev. B 110, 045114 (2024).
May-Mann, J., Stern, A., & Devakul, T. Theory of half-integer fractional quantum spin Hall insulator edges. Preprint at https://arxiv.org/abs/2403.03964 (2024).
Chen, F., Luo, W. W., Zhu, W., & Sheng, D. N. Robust non-Abelian even-denominator fractional Chern insulator in twisted bilayer MoTe2. Preprint at https://arxiv.org/abs/2405.08386 (2024).
Jian, C. M., & Xu, C. Minimal fractional topological insulator in half-filled conjugate moiré Chern bands. Preprint at https://arxiv.org/abs/2403.07054 (2024).
Liu, H., Liu, Z., & Bergholtz, E. J. Non-Abelian fractional Chern Insulators and competing states in flat moiré bands. Preprint at https://arxiv.org/abs/2405.08887 (2024).
Chiu, C. K., Teo, J. C. Y., Schnyder, A. P. & Ryu, S. Classification of topological quantum matter with symmetries. Rev. Mod. Phys. 88, 035005 (2016).
Maciejko, J., Qi, X. L. & Zhang, S. C. Magnetoconductance of the quantum spin Hall state. Phys. Rev. B 82, 155310 (2010).
Kondo, J. Resistance minimum in dilute magnetic alloys. Prog. Theor. Phys. 32, 37–49 (1964).
Costi, T. A. Kondo effect in a magnetic field and the magnetoresistivity of Kondo alloys. Phys. Rev. Lett. 85, 1504–1507 (2000).
Felsch, W. & Winzer, K. Magnetoresistivity of (La, Ce)Al2 alloys. Solid State Commun. 13, 569–573 (1973).
Lee, M. Electrolyte gate-controlled Kondo effect in SrTiO3. Phys. Rev. Lett. 107, 256601 (2011).
Ohkawa, F. J. Magnetoresistance of Kondo lattices. Phys. Rev. Lett. 64, 2300–2303 (1990).
Wang, Z., Barros, K., Chern, G. W., Maslov, D. L. & Batista, C. D. Resistivity minimum in highly frustrated itinerant magnets. Phys. Rev. Lett. 117, 206601 (2016).
Willett, R. et al. Observation of an even-denominator quantum number in the fractional quantum Hall effect. Phys. Rev. Lett. 59, 1776–1779 (1987).
Jain, J. K. Composite Fermions (Cambridge Univ. Press, 2007).
Moore, G. & Read, N. Nonabelions in the fractional quantum hall effect. Nucl. Phys. B 360, 362–396 (1991).
Nayak, C., Simon, S. H., Stern, A., Freedman, M. & Das Sarma, S. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 80, 1083–1159 (2008).
Lilly, M. P., Cooper, K. B., Eisenstein, J. P., Pfeiffer, L. N. & West, K. W. Anisotropic states of two-dimensional electron systems in high Landau levels: effect of an in-plane magnetic field. Phys. Rev. Lett. 83, 824–827 (1999).
Pan, W. et al. Strongly anisotropic electronic transport at Landau level filling factor ν = 9/2 and ν = 5/2 under a tilted magnetic field. Phys. Rev. Lett. 83, 820–823 (1999).
Samkharadze, N. et al. Observation of a transition from a topologically ordered to a spontaneously broken symmetry phase. Nat. Phys. 12, 191–195 (2016).
Wang, L. et al. One-dimensional electrical contact to a two-dimensional material. Science 342, 614–617 (2013).
Li, C. et al. Tunable superconductivity in electron- and hole-doped Bernal bilayer graphene. Nature 631, 300–306 (2024).
Tang, Y. et al. Simulation of Hubbard model physics in WSe2/WS2 moiré superlattices. Nature 579, 353–358 (2020).
Ciorciaro, L. et al. Kinetic magnetism in triangular moiré materials. Nature 623, 509–513 (2023).
Tang, Y. et al. Evidence of frustrated magnetic interactions in a Wigner–Mott insulator. Nat. Nanotechnol. 18, 233–237 (2023).
Tao, Z. et al. Observation of spin polarons in a frustrated moiré Hubbard system. Nat. Phys. 20, 783–787 (2024).
Mao, N. et al. Transfer learning relaxation, electronic structure and continuum model for twisted bilayer MoTe2. Commun. Phys. 7, 262 (2024).
Zhang, X. W. et al. Polarization-driven band topology evolution in twisted MoTe2 and WSe2. Nat. Commun. 15, 4223 (2024).
Jia, Y. et al. Moiré fractional Chern insulators. I. First-principles calculations and continuum models of twisted bilayer MoTe2. Phys. Rev. B 109, 205121 (2024).
Morales-Durán, N., Wei, N., Shi, J. & MacDonald, A. H. Magic angles and fractional Chern insulators in twisted homobilayer transition metal dichalcogenides. Phys. Rev. Lett. 132, 096602 (2024).
Song, X. Y., Zhang, Y. H. & Senthil, T. Phase transitions out of quantum Hall states in moiré materials. Phys. Rev. B 109, 085143 (2024).
Dong, J., Wang, J., Ledwith, P. J., Vishwanath, A. & Parker, D. E. Composite Fermi liquid at zero magnetic field in twisted MoTe2. Phys. Rev. Lett. 131, 136502 (2023).
Qiu, W. X., Li, B., Luo, X. J. & Wu, F. Interaction-driven topological phase diagram of twisted bilayer MoTe2. Phys. Rev. X 13, 041026 (2023).
Li, B., Qiu, W. X. & Wu, F. Electrically tuned topology and magnetism in twisted bilayer MoTe2 at νh = 1. Phys. Rev. B 109, L041106 (2024).
Fan, F. R., Xiao, C. & Yao, W. Orbital Chern insulator at ν = −2 in twisted MoTe2. Phys. Rev. B 109, L041403 (2024).
Liu, X. et al. Gate-tunable antiferromagnetic Chern insulator in twisted bilayer transition metal dichalcogenides. Phys. Rev. Lett. 132, 146401 (2024).
Wang, T. et al. Topology, magnetism and charge order in twisted MoTe2 at higher integer hole fillings. Preprint at https://arxiv.org/abs/2312.12531 (2023).
Yu, J. et al. Fractional Chern insulators versus nonmagnetic states in twisted bilayer MoTe2. Phys. Rev. B 109, 045147 (2024).
Wang, M., Wang, X., & Vafek, O. Phase diagram of twisted bilayer MoTe2 in a magnetic field with an account for the electron-electron interaction. Phys. Rev. B 110, L201107 (2024).
Reddy, A. P. & Fu, L. Toward a global phase diagram of the fractional quantum anomalous Hall effect. Phys. Rev. B 108, 245159 (2023).
Goldman, H., Reddy, A. P., Paul, N. & Fu, L. Zero-field composite Fermi liquid in twisted semiconductor bilayers. Phys. Rev. Lett. 131, 136501 (2023).
Wang, C. et al. Fractional Chern insulator in twisted bilayer MoTe2. Phys. Rev. Lett. 132, 036501 (2024).
Xu, C., Li, J., Xu, Y., Bi, Z. & Zhang, Y. Maximally localized Wannier functions, interaction models, and fractional quantum anomalous Hall effect in twisted bilayer MoTe2. Proc. Natl Acad. Sci. USA 121, e2316749121 (2024).
Sharma, P., Peng, Y., & Sheng, D. N. Topological quantum phase transitions driven by a displacement field in twisted MoTe2 bilayers. Phys. Rev. B 110, 125142 (2024).
Reddy, A. P., Alsallom, F., Zhang, Y., Devakul, T. & Fu, L. Fractional quantum anomalous Hall states in twisted bilayer MoTe2 and WSe2. Phys. Rev. B 108, 085117 (2023).
Abouelkomsan, A., Reddy, A. P., Fu, L. & Bergholtz, E. J. Band mixing in the quantum anomalous Hall regime of twisted semiconductor bilayers. Phys. Rev. B 109, L121107 (2024).
Li, B., & Wu, F. Variational mapping of Chern bands to Landau levels: application to fractional Chern insulators in twisted MoTe2. Preprint at https://arxiv.org/abs/2405.20307 (2024).
Xing, C. et al. Anomalous proximitized transport in metal/quantum magnet heterostructure Bi2Ir2O7/Yb2Ti2O7. Phys. Rev. Mater. 8, 114407 (2024).
Acknowledgements
We thank F. Wu, Z. Liu, X. Xu and M. Qin for helpful discussions. This work is supported by the National Key R&D Program of China (grant nos. 2022YFA1402702, 2022YFA1405400, 2021YFA1401400, 2021YFA1400100, 2022YFA1402404, 2019YFA0308600, 2022YFA1402400, 2020YFA0309000 and 2021YFA1202902), the National Natural Science Foundation of China (grant nos. 12350403, 92265102, 12174249, 12174250, 12141404, 12374045, 12374292 and 124B1030), the Innovation Program for Quantum Science and Technology (grant nos. 2021ZD0302600 and 2021ZD0302500), the Natural Science Foundation of Shanghai (grant nos. 24QA2703700, 22PJ1406700, 24LZ1401100 and 22ZR1430900). T.L., S.J. and X.L. acknowledge the Shanghai Jiao Tong University 2030 Initiative Program. T.L. and S.J. acknowledge the Yangyang Development Fund. N.M. acknowledges the financial support from the Alexander von Humboldt Foundation. Yixin Zhang and Yang Zhang acknowledge support from Max Planck partner lab grant for quantum materials. K.W. and T.T. acknowledge support from the JSPS KAKENHI (grant nos. 21H05233 and 23H02052) and World Premier International Research Center Initiative (WPI), MEXT, Japan. A portion of this work was carried out at the Synergetic Extreme Condition User Facility (SECUF, https://cstr.cn/31123.02.SECUF).
Author information
Authors and Affiliations
Contributions
T.L., S.J. and X.L. designed and supervised the experiment. J.X., F.L., F.X., X.C. and Z. Sun fabricated the devices. F.X., Z. Sun and J.L. performed the transport measurements. X.C and J.X. performed the optical measurements. F.X., X.C., T.L., S.J. and X.L. analysed the data. Yixin Zhang, N.M., N.P. and Yang Zhang performed theoretical studies. K.W. and T.T. grew the bulk hBN crystals. T.L. and Yang Zhang wrote the paper. All authors discussed the results and commented on the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks Su-Yang Xu, Kenji Yasuda and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Twist angle calibrations and contact resistance.
a, ρxx versus ν and B⊥ at T = 300 mK and D ≈ −275 mV/nm of device A. Clear quantum oscillations can be observed around ν = −1 when B⊥ above about 6 T, corresponding to a quantum mobility about 1500 cm2/V·s. The Landau Level filling factor νLL can be determined from the Hall resistance, which allows us to derive the gate geometric capacitance accurately. b, ρxx versus ν and B⊥ at T = 300 mK and D ≈ −410 mV/nm of device B. The twisted angles for device A and B are determined to be 3.15° ± 0.1° and 3.0° ± 0.1°, respectively. c, Two-terminal resistance as a function of ν at T = 1.2 K and B⊥= 0.1 T around D = 0. It is measured with contact 21 and contact 4 of device A with a constant bias current of approximately 1 nA. The measured two-terminal resistance includes contributions from both the sample resistance and the contact resistance of the two contacts used as the source and drain for transport measurements. Given that the contact resistance is in general high in TMDc devices, we can reasonably assume that it dominates the two-terminal resistance, except when the sample is tuned into an insulating state. d,e, Contact resistance in device A (d) and device B (e) at 1.7 K. For device A, the contact resistance is measured at ν = −1.4 and D = −116 mV/nm. For device B, the contact resistance is measured at ν = −4.2 and D = −30 mV/nm. During the measurement of contact resistance, only the specific contact is biased with a 1 mV dc voltage while all other contacts are grounded.
Extended Data Fig. 2 Characterizations of device B (3.0°).
a, Optical image of device B (3.0°). b, The schematic transport measurement configuration. Contacts in a and b are labeled by numbers. c,d, Longitudinal resistivity ρxx (c) and Hall resistivity ρxy (d) as a function of ν and D. ρxx is measured under zero magnetic field at 500 mK; ρxy is the antisymmetrized results under an out-of-plane magnetic field B⊥= ± 0.3 T at 500 mK. A built-in electric field D0 about 50 mV/nm has been subtracted for device B (3.0°).
Extended Data Fig. 3 Characterizations of device C (3.7°).
a, Optical image of device C (3.7°). b-f, MCD map as a function of ν and D measured at B⊥≈ 10 mT and T = 1.6 K (b), 2 K (c), 3 K (d), 4 K (e), 5 K (f). Ferromagnetism in the second moiré band spans approximately from ν ≈ −2.65 to −3.2. The maximum Cuire temperature of the second moiré band magnetism is about 5 K.
Extended Data Fig. 4 More characterizations of device A (3.15°).
a, Optical image of device A (3.15°). Contacts are labeled by numbers. b, MCD map as a function of ν and D measured at 1.6 K. c,d, Symmetrized ρxx (c) and antisymmetrized ρxy (d) at varying temperatures at ν ≈ −2.8. e, Symmetrized ρxx and antisymmetrized ρxy under \({B}_{\perp }\)= ± 0.3 T at D ≈ 0 V/nm and T = 0.6 K, 0.9 K, 1.2 K, respectively. f, Symmetrized ρxx and antisymmetrized ρxy under at D ≈ 0 V/nm and T =1.6 K with B⊥= 0.25 T, 0.5 T, 1 T, respectively.
Extended Data Fig. 5 Magnetoresistance at ν = −2 and −4 of device A (3.15°), and the transport gap fitting at ν = −2.
a-c, Rxx versus B|| and B⊥ at ν = −2 and D = −20 mV/nm (a), D = 260 mV/nm (b) and D = −300 mV/nm (c). d, Rxx versus B|| and B⊥ at ν = −4 at D = −200 mV/nm. The measurement temperature for a-d is 300 mK. e, Temperature dependence of Rxx at ν = −2 and D = −20 mV/nm of device A (3.15°). f, Temperature dependence of Rxx at ν = −2 and D = −650 mV/nm of device B (3.0°). Dashed lines in e and f are the fit to \({\rho }_{{xx}}{\propto e}^{-\varDelta /2{k}_{B}T}\), with \(\varDelta\) and \({k}_{B}\) denoting the transport gap and Boltzmann constant, respectively. We observe that below about 40 K, the temperature dependence of Rxx shown in e becomes metallic-like, presumably due to the interplay between bulk transport and edge transport of an IQSH insulator. Consequently, the thermal activation fitting range is very narrow in e, leading to a substantial uncertainty of the estimation for the real charge gap.
Extended Data Fig. 6 Magnetoresistance at ν = −2 and −4 of device B (3.0°) and at ν = −2 of device C (3.7°).
a,b, Angle-dependent magnetoresistance at ν = −2 (a) and ν = −4 (b) of device B (3.0°) at 300 mK. The definition of the tilt angle θ is schematically illustrated in the inset of a, where θ = 90° corresponds to the in-plane magnetic field configuration. c, Rxx versus B|| and B⊥ at ν = −2 and D ≈ 0 V/nm of device C (3.7°). d, Rxx as a function of θ at ν = −2 and D ≈ 0 V/nm of device C. The applied magnetic field Btotal is fixed at 0.4 T.
Extended Data Fig. 7 In-plane Magnetoresistance and nonlocal transport of device B (3.0°).
a, The in-plane magnetoresistance Rxx(B|| =0.3 T)/Rxx(B =0) versus ν and D measured at T = 500 mK. c, The ratio between nonlocal resistance and local resistance as a function of ν and D measured at T = 500 mK and zero magnetic field. b and d illustrate the measurement configurations in a and c, respectively.
Extended Data Fig. 8 Hartree-Fock simulation and schematic band structures of integer topological phases.
a, Hartree-Fock phase diagram at v = −2 and \(\epsilon =30\); b, Hartree-Fock band structure at v = −3 and \(\epsilon =20\) without magnetic field with non-polarized initial state, showing a partially polarized anomalous Hall metal; c, Hartree-Fock band structure with the same configuration but with \(\epsilon =30\), showing a nearly gapless IQAH state. d, Hartree-Fock band structure at and \(\epsilon =30\) with Zeeman energy \({E}_{z}\)= 2 meV, displaying a C = −1 Chern insulator from two occupied K valley bands with C = (1,−1), and one occupied K′ valley band with C = −1.
Extended Data Fig. 9 Chern state at ν = −3 of device B (3.0°).
a,b, ρxx (a) and ρxy (b) versus ν and B⊥ at T = 1.6 K and D ≈ 0 V/nm. Dashed lines represent the expected dispersions based on Streda formula for the IQAH state at ν = −1 with C = 1, the FQAH state at ν = −2/3 with C = 2/3, and the Chern state emerged under B⊥ at ν = −3 with C = −1, respectively. c, ρxx and ρxy versus B⊥ alone the Streda dispersion line of the Chern state at ν = −3. The ρxy approaches the expected quantized value of h/e2, and the ρxx is gradually vanishing with increasing B⊥. d, Temperature dependence of ρxx versus D at ν = −3 from T = 1.6 K to 30 K.
Extended Data Fig. 10 Out-of-plane magnetoresistance fitting, T dependence of ρxx under B⊥ at ν ≈ −5/2 of device A (3.15°).
a-c, ρxx versus B⊥ at ν = −2.3 (a), ν = −2.5 (b), ν = −2.7 (c). Dashed lines in a-c are the fitting curves of magnetoresistance with \({\rho }_{{\rm{xx}}}\left({B}_{\perp }\right)=a/{B}_{\perp }-b/{B}_{\perp }^{2}+c\). The measurements in a-c were performed at T = 300 mK and D ≈ 0 V/nm. d, Temperature dependent ρxx at ν ≈ −2.5 and D ≈ 0 V/nm under B⊥ = 0 T and 1 T, respectively.
Supplementary information
Supplementary Information
Supplementary Figs. 1 and 2.
Source data
Source Data Fig. 1
Source data for Fig. 1b–d.
Source Data Fig. 2
Source data for Fig. 2a,b.
Source Data Fig. 3
Source data for Fig. 3a–d.
Source Data Fig. 4
Source data for Fig. 4a–d.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Xu, F., Chang, X., Xiao, J. et al. Interplay between topology and correlations in the second moiré band of twisted bilayer MoTe2. Nat. Phys. 21, 542–548 (2025). https://doi.org/10.1038/s41567-025-02803-1
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/s41567-025-02803-1
This article is cited by
-
Observation of ferromagnetic phase in the second moiré band of twisted MoTe2
Nature Communications (2025)
-
Hidden states and dynamics of fractional fillings in twisted MoTe2 bilayers
Nature (2025)
-
Twisted path to Landau levels
Nature Physics (2025)
-
Microscopic signatures of topology in twisted MoTe2
Nature Physics (2025)
-
Real-space study of monolayer hBN encapsulated bilayer MoTe2 devices
Quantum Frontiers (2025)