Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Robust supermoiré pattern in large-angle single-twist bilayers

Nature Physics volume 21, pages 1085–1092 (2025)Cite this article

Subjects

Abstract

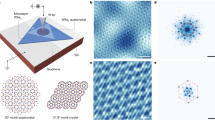
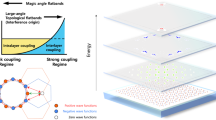
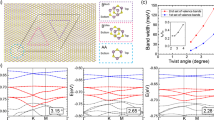
Forming long-wavelength moiré superlattices in van der Waals bilayers that have a small-angle twist between the two layers has been a key approach for creating moiré flat bands. However, for small twist angles, strong lattice reconstruction creates domain walls and other forms of disorder in the moiré pattern, posing considerable challenges for engineering such platforms. At large twist angles, the lattices are more rigid, but it is difficult to produce flat bands in shorter-wavelength moiré superlattices. Here we introduce an approach for tailoring robust supermoiré structures in bilayers of transition-metal dichalcogenides using only a single twist near a commensurate angle. Structurally, we show the spontaneous formation of a periodic arrangement of three inequivalent commensurate moiré stackings, where the angle deviation from the commensurate angle determines the periodicity. Electronically, we reveal a large set of van Hove singularities that indicate strong band hybridization, leading to flat bands near the valence band maximum. Our study extends the study of the interplay among band topology, quantum geometry and moiré superconductivity to the large twist angle regime.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: CM and SM patterns in near 32.2° tWSe2.
Fig. 2: Gliding translation relation and SM symmetry.
Fig. 3: Dense VHSs in the SM lattice.
Fig. 4: Continuum model for the SM lattice.
Fig. 5: Quasiparticle interference in a θt ≈ 31.1° SM.

Similar content being viewed by others

Data availability

Source data for the plots in Supplementary Information are available upon request. Other data are available via figshare at https://doi.org/10.6084/m9.figshare.28558070 (ref. 59). Source data are provided with this paper.

Code availability

The codes described in Supplementary Information are available upon reasonable request.

References

  1. Bistritzer, R. & MacDonald, A. H. Moiré bands in twisted double-layer graphene. Proc. Natl Acad. Sci. USA 108, 12233–12237 (2011).

    Article  ADS  Google Scholar 

  2. Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).

    Article  ADS  Google Scholar 

  3. Park, H. et al. Observation of fractionally quantized anomalous Hall effect. Nature 622, 74–79 (2023).

    Article  ADS  Google Scholar 

  4. Zeng, Y. et al. Thermodynamic evidence of fractional Chern insulator in moiré MoTe2. Nature 622, 69–73 (2023).

    Article  ADS  Google Scholar 

  5. Tsui, Y.-C. et al. Direct observation of a magnetic-field-induced Wigner crystal. Nature 628, 287–292 (2024).

    Article  ADS  Google Scholar 

  6. Craig, I. M. et al. Local atomic stacking and symmetry in twisted graphene trilayers. Nat. Mater. 23, 323–330 (2024).

    Article  ADS  Google Scholar 

  7. Devakul, T. et al. Magic-angle helical trilayer graphene. Sci. Adv. 9, eadi6063 (2023).

    Article  Google Scholar 

  8. Uri, A. et al. Superconductivity and strong interactions in a tunable moiré quasicrystal. Nature 620, 762–767 (2023).

    Article  ADS  Google Scholar 

  9. Hao, Z. et al. Electric field–tunable superconductivity in alternating-twist magic-angle trilayer graphene. Science 371, 1133–1138 (2021).

    Article  ADS  Google Scholar 

  10. Kim, H. et al. Evidence for unconventional superconductivity in twisted trilayer graphene. Nature 606, 494–500 (2022).

    Article  ADS  Google Scholar 

  11. Turkel, S. et al. Orderly disorder in magic-angle twisted trilayer graphene. Science 376, 193–199 (2022).

    Article  ADS  Google Scholar 

  12. Grover, S. et al. Chern mosaic and Berry-curvature magnetism in magic-angle graphene. Nat. Phys. 18, 885–892 (2022).

    Article  Google Scholar 

  13. Weston, A. et al. Atomic reconstruction in twisted bilayers of transition metal dichalcogenides. Nat. Nanotechnol. 15, 592–597 (2020).

    Article  ADS  Google Scholar 

  14. Gadelha, A. C. et al. Localization of lattice dynamics in low-angle twisted bilayer graphene. Nature 590, 405–409 (2021).

    Article  ADS  Google Scholar 

  15. Li, E. et al. Lattice reconstruction induced multiple ultra-flat bands in twisted bilayer WSe2. Nat. Commun. 12, 5601 (2021).

    Article  ADS  Google Scholar 

  16. Li, Y. et al. Tuning commensurability in twisted van der Waals bilayers. Nature 625, 494–499 (2024).

    Article  ADS  Google Scholar 

  17. Koren, E. et al. Coherent commensurate electronic states at the interface between misoriented graphene layers. Nat. Nanotechnol. 11, 752–757 (2016).

    Article  ADS  Google Scholar 

  18. Bistritzer, R. & MacDonald, A. H. Transport between twisted graphene layers. Phys. Rev. B 81, 245412 (2010).

    Article  ADS  Google Scholar 

  19. Mele, E. J. Commensuration and interlayer coherence in twisted bilayer graphene. Phys. Rev. B 81, 161405 (2010).

    Article  ADS  Google Scholar 

  20. Zhao, X. et al. Unveiling atomic-scale moiré features and atomic reconstructions in high-angle commensurately twisted transition metal dichalcogenide homobilayers. Nano Lett. 21, 3262–3270 (2021).

    Article  ADS  Google Scholar 

  21. Jiang, Y. et al. Electron ptychography of 2D materials to deep sub-ångström resolution. Nature 559, 343–349 (2018).

    Article  ADS  Google Scholar 

  22. Nguyen, K. X. et al. Achieving sub-0.5-angstrom–resolution ptychography in an uncorrected electron microscope. Science 383, 865–870 (2024).

    Article  ADS  Google Scholar 

  23. Liu, Y. et al. Pair density wave state in a monolayer high-Tc iron-based superconductor. Nature 618, 934–939 (2023).

    Article  ADS  Google Scholar 

  24. Chen, Z. et al. Mixed-state electron ptychography enables sub-angstrom resolution imaging with picometer precision at low dose. Nat. Commun. 11, 2994 (2020).

    Article  ADS  Google Scholar 

  25. Sung, S. H. et al. Torsional periodic lattice distortions and diffraction of twisted 2D materials. Nat. Commun. 13, 7826 (2022).

    Article  ADS  Google Scholar 

  26. Kim, J. et al. Anomalous optical excitations from arrays of whirlpooled lattice distortions in moiré superlattices. Nat. Mater. 21, 890–895 (2022).

    Article  ADS  Google Scholar 

  27. Ugeda, M. M. et al. Giant bandgap renormalization and excitonic effects in a monolayer transition metal dichalcogenide semiconductor. Nat. Mater. 13, 1091–1095 (2014).

    Article  ADS  Google Scholar 

  28. Chen, P. et al. Tunable moiré superlattice of artificially twisted monolayers. Adv. Mater. 31, 1901077 (2019).

    Article  Google Scholar 

  29. Zhang, C. et al. Probing critical point energies of transition metal dichalcogenides: surprising indirect gap of single layer WSe2. Nano Lett. 15, 6494–6500 (2015).

    Article  ADS  Google Scholar 

  30. Galperin, M., Ratner, M. A. & Nitzan, A. Inelastic electron tunneling spectroscopy in molecular junctions: peaks and dips. J. Chem. Phys. 121, 11965–11979 (2004).

    Article  ADS  Google Scholar 

  31. Klein, J., Léger, A., Belin, M., Défourneau, D. & Sangster, M. J. L. Inelastic-electron-tunneling spectroscopy of metal-insulator-metal junctions. Phys. Rev. B 7, 2336–2348 (1973).

    Article  ADS  Google Scholar 

  32. Stipe, B. C., Rezaei, M. A. & Ho, W. Single-molecule vibrational spectroscopy and microscopy. Science 280, 1732–1735 (1998).

    Article  ADS  Google Scholar 

  33. Wu, F., Lovorn, T., Tutuc, E., Martin, I. & MacDonald, A. H. Topological insulators in twisted transition metal dichalcogenide homobilayers. Phys. Rev. Lett. 122, 086402 (2019).

    Article  ADS  Google Scholar 

  34. Morales-Durán, N., Wei, N., Shi, J. & MacDonald, A. H. Magic angles and fractional Chern insulators in twisted homobilayer transition metal dichalcogenides. Phys. Rev. Lett. 132, 096602 (2024).

    Article  ADS  Google Scholar 

  35. Gao, Q., Dong, J., Ledwith, P., Parker, D. & Khalaf, E. Untwisting moiré physics: almost ideal bands and fractional Chern insulators in periodically strained monolayer graphene. Phys. Rev. Lett. 131, 096401 (2023).

    Article  ADS  Google Scholar 

  36. Balents, L., Dean, C. R., Efetov, D. K. & Young, A. F. Superconductivity and strong correlations in moiré flat bands. Nat. Phys. 16, 725–733 (2020).

    Article  Google Scholar 

  37. Yankowitz, M., McKenzie, D. & LeRoy, B. J. Local spectroscopic characterization of spin and layer polarization in WSe2. Phys. Rev. Lett. 115, 136803 (2015).

    Article  ADS  Google Scholar 

  38. Hoffman, J. E. et al. Imaging quasiparticle interference in Bi2Sr2CaCu2O8+δ. Science 297, 1148–1151 (2002).

    Article  ADS  Google Scholar 

  39. Foutty, B. A. et al. Mapping twist-tuned multiband topology in bilayer WSe2. Science 384, 343–347 (2024).

    Article  ADS  Google Scholar 

  40. Zhang, F. et al. Experimental signature of layer skyrmions and implications for band topology in twisted WSe2 bilayers. Preprint at https://arxiv.org/abs/2406.20036 (2025).

  41. Redekop, E. et al. Direct magnetic imaging of fractional Chern insulators in twisted MoTe2. Nature 635, 584–589 (2024).

    Article  Google Scholar 

  42. Xia, Y. et al. Superconductivity in twisted bilayer WSe2. Nature https://doi.org/10.1038/s41586-024-08116-2 (2024).

  43. Guo, Y. et al. Superconductivity in 5.0° twisted bilayer WSe2. Nature 637, 839–845 (2025).

    Article  Google Scholar 

  44. Lin, Y.-C. et al. Realizing large-scale, electronic-grade two-dimensional semiconductors. ACS Nano 12, 965–975 (2018).

    Article  Google Scholar 

  45. Wang, L. et al. One-dimensional electrical contact to a two-dimensional material. Science 342, 614–617 (2013).

    Article  ADS  Google Scholar 

  46. Liu, S. et al. Two-step flux synthesis of ultrapure transition-metal dichalcogenides. ACS Nano 17, 16587–16596 (2023).

    Article  Google Scholar 

  47. Tate, M. W. et al. High dynamic range pixel array detector for scanning transmission electron microscopy. Microsc. Microanal. 22, 237–249 (2016).

    Article  ADS  Google Scholar 

  48. Yin, X., Shi, C., Han, Y. & Jiang, Y. PEAR: a robust and flexible automation framework for ptychography enabled by multiple large language model agents. Preprint at https://arxiv.org/abs/2410.09034 (2024).

  49. Han, Y. et al. Strain mapping of two-dimensional heterostructures with subpicometer precision. Nano Lett. 18, 3746–3751 (2018).

    Article  ADS  Google Scholar 

  50. Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009).

    Article  Google Scholar 

  51. Giannozzi, P. et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 29, 465901 (2017).

    Article  Google Scholar 

  52. Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).

    Article  ADS  Google Scholar 

  53. Hamann, D. R. Optimized norm-conserving Vanderbilt pseudopotentials. Phys. Rev. B 88, 085117 (2013).

    Article  ADS  Google Scholar 

  54. Van Setten, M. J. et al. The PseudoDojo: training and grading a 85 element optimized norm-conserving pseudopotential table. Comput. Phys. Commun. 226, 39–54 (2018).

    Article  ADS  Google Scholar 

  55. Grimme, S., Antony, J., Ehrlich, S. & Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H–Pu. J. Chem. Phys. 132, 154104 (2010).

    Article  ADS  Google Scholar 

  56. Medeiros, P. V. C., Stafström, S. & Björk, J. Effects of extrinsic and intrinsic perturbations on the electronic structure of graphene: retaining an effective primitive cell band structure by band unfolding. Phys. Rev. B 89, 041407 (2014).

    Article  ADS  Google Scholar 

  57. Medeiros, P. V. C., Tsirkin, S. S., Stafström, S. & Björk, J. Unfolding spinor wave functions and expectation values of general operators: introducing the unfolding-density operator. Phys. Rev. B 91, 041116 (2015).

    Article  ADS  Google Scholar 

  58. Iraola, M. et al. IrRep: symmetry eigenvalues and irreducible representations of ab initio band structures. Comput. Phys. Commun. 272, 108226 (2022).

    Article  MathSciNet  Google Scholar 

  59. Li, Y. et al. Data for ‘Robust super-moiré pattern in large-angle single-twist bilayers’. figshare https://doi.org/10.6084/m9.figshare.28558070 (2025).

Download references

Acknowledgements

We acknowledge Y.-W. Son for a useful discussion. Y.L., F.Z., H.K. and C.-K.S. are mainly supported by the NSF through the Center for Dynamics and Control of Materials: an NSF Materials Research Science and Engineering Center (Cooperative Agreement No. DMR-2308817) and partially by the US Air Force (Grant No. FA2386-21-1-4061), NSF (Grant Nos. DMR-1808751 and DMR-2219610) and the Welch Foundation (Grant No. F-2164). C.S. and Y.H. acknowledge support from the NSF (Grant No. CMMI-2239545) and the Welch Foundation (Grant No. C-2065). V.-A.H. and F.G. were supported by the Welch Foundation (Grant No. F-2139-20230405). V.-A.H. and F.G. acknowledge the National Energy Research Scientific Computing Center (a DOE Office of Science User Facility supported under Contract No. DE-AC02-05CH11231) and the Texas Advanced Computing Center at the University of Texas at Austin for providing computational resources. X. Liu and X. Li were partially supported by the Department of Energy, Office of Basic Energy Sciences (Grant No. DE-SC0019398 for device fabrication) and the Welch Foundation chair (Grant No. F-0014 for sample preparation). C.D. and J.A.R. were supported by the Penn State Center for Nanoscale Science (NSF Grant No. DMR-2011839) and the Penn State 2DCC-MIP (NSF Grant No. DMR-1539916). Y.-C.L. acknowledges the support from the Center for Emergent Functional Matter Science of NYCU and the Yushan Young Scholar Program from the Ministry of Education of Taiwan. L.N.H., M.H., J.H. and K.B are supported by the NSF MRSEC programme at Columbia through the Center for Precision-Assembled Quantum Materials (NSF Grant No. DMR-2011738). Y.X., Q.G. and E.K. are supported by the NSF through the Center for Dynamics and Control of Materials: an NSF Materials Research Science and Engineering Center (Cooperative Agreement No. DMR-2308817).

Author information

Author notes

  1. These authors contributed equally: Yanxing Li, Chuqiao Shi, Fan Zhang, Xiaohui Liu.

Authors and Affiliations

  1. Department of Physics, The University of Texas at Austin, Austin, TX, USA

    Yanxing Li, Fan Zhang, Xiaohui Liu, Yuan Xue, Viet-Anh Ha, Nicolás Morales-Durán, Hyunsue Kim, Xiaoqin Li, Feliciano Giustino & Chih-Kang Shih

  2. Department of Materials Science and NanoEngineering, Rice University, Houston, TX, USA

    Chuqiao Shi & Yimo Han

  3. Oden Institute for Computational Engineering and Sciences, The University of Texas at Austin, Austin, TX, USA

    Viet-Anh Ha & Feliciano Giustino

  4. Department of Physics, Harvard University, Cambridge, MA, USA

    Qiang Gao & Eslam Khalaf

  5. Department of Materials Science and Engineering, Pennsylvania State University, University Park, PA, USA

    Chengye Dong & Yu-Chuan Lin

  6. Two-Dimensional Crystal Consortium, The Pennsylvania State University, University Park, PA, USA

    Chengye Dong & Joshua A. Robinson

  7. Department of Materials Science and Engineering, National Yang Ming Chiao Tung University, Hsinchu, Taiwan

    Yu-Chuan Lin

  8. Department of Applied Physics and Applied Mathematics, Columbia University, New York City, NY, USA

    Luke N. Holtzman & Katayun Barmak

  9. Center for Computational Quantum Physics, Flatiron Institute, New York, NY, USA

    Nicolás Morales-Durán

  10. Advanced Photon Source, Argonne National Laboratory, Lemont, IL, USA

    Yi Jiang

  11. Department of Mechanical Engineering, Columbia University, New York City, NY, USA

    Madisen Holbrook & James Hone

Authors
  1. Yanxing Li
    View author publications

    Search author on:PubMed Google Scholar

  2. Chuqiao Shi
    View author publications

    Search author on:PubMed Google Scholar

  3. Fan Zhang
    View author publications

    Search author on:PubMed Google Scholar

  4. Xiaohui Liu
    View author publications

    Search author on:PubMed Google Scholar

  5. Yuan Xue
    View author publications

    Search author on:PubMed Google Scholar

  6. Viet-Anh Ha
    View author publications

    Search author on:PubMed Google Scholar

  7. Qiang Gao
    View author publications

    Search author on:PubMed Google Scholar

  8. Chengye Dong
    View author publications

    Search author on:PubMed Google Scholar

  9. Yu-Chuan Lin
    View author publications

    Search author on:PubMed Google Scholar

  10. Luke N. Holtzman
    View author publications

    Search author on:PubMed Google Scholar

  11. Nicolás Morales-Durán
    View author publications

    Search author on:PubMed Google Scholar

  12. Hyunsue Kim
    View author publications

    Search author on:PubMed Google Scholar

  13. Yi Jiang
    View author publications

    Search author on:PubMed Google Scholar

  14. Madisen Holbrook
    View author publications

    Search author on:PubMed Google Scholar

  15. James Hone
    View author publications

    Search author on:PubMed Google Scholar

  16. Katayun Barmak
    View author publications

    Search author on:PubMed Google Scholar

  17. Joshua A. Robinson
    View author publications

    Search author on:PubMed Google Scholar

  18. Xiaoqin Li
    View author publications

    Search author on:PubMed Google Scholar

  19. Feliciano Giustino
    View author publications

    Search author on:PubMed Google Scholar

  20. Eslam Khalaf
    View author publications

    Search author on:PubMed Google Scholar

  21. Yimo Han
    View author publications

    Search author on:PubMed Google Scholar

  22. Chih-Kang Shih
    View author publications

    Search author on:PubMed Google Scholar

Contributions

C.-K.S. and Y.L. conceived the experiment. Y.L. and F.Z. carried out the STM and STS measurements. C.S. and Y.H. carried out the STEM measurements. C.S. and Y.J. performed the electron ptychography reconstruction. Y.X., Q.G. and E.K. performed the theoretical model calculations. N.M.-D. was involved in the discussion of the continuum model of TMDs. V.-A.H. and F.G. performed the density functional theory calculations. Y.-C.L. synthesized the twisted WSe2 bilayers. C.D. prepared the graphitic buffer layer/SiC. J.A.R. supervised the sample preparation effort. H.K. annealed and pretreated the samples. X. Liu and Y.L. prepared the exfoliated samples for STEM and STM under the supervision of X. Li. L.N.H., M.H., K.B. and J.H. synthesized the WSe2 bulk crystals. Y.L., F.Z., Y.H., C.S. and C.-K.S. analysed the STM and STEM data. Y.L., C.S., Y.H., E.K. and C.-K.S. wrote the paper with contributions from all authors.

Corresponding authors

Correspondence to Yimo Han or Chih-Kang Shih.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks Jiamin Xue and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 STM/S measurement of a fabricated θt ≈ 31.5° twisted bilayer WSe2 SM.

a, An STM image of the 31.5° twisted bilayer WSe2, showing a <1011 cm−2 low density of defects thanks to the high-quality bulk crystal WSe2 (VBias = −0.98 V, I = 100 pA). b, An in-gap taken STM topography image of θt ≈ 31.5° tWSe2 (VBias = −0.6 V, I = 100 pA), revealing unambiguous SM patterns. c, The FFT image of b. The black squares, blue circles, and red diamonds represent top layer WSe2 Bragg peaks, second order and first order tWSe2 moiré, with SM splitting, respectively. d, Filtered iFFT image using the FFT peaks in red diamonds. e, The logarithmic scale constant height STS taken in the pristine region (Vset = −2.0 V, I = 100 pA, Vamp = 29 mV). Blue and green arrows represent the \({\Gamma }_{1}\) and KVBM respectively. f, The constant current STS taken at the same site (Vint = −1.4 V, I = 50 pA, Vamp = 19 mV). Blue and green arrows represent the \({\Gamma }_{1}\) and KVBM respectively. Scale bars: 3 nm.

Extended Data Fig. 2 Quasiparticle interferences measurement and analysis on the fabricated θt ≈ 31.5° twisted bilayer WSe2 SM.

a–c, The constant current dI/dV mappings taken at −1.0 V (a), −0.98 V (b), and −0.96 V (c) (I = 100 pA, Vamp = 20 mV). d, Schematic of the intra-K-valley scattering in θt ≈ 31.5° SM. The purple and grey BZs depict the CM and SM BZs, respectively. ∆SM is the SM minigap while ∆CM is the CM minigap. The blue arrow exhibits the q vector from intra-K-valley scatterings. The SM γ overlaps with CM Γm and Km valleys. e–g, The FFT images of a-c, Red boxes label the regions of quasiparticle interference q vector rings near the center. Insets: magnified near-zero FFT frequency images in the red boxes, showing the rings of quasiparticle interference. h, E v.s. q/2 plot extracted from the quasiparticle interferences of θt ≈ 31.5° tWSe2 sample. The quasiparticle interferences measured under 77K can infer the intra-K-valley scatterings information. The blue curve shows the parabolic fitting of K-valley band dispersion from the three quasiparticle interference measurement dots. The fitted effective mass and KVBM energy levels are meff = 0.55 ± 0.1, EKVBM = −0.925 ± 0.1 eV. The vertical error bars, shown as grey lines, are set as 20 meV in E due to local field fluctuation. The horizontal error bars, also shown as grey lines, are from the q estimations in each Fourier transferred images, which is limited by the image resolution, field of view and quasiparticle interference ring width. Scale bars: a, b, c, 3 nm.

Supplementary information

Supplementary Information

Supplementary Figs. 1–27 and Notes 1–6.

Source data

Source Data Fig. 3

Statistical source data.

Source Data Fig. 4

Statistical source data.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, Y., Shi, C., Zhang, F. et al. Robust supermoiré pattern in large-angle single-twist bilayers. Nat. Phys. 21, 1085–1092 (2025). https://doi.org/10.1038/s41567-025-02914-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41567-025-02914-9

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing