Abstract
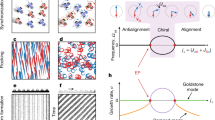
Motility-induced phase separation occurs in assemblies of self-propelled units when activity is coupled negatively to density. By contrast, the consequences of a positive coupling between density and activity on the collective behaviour of active matter remain unexplored. Here we show that collective activity can emerge from such a positive coupling among non-motile building blocks. We perform experiments with self-sustained oscillators powered by contact-charge electrophoresis. Although the oscillators are non-motile by design, they spontaneously form an active gas when confined together. The super-elastic nature of collisions constitutes a positive density–activity coupling and underlies the active gas properties. Elucidating the origin of binary collisions allows us to precisely control the structure of the active gas and its eventual crystallization. Beyond considering the overlooked positive coupling between density and activity, our work suggests that rich collective properties can emerge not only from the symmetry of interactions between active building blocks but also from their adaptable and responsive behaviour.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
As the raw datasets generated during the current study comprise several terabytes of data, it is not possible to share them on a public repository. However, they are available from the corresponding authors on reasonable request. Source data for the figures are provided with this paper and are available via figshare at https://doi.org/10.6084/m9.figshare.28661015 (ref. 45).
References
Toner, J., Tu, Y. & Ramaswamy, S. Hydrodynamics and phases of flocks. Ann. Phys. 318, 170–244 (2005).
Bricard, A., Caussin, J. B., Desreumaux, N., Dauchot, O. & Bartolo, D. Emergence of macroscopic directed motion in populations of motile colloids. Nature 503, 95–98 (2013).
Doostmohammadi, A., Ignés-Mullol, J., Yeomans, J. M. & Sagués, F. Active nematics. Nat. Commun. 9, 3246 (2018).
Duclos, G. et al. Topological structure and dynamics of three-dimensional active nematics. Science 367, 1120–1124 (2020).
Alert, R., Casademunt, J. & Joanny, J. F. Active turbulence. Annu. Rev. Condens. Matter Phys. 13, 143–170 (2022).
Deseigne, J., Dauchot, O. & Chaté, H. Collective motion of vibrated polar disks. Phys. Rev. Lett. 105, 098001 (2010).
Suzuki, R., Weber, C. A., Frey, E. & Bausch, A. R. Polar pattern formation in driven filament systems requires non-binary particle collisions. Nat. Phys. 11, 839–843 (2015).
Yan, J. et al. Reconfiguring active particles by electrostatic imbalance. Nat. Mater. 15, 1095–1099 (2016).
Najma, B., Wei, W. S., Baskaran, A., Foster, P. J. & Duclos, G. Microscopic interactions control a structural transition in active mixtures of microtubules and molecular motors. Proc. Natl Acad. Sci. USA 121, e2300174121 (2024).
Maitra, A., Lenz, M. & Voituriez, R. Chiral active hexatics: giant number fluctuations, waves, and destruction of order. Phys. Rev. Lett. 125, 238005 (2020).
Aubret, A., Martinet, Q. & Palacci, J. Metamachines of pluripotent colloids. Nat. Commun. 12, 6398 (2021).
Baconnier, P. et al. Selective and collective actuation in active solids. Nat. Phys. 18, 1234–1239 (2022).
Giomi, L., Toner, J. & Sarkar, N. Long-ranged order and flow alignment in sheared p-atic liquid crystals. Phys. Rev. Lett. 129, 067801 (2022).
Armengol-Collado, J. M., Carenza, L. N., Eckert, J., Krommydas, D. & Giomi, L. Epithelia are multiscale active liquid crystals. Nat. Phys. 19, 1773–1779 (2023).
Mijalkov, M., McDaniel, A., Wehr, J. & Volpe, G. Engineering sensorial delay to control phototaxis and emergent collective behaviors. Phys. Rev. X 6, 011008 (2016).
Lavergne, F. A., Wendehenne, H., Bäuerle, T. & Bechinger, C. Group formation and cohesion of active particles with visual perception–dependent motility. Science 364, 70–74 (2019).
Alston, H., Parry, A. O., Voituriez, R. & Bertrand, T. Intermittent attractive interactions lead to microphase separation in nonmotile active matter. Phys. Rev. E 106, 034603 (2022).
van Kesteren, S., Alvarez, L., Arrese-Igor, S., Alegria, A. & Isa, L. Self-propelling colloids with finite state dynamics. Proc. Natl Acad. Sci. USA 120, e2213481120 (2023).
Ketzetzi, S. et al. Self-reconfiguring colloidal active matter. Preprint at https://arxiv.org/abs/2501.00672 (2024).
Parsek, M. R. & Greenberg, E. Sociomicrobiology: the connections between quorum sensing and biofilms. Trends Microbiol. 13, 27–33 (2005).
Guttenplan, S. B. & Kearns, D. B. Regulation of flagellar motility during biofilm formation. FEMS Microbiol. Rev. 37, 849–871 (2013).
Grobas, I., Polin, M. & Asally, M. Swarming bacteria undergo localized dynamic phase transition to form stress-induced biofilms. eLife 10, e62632 (2021).
Worlitzer, V. M. et al. Biophysical aspects underlying the swarm to biofilm transition. Sci. Adv. 8, eabn8152 (2022).
Farrell, F., Marchetti, M., Marenduzzo, D. & Tailleur, J. Pattern formation in self-propelled particles with density-dependent motility. Phys. Rev. Lett. 108, 248101 (2012).
Theurkauff, I., Cottin-Bizonne, C., Palacci, J., Ybert, C. & Bocquet, L. Dynamic clustering in active colloidal suspensions with chemical signaling. Phys. Rev. Lett. 108, 268303 (2012).
Buttinoni, I. et al. Dynamical clustering and phase separation in suspensions of self-propelled colloidal particles. Phys. Rev. Lett. 110, 238301 (2013).
Cates, M. E. & Tailleur, J. Motility-induced phase separation. Annu. Rev. Condens. Matter Phys. 6, 219–244 (2015).
Bäuerle, T., Fischer, A., Speck, T. & Bechinger, C. Self-organization of active particles by quorum sensing rules. Nat. Commun. 9, 3232 (2018).
Liu, G. et al. Self-driven phase transitions drive Myxococcus xanthus fruiting body formation. Phys. Rev. Lett. 122, 248102 (2019).
Tobazéon, R. Electrohydrodynamic behaviour of single spherical or cylindrical conducting particles in an insulating liquid subjected to a uniform dc field. J. Phys. D 29, 2595 (1996).
Mersch, E. & Vandewalle, N. Antiphase synchronization of electrically shaken conducting beads. Phys. Rev. E 84, 061301 (2011).
Drews, A. M., Cartier, C. A. & Bishop, K. J. Contact charge electrophoresis: experiment and theory. Langmuir 31, 3808–3814 (2015).
Eslami, G., Esmaeilzadeh, E. & Pérez, A. T. Modeling of conductive particle motion in viscous medium affected by an electric field considering particle-electrode interactions and microdischarge phenomenon. Phys. Fluids 28, 107102 (2016).
Dou, Y., Pandey, S., Cartier, C. A., Miller, O. & Bishop, K. J. Emergence of traveling waves in linear arrays of electromechanical oscillators. Commun. Phys. 1, 85 (2018).
Han, M. et al. Fluctuating hydrodynamics of chiral active fluids. Nat. Phys. 17, 1260–1269 (2021).
O’Keeffe, K. P., Hong, H. & Strogatz, S. H. Oscillators that sync and swarm. Nat. Commun. 8, 1504 (2017).
Zhang, Y. & Fodor, É. Pulsating active matter. Phys. Rev. Lett. 131, 238302 (2023).
Saint Jean, M., Guthmann, C. & Coupier, G. Relaxation and ordering processes in ‘macroscopic Wigner crystals’. Eur. Phys. J. B 39, 61–68 (2004).
Coupier, G. Élasticité et ancrage dans des cristaux de Wigner macroscopiques: un système modèle pour l’étude du piégeage faible. PhD thesis, Univ. Pierre et Marie Curie, Paris (2006).
Galatola, P., Coupier, G., Saint Jean, M., Fournier, J. B. & Guthmann, C. Determination of the interactions in confined macroscopic Wigner islands: theory and experiments. Eur. Phys. J. B 50, 549–557 (2006).
Schindelin, J. et al. Fiji: an open-source platform for biological-image analysis. Nat. Methods 9, 676–682 (2012).
Crocker, J. C. & Grier, D. G. Methods of digital video microscopy for colloidal studies. J. Colloid Interface Sci. 179, 298–310 (1996).
Blair, D. & Dufresne, E. The MATLAB Particle Tracking Code Repository http://physics.georgetown.edu/matlab (2008).
Longuet-Higgins, H. C. A computer algorithm for reconstructing a scene from two projections. Nature 293, 133–135 (1981).
Le Blay, M., Saldi, J. H. K. & Morin, A. Control of collective activity to crystallize an oscillator gas. figshare https://doi.org/10.6084/m9.figshare.28661015 (2025).
Acknowledgements
We thank M. van der Veen, B. Durà Faulì and C. M. Meulblok for help with the preliminary experiments. We thank P. J. van Veldhuizen and R. Koehler from the Leiden Institute of Physics Electronics Department and R. Schrama and G. Verdoes from the Fine Mechanical Department for their help and expertise in developing the experimental set-up. We thank D. Kraft and J. Palacci for helpful comments and D. Bartolo and M. van Hecke for insightful discussions.
Author information
Authors and Affiliations
Contributions
M.L.B. and J.H.K.S. contributed equally to this work. A.M. and M.L.B. designed the project. M.L.B. and J.H.K.S. performed the experiments. A.M. performed the finite-element simulations. J.H.K.S. performed the numerical simulations. All authors discussed the results and wrote the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks Corentin Coulais and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Individual oscillators under constant electric field.
(a-c) The steady-state of self-sustained oscillation is quickly reached after the electric field (EDC = 0.77 kV mm−1) is applied (t = 0). (a) The particle elevation as a function of time is nearly triangular. (b) Correspondingly, the particle phase is nearly linear in the interval [0,2π[. (c) The instantaneous oscillation period T(t) = t(θ + 2π) − t(θ) decays to the steady-state value To in ~ 50 ms. (d) The period of oscillation To of a single oscillator is (yellow dots) is determined by the electric field amplitude EDC as 1/To ∝ EDC (black line). This scaling is consistent with dissipation dominated by inelastic collisions with the electrodes rather than fluid drag. Oscillations occur above a threshold value for the electric field E⋆ = 0.72 kV mm−1 materialized by the grey area. The red dots correspond to the average period of oscillations measured in the collective with packing fraction ϕ = 9%.
Extended Data Fig. 2 Dynamics of binary collisions.
The joint probability density of (Δxij, Δθij) reveals that initially steady particles typically synchronize to Δθij = π and then attract. Over 200 collisions between initially static particles are analysed. As in the main text, Δxij = xj − xi − 2R and Δθij = θj − θi. The experimental path of highest probability is drawn on the Main-text Fig. 3(c).
Extended Data Fig. 3 Binary collisions at the onset of the active gas.
(a) Snapshot of the system corresponding to the first binary collision (highlighted in green) after application of the electric field. (b) Close-up showing the trajectories of the two particles colliding in (a). Red circles indicate their initial positions. Orange circles and crosses indicate their positions at contact. After their super-elastic collision, the two particles move quickly away from each others. (c) Elevation of the two particles as a function of time reconstructed from stereo-imaging (t = 0 when the field is applied). Before they collide, the two particles oscillate in phase opposition.
Extended Data Fig. 4 Individual oscillator under alternative electric field.
Top row: schematics of the electric field signals with varying modulation frequency ωE. Bottom row: experimental trajectories of individual oscillators under these conditions. Oscillator heights z under a square wave with increasing modulation frequency ωE. The values of ωE (and corresponding colours) correspond to the data on the oscillator collective reported in the Main-text Fig. 4(a). The dotted black line aids visibility. Importantly, the active gas-crystal transition occurs at ω⋆ where the individual dynamics does not change qualitatively: the transition is a true collective phenomenon. EAC = 1 kV mm−1.
Extended Data Fig. 5 Decrease in kinetic energy across the active gas-crystal transition.
The in-plane kinetic energy decreases sharply with the modulation frequency ωE until ω⋆. This decrease is concomitant with the decrease in the collision rate reported in the Main-text Fig. 4(d): limiting the number of super-elastic collision is effective in taming collective activity.
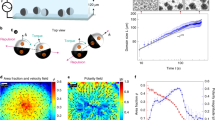
Extended Data Fig. 6 Finite size analysis of the active gas.
(a) Experimental snapshot of an active gas composed of 919 particles at a density ϕ = 9%. Red circles indicate the detected particles. Squares materialize the different box sizes used for the analysis of finite-size effects in panels (b-d). We use the same colour code from the smallest box (green) to the largest box (deep blue). (b) Mean speeds 〈v〉 for different box sizes as a function of the side-lengths of the box. No significant difference is found among the different box sizes (coloured dots), nor with the smaller system used in the main text (red cross). The errorbars show one standard deviation of uncertainty. The statistics have been derived from \({N}_{{\rm{samples}}}={\Sigma }_{i = 1}^{{N}_{{\rm{frames}}}}\,{N}_{{\rm{particles}},{\rm{i}}}\) samples, where Nframes is the total number of frames and Nparticles,i is the total number of particles that have a well-defined velocity within the different box sizes at each frame i. For the system composed of 919 particles, Nframes = 348729. The total samples sizes for increasing box sizes are Nsamples = 169644, 1074496, 4274413, 9555308, respectively. The total number of frames for the system composed of 91 particles is Nframes = 95183. Its total samples size is Nsamples = 8661653. (c) Probability density functions P(vx,y) of the velocity components vx and vy for the different box sizes. The probability density functions are independent on the size of the box, suggesting that finite-size effects are negligible. (d) The two-point velocity correlation Cvv(r) for different box sizes. There are virtually no velocity correlations at distances greater than one particle diameter r/2R = 1. This extremely short correlation length validates that the active gas statistics reported in the Main text are not influenced by finite-size effects.
Supplementary information
Supplementary Information
Supplementary Figs. 1–4.
Supplementary Video 1
Collective activity: this video demonstrates the concept behind collective activity. An active gas emerges from otherwise noiseless oscillators at high densities.
Supplementary Video 2
Active oscillator gas: this video illustrates the athermal nature of the oscillator gas: (1) the coexistence between stationary (blue) and moving (green) particles; and (2) the breaking of time-reversal symmetry.
Supplementary Video 3
Binary collisions at the onset of the active gas: this video illustrates that binary collisions occur at the onset of the active gas.
Supplementary Video 4
Reversible melting transition: this video illustrates how the control of collective activity leads to the structuring of the oscillator gas and its eventual crystallization.
Source data
Source Data Source Data Figs. 1–4
Single Excel file containing source data for Figs 1–4.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Le Blay, M., Saldi, J.H.K. & Morin, A. Control of collective activity to crystallize an oscillator gas. Nat. Phys. 21, 1412–1419 (2025). https://doi.org/10.1038/s41567-025-02957-y
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/s41567-025-02957-y