Main

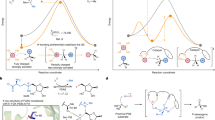
According to valence bond theory, the fission of σ-bonds from their ground (S0) or lowest excited states (S1, T1) through a single elementary step cannot be heterolytic in nature if their constituents are identical (that is, symmetric σ-bonds, Fig. 1)1,2. This exclusion criterion1 has profoundly shaped scientists’ notion of σ-bonds as being amenable or unamenable to single-step heterolysis (Fig. 1a,b). In organic molecules, σ-bonds susceptible to unimolecular heterolysis are typically composed of carbon-bound heteroatoms (that is, heteronuclear σ-bonds) with distinct differences in electronegativity relative to carbon, showing, in part, large dipole moments along the carbon–element axis (that is, heteropolar σ-bonds)2. Until today, experimental studies on single-step thermal and photochemical heterolyses have only focused on heteropolar σ-bonds but left analogous reactions of symmetric and homopolar σ-bonds (meaning, bond constituents with similar electronegativity and equal fugality3) virtually uninvestigated. From a methodological viewpoint, this state of affairs is very deplorable, because an immense synthetic potential may arise from the ionic fission of symmetric and homopolar σ-bonds. More concretely, supposing that such a polar cleavage requires an activation principle that is fundamentally different from conventional protocols (that is, single-step thermal or photochemical), it is expected that such a putative orthogonality enables σ-bond cleavage even in the presence of various other functionalities, and thus probably results in high regioselectivity and chemospecificity concomitant with elevated reactivity9,10.

Fig. 1: Representation of potential energy surfaces for homo- and heteronuclear σ-bond fission and conceptualization of SDET-induced σ-bond net heterolysis.
figure 1

a, Heteropolar σ-bond constitution leads to intersection of the S0 and S1 surfaces in solution, resulting in heterolysis by means of avoided surface crossing2. The T1 surface is omitted for clarity. b, Thermal and photochemical single-step fissions of symmetric and homopolar σ-bonds exclusively proceed along the homolytic S0 or T1 surfaces. The vertical singlet σ → σ* excitation energy of symmetric σ-bonds is smaller than the heterolytic σ-bond dissociation (diss.) energy1 due to electric potential and solvent reorganization energies5,6 needed to form ambipolar ion pairs10. c, Coincidental photoexcitation of one radical next to its homonuclear ground state radical partner inside a solvent cage leads to symmetry breaking7 and elevation onto the heterolytic S1 potential surface after electron transfer. d, Enhanced reaction control in the polar fission of σ-bonds by selective irradiation (green and bordeaux-coloured pathways) of incipient, σ-bond-derived radicals in contrast to direct σ-bond photolysis. ET, electron transfer.

Full size image

On the basis of these notions, we wondered whether symmetric σ-bonds may deviate from their natural tendency to solely undergo single-step homolysis (Fig. 1b) but instead engage in a two-step heterolytic pathway if the bond activation would consist of two separate stimuli (Fig. 1c). We posited that the first stimulus, for example, thermal excitation, would result in the expected homolysis to furnish a radical pair (for example, two doublets). Subsequent photoexcitation (second stimulus) of one of the incipient radicals at a proper wavelength (Fig. 1c,d) would result in a stimulated doublet–doublet electron transfer (SDET), and consequently in a net σ-bond heterolysis.

Mechanistically, this cleavage can be regarded as an ampholysis reaction due to the formation of a constitutionally identical pair of ions with opposite charges through a sequence featuring elements of both homolysis and heterolysis11. This scenario is remarkable, as related two-step heterolyses are only known to proceed with heteropolar σ-bonds12,13. In such cases, the direction of the electron transfer is determined by the nature of the heteropolar radical pair (that is, unidirectional electron transfer from the electropositive to the electronegative radical).

Given that the photoexcitation step is coincidental and only likely to occur in one of the incipient radical pair members at any given time, symmetry restrictions imposed by valence bond or molecular orbital theory on the single-step heterolysis of symmetric σ-bonds no longer apply1,6,7, as the electron transfer occurs only after the homolysis (Fig. 1c,d). Mechanistically similar electron transfers induced by coincidental, photochemical symmetry breaking were also reported for pairs of identical closed-shell molecules8,14, which lends plausibility to the postulate that sufficiently longevous radical pairs with unequal electronic or vibrational configurations may show an analogous behaviour.

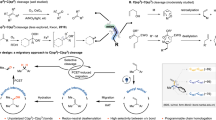
Projection of this mechanistic hypothesis to non-symmetric, yet homopolar carbon–element σ-bonds2 as targets for the SDET activation is expected to give controlled access to reactive carbenium intermediates from substrates that are inherently non-electrophilic. Consequently, these intrinsically inert substrates can engage in reaction manifolds that are typically observed only with heteropolar analogues, for example, in SN1 reactions (that is, atypical SN1 reactions) and 1,2-additions. On the basis of these considerations, we present herein a detailed mechanistic and synthetic study on the SDET activation of symmetric and homopolar selenium–selenium and carbon–selenium σ-bonds, respectively. We have identified relevant radical intermediates and deciphered their light-driven interconversion into highly reactive ion pairs, providing a profound groundwork for the design of unprecedented SN1 reactions at non-electrophilic carbon centres carrying arylselanes as SDET-controlled leaving groups.

To assess the feasibility of the proposed SDET-induced ampholysis of symmetric σ-bonds, organic diselanes were chosen as suitable substrates. Previous reports by Xu et al.15 showed that both aliphatic and aromatic diselanes readily undergo photochemical Se–Se σ-bond interchange through dynamic covalent reactions16. At room temperature and 5 mM concentration, the Se–Se σ-bond interchange of aliphatic diselanes was detected only under irradiation with ultraviolet or visible light15. This outcome was shown to be independent from all tested solvents (that is, chloroform, acetone, acetonitrile and methanol).

In a recent study from our laboratories on selenohydrins17, we demonstrated that certain closed- and open-shell selenium species function as effective H-bond acceptors, and that fluorous alcoholic solvents such as 1,1,1,3,3,3-hexafluoropropan-2-ol (HFIP) have a stabilizing effect17,18,19,20,21 on Se radical cations. To test whether akin solvent effects are operative with neutral Se radicals, equimolar solutions of diphenyldiselane (1a) and dibenzyldiselane (1b) were separately stirred in HFIP and propan-2-ol (19 °C, 0.5 M) in the dark. The degree of Se–Se σ-bond interchange (Fig. 2a) was monitored by 1H nuclear magnetic resonance (NMR) spectroscopy. After 3 h, corresponding interchange product 1c was formed in each solvent with exchange percentages (that is, measured ratio of (1c:(1a + 1b)) × 100% relative to the statistical ratio of (2:(1 + 1)) × 100%, Supplementary Table 16) ranging between 78 and 91%. In addition to 1c, formation of benzylphenylselane and dibenzylselane was detected, which accounted for 2 to 9% of the consumed starting material. A similar outcome (85% Se–Se exchange) was observed when the σ-bond exchange was allowed to run for only 15 min in CDCl3 in the dark, indicating that thermal Se–Se σ-bond homolysis is feasible22 in protic and/or acidic solvents (pKa,\({\text{CHCl}}_{3}\) = 13.6)23 under experimental conditions. As expected, addition of 2,2,6,6-tetramethylpiperidinyl-1-oxyl (TEMPO) or galvinoxyl as radical scavengers markedly reduced the degree of Se–Se interchange (54 and 58%, respectively, Supplementary Table 16, entries 7 and 8). To test whether homopolar C–Se σ-bonds may also undergo homolysis under thermal conditions, 1-deuterocyclohex-2-en-1-yl(phenyl)selane (2a–1d) was stirred at 0.5 M concentration in both neat propan-2-ol and HFIP in the dark (Fig. 2b and Supplementary Table 15). No C–Se scrambling was observed in propan-2-ol in the course of 3 h. Addition of trifluoroacetic acid (TFA) (0.5 equiv.) to this solution did not alter this outcome, suggesting that Brønsted-acid-catalysed C–Se heterolysis does not play a decisive role under the tested conditions. Notably, performing C–Se scrambling in HFIP without acid additives resulted in 10% σ-bond interchange under otherwise unaltered conditions (Fig. 2b and Supplementary Table 15). Addition of 0.5 equiv. of TFA to 2a–1d in HFIP led to 96% σ-bond interchange (that is, 48% of 2a–3d) within less than 300 s in the dark. In the presence of TEMPO, the interchange was reduced to 78% and the formation of a TEMPO/cyclohex-2-en-1-yl recombination adduct was detected by electrospray ionization high resolution mass spectrometry (Supplementary Information, page 15), which is congruent with a radical nature of the exchange reaction. In combination with our previous findings17, these results strongly support our hypothesis on the stabilizing effect of fluorous alcoholic solvents on selenium radical intermediates. To substantiate this assumption, we quantified the stabilization energies exerted by HFIP and propan-2-ol on PhSe• and the cyclohexenyl radical by computation, using the B3LYP-D3/def2-TZVP//CPCM level of theory (Supplementary Table 21)24,25,26,27,28. These calculations show that HFIP indeed stabilizes both radical species slightly more effectively than propan-2-ol. Moreover, the increased chemical stability of the radicals after HFIP solvation can be rationalized by a substantial lowering of the singly occupied molecular orbital energies in both the allylic and the selenyl radical, resulting in a deceleration of the unproductive radical recombination (Supplementary Fig. 31). However, we interpret the benign impact of HFIP predominantly as a kinetic solvent effect20.

Fig. 2: Se–Se and C–Se σ-bond exchange experiments.
figure 2

a, Composition of solutions initially containing a 1:1 mixture of 1a and 1b as starting materials at 19 °C in HFIP and iPrOH. After 180 min, formation of 1c and monoselanes is observed through Se–Se and Se–C σ-bond interchange, respectively. Numbers in the pie charts refer to relative amounts of 1a (dark blue), 1b (medium blue) and 1c (light blue) in solution. b, Composition of solutions containing 2a–1d as the starting material at 19 °C in HFIP and iPrOH after 180 min.

Full size image

As detailed in the Methods section, we showed that PhSe• (λmax = 490 nm) absorbs even above 500 nm, which is far more bathochromic than the absorptions of diselane 1a itself, the selenium-centred ions resulting from the proposed SDET, and cyclohexenyl radical 5a• (Fig. 3, Extended Data Fig. 1, Methods, and Supplementary Fig. 23). We therefore conducted next computations on the excited states of PhSe• (Supplementary Fig. 27) and its associated deactivation pathways (Supplementary Fig. 28) to determine the photochemically active states. Irradiation at wavelengths around 500 nm mainly populates the bright D3 state (Supplementary Fig. 27a), which is of πp excitation character (Supplementary Fig. 27b). The D2 state is also of πp excitation character but has a larger charge-transfer contribution (Supplementary Fig. 27b,c), which is consistent with its low extinction coefficient. Notably, in contrast to the D3 and D2 states, the D1 state shows a nSep charge-transfer character, which results in the localization of spin density in a p orbital at the Se atom that is orthogonal to the adjacent π system of the phenyl ring (Supplementary Fig. 27d). Given the large excitation energy difference between the D2 and the D1 state (2.09 versus 0.43 eV), we assessed their deactivation pathways next to ascertain their potential contribution to the subsequent SDET process (Supplementary Fig. 28). To this end, we could determine a substantial activation barrier (0.83 eV) for the non-radiative deactivation of a vibrationally cooled D2 state to the D1 state, suggesting that at least a part of the excited PhSe• radicals may react from the D2 state directly in an anti-Kasha manner29,30.

Fig. 3: Thermodynamic evaluation of a thermal electron transfer versus SDET between 5a• and •SePh, and transient absorption spectra of the SDET-induced ampholysis of 1a.
figure 3

Potentials shown refer to reduction potentials, whereas the index indicates whether the respective species is oxidized (ox) or reduced (red) in the reaction. Gibbs free energies ΔGET and ΔGSDET were calculated according to ΔG = −F• (E0red − E0ox). a, Thermal electron transfer is endergonic by 9.7 kcal mol−1. b, SDET process is exergonic by −3.8 kcal mol−1 from the D1 state and −41.3 kcal mol−1 from the D2 state. Parabola for the D2 state is not shown, but the arrows representing the vertical excitation into the D3 state and relaxation from the D2 state are shown in grey. c, Transient absorption (TA) spectra after photoexcitation of a sample of (PhSe)2 in HFIP with an ultrafast laser (central wavelength 340 nm, pulse duration 100 fs). The olive spectrum was recorded on a µs time scale after excitation at 355 nm and matches the end of the fs-transient absorption, indicating that the electron transfer stops after the end of vibrational cooling.

Full size image

On the basis of this analysis, we computed the standard absolute reduction potentials (E0) of the D0, D1, and D2 states of PhSe•, which amount to 4.33, 4.91, and 6.54 eV, respectively (Fig. 3a and Supplementary Information, Chapter 9). Considering the computationally estimated ground state reduction potential 5a+|5a• (E0 = 4.75 eV), the Gibbs free energy of an electron transfer (ΔGET) from 5a• to PhSe• in their respective electronic ground states is endergonic by 9.7 kcal mol−1 (that is, 0.42 eV, Fig. 3a), whereas after irradiation at 500 nm the corresponding SDET (ΔGSDET) becomes overall exergonic by −3.8 kcal mol−1 from the D1 state and −41.3 kcal mol−1 from the D2 state (Fig. 3b). These values suggest that allylic selanes such as 2a can principally engage in atypical SN1 reactions when exposed to nucleophiles under SDET conditions.

Eventually, two questions remained: (1) is it possible to obtain direct spectroscopic evidence for the SDET-induced Se–Se σ-bond ampholysis of 1a, and can the resulting PhSe+/PhSe− ion pair be intercepted by suitable reaction partners? (2) Can the archetypical reactivity profile of heteropolar carbon(sp3)–halogen σ-bonds (for example, halogen being Br) be emulated by SDET-induced net heterolysis of a homopolar carbon–selenium σ-bond (Fig. 4a), and can this concept indeed be used to conduct atypical SN1 and 1,2-addition reactions (Fig. 4b, Extended Data Figs. 2 and 3)?

Regarding question (1) we learned that 1a shows a signal of vibrationally excited (that is, hot) PhSe• arising at some point within 2 ps after excitation at 340 nm (Fig. 3c). Some tens of ps later, the spectrum turns into a double-peak structure, in which the rising absorption at 400 nm indicates the formation of PhSe+. Related photolyses of monoselanes do also show the formation PhSe• radicals but not that of PhSe+. We interpret this outcome as a result of a fast vibrational relaxation relative to diffusion. Meaning that if vibrationally relaxed (that is, cold) PhSe• radicals meet by diffusion, electron transfer is no longer energetically feasible. However, if vibrationally or electronically excited PhSe• radicals are generated by coincidental excitation in proximity to cold ones (that is, transient coexistence of two spatially close radicals only differing in their state populations), the electron transfer can occur. Therefore, the resulting SDET-induced net heterolysis offers an expedient and chemospecific means to edit the fission of symmetric and homopolar σ-bonds by means of state-directed poling of the incipient radical pair (that is, directional charge separation between state-differentiated, former bond members). In total, this lends plausibility to the overthrowing idea that the SDET principle might indeed be applicable to other kinds of homopolar σ-bond constitutions as long as they are susceptible to similar two-step activations. It is important to point out that the observed requirement for keeping the state-differentiated radical pair members in close proximity to one another is most probably key to establish chemospecificity31. More concretely, provided that radical recombination before the SDET or back electron transfer and filial ion pair recombination after the SDET are the only unproductive processes kinetically feasible under said diffusion restrictions, unwanted detrimental side reactivity of the electrophile becomes improbable.

Next, we subjected diselane 1a to 5-phenylpent-3-enoic acid (6a) (1.0 equiv.) in HFIP in the presence of TFA (0.5 equiv.) at 528 nm irradiation to test whether corresponding lactone 7a is formed as a result of the anticipated 1,2-anti-addition of the SDET-generated PhSe+ cation onto the alkene moiety (Extended Data Fig. 2a). To our delight, product 7a was produced in 27% after 24 h. Changing to 447 nm irradiation gave clean access to lactone 7a in an increased yield of 72% at 77% conversion. Switching from TFA to methanesulfonic acid (MSA) led to quantitative product formation. In the absence of any acid additive, formation of product 7a (61%) was still observed at full conversion alongside with butenolide 8a (21% yield, entry 4). This outcome strongly supports our interpretation that the σ-bond ampholysis is not a consequence of Brønsted-acid catalysis. This notion is further corroborated by the fact that without light, but in the presence of either acid additive (TFA or MSA), no substantial product formation was recorded (entries 5 and 6; Supplementary Information, Chapter 7.6). We propose that the acid additive, together with the solvent, serves two purposes: (1) it kinetically assists in the Se–Se homolysis step (vide supra) and (2) it enhances the protonation of the PhSe− anion after the SDET event, thus precluding it from recombination with its counterion. Consequently, these data show that net heterolyses of symmetric σ-bonds are indeed possible through SDET activation.

Encouraged by the observation that butenolide 8a can be directly accessed from enoic acid 6a, we next tested whether the SDET principle could be further elaborated into a catalytic regime32, in which lactone 7a only serves as an intermediate en route to butenolide 8a (Extended Data Fig. 2b and Supplementary Tables 3–9). After minor modifications of the reaction conditions (405 nm, 35 °C), compound 8a was obtained in 67% using only 5 mol% of diselane 1a. This finding represents an example of a Lewis acid whose activity is reversibly elicited by a photochemical stimulus (that is, photo-Lewis acid)33,34,35,36,37. This new photo-Lewis-acid protocol also proved suitable for an exemplary series of other enoic acids 6b–f (Extended Data Fig. 2b), which prefigures the potential that SDET-induced ampholyses might unfold in the realm of dinuclear catalysis38,39,40,41.

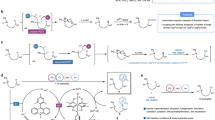
To address question (2), we compared the electrophilic reactivity profile of SDET-activated allylselane 2a with that of 3-bromocyclohex-1-ene (9) (Fig. 4a and Supplementary Information, Chapter 12). In HFIP, compounds 2a and 9 showed similar outcomes with regard to crude yields (84 and >99%, respectively) and N2/N1 regioselectivities (N1 in light blue, N2 in dark blue). When electrophile 9 was reacted in acetonitrile in the presence of K2CO3 as a base, the yield remained high (85%) but the selectivity for N2 allylation decreased to 41%, emphasizing the decisive impact of HFIP on the regioselectivity. Comparison of allyl(aryl)selane 2a and bromide 9 in their reactivities towards less reactive N-nucleophiles revealed that the SDET activation provided superior yields in both tested cases, that is, aniline 3j (82 versus 16%) and tosylsulfonamide 3r (96 versus 24%, Fig. 4a and Supplementary Tables 24 and 25).

Fig. 4: Comparative reactivity study of 2a versus 9 and SDET-induced atypical SN1 amination of allyl- and alkyl(aryl)selanes.
figure 4

a, Reactivity comparison between 2a and 9. Pie charts indicate regioselectivity ratios of N1 substitution (light blue) versus N2 substitution (dark blue). Yields were determined by 1H NMR spectroscopy using 1,3-dinitrobenzene as an internal standard. Additive A, 50% TFA; additive B, 1 equiv. K2CO3; ACN, acetonitrile. b, Exemplary series of SDET-induced allylations of azoles. Yields refer to isolated compounds.

Full size image

To ensure that the SN1 reaction is driven only within the absorption window of PhSe• (300 to 630 nm), the experiment was repeated with an optical filter setup that allowed irradiation within segments of an overall spectral range between 580 and 930 nm with varying LEDs (Supplementary Information and Supplementary Table 14, entries 1–8). Irradiation between 580 and 710 nm furnished product 4aa in an unaltered yield of 84%. Changing the window to 630–710 nm (630 nm represents the endpoint of the absorption band of PhSe•) led to a substantial decrease in the conversion and yield to 8 and 6%, respectively (Supplementary Table 14, entry 6). Using an irradiation window from 700 to 810 nm only led to background reactivity (Supplementary Table 14, entry 4) with less than 5% conversion. These outcomes substantiate our hypothesis that the requisite cation 5a+ is indeed only generated in response to PhSe• being excited with a suitable wavelength followed by a SDET. In addition, the key effect of HFIP relative to iPrOH (and other solvents, Supplementary Table 11) was confirmed, as the yield dropped down to 10% in the latter solvent under otherwise unaltered conditions. Other azoles were also effective and provided target structures 4ab–ai in isolated yields ranging from 39 to 85% (Fig. 4b).

Non-heteroaromatic N-nucleophiles such as hydrazides 3o–q, anilines 3j–n, and sulfonamides 3r–t were also readily converted into their respective allylation products 4aj–at (yield 31 to 90%, Extended Data Fig. 3). In addition to allylations (4aa–cr), the SDET protocol proved also effective for alkylations using alkylselanes 2d–f, which provided access to secondary sulfonamides 4dr–fr in isolated yields of up to 70%. Notably, substitution was even possible at the bridgehead carbon atom of bicyclo[2.2.2]octane 2f, furnishing product 4fr in 20% along with 20% of HFIP ether 4fr’ within 6 days reaction time. According to Bartlett and Knox10, such SN1 reactions are typically unfeasible under conventional SN conditions due to an increase in strain energy during the departure of the nucleofuge9. Single-step heterolyses at such positions are only known to be possible with very strong leaving groups such as N2+ (that is, strongly heteropolar C–N σ-bond)42,43. Our results indicate that this level of very high nucleofugality can indeed be emulated even with homopolar σ-bonds under SDET conditions, which is exemplarily further demonstrated in other SN1 reactions typical to carbenium ions, such as Friedel–Crafts alkylations (Supplementary Information, Chapter 4.4 and Supplementary Scheme 3).

In summary, we have presented a comprehensive mechanistic and methodical study on the net heterolysis of symmetric and homopolar σ-bonds by means of SDET. Symmetric Se–Se single bonds (exemplified by diselane 1a) can undergo stimulated ampholysis into Se-centred ion pairs; an outcome that has—to the best of our knowledge—never been shown with any kind of symmetric single bond. This finding complements long-standing notions on the general possibility of splitting symmetric and homopolar σ-bonds into (ambi)polar fragments in a unimolecular manner by sequential energy input (thermal or photochemical) by way of transient radical formation and subsequent differentiation of their electronic and/or vibrational state populations. The implications of our findings are in as far long-ranging as, in theory, the SDET-activation principle might be applicable to other pairs of equally electronegative nuclei (for example, bimetallic complexes38,39,40,41, nitrogen–nitrogen44,45, carbon–carbon44,45). This prospect may enable heretofore unexplored, inimitable reaction manifolds that are elusive to processes exclusively operating through thermal or photochemical single activation. The plausibility of this prospect was exemplified by (1) an atypical 1,2-anti-addition of diselane 1a to enoic acid 6a (Extended Data Fig. 2a), (2) the implementation of the ampholytic poling principle into catalytic manifolds (Extended Data Fig. 2b) and (3) highly chemospecific SN1 reactions of allyl- and alkyl(aryl)selanes with N and C nucleophiles (Fig. 4b, Extended Data Fig. 3 and Supplementary Scheme 3), which in total underscores the unique synthetic utility of the SDET approach. Future investigations in our groups will focus on the implementation of the SDET concept in new catalytic transformations and its generalization onto other geminate, incipient radical species.

Methods

Absorption spectra of reaction constituents in the SDET-induced net heterolysis

We first characterized the anticipated selenium intermediates resulting from the proposed SDET-induced net heterolysis of diselane 1a (that is, PhSe•, PhSe− and PhSe+, Extended Data Fig. 1a,b) in more detail. Investigations began with the elucidation of the spectral signatures of the expected intermediates and the identification of potential absorption overlaps under the reaction conditions between them or with any other reaction constituent (for example, nucleophile 3a or product 4aa, Extended Data Fig. 1). Ito and Tojo et al. reported a λmax for PhSe• of 450 and 490 nm, with a measurable absorption up to 630 nm (refs. 46,47). Furthermore, Lewis et al. documented two absorption maxima for PhSe− at 227 and 295 nm (ref. 48). To determine the wavelength at which the absorption of PhSe− potentially overlaps with that of PhSe•, we generated NaSePh from (PhSe)2 and NaBH4. The corresponding absorption spectrum of PhSe− showed a signature only below 350 nm (Extended Data Fig. 1b, middle), thus confirming that co-excitation of both selenium species above 350 nm is impossible. Analogously, the spectral signatures of PhSe+ (recorded from a mixture of N-phenylselanylphthalimide and MSA) range up to 500 nm (Extended Data Fig. 1b).

The unambiguity of our spectral assignment for the radical and ionic selenium species (Extended Data Fig. 1a,b) was also corroborated by computational means (Supplementary Figs. 22–24). The absorption spectra of PhSe• (λmax of 490 nm) and PhSe− (λmax of 295 and 227 nm in MeCN)48 were reproduced by single reference computational methods (Supplementary Figs. 22 and 24) with error margins below 0.25 eV, which marks a high level of accuracy given the current state of the art for the simulation of such systems49. The spectral simulation of PhSe+, on the other hand, was found to be complicated by the electronic configuration of this heavy ion, requiring multireference treatment to accurately reproduce the experimental spectrum computationally (Supplementary Information, Chapter 8). Considering the body of spectroscopic and computational data, it stands to reason that photoexcitation of PhSe• between 500 and 630 nm does not lead to substantial overlap with the observed absorption spectra of the presumed filial selenium ion pair (PhSe−/PhSe+) and of (PhSe)2 itself, which does not exceed 430 nm (Extended Data Fig. 1b, bottom).

An analogous spectral analysis was also conducted for the cyclohexenyl intermediates 5a• and 5a+ (that is, homopolar–heteronuclear case, Extended Data Fig. 1d), which were expected to result from the SDET-fragmentation of substrate 2a. Schuler et al. reported radical 5a• to possesses a λmax of 240 nm with an absorption range of only up to 320 nm (ref. 50). Carbocation 5a+, generated by us in situ from 3-chlorocyclohex-1-ene in the presence of AgPF6, shows similar spectral features as its radical congener, which do not exceed 300 nm (Extended Data Fig. 1d, top). In conclusion, both results confirm that—apart from PhSe•—none of the reactants, solvent, additives (Extended Data Fig. 1c,d) and conceivably relevant reactive intermediates show a pronounced absorption at wavelengths greater than 500 nm.