Abstract
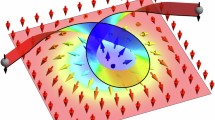
The coupling of conduction electrons and magnetic textures leads to quantum transport phenomena described by the language of emergent electromagnetic fields1,2,3. For magnetic skyrmions, spin-swirling particle-like objects, an emergent magnetic field is produced by their topological winding4,5,6, resulting in the conduction electrons exhibiting the topological Hall effect (THE)7. When the skyrmion lattice (SkL) acquires a drift velocity under conduction electron flow, an emergent electric field is also generated8,9. The resulting emergent electrodynamics dictate the magnitude of the THE by the relative motion of SkL and conduction electrons. Here we report the emergent electrodynamics induced by SkL motion in Gd2PdSi3, facilitated by its giant THE10,11. With increasing current excitation, we observe the dynamic transition of the SkL motion from the pinned to creep regime and finally to the flow regime, in which the THE is totally suppressed. We argue that the Galilean relativity required for the total cancellation of the THE may be generically recovered in the flow regime, even in complex multiband systems such as the present compound. Moreover, the observed THE voltages are large enough to enable real-time measurement of the SkL velocity–current profile, which shows the inertial-like motion of the SkL in the creep regime, appearing as the current hysteresis of the skyrmion velocity.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
All experimental data to reproduce the figures are available from Zenodo50 (https://doi.org/10.5281/zenodo.11408317).
Change history
29 November 2024
A Correction to this paper has been published: https://doi.org/10.1038/s41586-024-08235-w
References
Baskaran, G. & Anderson, P. W. Gauge theory of high-temperature superconductors and strongly correlated Fermi systems. Phys. Rev. B 37, 580–583 (1988).
Nagaosa, N., Sinova, J., Onoda, S., MacDonald, A. H. & Ong, N. P. Anomalous Hall effect. Rev. Mod. Phys. 82, 1539–1592 (2010).
Nagaosa, N. & Tokura, Y. Emergent electromagnetism in solids. Phys. Scr. 2012, 014020 (2012).
Nagaosa, N. & Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotechnol. 8, 899–911 (2013).
Mühlbauer, S. et al. Skyrmion lattice in a chiral magnet. Science 323, 915–919 (2009).
Yu, X. Z. et al. Real-space observation of a two-dimensional skyrmion crystal. Nature 465, 901–904 (2010).
Neubauer, A. et al. Topological Hall effect in the A phase of MnSi. Phys. Rev. Lett. 102, 186602 (2009).
Zang, J., Mostovoy, M., Han, J. H. & Nagaosa, N. Dynamics of skyrmion crystals in metallic thin films. Phys. Rev. Lett. 107, 136804 (2011).
Schulz, T. et al. Emergent electrodynamics of skyrmions in a chiral magnet. Nat. Phys. 8, 301–304 (2012).
Kurumaji, T. et al. Skyrmion lattice with a giant topological Hall effect in a frustrated triangular-lattice magnet. Science 365, 914–918 (2019).
Hirschberger, M. et al. High-field depinned phase and planar Hall effect in the skyrmion host Gd2PdSi3. Phys. Rev. B 101, 220401 (2020).
Cohen, E. et al. Geometric phase from Aharonov–Bohm to Pancharatnam–Berry and beyond. Nat. Rev. Phys. 1, 437–449 (2019).
Aharonov, Y. & Bohm, D. Significance of electromagnetic potentials in the quantum theory. Phys. Rev. 115, 485–491 (1959).
Berry, M. V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. A Lond. Math. Phys. Sci. 392, 45–57 (1997).
Xiao, D., Chang, M.-C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959–2007 (2010).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Armitage, N. P., Mele, E. J. & Vishwanath, A. Weyl and Dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 90, 015001 (2018).
Ohgushi, K., Murakami, S. & Nagaosa, N. Spin anisotropy and quantum Hall effect in the kagomé lattice: Chiral spin state based on a ferromagnet. Phys. Rev. B 62, R6065–R6068 (2000).
Taguchi, Y., Oohara, Y., Yoshizawa, H., Nagaosa, N. & Tokura, Y. Spin chirality, Berry phase, and anomalous Hall effect in a frustrated ferromagnet. Science 291, 2573–2576 (2001).
Nagaosa, N. Emergent inductor by spiral magnets. Jpn. J. Appl. Phys. 58, 120909 (2019).
Yokouchi, T. et al. Emergent electromagnetic induction in a helical-spin magnet. Nature 586, 232–236 (2020).
Jiang, W. et al. Direct observation of the skyrmion Hall effect. Nat. Phys. 13, 162–169 (2017).
Litzius, K. et al. Skyrmion Hall effect revealed by direct time-resolved X-ray microscopy. Nat. Phys. 13, 170–175 (2017).
Rößler, U. K., Bogdanov, A. N. & Pfleiderer, C. Spontaneous skyrmion ground states in magnetic metals. Nature 442, 797–801 (2006).
Heinze, S. et al. Spontaneous atomic-scale magnetic skyrmion lattice in two dimensions. Nat. Phys. 7, 713–718 (2011).
Moreau-Luchaire, C. et al. Additive interfacial chiral interaction in multilayers for stabilization of small individual skyrmions at room temperature. Nat. Nanotechnol. 11, 444–448 (2016).
Matsui, A., Nomoto, T. & Arita, R. Skyrmion-size dependence of the topological Hall effect: A real-space calculation. Phys. Rev. B 104, 174432 (2021).
Kimbell, G., Kim, C., Wu, W., Cuoco, M. & Robinson, J. W. A. Challenges in identifying chiral spin textures via the topological Hall effect. Commun. Mater. 3, 19 (2022).
Woo, S. et al. Observation of room-temperature magnetic skyrmions and their current-driven dynamics in ultrathin metallic ferromagnets. Nat. Mater. 15, 501–506 (2016).
Juge, R. et al. Current-driven skyrmion dynamics and drive-dependent skyrmion Hall effect in an ultrathin film. Phys. Rev. Appl. 12, 044007 (2019).
Peng, L. et al. Dynamic transition of current-driven single-skyrmion motion in a room-temperature chiral-lattice magnet. Nat. Commun. 12, 6797 (2021).
Hirschberger, M. et al. Skyrmion phase and competing magnetic orders on a breathing kagomé lattice. Nat. Commun. 10, 5831 (2019).
Khanh, N. D. et al. Nanometric square skyrmion lattice in a centrosymmetric tetragonal magnet. Nat. Nanotechnol. 15, 444–449 (2020).
Takagi, R. et al. Square and rhombic lattices of magnetic skyrmions in a centrosymmetric binary compound. Nat. Commun. 13, 1472 (2022).
Okubo, T., Chung, S. & Kawamura, H. Multiple-q states and the skyrmion lattice of the triangular-lattice Heisenberg antiferromagnet under magnetic fields. Phys. Rev. Lett. 108, 017206 (2012).
Leonov, A. O. & Mostovoy, M. Multiply periodic states and isolated skyrmions in an anisotropic frustrated magnet. Nat. Commun. 6, 8275 (2015).
Inosov, D. S. et al. Electronic structure and nesting-driven enhancement of the RKKY interaction at the magnetic ordering propagation vector in Gd2PdSi3 and Tb2PdSi3. Phys. Rev. Lett. 102, 046401 (2009).
Hayami, S. & Motome, Y. Multiple-Q instability by (d − 2)-dimensional connections of Fermi surfaces. Phys. Rev. B 90, 060402 (2014).
Wang, Z., Barros, K., Chern, G.-W., Maslov, D. L. & Batista, C. D. Resistivity minimum in highly frustrated itinerant magnets. Phys. Rev. Lett. 117, 206601 (2016).
Iwasaki, J., Mochizuki, M. & Nagaosa, N. Universal current-velocity relation of skyrmion motion in chiral magnets. Nat. Commun. 4, 1463 (2013).
Schütte, C., Iwasaki, J., Rosch, A. & Nagaosa, N. Inertia, diffusion, and dynamics of a driven skyrmion. Phys. Rev. B 90, 174434 (2014).
Grüner, G. The dynamics of charge-density waves. Rev. Mod. Phys. 60, 1129–1181 (1988).
Metaxas, P. J. et al. Creep and flow regimes of magnetic domain-wall motion in ultrathin Pt/Co/Pt films with perpendicular anisotropy. Phys. Rev. Lett. 99, 217208 (2007).
Anderson, P. W. & Kim, Y. B. Hard superconductivity: theory of the motion of Abrikosov flux lines. Rev. Mod. Phys. 36, 39–43 (1964).
Fröhlich, H. On the theory of superconductivity: the one-dimensional case. Proc. R. Soc. A Lond. Ser. Math. Phys. Eng. Sci. 223, 296–305 (1954).
Lee, P. A., Rice, T. M. & Anderson, P. W. Conductivity from charge or spin density waves. Solid State Commun. 14, 703–709 (1974).
Psaroudaki, C., Hoffman, S., Klinovaja, J. & Loss, D. Quantum dynamics of skyrmions in chiral magnets. Phys. Rev. X 7, 041045 (2017).
Iwasaki, J., Mochizuki, M. & Nagaosa, N. Current-induced skyrmion dynamics in constricted geometries. Nat. Nanotechnol. 8, 742–747 (2013).
Büttner, F. et al. Dynamics and inertia of skyrmionic spin structures. Nat. Phys. 11, 225–228 (2015).
Birch, M. T. Dataset for: Dynamic transition and Galilean relativity of current-driven skyrmions. Zenodo https://doi.org/10.5281/zenodo.11408317 (2024).
Acknowledgements
We thank the CEMS Semiconductor Science Research Support Team for the assistance in the use of cleanroom facilities. We also thank S. H. Moody for the schematic spin texture images. We thank X. Z. Yu and her team for the use of the FEI Helios 5UX focused ion beam system. We thank T. Sato and F. Kagawa for the lending of a previous Gd2PdSi3 device and for their advice. We are grateful to all members of the CEMS for their discussions. This work was supported by JSPS KAKENHI (grant no. 23H05431) and JST CREST (grant nos. JPMJCR1874 and JPMJCR20T1). N.N. was supported by the RIKEN TRIP initiative and JSPS KAKENHI (grant nos. 24H00197 and 24H02231).
Author information
Authors and Affiliations
Contributions
M.T.B. and Y. To conceived the project. A.K. and Y. Ta grew the bulk Gd2PdSi3 single crystal. M.T.B. fabricated the focused ion beam devices. M.T.B. performed the measurements and analysis with support from I.B., Y.F., M.K. and M.H.; N.N. developed the theoretical models; and M.T.B., N.N. and Y. To interpreted the data and wrote the paper, along with contributions from all other co-authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Characterization of the focused ion beam-fabricated Gd2PdSi3 devices.
a-e, Scanning electron microscopy images of the fabricated Gd2PdSi3 devices. Relevant sample dimensions are labelled, and the scale bar is 5 μm. f-j, Longitudinal resistivity ρxx measured as a function of decreasing temperature T at a selection of applied magnetic fields, for devices 0 to 4, respectively.
Extended Data Fig. 2 Additional skyrmion velocity measurements via the nonlinear topological Hall effect – device 1.
a, The change in the measured Hall resistivity, Δρyx(J) = ρyx(J) − ρyx(J→0), at 2.5 K measured as a function of the applied magnetic field \(B\) at different DC current densities, JDC, for device 1. The boundaries between the ground state magnetic phases are labelled by the grey dashed lines. The vertical solid grey lines highlight fields considered in later panels. b, The topological Hall resistivity \({\rho }_{{yx}}^{{\rm{THE}}}\) plotted as a function of JDC for selected \(B\) between 0.86 and 1.44 T. c, The calculated skyrmion velocity vSk plotted as a function of JDC for selected B between 0.86 and 1.44 T. The electron drift velocity, ve, is plotted as the dotted/dashed line, calculated from the measured charge carrier density. d-f, The same as a-c, but at 5.0 K.
Extended Data Fig. 3 Additional skyrmion velocity measurements via the nonlinear topological Hall effect – device 2.
a, The change in the measured Hall resistivity, Δρyx(J) = ρyx(J) − ρyx(J→0), at 2.5 K measured as a function of the applied magnetic field \(B\) at different DC current densities, JDC, for device 1. The boundaries between the ground state magnetic phases are labelled by the grey dashed lines. The vertical solid grey lines highlight fields considered in later panels. b, The topological Hall resistivity \({\rho }_{{yx}}^{{\rm{THE}}}\) plotted as a function of JDC, for selected B between 0.81 and 1.41 T. c, The calculated skyrmion velocity, vSk, plotted as a function of JDC for selected B between 0.81 and 1.41 T. The electron drift velocity, ve, is plotted as the dotted/dashed line, calculated from the measured charge carrier density. d-f, The same as a-c, but at 5.0 K.
Extended Data Fig. 4 Additional skyrmion velocity measurements via the nonlinear topological Hall effect – device 3 and 4.
a, The Hall resistivity ρyx measured at 2.5 K as a function of the applied magnetic field \(B\) at three current densities JDC for device 3. b, The change in the Hall resistivity Δρyx(J) = ρyx(J) − ρyx(J→0), normalized by the zero current limit value of the Hall resistivity, ρyx(J→0), measured as a function of JDC, at 2.5 K and various applied fields in device 3. c, The skyrmion velocity, vSk, plotted as a function of J, calculated from the data in b, for various applied fields in device 3. d-f, The same as a-c, but for device 4.
Extended Data Fig. 5 Sample dependence of the current density threshold to enter the flow regime.
The estimated current density threshold to enter the flow regime, \({J}_{{\rm{th}}}^{{\rm{F}}}\), at an applied field of 1.3 T and sample temperature of 2.5 K, plotted as a function of the cross sectional area A of each FIB device 1–4. Error bars show the standard error. An approximate fitted linear trend is plotted as the solid line.
Extended Data Fig. 6 Analysis of the oscilloscope Hall measurements.
In all panels, the solid grey line plots the applied current density J with a peak \({J}_{{\rm{AC}}}^{\max }\) of 1.9 × 109 Am−2. a, The measured Hall voltage response \({V}_{{yx}}^{{\rm{raw}}}\) of device 2, measured at 2.5 K and with an AC current at 125 Hz (corresponding to a dJ/dt = 1 × 1012 Am−2s−1), plotted as a function of θ = ωt. Data were acquired at both ± 1.0 T, displayed as the red and blue lines respectively. b, The voltage traces acquired at ± 1.0 T were antisymmetrized, yielding \({V}_{{yx}}^{{\rm{asym}}}\) (purple line). The estimated contribution from the ordinary Hall effect (OHE) is plotted (orange line). c, The contribution from the topological Hall effect (THE) was acquired by subtracting this estimated OHE signal. d, The calculated topological Hall effect resistivity \({\rho }_{{yx}}^{{\rm{THE}}}\) plotted as a function of \(\theta \). e, The calculated skyrmion velocity vSk plotted as a function of \(\theta \). f-j, The same as a-e, but measured with J oscillating at a frequency of 12,500 Hz (corresponding to a dJ/dt = 1 × 1014 Am−2s−1). The anstisymmetrization process removes any contributions from extrinsic capacitance/impedance from the measurement circuit (which exhibits a constant value with \(B\)).
Extended Data Fig. 7 Field-dependent oscilloscope Hall voltage measurements.
a-e, The antisymmetrized and isolated topological Hall voltage response \({V}_{{yx}}^{{\rm{THE}}}\) of device 2, measured at 2.5 K, and plotted as a function of time \(t\). Data were acquired at a range of applied fields between 1.0 and 1.4 T, as shown by each panel respectively. The dashed grey line plots the corresponding applied sinusoidal current density J with a peak \({J}_{{\rm{AC}}}^{\max }\) of 1.5 × 109 Am−2, and a frequency of 111 Hz. f-j, The calculated topological Hall effect resistivity \({\rho }_{{yx}}^{{\rm{THE}}}\) at each field, plotted as a function of t. k-o, The calculated skyrmion velocity vSk at each field. The electron drift velocity, ve calculated from the applied J, is plotted as the dashed grey line. p, q, \({V}_{{yx}}^{{\rm{THE}}}\) and vSk plotted as a function of the applied J for each applied magnetic field.
Extended Data Fig. 8 Frequency-dependent oscilloscope measurements of the Hall voltage at 1.0 T.
a-h, The antisymmetrized topological voltage response \({V}_{{yx}}^{{\rm{THE}}}\) of device 2, measured at 2.5 K and 1.0 T, plotted as a function of time t. Data were acquired with a sinusoidal current density, with peak amplitude \({J}_{{\rm{AC}}}^{\max }\) of 1.5 × 109 Am−2, and frequencies between 10 and 5,011 Hz. The horizontal dashed lines highlight the inflection points of the voltage response at low frequencies. At high frequencies, the nonlinearity of the voltage response appears delayed owing to the inertial-like motion of the skyrmion lattice in the creep regime.
Extended Data Fig. 9 Frequency-dependent oscilloscope measurements of the Hall voltage at 1.3 T.
a-h, The antisymmetrized topological voltage response \({V}_{{yx}}^{{\rm{THE}}}\) of device 2, measured at 2.5 K and 1.3 T, plotted as a function of time t. Data were acquired with a sinusoidal current density (solid grey line), with peak amplitude \({J}_{{\rm{AC}}}^{\max }\) of 1.5 × 109 Am−2, and frequencies between 10 and 5,011 Hz. The horizontal dashed lines highlight the inflection points of the voltage response at low frequencies. At high frequencies, the nonlinearity of the voltage response is delayed due to the inertial-like motion of the skyrmion lattice in the creep regime.
Extended Data Fig. 10 Frequency-dependent oscilloscope measurements of the Hall I-V characteristic and skyrmion velocity profile.
a-e, The isolated \({V}_{{yx}}^{{\rm{THE}}}\) measured for an applied oscillating triangle wave current density J with peak amplitude \({J}_{{\rm{AC}}}^{\max }\) of 1.9 × 109 Am−2, with current sweep rates dJ/dt between 1 × 1012 and 1 × 1014 Am−2s−1. The corresponding frequencies are labelled. The grey lines plot the antisymmetrized voltage signal \({V}_{{yx}}^{{\rm{asym}}}\) before the ordinary Hall effect subtraction. f-j, The calculated skyrmion velocities vSk plotted as a function of J for each dJ/dt. The estimated electron drift velocity ve is plotted as the grey line.
Supplementary information
Supplementary Information
This file contains Supplementary Notes 1−4 and Supplementary Figs. 1−8.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Birch, M.T., Belopolski, I., Fujishiro, Y. et al. Dynamic transition and Galilean relativity of current-driven skyrmions. Nature 633, 554–559 (2024). https://doi.org/10.1038/s41586-024-07859-2
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/s41586-024-07859-2