Main

El Niño events can reach extreme magnitude, as during the record-breaking events of 1982, 1997 and 2015, when extremely warm temperatures in the equatorial Pacific (≥2 K in the central Pacific7) drove highly disruptive environmental changes, including bleaching and widespread coral mortality8, tropical forest fires, heat waves9 and ice-shelf instability. Limited observations hinder our understanding of these extreme El Niño events because only three such events have been fully observed, to our knowledge, since the advent of satellite and moored observations2. Models predict increasing rainfall and sea-surface temperature (SST) variability under greenhouse warming10, potentially linked with stronger or more frequent extreme El Niño events. However, these predictions cannot be validated using historical records because of uncertainties in the forced response combined with high levels of unforced El Niño–Southern Oscillation (ENSO) variability2. This issue can be addressed by studying changes in ENSO during past geological intervals when the climate was substantially different from what it is today. However, contradictory palaeoclimatic evidence and uncertain mechanisms have complicated this approach5. Holocene records suggest a highly variable ENSO phenomenon, largely insensitive to external forcings3,11. Records from the last glacial period show large, potentially forced changes in ENSO variability, although a systematic, model-based attribution of these changes has not been carried out so far12,13,14,15. Furthermore, a lack of common mechanisms linking past and future changes has prevented the use of any reconstructions of past ENSO variability to directly validate the multiple mechanisms controlling ENSO changes under future warming.

We addressed this problem using climate model simulations of key intervals spanning the past 21,000 years (or 21 kilo-annum before present (ka BP))—a period in the history of Earth when global climate experienced substantial changes. We studied common mechanisms between past and future changes in ENSO using additional simulations of greenhouse warming under doubling and quadrupling CO2 concentrations. These simulations are comparable to medium-range and high-emission scenarios, respectively. All simulations were performed with Community Earth System Model v.1.2 (CESM1.2), a model that realistically simulates key ENSO dynamics, including asymmetric event evolution16 and drivers of extreme El Niño events (Methods). We focus on SST variability over the Niño–3.4 region in the central equatorial Pacific (170° W–120° W, 5° S–5° N), where strong ocean–atmosphere interactions give rise to El Niño and La Niña events. We quantify the strength of the different feedbacks involved in the growth of El Niño events to identify common mechanisms driving changes across climatic states. Our technique considers seasonality and asymmetries in the evolution of El Niño and La Niña, which is a marked improvement compared with the previous work4,17. Finally, we validate the simulations against existing and new reconstructions of past climate variability from multiple sites across the tropical Pacific that unambiguously capture changes in ENSO compared with other sources of variability. All reconstructions are based on the individual foraminiferal analyses (IFA) technique that can estimate past interannual ocean temperature and, thus, ENSO variability12,13,14,18,19. Our validation considers the site-specific influence of ENSO on surface and subsurface temperature variations, and rigorous statistical tests of the influence of externally forced changes in variability, including changes in the seasonal cycle (Methods).

Simulated ENSO variability since Last Glacial Maximum

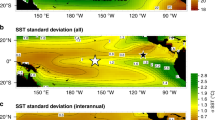
Our simulations show that the ENSO phenomenon can experience pronounced changes over a wide range of past and future climate states. Overall levels of ENSO variability increase under greenhouse warming and decrease under glacial conditions (Fig. 1a, bars). These changes—quantified by the standard deviation of SST variability over the Niño–3.4 region—are sufficiently large relative to unforced levels of variability (Fig. 1a, whiskers) and can, therefore, be used for validation against palaeoclimate reconstructions. Simulated ENSO variability reaches its lowest intensity under glacial and deglacial conditions, followed by a rapid increase to near-modern levels of variability as the climate responds to interglacial conditions (Fig. 1a). The simulated ENSO variability shows a weaker upward trend under Holocene conditions, reaching the maximum amplitude for modern, preindustrial conditions (Fig. 1a, 0 ka BP interval). Greenhouse warming results in a pronounced increase in ENSO variability comparable to but not as large as the reductions under glacial conditions.

Fig. 1: Simulated ENSO variability under past and future climate states.
figure 1

a, ENSO variability simulated by CESM1.2 for climate intervals characterized by altered glacial, orbital and greenhouse gas conditions over the past 21 ka BP and under a doubling of atmospheric CO2 concentrations (2×CO2). The level of ENSO variability in each climatic interval is computed as the standard deviation of simulated monthly SST anomalies averaged over the Niño–3.4 region (170° W–120° W, 5° S–5° N). The box-and-whisker diagrams indicate the distribution of standard deviation values for randomly selected 100-year intervals from each simulation (in which the box depicts the interquartile range and the whiskers extend to show the full distribution). b, Frequency distribution of simulated Niño–3.4 SST anomalies averaged from November to January, when ENSO events peak. c, The contrast between the preindustrial (PI) and LGM (21 ka BP) simulations. d, Relationship between the mean amplitude of simulated ENSO events and the percentage of El Niño events that reach extreme amplitude. El Niño events are identified as those with peak amplitude, measured by the Niño–3.4 SST averaged from November to January, larger than 0.5 K. Extreme El Niño events are computed as those with peak amplitude exceeding 2 K.

Full size image

The broad levels of ENSO variability simulated in each climatic state are directly linked to the frequency of extreme El Niño. In climates with higher ENSO variability, SST variability has a distribution with heavier, not longer, tails (Fig. 1b). This indicates that extreme El Niño events become more frequent, but their maximum amplitude does not change. Under greenhouse warming, the mean amplitude of extreme El Niño, defined as events with peak amplitude larger than 2 K, decreases slightly (Fig. 1b). Our simulations show that the overall levels of ENSO variability are governed by how often extreme El Niño events are triggered. The lowest levels of ENSO variability occur in intervals with no (or very few) extreme El Niño events (for example, 15 ka BP) relative to preindustrial conditions. Conversely, the highest variability occurs in response to greenhouse warming, with one in two events reaching extreme amplitude. The frequency of occurrence of extreme El Niño and overall ENSO variability are highly correlated across all simulations (r = 0.98, p-value < 0.01; Fig. 1d), indicating that this relationship is independent of the type of forcing.

The magnitude of the simulated glacial–interglacial changes is much larger than that for other intervals and, therefore, potentially detectable using reconstructions of past ENSO variability. By contrast, the increase in ENSO variability in response to changing Holocene forcings is much weaker and detectable only because of the length of our simulations. This forced trend is overwhelmed by unforced variability—with a wide range of values of ENSO amplitude simulated over 100-year periods (Fig. 1a, error bars). This response is consistent with the palaeoclimate records derived from fossil corals and bivalves, suggesting a highly variable ENSO phenomenon during this interval3,20,21 and, therefore, limited detectability of forced changes using available palaeodata22. Accordingly, owing to the availability of multiple IFA reconstructions and the large, therefore detectable, simulated changes, we focus our investigation on the Last Glacial Maximum (LGM)—the interval 21 ka BP, when ice sheets reached their maximum extent and CO2 concentrations were low (about 180 ppm). This analysis excludes the influence of freshwater forcing, which potentially drove changes in ENSO during deglacial intervals14,23,24. However, the paucity of a well-dated coverage of IFA records during these intervals prevents robust attribution of changes compared with using IFA data from the LGM.

Reconstructed LGM ENSO variability

IFA reconstructions collectively support the model inference that ENSO variability was weaker under LGM conditions. The IFA technique reconstructs surface and subsurface temperature variability, taking advantage of the near-monthly lifespan of planktic foraminifera12,19 and the depth-dependent calcification habitats of various species25. We quantified past ENSO variability using IFA data from a network of eight records spanning key locations and depths in the tropical Pacific (Extended Data Table 3). Our analysis included new IFA data from the centre of action of ENSO in the central equatorial Pacific (Figs. 2 and 3) combined with published IFA data from other ENSO-sensitive locations. The new IFA was generated using surface-dwelling Globigerinoides ruber tests from central equatorial Pacific sediments in which ENSO variability is dominant relative to the annual cycle of the Pacific cold tongue26 (1.27° N, 157.26° W, 2,850 m depth). Previously existing IFA data were generated with four different planktic species allowing us to sample different habitat depths over the water column12,13,14,18.

Fig. 2: Model–data comparison for changes in Pacific Ocean upper water-column temperature variability during the LGM relative to modern conditions.
figure 2

a–c, Depth-averaged changes in 0–30 m (a), 40–80 m (b) and 100–150 m (c) temperature variability simulated by CESM1.2 under 21 ka BP (LGM) and 0 ka BP (preindustrial; PI) background conditions. These depth ranges were chosen based on species-specific foraminiferal calcification habitats (Methods). Changes in variability were calculated as the difference in standard deviation (1σ) between the simulations at each grid point. Hatching denotes those regions in which changes in seasonal variability dominate the overall change in variability (that is, the sign of 1σ change in interannual temperature anomalies is opposite to the change in overall variability). Sites of IFA reconstructions12,13,14,18 (Extended Data Table 3), including new measurements from the central Pacific (IFA based on G. ruber shown as a circle with a yellow border in a) depict the 1σ change in inferred temperature variability during the LGM, where the symbols indicate different species used for IFA.

Source Data

Full size image
Fig. 3: Reduced glacial temperature variability inferred from central and eastern equatorial Pacific IFA records.
figure 3

a–d, Histograms and box-and-whisker plots (box represents the interquartile range and whiskers represent the full distribution minus outliers—depicted in b and d) of IFA anomalies for the late Holocene (LH; red) and LGM (blue) intervals from central (CEP; ML-1208: IFA-δ18O (a); this study—where δ18O is negatively correlated with temperature) and eastern equatorial Pacific sediments (EEP; ODP Site 849: IFA-Mg/Ca-temperature (c); ref. 12; see Extended Data Table 3 for details). e,f, Resampled histograms of simulated changes (1σ; percentage change from the 0 ka simulation) in site-based temperature variability detectable using the IFA technique19,52 in two scenarios: (1) changes between the 21 ka and 0 ka preindustrial (PI) simulation at each site (teal) and (2) year-to-year variability from the PI simulation imposed on the local annual cycle from the LGM simulation (dark blue) to test whether changes in seasonal variability can explain the observed changes. Reconstructed change (1σ; %) in temperature variability inferred from IFA at the sites are also depicted (around 40% at ODP Site 849, EEP, and about 30% at ML1208, CEP). g,h, Quantile–quantile plots of late Holocene versus LGM IFA data (markers) and their regression lines (purple dashed lines), with uncertainty envelopes generated from bootstrap resampling (n = 10,000) of seasonal-only versus full-variability scenarios described above. All foraminiferal carbonate δ18O values are reported in permille relative to Vienna Pee Dee Belemnite (VPDB).

Source Data

Full size image

Changes in temperature variability during the LGM show striking agreement with our simulation. Depth-stratified estimates of simulated changes in temperature variability between the LGM and preindustrial simulation show how the different sites capture interannual versus seasonal variability (Fig. 2, hatching, and Extended Data Fig. 1). New data from the central equatorial Pacific site and existing data from ODP Site 849 in the eastern equatorial Pacific show unambiguous evidence of externally forced reductions in ENSO variability (Figs. 2 and 3 and Methods). The distributions of anomalies for both the late Holocene baseline and the LGM show distinct agreement with simulated variability at both sites (compare Fig. 3a–d with Fig. 1b). Both sites show pronounced glacial reductions in the tails of the distributions, particularly the warm ones (Figs. 1b and 3g–h). This indicates that extreme El Niño and, to a lesser degree, La Niña were less frequent during the LGM. Statistical resampling of simulated temperature variability at species-specific depths shows low probabilities (≥16%) that IFA changes at these sites arose from unforced variability or because of changes in seasonality (Fig. 3e,f, red lines compared with green distributions). That is, each site shows a high probability (84% and 88%, respectively) that the IFA changes reflect externally forced changes in ENSO. Together, the IFA changes show a ≥98% joint probability of externally forced reductions in ENSO variability during the LGM. Moreover, reductions in the warmest quantiles of glacial IFA anomalies relative to late Holocene values (Fig. 3g,h) suggest that extreme El Niño events were suppressed under LGM conditions, in line with the proposed mechanism.

Extreme ENSO and the Bjerknes feedback

The growth of El Niño events is driven by the Bjerknes feedback—the positive feedback loop between SSTs, winds and ocean currents in the equatorial Pacific. Unlike La Niña events, which are triggered by a preceding El Niño, El Niño events are initiated when random, stochastic fluctuations in the trade winds weaken the equatorial currents that normally keep warm waters confined to the western Pacific. As the equatorial currents weaken, warm pool waters expand eastward, shifting atmospheric convection to the central Pacific. These responses weaken the trade winds, reinforcing the initial response triggered by stochastic wind variability. This mechanism dominates the growth of simulated extreme El Niño events in agreement with observational studies (Extended Data Figs. 2–4). Variations in the depth of the thermocline across the basin, the mechanism underlying conceptual models of ENSO27, play a lesser part restricted to amplifying warming in the eastern equatorial Pacific when warm pool waters expand sufficiently eastwards (Extended Data Fig. 4). This highlights the importance of using a comprehensive model such as CESM1.2, with its ability to realistically simulate the complex spatial dynamics of extreme El Niño, to study the past and future changes in ENSO (for further details, see the Methods). For these reasons, we quantified the strength of the Bjerknes feedback as the growth rate of positive SST anomalies in the equatorial Niño–3.4 region due to the thermal advection by anomalous currents (Fig. 4a). This approach captures the effect of zonal currents in the eastward expansion of warm pool waters during El Niño events (Methods). This mechanism is shown in Fig. 5.

Fig. 4: Simulated ocean and atmosphere processes driving extreme El Niño across past and future climate states.
figure 4

a, Growth rate of positive SST anomalies over the central equatorial Pacific driven by zonal displacements of the western Pacific warm pool, in which values during June–September capture the strength of the positive Bjerknes feedback driving the growth of El Niño events. The growth rates are computed over the equatorial Niño–3.4 region (170° W–120° W; 2.5° S–2.5° N) in which air–sea coupling is the strongest. This narrower region isolates the effect of variations in equatorial currents on zonal thermal advection. b, Relationship between the mean amplitude of simulated El Niño events and the strength of the Bjerknes feedback (June–September growth rates) across climatic states. c, Strength of the Bjerknes feedback across climatic states (black) and the contribution from mechanical coupling (magenta), wind–SST coupling (blue) and thermal coupling (green). The amplitude of ENSO variability (Fig. 1) in each interval is highly correlated with the strength of the Bjerknes feedback. d, Processes controlling the strength of the Bjerknes feedback across climatic states. The averaged mixed layer depth over the equatorial Niño–3.4 region (blue) controls the strength of mechanical coupling. The extent of the warm pool, measured by the longitude of its eastern edge (orange), controls the strength of the wind–SST coupling. The edge of the warm pool is defined as the easternmost longitude along the equator exhibiting ascending motion in the mid-atmosphere (Methods). The depth of the mixed layer is defined based on a 0.5-K threshold. These climatic features are ultimately related to the strength of the trade winds across the equatorial Pacific (dark blue; 2.5° S–2.5° N)—a measure of the strength of the Pacific Walker circulation.

Full size image
Fig. 5: Coupled ocean and atmosphere processes involved in the growth of extreme El Niño under altered climate states.
figure 5

Schematic of the proposed mechanism of extreme El Niño growth and its coupling with the Bjerknes feedback under current climate conditions (middle) and the proposed mean state control under glacial (left) and greenhouse (right) conditions. A weak Bjerknes feedback operates under glacial conditions and serves to weaken extreme El Niño growth and frequency owing to a contracted warm pool, strong SST gradient, and a deep mixed layer driven by an intensified Pacific Walker circulation. Under future greenhouse warming, a weakened Walker circulation leads to stronger mechanical coupling and an enhanced Bjerknes feedback in the equatorial Pacific, which increases the propensity of extreme El Niño growth.

Full size image

Our simulations show that the strength of the Bjerknes feedback in each climate state is correlated with the fraction of El Niño events that reach extreme amplitude (≥2 K; ref. 7). Warmer climates show the strongest growth rate of simulated SST anomalies in the central Pacific, particularly during boreal summer when El Niño events develop (Fig. 4a). By contrast, these growth rates are negligible under glacial conditions. Their summertime magnitude—the strength of the Bjerknes feedback—is highly correlated (r = 0.98, p-value < 10−6) with the mean amplitude of El Niño events in each climatic state (Fig. 4b). This relationship supports a causal link between the changes in the strength of the Bjerknes feedback and the frequency of El Niño events that reach extreme amplitude. The higher growth rates during boreal summer are consistent with the notion that stochastic wind variability during this season has the largest impact on the amplitude of extreme El Niño28. Extreme El Niño events are not very frequent under preindustrial conditions because sustained levels of wind fluctuations are required to activate the Bjerknes feedback28. Under glacial conditions, the Bjerknes feedback is very weak (Fig. 4b) and thus rarely activated. As a result, the frequency of extreme El Niño decreases to less than 20% compared with preindustrial levels. By contrast, under greenhouse warming, a stronger Bjerknes feedback is more easily activated. As a result, more than 50% of simulated El Niño events reach extreme amplitude. The fact that ENSO variability does not vanish when the Bjerknes feedback is very weak or negligible (for example, 12 ka BP, 15 ka BP and 18 ka BP intervals) indicates that all simulations have sufficient levels of stochastic variability controlled by other processes operating in the climate system.

Past and future ENSO feedbacks

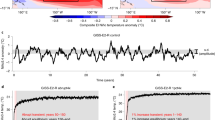
The strength of the Bjerknes feedback is the main control knob of ENSO variability across climatic states. Other positive and negative feedbacks involved in ENSO have a lesser influence. For instance, atmospheric damping, a main control on the amplitude of El Niño and La Niña events on par with the Bjerknes feedback29, has a lesser influence on the simulated response. This negative feedback is weaker in colder climates and stronger in warmer climates (Extended Data Fig. 2a) and, therefore, cannot explain the changes in ENSO. A weaker negative feedback under glacial conditions would favour the growth of El Niño events, allowing them to reach extreme amplitude. Conversely, stronger negative feedback under warming would dampen the growth of El Niño—this negative feedback starts playing a dominant part when CO2 concentrations reach four times preindustrial values (4×CO2) (Extended Data Fig. 2). Under these high levels of greenhouse forcing, our model simulates reductions in the amplitude of extreme El Niño (Extended Data Fig. 3b,c) because intensified atmospheric damping overwhelms the more modest increase in the strength of the Bjerknes feedback (Extended Data Fig. 2d).

Atmospheric damping becomes dominant under the 4×CO2 forcing scenario because the intensified warming over the central and eastern equatorial Pacific30,31 reduces the peak amplitude of El Niño. This behaviour is consistent with previous work showing that the peak amplitude of El Niño events is limited by the temperature of warm pool waters32. Under current and preindustrial conditions, observed and simulated El Niño reach this limit in the central equatorial Pacific—not in the eastern side of the basin, where temperatures remain colder than the warm pool, even at the peak of the record-breaking El Niño of 1997 (Extended Data Fig. 2e, blue and black curves). As the climate warms under 2×CO2 forcing, the Pacific cold tongue warms faster than the western Pacific warm pool, potentially limiting the amplitude of El Niño. However, as the cold tongue warms, peak El Niño temperatures shift eastwards (Extended Data Fig. 2e, red curves), allowing events to continue to reach similar amplitudes as under preindustrial conditions (Extended Data Fig. 3c, red and blue curves). Therefore, under 2×CO2, extreme El Niño events reach a similar amplitude as under preindustrial conditions, but they become more frequent because of stronger Bjerknes feedback. This explains the minimal influence of atmospheric damping on El Niño peak amplitude under moderate levels of warming produced by 2×CO2 forcing. Furthermore, the interplay between these mechanisms explains the thicker, yet slightly shorter, warm tail of the distribution of Niño–3.4 SST anomalies (Extended Data Fig. 2c).

Under 4×CO2, El Niño events shift further to the east, where their peak amplitude starts reaching warm pool temperatures (Extended Data Fig. 3c, green curve). This makes atmospheric damping stronger and, therefore, the dominant mechanism at this level of CO2 forcing. This dominant effect of atmospheric damping explains the robust model projections of ENSO reductions under 4×CO2 levels33. At moderate, more plausible 2×CO2 levels, the opposing effects between changes in atmospheric damping and the Bjerknes feedback might explain model uncertainty34,35, making validation against past changes important. Thus, the challenge for models is simulating changes in ENSO under more moderate CO2 forcing36,37—for which our palaeo-validation is key to identifying responses associated with the proposed mechanism.

To determine how changes in the climate of the tropical Pacific alter the frequency of extreme El Niño, we quantified the strength of coupled processes involved in the Bjerknes feedback. We find that mechanical coupling between winds and ocean currents is the dominant physical process driving changes in growth rates associated with this positive feedback (Fig. 4c, magenta curve compared with black curve; see the Methods for details). This mechanical coupling of currents and winds is the weakest under glacial conditions, with reductions of up to 60%, and the strongest under greenhouse warming, increasing by more than 70%, relative to PI conditions (Fig. 4c). Low mechanical coupling under glacial conditions hinders the eastward expansion of the warm pool during the onset of El Niño and explains why fewer events reach peak amplitude. Conversely, high mechanical coupling under greenhouse warming favours the eastward expansion of the warm pool and the activation of the Bjerknes feedback. The responsiveness of winds to SST anomalies also plays an important part in the strength of the Bjerknes feedback. This wind–SST coupling is also weaker under glacial conditions and stronger under greenhouse warming (Fig. 4c, blue curve). Together, these two coupled processes explain most of the changes in the strength of the Bjerknes feedback across climatic states (Fig. 4c, black curve). The Bjerknes feedback is also controlled by the magnitude of the climatological SST contrast across the equatorial Pacific because this gradient governs the thermal advection by anomalous currents. This thermal coupling is stronger under glacial conditions and weaker under interglacial conditions (Fig. 4c, green curve) and, therefore, cannot explain the simulated pattern of changes in extreme El Niño.

Glacial ENSO and the Walker circulation

The strength of the coupling mechanisms, and, therefore, the frequency of extreme El Niño events across cold and warm climates, is ultimately tied to the strength of the Pacific Walker circulation. This influence is mediated by the changes in the depth of the oceanic mixed layer and the climatological extent of the warm pool. Warmer climates are characterized by a weaker Walker circulation, shallow oceanic mixed layer and an eastward expanded warm pool, whereas the opposite occurs for glacial climates (Fig. 4d). In warmer climates, wind fluctuations transfer momentum to a thinner layer of upper ocean waters making zonal currents more responsive to wind variations during the onset of El Niño. Moreover, winds are more responsive to SST anomalies because an eastward expanded warm pool favours convection over a larger area along the equatorial Pacific. Both factors promote rapid expansions of the warm pool during the onset of El Niño, allowing more events to reach extreme amplitude (Fig. 5). The opposite scenario occurs under glacial conditions, in which the onset of extreme El Niño is hindered by less responsive ocean currents and winds because of a deeper mixed layer and a contracted warm pool—both driven by a stronger Walker circulation (Fig. 5).

The simulated changes are supported by evidence of a deeper thermocline across the equatorial Pacific during the LGM, a response indicative of a deeper mixed layer and unambiguously linked to a stronger Walker circulation38—both important elements of the proposed mechanism. A recent compilation of subsurface proxies shows a deeper thermocline over the eastern Pacific39. Independent estimates show evidence of a deeper thermocline over the western side of the basin40,41. By contrast, the simulated pattern of enhanced equatorial cooling—a metric also related to the strength of the Walker circulation—has less conclusive support from proxies. Individual temperature records generally disagree regarding the pattern of surface-ocean cooling42. However, data assimilation reconstructions of the LGM, which factor in spatial undersampling of proxies alongside proxy uncertainty and biases, support the pattern of enhanced equatorial cooling associated with a stronger Walker circulation43,44 (Methods). Our mechanism based on zonal advective processes clarifies a previously proposed link between levels of ENSO variability and depth of the mixed layer15. A deeper thermocline, such as during the LGM, would reduce mixing in the upper ocean, whereas the stronger Walker circulation and associated surface winds would enhance turbulent mixing, both acting to deepen the mixed layer. Together with the large reductions in ENSO variability inferred from IFA, these lines of evidence support our conclusion that mechanical and wind–SST coupling are the primary control knobs on ENSO variability.

Palaeo-constraints on future dynamics

Despite the complexity of feedbacks driving the growth and decay of El Niño and La Niña45, we identify a single mechanism connecting past and future changes. This mechanism is consistent with the dynamics of observed extreme El Niño events, which develop when warm pool waters expand rapidly eastwards because of strongly coupled ocean currents and winds29,46. This mechanism is realistically simulated by our model, consistent with the emerging paradigm that ENSO is not a cycle; instead, it is best described as a series of events47. Observed and simulated ENSO variability is energized every time an El Niño event is excited by stochastic forcing, triggering a subsequent La Niña, with the cycle breaking down as conditions return to neutral without triggering a subsequent El Niño event45,48. This asymmetric evolution is key to quantifying the strength of coupled feedbacks because each phase is triggered by different physical processes. Together, the existence of a single mechanism controlling ENSO variability across a range of cold and warm climatic states, combined with the robust evidence of weaker ocean temperature variability during the last glacial interval, supports our prediction of an increased risk of extreme El Niño frequency under continued greenhouse warming.

Our novel prediction verification using palaeoceanographic data enabled us to provide firm constraints on model projections of increasing ENSO variability in a warming climate. Global models are starting to converge about stronger ENSO variability in the future37. However, their response needs validation against observed changes because of the highly variable nature of ENSO49. Ongoing greenhouse warming has not resulted in a discernible weakening of the Walker circulation as predicted by models because natural variability or aerosol forcing might be delaying the emergence of this response50. This model prediction, however, is supported by palaeoclimatic evidence of a weakened east–west gradient across the Pacific and a weaker Walker circulation during the Pliocene51, the most recent geological interval when CO2 levels were comparable to our idealized 2×CO2 scenario. The mechanism governing the past and future changes is also supported by evidence of a stronger Walker circulation during the LGM, seen as a deeper equatorial thermocline during this interval39,40,41. Despite the multiple forcings driving glacial cooling, our results indicate that global mean temperatures by their effect on the Walker circulation30,34 are the main control on ENSO variability. Stabilizing CO2 concentrations in the atmosphere well below two times preindustrial values (560 ppm) is, therefore, essential to mitigate the heightened risk of increasing climate extremes posed by more frequent extreme El Niño events.

Methods

Numerical simulations

Simulations of global climate were run for eight distinct intervals selected every 3 ka from the LGM (21 ka BP) to modern or preindustrial conditions (0 ka BP). The numerical model—CESM1.2—simulates the coupled interactions between the atmosphere, land, ocean and sea ice. Together, these simulations resolve changes in climate since the LGM driven by the collapse of ice sheets, increasing atmospheric CO2 and orbitally driven changes in insolation. The simulations do not include freshwater forcing associated with iceberg discharges, an important driver of the abrupt events that punctuated the deglaciation. Our analysis does not consider changes in response to this forcing mechanism because of limited reconstructions of past ENSO variability during these events. Each simulation was run with specific boundary conditions corresponding to the interval (Extended Data Table 1), including modifications to (1) the distribution of seasonal and latitudinal insolation due to changes in the orbit of Earth; (2) greenhouse gas (GHG) concentrations based on ice core measurements; (3) the effect of altered sea level on coastlines and key ocean passages; and (4) the topography and ice extent of continental ice sheets. The implementation of these boundary conditions follows the same procedure as in previous simulations of the LGM using CESM1 (ref. 53) outlined in more detail below. All simulations are nearly equilibrated (Extended Data Table 2).

Boundary conditions for simulations

Ice sheet topography and land surface glacier extent were prescribed based on the ICE-6G_C reconstruction54,55. This reconstruction provides ice sheet extent, land surface elevation and land–sea mask for the Laurentide, Fennoscandian, Patagonian and Antarctic ice sheets for all simulated intervals. For glacial intervals, we included prescribed ice shelves over the western Labrador Sea following previous work56 showing that this alleviates numerical instabilities associated with very steep topography. For each simulation, the topography of the atmospheric component of CESM1.2 was uniformly elevated based on the magnitude of relative sea level (Extended Data Table 1) to represent the effect of a higher land surface. The land–sea mask was also modified in both the atmosphere and land components of CESM1.2 to represent the effect of lowered sea levels exposing continental shelves globally. The ICE-6G_C land–sea mask was used globally, except the Maritime Continent, where the land–sea mask was defined following previous work demonstrating the importance of shelf exposure on tropical climate changes57.

The bathymetry of the ocean component was also modified based on the past relative sea level58 following a previous work simulating the LGM57. This resulted in the exposure of the continental shelves with partial or full closure of several key oceanic passages depending on the magnitude of the relative sea level of each interval (Extended Data Table 1). The bathymetry around the Maritime Continent was further modified following previous work57 with the objective of representing the effect of lower sea level on the Indonesian Throughflow (ITF). The bathymetry of other key passages of the world ocean, such as the Bering Strait, Korea Strait or the Northwest Passage, was modified to ensure a realistic timing of the closure or opening of these passages. The effect of altered tidal mixing due to exposed shelves was implemented for the glacial intervals (15 ka, 18 ka and 21 ka—see Extended Data Table 1) using LGM dissipation rates57. Parametrized overflows in the Ross and Weddell Seas were removed in the glacial simulations (15 ka, 18 ka and 21 ka) because the associated ice shelves extended over the overflow source regions. The Denmark Strait and Iceland–Scotland overflows were kept unchanged as in the 0 ka simulation.

Vegetation was prescribed to be the same as in the 0 ka simulation, except for the regions covered by the ice sheets or those exposed because of lowered sea levels. Different plant functional types (PFTs) were prescribed over exposed shelves according to the latitude. C3 Arctic grass PFT was applied over the shelves polewards from 60°. C3 grass PFT was applied over shelves polewards from 30°. An equal mix of tropical deciduous trees and C4 tropical grass was prescribed over tropical shelves (towards the equator from 30°), including the Sunda and Sahul shelves57. The remaining surface properties, such as albedo or surface roughness, are computed by the land component of CESM1.2 based on the soil and plant properties and passed to the atmosphere component by the coupler. The vegetation phenology, including the total leaf and stem area indices and canopy heights, was prescribed and does not respond to changes in climate.

Concentrations of key greenhouse gases, CO2, CH4 and N2O, were altered for each simulation based on ice core measurements59 (Extended Data Table 1). The concentrations of other greenhouse gases, such as chlorofluorocarbons, were set to zero in all simulations. Ozone concentrations were kept at 1850 CE (common era) values in all simulations. CESM1.2 was configured to run with its prognostic aerosol module requiring prescribed emissions of aerosols and dust. These processes are likely to be of second order relative to the magnitude of Northern Hemisphere cooling caused directly by the higher albedo of ice sheets. Therefore, all our simulations were run with the same dust emissions as in the 0 ka simulation.

The 0 ka simulation corresponds to preindustrial conditions and was, therefore, run with external forcings (solar irradiance, orbit, greenhouse gases, dust and other aerosol emissions, ozone and land use) set constant to 1850 CE values. The 2×CO2 simulation was identical to this 0 ka simulation except for the doubling of CO2 to 580 ppm. The solar flux was kept constant at 1,365 W m−2 in all simulations.

Model initiation and climate equilibration

The 0 ka and 21 ka simulations were initialized from the existing simulations performed with CESM1.2 under slightly different boundary conditions53 and were run until the surface climate reached a new equilibrium. This was particularly important for the 21 ka simulation that uses a different ice sheet reconstruction than the existing one used for initialization. To efficiently reach the equilibrated climate states, each of the remaining simulations was initialized starting from either the 0 ka or 21 ka simulations as listed in Extended Data Table 2. All simulations were run until the surface climate and oceanic processes controlling tropical climate, such as the depth of the thermocline (ZTC) in the equatorial Pacific or the Atlantic Meridional Overturning Circulation (AMOC), reached equilibrium. All analyses were performed using output from the past 500 years of nearly equilibrated climate. The preindustrial, 0 ka simulation was run for 1,500 years to obtain a robust baseline of the range of unforced temperature variability to accurately assess forced changes in the remaining simulations. All simulations exhibit minimal drift in global mean surface temperature, tropical mean surface temperature, the depth of the equatorial thermocline in the Pacific and the strength of the AMOC during the periods used in the analyses (Extended Data Table 2).

Observational data

Ocean temperature and current data from the ORAS3 and ORAS5 reanalyses60 were used for validation of key features of the simulation of extreme El Niño by CESM1. These datasets are used to evaluate the zonal and vertical thermal advection between the observed and simulated extreme El Niño events. Zonal thermal advection is computed for the extreme El Niño events of 1972, 1982, 1997 and 2015 using monthly mean temperature and zonal current fields from ORAS3 and ORAS5. Vertical thermal advection is computed for the events of 1972, 1982 and 1997 because the vertical velocity needed to compute this quantity is available only from the ORAS3 dataset, which extends to the year 2009, thus excluding the 2015 event. Other diagnostics involving subsurface temperature, such as the zonally averaged thermocline depth, were computed using ORAS3 data from 1959 to 2009. Diagnostics involving SST were computed using the Extended Reconstructed Sea Surface Temperature v.5 (ERSST5; ref. 61). This dataset spans from 1871 to 2020, providing three nonoverlapping 50-year intervals to evaluate the simulated ENSO against different levels of observed variability.

Climate indices and diagnostics

Our analysis includes several variables and indices computed from the model output. The depth of the mixed layer (MLD) was computed as the depth at which the ocean temperature increases by 0.5 °C relative to the previous level. The depth of the thermocline (ZTC) is computed as the depth of the maximum vertical temperature gradient. This metric captures the depth of this ocean interface independently of the climate state31. The zonal extent of the Western Pacific Warm Pool (WPWP) is computed as the longitude along the equator where rainfall values averaged from 2.5° N to 2.5° S reach 5 mm day−1. This definition of the eastward extent of the WPWP tracks the area characterized by ascending motion measured by the simulated vertical velocity (ω). The strength of the equatorial trade winds, a measure of the intensity of the Pacific Walker circulation, is computed as the simulated zonal wind stress averaged over the 180°–110° W; 2.5° S–2.5° N) region. The calculation of several key terms of the temperature equation involved in the heat budget of the oceanic surface layer, including thermal advection and sea–air heat fluxes, is outlined below.

For each climatic state, the variability associated with the ENSO phenomenon was quantified using anomalies relative to the monthly mean seasonal cycle of the corresponding timeslice simulation. The average amplitude of ENSO variability was quantified as the standard deviation of the Niño–3.4 SST index. This index is defined as the monthly mean SST anomalies averaged over the central equatorial Pacific (170° W–120° W; 5° S–5° N). The standard deviation of this index includes variability at all timescales other than seasonal, but it is dominated by the interannual variations associated with El Niño and La Niña events. The zonal extent of the Niño–3.4 region captures the bulk of the SST variability in all simulations because the changes in variability are spatially stationary, that is, the variability increases and decreases while keeping its spatial pattern largely unaltered. A zonal mean thermocline depth index is computed by averaging ZTC anomalies across the equatorial Pacific (140° E–80° W; 5° N–5° S). Under preindustrial or modern climatic conditions, this index is highly correlated with the Warm Water Volume index based on the depth of the 20 °C isotherm (D20) commonly used to study the oscillatory dynamics of ENSO. However, our definition can be applied to different climatic states because it does not require a 20 °C isotherm coinciding with the thermocline in the equatorial Pacific.

New and existing palaeoceanographic reconstructions of tropical Pacific variability during the LGM

We developed new IFA reconstructions using Globigerinoides ruber tests in well-dated62 late Holocene and LGM sediments from the central equatorial Pacific, using cores ML1208-21MC and 20BB collected from the Line Islands Ridge26. We picked individuals of Globigerinoides ruber (white variety) from the 350–450 µm size fraction, focusing on sensu stricto morphotypes when possible26. IFA-δ18O (reported in permille relative to Vienna Pee Dee Belemnite: ‰, VPDB) was measured at the University of Arizona Paleo² Laboratory using a Kiel IV Carbonate Device and a Thermo MAT253 + IRMS setup63, with δ18O analytical uncertainty of 0.06‰ (VPDB). We interpret IFA-δ18O anomalies as quantitative changes in temperature anomalies, as the influence of seawater δ18O on carbonate-δ18O variability is minor at this location19,42. Available reconstructions12,13,14,18 (Extended Data Table 3) of temperature variability using IFA-Mg/Ca and IFA-δ18O were also used in our analysis. The IFA technique takes advantage of the near-monthly lifespan of planktic foraminifera, in which numerous specimens from a sedimentary layer are analysed to approximate the distribution of monthly temperature variability in that period19,64. Proxy system modelling demonstrates that the IFA technique reliably captures changes in ENSO intensity at a site as long as the overall variability is dominated by interannual fluctuations19,52,65. Temperature anomalies were calculated relative to mean values, using temperature calibrations reported by the authors. The impact of various calibrations on the resultant IFA variability is minor to negligible after removing the mean values52,64. These datasets12,13,14,18, including our new measurements, span six different locations and are composed of temperature-sensitive IFA-δ18O and Mg/Ca measurements using four different species of foraminifera that calcify in the upper ocean. The species include Globigerinoides ruber, Trilobatus sacculifer, Neogloboquadrina dutertrei and Globorotalia tumida (Extended Data Table 3).

Model evaluation

Simulated changes in temperature variability between the 21 ka BP and 0 ka BP timeslices were compared relative to reconstructed changes using IFA from LGM and late Holocene sediments. The intervals corresponding to deglacial conditions (18 ka, 15 ka and 12 ka) exhibit the largest simulated changes due to a combination of glacial and orbital forcings, but there are few-to-no palaeoreconstructions of ENSO variability from these intervals without an influence from freshwater forcing14,24,66 and its influence on the AMOC. There is a wealth of coral and mollusc records of palaeo-ENSO variability from the Holocene20,21,22, but the model and data evidence point to changes dominated by natural multi-decadal to longer variations in levels of ENSO variability. The IFA reconstructions span multiple sites and depths at which seasonal to interannual processes are dynamically heterogeneous and capture unique aspects of glacial and modern El Niño variability and extremes (Fig. 2). Simulated ocean temperatures at the grid-point location of the core were used to compare temperature variability derived from surface-ocean IFA. Specific depth ranges were chosen for comparison based on recent global core-top estimates of apparent calcification depths25,67 (Extended Data Fig. 1). Changes in temperature variability using depth-stratified averages of 0–30 m, 40–80 m and 100–150 m were calculated in the simulations to compare with Globigerinoides ruber, Trilobatus sacculifer and Neogloboquadrina dutertrei, and Globorotalia tumida, respectively (Fig. 2). We further investigated site-based model–data responses at two locations at which the simulated signal of ENSO-driven changes relative to the calcification depth of foraminifera (and associated uncertainty; see Extended Data Fig. 1) was unambiguous: our central equatorial Pacific site ML2108-21MC/20BB and IODP Site 849 in the eastern equatorial Pacific12. At each site, the distributions of simulated variability were computed in the following scenarios: (1) changes between the 0 ka and 21 ka simulation (purple distribution and quantile–quantile uncertainty envelope in Fig. 3) and (2) seasonal variability under 21 ka conditions imposed with interannual anomalies from the 0 ka simulation (green distribution and quantile envelope in Fig. 3). These scenarios provide a statistical null hypothesis in which the IFA-inferred changes in variability may arise from changes in the local annual cycle. Bootstrap Monte Carlo simulations (n = 10,000) were performed for each scenario resampling the simulated variability according to the number of IFA samples generated by each study for the late Holocene and LGM datasets (Extended Data Table 3). Analytical uncertainty (1σ) values of 0.1‰ (ML1208) and 0.15 mmol mol−1 (ODP Site 849) were incorporated into each realization. Finally, we computed the probability that each scenario explains the IFA-inferred changes in variability at each site (as % change; Fig. 3).

Coupled feedbacks

The strength of the Bjerknes feedback was estimated using output from each simulation applying a technique that accounts for asymmetries between El Niño and La Niña as well as their seasonality48. These calculations are based on the anomalous zonal thermal advection because this process drives the largest positive tendency during the growth of positive SST anomalies (Extended Data Fig. 4). Further details on the heat budget calculation are available below. All simulations show that the anomalous temperature tendency because of thermal advection by zonal currents is positively correlated with positive SST anomalies in the equatorial Niño–3.4 region, consistent with a positive Bjerknes feedback. This relationship indicates that during growing El Niño events, zonal currents weaken driven by the weakening trade winds, reducing the climatological cooling at the edge of the warm pool. This response translates into a warming of the central equatorial Pacific driving a further weakening of the trade winds and equatorial currents, feeding back into the expanding warm pool during the growth of an El Niño event. Partial least-square regression was used to compute the slope between the positive temperature tendency associated with the zonal thermal advection and the positive equatorial Niño–3.4 SST anomaly. This slope represents the growth rate of SST anomalies in the central equatorial Pacific driven by zonal thermal advection associated with the expansion of the warm pool. This growth rate is the main process contributing to the Bjerknes feedback and reaches the peak amplitude during boreal summer when El Niño events grow (Fig. 4a). The strength of the Bjerknes feedback (Fig. 4b) is computed using the slope of those same quantities (zonal thermal advection versus the positive Niño–3.4 SST anomaly), but averaged from June to September before computing the slope. Damping rates associated with air–sea heat fluxes were computed as the slope between negative surface air–sea heat fluxes and the positive SST anomaly averaged over the equatorial Niño–3.4 SST region used to compute the thermal advection. The strength of this negative feedback was computed for both the growth phase of El Niño (June–September) and for its peak (November–January).

Coupling mechanisms

Wind–SST coupling is estimated as the slope between positive zonal wind stress anomalies and positive SST averaged over the central equatorial Pacific and from June to September. Mechanical coupling is estimated as the slope between positive zonal current and zonal wind stress anomalies averaged over the central equatorial Pacific and from June to September. Thermal coupling is the slope between the positive zonal thermal advection and zonal current anomalies averaged over the central equatorial Pacific and from June to September. For all three responses involved in the feedback loop, the slope or coupling coefficient is computed using partial least-square regression between the positive anomalies involved in the growth of El Niño during boreal summer, that is, quantities averaged from June to September. The product of the three couplings is equivalent to the growth rate associated with the Bjerknes feedback. The influence of each of these coupling mechanisms on the Bjerknes feedback is isolated by keeping the other two couplings at the value for the 0 ka BP interval and then calculating the growth rate associated with each individual coupling (Fig. 4b).

ENSO heat budget

We computed the different advection terms of the temperature equation and integrated them vertically over a layer of constant depth approximating the oceanic mixed layer. These terms with the surface heat fluxes closely balance the time tendency of the vertically integrated ocean temperature. The resulting heat budget can be used to quantify the influence of different physical processes driving SST anomalies associated with ENSO because the time tendency is nearly equal to the tendency of SST (times the depth of the layer). The surface layer was defined as one vertical level (10 m) deeper than the climatological annual mean MLD in each simulation. Using a stationary layer provides accurate results on interannual timescales, despite ignoring the influence of a temporally varying mixed layer on the entrainment of colder thermocline waters68. The vertically averaged temperature tendencies are averaged over an equatorial Niño–3.4 region (170° W–120° W; 2.5° S–2.5° N) where air–sea coupling is the strongest. This region is meridionally narrower than the typical Niño–3.4 regions to isolate the effect of variations in equatorial currents on the zonal thermal advection. This region also captures the variability associated with vertical thermal advection. However, the influence of these processes is smaller for El Niño events (Extended Data Fig. 3) and is, therefore, not included in the estimates of El Niño growth rates.

Simulated ENSO dynamics

CESM1.2 provides a highly realistic simulation of ENSO dynamics, including asymmetries in amplitude and duration of its warm El Niño and cold La Niña phases16. These features of the simulation of ENSO vastly improve on CCSM3, a previous version of this model used to simulate the past 21,000 years (ref. 4). That model simulated an excessively oscillatory, regular and symmetric ENSO69, precluding its use for investigating changing extremes. CESM1.2 simulates a lagged autocorrelation function of the Niño–3.4 SST index with a negative peak at about a 2-year lag is in striking agreement with observations (Extended Data Fig. 4a, purple and orange curves). The decay at longer lags and overall shape of the simulated and observed autocorrelation functions indicate that ENSO is not a self-sustained oscillation. This is a vast improvement relative to CCSM3 (Extended Data Fig. 4a, green curve), which simulated a Niño–3.4 SST index with autocorrelation at multiple, periodic peaks reflective of oscillatory behaviour. Similar improvements are seen in the lagged correlation between the Niño–3.4 SST index and the zonally averaged thermocline depth, a metric of the influence of thermocline depth anomalies on the evolution of ENSO events. CESM1.2 shows a low positive correlation at negative lags, similar to observations, and an improvement relative to CCSM3, in which the correlation is much higher. The low correlation of CESM1.2 is consistent with the secondary role played by thermocline variations in the onset of extreme El Niño (Extended Data Fig. 4b). Apart from a more realistic evolution of events, CESM1.2 also simulates ENSO with improved statistics of extremes. CESM1.2 simulates a distribution of the Niño–3.4 SST index with a heavier tail for positive anomalies associated with extreme El Niño (Extended Data Fig. 4c). This is also seen in the values of the skewness of this index, which are positive for CESM1.2, as observed, and unlike CCSM3, which shows negligible skewness indicative of non-frequent extreme El Niño events (Extended Data Fig. 4d).

CESM1.2 simulates physical processes driving extreme El Niño in striking agreement with observed events. Composite analysis of simulated and observed events shows that zonal thermal advection plays a much larger part than vertical thermal advection in the onset of extreme El Niño. In both CESM1.2 and nature, warming of the Niño–3.4 region (Extended Data Fig. 3, blue curves) is preceded by the positive zonal thermal advection (Extended Data Fig. 3, left, green curves) associated with positive zonal current anomalies, that is, weaker equatorial currents (Extended Data Fig. 3, left, red curves). These processes reflect the eastward expansion of the WPWP driving the onset of El Niño. Zonal thermal advection and the eastward expansion of the WPWP played a key part in the onset of the extreme El Niño events of 1997 and 2015 (refs. 29,46). By contrast, the magnitude of the vertical thermal advection is much smaller (Extended Data Fig. 3, right, green curves), indicative of the lesser role played by variations in the depth of the thermocline (Extended Data Fig. 3, right, red curves) in the onset of El Niño. This process, however, plays a dominant part in the onset of La Niña, as seen by the large, negative vertical thermal advection leading to La Niña events following the peak of an El Niño event.

This analysis is consistent with the emerging model that El Niño events are triggered by stochastic wind fluctuations and amplified by a positive Bjerknes feedback involving the expansion of the WPWP with a lesser role45 for subsurface thermal anomalies generated by a preceding La Niña, as indicated by many theories of ENSO27. By contrast, large negative thermocline depth anomalies and associated negative vertical thermal advection do play a part in the onset of La Niña (Extended Data Fig. 3, right). This suggests that the oscillatory dynamics underpinning conceptual models of ENSO operate only in the transition from El Niño to La Niña, but not the other way around because La Niña events cannot trigger48 a subsequent El Niño. Because of this, the onset of El Niño events requires stochastic wind variability to excite the Bjerknes feedback by changes in zonal currents and associated zonal advection of warm pool waters1.

Pacific Ocean mean state at 21 ka

The main text demonstrates model–data parity between reconstructed and simulated ocean temperature variability in the surface and subsurface Pacific Ocean under LGM boundary conditions using CESM1.2 and IFA. Additional assessments of the 21 ka simulation are previously published53,57; ref. 53 also validated simulated LGM patterns in the Indo-Pacific using a network of mean annual temperature proxies. However, assessments of the pattern and magnitude of mean annual temperature changes across the Pacific Ocean are more challenging because of both larger gaps in the proxy record43 owing to the size of the basin and large multiproxy uncertainty arising from conflicting proxy reconstructions42,43,70. Furthermore, seasonal and depth-related biases in different proxies71—including their stationarity72—in tandem with calibration uncertainties73,74 complicate estimates of mean SST change. Recent applications of palaeoclimate data assimilation techniques have made marked advances in circumventing the aforementioned biases by explicitly incorporating proxy system models to blend model output and palaeoproxy information43. Moreover, data assimilation techniques provide globally complete reconstructions by leveraging local and remote information arising from available proxies. A recent assessment of four independent palaeoclimate assimilation reconstructions of the LGM (using both inverse and forward modelling of proxies) indicates that SSTs in the eastern tropical Pacific cooled more than the western Pacific44 after accounting for proxy and spatial biases. This inference (see multimodel mean in fig. 1e in ref. 44) is in striking agreement with the simulated pattern and magnitude of surface-ocean cooling in our simulations. In CESM1.2, the eastern equatorial Pacific cooling response is associated with a deeper thermocline during the LGM57 (Fig. 4). Whereas available estimates of changes in LGM thermocline depths have also been largely equivocal40,75,76, recent reappraisals of proxy data in the eastern39 and western41 tropical Pacific strongly support a deeper thermocline. Moreover, CESM1.2 shows thermocline deepening in the southern tropical western Pacific41 and shoaling in the off-equatorial northern tropical Pacific and in the southwest Pacific (see fig. 8a in ref. 57), both features that are observed in proxy reconstructions40,41,75,76. Accordingly, we suggest that these lines of evidence point to a thicker mixed layer across the Pacific40 during the LGM, with a more substantial deepening of the thermocline in the eastern equatorial Pacific39, pointing towards a stronger Walker circulation26, as observed in the CESM1.2. simulations.