Abstract
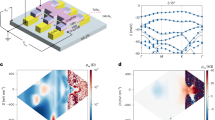
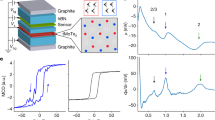
Orbital magnetization provides a sensitive probe of topology and interactions, with particularly rich phenomenology in Chern insulators in which the topological edge states carry large equilibrium currents. Here we use a nanoscale superconducting sensor1,2 to map the magnetic fringe fields in twisted bilayers of MoTe2, in which transport3,4 and optical sensing5,6 experiments have revealed the formation of fractional Chern insulator (FCI) states at zero magnetic field. We observe oscillations in the local magnetic field associated with fillings ν = −1, −2/3, −3/5, −4/7 and −5/9 of the first moiré hole band, consistent with the formation of FCIs at these fillings. We determine the local thermodynamic gaps of the most robust FCI state at ν = −2/3, finding −2/3Δ as large as 7 meV. We also characterize sample spatial disorder, which is dominated by both inhomogeneity in the effective unit cell area7 as well as inhomogeneity in the band edge offset and bound dipole moment. Our results highlight both the challenges posed by structural disorder in the study of twisted homobilayer moiré systems and the opportunities afforded by the robust nature of the underlying correlated topological states.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
All data are available at Dryad (https://doi.org/10.5061/dryad.0zpc86769) (ref. 47).
Code availability
All the software supporting the data processing pipeline is available at Zenodo (https://doi.org/10.5281/zenodo.13621665) (ref. 48).
References
Finkler, A. et al. Self-aligned nanoscale SQUID on a tip. Nano Lett. 10, 1046–1049 (2010).
Vasyukov, D. et al. A scanning superconducting quantum interference device with single electron spin sensitivity. Nat. Nanotechnol. 8, 639–644 (2013).
Park, H. et al. Observation of fractionally quantized anomalous Hall effect. Nature 622, 74–79 (2023).
Xu, F. et al. Observation of integer and fractional quantum anomalous Hall effects in twisted bilayer MoTe2. Phys. Rev. X 13, 031037 (2023).
Cai, J. et al. Signatures of fractional quantum anomalous Hall states in twisted MoTe2. Nature 622, 63–68 (2023).
Zeng, Y. et al. Thermodynamic evidence of fractional Chern insulator in moiré MoTe2. Nature 622, 69–73 (2023).
Uri, A. et al. Mapping the twist-angle disorder and Landau levels in magic-angle graphene. Nature 581, 47–52 (2020).
Spanton, E. M. et al. Observation of fractional Chern insulators in a van der Waals heterostructure. Science 360, 62–66 (2018).
Cao, Y. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018).
Chen, G. et al. Evidence of a gate-tunable Mott insulator in a trilayer graphene moiré superlattice. Nat. Phys. 15, 237–241 (2019).
Regan, E. C. et al. Mott and generalized Wigner crystal states in WSe2/WS2 moiré superlattices. Nature 579, 359–363 (2020).
Tang, Y. et al. Simulation of Hubbard model physics in WSe2/WS2 moiré superlattices. Nature 579, 353–358 (2020).
Wang, L. et al. Correlated electronic phases in twisted bilayer transition metal dichalcogenides. Nat. Mater. 19, 861–866 (2020).
Shimazaki, Y. et al. Strongly correlated electrons and hybrid excitons in a moiré heterostructure. Nature 580, 472–477 (2020).
Xu, Y. et al. Correlated insulating states at fractional fillings of moiré superlattices. Nature 587, 214–218 (2020).
Sharpe, A. L. et al. Emergent ferromagnetism near three-quarters filling in twisted bilayer graphene. Science 365, 605–608 (2019).
Serlin, M. et al. Intrinsic quantized anomalous Hall effect in a moiré heterostructure. Science 367, 900–903 (2020).
Chen, G. et al. Tunable correlated Chern insulator and ferromagnetism in a moiré superlattice. Nature 579, 56–61 (2020).
Li, T. et al. Quantum anomalous Hall effect from intertwined moiré bands. Nature 600, 641–646 (2021).
Anderson, E. et al. Programming correlated magnetic states with gate-controlled moiré geometry. Science 381, 325–330 (2023).
Xie, Y. et al. Fractional Chern insulators in magic-angle twisted bilayer graphene. Nature 600, 439–443 (2021).
Ji, Z. et al. Local probe of bulk and edge states in a fractional Chern insulator. Preprint at https://arxiv.org/abs/2404.07157 (2024).
Lu, Z. et al. Fractional quantum anomalous Hall effect in multilayer graphene. Nature 626, 759–764 (2024).
Li, H., Kumar, U., Sun, K. & Lin, S.-Z. Spontaneous fractional Chern insulators in transition metal dichalcogenide moiré superlattices. Phys. Rev. Res. 3, L032070 (2021).
Dong, Z., Patri, A. S. & Senthil, T. Theory of quantum anomalous Hall phases in pentalayer rhombohedral graphene moiré structures. Preprint at https://arxiv.org/abs/2311.03445 (2023).
Dong, Z., Patri, A. S. & Senthil, T. Stability of anomalous Hall crystals in multilayer rhombohedral graphene. Preprint at https://arxiv.org/abs/2403.07873 (2024).
Wang, C. et al. Fractional Chern insulator in twisted bilayer MoTe2. Phys. Rev. Lett. 132, 036501 (2024).
Yu, J. et al. Fractional Chern insulators versus nonmagnetic states in twisted bilayer MoTe2. Phys. Rev. B 109, 045147 (2024).
Morales-Durán, N., Wei, N., Shi, J. & MacDonald, A. H. Magic angles and fractional Chern insulators in twisted homobilayer transition metal dichalcogenides. Phys. Rev. Lett. 132, 096602 (2024).
Jia, Y. et al. Moire fractional Chern insulators. I. First-principles calculations and continuum models of twisted bilayer MoTe2. Phys. Rev. B 109, 205121 (2024).
Sheng, D. N., Reddy, A. P., Abouelkomsan, A., Bergholtz, E. J. & Fu, L. Quantum anomalous Hall crystal at fractional filling of moiré superlattices. Phys. Rev. Lett. 133, 066601 (2024).
Dong, J. et al. Anomalous Hall crystals in rhombohedral multilayer graphene. I. Interaction-driven Chern bands and fractional quantum Hall states at zero magnetic field. Preprint at https://arxiv.org/abs/2311.05568 (2023).
Soejima, T. et al. Anomalous Hall crystals in rhombohedral multilayer graphene. II. General mechanism and a minimal model. Preprint at https://arxiv.org/abs/2403.05522 (2024).
Goldman, H., Reddy, A. P., Paul, N. & Fu, L. Zero-field composite Fermi liquid in twisted semiconductor bilayers. Phys. Rev. Lett. 131, 136501 (2023).
Anahory, Y. et al. SQUID-on-tip with single-electron spin sensitivity for high-field and ultra-low temperature nanomagnetic imaging. Nanoscale 12, 3174–3182 (2020).
Dong, J., Wang, J., Ledwith, P. J., Vishwanath, A. & Parker, D. E. Composite Fermi liquid at zero magnetic field in twisted MoTe2. Phys. Rev. Lett. 131, 136502 (2023).
Jain, J. K. Composite-fermion approach for the fractional quantum Hall effect. Phys. Rev. Lett. 63, 199–202 (1989).
Deilmann, T., Krüger, P. & Rohlfing, M. Ab initio studies of exciton g factors: monolayer transition metal dichalcogenides in magnetic fields. Phys. Rev. Lett. 124, 226402 (2020).
Woźniak, T., Faria Junior, P. E., Seifert, G., Chaves, A. & Kunstmann, J. Exciton g factors of van der Waals heterostructures from first-principles calculations. Phys. Rev. B 101, 235408 (2020).
Robert, C. et al. Measurement of conduction and valence bands g-factors in a transition metal dichalcogenide monolayer. Phys. Rev. Lett. 126, 067403 (2021).
Morf, R. & Halperin, B. I. Monte Carlo evaluation of trial wave functions for the fractional quantized Hall effect: disk geometry. Phys. Rev. B 33, 2221–2246 (1986).
Yang, F. et al. Experimental determination of the energy per particle in partially filled Landau levels. Phys. Rev. Lett. 126, 156802 (2021).
Grover, S. et al. Chern mosaic and Berry-curvature magnetism in magic-angle graphene. Nat. Phys. 18, 885–892 (2022).
Nakamura, J., Liang, S., Gardner, G. C. & Manfra, M. J. Direct observation of anyonic braiding statistics. Nat. Phys. 16, 931–936 (2020).
Huber, M. E. et al. DC SQUID series array amplifiers with 120 MHz bandwidth. IEEE Trans. Appl. Supercond. 11, 1251–1256 (2001).
Tschirhart, C. L. et al. Imaging orbital ferromagnetism in a moiré Chern insulator. Science 372, 1323–1327 (2021).
Redekop, E. et al. Direct magnetic imaging of fractional Chern insulators in twisted MoTe2. Dryad https://doi.org/10.5061/dryad.0zpc86769 (2024).
Redekop, E. et al. Direct magnetic imaging of fractional Chern insulators in twisted MoTe2. Zenodo https://doi.org/10.5281/zenodo.13621665 (2024).
Acknowledgements
We thank L. Fu, T. Wang and M. Zaletel for the discussions. Work at UCSB was primarily supported by the Army Research Office under award no. W911NF-20-2-0166. E.R. and O.S. acknowledge support by the National Science Foundation through Enabling Quantum Leap: Convergent Accelerated Discovery Foundries for Quantum Materials Science, Engineering and Information (Q-AMASE-i) award no. DMR-1906325. A.F.Y. acknowledges additional support from the Gordon and Betty Moore Foundation EPIQS programme under award no. GBMF9471. A.F.Y. also acknowledges the support of the W. M. Keck Foundation under award no. SB190132 for the development of SQUID microscopy techniques. Work at the University of Washington was supported by DoE BES under award no. DE-SC0018171. Device fabrication used the facilities and instrumentation supported by NSF MRSEC DMR-230879. K.W. and T.T. acknowledge support from the Elemental Strategy Initiative conducted by the MEXT, Japan (grant no. JPMXP0112101001) and JSPS KAKENHI (grant nos. 19H05790, 20H00354 and 21H05233).
Author information
Authors and Affiliations
Contributions
E.R., A.F.Y. and X.X. initiated the experiment. H.P., J.C. and E.A. prepared the samples. K.W. and T.T. grew the hBN crystals. E.R. and C.Z. performed the measurements and data analysis. O.S., T.A., G.B. and S.S. prepared the nanoSQUID-on-tip. E.R., T.A. and O.S. developed the nanoSQUID microscope. M.E.H. provided Series SQUID Array Amplifiers for the nSOT readout. E.R. and A.F.Y. wrote the paper with input from all other authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks Yonglong Xie and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 SQUID sensitivity.
(a) SEM image of the nSOT sensor used in most of the current work, highlighting the superconducting weak links on the tip apex. (b) Typical sensitivity of the nSOT as a function of the frequency. 1/f noise dominates at frequencies below 1 kHz and decays below the instrumentation noise floor above 2 kHz allowing for ultra-high magnetic field sensitivity well below 1nT/\(\sqrt{{\rm{Hz}}}\).
Extended Data Fig. 2 Devices.
(a) Optical micrograph of Device A (corresponding to device D(3.7°) from ref. 3); (b) Device B (corresponding to device from ref. 5); (c) Device C. Scale bar is 10 μm; (d) δBn phase diagram measured in Device A, (e) Device B, and (f) device C. All devices show signals near ν = − 1 and ν = − 2/3 characteristic of Chern insulators.
Extended Data Fig. 3 Chemical potential sensing and band edge offset.
(a) δBb for device C as a function of V ≡ vt + vb and vt − vb in the configuration with the sample grounded. The phase diagram exhibits both MoTe2 features described in the main text as well as features associated with Landau levels of the top graphite gate. The band edge is visible as a kink in the constant top gate carrier density trajectory, marked as a dashed blue line, with the offset V0 corresponding to the voltage that separates the regime where tMoTe2 is insulating and the regime where it is hole-doped. The value obtained using this method agrees with that described in the main text using the ν = − 1 and ν = − 2/3 gap densities. (b) Schematic of the electric field in the hole-doped tMoTe2 regime. Here modulations of the bottom gate produce electric fields δEb which are screened by the tMoTe2 layer. In this regime, the top gate density nt is tuned solely by Vt, and trajectories of constant nt follow slope − 1 on the diagram in panel a. (c) Schematic of the electric field in the insulating tMoTe2 regime. Here δEb penetrates the tMoTe2, so that nt is tuned by both vt and vb. In this regime, constant-nt lines have slope 0 in panel a.
Extended Data Fig. 4 Chern insulator signal dependence on the displacement field.
(a) Signal δBn as a function of charge carrier density and electric displacement field; (b) Minimum value of δBn in a window around ν = − 1 gap along displacement field axis. The positions of the values are shown on a. The signal from the gap decays slightly as a function of displacement field, remaining finite up to the first order phase transition induced by layer polarization.
Extended Data Fig. 5 First order valley polarization transition at ν = − 1.
(a) δBn near the valley polarization transition in the vicinity of ν = − 1 at point “a” in panel c. (b) δBn measured at point “b”, approximately 200 nm away from point “a”. Both panel a and b show a sharp first-order-like signal on the boundary of the ν = − 1 Chern insulator peak, but these transitions appear at slightly different values of D and ne. (c) Reconstructed magnetization in the point indicated by the “×” on panels a and b. The measured m at position “a” is consistent with zero to within our experimental error, and we find no evidence for non-zero net magnetization in the high ∣D∣ phases. The non-zero signal observed in δBn at that position is associated with fringe AC magnetic fields arising from areas where where the “×” position in parameter space corresponds to the valley transition.
Extended Data Fig. 6 Magnetization reconstruction.
(a) Schematic of analysis to reconstruct the magnetization. We measure the local magnetic field δBs in response to a modulated sample voltage δvs; data is from Device B, with scale bar of 2 μm. An FFT-based algorithm (see Methods) can be used to directly compute the corresponding δms, which may then be integrated over vs to obtain m. Alternatively, the δBs signal may be integrated over Vs to obtain B, which can in some cases be compared to the directly measured BDC; this can them be processed by the FFT algorithm to produce the same m. (b) Comparison of the measured δBs (orange) and the reconstructed δms (blue) as a function of the filling factor ν at a single given spatial location. While qualitative features are preserved, but of course quantitative features differ.
Extended Data Fig. 7 Gap reconstruction in device C.
(a) δBn with an applied modulation of δn ≈ 1.5 × 1010 cm−2; (b) Spatial distribution of δmb in the vicinity of ν = − 1 gap. The dashed line outlines the region of the device in the ν = − 1 gap. Scale bar is 500 nm; (c) Spatial distribution of δmb in the vicinity of ν = − 2/3 gap. The dashed line outlines the region of the device in the ν = − 2/3 gap; (d) Reconstructed magnetization drop of Δm = 1.3μB/u. c. corresponding to the thermodynamic gap −1Δ = 13 meV across the ν = − 1 gap in the point circled on b; (e) Reconstructed magnetization drop of Δm = 0.3μB/u. c. corresponding to the thermodynamic gap −2/3Δ = 5 meV across the ν = − 2/3 gap in the point circled on c.
Extended Data Fig. 8 Magnetization near ν = − 1 and ν = − 2/3.
(a) Spatial image corresponding to Δm = m(ne = 3.8 × 1012 cm−2) − m(ne = 3.6 × 1012 cm−2) near filling ν = − 1. Scale bar is 500 nm; (b) Spatial image corresponding to m(ne = 2.55 × 1012 cm−2) − m(ne = 2.35 × 1012 cm−2), near filling ν = − 2/3 in the same region as panel a. Scale bar is 500 nm; (c) Δm(ne) (referenced to the center of the local ν = − 1 gap) measured at 25 points within the red square in panel a. The black curve is the average. Red stars indicate the charge carrier densities used to determine spatial distribution of Δm in panel a; (d) Δm(ne) (referenced to the center of the local ν = − 2/3 gap) measured at 25 points within the red square in panel b. The black curve is the average. Red stars indicate the charge carrier densities used to determine spatial distribution of Δm in panel b; (e) Δm(ne) (referenced to the center of the local ν = − 1 gap) measured at 25 points within the green square in panel a. The black curve is the average. Red stars indicate the charge carrier densities used to determine spatial distribution of Δm in panel a; (f) Δm(ne) (referenced to the center of the local ν = − 2/3 gap) measured at 25 points within the green square in panel b. The black curve is the average. Red stars indicate the charge carrier densities used to determine spatial distribution of Δm in panel b.
Extended Data Fig. 9 Estimating systematic error due to padding assumptions.
(a) Magnetization change Δm (referenced to the center of the ν = − 1 gap) in the same location as that shown in Fig. 3 for the three different padding assumptions described in panels c, d, and e. (b) Magnetization change Δm (referenced to the center of the ν = − 2/3 gap) in the same location as that shown in Fig. 3 for the three different padding assumptions described in panels f, g, and h. (c) Top row: measured BDC with zero padding assumption across the ν = − 1 gap. Scale bar is 600 nm. Left and right panels correspond to ne values shown by dotted lines in panel a. Bottom row: reconstructed magnetization in the measured range at the same positions, with the zero padding assumption. The magnetization change across the gap is 1.61 μB/u.c. Scale bar is 200 nm. (d) Same as panel c, except with the padding assumption that data extends to the right and left of measured area as shown. The magnetization change across the gap is 1.66 μB/u.c. (e)Same as panels c and d but with additional padding as shown. Magnetization change across the gap is 1.57 μB/u.c. (f) Top row: measured BDC with zero padding assumption across the ν = − 2/3 gap. Left and right panels correspond to ne values shown by dotted lines in panel b. Bottom row: reconstructed magnetization in the measured range at the same positions, with the zero padding assumption. The magnetization change across the gap is 0.52 μB/u.c. (g) Same as panel f, with the same padding assumption as panel d. Magnetization change across the gap is 0.52 μB/u.c.; (h) Same as panels f-g but with the same padding assumption as in panel e. Magnetization change across the gap is 0.58 μB/u.c.
Supplementary information
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Redekop, E., Zhang, C., Park, H. et al. Direct magnetic imaging of fractional Chern insulators in twisted MoTe2. Nature 635, 584–589 (2024). https://doi.org/10.1038/s41586-024-08153-x
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/s41586-024-08153-x
This article is cited by
-
Microscopic signatures of topology in twisted MoTe2
Nature Physics (2025)
-
Interplay between topology and correlations in the second moiré band of twisted bilayer MoTe2
Nature Physics (2025)
-
Experimental signature of layer skyrmions and implications for band topology in twisted WSe2 bilayers
Nature Physics (2025)
-
Ferromagnetism and topology of the higher flat band in a fractional Chern insulator
Nature Physics (2025)
-
Observation of ferromagnetic phase in the second moiré band of twisted MoTe2
Nature Communications (2025)