Main

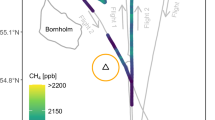
Subsea natural gas leaks from pipeline ruptures and well blowouts can emit large quantities of methane (CH4) to the ocean and atmosphere. Prominent examples are the 22/4b well blowout20,21, the Deepwater Horizon oil disaster22,23 and the Elgin rig blowout24. The Nord Stream 1 and 2 twin pipeline systems (NS1 and NS2) are a network of offshore pipelines underlying the Baltic Sea that connect the Russian natural gas supply with Europe25,26,27. On 26 September 2022, damage to both NS1 and NS2 occurred in a series of underwater explosions, resulting in the leakage of natural gas (Fig. 1). The first explosion occurred at 00:03 UTC southeast of the Danish Island of Bornholm in the Bornholm Basin, rupturing pipeline A of the twin NS2 pipeline system (NS2A) at approximately 70 m depth28,29,30. This explosion destroyed approximately 10 m of the pipeline31. At 17:03 UTC, multiple explosions to the northeast of Bornholm ruptured both NS1 pipelines (NS1A and NS1B) at depths of approximately 75 m (ref. 30) and caused a smaller partial rupture in the NS2A pipeline to the north of the previous NS2A leak31,32. These explosions destroyed 200–300 m of the NS1A and NS1B pipelines31. The NS2B pipeline remained undamaged33.

Fig. 1: Location of the Nord Stream gas leak sites in the Baltic Sea.
figure 1

The first rupture occurred to the southeast of Bornholm on NS2A (54° 52.6′ N, 15° 24.6′ E)28. The remaining three ruptures occurred to the northeast of Bornholm on NS1A (55° 33.4′ N, 15° 47.3′ E)32, NS1B (55° 32.1′ N, 15° 41.9′ E)32 and NS2A (55° 32.45′ N, 15° 46.47′ E)32. The locations of marine (SOOP, ocean glider and CTD, see text) and airborne (HELiPOD, see text) observations are depicted. The inset map on the right offers a detailed view of the sampling locations for the CTD casts, ocean glider and HELiPOD observations near the leak sites. The tall towers located at the ICOS BIR, HTM, NOR and UTO observatory stations and an atmospheric monitoring location located at the Norwegian Institute for Air Research (NILU) in Kjeller are shown. The ICOS ZEP observatory station is located to the north of the map area in Svalbard, Norway.

Full size image

Although not operational at the time, both NS1 and NS2 pipeline systems were filled with pressurized natural gas1,2,3,4,5. The natural gas released from the ruptured pipelines was predominantly CH4 along with small amounts of ethane, nitrogen and other hydrocarbons34. The emitted gas was seen bubbling through the sea surface above the four rupture sites, creating bulging mounds of foamy seawater of up to several hundred metres in diameter, which lasted for approximately 1 week. Given the magnitude, persistence and visibility of the emitted gas, there was an immediate desire to estimate the amount of CH4 emitted to the atmosphere to understand the potential environmental and climatic impact1,2,3,4,5.

A wide range of bottom-up and top-down approaches were used to estimate the various components of CH4 emissions from the event (Supplementary Table 1). Bottom-up pipeline emissions estimates, quantifying the amount of CH4 contained in (or released from) the pipelines before (or after) rupturing, were derived from volumetric calculations and simulations based on pipeline physical parameters and information from pipeline operators1,2,3,4,5,6,7,8. Top-down estimates, quantifying the amount of CH4 released from the pipelines to the Baltic Sea and atmosphere, were derived from marine and ship-based measurements9,10; airborne in situ measurements11; satellite measurements8,12,13,14; and atmospheric CH4 measurements captured by tall tower observatory stations within the European Integrated Carbon Observation System (ICOS)8,15,16,17,18. Top-down approaches had varying spatiotemporal coverage of the leaks and used a diverse set of measurement platforms. The top-down approaches used to inform our analysis are shown in Fig. 2.

Fig. 2: Overview of measurement approaches applied in our analysis and the period(s) over which the measurements were taken.
figure 2

a, Bottom-up and top-down measurement approaches applied in our analysis of the Nord Stream pipeline leaks. The numbers 1–15 correspond to each measurement approach. b, The period(s) over which the measurements were taken. See text and Supplementary Table 1 for details on each approach. Although shown, the results of a second airborne campaign on 16 and 17 November 2022 using HELiPOD, and a second marine campaign deploying CTD casts between 9 and 12 January 2023 have not been published and are not otherwise available. MetOp-B and Sentinel-2B satellite icons adapted with permission from the European Space Agency (ESA) and ESA/ATG Medialab. GHGSat Satellite icon adapted from GHGSat.

Full size image

Reported bottom-up estimates across the three ruptured pipelines range from 230 to 509 thousand metric tons (kt) of CH4 (refs. 1,2,3,4,5,6,7,8). An initial report in February 2023 documenting top-down estimates concluded that 75–230 kt of CH4 was emitted to the atmosphere35. However, cautious interpretation of these initial bottom-up and top-down estimates is required because of the methodological limitations and assumptions inherent to each approach, as well as the need to contextualize the estimates in both space and time. Supplementary Table 1 presents all available bottom-up and top-down estimates, including those reported in this paper, and outlines the limitations and contributions of each approach to quantifying atmospheric CH4 emissions from the leaks.

Here we integrate bottom-up pipeline rupture emission-rate simulations with marine CH4 dissolution estimates9 to model the time series of atmospheric emissions from the leaks. We verify our simulated atmospheric emission rates over time by comparing them with point-in-time atmospheric emission-rate estimates derived from airborne measurements11 and point-source imaging satellites8,12,13, as well as cumulative emissions estimates, acquired from atmospheric inversion methods using satellite and tall tower observations that incorporate revised a priori (prior) atmospheric emission rates. Agreement between our simulated atmospheric emissions and top-down atmospheric estimates across multiple spatiotemporal domains demonstrates that our synthesis provides a more reliable estimate of atmospheric CH4 emissions from the leaks than previous studies.

Emissions from the ruptured pipelines

Using the volume of natural gas in each pipeline (Extended Data Table 1) and its composition (Extended Data Table 2), we estimate that 496 ± 14 kt of CH4 was contained in the three pipelines before rupturing (Methods and Extended Data Table 3). Subsequently, we use PBREAK36 and the Code for Analysis of Thermal Hydraulics during Accident and for Reactor safety Evaluation (CATHARE)37 to simulate post-rupture pipeline CH4 emission rates from NS1A, NS1B and NS2A (Methods and Supplementary Method 1). In both simulations, pipeline CH4 emission rates from NS1A and NS1B are each about 1 × 105 t h−1 in the seconds after rupturing (Extended Data Fig. 1). These decrease to about 1 × 104 t h−1 after 2 h and about 1 × 103 t h−1 over the following 2 days. Pipeline emission rates from NS2A are about 7 × 104 t h−1 in the initial seconds, decreasing to about 1 × 104 t h−1 after 30 min and about 1 × 103 t h−1 after 30 h. The potential impact of the partial northern rupture in NS2A on emission rates from the southern NS2A leak site is probably minor (Supplementary Discussion 1). PBREAK modelling indicates that leaking stopped on 1 October for NS2A and on 2 October for NS1A and NS1B. These timelines are consistent with reports that the pressure in NS2A stabilized on 1 October38, and sea foam patch observations indicating that bubbling at the NS1A leak site had ceased by 06:00 UTC on 3 October (A. Sundberg, personal communication). CATHARE modelling suggests leaking extended one day longer compared with PBREAK. Nonetheless, time series of landfall pipeline pressures simulated using CATHARE are broadly consistent with reports from pipeline operators (Extended Data Fig. 2). CH4 hydrate formation was unlikely to impact our simulated pipeline emission rates (Supplementary Discussion 2).

Our PBREAK simulations estimate that a total of 457 ± 14 kt of CH4 was released from the pipelines following the ruptures. CATHARE modelling indicates a larger total of 472 ± 14 kt. From both simulations, we estimate 23 ± 1 kt remained within the three pipelines once pressure stabilized at the seafloor (Extended Data Table 3) and, of this, <1 kt was subsequently displaced by seawater (Extended Data Fig. 2). The differences between pre-rupture pipeline inventories and post-rupture estimates of CH4 contained in the pipelines are used to derive discrepancies in the total mass of CH4 released from the pipelines in our simulations (Extended Data Table 3). Owing to its lower mass discrepancy, we consider the CATHARE estimate (472 ± 14 kt) to be a more accurate estimation of CH4 released from the 3 ruptured pipelines (Supplementary Discussion 3).

Marine and ship-based estimates

At each rupture site, the leaked gas was transported to the sea surface via rapidly ascending plumes of bubbles39. During this period, the Bornholm Basin showed strong vertical temperature and salinity gradients creating a distinct three-layer system separated by a thermocline (about 30–40 m depth) and halocline (about 50 m depth)9,10. During its ascent through the water column, a fraction of the CH4 was dissolved, advected and mixed in each of the three layers (Fig. 2a). A fraction of the dissolved CH4 was outgassed to the atmosphere via air–sea gas exchange from the mixed surface layer. The presence of a thermocline and halocline during this time inhibited direct mixing between seawater layers and resulted in the build-up of dissolved CH4 at mid-depths9. By January 2023, the seawater column shifted to a two-layer structure in the absence of a thermocline, vertically deepening the mixed surface layer and facilitating further outgassing of dissolved CH4 (refs. 9,10).

The shallow depth of the ruptures (70–80 m) allowed the plumes to rise quickly through the water column, causing only a small fraction of the total CH4 released from the pipelines to dissolve. Microbial CH4 oxidation was probably most prominent below the halocline, where ventilation to the atmosphere is minimal, and the highest abundance of indigenous methanotrophic communities is found in the Bornholm Basin40. This contrasts with the Deepwater Horizon blowout, where a substantial component of the CH4 had dissolved in deep seawater (>1,000 m depth), which allowed large quantities of CH4 to undergo oxidation in the water column23.

Dissolved CH4 concentrations were continuously measured near the northernmost leaks between 5 October 2022 and 2 January 2023 using an autonomous SeaExplorer glider equipped with a Franatech METS CH4 sensor9 (Figs. 1 and 2, and Supplementary Method 2). Concurrently, sea-surface CH4 partial pressures were measured using an underway analytical system onboard the ship of opportunity (SOOP) Finnmaid (DE-SOOP-Finnmaid), which passed the leak sites twice every 3 days. The glider and SOOP observations were used to establish the vertical and horizontal subsea CH4 plume structures and set initial conditions for an oceanic chemical fate and transport model driven by the PBREAK and CATHARE pipeline emission rates derived from the present study. The modelling suggests between 9 kt and 15 kt of the CH4 released from the ruptured pipelines was dissolved in the Baltic Sea, of which 8–13 kt was outgassed to the atmosphere at rates of up to 74 t h−1 (Fig. 3).

Fig. 3: Net atmospheric CH4 emission rates.
figure 3

The net atmospheric CH4 emission rates were derived using PBREAK (P-NAERNSx; orange) and CATHARE (C-NAERNSx; blue) for the NS1A, NS1B and NS2A pipelines compared with top-down emission rates. The shaded regions represent the upper and lower uncertainty bounds for P-NAERNSx, C-NAERNSx and sea-surface outgassing9. Satellite estimates8,12,13 are only comparable to the NS2A emission rates. The error bars on the y axis for satellite estimates represent 1σ standard deviation. The x-axis error bars for the L8 and S-2B ensemble estimate represent the time span between the two satellite detections. The symbol and error bars for the airborne estimate represent the central (average) estimate and range reported in ref. 11, respectively. It is noted that sea-surface outgassing rates modelled by ref. 9 extend beyond 6 October 2022, which are not shown here.

Source Data

Full size image

The seawater column near the northernmost leaks was sampled for dissolved CH4 concentrations and stable carbon isotopic signatures between 3 and 5 October 2022 using conductivity, temperature and depth (CTD) casts deployed from the RV Skagerak10 (Figs. 1 and 2, and Supplementary Method 3). Subsea plume simulations, corroborated by fossil CH4 isotopic signatures, suggest that 9% of dissolved CH4 from the ruptured pipelines was transported by currents to 16 of 20 sampling sites. Using the average and maximum dissolved CH4 concentration measured across sampling sites, the amount of dissolved CH4 was extrapolated to be 10 kt and 55 kt, respectively10. In our analysis, we consider the 10-kt estimate to be more credible because maximum dissolved CH4 concentrations did not persist over all sampling locations. Atmospheric CH4 concentrations were also measured onboard RV Skagerak near several CTD sampling sites using a Picarro G2132-i laser spectrometer10. Estimated sea-surface CH4 outgassing rates ranged from 0.5 × 10−3 t h−1 km−2 and 5 × 10−3 t h−1 km−2. Although providing further evidence of outgassing, these rates have not been spatially modelled beyond the extent of CTD sampling sites to other regions shown to have undergone outgassing9,11, thus limiting their ability to inform gross outgassing rates over the Baltic Sea.

Bottom-up bubble-plume simulations suggest that about 11 kt of the CH4 released from the ruptured pipelines was dissolved in the Baltic Sea, of which about 3 kt was oxidized and about 8 kt outgassed to the atmosphere39. However, this modelling assumes that 215 kt of CH4 was released from the pipelines (Supplementary Table 1). Our modelling indicates over twice this amount was released from the pipelines. Therefore, we refrain from using these estimates in our analysis, except for providing an estimate of microbial CH4 oxidation based on the percentage relative to total pipeline emissions (about 1%)39.

Simulated atmospheric emissions

Satellite and tall tower observations8,14,15,16,17,18 showed that once the CH4 had escaped the water column, the plumes were transported across various parts of Scandinavia and the North Sea between 26 September and 1 October. Our simulated pipeline emission rates cannot be directly compared with top-down quantifications of these plumes because they do not account for CH4 dissolution in the water column during the plumes’ ascent. Consequently, we use modelled CH4 dissolution rates9 to calculate the CH4 emission rate expected to reach the atmosphere directly from each pipeline (NSx), called herein the net atmospheric emission rate (P-NAERNSx for PBREAK and C-NAERNSx for CATHARE; Methods and Fig. 3). We also calculated the combined sum of net atmospheric emissions from all three pipelines (P-NAEAll and C-NARAll; Methods and Fig. 4), to allow for direct comparison with satellite and tall tower inversion approaches, which do not distinguish between the total amount of atmospheric CH4 emissions from the individual pipelines.

Fig. 4: Comparison of net atmospheric emissions derived using PBREAK and CATHARE with satellite and tall tower estimates used in our analysis.
figure 4

Total CH4 emissions from the Aliso Canyon blowout45 are shown for comparison. The symbols and error bars for inversions 1, 2 and 4–6 represent central (average) estimates and ranges, respectively. It is noted that initial tall tower inverse estimates are not plotted here, nor inversion 3, which derives only a minimum estimate of atmospheric CH4 emissions (see text and Supplementary Table 1).

Source Data

Full size image

Comparison with atmospheric measurements

Airborne estimate

Atmospheric CH4 concentration enhancements and meteorological parameters near all leak sites were measured on 5 October 2022 using the helicopter borne sonde HELiPOD41 equipped with a Picarro G2401-m laser spectrometer11 (Figs. 1 and 2, and Supplementary Method 4). An emission rate of 19–48 t h−1 was derived using an inverse model of atmospheric transport. By 5 October, the pipeline leaks had ceased, meaning the atmospheric CH4 enhancements measured by HELiPOD were derived from the outgassing of dissolved CH4 rather than from direct emission via bubbling. Thus, no direct comparison with P-NAERNSx and C-NAERNSx can be made. Nonetheless, considering random uncertainties, the lower bound (19 ± 5 t h−1) is consistent with the glider and SOOP outgassing estimate on 5 October9 (11–18 t h−1; Fig. 3).

Satellite point-source estimates

The Planet, Landsat 8 (L8), GF5-02-AHSI, Sentinel-2 and Sentinel-1 satellite platforms acquired imagery of the pipeline leak sites between 26 September and 1 October8. However, emission-rate quantification was achieved for only the southern NS2A leak on 29 and 30 September using L8 and Sentinel-2B (S-2B) nadir observations8,12 and sun-glint measurements with the GHGSat constellation13. Over sea, the reflected signal detected by Earth-surface imaging satellites is ordinarily too low at nadir to detect any useful CH4 signal. However, the bright patch of sea foam caused by the NS2A leak created enough reflectance to detect CH4 using L8 and S-2B. The NS1A, NS1B and northern NS2A leaks could not be sampled by high-resolution satellites owing to cloud coverage during the entire emission event.

An emission rate of 72 ± 38 t h−1 was derived by applying the integrated mass enhancement (IME) method42 to S-2B nadir observations over the southern NS2A leak on 30 September at 10:07 UTC8 (Fig. 2 and Supplementary Method 5). The upper range of this estimate is consistent with P-NAERNSx (86–115 t h−1; Fig. 3 and Extended Data Table 4). An emission rate of 502 ± 464 t h−1 was also derived by applying multi-band single-pass43 and specifically calibrated IME methods42 to L8 and S-2B satellite nadir observations over the southern NS2A leak on 29 September (09:56 UTC) and 30 September (10:07 UTC)12 (Fig. 2 and Supplementary Method 6). This estimate addresses methodological limitations detailed in ref. 8 by using a calibration procedure that accounts more rigorously for spectral interferences from sea-surface bubbling, and provides a comprehensive uncertainty estimate. The lower range of this estimate is consistent with P-NAERNS2A (85–258 t h−1; Fig. 3 and Extended Data Table 4).

Three plume detections of the southern NS2A leak were obtained from available cloud-free acquisitions from the GHGSat constellation at 08:51, 10:26 and 12:54 UTC on 30 September (GHGSat-C2, -C1 and -C4, respectively) using a sun-glint configuration13 (Fig. 2 and Supplementary Method 7). An emission rate for the C2 observation was not achieved because the signal was too low (high scattering angle and low surface reflectivity). The C1 observation had the highest signal of the three observations, and comprised a steady streamlined plume that spanned the length of the observation13. The emission rate for C1 (84 ± 24 t h−1) is within 1σ uncertainty of P-NAERNS2A (84–113 t h−1; Fig. 3 and Extended Data Table 4). In contrast, the plume detected in C4 had a lower signal strength compared with C1 and comprised a more dispersed plume, possibly owing to increased atmospheric turbulence, as emission rates slowed near the later stages of the leak. These factors may contribute to discrepancies between the C4 emission rate (24 ± 8 t h−1) and P-NAERNS2A (72–101 t h−1; Fig. 3 and Extended Data Table 4). The next clear-sky GHGSat observation was on 3 October, which indicated that the leak had subsided.

Satellite estimates using IASI

The Infrared Atmospheric Sounding Interferometer (IASI) onboard Eumetsat’s MetOp-B satellite detected elevated CH4 over the Baltic Sea around 07:30 UTC on 26 September14. CH4 plumes were either not or only partially visible from space as they moved over land owing to cloud cover over Scandinavia later on 26 and 27 September. However, on 28 September, IASI observed large enhancements (>200 ppb) of column averaged CH4 (XCH4) off the west coast of Norway. Using their own emission priors, ref. 14 combined the XCH4 enhancements with an atmospheric transport model in an inversion framework to obtain an estimate of 219–427 kt. Here we re-evaluate these results using P-NAERNSx and C-NAERNSx as priors (inversion 1; Methods). Our revised posterior atmospheric emission of 281–346 kt has reduced uncertainty compared with the initial estimate and is consistent with equivalent P-NAEAll and C-NAEAll until 28 September (311–326 kt and 301–336 kt; Fig. 4 and Extended Data Table 4).

The IME method was also applied to IASI XCH4 enhancements to derive an estimate of 30 ± 1 kt on 26 September17. Although this is broadly consistent with P-NAEAll and C-NAEAll, similarly derived estimates on 27 and 28 September (16 ± 1 kt, and 161 ± 4 kt and 77 ± 2 kt) are lower than P-NAEAll and C-NAEAll (Extended Data Table 4). We note the IME method as applied by ref. 14 cannot account for IASI’s vertical sensitivity, which is highest in the upper troposphere, and that these enhancements may comprise only partial plume observations owing to cloud cover (Supplementary Table 1). Both methodological limitations can lead to an underestimate of atmospheric emissions, preventing us from using these quantifications to verify our simulated atmospheric emissions.

Tall tower inversion estimates

Regionally enhanced atmospheric CH4 concentrations were detected across multiple tall towers within the ICOS observation network, including the Norunda (NOR), Hyltemossa (HTM), Birkenes (BIR), Utö-Baltic Sea (UTO) and Zeppelin (ZEP) observatory stations, and a station located in Kjeller, Norway (Figs. 1 and 2). Atmospheric monitoring stations in Finland and Estonia also detected CH4 enhancements6. Unfortunately, enhancements from the Nord Stream plumes were detected for only short periods (Extended Data Fig. 4) because wind directions frequently changed during the event. Moreover, their narrow structure meant small changes in the advecting field moved the plumes away from the stations. Relating simulated plumes to the ICOS observations has proved challenging6,8,15,16,17,18, particularly because of meteorological uncertainty, which can lead to large spatiotemporal errors in each plume’s location (for example, Extended Data Fig. 5), as well as uncertainty in the plume injection height above each leak site6. It is also noteworthy that the automated processing routines for the near-real-time ICOS tall tower data had filtered out very high CH4 concentrations, which are now included in Level 2 release ICOS CH4 time series44 (Extended Data Fig. 4). Nonetheless, attempts were made to provide initial atmospheric emissions estimates using various inversion frameworks to near-real-time ICOS observations applying constant8,15,16 and exponential17,18 priors. Central estimates from these initial approaches range from 56 kt to 226 kt, with a mean (±1σ) of 165 ± 64 kt (refs. 8,15,16,17,18; Supplementary Table 1).

Here we report five tall tower inversion estimates using quality-controlled ICOS CH4 time series44 that apply P-NAERNSx and/or C-NAERNSx as the prior (inversions 2–6; Methods). Inversions 2, 4 and 6 are reanalyses of previous inversions8,16,17,18. Our inversions use a range of atmospheric transport models and are driven by different meteorological data at varying model resolutions. Apart from inversion 3, which derives a lower bound of atmospheric emissions up to 1 October (≥230 kt; Methods), central estimates from inversions 2, 4, 5 and 6 range from 267 kt to 716 kt CH4, with a mean (±1σ) of 430 ± 216 kt. Although our mean estimate has large uncertainty, it is consistent with P-NAEAll and C-NAEAll (434–456 kt and 448–471 kt; Fig. 4 and Extended Data Table 4). The mean difference of approximately 265 kt between our estimates and those in the literature illustrates the reliance of atmospheric inversion models on emission priors, especially when observations are sparse. We acknowledge that our mean estimate is caveated because it assumes equal performance across our inversions, which is unlikely given the methodologies varied (Supplementary Table 1). For example, the sparsity of observations leads to an overestimation in inversion 5 (740 ± 134 kt; Supplementary Discussion 4), which skews our mean estimate upwards. Notably, inversion 6 (155–450 kt), which uses a Bayesian data assimilation approach to quantify uncertainty in both the plume location based on an ensemble of meteorological forecasts and injection heights based on gas velocity rates from CATHARE simulations, is compatible with P-NAEAll and C-NAEAll.

Total atmospheric CH4 emissions

Using our modelled pipeline emissions in conjunction with marine estimates of dissolution, outgassing and microbial oxidation, we conservatively estimate that 465 ± 20 kt of CH4 was emitted to the atmosphere from the Nord Stream pipeline leaks (Table 1). Our simulated time series of atmospheric emissions broadly align with airborne, satellite and tall tower estimates over various points in time and space (Figs. 3 and 4, and Extended Data Table 4), indicating that this estimate is consistent with the available ensemble of atmospheric quantifications. Our analysis confirms that, to our knowledge, the leaks were the largest recorded emission of CH4 to the atmosphere from a single transient event. Our estimate is over 4 times greater than atmospheric emissions from the previous largest natural gas leak at the Aliso Canyon storage facility (approximately 100 kt of CH4)45. Remarkably, emissions from the 4-month-long Aliso Canyon leak were surpassed within just 1 day (Fig. 4). Despite their magnitude on short-term timescales, atmospheric emissions from the leaks are equivalent to about 1.2% of emissions from the natural gas sector, and only 0.3% of CH4 emissions from agriculture, for 202246. Moreover, they amount to only 0.1% of anthropogenic CH4 emissions for 202246. Equally, the small impact of the leaks on the anthropogenic CH4 budget highlights the large number of other CH4 sources that require mitigation globally.

Table 1 Atmospheric CH4 emissions budget from the Nord Stream pipeline leaks
Full size table

Top-down analysis of the event proved challenging because the leaks were short-lived and occurred near-simultaneously across four separate offshore locations. Time was needed to deploy instruments9,10,11 and task satellites to the leak sites, and there were several occasions where cloud coverage prevented satellite quantification8,12,13,14. This meant that some parts of the event were missed by individual approaches (Fig. 2). Importantly, the plumes were not transported consistently over tall tower monitoring stations, leading to considerable uncertainty across inversion estimates. These methodological constraints limit our ability to rely solely on top-down approaches to estimate the atmospheric emissions from the event (Supplementary Table 1). Nonetheless, the collective ensemble of top-down quantifications offers an invaluable way of ensuring that our modelled atmospheric emissions are reliable. More generally, our analysis highlights the benefits of applying diverse measurement approaches to verify bottom-up estimates in support of CH4 reduction commitments such as the Global Methane Pledge19. Developing and maintaining a varied measurement toolkit that allows for rapid detection and quantification of future ultra-emitter events—whether transient or persistent—remains an essential requirement to support meeting these ambitious targets.

Methods

Pre-rupture pipeline inventories

We estimate the mass of CH4 contained in each pipeline before rupturing using equation (1):

$${M}_{{\rm{NS}}x}={L}_{{\rm{NS}}x}\times {\rho }_{{\rm{NS}}x}\times 0.25\,\times {D}_{{\rm{NS}}x}^{2}\times {\rm{\pi }}\times {C}_{{\rm{NS}}x}/\mathrm{1,000}$$
(1)

where MNSx is the mass of CH4 contained within pipeline NSx (kt of CH4), LNSx is the total pipeline length in kilometres (km), ρNSx is the density of the natural gas mixture at the pressure and temperature within the pipeline (kg m−3), DNSx is the pipeline diameter (m), and CNSx is the percentage mass composition of CH4 in the natural gas (Extended Data Tables 1 and 2). In equation (1), we use ρNSx values from the gas mixture eventually used in the PBREAK simulations because our CATHARE simulations do not consider components in the mixture that make up less than 0.1% (Extended Data Table 2).

Pipeline emission simulation tools

We use PBREAK36 (version 2.28.3) and CATHARE (version CATHARE-337) to simulate pipeline rupture emission from NS1A, NS1B and NS2A. PBREAK is a mathematical model used to simulate the outflow of gas following the sudden puncture or rupture of a high-pressure transmission pipeline36,47,48,49. The model is embedded in the PIPESAFE Quantitative Risk Assessment software. CATHARE is a tool developed by the French Alternative Energies and Atomic Energy Commission used for thermal hydraulic simulations of multiphase flows (https://cathare.cea.fr)37,50,51,52,53. Both model pipeline depressurization as the one-dimensional flow of natural gas in a pipeline and solve a system of three conservation equations for mass, momentum and energy. The models use an equation of state to compute fluid properties (Supplementary Discussion 3). Further descriptions of each model, including their suitability for modelling subsea pipeline ruptures, are provided in Supplementary Method 1.

PBREAK

Within the PBREAK workflow, each pipeline is divided in N segments, and the nonlinear equations for continuity and mass balance, momentum and energy solved at each time step using an implicit finite-difference scheme36. These equations are solved every 1 s for the first 2 min, then every 30 s until the calculation finishes. The computation terminates when the internal pressure in all the lengths of each pipeline is equal to the external pressure. The model results are the variation with time of the outflow at the point of rupture coming from each branch of pipeline, and the cumulative flow from the beginning of the release.

CATHARE

We discretize each of the three pipelines into one-dimensional elements meshed with a series of cylinders. We define the cross-section (A), friction perimeter (χf) and roughness of the pipelines. In the case of monophasic calculations, CATHARE solves a system with three main variables (pressure P, enthalpy H and velocity V) and three conservation equations (equations (2)–(4): conservation of mass, momentum and energy):

$$A\times \frac{\partial \rho \,}{\partial t}+\frac{\partial (A\times \rho \times V)}{\partial z}=0$$
(2)
$$A\times \rho \times \left(\frac{\partial V\,}{\partial t}+V\times \,\frac{\partial V\,}{\partial z}\right)+A\times \frac{\partial P\,}{\partial z}=-\,{\chi }_{{\rm{f}}}\times {C}_{{\rm{f}}}\times \rho \times \frac{V| V| }{2}+A\times \rho \times \,{g}_{z}$$
(3)
$$A\times \frac{\partial }{\partial t}\left[\rho \times \,\left(H+\,\frac{{V}^{2}}{2}\right)\right]+\frac{\partial \,}{\partial z}\left[A\times \rho \times V\times \left(H+\,\frac{{V}^{2}}{2}\right)\right]-A\times \frac{\partial P\,}{\partial t}={{\chi }_{{\rm{c}}}\times q}_{{\rm{w}}}+A\times \rho \times V\times {g}_{z}$$
(4)

We add thermal structure to each of the cylinders by specifying their heating perimeter (χc). The heat conduction through the wall structures is resolved by a multilayer radial discretization and we define the heat exchange with an external fluid. The pipelines are assumed to be horizontal (gravity projection gz equal to 0 in equations (3) and (4)).

The one-dimensional elements use a first-order finite-volume scheme with a staggered mesh and the donor-cell principle. The time discretization is fully implicit. The mass and energy equations in CATHARE use a conservative form and are discretized to ensure mass and energy conservation. The wall conduction is implicitly coupled with the hydraulic calculations. The nonlinear system of equations is solved in several steps using an iterative Newton–Raphson method. The numerical resolution allows the model to consider sonic flow as a boundary condition during the pipeline rupturing.

The fluid equation of state is computed by coupling CATHARE with the REFPROP library from the National Institute of Standards and Technology54, which uses the GERG-2008 equation of state55 to compute properties (such as density ρ) for natural gas mixtures. We use two closure laws to model the interaction between the internal fluid and the pipe wall. Given the high gas velocity and the large pipe diameter, the flow is deemed fully turbulent throughout the transient (Reynold’s number exceeding 3,000). Therefore, the wall friction coefficient (Cf) is evaluated using the Colebrook factor56. The convective wall heat transfer (qw) is modelled using the Colburn correlation57.

To simulate the rupture, we use a numerical methodology previously applied to flow pipe breaks in a pressurized water reactor. As per previous applications, a very fine mesh of 10−5 m is used at the break side. From this point, the mesh size is gradually increased with a 1.05 adjacent cell size ratio up to 500 m, and then is kept constant until the other end. In the initial state, the velocity is zero all along the pipe and the pressure and temperature are initialized at their initial values. At the rupture location point, the pressure drops from the initial pressure to the outlet pressure (hydrostatic pressure at the seafloor) value in 10−3 s. To minimize the computation time, the time step at the beginning of the rupture is set to 10−5 s and progressively increased to 104 s. This procedure is applied to each side of the three pipelines to evaluate the evolution of the total gas flow rate as a function of time.

Sensitivity analysis

We assess uncertainty in our simulations by reperforming the PBREAK and CATHARE simulations using the upper and lower uncertainty bounds for the initial gas temperature, depth of rupture, post-rupture pipeline section lengths and natural gas composition (Extended Data Table 1). As the variables are independent, we sum the resulting deviations from reference emission rates in quadrature to derive the uncertainty at each time step of the simulation. We additionally assess the model uncertainty in CATHARE simulations by varying pipeline roughness, heat transfer coefficients, mesh number and break size (Supplementary Method 1). The CATHARE model uncertainties are summed in quadrature in addition to the uncertainties introduced by the model variables. We do not assess the model uncertainty in PBREAK as this functionality is not accessible to users of the software.

NAER and NAE

We calculate the rate of CH4 emission expected to directly reach the atmosphere (NAER) from each pipeline (NSx) over time, according to equation (5):

$${\rm{X}}\text{-}{{\rm{NAER}}}_{{\rm{NS}}x}={r}_{{\rm{NS}}x,t}-{d}_{{\rm{NS}}x,t}$$
(5)

where X- is the simulation (P- for PBREAK and C- for CATHARE), t is the simulation time step, n is the total number of simulation time steps, r is the pipeline CH4 emission rate (t h−1), and d is the CH4 dissolution rate9 for the equivalent simulation time step (t h−1). We compute equation (5) over the lower and upper uncertainty bounds of the pipeline emission rates to derive lower and upper bounds of P-NAERNSx and C-NAERNSx. In our paper, we use P-NAERNSx for comparison with top-down atmospheric emission-rate estimates because the pipeline emission rates derived from PBREAK modelling align better with timelines reported by the pipeline operators38 and leak site observations (A. Sundberg, personal communication). The cumulative sum of net atmospheric emissions for each pipeline and pipeline emission-rate simulation (P-NAENSx and C-NAENSx, in kt of CH4) is calculated using equation (6):

$${\rm{X}}\text{-}{{\rm{NAE}}}_{{\rm{NS}}x}=\mathop{\sum }\limits_{t=1}^{n}({r}_{{\rm{NS}}x,t}-{d}_{{\rm{NS}}x,t})$$
(6)

We sum the atmospheric CH4 emissions from all three pipeline leaks to derive P-NAEAll and C-NAEAll.

Inversion 1

Inversion 1 is derived from the reanalysis of a previous inversion14 (Supplementary Table 1). Briefly, IASI XCH4 data retrievals58,59 are combined with simulated mixing ratios produced by the TOMCAT offline chemical transport model60 in an inversion framework to optimally quantify the flux rate from the leaks. A global model simulation is carried out covering the period of 26–30 September 2022. The model’s horizontal resolution is approximately 1° × 1°, with 60 vertical levels between the surface and 0.1 hPa. The model dynamical time step is 5 min. The model is initialized with CH4 mixing ratios from ref. 61, which are optimized in the inversion. The fluxes of CH4 from sources other than the Nord Stream leaks are also based on that study, as are the atmospheric loss rates.

Here, both P-NAERNSx and C-NAERNSx and their uncertainties are used as priors in the inversions. Leak flux rates in each emission window (the first 5 min of each leak, the remainder of the first hour and then subsequent 3-h periods) are treated as constant within that window. To drive model transport, meteorological data from the European Centre for Medium-range Weather Forecasts (ECMWF) operational analyses are applied at the same horizontal resolution as the model. In total, we perform eight inversions using the P-NAERNSx and C-NAERNSx priors, with each one optimized against all individual IASI retrievals, or alternatively optimized against the mean XCH4 value in the region of the observed plume, with prior error covariances also tested. Our estimate represents the range across these eight inversions.

Inversion 2

Inversion 2 is derived from the reanalysis of a previous inversion18 (Supplementary Table 1), using CH4 concentrations from three ICOS stations (BIR, NOR and ZEP)62,63,64 and the Norwegian Institute for Air Research (NILU) between 26 and 30 September 2022. The Lagrangian Particle Dispersion Model FLEXPART65 is used to model atmospheric transport and is driven by meteorological data obtained from the ECMWF Integrated Forecasting System. A synthesis inversion approach assuming Gaussian errors is employed for the inverse modelling66. CH4 enhancements are derived by subtracting the average of time-series CH4 concentrations immediately before and after the plume passed at each station. We assemble the CH4 enhancements in an observation vector y and corresponding hourly emission rates into a state vector x and solve for the optimal estimation of x by minimizing the cost function J(x) in equation (7):

$$J(x)={(x-{x}_{{\rm{b}}})}^{{\rm{T}}}{B}^{-1}(x-{x}_{{\rm{b}}})+{(Hx-y)}^{{\rm{T}}}{R}^{-1}(Hx-y)$$
(7)

where xb is the prior estimate, T denotes the operation of matrix transposition, B is the prior error covariance matrix, H is the Jacobian matrix operator constructed using FLEXPART transport simulations, y is the concentration enhancement with respect to the background, and R is the observational covariance matrix. The optimal solution to equation (7) (\(\widehat{x}\)) is given by:

$$\widehat{x}={x}_{{\rm{b}}}+B{H}^{{\rm{T}}}{(HB{H}^{{\rm{T}}}+R)}^{-1}(y-H{x}_{{\rm{b}}})$$
(8)

The previous estimate18 used wind data at 1° resolution, and xb were derived by modelling flow rates from the depressurization based on initial reports of the pipeline volume, temperature, and pressure in the NS2A pipeline2. Here we use wind data at 0.2° resolution and both P-NAERNSx and C-NAERNSx for xb. Both forwards and backwards simulations are used. Error correlations of 10% for R are used for the inversions based on forward simulations, with no off-diagonal entries being non-zero. Simulations are produced for the transport operator H in forward mode at different resolutions. To account for the uncertainty in the prior, we perform six inversions using the upper, central and lower bounds of P-NAERNSx and C-NAERNSx. In addition, we estimate transport uncertainty using a variant of the statistical technique of resampling. We perform an initial inversion using all available time series for each station and then subsample the stations to obtain inversions using the same inversion parameters. We report the range across estimates derived using this approach.

Inversion 3

Inversion 3 is derived using CH4 concentrations from four ICOS stations (BIR, NOR, HTM and UTO)62,67,68,69 and the NILU between 26 September and 1 October 2022. We use the numerical weather prediction (NWP) model Icosahedral Non-hydrostatic Aerosols and Reactive Trace gases (ICON-ART)70,71 to model atmospheric transport. The model is run in limited area mode with 6.5-km resolution and initialized with NWP analysis fields. Using P-NAERNSx as the prior, we model the three-dimensional CH4 concentration field resulting from the leaks and compare hourly outputs with observations from the ICOS and NILU sites.

Owing to meteorological uncertainty, the timing of modelled and observed plume arrival differs. To allow for this uncertainty, the modelled signals from the leaks are integrated in time for each of the 5 measurement stations (mi, where i = 1, …, 5). The observed signals (oi, where i = 1, …, 5) are obtained analogously after subtracting the background from each observation time series. This background and its uncertainty are estimated for each station using the average and standard deviation of the September observations before arrival of the plume. Because the concentration scales with the emissions, an emission scaling factor is calculated for each station (si) as:

$${s}_{i}=\frac{{o}_{i}}{{m}_{i}}$$
(9)

Our posterior emissions estimate pi is derived by:

$${p}_{i}={s}_{i}\times e(t)$$
(10)

where e(t) is the time dependent P-NAERNSx.

Ideally, the scaling factors for all stations would agree, but they differ, probably because of a plume location error. To capture a wide range of plausible meteorological variability, we use an ICON-ART ensemble of 40 members and an additional deterministic run. The ensemble is constructed using operational weather forecasting methods and represents 40 slightly different, equally likely, meteorological initial conditions (k). The scaling factors derived from the ensemble members vary substantially. The minimum emission scaling needed to match the observed with the modelled integrated plume signal at a station is given by si = min(si, k (where k = 1, …, 40)). This way, the dominant meteorological uncertainty is regarded by providing lower bounds for the emissions at each station. Owing to the high response of concentration distribution to the meteorological uncertainty, there are cases where the modelled signal is close to zero owing to location error and scaling factors grow to infinity. Therefore, no upper bound can be derived.

Uncertainties aside from the meteorology are regarded as follows. For each ensemble member, the uncertainty of the prior emissions is propagated to mi by distinguishing the contributions of emissions from 14 time intervals. The uncertainty of each contribution to mi is bounded by the maximum relative prior uncertainty within the respective time interval. Summing these contributions yields upper bounds on the uncertainties of mi between 1% and 10%, depending on which part of the plume is observed. Here, the P-NAERNSx emission profiles representing the prior uncertainty are normalized to the total emissions because the inversion result is independent of the total prior emissions. A higher uncertainty of 6% to 34% is obtained for observations oi due to the background subtraction.

Our emissions estimate is the highest minimum pi derived across the measurement stations (in this case, BIR) rounded to the nearest 10 kt of CH4. Given the time dependency of emissions e(t) and allowing for meteorological transport uncertainty as used in NWP methods, this approach can only derive a lower bound of atmospheric emissions.

Inversion 4

Inversion 4 is derived from the reanalysis of a previous inversion8 (Supplementary Table 1), using CH4 concentrations from four ICOS stations (BIR, NOR, HTM and UTO)62,63,69,72 between 26 September and 1 October 2022. We use the Stochastic Time-Inverted Lagrangian Transport model (STILT)73,74 to model atmospheric transport. The STILT simulation is driven by 0.25° × 0.25° global meteorological fields from the National Centers for Environmental Prediction operational Global Forecast System75 analysis. CH4 concentration enhancements at the four stations are computed by subtracting the median of all September observations before 26 September from the time-series observations. The sensitivity of CH4 enhancements at ICOS stations to CH4 emission rates are computed with forward-mode STILT simulations by tracking the surface influence of 500 particles released from two leak points (one for the adjacent NS1A and NS1B leak sites, and one for the NS2A leak site). As for inversion 2, we solve a Bayesian inverse problem to estimate hourly CH4 emission fluxes from the two leak points using equations (7) and (8). The Jacobian matrix H in equations (7) and (8) is the sensitivity derived from the STILT simulations.

In the previous estimate8, xb were assumed to be zero because no credible prior information was available at the time of publication. Here, we use P-NAERNSx for xb. The prior error for the matrix H is considered to be the maximum uncertainty in the P-NAERNSx prior for emission rates >100 t h−1 (about 10%), and the observation error for the matrix R is 30 ppbv. We compute the uncertainty of the posterior estimate \(\hat{x}\) by analysing the posterior error covariance matrix (\(\widehat{S}\)) given by equation (11):

$$\hat{S}={({H}^{{\rm{T}}}\times {R}^{-1}\times H+{B}^{-1})}^{-1}$$
(11)

Inversion 5

Inversion 5 is derived using CH4 concentrations from three ICOS stations (BIR, NOR and HTM)76,77 between 26 September and 3 October 2022. We model atmospheric transport using the TNO LOTOS–EUROS chemistry transport model78,79 operated at 0.1° × 0.1° resolution. Meteorological fields are derived from the short-range ECMWF forecast. The CH4 concentration signal from non-Nord Stream sources are generated by the LOTOS–EUROS model using the CAMS-REGv5 emission inventory80 for anthropogenic emissions and the Copernicus Atmosphere Monitoring Service global atmospheric composition forecast81 for boundary conditions. Modelled CH4 concentrations from these sources are considered as background from which we derive CH4 enhancements from the leaks.

We produce two LOTOS–EUROS simulations using P-NAERNSx and C-NAERNSx, including their uncertainty, as the prior. Each simulation results in a total of 35 runs for each NS1 leak and 40 runs for the NS2A leak, leading to a total of 110 runs. For each simulation, a fitting routine is applied to derive an emissions estimate. The fitting is described by an Ax = B system, where A is the source receptor relations, x is the hourly emission enhancement and B is the hourly measurements from the three ICOS stations. The matrix A contains the concentrations simulated in each of our runs at the location of the three ICOS towers. The Ax = B system is underdetermined, and therefore a least-square fit is derived for x such that Ax is as close to B as possible. When the emission enhancements in x are multiplied with the initial emission strengths an estimate for the total emissions is obtained. The estimate uncertainty is the standard deviation across the fittings.

Inversion 6

Inversion 6 is derived from the reanalysis of previous inversions16,17 (Supplementary Table 1), using the temporal variation of CH4 concentrations from two ICOS stations (BIR and NOR)62,63 between 26 September and 3 October 2022. We conduct atmospheric transport simulations using the CHIMERE chemistry transport model82, with 0.2° horizontal resolution and vertical resolution divided into 29 vertical levels from the surface up to 300 hPa. Our CHIMERE simulations are driven by the Community Inversion Framework83. The meteorological fields are interpolated at the model resolution and are derived from 3-hourly operational forecasts sourced from ECMWF at a resolution of 0.15°. The CH4 concentration signal from non-Nord Stream sources is simulated using a standard regional configuration. Anthropogenic emissions other than Nord Stream are derived from EDGARv684 at 0.1° × 0.1° resolution. For natural emissions, such as natural fluxes from peatlands, inundated and mineral soils are taken from the JSBACH-HIMMELI model85. Geological emissions are a climatology based on ref. 86 and GCP-CH4 and scaled down to a global total of 15 Tg of CH4 in accordance with the maximum suggested by ref. 87. Ocean CH4 fluxes are a climatology based on ref. 88. Background concentrations at the side of the area-limited domain of CHIMERE are interpolated from the Copernicus Atmosphere Monitoring Service CH4 reanalysis89.

The previous estimates used a constant emission prior16, and an assumed exponential emission prior17. Our reanalysis uses C-NAERNSx as the emission prior. To ensure the posterior estimates are not biased by the confidence we have with C-NAERNSx values, we use C-NAERNSx temporal profiles and not the value of the rate. To do so, we carry out Monte Carlo simulations by multiplying the emission rate from C-NAERNSx by a random coefficient between 0 and 1.5. This allows to cover the lower and upper bounds of the C-NAERNSx priors. To account for uncertainties from meteorological data, we integrate 11 meteorological datasets from the ECMWF ensemble forecast. The 11 members from the ensemble forecast represent data slightly deviated from a standard case. In addition, CATHARE modelling indicates that the gas velocity exceeds 55 m s−1 during the first 24 h of at all leak sites. For that same period, gas temperatures did not exceed −35 °C owing to localized depressions between the pressure inside and outside the pipelines. Accordingly, we use the analytical solutions for turbulent buoyant plumes from circular sources to estimate the altitude the gas reached before dispersion.

To estimate atmospheric CH4 emissions, we generate 10,000 distinct scenarios. Each scenario is created by picking a random meteorological dataset from the 11 members and an altitude from 10 values between 0 m and 2,000 m for each day of the leaks. Finally, for each scenario, a reduction factor randomly fixed between 0 and 1.5 is assigned. For each scenario, we compute a probability expressing how much the scenario is close to the observations. Within the Bayesian data assimilation process, we evaluate the probability of the reduction coefficient knowing the probability of the scenario. The Bayesian probability is expressed as:

$$P(x| \,y)\,\propto \,P(\,y| x)\,\times \,P(x)\,\times \,P({\rm{alt}}| x)$$
(12)

where x is the reduction coefficient, alt is the altitude reached by the gas, and y is the comparison between the simulations and the observations for the selected stations. P(x|y) is assimilated to the posterior that we want to estimate, P(x) is the emission prior and P(alt|x) is the probability to reach an altitude knowing the rate. To evaluate equation (12), we use the analytical solutions for turbulent buoyant plumes from circular sources. The Bayesian data assimilation allows us to estimate the range and maximum probability of our posterior estimate.