Main

The number of quantum states available to a quantum computer, quantified by its Hilbert space dimension, is a fundamental and precious resource1,2. Crucially, the goal of achieving quantum advantage at scale relies on the ability to manipulate an exponentially large Hilbert space with subexponentially many operations. This large Hilbert space is typically realized using N qubits (two-level quantum systems), giving rise to a 2N-dimensional Hilbert space. However, most physical realizations of qubits have many more than two available states. These valuable extra quantum states often go untapped, because the methods for working with qudits (d-level quantum systems with d > 2) as the fundamental unit of quantum information are more complicated and less well developed than those for working with qubits23.

On the other hand, embracing these qudits could enable more efficient distillation of magic states24,25, synthesis of gates3,4, compilation of algorithms5,6,7, and simulation of high-dimensional quantum systems26,27. For these reasons, considerable experimental effort has been spent in recent years on developing qudit-based platforms for quantum computing, using donor spins in silicon8, ultracold atoms and molecules9,10, optical photons11,12, superconducting circuits13,14,15, trapped ions16,17, and vacancy centers18,19. If qudits are to be useful in the long run, however, quantum error correction (QEC) will be necessary.

In this work we experimentally demonstrate QEC of logical qudits with d > 2, using the Gottesman–Kitaev–Preskill (GKP) bosonic code20 to realize a logical qutrit (d = 3) and ququart (d = 4) encoded in grid states of an oscillator. Our optimized GKP qutrit (ququart) lived longer, on average, than the best physical qutrit (ququart) available in our system by a factor of 1.82 ± 0.03 (1.87 ± 0.03), making this one of only a handful of experiments to beat the break-even point of QEC for quantum memories22,28,29,30. This experiment represents a novel way of leveraging the large Hilbert space of an oscillator and builds on previous realizations of GKP qubits22,31,32,33,34,35,36 and bosonic codes28,29,37. Access to a higher-dimensional error-corrected manifold of quantum states may enable more hardware-efficient architectures for quantum information processing.

Error correction of GKP qudits

Our experimental device is the same as in ref. 22 and consists of a tantalum transmon38,39 dispersively coupled to a three-dimensional superconducting microwave cavity40, as shown in Fig. 1a. The cavity hosts an oscillator mode (described by Fock states \(\{| n\rangle :n\in {{\mathbb{Z}}}_{\ge 0}\}\) and mode operator a), which is used for storing our logical GKP states. The transmon hosts a qubit (described by ground and excited states {|g⟩, |e⟩} and Pauli operators σx,y,z), which is used as an ancilla for controlling the oscillator and performing error correction. The cavity has an energy relaxation lifetime of T1,c = 631 μs and Ramsey coherence time T2R,c = 1,030 μs, whereas the transmon has lifetime T1,q = 295 μs and Hahn-echo lifetime T2E,q = 286 μs (Supplementary Information section I).

Fig. 1: Stabilizing GKP qudits.
figure 1

a, Schematic of the experimental device. b, Geometric structure of the displacement operators that define the single-mode square GKP code. c, Circuit for one round of finite-energy GKP qudit stabilization, generalizing the SBS protocol43. The big ECD gate48 of amplitude \({{\ell }}_{d,\varDelta }=\sqrt{{\rm{\pi }}d}\cosh ({\varDelta }^{2})\) is approximately the stabilizer length. The small ECD gates of amplitude \({\varepsilon }_{d}/2=\sqrt{{\rm{\pi }}d}\sinh ({\varDelta }^{2})/2\) account for the envelope size Δ. At the end of SBS round j, the cavity phase is updated by ϕj (Methods). d, Measured real part of the characteristic function of the maximally mixed GKP qudit state for d = 1 to 4 with Δ = 0.3, prepared by performing 300 SBS rounds starting from the cavity in its vacuum state |0⟩.

Full size image

We employed the single-mode square GKP code20, which is designed to be translationally symmetric in phase space. The structure of the code comes from the geometric phase associated with displacement operators D(α) = exp(αa† − α*a) in phase space, as depicted in Fig. 1b. Two displacements commute up to a phase given by twice the area A they enclose, such that D(α1)D(α2) = exp(2iA)D(α2)D(α1) with \(A=\text{Im}[{\alpha }_{1}{\alpha }_{2}^{* }]\). The ideal code has stabilizer generators SX = D(ℓd) and SZ = D(iℓd), where ℓd is the stabilizer length. If these stabilizers are to have a common +1 eigenspace (the code space), they must commute, which means they must enclose an area πd in phase space for positive integer d, such that \({{\ell }}_{d}=\sqrt{{\rm{\pi }}d}\), where d is the dimension of the code space. The code words of this idealized logical qudit are grids of position eigenstates |q⟩, with form

$${| {Z}_{n}\rangle }_{d}\propto \mathop{\sum }\limits_{k=-\infty }^{\infty }| q=n\sqrt{2{\rm{\pi }}/d}+k\sqrt{2{\rm{\pi }}d}\rangle ,$$
(1)

where n = 0, 1, …, d − 1 and \(q=(a+{a}^{\dagger })/\sqrt{2}\) is the position operator. Note that with our choice of phase-space units, translations in position and displacements along the real axis of phase space differ in amplitude by a factor of \(\sqrt{2}\). The logical operators of the ideal code are the displacement operators \({X}_{d}=D(\sqrt{{\rm{\pi }}/d})\) and \({Z}_{d}=D({\rm{i}}\sqrt{{\rm{\pi }}/d})\), which act on the code space as

$$\begin{array}{l}{Z}_{d}{| {Z}_{n}\rangle }_{d}={({\omega }_{d})}^{n}{| {Z}_{n}\rangle }_{d},\\ {X}_{d}{| {Z}_{n}\rangle }_{d}={| {Z}_{(n+1)\text{mod}d}\rangle }_{d},\end{array}$$
(2)

where ωd = exp(2πi/d) is the primitive dth root of unity. These operators Zd and Xd are the generalized Pauli operators41,42, which are unitary but no longer Hermitian for d > 2. These operators obey the generalized commutation relation ZdXd = ωdXdZd, determined by the area these displacements enclose in phase space. Compared to GKP qubits, GKP qudits have a longer stabilizer length that is proportional to \(\sqrt{d}\), such that they encode information further out in phase space, and a shorter distance between logical states that is proportional to \(1/\sqrt{d}\).

In practice, we work with an approximate finite-energy version of this code, which is obtained by applying the Gaussian envelope operator EΔ = exp(−Δ2a†a) to both the operators and states of the ideal code43,44. The parameter Δ determines both the squeezing of individual quadrature peaks in the grid states as well as their overall extent in energy. For smaller Δ, the peaks are more highly squeezed and the states have more energy. On increasing d, we expect to require smaller Δ, as the logical states are more closely spaced and contain information further out in phase space (at higher energies). With smaller Δ, we expect the lifetime of our GKP qudits to decrease, as having more energy amplifies the rate of oscillator photon loss, and having information stored further out in phase space amplifies the effects of oscillator dephasing.

To stabilize the finite-energy GKP qudit manifold, we adapted the small-big-small (SBS) protocol43 to the stabilizer length \({{\ell }}_{d}=\sqrt{{\rm{\pi }}d}\), as shown in Fig. 1c. This circuit, consisting of echoed conditional displacement (ECD) gates \({\rm{ECD}}(\beta )=D(\beta /2)| e\rangle \langle g| +D(-\beta /2)| g\rangle \langle e| \) and ancilla qubit rotations Rφ(θ) = exp[i(σx cos φ + σy sin φ)θ/2], realizes an engineered dissipation onto the finite-energy GKP qudit manifold that removes the entropy associated with physical errors in the oscillator before they can accumulate into logical errors (Supplementary Information section II-A)32,43. In these expressions, β is the complex amplitude of the conditional displacement, φ is the azimuthal angle defining the rotation axis and θ is the rotation angle. This protocol is autonomous, requiring only a reset of the ancilla between rounds. We update the reference phase of the cavity mode between rounds to stabilize both quadratures in phase space (Methods).

To verify that this generalized SBS protocol works, we ran it for 300 rounds, starting with the cavity in vacuum, which prepared the maximally mixed state of the finite-energy GKP qudit \({\rho }_{d}^{{\rm{mix}}}\,=\)\((1/d){\sum }_{n=0}^{d-1}| {Z}_{n}\rangle \langle {Z}_{n}{| }_{d}\). We performed characteristic function tomography45 of \({\rho }_{d}^{{\rm{mix}}}\) prepared in this way, the results of which are shown in Fig. 1d. As expected from its definition \({\mathcal{C}}(\beta )=\langle D(\beta )\rangle \), the characteristic function of these states has peaks at the stabilizer lengths, which increase with d according to \({{\ell }}_{d}=\sqrt{{\rm{\pi }}d}\). The negative regions of \(\text{Re}[{\mathcal{C}}(\beta )]\) for odd d are a consequence of the geometric phase associated with displacement operators \(D({e}^{{\rm{i}}{\rm{\pi }}/4}\sqrt{2{\rm{\pi }}d})={(-1)}^{d}D(\sqrt{{\rm{\pi }}d})D({\rm{i}}\sqrt{{\rm{\pi }}d})\). However, it is interesting to note that the states \({\rho }_{d}^{{\rm{mix}}}\) for odd d have regions of Wigner negativity (Supplementary Information section II-B) and are, therefore, non-classical46.

Characterizing quantum memories

To characterize the performance of our logical qudits as quantum memories and establish the concept of QEC gain for qudits, we followed previous work22 and used the average channel fidelity \({{\mathcal{F}}}_{d}({\mathcal{E}},I)\), which quantifies how well a channel \({\mathcal{E}}\) realizes the identity I (ref. 47). Although \({{\mathcal{F}}}_{d}\) will have a non-exponential time evolution in general, it can always be expanded to short times dt as \({{\mathcal{F}}}_{d}({\mathcal{E}},I)\approx 1-((d-1)/d)\varGamma {\rm{d}}t\), where Γ is the effective decay rate of the channel \({\mathcal{E}}\) at short times. This rate Γ enables us to compare different decay channels on the same footing. In particular, we want to compare the decay rate \({\varGamma }_{d}^{{\rm{logical}}}\) of our logical qudit to \({\varGamma }_{d}^{{\rm{physical}}}\) of the best physical qudit in our system. We define the QEC gain as their ratio \({G}_{d}={\varGamma }_{d}^{{\rm{physical}}}/{\varGamma }_{d}^{{\rm{logical}}}\), and the break-even point is when this gain is unity.

The average channel fidelity can be expressed in terms of the probabilities \({\langle \psi | {\mathcal{E}}(| \psi \rangle \langle \psi | )| \psi \rangle }_{d}\) that our error-correction channel \({\mathcal{E}}\) preserves the qudit state |ψ⟩d, summed over a representative set of states {|ψ⟩d} (Supplementary Information section III). Each of these probabilities entails a separate experiment in which we prepare the state |ψ⟩d, perform error correction, and measure our logical qudit in a basis containing |ψ⟩d. Herein lies the primary experimental challenge of the present work: devising ways of measuring our logical GKP qudit in bases containing each state in our representative set {|ψ⟩d} using only binary measurements of our ancilla qubit.

For the qutrit in d = 3, our representative set of states are the bases {|Pn⟩3: n = 0, 1, 2} of Pauli operators \(P\in {{\mathcal{P}}}_{3}=\{{X}_{3},{Z}_{3},{X}_{3}{Z}_{3},{X}_{3}^{2}{Z}_{3}\}\), defined by P|Pn⟩3 = ωn|Pn⟩3 for ω = exp(2πi/3). The effective decay rate of our logical GKP qutrit can then be expressed as

$${\varGamma }_{3}^{{\rm{GKP}}}=\frac{1}{12}\sum _{P\in {{\mathcal{P}}}_{3}}\mathop{\sum }\limits_{n=0}^{2}{\gamma }_{{P}_{n}},$$
(3)

where \({\gamma }_{{P}_{n}}\) is the rate at which the state |Pn⟩3 decays to \({\rho }_{3}^{{\rm{mix}}}\). For the ququart in d = 4, our representative set of states consists of two types of bases. The first type are the bases {|Pn⟩4: n = 0, 1, 2, 3} of Pauli operators \(P\in {{\mathcal{P}}}_{4}=\{{X}_{4},{Z}_{4},\sqrt{\omega }{X}_{4}{Z}_{4},{X}_{4}^{2}{Z}_{4},\sqrt{\omega }{X}_{4}^{3}{Z}_{4},{X}_{4}{Z}_{4}^{2}\}\), defined by P|Pn⟩4 = ωn|Pn⟩4 for ω = i. The second type is what we call the ququart parity basis {|±, m⟩4: m = 0, 1} consisting of the simultaneous eigenstates of \({X}_{4}^{2}\) and \({Z}_{4}^{2}\), such that \({X}_{4}^{2}{| \pm ,m\rangle }_{4}=\pm {| \pm ,m\rangle }_{4}\) and \({Z}_{4}^{2}{| \pm ,m\rangle }_{4}={(-1)}^{m}{| \pm ,m\rangle }_{4}\). The effective decay rate of our logical GKP ququart can then be expressed as

$${\varGamma }_{4}^{{\rm{GKP}}}=\frac{1}{20}\left[\sum _{P\in {{\mathcal{P}}}_{4}}\mathop{\sum }\limits_{n=0}^{3}{\gamma }_{{P}_{n}}-\sum _{\begin{array}{c}s=\pm \\ m=0,1\end{array}}{\gamma }_{\pm ,m}\right],$$
(4)

where \({\gamma }_{{P}_{n}}\) (γ±,m) is the rate at which the Pauli eigenstate |Pn⟩4 (parity state |±, m⟩4) decays to \({\rho }_{4}^{{\rm{mix}}}\).

As a basis of comparison, the best physical qudit in our system is the cavity Fock qudit spanned by the states |0⟩, |1⟩, …, |d − 1⟩. The cavity hosting this qudit decoheres under both photon loss and pure dephasing at rates κ1,c = 1/T1,c and κϕ,c = 1/T2R,c − 1/2T1,c. From these measured rates, we can extrapolate the effective decay rate \({\varGamma }_{d}^{{\rm{Fock}}}\) of the cavity Fock qudit under these decoherence channels. For d = 2 through 4, we obtained \({\varGamma }_{2}^{{\rm{Fock}}}={(851\pm 9\mu {\rm{s}})}^{-1}\), \({\varGamma }_{3}^{{\rm{Fock}}}={(488\pm 7\mu {\rm{s}})}^{-1}\) and \({\varGamma }_{4}^{{\rm{Fock}}}={(332\pm 6\mu {\rm{s}})}^{-1}\).

Logical qutrit beyond break-even

To measure the effective decay rate of the logical GKP qutrit through equation (3), we needed to prepare all of the eigenstates of the Pauli operators in \({{\mathcal{P}}}_{3}\) and perform measurements in the basis of these Pauli operators. To prepare the eigenstates |Pn⟩3, we used interleaved sequences of ECD gates and transmon rotations, which enable universal control of the oscillator mode in the cavity48. We optimized depth-8 ECD circuits to implement the unitary that maps the cavity vacuum state |0⟩ to the desired state |Pn⟩3 with envelope size Δ = 0.32. The measured Wigner functions \(W(\alpha )=\langle D(\alpha ){e}^{i\pi {a}^{\dagger }a}D(\,-\alpha )\rangle \) of our prepared |P0⟩3 states are shown in Fig. 2a (see Supplementary Information section V-A for the other eigenstates). In general, the eigenstates |Pn⟩d are oriented in phase space in the direction of the displacement induced by Pd, where Xd displaces rightward, Zd displaces upward, and \({P}_{d}^{d-1}={P}_{d}^{-1}\).

Fig. 2: Realization of a logical GKP qutrit.
figure 2

a, State preparation of qutrit Pauli eigenstates |P0⟩3 with Δ = 0.32. b, Circuit for measuring a qutrit in the basis of Pauli operator P3 using an ancilla qubit, where \({\theta }_{0}=2\,\arctan (1/\sqrt{2})\). The first measurement distinguishes between the state |P0⟩3 and the subspace {|P1⟩3, |P2⟩3}, whereas the second distinguishes between |P1⟩3 and {|P0⟩3, |P2⟩3}. The Bloch spheres depict the trajectories taken by the ancilla when the qutrit is in each Pauli eigenstate. c, Backaction of the qutrit Pauli measurement in the Z3 basis, applied to the maximally mixed qutrit state. d, Decay of qutrit Pauli eigenstates |P0⟩3 under the optimized QEC protocol. The dashed black lines indicate a probability of 1/3. The solid grey lines are exponential fits. From left to right, we found \({\gamma }_{{X}_{0}}^{-1}=\mathrm{1,153}\pm 13\,\mu {\rm{s}}\), \({\gamma }_{{Z}_{0}}^{-1}=\mathrm{1,120}\pm 15\,\mu {\rm{s}}\), \({\gamma }_{X{Z}_{0}}^{-1}=743\pm 10\,\mu {\rm{s}}\) and \({\gamma }_{{X}^{2}{Z}_{0}}^{-1}=727\pm 11\,\mu {\rm{s}}\).

Full size image

We measured the GKP qutrit in Pauli basis P3 using the circuit shown in Fig. 2b. The generalized ancilla-qubit-controlled Pauli operators CP3 = |g⟩⟨g|I3 + |e⟩⟨e|P3 were realized with ECD gates, where Id is the identity operator in dimension d. Intuitively, as generalized Pauli operators on GKP qudits are implemented through displacements, the conditional versions of these displacements implement CPd operations, with some technical caveats (Methods). The idea of this circuit is to perform a projective measurement in the P3 basis using two binary measurements of the ancilla qubit. The first measurement determines whether the qutrit is in state |P0⟩3 or the {|P1⟩3, |P2⟩3} subspace, and the second determines whether the qutrit is in state |P1⟩3 or the {|P0⟩3, |P2⟩3} subspace. These two binary measurements uniquely determine the ternary measurement result in the P3 basis and collapse the qutrit state accordingly. Note that this circuit was constructed for the ideal code and incurs infidelity when applied to the finite-energy code. To verify that this circuit realizes the desired projective measurement, we prepared \({\rho }_{3}^{{\rm{mix}}}\), measured in the Z3 basis, and performed Wigner tomography of the cavity post-selected on the three measurement outcomes. The results of this measurement are shown in Fig. 2c (see Supplementary Information section V-B for the other Pauli bases).

With these techniques, we used a reinforcement learning agent21 to optimize the logical GKP qutrit as a ternary quantum memory following the method in ref. 22 (Methods). We then evaluated the optimal QEC protocol by preparing each eigenstate |Pn⟩3 for each \({P}_{3}\in {{\mathcal{P}}}_{3}\), implementing the optimized QEC protocol for a variable number of rounds, and measuring the final state in the P3 basis. Finally, we fitted an exponential decay to each probability \(\langle {P}_{n}| {\mathcal{E}}(| {P}_{n}\rangle \langle {P}_{n}| )| {P}_{n}\rangle \) to obtain \({\gamma }_{{P}_{n}}\). The results of this evaluation for the |P0⟩3 states are shown in Fig. 2d (the other results are given in Supplementary Information section V-C). As with the GKP qubit22,33, we found longer lifetimes for the ‘Cartesian’ eigenstates of X3 and Z3 than for the remaining ‘diagonal’ eigenstates, as the latter were more susceptible to both cavity photon-loss errors and ancilla bit-flip errors33. Using equation (3) with our measured rates \({\gamma }_{{P}_{n}}\), we obtained \({\varGamma }_{3}^{{\rm{GKP}}}={(886\pm 3\mu {\rm{s}})}^{-1}\). Comparing with \({\varGamma }_{3}^{{\rm{Fock}}}\), we obtained the QEC gain

$${G}_{3}={\varGamma }_{3}^{{\rm{Fock}}}/{\varGamma }_{3}^{{\rm{GKP}}}=1.82\pm 0.03,$$
(5)

which is well beyond the break-even point.

Logical ququart beyond break-even

We followed a similar procedure to measure the effective decay rate of our logical GKP ququart through equation (4) as we did for the qutrit, the main difference being that we needed to prepare and measure states in both the ququart parity basis and the Pauli bases \(P\in {{\mathcal{P}}}_{4}\). We again used depth-8 ECD circuits48 to prepare the Pauli eigenstates |Pn⟩4 and parity states |±, m⟩4 with Δ = 0.32. The measured Wigner functions of our prepared |P0⟩4 states and the |+, 0⟩4 state are shown in Fig. 3a (see Supplementary Information section VI-A for the remaining states). Again, the eigenstates |Pn⟩d are oriented in phase space in the direction of the displacement induced by Pd. By contrast, the parity states |±, m⟩ are uniform grids, equally oriented both horizontally and vertically.

Fig. 3: Realization of a logical GKP ququart.
figure 3

a, State preparation of ququart Pauli eigenstates |P0⟩4 and parity state |+, 0⟩4 with Δ = 0.32. b, Circuit for measuring a ququart in the basis of Pauli operator P4 using an ancilla qubit. The first measurement distinguishes between the even and odd states |Peven/odd⟩4, and the second measurement distinguishes between the remaining two states. The Bloch spheres depict the trajectories taken by the ancilla when the ququart is in each Pauli eigenstate. c, Backaction of the GKP ququart Pauli measurement in the Z4 basis applied to the maximally mixed ququart state. d, Circuit for measuring a ququart in the parity basis {|±, m⟩4: m = 0, 1}, where \({X}_{4}^{2}{| \pm ,m\rangle }_{4}=\pm {| \pm ,m\rangle }_{4}\) and \({Z}_{4}^{2}{| \pm ,m\rangle }_{4}={(-1)}^{m}{| \pm ,m\rangle }_{4}\). The first measurement determines the eigenvalue of \({X}_{4}^{2}\), and the second determines that of \({Z}_{4}^{2}\). e, Backaction of the GKP ququart parity measurement applied to the maximally mixed ququart state. f, Decay of ququart Pauli eigenstates |P0⟩4 and parity state |+, 0⟩4 under the optimized QEC protocol. The dashed black lines indicate a probability of 1/4. The solid grey lines are exponential fits. From left to right, we found \({\gamma }_{{X}_{0}}^{-1}=840\pm 8\,{\rm{\mu }}{\rm{s}}\), \({\gamma }_{{Z}_{0}}^{-1}=836\pm 9\,\mu {\rm{s}}\), \({\gamma }_{X{Z}_{0}}^{-1}=519\pm 6\,\mu {\rm{s}}\), \({\gamma }_{{X}^{2}{Z}_{0}}^{-1}\,=507\pm 9\,\mu {\rm{s}}\), \({\gamma }_{{X}^{3}{Z}_{0}}^{-1}=571\pm 7\,\mu {\rm{s}}\), \({\gamma }_{X{Z}_{0}^{2}}^{-1}=562\pm 9\,\mu {\rm{s}}\) and \({\gamma }_{+,0}^{-1}=607\pm 8\,\mu {\rm{s}}\).

Full size image

We measured the GKP ququart in Pauli basis P4 using the circuit shown in Fig. 3b. The first binary measurement of the ancilla qubit distinguishes between the even subspace {|P0⟩, |P2⟩} and odd subspace {|P1⟩, |P3⟩} by measuring whether \({P}_{4}^{2}=\pm 1\), and the second distinguishes between the remaining two states by measuring P4 = ±1 (if in the even subspace) or P4 = ±i (if in the odd subspace). To verify that this circuit realizes the desired projective measurement, we prepared \({\rho }_{4}^{{\rm{mix}}}\), measured in the Z4 basis, and performed Wigner tomography of the cavity post-selected on the four measurement outcomes. The results of this measurement are shown in Fig. 3c (see Supplementary Information section VI-B for the other Pauli bases).

We measured the GKP ququart in the parity basis {|±, m⟩4: m = 0, 1} using the circuit shown in Fig. 3d. The first binary measurement of the ancilla qubit determines whether \({X}_{4}^{2}=\pm 1\), and the second determines whether \({Z}_{4}^{2}=\pm 1\). To verify that this circuit realizes the desired projective measurement, we prepared \({\rho }_{4}^{{\rm{mix}}}\), measured in the parity basis, and performed Wigner tomography post-selected on the four measurement outcomes. The results of this measurement are shown in Fig. 3e. As with the qutrit, our logical ququart measurements were constructed for the ideal code, and they incur infidelity when applied to the finite-energy code.

With these techniques, we again used a reinforcement learning agent21 to optimize the logical GKP ququart as a quaternary quantum memory following the method in ref. 22 (Methods). We then evaluated the optimal QEC protocol by preparing each eigenstate |Pn⟩4 for each \({P}_{4}\in {{\mathcal{P}}}_{4}\) (plus the parity basis), implementing the optimized QEC protocol for a variable number of rounds, and measuring the final state in its corresponding basis. Finally, we fitted an exponential decay to each probability \(\langle {P}_{n}| {\mathcal{E}}(| {P}_{n}\rangle \langle {P}_{n}| )| {P}_{n}\rangle \) and \(\langle \pm ,m| \,{\mathcal{E}}(| \pm ,m\rangle \langle \pm ,m| )| \pm ,m\rangle \) to obtain \({\gamma }_{{P}_{n}}\) and γ±,m, respectively. The results of this evaluation for the |P0⟩4 states and |+, 0⟩4 state are shown in Fig. 3f (the remaining results are given in Supplementary Information section VI-C). Again, we found longer lifetimes for the Cartesian eigenstates of X4 and Z4 than for the remaining eigenstates. Using equation (4) with our measured rates \({\gamma }_{{P}_{n}}\) and γ±,m, we obtained \({\varGamma }_{4}^{{\rm{GKP}}}={(620\pm 2\mu {\rm{s}})}^{-1}\). Comparing with \({\varGamma }_{4}^{{\rm{Fock}}}\), we obtained the QEC gain

$${G}_{4}={\varGamma }_{4}^{{\rm{Fock}}}/{\varGamma }_{4}^{{\rm{GKP}}}=1.87\pm 0.03,$$
(6)

which is, again, well beyond the break-even point.

Discussion

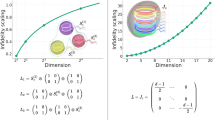
Notably, despite the increasing complexity of the code, we found that the QEC gain stayed roughly constant at about 1.8 as we increased the dimension of our logical GKP qudit from 2 to 4, as shown in Fig. 4a. Note that the gain G2 = 1.81 ± 0.02 that we achieved with the GKP qubit is less than the gain of 2.3 previously reported using the same device22, which was due to changes in both the device and the experimental conditions (see Supplementary Information section IV-C for details). Regardless, the measurements shown in Fig. 4a were taken under the same conditions, and they indicate that as we increased d from 2 to 4, the lifetime of our logical GKP qudit decreased at about the same rate as that of our cavity Fock qudit.

Fig. 4: Comparing GKP qudits.
figure 4

a, Effective lifetime of the physical cavity Fock qudit and logical GKP qudit for d ∈ {2, 3, 4}. The arrows indicate the QEC gain. b, Effective envelope size Δeff of the optimized GKP qudit for d ∈ {2, 3, 4}. c, Mean number of photons in the cavity for the optimized GKP qudit for d ∈ {2, 3, 4}.

Full size image

This decrease occurred because the GKP qudit states are more closely spaced and contain information further out in phase space for increasing d, which should require smaller Δ. To verify this, we prepared \({\rho }_{d}^{{\rm{mix}}}\) of our optimal GKP qudits and measured the central Gaussian peak of their characteristic functions for d = 2 through 4 (Supplementary Information). The width Δeff of this Gaussian is related to the parameter Δ and decreased with d, as shown in Fig. 4b, in agreement with our expectations. The average number of photons ⟨a†a⟩ in \({\rho }_{d}^{{\rm{mix}}}\) can also be inferred from this measurement of Δeff and is presented in Fig. 4c.

With a smaller Δ, our logical GKP qudits had more energy and were more highly squeezed, which should amplify the rates of cavity photon loss and dephasing. To corroborate this, we simulated our optimal QEC protocols and isolated the relative contributions of different physical errors to our overall logical error rates (Supplementary Information section VII). We found that the three largest sources of logical errors were transmon bit flips, whose relative contribution decreased as d was increased, cavity photon loss, whose relative contribution increased as d was increased, and cavity dephasing, which was the dominant source of error and whose relative contribution increased as d was increased. As our cavity dephasing was primarily due to the thermal population nth = 2.2 ± 0.1% of the transmon40, the lifetimes of our logical GKP qudits could be substantially improved by either reducing nth or using an ancilla that can be actively decoupled from the cavity when not in use49,50.

In summary, we have demonstrated QEC of logical qudits with d > 2, which represents a milestone achievement in the development of qudits for useful quantum technologies. Moreover, we have beaten the break-even point for QEC of quantum memories, a result few other experiments have accomplished22,28,29,30. These results rely upon many technical advances, such as our generalization of previous experimental methods22 and our invention of protocols for measuring qudits in generalized Pauli bases. Our work builds on the promise of hardware efficiency offered by bosonic codes22,28,29,31,32,33,34,35,36,37 and represents a novel way of leveraging the large Hilbert space of an oscillator. In exchange for a modest reduction in lifetime, we gained access to more logical quantum states in a single physical system. This could enable more efficient compilation of gates3,4 and algorithms5,6,7, alternative techniques for quantum communication51 and transduction52, and advantageous strategies for concatenation into an external multi-qudit code24,25. Such a concatenation requires entangling gates, which for GKP qudits can be realized with the same operations used for entangling GKP qubits20,53,54,55. With the realization of bosonic logical qudits, we have also established a platform for concatenating codes internally. By embedding a logical qubit within a bosonic logical qudit20,56,57,58, multiple layers of error correction can be implemented inside a single oscillator.

Methods

Phase update between stabilization rounds

The generalized SBS circuit in Fig. 1c realizes autonomous QEC of the finite-energy GKP code with respect to the ideal stabilizer \({S}_{X}=D(\sqrt{{\rm{\pi }}d})\) (ref. 43). The analogous circuit for \({S}_{Z}=D({\rm{i}}\sqrt{{\rm{\pi }}d})\) is obtained by updating the phase of all subsequent cavity operations by π/2, which transforms q → p and p → −q in the rotating frame of the cavity, where \(q=(a+{a}^{\dagger })/\sqrt{2}\) is the position of the cavity and \(p={\rm{i}}({a}^{\dagger }-a)/\sqrt{2}\) is the momentum. To mitigate the effects of experimental imperfections, we symmetrized the protocol by also performing QEC with respect to stabilizers \({S}_{X}^{\dagger }\) and \({S}_{Z}^{\dagger }\), which are related to the circuit in Fig. 1c by phase updates of π and 3π/2, respectively. The full protocol is periodic with respect to four SBS rounds, as each stabilizer (\({S}_{X},{S}_{Z},{S}_{X}^{\dagger },{S}_{Z}^{\dagger }\)) is measured once per period.

Ideally, we would measure the stabilizer SX by implementing the ancilla-controlled-stabilizer operation \(C{X}_{d}^{d}\), but in practice, we instead used \({\rm{ECD}}(\sqrt{{\rm{\pi }}d})=D(-\sqrt{{\rm{\pi }}d}/2)C{X}_{d}^{d}{\sigma }_{x}\) (refs. 33,48). For even dimensions d, the extra displacement \(D(-\sqrt{{\rm{\pi }}d}/2)\) is the ideal Pauli operator \({X}_{d}^{d/2}\), the effect of which can be tracked in software (a similar result holds for the other stabilizers). In this case, we are free to measure the stabilizers in any order. We chose to increment the cavity phase in each round according to

$${\phi }_{j}^{(d\,{\rm{even}})}={\rm{\pi }}/2,$$
(7)

which measures the stabilizers in the order SX, SZ, \({S}_{X}^{\dagger }\) and \({S}_{Z}^{\dagger }\). However, for odd d, the displacement \(D(-\sqrt{{\rm{\pi }}d}/2)\) takes us outside the code space, an effect we have to reverse before moving on to measure SZ. To do so, we incremented the cavity phase in each round according to

$${\phi }_{j}^{(d\,{\rm{o}}{\rm{d}}{\rm{d}})}=\left\{\begin{array}{cc}{\rm{\pi }}, & j\equiv 0\,({\rm{m}}{\rm{o}}{\rm{d}}\,4),\\ -{\rm{\pi }}/2, & j\equiv 1\,({\rm{m}}{\rm{o}}{\rm{d}}\,4),\\ {\rm{\pi }}, & j\equiv 2\,({\rm{m}}{\rm{o}}{\rm{d}}\,4),\\ {\rm{\pi }}/2, & j\equiv 3\,({\rm{m}}{\rm{o}}{\rm{d}}\,4),\end{array}\right.$$
(8)

which measures the stabilizers in the order SX, \({S}_{X}^{\dagger }\), SZ and \({S}_{Z}^{\dagger }\).

Compiling generalized controlled Pauli gates

The ancilla-controlled version of generalized Pauli operator \({P}_{d}={e}^{{\rm{i}}\varphi }{X}_{d}^{n}{Z}_{d}^{m}\) on the ideal GKP code is given by CPd = |g⟩⟨g| + |e⟩⟨e| eiϕD(βn)D(βm), where \({\beta }_{n}=n\sqrt{{\rm{\pi }}/d}\) and \({\beta }_{m}={\rm{i}}m\sqrt{{\rm{\pi }}/d}\). We compiled CPd in terms of ancilla rotations and a single ECD gate:

$${\rm{ECD}}({\beta }_{nm})=D(-{\beta }_{nm}/2)(| g\rangle \langle e| +| e\rangle \langle g| D({\beta }_{nm})),$$
(9)

where βnm = βn + βm. Using D(βnm) = exp(inmπ/d)D(βn)D(βm), this can be rewritten as

$${\rm{ECD}}({\beta }_{nm})=D(-{\beta }_{nm}/2){\sigma }_{z}({\varphi }_{nm})C{P}_{d}{\sigma }_{x},$$
(10)

where φnm = nmπ/d − φ and σz(θ) = |g⟩⟨g| + |e⟩⟨e| eiθ. Rearranging terms, we obtain

$$C{P}_{d}=D({\beta }_{nm}/2){\sigma }_{z}(-{\varphi }_{nm}){\rm{ECD}}({\beta }_{nm}){\sigma }_{x}.$$
(11)

In our experiments, we omitted the unconditional displacement D(βnm/2) when compiling CPd gates, which affected the backaction of our GKP qudit logical measurements (Figs. 2 and 3). In addition, we used the smallest amplitude ∣βnm∣ consistent with the Pauli operator Pd. As an example, for n = d − 1 and d > 2, we used \({\beta }_{nm}=-\sqrt{{\rm{\pi }}/d}+{\rm{i}}m\sqrt{{\rm{\pi }}/d}\) because \({X}_{d}^{d-1}={X}_{d}^{-1}\). We emphasize that this CPd gate is designed for the ideal GKP code and will necessarily incur infidelity when applied to the finite-energy code, but it may be possible to adapt this construction to the finite-energy case32,43,55.

Optimizing the QEC protocol

To optimize our generalized SBS protocol (Fig. 1c), we followed the method described in ref. 22, parametrizing the SBS circuit using 45 free parameters in total. Anticipating that the larger conditional displacements required for GKP qudit stabilization (nominally proportional to \(\sqrt{{\rm{\pi }}d}\)) would take longer to execute, we fixed the duration of each SBS round to be 7 μs (instead of 5 μs as in ref. 22).

We used a reinforcement learning agent to optimize our QEC protocol over these 45 parameters in a model-free way21. In each training epoch, the agent sends a batch of ten parametrizations pi to the experiment, collects a reward Ri for each, and updates its policy to increase the reward. For our reward, we measured the probability that the QEC protocol keeps our logical qudit in its initial state, operationally quantified by

$${R}_{i}=\frac{1}{2}[{\langle {Z}_{0}| {{\mathcal{E}}}_{{{\bf{p}}}_{i}}^{N}(| {Z}_{0}\rangle \langle {Z}_{0}| )| {Z}_{0}\rangle }_{d}+{\langle {X}_{1}| {{\mathcal{E}}}_{{{\bf{p}}}_{i}}^{N}(| {X}_{1}\rangle \langle {X}_{1}| )| {X}_{1}\rangle }_{d}],$$
(12)

where \({{\mathcal{E}}}_{{{\bf{p}}}_{i}}^{N}\) is the channel corresponding to N rounds of the SBS protocol parametrized by pi. For our optimal GKP qubit, we used N = 140 and 200 training epochs, for the qutrit, N = 80 and 200 training epochs, and for the ququart, N = 80 and 300 training epochs.

Regarding the scalability of this optimization method, we emphasize that the resources required for training our GKP qudits are the same as for the GKP qubit and that this training was implemented using off-the-shelf consumer electronics. Because the training was performed for individual qubits or qudits, we expect that it could be parallelized across an array of such systems, yielding a resource requirement that scales only linearly with the system size. We expect that applying reinforcement learning to optimize entangling gates will be more complicated than applying it to individual qubits or qudits.