Main

Quantum computing holds immense potential for solving complex problems beyond the reach of classical computers23,24. However, most practical quantum computing applications require gate error rates far below what current physical devices can achieve25. Quantum error correction (QEC) offers a solution to bridge this gap by encoding logical qubits across multiple physical qubits1,2. This encoding can exponentially suppress errors, provided the physical error rates are below a critical threshold26.

Realizing scalable, fault-tolerant quantum computation in practice requires overcoming several core challenges, including achieving low logical error rates with reasonable qubit overhead and performing logical operations efficiently. Considerable experimental progress has been made in recent years to address these challenges. Notably, scalable error suppression was recently demonstrated by increasing the size of a logical qubit encoded in the surface code8 using superconducting circuits27. QEC implementations with superconducting qubits5,6,7,28,29 have predominantly focused on the surface code9 or variants thereof30,31, although alternative approaches such as bosonic encodings are also being explored32,33. The surface code offers a high error threshold and is compatible with planar, four-nearest-neighbour architectures. However, it demands substantial qubit overhead and has limitations for certain logical operations34, motivating the investigation of alternative planar codes.

Colour codes10,35 allow for more efficient logical operations and require fewer qubits than the surface code to encode a logical qubit at a fixed code distance36. The smallest instance of the colour code, the Steane code37, has been implemented with trapped ions11,12 and neutral atoms18, demonstrating logical operations and logical circuits13,14,15,16,17,18,19. Colour codes can perform all Clifford gates38 within a single error correction cycle and support resource-efficient magic state injection protocols required to implement non-Clifford gates21,39,40. A recent breakthrough harnessed these features to reduce the overhead required for non-Clifford gate implementation in surface code architectures41,42. Colour codes also enable multi-qubit entangling operations with less space-time overhead because of their ability for simultaneous fault-tolerant multi-qubit Pauli measurements43.

However, colour codes have a stricter error threshold than surface codes because of their higher weight stabilizer measurements35. Moreover, these colour codes require more elaborate decoding strategies, and conventional colour code syndrome extraction circuits require higher connectivity than four-nearest-neighbour architectures35,44, which is difficult to realize on superconducting devices. As a result, error suppression by increasing the colour code size has not yet been demonstrated, to our knowledge, on any experimental platform.

Nevertheless, recent advances in superconducting qubit performance8, improvements in decoding algorithms39,40,45,46,47 and optimized error-syndrome extraction circuits44,47 now open new possibilities for implementing the colour code on existing hardware. Here we demonstrate building blocks of fault-tolerant quantum computation using the colour code on a superconducting processor. Specifically, we suppress logical errors by increasing code distance, characterize single-qubit logical Clifford gates, inject magic states and perform lattice surgery22 to demonstrate multi-logical-qubit operations. This comprehensive demonstration establishes the colour code as a promising approach for resource-efficient, fault-tolerant quantum computation on superconducting circuits.

Colour codes with superconducting qubits

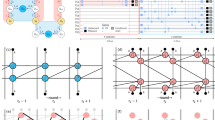
Triangular colour codes10,48 are two-dimensional topological stabilizer codes2. In these constructions, three tiles meet at each vertex of the lattice, and the tiles can be coloured (red, green and blue in this work) such that no two adjacent tiles share the same colour. Data qubits are located at each vertex of the lattice, and each tile has an X-type and a Z-type stabilizer.

Several such lattices exist, each with potentially different syndrome extraction circuits for stabilizer measurements47. Here we choose to implement a code based on a hexagonal lattice embedded in a square grid of qubits with a superdense syndrome extraction circuit47 (Fig. 1a,b). This choice is particularly attractive for superconducting qubits because it requires only nearest-neighbour connectivity on a square grid of qubits. Moreover, this choice enables simultaneous measurement of X- and Z-type stabilizers of each tile using two auxiliary qubits labelled X and Z in Fig. 1a, located at the centre of each tile. Conceptually, the two auxiliary qubits are prepared in a Bell pair, and each interact with the three nearest data qubits of the tile using the controlled-NOT (CNOT) gates to accumulate first the Z-type, then the X-type stabilizer, as shown in Fig. 1b. A Bell-basis measurement of the auxiliary qubits follows, allowing both stabilizers of the hexagon to be measured simultaneously up to Pauli corrections dealt with by a frame update47.

Fig. 1: Superdense colour code.
figure 1

a, Example tile in the bulk of a red, green and blue hexagonal lattice used for the superdense colour code. The lattice is embedded on a square grid of data qubits (golden circles labelled D1–D6) and X/Z auxiliary qubits (red, green and blue circles), with their connectivity indicated by solid grey lines. b, Superdense syndrome extraction circuit for the tile shown in a (see the main text). c, Distance-5 colour code qubit, with one of the distance-3 qubit subsets outlined in purple. Data qubits included in the logical operators XL and ZL are circled and connected by a solid black line. Red arrows indicate qubit pairs interchanged for the implementation of the colour code on our quantum device. d, Deformed code layout after interchanging the qubits to ensure that each readout line contains only data or auxiliary qubits. The readout lines are oriented diagonally from top left to bottom right (two dashed grey lines).

Full size image

This construction allows the encoding of a single distance-5 logical qubit using 19 data qubits and 18 auxiliary qubits (Fig. 1c). It consists of six weight-6 stabilizers (two per hexagonal tile) and 12 boundary weight-4 stabilizers (two per quadrilateral tile). The logical operators XL and ZL are defined as the product of the individual Pauli X and Z operators, respectively, of data qubits along a boundary of the triangle.

We implement this logical qubit on the 72-qubit Willow processor first introduced in ref. 8; see Supplementary Information section A for a summary of the device performance. The design of this processor favours the simultaneous readout of all qubits sharing a readout line to minimize measurement-induced dephasing. To accommodate this constraint, we swap the roles of auxiliary and data qubits for certain pairs of qubits, as indicated by the red arrows in Fig. 1c. This adjustment results in the code layout shown in Fig. 1d, in which each readout line contains only data qubits or auxiliary qubits, but no mixture of both. This ensures that all qubits on each readout line are measured either in each QEC cycle (auxiliary qubit readout line) or at the end of the protocol only (data qubit readout line). To avoid the use of costly swap gate decompositions, we use circuit transformations that add no additional operations and preserve the fault tolerance of the circuit, as detailed in Supplementary Information section B. Apart from these circuit transformations, the CNOT gates are compiled to a combination of native Hadamard gates and CZ gates; see Supplementary Information section B.3 for a full circuit diagram of a QEC cycle on the distance-5 logical qubit.

Distance scaling

First, we demonstrate that the colour code is a viable candidate for encoding logical qubits by testing its memory performance and scaling. Specifically, we preserve logical states in the X and Z bases through repeated cycles of error correction and suppress the logical error per cycle by increasing the code distance d from three to five. Here, the distance of the code corresponds to the minimum number of physical qubit errors required to cause an undetectable logical error. A distance d code can correct any (d − 1)/2 independent errors. We compare the performance of the distance-5 code to the average performance of three distance-3 colour code subsets. An example subset is shown with a purple outline in Fig. 1c,d, and a visual representation of all d = 3 subsets is presented in Supplementary Information section C. For each experimental run, we initialize the data qubits in a product state of the Z and X bases, project the logical qubit into the target logical state using a single cycle of stabilizer measurements, perform n − 1 additional cycles of error correction, and finally measure all data qubits in the Z and X bases. We obtain the logical operator value from the product of the relevant data qubits in this final measurement, and the run succeeds if the corrected logical measurement after decoding coincides with the target logical state; otherwise, a logical error has occurred.

For each error correction cycle, the auxiliary qubit readout outcomes correspond to the stabilizer values and indicate the parity of the involved data qubits (0 for even parity, 1 for odd parity). We construct the error syndrome, in which each element is obtained by comparing stabilizer values in two consecutive cycles and takes a value of 1 if a change of parity is detected and 0 otherwise. By averaging each syndrome element over 50,000 experimental runs, we obtain the average error detection probability Pd for each stabilizer in each cycle, see Fig. 2a for the error detection probabilities of the distance-5 X-basis state-preservation experiment and Supplementary Information section C.4 for others. We find that Pd remains nearly constant in the bulk of the error correction cycles, suggesting a stable error rate throughout the experiment. As expected, weight-6 stabilizers exhibit a higher error detection probability (Pd,6 = 0.149 when averaging over all cycles and stabilizers), compared with boundary weight-4 stabilizers (Pd,4 = 0.112), which involve fewer gates and are thus less susceptible to errors, as shown in Fig. 2b.

Fig. 2: Distance scaling experiment.
figure 2

a, Detection probability Pd as a function of QEC cycle n for individual stabilizers (faded lines) and their average (solid line) for an X-basis state-preservation experiment in a distance-5 colour code. Weight-6 stabilizers are coloured in red and weight-4 stabilizers are coloured in gold. b, Detection probability for each tile of the distance-5 colour code, averaged over cycles and bases. c, Measured logical error PL for distance-3 (green triangles) and distance-5 (blue pentagons) codes averaged over the X and Z bases. Faded symbols correspond to individual distance-3 subsets. The solid lines, shown for the averaged distance-3 code and the distance-5 code, are fits to \({P}_{{\rm{L}}}={\varepsilon }_{0}\times {(1-2\times {\varepsilon }_{d})}^{n}+1/2\), with fitting parameters ε0 and εd. d, Logical error per cycle, εd, compared with code distance, d. Same symbols as in c. e, Relative contributions of different error sources to the error budget for the colour code: CZ errors (CZ); errors from spurious interactions during two-qubit gates (CZ stray int.); leakage errors during two-qubit gates (CZ leakage); measurement errors (Meas.); single-qubit gate error (1Q); data-qubit idle error during measurement and reset of auxiliary qubits (Data idle); reset error (Reset); leakage due to incoherent heating from |1⟩ to |2⟩ (Heating). The relative contributions of the different error channels are indicated.

Full size image

Because each data qubit in the bulk participates in three stabilizers per basis (compared with two for the surface code), efficient matching-based decoders49,50 cannot be used directly47. Therefore, we use new decoding strategies35,44,47,51 to infer whether logical errors have occurred; see Supplementary Information section D for an overview of the different decoders used in this work.

To assess the performance of our colour code, we initialize the logical qubit, measure up to n = 29 cycles of error correction, and compute the logical error probability PL as a function of n. We then fit PL to obtain the logical error per cycle εd (ref. 5). We average the error per cycle of the three different distance-3 subsets to obtain \({\overline{\varepsilon }}_{3}\) and compute the error suppression factor \({\varLambda }_{3/5}={\overline{\varepsilon }}_{3}/{\varepsilon }_{5}\). With a neural-network decoder (AlphaQubit)51, we obtain Λ3/5 = 1.56(4) and ε5 = 0.0110(2).

This significant reduction in logical error with increasing distance suggests performance below the error correction threshold of the colour code, corroborated by Pauli simulations extrapolating to larger distances and varying noise strengths (see Supplementary Information section E). The observed error suppression factor is in reasonable agreement with the simulated error suppression factor \({\varLambda }_{3/5}^{{\rm{sim}}}=1.680(4)\). By varying the strength of individual error sources in simulations, we estimate their relative contributions to \(1/{\varLambda }_{3/5}^{{\rm{sim}}}\) (ref. 8). This analysis suggests that CZ gates are the primary contributors, accounting for about 39% of the error budget (including CZ-gate-induced leakage and stray interactions during CZ gates). The remaining contributions are approximately equally distributed among measurement errors, single-qubit gate errors, and data-qubit idle errors during the measurement and reset of auxiliary qubits.

Logical randomized benchmarking

Achieving fault-tolerant quantum computation requires not only correcting errors in idle logical qubits but also applying logical gates that do not spread errors. Transversal single-qubit logical gates52 achieve this by applying the desired gate independently to each physical data qubit, keeping potential errors isolated. They are inherently fault-tolerant, simple to implement and efficient, as they require only a single time step of physical gates.

An important advantage of the colour code over the surface code is its ability to perform all single-qubit logical Clifford gates transversely. Here, we implement all 24 gates of the Clifford group using a combination of Hadamard gates H, phase gates S, and Pauli operators, see Supplementary Information section F. We characterize the average error of transversal Clifford operations using logical randomized benchmarking20. In analogy to interleaved randomized benchmarking at the physical qubit level53, the protocol consists of applying multiple sequences of m randomly chosen logical Clifford gates, each followed by a final Clifford gate C−1 that inverts the sequence. The logical qubit is subsequently measured and compared with the initial logical state, |0L⟩. This process is repeated for various Clifford sequence lengths m, with a cycle of error correction between each Clifford gate. To obtain an estimate of the average error per logical Clifford gate, we compare these sequences with the reference sequences in which no Clifford gates are applied, that is, a standard |0L⟩ state-preservation experiment (Fig. 3a).

Fig. 3: Logical randomized benchmarking.
figure 3

a, Logical-qubit-level reference (Ref.; green) and interleaved randomized benchmarking (IRB; blue) circuit diagrams, consisting of error correction cycles (QEC), randomly selected Clifford gates (C1, …, Cm), a Clifford recovery gate C−1 and a Z basis measurement (MZ). b–d, Simplified circuit diagrams for a tile of the colour code indicating measurements included in an X-stabilizer error-detecting region spanning across two consecutive cycles without logical gate (b), and how it changes on the application of a logical Hadamard gate H (c), or a logical phase gate S (d) between two error correction cycles, see text for details. The green, blue and purple highlighted sections correspond to regions in which the detecting region is sensitive to Z, X and both X and Z errors, respectively. A CNOT gate symbol spanning three qubit wires indicates three consecutive CNOTs between the auxiliary qubit and its neighbouring data qubits. e, Measured fidelity (symbols) and exponential fits (solid lines) for the interleaved (blue) and reference (green) sequences compared with the number of logical Clifford gates m. The data are decoded using the neural-network decoder. Error bars represent the standard deviation of fidelity over 25 random Clifford sequences, each repeated 20,000 times.

Full size image

In a state-preservation experiment (no logical gates), subsequent measurements of the same auxiliary qubits are used to construct error syndrome elements. Applying a logical gate between error correction cycles transforms the stabilizers, changing how syndrome elements are constructed, as shown in Fig. 3b–d and explained in more detail in Supplementary Information section F.

We realize logical randomized benchmarking in a distance-3 colour code, varying the number of randomly chosen Clifford gates m = 0–10, with 25 random sequences for each m. When compiling these circuits to native physical operations available on our hardware, single-qubit gates implementing the transversal gate are potentially merged with those from adjacent error correction cycles to minimize the total number of operations per qubit. We observe an exponentially decaying randomized benchmarking fidelity, with the sequence, including transversal Clifford gates, decaying slightly faster than the reference idling experiment (Fig. 3e). We extract an average logical Clifford gate error εC, which quantifies the additional error introduced by the logical Clifford gate in each cycle. Using the neural-network decoder, we obtain εC = 0.0027(3). This is significantly lower than the logical error per cycle, \({\overline{\varepsilon }}_{3}=0.0171(3)\), underscoring the efficiency of implementing transversal single-qubit gates.

Magic state injection

Despite their efficient implementation, transversal gates cannot form a universal gate set52 required for arbitrary error-corrected quantum computation. For the colour code, extending the transversal gate set with a non-Clifford single-qubit T-gate (π/4 rotation around the z-axis) suffices to perform all single-qubit logical operations necessary for universal quantum computation. This gate can be implemented by preparing a high-fidelity resource magic state21 on an auxiliary logical qubit and consuming it in a gate teleportation protocol4,21. Preparing the high-fidelity magic state consists of two steps: first, injecting a magic state prepared on a physical qubit into a logical qubit, and second, distilling very high-fidelity magic states from an ensemble of faulty ones through magic state distillation21. Here, we focus on the state injection step.

We begin by preparing an arbitrary state |ψ⟩ on a single data qubit using Y- and Z-rotations, parameterized by the polar angle θ and azimuthal angle ϕ, respectively. We then grow into a distance-3 colour code by initializing the new data qubits pairwise into Bell states (Fig. 4a, purple ellipses), ensuring the X and Z operators of the injection qubit (indicated with a black arrow) deterministically extend to \({X}_{{\rm{L}}}\) and \({Z}_{{\rm{L}}}\) (ref. 39). Executing a single cycle of error correction thereafter projects the distance-3 colour code into |ψL⟩ (see Fig. 4b for a simplified circuit diagram and Supplementary Information section G for details). Because the protocol is applicable to arbitrary states and starts with a single physical qubit, an error on the injection data qubit cannot be detected. However, it has been shown to achieve lower error rates than other injection protocols for CSS codes39.

Fig. 4: Arbitrary state injection in a distance-3 colour code.
figure 4

a, Schematic of a distance-3 colour code. The arbitrary state |ψ⟩ is prepared on the data qubit indicated by a black arrow. The black line indicates the logical operators of the colour code, and the purple ellipses indicate Bell pairs, see the main text. b, Simplified circuit diagram for the state injection. Each line corresponds to one of the data qubits, on which we apply single-qubit Y- and Z-rotations (yellow boxes), Bell pair preparation circuits (purple boxes), a QEC cycle and a measurement in the X, Y or Z basis (MXYZ) for logical state tomography. c, Decoded (semi-transparent circles) and post-selected (solid dots) expectation value of the logical Pauli operators XL (blue), YL (red) and ZL (green) when sweeping the polar angle θ. The solid lines correspond to ideal expectation values. d, Decoded (semi-transparent circles) and post-selected (solid dots) infidelities for the prepared logical state |ψL⟩. e, Magic state |mL⟩ infidelity as a function of rejected data fraction for |AL⟩ (green squares), |HL⟩ (blue diamonds) and |TL⟩ (red triangles), see the main text and Supplementary Information section G. The dashed lines serve as a guide to the eye, and the error bars indicate a 95% bootstrapped confidence interval. Each state is shown on the Bloch sphere by an arrow of the corresponding colour.

Full size image

We characterize the injection of arbitrary states by sweeping the polar angle θ from 0 to 2π while keeping ϕ = 0 and performing logical tomography, measuring the expectation values of XL, YL and ZL. As expected for a rotation around the y-axis of the logical Bloch sphere, \(\langle {Z}_{{\rm{L}}}\rangle \) and \(\langle {X}_{{\rm{L}}}\rangle \) oscillate with sinusoidal shapes, whereas \(\langle {Y}_{{\rm{L}}}\rangle \) remains close to zero (Fig. 4c). From the measured values, we compute the state infidelity across the sweep, obtaining an average infidelity of 0.039(3) using the Möbius decoder (Chromobius)47 and 0.009(4) when post-selecting for runs without detectable errors (keeping on average 74.8% of the runs) (Fig. 4d). Note that post-selection is acceptable in this context because state injection protocols can be repeated until a high-fidelity resource state is achieved with high confidence54.

We perform a similar analysis for the azimuthal angle sweep and then focus on preparing specific magic states (see Supplementary Information section G). We examine |AL⟩, |HL⟩ and |TL⟩, corresponding to the +1 eigenstate of the XL + YL, XL + ZL, and XL + YL + ZL, operators, respectively. We achieve post-selection infidelities of \(0.000{8}_{-3}^{+15}\), \(0.004{1}_{-38}^{+37}\) and \(0.008{6}_{-65}^{+67}\) with retained data fractions of 75.2%, 74.6% and 75.7%, respectively. Here, the uncertainty represents a 95% confidence interval calculated using bootstrapping. We also explore partial post-selection, balancing data rejection with infidelity (Fig. 4e). These high-fidelity magic states surpass the threshold required for magic state distillation21,55, exceed the fidelities previously achieved in superconducting circuits and are on par with the best state injection implementations on other platforms (Supplementary Information section G).

State teleportation using lattice surgery

Lattice surgery22,39,43,56 enables the efficient realization of multi-qubit fault-tolerant operations, such as the CNOT gate, with only nearest-neighbour interactions. It performs these operations using fault-tolerant measurements of multi-qubit logical Pauli operators, combined with conditional operations based on the measurement outcomes.

Here, we showcase the lattice surgery framework using an MXX parity measurement, which measures the two-qubit Pauli operator XL1XL2, along with a classical Pauli frame update to teleport16,57 a logical state, |ψL⟩, from one logical qubit (L1) to another (L2), represented schematically in Fig. 5a. The protocol consists of simultaneously initializing L1 in |ψL⟩ and L2 in |0L⟩, measuring MXX by merging the two logical qubits for three cycles, followed by splitting them for one cycle (see Fig. 5b for a space-time visualization of the code evolution and Fig. 5c–e for spatial cuts at the key stages). The parity outcome m1 is determined from the product of the X-basis stabilizers introduced during the merge (Fig. 5d, hatched tiles) and the Bell measurement of two additional data qubits that are also introduced during the merge to extend the boundary stabilizers. Finally, L1 is measured in the Z basis and logical state tomography is performed on L2 to reconstruct the teleported state density matrix. The parity measurement outcome m1 and Z basis measurement outcome m2 of L1 are used in post-processing to apply a conditional Pauli frame update \({Z}_{{\rm{L}}}^{{m}_{1}}{X}_{{\rm{L}}}^{{m}_{2}}\) to the state of L2, effectively completing the teleportation of the logical operators indicated in Fig. 5c (black line) from L1 to L2. Further details and circuit-level diagrams are provided in Supplementary Information section H.

Fig. 5: State teleportation in the colour code using lattice surgery.
figure 5

a, Simplified circuit diagram to teleport a state |ψL⟩ from logical qubit L1 to a logical qubit L2 using an XX-parity measurement (MXX) realized by lattice surgery, and Pauli frame updates conditioned on the measurement outcomes m1 and m2 performed in post-processing (dashed boxes). b, Space-time block diagram showing the MXX lattice surgery operation, with horizontal cuts displaying the evolution of the stabilizers as a function of the QEC cycles, as detailed in c–e. c–e, Representation of the active qubits (coloured) and stabilizers before (c) and after (d) the merge operation, and after the split operation (e). The hatched tiles indicate stabilizers in the X basis only, whereas filled tiles indicate both X and Z stabilizers with support on its vertices. The black line indicates the teleported logical operator from L1 to L2, after the Pauli frame update. f–i, Measured (colour), simulated (black wireframe) and ideal (dotted grey wireframe) expectation values of the Pauli logical operators of L2 after teleporting state |0L⟩, |1L⟩, |+L⟩ and |−L⟩, respectively. j, Measured (gold bars) and simulated (black wireframe) teleported state fidelity F of the four logical X and Z eigenstates.

Full size image

We experimentally realize the teleportation protocol for four input states (|0L⟩, |1L⟩, |+L⟩ and |−L⟩) and measure the expectation value of the logical Pauli operators XL, YL and ZL of the output state. For each state, only the expectation value in its corresponding eigenbasis (Z basis for |0L⟩ and |1L⟩, X basis for |+L⟩ and |−L⟩) shows a large deviation from zero after decoding (Fig. 5f–i). The decoded eigenvalues are in general agreement with the ideal expectations (dotted grey wireframe) and reasonably match Pauli noise simulations based on device benchmarks (black wireframe), except for \(\langle {Y}_{{\rm{L}}}\rangle \) in the X-basis states, which we discuss in Supplementary Information section H.3. Calculating fidelity with the ideal logical states yields fidelities between 86.5(1)% and 90.7(1)% when decoded with the neural-network decoder (Fig. 5j). These measurements enable us to bound the average fidelity of the single-qubit teleportation channel, \({\mathcal{T}}\), at \(\overline{F}({\mathcal{T}}\,)\ge 84.7(1) \% \) (see Supplementary Information section H for details).

Discussion and outlook

In this work, we demonstrate key building blocks of fault-tolerant quantum computation using the colour code on a superconducting processor. Combining improved device performance, compact syndrome extraction circuits, and new decoding strategies, we achieve clear error suppression with Λ3/5 = 1.56(4) when scaling the code from distance-3 to distance-5. We characterize transversal single-qubit logical Clifford gates using randomized benchmarking. Furthermore, we demonstrate high-fidelity magic state injection and successfully teleport logical Pauli states between distance-3 qubits using lattice surgery.

These results highlight that QEC with superconducting qubits has reached a pivotal stage at which the noise threshold may no longer be the main driver of code choice, and efficient logical operations are a crucial factor. At present, the surface code achieves better logical error suppression (on the same processor, \({\varLambda }_{3/5}^{{\rm{surface}}}=2.31(2)\); ref. 8), but simulations suggest that improving physical error rates by about a factor of four could render the colour code more qubit-efficient than the surface code (Supplementary Information section I). Importantly, the efficient transversal Clifford gates of the colour code and more flexible lattice surgery would simplify algorithm implementations43. Colour codes also underpin the most efficient methods to generate high-fidelity magic states41,42, which could be used alongside surface code computation58,59,60. Quantifying the practical impact of these advantages for large-scale algorithms requires detailed resource estimation studies.

The key goals for future research with colour codes include increasing device performance and size, improving decoding speed and accuracy, demonstrating logical gate error suppression with growing code size, and characterizing more of the unique abilities of the colour code for logical gates. As hardware continues to improve, other quantum-error-correcting codes may also become available for practical implementation. Together, we expect these developments to accelerate progress towards scalable and resource-efficient fault-tolerant quantum computation.