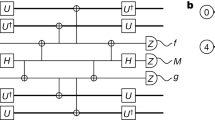
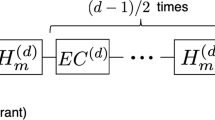
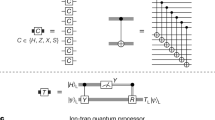
Abstract
Realizing universal fault-tolerant quantum computation is a key goal in quantum information science1,2,3,4. By encoding quantum information into logical qubits using quantum error correcting codes, physical errors can be detected and corrected, enabling a substantial reduction in logical error rates5,6,7,8,9,10,11. However, the set of logical operations that can be easily implemented on these encoded qubits is often constrained1,12, necessitating the use of special resource states known as ‘magic states’13 to implement universal, classically hard circuits14. A key method to prepare high-fidelity magic states is to perform ‘distillation’, creating them from multiple lower-fidelity inputs13,15. Here we present the experimental realization of magic state distillation with logical qubits on a neutral-atom quantum computer. Our approach uses a dynamically reconfigurable architecture8,16 to encode and perform quantum operations on many logical qubits in parallel. We demonstrate the distillation of magic states encoded in d = 3 and d = 5 colour codes, observing improvements in the logical fidelity of the output magic states compared with the input logical magic states. These experiments demonstrate a key building block of universal fault-tolerant quantum computation and represent an important step towards large-scale logical quantum processors.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
Peer reviewer reports are available. All data supporting the findings of this study are available from Zenodo at https://doi.org/10.1038/s41586-025-09367-3 (ref. 75).
References
Shor, P. W. Fault-tolerant quantum computation. In Proc. 37th IEEE Symposium on the Foundations of Computer Science 56–65 (IEEE, 1996).
Aharonov, D. & Ben-Or, M. Fault-tolerant quantum computation with constant error rate. SIAM J. Comput. 38, 1207–1282 (2008).
Gottesman, D. An introduction to quantum error correction and fault-tolerant quantum computation. Preprint at https://doi.org/10.48550/arXiv.0904.2557 (2010).
Campbell, E. T., Terhal, B. M., & Vuillot, C. Roads towards fault-tolerant universal quantum computation. Nature 549, 172–179 (2017).
Google Quantum AI and Collaborators. Quantum error correction below the surface code threshold. Nature 638, 920–926 (2025).
Google Quantum AI. Suppressing quantum errors by scaling a surface code logical qubit. Nature 614, 676–681 (2023).
Ryan-Anderson, C. et al. Implementing fault-tolerant entangling gates on the five-qubit code and the color code. Preprint at https://doi.org/10.48550/arXiv.2208.01863 (2022).
Bluvstein, D. et al. Logical quantum processor based on reconfigurable atom arrays. Nature 626, 58–65 (2024).
Putterman, H. et al. Hardware-efficient quantum error correction using concatenated bosonic qubits. Nature 638, 927–934 (2025)
Sivak, V. V. et al. Real-time quantum error correction beyond break-even. Nature 616, 50–55 (2023).
Paetznick, A. et al. Demonstration of logical qubits and repeated error correction with better-than-physical error rates. Preprint at https://doi.org/10.48550/arXiv.2404.02280 (2024).
Eastin, B. & Knill, E. Restrictions on transversal encoded quantum Gate Sets. Phys. Rev. Lett. 102, 110502 (2009).
Bravyi, S. & Kitaev, A. Universal quantum computation with ideal Clifford gates and noisy ancillas. Phys. Rev. A 71, 022316 (2005).
Gottesman, D. The Heisenberg representation of quantum computers. In Proc. XXII International Colloquium on Group Theoretical Methods in Physics (eds Corney, S. P. et al.) 32–43 (International Press, 1999)
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge Univ. Press, 2010).
Bluvstein, D. et al. A quantum processor based on coherent transport of entangled atom arrays. Nature 604, 451–456 (2022).
Bravyi, S. & Koenig, R. Classification of topologically protected gates for local stabilizer codes. Phys. Rev. Lett. 110, 170503 (2012).
Fowler, A. G., Mariantoni, M., Martinis, J. M. & Cleland, A. N. Surface codes: towards practical large-scale quantum computation. Phys. Rev. A 86, 032324 (2012).
Bombin, H. & Martin-Delgado, M. A. Topological quantum distillation. Phys. Rev. Lett. 97, 180501 (2006).
Litinski, D. Magic state distillation: not as costly as you think. Quantum 3, 205 (2019).
Gidney, C. & Fowler, A. G. Efficient magic state factories with a catalyzed |CCZ⟩ to 2|T⟩ transformation. Quantum 3, 135 (2019).
O’Gorman, J. & Campbell, E. T. Quantum computation with realistic magic-state factories. Phys. Rev. A 95, 032338 (2017).
Souza, A. M., Zhang, J., Ryan, C. A. & Laflamme, R. Experimental magic state distillation for fault-tolerant quantum computing. Nat. Commun. 2, 169 (2011).
Brown, N. C. et al. Advances in compilation for quantum hardware — a demonstration of magic state distillation and repeat-until-success protocols. Preprint at https://doi.org/10.48550/arXiv.2310.12106 (2023).
Postler, L. et al. Demonstration of fault-tolerant universal quantum gate operations. Nature 605, 675–680 (2022).
Ye, Y. et al. Logical magic state preparation with fidelity beyond the distillation threshold on a superconducting quantum processor. Phys. Rev. Lett. 131, 210603 (2023).
Gupta, R. S. et al. Encoding a magic state with beyond break-even fidelity. Nature 625, 259–263 (2024).
Chamberland, C. & Cross, A. W. Fault-tolerant magic state preparation with flag qubits. Quantum 3, 143 (2019).
Gidney, C., Shutty, N. & Jones, C. Magic state cultivation: growing T states as cheap as CNOT gates. Preprint at https://doi.org/10.48550/arXiv.2409.17595 (2024).
Daguerre, L. & Kim, I. H. Code switching revisited: low-overhead magic state preparation using color codes. Phys. Rev. Research 7, 023080 (2025).
Cain, M. et al. Correlated decoding of logical algorithms with transversal gates. Phys. Rev. Lett. 133, 240602 (2024).
Chao, R. & Reichardt, B. W. Fault-tolerant quantum computation with few qubits. npj Quantum Inf. 4, 42 (2018).
Kim, Y., Sevior, M. & Usman, M. Magic state injection on IBM quantum processors above the distillation threshold. Preprint at https://doi.org/10.48550/arXiv.2412.01446 (2024).
Laflamme, R., Miquel, C., Paz, J. P. & Zurek, W. H. Perfect quantum error correcting code. Phys. Rev. Lett. 77, 198–201 (1996).
Smith, S. C., Brown, B. J. & Bartlett, S. D. Mitigating errors in logical qubits. Commun. Phys. 7, 386 (2024).
Bombín, H., Pant, M., Roberts, S. & Seetharam, K. I. Fault-tolerant post-selection for low overhead magic state preparation. PRX Quantum 5, 010302 (2024).
Chao, R. & Reichardt, B. W. Quantum error correction with only two extra qubits. Phys. Rev. Lett. 121, 050502 (2018).
Ryan-Anderson, C. et al. Realization of real-time fault-tolerant quantum error correction. Phys. Rev. X 11, 041058 (2021).
Graham, T. M. et al. Midcircuit measurements on a single-species neutral alkali atom quantum processor. Phys. Rev. X 13, 041051 (2023).
Deist, E. et al. Mid-circuit cavity measurement in a neutral atom array. Phys. Rev. Lett. 129, 203602 (2022).
Singh, K. et al. Mid-circuit correction of correlated phase errors using an array of spectator qubits. Science 380, 1265–1269 (2023).
Lis, J. W. et al. Midcircuit operations using the omg architecture in neutral atom arrays. Phys. Rev. X 13, 041035 (2023).
Norcia, M. A. et al. Midcircuit qubit measurement and rearrangement in a 171Yb atomic array. Phys. Rev. X 13, 041034 (2023).
Bombín, H. Gauge color codes: optimal transversal gates and gauge fixing in topological stabilizer codes. New J. Phys. 17, 083002 (2015).
Kubica, A., Yoshida, B. & Pastawski, F. Unfolding the color code. New J. Phys. 17, 083026 (2015).
Chamberland, C. & Noh, K. Very low overhead fault-tolerant magic state preparation using redundant ancilla encoding and flag qubits. npj Quantum Inf. 6, 91 (2020).
Hirano, Y., Itogawa, T. & Fujii, K. Leveraging zero-level distillation to generate high-fidelity magic states. In IEEE International Conference on Quantum Computing and Engineering 843–853 (IEEE, 2024).
Itogawa, T., Takada, Y., Hirano, Y. & Fujii, K. Even more efficient magic state distillation by zero-level distillation. PRX Quantum 6, 020356 (2025).
Jones, C. Multilevel distillation of magic states for quantum computing. Phys. Rev. A 87, 042305 (2013).
Barredo, D., de Léséleuc, S., Lahaye, T. & Browaeys, A. An atom-by-atom assembler of defect-free arbitrary two-dimensional atomic arrays. Science 354, 1021–1023 (2016).
Endres, M. et al. Atom-by-atom assembly of defect-free one-dimensional cold atom arrays. Science 354, 1024–1027 (2016).
Kim, H. et al. In situ single-atom array synthesis using dynamic holographic optical tweezers. Nat. Commun. 7, 13317 (2016).
Ebadi, S. et al. Quantum phases of matter on a 256-atom programmable quantum simulator. Nature 595, 227–232 (2021).
Levine, H. et al. Dispersive optical systems for scalable Raman driving of hyperfine qubits. Phys. Rev. A 105, 032618 (2022).
Levine, H. et al. Parallel implementation of high-fidelity multiqubit gates with neutral atoms. Phys. Rev. Lett. 123, 170503 (2019).
Evered, S. J. et al. High-fidelity parallel entangling gates on a neutral-atom quantum computer. Nature 622, 268–272 (2023).
Ma, S. et al. High-fidelity gates and mid-circuit erasure conversion in an atomic qubit. Nature 622, 279–284 (2023).
Jandura, S. & Pupillo, G. Time-optimal two- and three-qubit gates for Rydberg atoms. Quantum 6, 712 (2022).
Scholl, P. et al. Erasure conversion in a high-fidelity Rydberg quantum simulator. Nature 622, 273–278 (2023).
Emerson, J. et al. Scalable noise estimation with random unitary operators. J Opt. B Quantum Semiclassical Opt. 7, S347 (2005).
Goto, H. Minimizing resource overheads for fault-tolerant preparation of encoded states of the Steane code. Sci. Rep. 6, 19578 (2016).
Mayer, K. et al. Benchmarking logical three-qubit quantum Fourier transform encoded in the Steane code on a trapped-ion quantum computer. Preprint at https://doi.org/10.48550/arXiv.2404.08616 (2024).
Gottesman, D. E. Stabilizer Codes and Quantum Error Correction. PhD thesis, California Institute of Technology (1997).
Cleve, R. & Gottesman, D. Efficient computations of encodings for quantum error correction. Physical Review A 56, 76–82 (1997).
Gidney, C. Stim: a fast stabilizer circuit simulator. Quantum 5, 497 (2021).
Bravyi, S. et al. Simulation of quantum circuits by low-rank stabilizer decompositions. Quantum 3, 181 (2019).
Javadi-Abhari, A. et al. Quantum computing with Qiskit. Preprint at https://doi.org/10.48550/arXiv.2405.08810 (2024).
Granade, C., Ferrie, C., & Flammia, S. T. Practical adaptive quantum tomography. New J. Phys. 19, 113017 (2017).
Rice, J. A. Mathematical Statistics and Data Analysis, 3rd edn, Vol. 371 (Thomson Brooks/Cole, 2007).
Schmied, R. Quantum state tomography of a single qubit: comparison of methods. J. Mod. Optics 63, 1744–1758 (2016).
Gurobi Optimization. Gurobi Optimizer Reference Manual (Gurobi Optimization, 2024).
Landahl, A. J., Anderson, J. T. & Rice, P. R. Fault-tolerant quantum computing with color codes. Preprint at https://doi.org/10.48550/arXiv.1108.5738 (2011).
Meister, N., Pattison, C. A. & Preskill, J. Efficient soft-output decoders for the surface code. Preprint at https://doi.org/10.48550/arXiv.2405.07433 (2024).
Gidney, C., Newman, M., Brooks, P. & Jones, C. Yoked surface codes. Nat. Commun. 16, 4498 (2025).
QuEra Computing and collaborators. Data for “Experimental demonstration of logical magic state distillation”. Zenodo https://doi.org/10.1038/s41586-025-09367-3 (2025).
Acknowledgements
We acknowledge the discussions with L. Jiang, M. Kang, G. Masella, C. Pattison, A. Piñeiro Orioli, Q. Xu and M. Yuan and technical contributions from I. Paus, C. Skinker and Q. Yu. This work, including the design, assembly and operation of the Gemini-class neutral-atom quantum computer, was supported by QuEra Computing. Pathfinding work at Harvard and MIT was supported by IARPA and the Army Research Office, under the Entangled Logical Qubits program (cooperative agreement no. W911NF-23-2-0219), the DARPA ONISQ program (W911NF2010021), the DARPA MeasQuIT program (HR0011-24-9-0359), the Center for Ultracold Atoms (an NSF Physics Frontiers Center, PHY-1734011), the National Science Foundation (grant no. PHY-2012023 and grant no. CCF-2313084), the Army Research Office MURI (grant no. W911NF-20-1-0082) and QuEra Computing. Z.H. acknowledges support from the NSF Graduate Research Fellowship Program (grant no. 2141064). D.B. acknowledges support from the NSF Graduate Research Fellowship Program (grant no. DGE1745303) and The Fannie and John Hertz Foundation. S.J.E. acknowledges support from the National Defense Science and Engineering Graduate (NDSEG) fellowship. T. Manovitz acknowledges support from the Harvard Quantum Initiative Postdoctoral Fellowship in Science and Engineering. M.C. acknowledges support from the Department of Energy Computational Science Graduate Fellowship (award no. DE-SC0020347).
Author information
Authors and Affiliations
Contributions
The QuEra Computing staff designed, built and ran the experiment and performed data analysis. P.S.R., J.M.R., P.N.J., Z.H., C.D., C.Z., K.-H.W., J.C., K.B., M. Kwon, T. Karolyshyn, P.W., M.C., S.J.E., A.A.G., M. Kalinowski, S.H.L., T. Manovitz, J.A.-G., J.I.B., L.B., B.B., A.B., A.C., R.J.D., F.F., C.F., P.F., D.H., M. Hamdan, J.H., N.H., M.-G.H., F.H., N.J., D.K., M. Kornjač, F.L., J. Long, J. Lopatin, P.L.S.L., X.-Z.L., T. Macrì, O.M., L.A.M.-M., X.M., S.O., E.O., D.P., Z.Q., V.S., A.S., M.S., N.S., H.T., N.W., Y.W., D.W.-L., T.W., J.W., A.Z., L.Z., M.G., A.K., N.G., V.V., T. Kitagawa, S.-T.W., D.B., M.D.L., A.L., H.Z. and S.H.C. discussed the results, revised and contributed to the writing of this paper.
Corresponding authors
Ethics declarations
Competing interests
M.G., V.V. and M.D.L. are co-founders and shareholders of QuEra Computing. Authors affiliated with QuEra Computing are employees or interns at QuEra Computing at the time of their contributions.
Peer review
Peer review information
Nature thanks Michael Vasmer and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Experimental layout of magic state distillation factory.
a, We arrange 7 to 17 87Rb atoms, each corresponding to a physical qubit, into a row. This horizontal register represents a logical qubit, tiled into 5 rows for a total of five logical qubits (LQ1 to LQ5). b, Encoding. Once the register of physical qubits is prepared, we coherently rearrange atoms to perform two-qubit entangling gates using the Rydberg blockade mechanism. We break up the circuit into “layers” each containing one set of local rotations, transport, and CZ gates. c, Coherent movement of logical qubits to perform transversal CZ gates. In the case of 5-to-1 distillation, this is achieved in three layers. The circuit as drawn here corresponds 1 to 1 to the atom layout, whereas in Fig. 3 logical qubits LQ1 and LQ2 are swapped for clarity. d, Global measurement of qubits after circuit execution.
Extended Data Fig. 2 Experimental layout of d = 5 encoding.
The arbitrary-state encoding circuit for the d = 5 color code (left) is comprised of five entangling gate layers, illustrated by averaged images of the corresponding atom configurations (right), and local gates between the layers. We execute encoding with 5x parallelism, one instance per row (LQ1 to LQ5). The horizontal AOD trap array is tiled vertically by the second AOD. For each layer, atoms start in SLM sites, we apply local rotations, pick up and move atoms to their gate location, execute parallel CZ gates, echo (omitted for clarity), and finally move back to SLM sites.
Extended Data Fig. 3 Encoded magic state fidelity and stabilizers.
a, Spatial dependence of distance-3 magic state encoding fidelity, for the experimental run with no added coherent error. Logical qubits numbered 1-5 and 6-10 are the input qubits to two parallel distillation circuits. We observe some spatial dependence on both the fidelity and perfect stabilizer rate, which we attribute to local single-qubit gate inhomogeneity and two-qubit gate inhomogeneity. b, Time dependence of distance-3 color code stabilizers, for the experimental run with no added coherent error. Time traces are averaged with window size of 100. c,d, Same as a and b for distance-5.
Extended Data Fig. 4 Additional decoding results.
a, Simulated injected and distilled magic state fidelities as a function of global rescaling of physical error rates, when no stabilizer postselection is applied. Relative to our error model for decoding, the physical error rates have been further increased by 1.25 × to match the experimental injected and distilled fidelities. b, Simulation and experimental data in table format for d = 3, sorted into bins corresponding to 3 × 5 = 15 stabilizers and 5 logical observables, for a total of 220 bins. We see good agreement between simulation and experiment. c, Sliding-scale postselection of experimental distillation fidelity with added input errors. Fidelity of the output magic state (blue line) as a function of the total accepted fraction. The accepted fraction range decreases with added errors due to the factory acceptance rate decreasing. Horizontal line segments indicate the error corrected fidelity of the factory input states (green). Shaded regions indicate 68% confidence intervals.
Extended Data Fig. 5 Comparison of different fidelity estimation methods for d = 5 distillation.
For low accepted fractions, the small number of samples causes the maximum likelihood estimate (red, allowed to exceed 1 here) and Bayesian estimates (blue) to differ noticeably, since the latter will be influenced by the prior. In our figures in the main text, we therefore focus on the region in which the two methods give consistent estimates. Horizontal line indicates the error corrected fidelity of the factory input states (green). Shaded regions indicate 68% confidence intervals.
Supplementary information
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Sales Rodriguez, P., Robinson, J.M., Jepsen, P.N. et al. Experimental demonstration of logical magic state distillation. Nature 645, 620–625 (2025). https://doi.org/10.1038/s41586-025-09367-3
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/s41586-025-09367-3