Main

Quantum correlations and entanglement are now actively explored to improve precision measurements in a variety of quantum systems. For example, in so-called spin squeezed states9,13, quantum correlations are generated to reduce (squeeze) the quantum projection noise along a certain quadrature of the collective spin, thereby improving the precision of measurements along that quadrature. Recently, spin squeezing has been realized in several experimental platforms, including cavity-QED systems14,15, Rydberg atoms16,17,18, trapped ions19, Bose–Einstein condensates20, superconducting qubits21 and atomic vapour cells22, with broad applications, including atomic clocks14,18, magnetometry20,22 and matter-wave interferometry15. Although these approaches can be effective in systems with a high degree of isolation and control, an alternative strategy—signal amplification12,23—focuses on using many-body dynamics for amplifying the measured signal, rather than reducing quantum noise (Fig. 1a). While complementary to spin squeezing, the key feature of this approach is the improved robustness against technical noise during readout, which makes it applicable to a much broader class of quantum systems that do not naturally support high-fidelity quantum limited measurements under ambient conditions24.

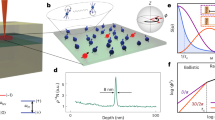
Fig. 1: Engineering uniform-signed twisting interactions.
figure 1

a, Concept of signal amplification. Different sensing signals lead to different states on the Bloch sphere, and the distance between them can be amplified under many-body interaction, resulting in enhanced sensitivity. The finite extent of the states represents technical noises during readout. The exact protocol with which we achieve signal amplification is shown in Fig. 4a. b, Schematic of the experimental system. The transparent box represents the diamond sample, with interacting NV centres confined in a 2D plane within it. An external field (blue arrow) is used to change the quantization axis from the native axis (ηnative, black) to the normal vector of the plane (ηeff, purple). Furthermore, a pulsed field (red, generated by the two wires below the diamond) is turned on during the initialization and readout, leading to a total field along the NV axis, which is required for high-quality initialization and readout. c, Angular dependence of the Ising part (green) and exchange part (yellow) of the dipolar interaction for the native quantization axis. The colour in the inset indicates the sign of AZZ − AXY, which controls the OAT dynamics (see the main text). d, Same as c, but for the engineered quantization axis ηeff. The residual angular dependence is a consequence of the spin-1 nature of NV centres.

Full size image

Here we develop and demonstrate a method for signal amplification in a two-dimensional (2D) ensemble of electronic spins associated with nitrogen–vacancy (NV) centres in diamond at room temperature. Featuring long coherence times and well-developed quantum control techniques, such a system has recently emerged as a promising platform for micro- and nanoscale magnetic sensing applications1,2,3,4,5,6,7. Despite the many applications of these solid-state quantum sensors, signal amplification has not yet been realized in these systems because of the short-ranged, anisotropic nature of the dipolar interaction and the faster decoherence compared with atomic platforms that are better isolated. Our approach overcomes these challenges through a combination of dynamical control of the quantization axis to ameliorate the dipolar anisotropy and Floquet engineering of two-axis-twisting (TAT)9 dynamics that exhibit fast amplification. Combining these techniques with time-reversed dynamics, we demonstrate a signal amplification of 6.7(6)%. In contrast to previous approaches involving a symmetric time-reversed echo25,26, we observe that the optimal amplification occurs under an asymmetric echo, in which the backward evolution time equals twice the forward evolution time. We show that these observations can be understood as resulting from the time-reversed mirror symmetry of the underlying Hamiltonian, which yields a generic, robust mechanism for quantum enhancement in precision measurements. These results provide opportunities for new applications involving entanglement-enhanced sensing in the solid state under ambient conditions.

Many-body spin sensors in diamond

Our experiments use a high-density, dipolar-interacting ensemble of electronic spins associated with NV centres in diamond. To enhance metrological sensitivity through interactions, a common approach is to evolve the system under one-axis-twisting (OAT) or TAT Hamiltonians9. A unique challenge for dipolar interactions is their anisotropic nature, which causes spin pairs separated along and perpendicular to their quantization axis to interact with opposite signs (that is, ferromagnetic compared with anti-ferromagnetic coupling). This leads to net zero twisting when averaging over all orientations of spin pairs in three-dimensional spin ensembles. To overcome the dipolar anisotropy, we confine the NV centres to a 2D plane, achieved by nitrogen δ-doping27,28 during diamond chemical vapour deposition (CVD) growth (see Methods for details). The resulting sample consists of a positionally disordered NV ensemble distributed within a 9-nm-thick (full-width at half-maximum; FWHM) layer, which is thinner than the typical NV–NV spacing (about 17 nm), so that the geometry is approximately 2D.

The dipolar anisotropy can be mitigated if the quantization axis of the NV centres is perpendicular to the 2D plane, corresponding to (111) crystal axis orientation, as the separation of spin pairs would be predominantly perpendicular to the quantization axis. While fabrication techniques for growing such (111)-oriented samples are under active development29, here we subject a (100)-oriented diamond to a strong (about 890 G, chosen to maximize the qubit frequency within technical constraints) magnetic field Bext (Fig. 1b, blue vector), changing the quantization axis from the native orientation (ηnative, black) to the plane normal (ηeff, purple). This configuration is motivated by the observation that the native quantization axis, tilted at 55° from the plane normal, results in a mixed-signed and net zero dipolar interaction when averaged over the 2D plane (Fig. 1c). Although the engineered quantization axis (ηeff) overcomes such problem (Fig. 1d), the off-axis (that is, not along the native NV axis) component of Bext mixes the m = 0 and m = ±1 NV spin states, and thus disrupts the native initialization and readout mechanisms of NV30,31. Therefore, during initialization and readout, we cancel this off-axis field by turning on an auxiliary pulsed B field (Fig. 1b, red), which is adiabatically switched off in the middle to evolve the system under the twisting dynamics associated with the quantization axis ηeff. With the pulsed field, we improve the initial spin polarization by a factor of 4 (Extended Data Fig. 1d), which yields a 4,000-fold improvement in data averaging speed (Supplementary Information).

Engineering OAT and TAT dynamics

To explain how OAT dynamics emerge from dipolar interactions, we decompose the XXZ Hamiltonian— derived from the secular approximation32 (Supplementary Information)—into a Heisenberg term and a twisting term

$${\widehat{H}}_{{\rm{XXZ}}}=\sum _{i < j}[\,{J}_{ij}^{{\rm{Heis}}}{\widehat{{\boldsymbol{\sigma }}}}_{i}\cdot {\widehat{{\boldsymbol{\sigma }}}}_{j}+{J}_{ij}^{{\rm{Twist}}}{\widehat{\sigma }}_{i}^{z}{\widehat{\sigma }}_{j}^{z}],$$
(1)

where i, j index the spins (omitted from now on for simplicity), \({\widehat{\sigma }}_{i}^{x,y,z}\) are the Pauli operators defined on the m = 0, −1 electronic ground states of NV centres, and \({J}_{ij}^{{\rm{H}}{\rm{e}}{\rm{i}}{\rm{s}}}\,\equiv {A}_{\eta }^{XY}({\hat{r}}_{ij})/{r}_{ij}^{3}\), \({J}_{ij}^{{\rm{T}}{\rm{w}}{\rm{i}}{\rm{s}}{\rm{t}}}\,\equiv ({A}_{\eta }^{ZZ}({\hat{r}}_{ij})-{A}_{\eta }^{XY}({\hat{r}}_{ij}))/{r}_{ij}^{3}\) are defined with \({A}_{\eta }^{XY}\), \({A}_{\eta }^{ZZ}\) being the coefficients of the exchange and Ising parts of the dipolar coupling (Fig. 1c,d; see Supplementary Information for calculations). In this decomposition, the Heisenberg term does not affect the early-time dynamics of a spin-polarized initial state (which is an eigenstate of it), and the second term is a short-ranged OAT Hamiltonian. Therefore, as long as (AZZ − AXY) does not average to zero—as is the case for the interaction in Fig. 1d—twisting dynamics can be obtained following an average over all spin pairs.

To observe the OAT dynamics experimentally, we further suppress the on-site disorder with an XY8 pulse sequence33 and measure the dynamics of a series of initial states polarized in the Y–Z plane (Fig. 2a). Here we see that initial states prepared in the upper hemisphere rotate anticlockwise, whereas the initial states in the lower hemisphere rotate clockwise, consistent with the OAT dynamics. To further quantify the amount of twisting, the twisting signal, defined as the X polarization generated by the twisting dynamics, is measured on the same set of initial states (Fig. 2b). To be robust against systematic global rotations originating from pulse errors (Methods and Extended Data Fig. 8), the signal is averaged over pairs of antipodal states (\(\widehat{\rho }\) and \({\widehat{\rho }}_{{\rm{i}}{\rm{n}}{\rm{v}}}\) in Fig. 2a). As expected, the data show a Z-dependent twisting rate at early times, until eventually decaying after the interaction limited T2 (about 5 μs). To gain further evidence that the observed dynamics originate from dipolar interactions, we perform the same measurement at the native quantization axis ηnative (Fig. 2b, inset), in which no twisting dynamics are expected because of the dipolar anisotropy. The sharp contrast between them unambiguously rules out any alternative explanations based on systematic imperfections in the experiment.

Fig. 2: OAT dynamics.
figure 2

a, Measured polarization dynamics of a series of initial states (left) in the Y–Z plane after 2.7 μs evolution (right). The red circles represent the initial states on the front side, and the blue circles represent the initial states on the back side of the Bloch sphere. b, Twisting signal (in units of Bloch sphere radius) for the initial states in a with varying tilting angles from the equator to Z-axis. The signal is averaged between antipodal pairs on the Bloch sphere (\(\widehat{\rho }\) and \({\hat{\rho }}_{{\rm{i}}{\rm{n}}{\rm{v}}}\) in a) to cancel the effects from global rotations originating from pulse errors (Methods). The curves are predictions from our most realistic model of the system (Methods). Inset, same experiment with native quantization axis. Errors represent 1 s.d. accounting statistical uncertainties.

Full size image

The resulting OAT dynamics can, in principle, be used for signal amplification in sensing experiments. This is quantified by the distance

$$D\equiv \sqrt{{(\Delta X)}^{2}+{(\Delta Y)}^{2}+{(\Delta Z)}^{2}}$$
(2)

between two states that experienced opposite sensing rotations ±δθ (Fig. 1a), where ΔX, ΔY and ΔZ are defined as the difference of the spin polarization between these two states. Under OAT dynamics, this distance is amplified for a pair of states initially separated along the Z-direction (Fig. 1a), as a non-zero ΔX is generated during the dynamics, whereas the initial ΔZ is conserved. However, for the relatively weak twisting observed (Fig. 2b), the amplification will be very small, as the increase of D is second-order in ΔX. This small amplification can be easily overwhelmed by imperfect Z conservation coming from finite T1 relaxation time and other imperfections. Therefore, dynamics that exhibit first-order amplification, such as TAT dynamics (see the flow diagram in Fig. 3b, inset), are more desirable.

Fig. 3: TAT dynamics.
figure 3

a, Measured polarization dynamics of a series of states that initially reside on two circles around ±Y-axis (left), after evolving for 4.3 μs under the TAT dynamics (right). Red (blue) circles represent initial states on the front (back) side of the Bloch sphere. The Floquet pulse sequence used to engineer the TAT Hamiltonian is plotted on the bottom, with upward blue rectangles representing pulses along +X-axis and downward red rectangles representing pulses along −Y-axis. b, Measured distance (in units of Bloch sphere radius) between the initial state pairs with corresponding colours in the left inset, as a function of time evolved under the TAT dynamics. The initial states are tilted by 15° away from the ±Y-axis, leading to the initial distance 2sin(15°) ≈ 0.52. The curves are predictions from our most realistic model of the system (Methods). Insets, Bloch sphere representation of the local semi-classical flow under the TAT dynamics, and the same experiment with native quantization axis. Errors represent 1 s.d. accounting statistical uncertainties.

Full size image

The dipolar TAT Hamiltonian

$${\widehat{H}}_{{\rm{TAT}}}={J}^{{{\rm{Heis}}}^{{\prime} }}\widehat{{\boldsymbol{\sigma }}}\cdot \widehat{{\boldsymbol{\sigma }}}+\lambda {J}^{{\rm{Twist}}}({\widehat{\sigma }}^{z}{\widehat{\sigma }}^{z}-{\widehat{\sigma }}^{x}{\widehat{\sigma }}^{x})$$
(3)

can be engineered from the OAT Hamiltonian (equation (1)) by Floquet engineering34,35. Motivated by the requirement to break the U(1) symmetry and the good decoupling properties of XY16 sequence33, we designed a pulse sequence in which every π-pulse along the X-direction is replaced by a 3π-pulse (Fig. 3a, bottom), which explicitly breaks the symmetry between X-pulses and Y-pulses, while preserving the structures responsible for good decoupling properties. The exact TAT Hamiltonian, with \({J}^{{{\rm{Heis}}}^{{\prime} }}\equiv \,{J}^{{\rm{Heis}}}+\frac{1}{3}{J}^{{\rm{Twist}}}\) and λ = 2/9, is then achieved by choosing appropriate values for the pulse durations and spacings (Methods).

To confirm the engineering of TAT dynamics, we prepare a series of initial states residing on two circles around the ±Y-axis of the Bloch sphere, and measure their dynamics after a 4.3-μs evolution (Fig. 3a). These states, which initially form two circles, deform into two ellipses with perpendicular major axes, consistent with the predicted semi-classical flow (that is, mean-field spin dynamics under the corresponding classical Hamiltonian, Fig. 3b, left inset). Motivated by the goal of signal amplification, we further prepare initial states tilted by 15° from the ±Y-axis into the local amplifying and deamplifying directions (that is, X ± Z), shown as the coloured dots in Fig. 3b (left inset). We then measure the distance (equation (2)) between the two states in each pair with the same colour, as a function of evolution time. As shown in Fig. 3b (left inset), the distances of the yellow and red pairs are expected to amplify, whereas the distances of the purple and blue pairs are expected to deamplify. In Fig. 3b, this shows up as a clear separation between the distances of the amplifying pairs and the distances of the deamplifying pairs, in sharp contrast to the no-separation case observed at the native quantization axis (right inset). The data show good agreement with theory, and 3.4(8)% early-time amplification.

Enhancing amplification through time-reversed echo

To further enhance signal amplification, we note that the effects of interactions in the TAT Hamiltonian are twofold: First, the mean-field TAT flow (Fig. 3b, left inset) leads to an increase of the distance (of the amplifying pairs). Second, the short-ranged nature of the dipolar interaction and the associated lack of total spin conservation also lead to a rapid decay of the Bloch vector length36,37, and thus a decrease of the distance. Motivated by the competition between these two mechanisms, we next investigate whether a time-reversed echo protocol could improve the amplification, as the decay can be (partially) reversed.

Specifically, we use the echo protocol shown in Fig. 4a, in which a sensing rotation towards the local amplifying direction (simulated by explicit microwave driving) is sandwiched between a pair of forward and backward evolutions under the TAT Hamiltonian, engineered through Floquet sequences. Although these echo protocols are typically implemented with equal duration of forward (t+) and backward (t−) evolutions12,25,26, we explore more general asymmetric echoes, where t+ and t− are swept independently. To realize the time-reversed dynamics, we used a π/2-pulse to switch \({\widehat{\sigma }}^{x}\) and \({\widehat{\sigma }}^{z}\). Although the Heisenberg term \(\widehat{{\boldsymbol{\sigma }}}\cdot \widehat{{\boldsymbol{\sigma }}}\) cannot be reversed, it has a trivial effect on early-time dynamics for spin-polarized initial states.

Fig. 4: Time-reversed echo experiments.
figure 4

a, The protocol of time-reversed echo, in which a sensing rotation towards the local amplifying direction (purple pulse, simulated by explicit microwave driving) is sandwiched between forward (t+) and backward (t−) evolutions under the TAT Hamiltonian. The reversal is achieved by a π/2 pulse around the Y-axis, which switches \({\widehat{\sigma }}^{x}\) with \({\widehat{\sigma }}^{z}\) and thereby transforms the Hamiltonian from \(\widehat{{\boldsymbol{\sigma }}}\cdot \widehat{{\boldsymbol{\sigma }}}+\lambda ({\widehat{\sigma }}^{z}{\widehat{\sigma }}^{z}-{\widehat{\sigma }}^{x}{\widehat{\sigma }}^{x})\) to \(\widehat{{\boldsymbol{\sigma }}}\cdot \widehat{{\boldsymbol{\sigma }}}-\lambda ({\widehat{\sigma }}^{z}{\widehat{\sigma }}^{z}-{\widehat{\sigma }}^{x}{\widehat{\sigma }}^{x})\). b, Measurement of the Y revival under the time reversal, without the sensing step (δθ = 0). The black curve is the reference decay without time reversal, and each of the other curves corresponds to dynamics reversed at a different t+, indicated by the leftmost point on the curve (for example, for the brown curve, t+ = 4.3 μs, as indicated by the brown horizontal arrows). c, Signal amplification measurement (in units of Bloch sphere radius) sweeping both t+ and t−, with sensing angle δθ = 15°. Each curve represents a different t+, similar to b. The downward blue arrow indicates the point with maximum amplification, relative to the non-interacting reference at t+ = t− = 0. The distance is averaged between the two amplifying pairs (Fig. 3b). d, Data in c replotted to compare the amplification without echo (black), with symmetric echo (brown) and with asymmetric echo (green). e, Mirror reflection (\({\mathcal{R}}\)) of the TAT dynamics, which reverses the direction of semi-classical flow and exchanges the sensing (\(\widehat{S}\)) and measurement (\(\widehat{M}\)) operators, represented here by their Pauli basis decompositions. This mirror reflection, when combined with time reversal (not drawn), which restores the original flow direction, forms a fundamental symmetry of the system. The directions of \(\widehat{S}\) and \(\widehat{M}\) are chosen as their local amplifying directions (that is, the TAT flow leads to amplification for sensing rotation around \(\widehat{S}\) and projective measurement along \(\widehat{M}\)). f, The symmetry in e maps the sensing operator \(\widehat{S}({t}_{+})\) to \(\widehat{M}(-{t}_{+})\) and the measurement operator \(\widehat{M}({t}_{+}-{t}_{-})\) to \(\widehat{S}({t}_{-}-{t}_{+})\), transforming the original asymmetric echo (top) to an equivalent protocol (bottom) with a modified forward evolution time \({t}_{+}^{{\prime} }={t}_{-}-{t}_{+}\), ensuring equal amplitude of amplification between them. Errors in the figure represent 1 s.d. accounting statistical uncertainties.

Full size image

To verify the time-reversal protocol, we first measure the revival of the initial state polarized along the Y-axis following the time reversal, without the intermediate sensing step. As shown in Fig. 4b, the Y polarization decays under the TAT Hamiltonian during t+, and then revives at t− = t+, confirming the validity of our implementation. We then apply the echo protocol to signal amplification, measuring the distance between the two states in each amplifying pair (Fig. 3b) prepared by opposite sensing rotations ±δθ (purple pulse in Fig. 4a). The average distance between the two amplifying pairs is shown in Fig. 4c, in which the leftmost point with t+ = t− = 0 corresponds to the non-interacting case, thus serving as a reference for measuring amplification. We observe a maximum amplification of 6.7(6)% at (t+, t−) = (0.864, 1.728) μs; and for sufficiently long evolution times (t+ > 0.5 μs), we find that optimal signal amplification occurs at t− = 2t+, in contrast to the conventional echo, in which t− = t+. This amplification would directly translate into an equivalent enhancement in the sensing signal-to-noise ratio, as the readout noise of NV ensembles is dominated by photon shot noise24, which is not affected by spin dynamics (Extended Data Fig. 3).

Discussion and outlook

We next turn to interpretations of the experimental results. We first note that the symmetric echo protocol is known to provide a Heisenberg-limited sensitivity and an \({\mathcal{O}}(\sqrt{N})\) amplification if the qubits in the system are all-to-all coupled12. However, our observations demonstrate that in the disordered, short-range coupled system, it performs poorly and does not lead to any amplification (Fig. 4d). By contrast, the asymmetric echo with t+ = t−/2, which was also recently predicted theoretically to give a Heisenberg-limited sensitivity in the all-to-all interacting case38, outperforms both the symmetric echo and non-echo protocols in our experiments (Fig. 4d).

The superior performance of the asymmetric echo can be understood as a consequence of a (time-reversed) mirror symmetry of the underlying Hamiltonian. As shown in Fig. 4e, the dynamics under the TAT Hamiltonian remain invariant— up to a reversal of direction—under reflection about the Y–Z plane (the green shade, \({\mathcal{R}}\)). This mirror reflection, when combined with time reversal, restores the original flow direction and forms a fundamental symmetry of the system. Notably, this symmetry involves flipping the time coordinate (t ↔ −t) and exchanging the sensing (\(\widehat{S}\)) and measurement (\(\widehat{M}\)) operators (Fig. 4e). Applying these two rules to the asymmetric echo (Fig. 4f), the sensing operator at time t+ (that is, \(\widehat{S}({t}_{+})\)) is mapped to \(\widehat{M}(-{t}_{+})\), whereas the measurement operator at t+ − t− is mapped to \(\widehat{S}({t}_{-}-{t}_{+})\), effectively transforming the original asymmetric echo into an equivalent protocol with a modified forward evolution time \({t}_{+}^{{\prime} }={t}_{-}-{t}_{+}\). As a result, the amplification amplitude—defined as \(| \chi | \equiv | d\langle \widehat{M}\rangle /d({\rm{\delta }}\theta )| \)—remains the same in these two cases (that is, \(| \chi ({t}_{+},{t}_{-})| =| \chi ({t}_{-}-{t}_{+},{t}_{-})| \)). At the time \({t}_{+}=\frac{{t}_{-}}{2}+{\epsilon }\), this relation transforms to \(|\chi (\frac{{t}_{-}}{2}+{\epsilon },{t}_{-})|=|\chi (\frac{{t}_{-}}{2}-{\epsilon },{t}_{-})|\), guaranteeing a symmetry of amplification around t+ = t−/2 and thus an extremum at this point (see Supplementary Information for rigorous derivation).

To explain why the extreme value is a local maximum (instead of a local minimum) in our experiments, we turn to a microscopic model of the positionally disordered spin ensemble governed by the TAT Hamiltonian. In such a system, we find that the naturally occurring strongly coupled pairs of spins—the so-called spin dimers37,39,40—dominate the dynamics, and that the observed maximum amplification at t+ = t−/2 can be explained by the refocusing of dimers with widely spread coupling strength (see Extended Data Fig. 5 and Supplementary Information for detailed discussions). This conclusion is further supported by modifying the Hamiltonian such that a local minimum is obtained, as the original maximum splits into two peaks under the modified refocusing conditions (Extended Data Fig. 5g,h). We also note that for systems not dominated by dimers (for example, spins on a lattice), a local maximum is generically expected, as supported by our numerical simulations (Extended Data Fig. 4).

Our results can be extended in several directions. A natural goal is to realize larger, scalable (that is, improve with system size N) amplification, to achieve practical benefits. A promising approach is to engineer interactions that support XY ferromagnetic ordering41,42. Although positional disorder may pose a challenge43 for realizing scalability in the thermodynamic limit, our numerical simulations at intermediate system size (N = 200; Extended Data Fig. 7a) support a substantial enhancement of amplification. This can be explored experimentally by using recent advances in CVD growth of (111)-oriented diamonds29 (see Extended Data Fig. 7 and Supplementary Information). Moreover, overcoming positional disorder—the primary limitation in the system (Extended Data Fig. 6)—presents another opportunity for improvement. This challenge motivates exploring controlled NV creation44, or integration with strong magnetic field gradients to investigate mechanisms robust to positional disorder (N.T.L. et al., manuscript in preparation). From a practical standpoint, another interesting direction is to combine our approach with other sensitivity-enhancing techniques (for example, improved spin readout24,45). This combination could enable exploring new opportunities beyond signal amplification, because quantum projection noise would become comparable to technical noise in these cases. Ultimately, combined with other features of solid-state quantum sensors, such as the ability to bring the sensors to close proximity with sensing targets6 and the injection of sensor-containing nanoparticles for in vivo measurements7,46, signal amplification can lead to practical advances in nanoscale imaging technologies for novel condensed matter materials and biological structures.

Beyond the direct applications to dense NV ensembles, the present observations demonstrate a generic and robust mechanism for exploiting metrologically useful entanglement, applicable to a wide variety of sensing platforms. In particular, the time-reversed mirror symmetry applies to a vast majority of Hamiltonians used for entanglement-enhanced sensing, including the OAT Hamiltonian, TAT Hamiltonian, LMG Hamiltonian26 and even a cubic XYZ Hamiltonian47, suggesting the generality of the observed optimal amplification under asymmetric echo (Extended Data Fig. 4). As discussed in ref. 38 and our complementary work (N.T.L. et al., manuscript in preparation), asymmetric echo with t+ = t−/2 can be exploited in systems exhibiting collective dynamics, theoretically enabling Heisenberg-limited sensing and an \({\mathcal{O}}(N)\) amplification, in platforms ranging from polar molecules48 to trapped ions49 and cavity-QED systems25.

Methods

Diamond sample

Diamond homoepitaxial growth and delta doping28 were performed by plasma-enhanced chemical vapour deposition using a SEKI SDS6300 reactor on a (100)-oriented electronic grade diamond substrate (Element Six). Before growth, the substrate was subjected to fine-polishing by Syntek to a surface roughness of about 200–300 pm, followed by a 4−5 μm etch to relieve polishing-induced strain. The growth conditions consisted of a 750-W plasma containing 0.1% 12CH4 in 400 sccm H2 flow held at 25 torr and about 790 °C according to a pyrometer. An approximately 420-nm-thick isotopically purified (99.998% 12C) epilayer was grown. During the nitrogen δ-doping period of growth, 15N2 gas (1.0% of the total gas content) is introduced into the chamber for 30 min. After growth, the sample was characterized with secondary ion mass spectrometry (Extended Data Fig. 2a) to estimate the isotopic purity, epilayer thickness and the thickness of the δ-doped layer (8–10 nm FWHM).

The diamond was further subjected to electron irradiation and annealed to generate enhanced NV centre concentrations. Irradiation was performed with the 200 keV electrons of a transmission electron microscope (TEM; ThermoFisher Talos F200X G2 TEM). The irradiation time was varied to create spots that range in dose from 1017 to 1021 e− cm−2, and the presented experiments are performed at a spot with a dose of 2.8 × 1020 e− cm−2. The sample then underwent subsequent annealing at 850 °C for 6 h in an Ar/H2 atmosphere, during which the vacancies diffuse and form NV centres. After irradiation and annealing, the sample was cleaned in a boiling triacid solution (1:1:1 H2SO4:HNO3:HClO4) and annealed in air at 450 °C for oxygen termination of the surface and stabilize the negative NV− charge state for further measurements.

The density of NV centres in the δ-doped layer is estimated based on the XY8 decay timescale measured under the native quantization axis (ηnative), which is dominated by dipolar interaction between them. Here we observe a decay timescale of 6.5 μs (Extended Data Fig. 2b), corresponding to a single-group NV− areal density of 19 ppm nm (therefore, the total density of all four groups of NV− is 76 ppm nm). Similarly, the density of substitutional nitrogen (P1 centres) is estimated based on Ramsey decay timescale (\({T}_{2}^{* }\)) measured under ηnative, assuming that the on-site disorder felt by NV− is dominated by dipolar interaction with these spins. Here we observe \({T}_{2}^{* }=309\,{\rm{n}}{\rm{s}}\) (Extended Data Fig. 2c), leading to an upper bound of the P1 areal density of 230 ppm nm. The conversion between the decay timescales and the densities is obtained empirically based on numerical simulations.

Circuit designs for pulsed current

The pulsed current is controlled by a custom voltage-controlled current source (Extended Data Fig. 1b), with a 3-μs rising time and a 7-μs falling time. These times are much slower than the qubit frequency (712.24 MHz) but much faster than the T1 time (0.94 ms), ensuring adiabatic switching of quantization axis while avoiding significant polarization loss during the process. The pulsed current is combined with the microwave driving using a bias-tee (Extended Data Fig. 1a), and then delivered to the diamond through a coplanar waveguide (CPW). At the centre of the CPW, the current flows through two parallel wires (Extended Data Fig. 1c), and the presented experiments are done at a confocal spot between them. The thicknesses of these two wires are 10 μm and 4 μm, and the gap between them is 6 μm. These dimensions are optimized for the direction and strength of the pulsed field, and the homogeneity of the Rabi drive.

In the experiment, a pulsed field with strength 168 G and direction 23° below the horizontal plane is generated by a 1 A current, resulting in a qubit frequency fqubit = 712.24 MHz during the twisting dynamics and fread = 660 MHz during the initialization and readout. Operating at about 25% duty cycle, the pulsed current leads to significant heating. To prevent thermal failure of the coil, the circuit was fabricated on a sapphire substrate with a heat conductivity one order of magnitude better than glass. With the help of the pulsed field, the spin polarization is improved by a factor of 4 (Extended Data Fig. 1d).

Floquet sequences timings

The timings in the TAT (and time-reversed TAT) engineering pulse sequence (Fig. 3a, bottom) are chosen as tπ = 12 ns and τ = 3 ns, where tπ and τ are π-pulse duration and pulse spacing, respectively. This choice is made through the following considerations. First, to ensure the generation of the TAT Hamiltonian, the effective time spent in the X, Y and Z frames must satisfy tx + tz = 2ty (ref. 10), which dictates the ratio between tπ and τ. Second, it is desirable to repeat the sequence as fast as possible, to decouple the high-frequency components of on-site disorder and thereby improve the coherence properties. Third, the off-axis magnetic field used in this work leads to complicated nuclear spin dynamics (Supplementary Information), in which accidental entanglement between the NV electronic spin and nuclear spin could happen when the Floquet period matches the nuclear spin precession period, which happens around tπ = 24 ns (see Supplementary Information for discussions). The choice of pulse timings needs to avoid these special durations to effectively decouple the nuclear spins. Finally, to prevent neighbouring pulses from overlapping due to finite rising and falling time, τ cannot be smaller than 3 ns experimentally. The above considerations together lead to the timing choice in the experiment. The timings in the OAT dynamics are chosen arbitrarily as tπ = 38 ns and τ = 46 ns and did not require extensive optimization.

Controlling systematic errors

Owing to the relatively small amplification observed in this work, it is crucial to understand and control potential systematic errors to make trustworthy interpretations of the experimental data. First, the slow drift of the laser power causes the drift of fluorescence (FL) intensity. This is overcome by differential readout, in which we pair up each measurement with a variant of itself with an additional π-pulse before the readout, and focus on the contrast (that is, fractional difference of the FL) instead of the raw FL values. This significantly reduces the effects of FL drift, but we still observe residual drift of the full contrast (that is, contrast between +Z and −Z states), coming from different saturation levels of the single photon counting module under different FL intensity. This residual effect is further normalized out by interleaving the main experiments with measurements of the full contrast, on a time scale of 4 ms, which is much faster than the drift timescale. Similarly, we also interleave the main experiments with measurements of qubit frequency and Rabi frequency, and use feedback to stabilize them. The qubit frequency is stabilized to within ±0.3 MHz, which is much smaller than the on-site disorder. The Rabi frequency is stabilized to within ±0.5%. Finally, the relative concentration of the charge states NV− and NV0 is controlled by fixing the duty cycle of laser illumination across all data points, whereas any residual drift of the charge state concentration is further accounted for by the full contrast normalization discussed above.

Apart from the drift effects mentioned above, an important source of systematic error in the extraction of OAT signal (Fig. 2b) is the global rotation of the Bloch sphere, coming from accumulated coherent pulse errors. As shown in Extended Data Fig. 8a, these rotations could locally mimic the twisting dynamics. This is overcome by averaging the measured X polarization on antipodal pairs on the Bloch sphere, because antipodal pairs remain antipodal under global rotations.

Although the distance measurements (Figs. 3 and 4) are naturally insensitive to global rotations, problems can arise if the rotations are too large. As an extreme example, if a net π/2 rotation angle is accumulated along the Y-axis, the amplifying pairs will transform into the deamplifying pairs and thereby affect the efficiency of amplification. Moreover, distortions of the pulse envelope along the microwave circuit lead to (small) overlaps of the sensing pulse with surrounding Floquet pulses, which could affect the effective sensing angle through interference. To control the pulse distortions, we measured the S parameter of the microwave circuit in the Fourier domain with a vector network analyser (assuming the distortions to be predominantly linear) and pre-distorted the waveform sent to the arbitrary waveform generator with the inverse transformation to cancel the distortions. The effects of pulse pre-distortion are shown in Extended Data Fig. 9. To be extra cautious, we further cancel the effects of the residual (tiny) pulse overlaps by averaging the measured distance between the two experiments shown in Extended Data Fig. 10, in which the overlap between the sensing pulse and surrounding pulses are negated, whereas the engineered Hamiltonian is kept the same.

Numerical models

All numerical simulations in this work are done using the cluster discrete truncated Wigner approximation (cluster-DTWA) method50,51, with each cluster including two spins. The clustering strategy we use is the same as in ref. 51, which has been shown to give high-accuracy results in strongly disordered systems. In our most realistic model, which was used to generate the theory predictions in Figs. 2b and 3b, we considered the imperfections coming from finite 2D layer thickness, static on-site disorder, dynamical on-site disorder and imperfect spin polarization, apart from the ideal Hamiltonian evolution. Here, the 2D layer thickness (9 nm, FWHM) is measured with secondary ion mass spectroscopy, the static on-site disorder (1.0 MHz, FWHM) is characterized through Ramsey measurements, the dynamical on-site disorder (0.019 MHz MHz−1/2 around the filter function peak fpeak = 37 MHz) is characterized through spin-locking measurements52, and the spin polarization (75%) is estimated based on the NV rate equation53 prediction (85%) and measured contrast loss (10%) during the quantization axis switching. The effects of these imperfections on amplification are studied numerically by turning them off one by one in the simulations, as shown in Extended Data Fig. 6. All reported simulations in this work have system size N = 200 (except the 2D lattice cases, in which N = 196).