Main

The human ear features an ingenious preprocessing system: hair cells on the cochlea’s basilar membrane decompose sound into frequency components and transduce mechanical vibrations into electrical signals7, which the auditory nerve transmits to the brain in the form of neural spikes8 (Fig. 1a). As the hair cell vibrations do not increase linearly with the sound intensity and the cochlea shows an active feedback mechanism, non-harmonic frequencies (distortions) are generated. This compressive nonlinearity is crucial for the sensitivity, frequency selectivity and dynamic range in hearing9. In-ear preprocessing thus enables real-time, low-power encoding, which greatly reduces the data required to represent sound.

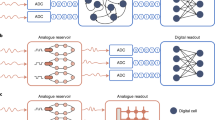
Fig. 1: Speech-recognition approaches.
figure 1

a, When two frequencies f1 and f2 (f2 > f1) enter the human ear, distortion products, such as 2f1 − f2 are generated due to nonlinear active feedback in the cochlea52. Hair cells connected to the auditory nerve endings (1 to n) convert the incoming time-domain acoustic signal into frequency-domain electrical spike-encoded information (features) to be further processed (classified) by the brain. b, Time-frequency digital processing. After analogue-to-digital conversion (ADC), frequency decomposition by a feature-extracting model F(f(t)), such as Lyon’s artificial cochlea model53, is required before classification. c, Time-domain digital processing. Top, in addition to classification, a neural network performs feature extraction by learning (band-pass) filters in the time domain. Bottom, an analogue filterbank extracts frequency features directly from the time-domain analogue signal before classification. d, Reservoir computing. After feature extraction in the time (top) or frequency (bottom) domain, the preprocessed data are used as inputs (in1,..., inN) to a reservoir that increases the dimensionality (represented by φ), simplifying classification. e, Time-domain analogue processing (this work). Reconfigurable nonlinear-processing units (RNPUs) extract temporal features, simplifying classification without the need for extra preprocessing. An analogue in-memory computing (AIMC) chip based on a memristive crossbar array performs the classification.

Full size image

Computerized audio signal processing, particularly automatic speech recognition (ASR), commonly incorporates three domain conversions (Fig. 1b). First, a microphone converts sound into an electrical signal; second, this signal is digitized using an analogue-to-digital converter (ADC); and third, a short-term Fourier transform is applied. Time-domain to frequency-domain conversion is an important part of the feature extraction stage, which—possibly in combination with further nonlinear data transformations—substantially simplifies the subsequent classification stage10. The latter can be accomplished by an artificial neural network, such as a transformer11, a convolutional neural network (CNN)12, a recurrent neural network13 or a combination of those14,15.

ASR models are typically run on specialized hardware, including application-specific-integrated-circuit accelerators, such as neural engines16, graphics processing units or tensor processing units. Demand for edge ASR is rising in applications such as always-on e-health systems17, offline voice assistants16 and fault detection18, in which latency, privacy and limited connectivity matter, requiring real-time, ultra-low-power computing. However, digital temporal-signal processing at the edge is challenging due to expensive domain conversions, complex feature-extraction algorithms19 and the von Neumann bottleneck. Although combined feature extraction and classification in the time domain (Fig. 1c, upper part) omits the time to frequency-domain conversion by porting the feature extraction to a neural network20, it generally requires larger neural networks to extract features from raw data21. These difficulties have led to a growing interest in alternative, more efficient approaches22,23.

Apart from the conventional (that is, fully digital) approaches of Fig. 1b,c (top), emerging ASR can roughly be divided into three categories: artificial cochlea models in combination with spiking neural networks, closest to human hearing24 (Fig. 1a); analogue filterbanks19,25 (Fig. 1c, bottom); and reservoir computing26 (Fig. 1d). Artificial cochlea implementations perform feature extraction by converting analogue signals into ‘spike grams’24. Despite the similarity to biology, a spiking hardware classifier realized with, for example, a digital spiking neural network is required. Lower classification accuracies with spiking features, compared with time-domain or frequency-domain features, suggest that the classification step is more difficult27. Although analogue filterbanks (Fig. 1c, bottom) do not require digitization for feature extraction, recent demonstrations still require digital classifiers25. In reservoir computing28 the reservoir first projects the temporal input into a higher-dimensional feature space, enabled by its recurrent (multi-timescale) time dynamics, followed by a linear classification layer. However, high classification accuracy requires a complex classification step when the reservoir is fed with time-domain input, for example, a deep CNN22. Alternatively, expensive preprocessing, such as using the mel-frequency cepstral coefficients, is needed when feeding the reservoir with frequency-domain features29. Despite promising classification results obtained on the TI-46-Word spoken digit task30, edge conditions demand hardware that is not only accurate but also compact and efficient. This requires an approach that simultaneously addresses domain conversions, efficient feature extraction and the von Neumann bottleneck.

In this Article, we present an ASR architecture based on two emerging in-materia computing paradigms. First, analogue time-domain feature extraction is achieved through a circuit that incorporates one or more reconfigurable nonlinear-processing units (RNPUs)3 working at room temperature. Serving as the core of a low-power analogue circuit, the RNPU uniquely establishes biologically plausible feature extraction through a recurrent nonlinear transformation with adjustable frequency selectivity and tuneable characteristic timescales in the millisecond range. Second, for the classification based on the extracted features, we implement a CNN on an analogue in-memory computing (AIMC)5 chip. Crossbar arrays of synaptic unit cells based on phase-change memory (PCM) devices perform matrix-vector multiplication (MVM) operations for the CNN, mitigating the von Neumann bottleneck. We assess the performance of these combined in-materia approaches using two benchmarks: the TI-46-Word spoken digits and Google Speech Commands (GSC) datasets, achieving near-software-equivalent accuracies of 96.2% and 89.3%, respectively.

Time-domain processing with RNPUs

RNPUs possess the three characteristics crucial for biologically plausible time-domain speech recognition: frequency selectivity, tuneable nonlinearity and sensory memory on the millisecond timescale relevant to audio processing. Figure 2a shows a false-colour atomic-force-microscopy image of an RNPU and the measurement circuitry (Methods). The active region of the RNPU consists of a lightly doped silicon region, surrounded by eight electrodes (one input, one output, six controls). The RNPU features a complex energy landscape and highly nonlinear charge transport, which can be tuned by means of control voltages to enable specific functionalities such as Boolean logic, nonlinear classification and feature extraction31 (see Methods for fabrication and room-temperature operation details).

Fig. 2: Tuneable nonlinearity and short-term memory characterization of an RNPU at room temperature.
figure 2

a, Atomic-force-microscopy image of an eight-electrode RNPU and schematic measurement circuit with external capacitance Cext (roughly 10–100 pF) and a greater than 1 GΩ input impedance buffer. Scale bar, 500 nm. b, Fourier transform of a two-tone input signal (blue, f1 and f2) and the RNPU response (orange), showing (sub)harmonics and distortions. Input and output signals are sampled at a fixed sampling rate of 25 kS s−1. Similar to the frequency response of a human cochlea, the output signal contains distortion products \(|(n+1){f}_{1}-n{f}_{2}|\) of progressively higher frequencies and lower magnitudes. Inset, histogram of time constants (τ is the time for the output to reach 63% of Vmax) of Vout(t) in response to a 1-V step input with a rising time of less than 20 μs for 500 randomly configured control-voltage sets. c, (i) Power spectral density of chirp input voltage signal \({V}_{{\rm{in}}}(t)=A\sin \,\left[2{\rm{\pi }}{f}_{0}\left(\frac{{k}^{t}-1}{\mathrm{ln}(k)}\right)+{\varphi }_{0}\right]\), with A = 0.75 V the amplitude, f0 = 100 Hz the starting frequency, \(k={\left(\frac{{f}_{1}}{{f}_{0}}\right)}^{\frac{1}{T}}\) the rate of exponential change in frequency, \({\varphi }_{0}=-\frac{{\rm{\pi }}}{2}\) the initial phase at t = 0, f1 = 2 kHz the final frequency and T = 1 s the signal duration. (ii) Power spectral density of output voltage Vout(t) in response to the input signal of (i) with 0 V on all controls, showing up to five harmonics. (iii) Idem for a set of random control voltages. (iv) Idem, for a different set of random control voltages.

Full size image

In our earlier work on static (time-independent) tasks3, we operated the RNPUs (then referred to as dopant network processing units) at 77 K with voltage input and current output, using a transimpedance amplifier (Extended Data Fig. 1), effectively shorting the stray capacitance of the readout circuit and minimizing the response time. Here, we operate at room temperature using a modified fabrication process avoiding hydrofluoric acid etching, probably enhancing the role of Pb centres (dangling bonds at the Si–SiO2 interface). Carrier transport in the devices now shows an activation energy of roughly 0.4 eV and shows nonlinear behaviour, possibly because of a combination of trap-assisted transport and space-charge-limited-current mechanisms (Methods). Furthermore, we measure the output as a voltage (Methods). Specifically, we use a buffer circuit with a large input impedance (greater than 1 GΩ) at the RNPU output, so that the external capacitance Cext (roughly 10–100 pF) can no longer be neglected (Fig. 2a). Together with the intrinsic nonlinear RNPU resistance and capacitance, these features give rise to a highly nontrivial temporal response with a tuneable characteristic timescale in the milliseconds range. In the inset of Fig. 2b, we show the distribution of these timescales, corresponding to 500 sets of random control voltages.

Figure 2b shows the response of the RNPU circuit to a two-tone input, in which a signal with two frequencies (f1 = 74 Hz, f2 = 174 Hz) is fed to the RNPU input (blue). The Fourier transform of the output signal is shown in orange, with distortion magnitudes tuneable by means of the control voltages. Figures 2c(ii)–(iv) show the output spectrograms for three different sets of control voltages in response to an exponential chirp input signal (Fig. 2c(i)). In Fig. 2c(ii), all control voltages are set to 0 V with respect to ground. The output voltage contains up to the fifth harmonic of the input signal, indicating the presence of strong nonlinearities. These harmonics can be tuned by the control voltages, as shown in Figs. 2c(iii) and 2c(iv). For example, harmonics can be selectively created or removed, including the fundamental tone.

The RNPU output voltage is determined by the complex potential landscape of the active region, which in turn depends on the potential at each electrode. Similar to a state-dependent system, changes in the charge stored at the output capacitor Cext alter the potential at the output electrode, which in turn modifies the circuit characteristics (for example, τ). This effectively forms a nonlinear active feedback system that introduces recurrency and short-term memory (Fig. 3b). In concrete, the charge on Cext at time t = t0 influences the RNPU behaviour at t = t0 + Δt, given Δt ≲ RRNPU(t0) Cext, where RRNPU(t0) is the RNPU resistance measured at t = t0 between the input and output electrodes with control voltages VC1, VC2, …VC6. Details on the RNPU’s variable-impedance-based fading memory are provided in the Methods and Extended Data Figs. 2 and 3.

Fig. 3: RNPU analogue feature extraction for speech recognition.
figure 3

a, t-distributed stochastic neighbour embedding (t-SNE) visualization for the female subset of the TI-46-Word spoken digit dataset before RNPU preprocessing. b, Schematic of RNPU (nonlinear function noted as f(.)) fed with analogue time-dependent input x(t) (blue electrode), voltage measured at the orange electrode and constant control voltages (black electrodes). Every set of control voltages results in a unique transformed signal (green and red curves shown as examples) and forms an output channel with a ten times lower sample rate compared with the raw input signal (Methods). c, t-SNE visualization after RNPU preprocessing (1 configuration out of 32 sets of randomly chosen control voltages). The output data show that the RNPU preprocessing helps clustering utterances of the same digit, simplifying later classification. d, Comparison of the TI-46-Word classification accuracy for linear and CNN classifier models without (green, software model) and with (blue, software model and orange, hardware-aware (HWA) trained model) RNPU preprocessing for 16, 32 and 64 RNPU channels (CHNL). The all-hardware (RNPU with the AIMC classifier) result (orange) is presented as the mean ±1 standard deviation over 10 inference measurements. e, Comparison of the Google Speech Commands (GSC) keyword spotting (KWS) classification accuracy with and without RNPU preprocessing with four-layer, five-layer and six-layer CNNs. RNPU preprocessing allows for achieving higher accuracies with classifiers requiring over twice fewer MAC operations. M, million.

Full size image

Frequency selectivity and short-term (fading) memory are key characteristics of neural network models for temporal data processing12. For example, CNN models use large kernel sizes for the first convolution layer, typically a roughly 10-ms receptive field, to capture temporal features from raw audio21. The first layer extracts low-level features, whereas the deeper layers with smaller kernel sizes construct higher-level features and perform classification. The overall accuracy of an end-to-end CNN classifier remains high even when the initial layer is randomly initialized or only lightly trained12. Leaving the first layer untrained, that is, feature extraction with random software filterbanks can reduce the training costs32. In the inference phase, however, the first layer is the most computationally expensive part of the network as the large kernel size demands many multiply–accumulate (MAC) operations. For example, in a five-layer CNN for raw audio classification, for inference of a single input sample, the first layer accounts for roughly 75% of all MAC operations.

Speech recognition and keyword spotting

We now propose an RNPU circuit to implement an in-materia time-domain feature extractor and combine it first with a software classifier model (we discuss an in-materia classifier below). To benchmark this hybrid system, we use the TI-46-Word spoken digits and a subset of the GSC datasets (Methods). These datasets are processed 64 times by a single RNPU circuit, each process step is referred to as a channel (Fig. 3b) and has a different set of random control voltages (in a device-dependent voltage range, Methods). Alternatively, one could obtain 64 channels by using 64 different, randomly initialized RNPUs in parallel. Also, instead of randomly initialized RNPUs, one could use RNPUs with control voltages trained in an end-to-end fashion together with the software classifier, using backpropagation (Extended Data Fig. 4).

To visualize the impact of RNPU preprocessing, we use t-distributed stochastic neighbour embedding (t-SNE), which is a statistical method for visualizing high-dimensional data33 (we also used universal manifold approximation and projection, Extended Data Fig. 5). Figure 3a shows the t-SNE visualization of the original (raw) TI-46-Word audio dataset. Every individual sample is fed to the circuit shown in Fig. 3b. When visualizing one of the output channels in Fig. 3c, several digits, such as ‘six’, ‘eight’ and ‘nine’, form well-defined clusters compared with the original dataset, whereas others remain more scattered. The results of the RNPU preprocessing (illustrated by the green and red traces in Fig. 3b) contain fingerprints (or low-level features) of the input data. Similar to contrastive learning34, RNPU preprocessing puts same-labelled instances of the dataset closer together in time-domain representation space while keeping dissimilar instances apart.

To study the impact of RNPU preprocessing on the overall classification performance, we examined several simple classifier models, with and without RNPU preprocessing (Methods). As shown for TI-46-Word in Fig. 3d, a single-layer linear model performs poorly on the raw data (green, roughly 18%). An extra single convolutional layer with 64 output channels after (green), or 32-channel RNPU preprocessing (blue) before, the linear model improves the overall classification accuracy to roughly 60%. The backpropagation-trained CNN outperforms preprocessing by randomly initialized RNPUs by only 3% point. If we combine 16-channel RNPU preprocessing with a 1-layer CNN, we achieve 95.1% accuracy, with only around 4,000 learnable parameters. For comparison, recent studies on a 500-sample subset of the TI-46-Word spoken digits dataset with 4,096 learnable parameters reported 78% without35 and 97% with36 frequency-domain feature extraction. We obtain higher accuracies with 32 or 64 channels, using a 2-layer or 3-layer CNN software model. With 64-channel RNPU-preprocessed data and a 2-layer (and also 3-layer) CNN, we obtain 98.5% accuracy, comparable to the best all-software models, such as long short-term memory36.

RNPU preprocessing similarly enhances the classification accuracy for complex keyword spotting (KWS) tasks using a subset of the GSC dataset while reducing the required CNN operations by more than a factor of two (Fig. 3e). A 5-layer CNN with a roughly 10-ms first-layer receptive field20, requires roughly 5 million MAC operations and gives 84.5% accuracy for the same subset. By comparison, a 4-layer CNN with 64-channel RNPU preprocessing requires only 2.28 million MAC operations and achieves a comparable 83.5% accuracy. This increases to 91.1%, close to the state-of-the-art, all-software value 92.4%, with RNPU-preprocessed data and a compact 6-layer CNN. RNPU preprocessing combined with the same CNN architecture using the Swish activation function37 instead of a hyperbolic tangent, achieves the highest classification accuracy of 93.1%.

Frequency selectivity, compressive nonlinearity and recurrency are key in the RNPU preprocessing. In the Methods, we compare different filterbanks of low-pass and band-pass filters with one or more of these characteristics. Furthermore, there we use 64 different reservoir models for the feature-extraction stage and compare them with other methods. Extended Data Table 1 compares inference accuracy across preprocessing methods using the same classifier, highlighting the superior performance of RNPUs.

Mapping the classifier model on an AIMC chip

As discussed above, RNPU preprocessing effectively extracts time-domain acoustic features, substantially simplifying the task for the classifier. The classifier model typically consumes roughly 40% of the total power in an ASR system25. In traditional deep neural network implementations, energy consumption is dominated by memory access and data transfer between the processor and memory units38. We leverage AIMC, another in-materia computing paradigm, to address this challenge. AIMC enables computation within non-volatile memristive devices that hold the neural network weights39,40,41. Below, we discuss the results of a classifier model trained with the RNPU features implemented on the IBM HERMES project AIMC chip5 (Fig. 4a, through a digital interface as the RNPU and AIMC chips are at present physically separated).

Fig. 4: Schematic of a hybrid CNN architecture for in materia speech recognition.
figure 4

a, A schematic illustration of one core of the IBM HERMES project AIMC chip and its architecture containing 256 × 256 synaptic unit cells, each comprising four PCM devices organized in a differential configuration, ADC and/or digital-to-analogue converter (DAC) arrays and on-chip local digital processing units. b, Classifier architecture for the TI-46-Word dataset. A 64-channel RNPU preprocessing step converts audio signals into 64-D input to the AIMC chip with a downsampling rate of 10 (details in Extended Data Fig. 3). Batch normalization, activation functions and pooling operations are performed off-chip. c, Schematic representation of resource use for the three-layer CNN classifier in b for the TI-46-Word implemented on two tiles of the AIMC chip. d, CNN architecture for the GSC KWS task. After 64-channel RNPU preprocessing, a 6-layer CNN maps the inputs into 11 classes of known or 1 class of unknown targets. e, The mapping of CNN layers on the AIMC chip. In a fully pipelined implementation, 18 cores (out of 64) of the AIMC chip will be used. f, The confusion matrix of the GSC KWS task with HWA model training. Conv., convolution layer; FC, fully connected layer.

Full size image

First, we implemented the CNN model illustrated in Fig. 4b on the AIMC chip for TI-46-Word classification, which is trained with 64 RNPU channels (Extended Data Fig. 6). The training includes a standard and a hardware-aware (HWA) retraining phase to enhance the network model’s resilience to AIMC noise42. We used the open-source IBM analogue hardware acceleration kit43,44 to add weight and activation noise, perform weight clipping and incorporate ADC quantization noise during the retraining phase (Methods). The learned network weights are transferred to each PCM-based synaptic unit cell as analogue conductance values (illustrated in Fig. 4a) using gradient-descent-based programming (GDP)45. The resource use of this model is shown in Fig. 4c. We use only a fraction of two cores out of the chip’s 64, highlighting the compactness of the model. The two combined in-materia systems achieve a near-software inference accuracy (96.2 ± 0.8% averaged more than 10 repetitions, compared with 98.5% for the RNPU with a software classifier) while performing roughly 95% of total operations on new material systems and offloading less than 5% to digital processors.

Similarly, Fig. 4d illustrates a six-layer CNN for the GSC KWS task implemented on the AIMC chip with its resource mapping shown in Fig. 4e. Although the AIMC chip has been measured through time-multiplexing, a fully pipelined implementation, in which every layer is realized by a unique in-memory computing core, requires only 18 cores (out of 64): that is, less than 29% resource use. This small footprint implies that an optimized AIMC chip can be much more compact. The confusion matrix is shown in Fig. 4f, where the ‘unknown’ class represents several utterances, such as numbers from zero to nine.

Discussion

This study demonstrates bio-plausible, time-domain speech recognition using two in-materia computing hardware systems for both feature extraction and classification. The 96.2% and 89.3% end-to-end, all-hardware accuracies (that is, RNPU preprocessing + AIMC classification) obtained for the TI-46-Word and GSC KWS tasks are comparable to those of state-of-the-art software models that have roughly 10 times more learnable parameters36, and only roughly 2% lower than when the classifier is implemented in software (that is, RNPU + software classification). Including RNPUs in end-to-end training (Extended Data Fig. 4)—rather than leaving them untrained—as well as optimizing the AIMC HWA retraining phase, specifically for temporal data processing, can further improve these results. Our approach achieves high classification rates without the necessity for costly digital feature extraction46 or a complex classifier model22.

We have evaluated the overall system-level efficiency, considering a raw audio waveform as input and a classification label as output (Methods). The analysed system comprises RNPU feature extraction circuits, a digital interface with ADCs47 (or equivalently an analogue interface with sample-and-hold circuits) and the IBM HERMES project AIMC chip. Among feature-extraction methods, frequency-domain preprocessing involves similar nonlinearity to RNPUs, simplifying the classification step10. However, state-of-the-art digital implementation requires roughly 10 µW of power and roughly 0.5 mm2 of silicon area with a latency of more than 10 ms (ref. 64). By contrast, our RNPU feature-extraction circuit consumes roughly 300 nW (more than 30× lower, Methods and Extended Data Fig. 7), uses roughly 1 µm2 of silicon per RNPU channel (roughly 100 µm2 if external capacitance is needed) and operates in real time, hence introducing no latency to the overall system.

As detailed in the Methods, the AIMC chip consumes roughly 78 μJ (and can be optimized to less than 10 μJ) per inference with submillisecond delay (348 μs). In comparison, a digital state-of-the-art recurrent neural network classifier with band-pass filterbanks for feature extraction consumes roughly 5.2 μJ with a roughly 10-ms delay for computations48. Our system’s overall energy-delay product, including the interface, outperforms the state-of-the-art digital KWS chip in 22-nm technology49 by roughly 8.5 times (Extended Data Table 2). With AIMC enhancements considered (Methods) a conservative future estimate places the energy per inference in the range of roughly 10 μJ, which would make AIMC systems competitive with state-of-the-art ASR processors also in terms of energy efficiency. Furthermore, RNPUs and AIMC have the advantage of high integration density, that is, weight or computation capacity per area50, compared with other complementary metal-oxide-semiconductor technologies. The low power consumption of RNPUs allows for bonding AIMC and RNPU chips through 3D heterogenous integration, enabling a compact computing system.

As every RNPU is unique, RNPU-based feature extraction will always require the subsequent classifier to be trained accordingly. For real-life applications, it will be practical if this training is performed online in an adaptive fashion. Whereas the inability to copy the parameters from one system to another is a disadvantage, it could be an asset for applications in which safety and privacy are critical. At present, the RNPU and AIMC layers are still physically separated. However, backend-of-the-line and heterogeneous integration51 should allow for integration of RNPUs and AIMC on the same chip. Also, a single physical RNPU has been time-multiplexed in this work. To fully exploit our platform’s potential, we need to scale up RNPU circuits in mainstream complementary metal-oxide-semiconductor technology and use parallel multi-channel feature extraction. Although we have benchmarked our method for a speech-recognition task, we expect it to be generally applicable to temporal-signal processing at the edge, such as video or electroencephalogram and/or electrocardiogram data classification. Our results demonstrate that combining two in-materia computing hardware platforms for feature extraction and classification can simultaneously address efficiency, accuracy and compactness, paving the way towards postconventional heterogeneous computing systems for sustainable edge computing.

Methods

RNPU fabrication and room-temperature operation

A lightly n-doped silicon wafer (resistivity ρ ≈ 5 Ω cm) is cleaned and heated for 4 h in a furnace at 1,100 °C for dry oxidation, producing a 280-nm thick SiO2 layer. Photolithography and chemical etching are used to selectively remove the silicon oxide. A second, 35 nm SiO2 layer is needed for the desired dopant concentration. Ion implantation of B+ ions is performed at 9 keV with a dose of 3.5 × 1014 cm−2. After implantation, rapid thermal annealing (1,050 °C for 7 s) is carried out to activate the dopants. The second oxide layer is removed by buffered hydrofluoric acid (1:7; 45 s) and then the wafer is diced into 1 cm × 1 cm pieces. E-beam lithography and e-beam evaporation are used, respectively, for creating the (1.5 nm Ti/25 nm Pd) electrodes. Finally, reactive-ion etching (CHF3 and O2, (25:5)) is used to etch (30–40 nm) the silicon until the desired dopant concentration is obtained.

We have consistently realized room-temperature functionality for both B-doped and As-doped RNPUs using a fabrication process that is slightly different from the previous work3. The main difference is that we do not hydrofluoric acid-etch the top layer of the RNPU after reactive-ion etching, which we expect to lead to an increased role of Pb centres54. The observed activation energy of roughly 0.4 eV for both B-doped and As-doped devices agrees with their position in the Si bandgap and their ambipolar electronic activity. Depending on the relative concentration of intentional and unintentional dopants, and the voltages applied, we argue that both trap-assisted transport and trap-limited space-charge-limited-current55 transport mechanisms can play a role and contribute to the observed nonlinearity at room temperature. A detailed study of the charge transport mechanisms involved will be presented elsewhere.

RNPU measurement circuitry

We use a National Instruments C-series voltage output module (NI-9264) to apply input and control voltages to the RNPU. The NI-9264 is a 16-bit digital-to-analogue converter with a slew rate of 4 V μs−1 and a settling time of 15 μs for a 100-pF capacitive load and 1 V step. As shown in Fig. 2a, a small parasitic capacitance (roughly 10–100 pF) to ground is present at the RNPU output. In contrast to the previous study3, we do not measure the RNPU output current but the output voltage, without amplification. In refs. 3,4,31, the device output was virtually grounded by the operational amplifier used for current-to-voltage conversion (Extended Data Fig. 1). Thus, the external capacitance was essentially short-circuited to ground, and no time dynamics was observed. In the present study, we directly measure and digitize the RNPU output voltage with the National Instruments C-series voltage input module (NI-9223; input impedance greater than 1 GΩ). A large input impedance, that is, more than ten times the RNPU resistance, is necessary to ensure that the time dynamics of the RNPU circuit is measurable.

Recurrent fading memory in RNPU circuit

In an RNPU, the potential landscape of the active region, which is dependent on the potential of the surrounding electrodes, determines the output voltage. In the static measurement model, the output electrode is virtually grounded. In the dynamic measurement mode (this work), however, the output electrode has a finite potential that we read with the ADC. This potential is the charge stored on the capacitor divided by the capacitance \(\left({V}_{{\rm{out}}}=\frac{Q}{{C}_{{\rm{ext}}}}\right)\). The charge on the capacitor, and hence Vout, depends on the previous inputs. The short-term (fading) memory of the circuit is therefore recurrent in nature, that is, previous inputs influence the present physical characteristics of the circuit over a typical timescale given by the time constant. More specifically, as shown in Fig. 3, an RNPU circuit is a stateful system in which the current behaviour is influenced by past events within a range of tens of milliseconds.

Extended Data Fig. 2a shows an input pulse series with a magnitude of 1 V (orange) and the output measured from the RNPU (blue). Extended Data Fig. 2b,c zoom in on the RNPU response. For each panel, we fit an exponential to extract the time constant. The time constant changes over time for the same repetitive input stimulus. We explain this by the output capacitor holding some charge from previous input pulses when the next input pulse arrives. On its turn, the potential landscape of the device is affected by the stored charge, resulting in different intrinsic RNPU impedance values.

Extended Data Fig. 3 emphasizes the nonlinearity of the RNPU response, which affects the (dis)charging rate of the RNPU circuit. A series of step functions are fed to the device (orange), and the output is measured and normalized to 1 V for better visualization (blue). Each step function has a 200 mV larger magnitude compared with the previous one. The charge stored on the capacitance, read as ADC voltage, is different for each step function, indicating that the RNPU responds to the input nonlinearly, and thus, the time constant for each input step is different. In summary, these two experiments show that the RNPU behaviour is nonlinear, dependent on both the input at t = t0 and on preceding inputs.

TI-46-Word spoken digit dataset

The audio fragments of spoken digits are obtained from the TI-46-Word dataset1, available at https://catalogue.ldc.upenn.edu/LDC93S9. To reduce the measurement time, we use the female subset, which contains a total of 2,075 clean utterances from 8 female speakers, covering the digits 0 to 9. The audio samples have been amplified to an amplitude range of −0.75 V to 0.75 V to match the RNPU input range and trimmed to minimize the silent parts by removing data points smaller than 50 mV (again for reducing measurement time). We used stratified randomized split to divide the dataset into train (90%) and test (10%) subsets.

GSC dataset

The GSC2 dataset (available at https://www.tensorflow.org/datasets/catalog/speech_commands), is an open-source dataset containing 65,000 1-s audio recordings spoken by more than 1,800 speakers. Although the dataset comprises thousands of audio recordings, to reduce our measurement time, we selected a subset of 6,000 recordings (100 min of audio, total 64 × 100 ≈ 106 h of measurement), comprising 200 recordings per class (total 30 classes). Then, we used 11 classes as keywords and the rest as unknown (shown in Fig. 4f). No preprocessing, such as trimming silence or normalizing data, was applied to this subset before RNPU measurements. The dataset was divided into training (90%) and testing (10%) sets to assess the performance of our system. It is worth mentioning that the GSC dataset is commonly used to evaluate KWS systems that are tuned for high precision, that is, low false-positive rates. The analysis of our HWA trained model reveals that in addition to the high classification accuracy of roughly 90% (shown in Fig. 3e), the weighted F1-score for false-positive detections is roughly 91.3%.

RNPU optimization

The RNPU control electrodes are used to tune the functionality for both the linear and nonlinear operation regimes. Applying control voltages greater than or roughly equal to 500 mV pushes the RNPU into its linear regime. Furthermore, higher control voltages make the device more conductive, leading to a faster discharge of the external capacitor and, thus, a smaller time constant. In this work, we randomly choose control voltages between −0.4 V and 0.4 V except for the end-to-end training of neural networks with RNPUs in the loop (Extended Data Fig. 4). For electrodes directly next to the output, we reduce this range by a factor of two because these control voltages have a stronger influence on the output voltage.

Software-based feedforward-neural network training and inference

To evaluate the RNPU performance in reducing the classification complexity, we combined the RNPU preprocessing with two shallow ANNs: (1) a one-layer feedforward, and (2) a one-layer CNN. We trained these two models for the TI-46-Word spoken digits dataset with both the original (raw) dataset and the 32-channel RNPU-preprocessed data. For all evaluations, we used the AdamW optimizer56 with a learning rate of 10−3 and a weight decay of 10−5 and trained the network for 200 epochs.

  • Linear layer with the original dataset. Each digit (0 to 9) in the dataset consists of an audio signal of 1 s length sampled at a 12.5 kS s−1 rate. Thus, 12,500 samples have to be mapped into 1 of 10 classes. The linear layer, therefore, has 12,500 × 10 = 125,000 learnable parameters followed by 10 log-sigmoid functions.

  • Linear layer with the RNPU-preprocessed data. A 10-channel RNPU preprocessing layer with a downsampling rate of 10× converts an audio signal with a shape of 12,500 × 1 into 1,250 × 10. Then, the linear layer with 1,250 × 10 × 10 = 125,000 learnable parameters is trained. This model gives roughly 57% accuracy, which is 2% less than the 32-channel result reported in Fig. 3.

  • CNN with the original dataset. The CNN model contains a 1D convolution layer with one input channel and 32 output channels, kernel size of 8, with a stride of 1, followed by a linear layer and log-sigmoid activation functions mapping the output of the convolution layer into 10 classes. The 1-layer CNN with 32 input and output channels has roughly 4,500 learnable parameters.

  • CNNs with the RNPU-processed data. The CNN models used with RNPU-preprocessed data contain 1 (or 2) convolution layers with 16, 32 and 64 input channels and 32 output channels followed by a linear layer. Similar to the previous model, we used a kernel size of eight with a stride of one for each convolution kernel. The 1-layer CNN with 16, 32 and 64 channels has roughly 4,500, 8,600 and 16,900 learnable parameters, respectively.

Comparison with filterbanks and reservoir computing

Low-pass and band-pass filterbanks

The RNPU circuit of Fig. 2a would behave like an ordinary low-pass filter if the RNPU is assumed to be an adjustable linear resistor. If so, RNPUs with different control voltages could be used to realize filters with different cut-off frequencies, thus forming a low-pass filterbank. However, as argued above, the RNPU cannot be considered merely a simple linear resistive element.

Figure 2b shows the time constant of the voltage output of the circuit when the input stimulus is a voltage step of 1 V. When converting the time constants into frequency assuming a linear response, the cut-off frequency of corresponding low-pass filters can be calculated as \({f}_{{\rm{cut}}-{\rm{off}}}=\frac{1}{2{\rm{\pi }}RC}\), where R and C are the values of the device resistance and the capacitance, respectively. Given the range of the time constants in Fig. 2b, the highest and lowest cut-off frequencies of such filters are

$$\begin{array}{c}{f}_{{\rm{cut}}-{\rm{off}},{\rm{high}}}=\frac{1}{2{\rm{\pi }}RC}=\frac{1}{2{\rm{\pi }}\times 12\times {10}^{-3}}=13\,{\rm{Hz}},\\ {f}_{{\rm{cut}}-{\rm{off}},{\rm{low}}}\frac{1}{2{\rm{\pi }}\times 34\times {10}^{-3}}=4\,{\rm{Hz}},\end{array}$$

which are below the lowest frequency the human ear can detect (20 Hz). We used this cut-off frequency range to evaluate the classification accuracy when using a linear low-pass filterbank as feature extractor (Extended Data Table 1). However, the simulation results give roughly 75% classification accuracy. This indicates that the RNPU circuit does not simply construct a linear low-pass filter with the control voltages only changing the cut-off frequency, but rather a nonlinear filterbank that mimics biological cochlea by generating distortion products.

Nonlinear low-pass filterbanks

To study the effects of nonlinear filtering on the feature extraction step, and consecutively, on the classifier performance, we have introduced biologically inspired distortion products to the output of a linear filter, more specifically, distortion products of progressively higher frequency and lower magnitude. These properties are similar to the nonlinear properties of the RNPUs. Note that we only intend to qualitatively describe the effect of distortion products on the classification accuracy here, and not to quantitatively represent the RNPU circuit.

The nonlinear filterbanks are constructed by adding nonlinear components to the output of a linear time-invariant (LTI) filter. These nonlinear components include (1) harmonic or subharmonic addition and (2) delayed input. In the frequency domain, we progressively decrease the magnitude of the nonlinear components as their frequency increase (Extended Data Table 3).

  1. (1)

    Harmonic or subharmonic: given the input audio signal of xin(t), first, we calculate the Fourier transform of the output of the LTI low-pass filter F(LPF(xin(t))). Then, for a specific range of frequencies, for example, from the first to the hundredth frequency bin ([f0, f100]), we add that frequency component to the frequency harmonic at the harmonic or subharmonic position (2 × f0, 3 × f0, …) divided by the order of the harmonic (1/n for n × f0). The pseudo-code of this approach is shown in Extended Data Table 3.

  2. (2)

    Delayed inputs: the second nonlinear property of this nonlinear filtering is to add the delayed output of each filter (with 30% of the magnitude) to the next filter channel for a channel greater than one. Although this nonlinear inter-channel crosstalk does not occur in the RNPU circuit, our experiments have shown that this nonlinearity can help improve the classification accuracy. The time delayed has been chosen to be 10 samples, given the 1,250 S s−1 sampling rate (which is the rate after downsampling the filtered signal).

To evaluate the capability of linear and nonlinear low-pass filterbanks in acoustic feature extraction, we used a similar pipeline for RNPU-processed data, that is, a 1-layer CNN with a kernel size of 3, a tanh activation function trained for 500 epochs with the AdamW57 optimizer and a learning rate and weight decay of 0.001. We have also used the OneCycleLR scheduler58 with a maximum learning rate of 0.1 and a cosine annealing strategy. The classifier model has been intentionally kept simple to limit its feature-extraction capabilities so that we can better evaluate different preprocessing methods.

We examined linear low-pass filterbanks under two scenarios: (1) setting the cut-off frequencies according to the RNPU circuit time constants, that is, 4 Hz and 13 Hz, for lower and higher limits, respectively, and (2) setting a wider range of cut-off frequencies, that is, 20 and 625 for the lower and higher limits, respectively. The higher limit for the latter case is based on the Nyquist frequency given the 1,250 S s−1 sampling rate. The inference accuracy results for the same TI-46-Word benchmark test are summarized in Extended Data Table 1.

Nonlinear band-pass filterbanks

The hair cells of the basilar membrane in the cochlea convert acoustic vibrations into electrical signals nonlinearly, in which small displacements cause a notable change in the output at first. However, as the displacements increase, this rate slows down and eventually approaches a limit. It has been proposed that this with nonlinearity (CN) can be modelled as a hyperbolic tangent (tanh) function. Similar to nonlinear low-pass filterbanks, we implemented a nonlinear band-pass filterbank as a model for auditory filters in the mammalian auditory system. The model is constructed by an LTI filterbank of band-pass filters (fbband-pass) initialized with gammatone within 20 Hz to 625 Hz followed by the tanh nonlinearity described as follows:

$${f}_{{\rm{CN}}}(X)=\frac{1}{2}\times \tanh ({{fb}}_{{\rm{band}}-{\rm{pass}}}(X)+1),$$

where X represents the input audio signal. For simulations with this nonlinear band-pass filterbank, we use the same classifier model (1-layer CNN) with the same hyperparameters described before. The performance of this nonlinear filterbank is summarized in Extended Data Table 1. Adding the tanh nonlinearity increases the overall classification accuracy to more than 93%, which is notably higher than the LTI band-pass filterbank but still less than the value obtained with RNPU preprocessing.

Reservoir computing

Here we make a comparison with reservoir computing, in particular with echo state networks (ESNs). ESNs are reservoir computing-based frameworks for time-series processing, which are essentially randomly initialized recurrent neural networks59. ESNs offer nonlinearity and short-term memory essential for projecting input data into a high-dimensional feature space, in which the classification of those features becomes simpler. As reported in the main text, most reservoir computing solutions for speech recognition rely on frequency-domain feature extraction. More specifically, a reservoir is normally used to project pre-extracted features into a higher-dimensional space and then a classifier, often a linear layer, is used to perform the classification.

Here, we compare the efficacy of ESNs for acoustic feature extraction to RNPUs and filterbanks. Using the ReservoirPy Python package60, we modelled 64 different reservoirs initialized with random conditions for neuron leak rate (lr), spectral radius of recurrent weight matrix (sr), recurrent weight matrix connectivity (rc_connectivity) and reservoir activation noise (rc_noise). Then, the same dataset as described in the main text is fed to all these reservoir models, and the output is used for classification. The reservoir maps the input to output with a downsampling rate of ten times, the same as for RNPUs and filterbanks. The performance of using reservoirs as feature extractors is summarized in Extended Data Table 1. Notably, this approach performs the poorest among other feature extractors. We attribute this low classification rate to the absence of bio-plausible mechanisms for acoustic feature extraction in the reservoir system. More specifically, although a reservoir projects the input into a higher-dimensional space, the lack of compressive linearity, a recurrent form of feedback from the output, and frequency selectivity make acoustic feature extraction with reservoirs less effective compared with other solutions.

AIMC CNN model development

We implemented two CNN models for classification of the TI-64-Word spoken digits dataset on the AIMC chip with 2-layer and 3-layer convolutional layers, trained with 32 and 64 channels of RNPU measurement data, respectively. Extended Data Fig. 3 illustrates the architecture of the 3-layer convolution layer with 64 RNPU channels (roughly 65,000 learnable parameters). The first AIMC convolution layer receives the data from the RNPU with dimensions of 64 × 1,250. To implement this layer with a kernel size of 8, 64 × 8 = 512 crossbar rows are required. To optimize crossbar array resource use, this layer has 96 output channels. Thus, in total, 512 rows and 96 columns of the AIMC chip are used (Fig. 4c) to implement this layer. The second and third convolution layers both have a kernel size of three. Considering the 96 output channels, each layer requires 96 × 3 = 288 crossbar rows (Fig. 4c). Finally, the fully connected layer is a 36 × 10 feedforward layer.

AIMC training and inference

The AIMC training, done in software, consists of two phases: a full-precision phase and a retraining phase, each performed for 200 epochs. The retraining phase is performed to make the classifier robust to weight noise arising from the non-ideality of the PCM devices and the 8-bit input-quantization. During this second phase, we implement two steps: (1) in every forward pass, random Gaussian noise with a magnitude equalling 12% of the maximum weight is added to each layer of the network, as well as Gaussian noise with a standard deviation of 0.1 is added to the output of every MVM to make the model more robust to noise, and (2) after each training batch, weights and biases are clipped to 1.5 × σW implementing the low-bit quantization, where σW is the standard deviation of the distribution of weights.

RNPU static power measurement

To estimate the RNPU energy efficiency, we measured the static power consumption, Pstatic, for ten different sets of random control voltages and averaged the results. In every configuration, a constant d.c. voltage is applied to each electrode, and the resulting current through every electrode is measured sequentially using a Keithley 236 source measure unit. Pstatic is calculated according to

$${P}_{{\rm{static}}}=\mathop{\sum }\limits_{k=0}^{N-1}{V}_{i}{I}_{i},$$

where N = 8 is the number of electrodes of the device.

As illustrated in Extended Data Fig. 2, the average static power consumption <Pstatic> of the measured RNPU is roughly 1.9 nW. For an estimate of the RNPU power efficiency, we use a conservative value of 5 nW, leading to 320 nW for 64 RNPUs in parallel, which is roughly 3 times lower than realized with analogue filterbanks reported in ref. 25. However, it is worth emphasizing that the advantage of RNPU preprocessing extends beyond this improvement by simplifying the classification step, as illustrated in Fig. 2.

System-level efficiency analysis

The 6-layer CNN model for the GSC dataset, implemented on the IBM HERMES project chip, possesses roughly 470,000 learnable parameters and requires 120 M MAC operations per RNPU-preprocessed audio recording (all audio recordings have a duration of 1 s). On deployment of the AIMC chip, the model occupies 18 out of the available 64 cores (28% of the total number of cores), as depicted in Fig. 4e. Since the present chip is not designed and optimized for the studied tasks, but rather serves a general purpose, in each core some memristive devices remain unused causing the efficiency to drop.

In this regard, it is necessary to mention that we use experimental measurement reports from ref. 5 when the chip operates in one-phase read mode, although the reported inference accuracies are for the four-phase mode. The latter approach reduces the chip’s maximum throughput and energy efficiency by roughly four times, while accounting for circuit and device non-idealities. Our decision to report the results based on the one-phase read mode is recently supported by the literature57, as evidenced by the experimental demonstration of a new analogue or digital calibration procedure on the same IBM HERMES project chip. This procedure has been shown to achieve comparable high-precision computations in the one-phase read mode as those achieved in the four-phase model.

Convolution layers 0 to 3 in Fig. 4d of the main text require 1977, 492, 121 and 28 MVMs per number of occupied cores, respectively. Therefore, the total number of MVMs (including two fully connected layers) is \(\mathop{\sum }\limits_{l=0}^{5}{{\rm{MVMs}}}_{l}\times {\rm{num}}\_{\rm{cores}}={\rm{5,861}}\). The IBM HERMES project chip consumes 0.86 µJ at full use (for all 64 cores) for MVM operations with a delay of 133 ns. Consequently, the classifier model consumes \(\frac{5,\,861}{64}\times 0.86\,{\rm{\mu }}{\rm{J}}=78.7\,{\rm{\mu }}{\rm{J}}\). Similarly, the end-to-end latency can be calculated as \(\mathop{\sum }\limits_{l=0}^{5}{{\rm{MVMs}}}_{l}\times 133\,{\rm{ns}}=2,\,619{\rm{\times }}133\,{\rm{ns}}=348.3\,{\rm{\mu }}{\rm{s}}\). Note that a layer (weight) matrix is typically partitioned into submatrices to be fitted on the AIMC crossbar core57. In our calculations, we assume that these submatrices are mapped to different cores and, therefore, the partial block-wise MVMs are executed in parallel.

Our evaluation approach stands on the conservative side for MVM energy consumption; for instance, we assume energy consumption of one core for linear layers with 17,152 learnable parameters (out of 262,144 memristive devices of a core, which is only 6.5% use). However, we assume negligible energy consumption due to (local) digital processing, which rounds for roughly 7% of the total energy consumption (28% core use × 27% local digital processing unit’s part out of total static power consumption). Further, because of batch-norm and maximum-pooling layers, we buffered MVM results of each layer on memory, which introduces extra delay to the computations. However, for real-world tasks, we can avoid CNNs but rather use large multilayer perceptrons or recurrent neural networks instead.

Comparing energy consumption and latency with state of the art

We conducted a comparative analysis of the system-level energy consumption and latency of our architecture with other state-of-the-art speech-recognition systems, summarized in Extended Data Table 2. Dedicated digital speech-recognition chips consume the lowest amount of energy per inference. Nevertheless, because of the long latency of computations, their energy-delay product) is markedly high. A recent KWS task implemented on an AIMC-based chip has shown classification latency reduction, specifically, 2.4 μs compared with a 16-ms delay of digital solutions. However, this approach is based on extensive preprocessing that includes extracting mel-frequency cepstral coefficient features and pruning the features to increase the classification accuracy. Furthermore, not reporting the energy consumption, and only considering the classification latency (excluding preprocessing) are the reasons that make a direct comparison impossible.

It is worth mentioning that our energy estimate for the AIMC classification stage is based on experimental measurements from a prototype AIMC tile5. Similar to any emerging technology, we anticipate that these energy figures will notably improve as the technology matures beyond the prototyping stage39. These improvements are expected to occur at not only the peripheral circuitries, but also at the PCM device level: active efforts are already underway in both areas.

In AIMC, integration time and the ADC power consumption are major sources of the total energy consumption. In the AIMC chip used in this work, clock transients and the bit-parallel vector encoding scheme limit the MVM latency to roughly 133 ns. However, bit-serial encoding scheme and increasing the clock frequency is now being explored to reduce the integration time below around 50 ns. Furthermore, ADCs at the moment account for up to 50% of the total power consumption5. Efforts are underway to adopt time-interleaved, voltage-based ADCs, potentially in a design that avoids power-hungry components, such as operational transimpedance amplifiers. These design improvements will substantially reduce power consumption while also further improving conversion speeds through a single ADC conversion for signed inputs. Furthermore, introducing power gating techniques, which are not implemented at present, can further reduce ADC energy usage during idle periods.

At the PCM device level optimization, research is being conducted to reduce the conductance values of the programmable non-volatile states. Recent experimental measurements have shown that a more than ten times reduction in the conductance values can be achieved61, which can lead to proportional improvements in energy efficiency at the crossbar level. Taking all these enhancements into account, a conservative future estimate places the energy per inference in the range of roughly 10 μJ, which would also make AIMC systems competitive with state-of-the-art ASR processors in terms of energy efficiency.