Transitions in dynamical regime and neural mode during perceptual decisions

Abstract

Perceptual decision-making is thought to be mediated by neuronal networks with attractor dynamics^1,2. However, the dynamics underlying the complex neuronal responses during decision-making remain unclear. Here we use simultaneous recordings of hundreds of neurons, combined with an unsupervised, deep-learning-based method, to discover decision-related neural dynamics in the rat frontal cortex and striatum as animals accumulate pulsatile auditory evidence. We found that trajectories evolved along two sequential regimes: an initial phase dominated by sensory inputs, followed by a phase dominated by autonomous dynamics, with the flow direction (that is, neural mode) largely orthogonal to that in the first regime. We propose that this transition marks the moment of decision commitment, that is, the time when the animal makes up its mind. To test this, we developed a simplified model of the dynamics to estimate a putative neurally inferred time of commitment (nTc) for each trial. This model captures diverse single-neuron temporal profiles, such as ramping and stepping^3,4. The estimated nTc values were not time locked to stimulus or response timing but instead varied broadly across trials. If nTc marks commitment, evidence before this point should affect the decision, whereas evidence afterwards should not. Behavioural analysis aligned to nTc confirmed this prediction. Our findings show that decision commitment involves a rapid, coordinated transition in dynamical regime and neural mode and suggest that nTc offers a useful neural marker for studying rapid changes in internal brain state.

Main

Theories of attractor dynamics have been successful at capturing several brain functions⁵, including motor planning⁶ and neural representations of space^7,8. Attractors are a set of states towards which a system tends to evolve from a variety of starting positions. In these theories, computations of a brain function are carried out using the temporal evolution or the dynamics of the system. Experimental findings support the idea that the brain uses systems with attractor states for computations underlying working memory⁶ and navigation⁷. These theories often focus on the low-dimensional nature of neural population activity^2,9,10 and account for responses across a large number of neurons using a dynamical system model in which the variable has only a few dimensions^7,11,12,13.

Attractor network models have also been proposed to underlie perceptual decision-making: the process by which noisy sensory stimuli are categorized to select an action or mental proposition. In these hypotheses, the network dynamics carry out the computations needed in decision formation^1,2,14,15,16, such as accumulating sensory evidence and committing to a choice. Although some experimental evidence favours a role of attractors in perceptual decisions^2,16,17, the actual population-level dynamics underlying decision-making have not been directly estimated. Knowledge of these dynamics would directly test the current prevailing attractor hypotheses, provide fundamental constraints on neural circuit models and account for the often complex temporal profiles of neural activities.

A separate line of work involves tools, sometimes based on deep learning, for discovering the low-dimensional component of neural activity in a data-driven manner^10,18,19. In this approach, the spike trains of many simultaneously recorded neurons are modelled as being a function of a few latent variables that are shared across neurons.

To combine both lines of work, we used an innovative method²⁰ that estimates, from the spike trains of simultaneously recorded neurons, the dynamics of a low-dimensional variable z, given by:

$$\dot{{\bf{z}}}=F({\bf{z}},{\bf{u}})+{\boldsymbol{\eta }},$$

(1)

where u are external inputs, η is noise and, when applied to perceptual decisions, z represents the dynamical state of the decision process of the brain at a given time (Fig. 1a–c). The instantaneous change of the decision variable or its dynamics is given by ż, which depends on z itself, and u and η. This approach aims to estimate the function F and, through it, capture the nature of decision-making neural dynamics.

Fig. 1: Attractor models of decision-making were tested by recording from the rat frontal cortex and striatum.

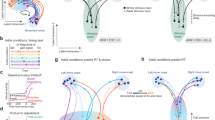
a, Rats were trained to accumulate auditory pulsatile evidence over time. While keeping its head stationary, the rat listened to randomly timed clicks played from loudspeakers on its left (L) and right (R). At the end of the stimulus, the rat received a water reward for turning to the side with more clicks. The earliest time when a rat could respond was fixed at 1.5 s relative to the moment of inserting its nose in the centre port (that is, not a reaction time paradigm). b, Behavioural performance in an example recording session. Dashed reference lines at abscissa = 0 and ordinate = 0.5. c, The decision process is modelled as a dynamical system. Right, the blue and red arrows represent the change in the decision variable in the presence of a left or right, respectively. z₁, z dimension 1; z₂, z dimension 2. d, Autonomous dynamics illustrated using the bistable attractor hypothesis. In the velocity vector field (that is, flow field; left), the arrow at each value of the decision variable z indicates how the instantaneous change depends on z itself. The orientation of the arrow represents the direction of the change, and its size represents the speed, also quantified using a heat map (right). e, Changes in z driven solely by external sensory inputs (example of bistable attractors). f, Bistable attractor hypothesis of decision-making, with directions of the input dynamics (based on ref. ¹). g, A hypothesis supposing a line attractor in the autonomous dynamics on the basis of the DDM of decision behaviour (based on ref. ²³). h, Recurrent neural networks can be trained to make perceptual decisions using a line attractor that is not aligned to the input dynamics (non-normal; based on ref. ²). i, Unsupervised discovery (this study) of dynamics that have not been previously considered. j, Six interconnected frontal cortical and striatal regions are examined here. vStr, ventral striatum. k, Neuropixels recordings (318 ± 147 neurons per session per probe, mean ± s.d.) from 12 rats in total (two to three regions per rat). AP, anteroposterior; ML, mediolateral.

Differentiating dynamical hypotheses

The function F is useful for distinguishing among hypotheses of decision-making. F can be dissected into two components: autonomous dynamics and input-driven dynamics. Autonomous dynamics are dynamics in the absence of sensory inputs u (that is, F(z, 0); Fig. 1d and Extended Data Fig. 1a,b). Input dynamics are changes in z driven by u, which can be distinguished from autonomous dynamics as F(z, u) − F(z, 0). Input dynamics can depend on z (Fig. 1e and Extended Data Fig. 1c–e).

Many of the prevailing neural attractor hypotheses have been inspired by a classic and successful behavioural-level model, the drift diffusion model (DDM)^21,22. In the behavioural DDM, a scalar (that is, one-dimensional) decision variable z is driven by sensory evidence inputs (Extended Data Fig. 6a,b). For example, for decisions between go right versus go left, momentary evidence for right (left) might drive z in a positive (negative) direction. Through these inputs, the momentary evidence accumulates over time in z until the value of z reaches an absorbing bound, a moment thought to correspond to decision commitment and after which inputs no longer affect z. Different bounds correspond to different choice options: a positive (or negative) bound would correspond to the decision to go right (or go left). A straightforward implementation of the DDM in neural population dynamics, which we refer to as the DDM line attractor, would posit a line attractor in neural space, with the position of the neural state z along that line representing the value of z and two point attractors at the ends of the line representing the decision commitment bounds²³ (Fig. 1g). Another hypothesis approximates the DDM process using bistable attractors¹, with each of the two attractors representing each of the decision bounds and, in between the two attractors, a one-dimensional stable manifold of slow autonomous dynamics that corresponds to the evidence accumulation regime (Fig. 1f). In both the DDM line attractor and bistable attractor hypotheses, evidence inputs are aligned with the slow dynamics manifold and the attractors at its end points. A third hypothesis, inspired by trained recurrent neural networks, also posits a line attractor (Fig. 1h) but allows for evidence inputs that are not aligned with the line attractor and that accumulate over time through non-normal autonomous dynamics². In all three hypotheses, the one-dimensional line attractor and/or slow manifold is stable, meaning that autonomous dynamics flow towards it (Fig. 1f–h). Because these three hypotheses were each designed to explain a particular set of the phenomena observed in decision-making experiments, a broader range of experimental observations could suggest dynamics that have not been previously considered. As but one example, autonomous dynamics may contain discrete attractors that do not lie at the end points of a one-dimensional slow dynamics manifold; many other arrangements are possible. In the data-driven approach we describe below, F is estimated purely from the spiking data and the timing of sensory input pulses, without incorporating any assumptions from the behavioural DDM or other existing hypotheses.

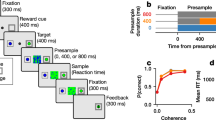
Dissociating between autonomous and input dynamics requires neural recordings during a decision unfolding over a time period that includes intervals both with and without momentary evidence inputs. We trained rats to perform a task in which they listened to randomly timed auditory pulses played from their left and their right and reported the side on which more pulses were played²⁴ (Fig. 1a). The stochastic pulse trains allow us to sample neural responses time locked to pulses, which are useful for inferring input-driven dynamics, and also the neural activity in the intervals between pulses, which is useful for inferring autonomous dynamics. Expert rats are highly sensitive to small differences in auditory pulse number (Fig. 1b and Extended Data Fig. 2a), and the behavioural strategy of rats in this task is typically well captured by gradual accumulation of evidence, which is at the core of the DDM^24,25,26.

While the rats performed this task, we recorded six frontal cortical and striatal regions with chronically implanted Neuropixels probes (Fig. 1j,k and Extended Data Fig. 2b). The frontal orienting fields (FOF) and the anterior dorsal striatum (dStr) are known to be causally necessary for this task and are interconnected^27,28,29. The dorsomedial frontal cortex (dmFC) is a major anatomical input to the dStr³⁰, as confirmed by our retrograde tracing (Extended Data Fig. 2c), and is also causally necessary for the task (Extended Data Fig. 2d). The dmFC is interconnected with the medial prefrontal cortex (mPFC) and, less densely, the FOF, the primary motor cortex (M1)³¹ and the anterior ventral striatum³⁰.

Unsupervised discovery of dynamics

To test the attractor hypotheses and allow discovery of dynamics not previously considered, a flexible yet interpretable method was needed. We used an innovative deep learning method (flow field inference from neural data using deep recurrent networks; FINDR²⁰) that infers the low-dimensional stochastic dynamics that best account for population spiking data. The low dimensionality of the description is critical for interpretability. Prominent alternative deep-learning-based approaches for inferring neural latent dynamics involve models in which these latent dynamics have hundreds of dimensions and are deterministic¹⁸. By contrast, FINDR infers latent dynamics that are low dimensional and stochastic. The stochasticity in the latent dynamics accounts for noise in the decision process that contributes to errors. FINDR approximates the decision-relevant dynamics F with a gated multilayer perceptron network³² and noise η as a Gaussian with diagonal covariance (equation (1) and Fig. 2a). The firing rate of each neuron at each time point is modelled as a weighted sum of the z variables, followed by a softplus nonlinearity, which can be thought of as approximating neuronal current–frequency curves⁶ (Fig. 2b). The weighting for each neuron (vector w_n for neuron n, comprising the nth row of a weight matrix W; Fig. 2b) is fit to the data. To aid the interpretability of z, we transform W after training such that its columns are orthonormal and it therefore acts as a rotation. As a result, angles and distances in z are preserved in Wz (neural space before softplus). Before learning F and W, we separately account for the decision-irrelevant, deterministic but time-varying baseline firing rate for each neuron (baseline in Fig. 2b) so that FINDR can focus on the choice formation process.

Fig. 2: Unsupervised discovery shows transitions in dynamical regime and neural mode underlying the shift from evidence accumulation to decision commitment.

a, Decision-relevant dynamics are inferred using FINDR²⁰. b, FINDR learns the decision variable z that best captures neural spiking activity. Each neuronal spike count at a given time step is modelled as a Poisson random variable with the rate given by an affine transformation of z at that time step, followed by the softplus nonlinearity. The grey box indicates the decision variable z at an example time step, and the yellow box indicates the spike counts at that time step. A time-varying baseline is learnt for each neuron to capture the decision-irrelevant component of its activity. c–h, Vector field inferred from 96 simultaneously recorded choice-selective neurons in the dmFC and the mPFC from a representative session. Only the portion of the state space visited by at least 50 of 5,000 simulated 1-s trajectories (sample zone) is shown. c, Autonomous dynamics. d, Speed of autonomous dynamics. e, Input dynamics for left and right clicks. If u = [1;0] indicates a left click input, F(z, [1;0]) − F(z, 0) is the input dynamics given a left click. However, the average left input dynamics depend on the frequency of left clicks, given by p(u = [1;0]|z). Therefore, we compute the average left input dynamics F(z, left) − F(z, 0) as p(u = [1;0]|z)(F(z, [1;0]) − F(z, 0)). We compute the average right input dynamics similarly, with u = [0;1]. f, Speed of input dynamics. g, Difference in speed between autonomous and input dynamics. h, Initially, z is strongly driven by inputs, and its trajectories develop along the evidence accumulation axis aligned with the direction of input dynamics. At a later time, the trajectories become largely insensitive to the inputs and are instead driven by autonomous dynamics to evolve along the decision commitment axis aligned with the direction of autonomous dynamics.

We first confirmed that, in synthetic data, the velocity vector fields (flow fields) inferred by FINDR can distinguish between existing attractor hypotheses (Extended Data Fig. 1f–h). Next, we turned to the recorded spiking data and confirmed that FINDR provides a good fit to the heterogeneous single-trial firing rates of individual neurons and to the complex dynamics in their peristimulus time histograms (PSTHs) conditioned on the sign of the evidence (Extended Data Fig. 3a–d). We found that two latent dimensions suffice to capture our data well (Extended Data Fig. 3e–i). For models with more than two latent dimensions, the latent dynamics are still mostly confined to two dimensions, and this two-dimensional manifold is approximately an attractor (Extended Data Fig. 3h–k).

Figure 2c–h shows a representative recording session from the dmFC and the mPFC. We found that, generally, two-dimensional input-driven dynamics and autonomous dynamics inferred by FINDR were not described well by the existing hypotheses: in all three hypotheses illustrated in Fig. 1d–h, there is a one-dimensional stable manifold that either is or approximates a line attractor. By contrast, even though, over the first 330 ms, the average trajectories evolve along an approximately straight line (Fig. 2h), the line is not a one-dimensional attractor, and individual trials diverge from it. Furthermore, in all three hypotheses in Fig. 1d–h and in all other hypotheses we are aware of, autonomous dynamics play an important part throughout the entire decision-making process. For example, autonomous dynamics are what enforce the stability of the one-dimensional slow manifolds in Fig. 1d–h. By contrast, at least in the space of the latent variable z, FINDR-inferred dynamics suggest that, initially, motion in neural space is dominated and driven by inputs to decision-making regions (that is, by the input-dependent dynamics), not the autonomous dynamics, which are slow in both dimensions (Fig. 2c–h), not only one. Later in the decision-making process, the balance between autonomous versus input-driven dynamics inverts, and it is the autonomous dynamics that become dominant. Plots in Fig. 2g show the difference in magnitude between autonomous and input-driven dynamics (indicated with the colour scale) on the z plane. The initial dominance of the input-driven dynamics can be seen in the zone near the (0, 0) origin at the negative end of the colour scale. The later dominance of autonomous dynamics can be seen in the right and left edges of the sampled region, reached later in the decision-making process, at the opposite end of the colour scale. Moreover, the direction of instantaneous change driven by the inputs (slightly clockwise from horizontal in Fig. 2e) is not aligned with the direction of the strongest autonomous dynamics in the left and right edges of the sampled region (slightly anticlockwise from vertical in Fig. 2c). The curved trial-averaged trajectories of z emerge from this non-alignment in the input direction and the autonomous direction later in the decision-making process. The change from an input-dominated to an autonomous-dominated dynamical regime and the sharp turn in the direction of the neural trajectories in Fig. 2c–h were observed consistently across rats and behavioural sessions (Fig. 3a–d). These observations were robust to several different initializations of the neural networks in FINDR, the order of minibatches during training and how datasets were split into training and test sets (Extended Data Fig. 4). They are therefore a consistent finding of the analysis.

Fig. 3: FINDR shows transitions in dynamical regime and neural mode consistently across sessions and better captures the data than a constrained model based on previous hypotheses.

a, To quantify how speed difference between autonomous and input dynamics evolves over a trial, we identify the time point when the latent trajectories curve (stars) and compute the speed difference in Fig. 2g before and after this point. The latent trajectories are trial-averaged, sorted by evidence strength. The trial-averaged trajectories and stars are coloured as in Fig. 2h. b, The peak is defined as the time of maximum curvature in the trial-averaged trajectories. Time periods are defined relative to this peak (before peak and after peak) and to trial start and end (early and late) for c,d. Black star symbol represents the peak of average trajectory curvature. c, We compute the normalized difference in speed between autonomous and input dynamics for five different time periods (start (time = 0 s), early, before peak, after peak and late) from vector fields inferred from sessions with more than 30 recorded neurons, over 400 trials during which the animal performed with more than 80% accuracy (n = 27 sessions). The dashed line indicates normalized difference of 0. CI, confidence interval. d, For sessions in which FINDR with the two-dimensional decision variable z fit significantly better than FINDR with one-dimensional z (n = 21 of 27; Extended Data Fig. 3), we measured the direction of motion of the trial-averaged trajectories and its angle with respect to the z₁ axis for different time periods (curving of trial-averaged trajectories across 21 sessions). e, cFINDR captures previous hypotheses and replaces the neural network parametrizing F with a combination of line attractor dynamics (specified by QΛQ⁻¹, with the diagonal matrix Λ having one zero and one negative eigenvalue) and bistable attractor dynamics (specified by a nonlinear function φ; Methods). f, Autonomous dynamics inferred by cFINDR and FINDR are shown for a representative session, with vector field outside the sample zone in grey. g, The coefficient of determination (R²) of the evidence–sign conditioned PSTH computed using fits of FINDR is significantly greater than those computed using fits of cFINDR (across 27 sessions, two-sided Wilcoxon signed-rank test).

To perform a head-to-head comparison with the three hypotheses in Fig. 1d–h, we constructed a variant of FINDR in which the network parametrizing F was replaced by a parametrization of the dynamics constrained to describe those three hypotheses (Fig. 3e,f and Extended Data Fig. 5). If the data were described well by one of these hypotheses, we would expect this variant (which we refer to as cFINDR, for constrained FINDR) to fit the data well, particularly out of sample, because it has far fewer parameters than FINDR. However, unconstrained FINDR consistently fit the data better than cFINDR, confirming that previous hypotheses do not adequately capture the data. Although one of the hypotheses (Fig. 1h, suggesting non-normal dynamics with a line attractor) can generate curved trial-averaged trajectories apparently similar to those we see in the data (Fig. 3e,f and Extended Data Fig. 5g), there is a key difference, which is that, in this particular hypothesis, the turn from the initial flow direction induced by the inputs happens early, because the autonomous dynamics causing it are strong the moment the latent state departs from the line attractor. However, our data suggest that there is a more prolonged initial phase of flow along the input directions before the turn, with the stronger autonomous dynamics happening much later in the decision-making process. We believe that this underlies the much better fits to the data for FINDR than those for cFINDR.

A recent study³³ described neural trajectories that were described well by non-normal dynamics^34,35. Consistent with this, the two-dimensional FINDR-inferred autonomous dynamics around the origin are also non-normal (Extended Data Fig. 10b,c), although with a key difference with respect to refs. ^33,34,35, which is that here the origin is unstable (Extended Data Fig. 10a,e).

Unsupervised inference of dynamics underlying decision-making, based only on spiking activity and sensory evidence inputs, thus suggests that the process unfolds in two separate sequential regimes. In the initial regime, dynamics are largely determined by the inputs, with autonomous dynamics playing a minor role. The sensory evidence inputs (right and left clicks) drive the decision variable to evolve along an axis, parallel to the directions of the input dynamics, that we will term the evidence accumulation axis. In the second, later regime, these characteristics reverse; the trajectories representing the evolution of the decision variable become largely independent of the inputs and are instead mostly determined by autonomous dynamics. We will term the straight line along the direction of the autonomous dynamics in the later regime the decision commitment axis. Of note, the evidence accumulation axis and the decision commitment axis are not aligned with each other. During the regime transition, the trajectories in z veer from evolving along the evidence accumulation axis to developing along the decision commitment axis. In neural space, this will equate to a transition from evolving along one mode (that is, a direction in neural space), corresponding to evidence accumulation, to another mode that, as explained below, we believe may correspond to decision commitment.

Although derived entirely from unsupervised analysis of neural spiking activity and auditory click times, these two regimes are reminiscent of the two regimes of the behavioural DDM: namely, an initial regime in which momentary sensory inputs drive changes in the state of a scalar decision variable z and a later regime, after z reaches a bound, in which the state becomes independent of sensory inputs (Extended Data Fig. 2e,f). The correspondence between the two regimes inferred from spiking activity and the behavioural DDM suggests that the transition between regimes may correspond to the moment of decision commitment. It further suggests that a modified neural implementation of the DDM, focusing on key aspects of the two regimes, could be a simple model that captures many aspects of the neural data, although having far fewer parameters than FINDR and thus greater statistical power. We next develop this model and show that it can be used to precisely infer the regime transition time in each trial and test the proposal that this transition corresponds to decision commitment.

Simplified model of decision dynamics

FINDR-inferred vector fields show a rapid shift from strongly input-driven to autonomous-dominant dynamics, analogous to the transition from evidence accumulation to decision commitment in the behavioural DDM (Fig. 4a,b). The DDM captures behaviour in a wide range of decision-making tasks, including tasks in which the stimulus duration is determined by the environment^{24,25,28,36,37}, as used here. This suggests that the FINDR-inferred dynamics may be approximated by a simplified model in which the decision variable evolves as in the behavioural DDM.

Fig. 4: A simplified model captures discovered dynamics and diverse neuronal profiles.

a, The velocity vector field of both the discovered dynamics and the DDM line attractor can be partitioned into evidence accumulation (EA) and decision commitment (DC) regimes. b, The MMDDM, a simplified model of the discovered dynamics. As in the behavioural DDM, momentary evidence (u) and noise (η) accumulate over time in the decision variable (z) until z reaches either the left (−B) or right (+B) bound. At this moment, the animal commits to a decision: z becomes fixed and unresponsive to further input. Also at this moment, the encoding weight (w) of each neuron shifts from w_EA to w_DC, changing how z maps to the predicted Poisson firing rate y through softplus nonlinearity h and baseline b. c, MMDDM captures heterogeneous single-neuron profiles. A ramp PSTH arises when w_EA and w_DC are equal. d, A decay profile emerges when w_DC is zero because, over time, more trials reach the bound where encoding of z vanishes. e, A delay profile results from setting w_EA to zero because, early in the trial, it is unlikely to have reached the bound. f, ‘Flip’ is produced by setting w_EA and w_DC to have opposite signs. g, MMDDM captures heterogeneity in single-neuron temporal profiles. Shading represents 95% bootstrap CI of the mean; the solid line is the model prediction. h, MMDDM has a higher out-of-sample likelihood than a one-dimensional DDM without a neural mode switch. i, MMDDM achieves a higher goodness-of-fit R² value of the choice-conditioned PSTHs. h,i, P values were computed using two-sided sign tests. j, Model prediction (pred.) and observed psychometric function for one example session. The shaded areas are the 95% bootstrap CI of the mean; the solid line is the model prediction.

The regime transition coincides with rapid reorganization in the neuronal population representation of the decision process. To quantify this reorganization, we treat the activity of each neuron as a dimension in neural space, with axes in this space as neural modes. Seen in this way, the shift from evidence accumulation to decision commitment is coordinated with a fast transition in the neural mode, analogous to the rapid change in neural modes from motor preparation to motor execution³⁸. This motivates whether a simplified model based on a rapid, coordinated transition in both dynamical regime and neural mode can capture the key features of FINDR-inferred dynamics and broader experimental observations.

In what we will call the multimode or minimally modified DDM (MMDDM), a scalar decision variable z evolves just as in the behavioural DDM, governed by three parameters (Fig. 4b, Extended Data Fig. 6a,b and the Methods). The key addition is that neurons encode z differently before and after the decision commitment bound is reached. Each neuron has two weights: w_EA for the evidence accumulation phase and w_DC for the decision commitment phase. When w_EA and w_DC are constrained to be the same, the MMDDM reduces to a standard DDM with a single neural mode. In the DDM line attractor hypothesis in Fig. 1g, if the autonomous dynamics towards the line attractor are strong relative to the noise, trajectories will be largely one dimensional, which are approximated well by a single-mode DDM. Because neurons multiplex both decision-relevant and decision-irrelevant signals^39,40, MMDDM includes terms for spike history and, similar to FINDR, decision-irrelevant baseline changes (Extended Data Fig. 6c–f). All parameters are fit jointly for each session using both neural activity and behavioural choices.

MMDDM can account for a broader range of neuronal profiles (Fig. 4c–g) than the single-mode DDM, which captures only ramp-like neuronal temporal profiles (Extended Data Fig. 2e–l). In the vast majority of recording sessions, the data are better fit by MMDDM than by the single-mode DDM (cross-validated; Fig. 4h,i). The model also accurately captures the choice data (Fig. 4j and Extended Data Fig. 6g) and reproduces vector fields that closely resemble those inferred from real spike trains (Extended Data Fig. 6h). Additional validations are shown in Extended Data Fig. 6i–n. Finally, because the end of the stimulus was fixed across trials relative to fixation onset, stimulus offset was not included as an input in MMDDM, consistent with the lack of abrupt neural changes at stimulus offset (Extended Data Fig. 9).

nTc

In MMDDM, the transition from evidence accumulation to decision commitment and a consequent switch from w_EA to w_DC directly implement a change in neural mode between the two phases of the trial, which was previously suggested^9,41. However, it remains unclear whether this neural mode change corresponds to the animal making up its mind, in part because no method has been developed previously to precisely estimate its timing in single trials. The behavioural DDM, without neural data, can provide a rough estimate of the moment of commitment (Fig. 5a, dashed grey line). But on the basis of the hypothesis that the time of the neural mode change corresponds to the time of commitment and, using data from many simultaneously recorded neurons, MMDDM allows a far more precise estimate per trial (Fig. 5a, orange line). We refer to this moment as nTc. Surprisingly, nTc varied widely across trials. It was not time locked to stimulus onset (Fig. 5b), stimulus offset (Extended Data Fig. 7n) or the onset of the decision-reporting motor response (Fig. 5c). Instead, nTc seemed to be an internally timed event. nTcs also occurred well after the onset of perimovement kernels inferred from generalized linear models of single-neuron spike trains⁴⁰ (Extended Data Fig. 8), indicating that nTcs do not reflect the initiation of action plan encoding.

Fig. 5: nTc marks the moment of internal decision commitment.

a, Example trial. The inferred time of commitment is far more precise when neural activity is used (nTc, orange line) than when it is inferred solely from sensory stimulus timing and choice behaviour (dashed grey line). b, Distribution of estimated nTc values relative to stimulus onset. Among the 34.7% of trials in which commitment times could be detected, nTc varied widely relative to the onset of auditory click trains. The decline in nTc frequency over time reflects randomized stimulus durations (0.2–1.0 s). c, Distribution of nTc values relative to movement onset to report the decision of the animal (exiting centre fixation port). As in b, nTc timing also varies widely across trials. The leftmost bin includes trials in which the nTc occurred more than 1 s before movement. d, Supporting the interpretation of nTc as a decision commitment and, despite the highly variable timing of nTc, sensory evidence presented before nTc affects the decision of the animal but evidence presented after nTc does not (weight of clicks on choice inferred using logistic regression). Trials for which the estimated time of commitment occurred at least 0.2 s before stimulus offset and 0.2 s or more after stimulus onset were included for this analysis (9,397 of 55,057 trials across 115 sessions with 12 rats). The green line is the prediction from the MMDDM model fit to the data. e, Behavioural accuracy was lower in trials in which nTc could not be identified. Predictions were made by fitting MMDDM to the data, simulating trials from the fitted models and applying the same nTc detection procedure as that used for real data. Dashed reference lines at abscissa = 0 and ordinate = 0.5. f, nTc was more likely to be identified in trials with stronger evidence. For each evidence strength bin, the fraction of trials with an identified nTc was divided by the overall trial fraction across all bins, which was lower in the data than in the model predictions. Black circles and green lines indicate the mean across sessions. Black error bars and green shading indicate the 95% bootstrap confidence of the mean. Dashed reference lines at ordinate = 1.0.

A core prediction of the hypothesis that nTc marks the time of internal decision commitment is that, after nTc, auditory click stimuli should stop influencing the behavioural choice, because the animal will have already made up its mind. The single-trial estimates of nTc that MMDDM provides can be used to test this prediction: we time align the sensory stimulus data of each trial to the neurally estimated nTc and then behaviourally measure the weight with which stimulus fluctuations at each time point affect choice (that is, the psychophysical kernel⁴²; Methods). Remarkably, as predicted, we found that the psychophysical weight of stimulus fluctuations on the choice of the animal diminished abruptly to zero after nTc (Fig. 5d and Extended Data Fig. 7). Because these commitment times varied widely across trials (Fig. 5b,c), the abrupt drop in psychophysical weight cannot be observed without the single-trial nTc estimates. If we instead align trials to the stimulus onset, we obtain a smooth psychophysical kernel (Extended Data Fig. 7e–h), as observed in previous studies lacking access to nTc²⁴.

nTc showed further hallmarks of being a marker of commitment: First, for a given evidence strength, trials without commitment are predicted to be more likely to involve noise acting against the sensory evidence, leading to lower accuracy. Consistent with this prediction, accuracy was lower in trials when nTc could not be identified (Fig. 5e). Second, commitment should occur more often when evidence is stronger, and, accordingly, nTc was more frequently detected in trials with stronger evidence (Fig. 5f). Additional hallmarks are shown in Extended Data Fig. 7i–q. Together, these results offer behavioural support for an internally timed commitment event, after which sensory inputs are ignored, and the timing of which can be inferred from spiking data using nTc.

Abrupt and gradual shifts at commitment

Perceptual decision-making involves a diversity in the temporal profiles of choice-selective neurons, with some showing a ramp-to-bound profile, others exhibiting a step-like profile and some falling in between a ramp and a step^3,4. We found that the continuum of ramping and stepping profiles can be captured by a rapid reorganization in population activity at the time of decision commitment, as described by MMDDM. We grouped neurons by whether they were estimated to be more, less or similarly engaged in evidence accumulation relative to decision commitment (|w_EA| > |w_DC|, |w_EA| ≈ |w_DC| and |w_EA| < |w_DC|, respectively, in MMDDM fits). We then computed the pericommitment neural response time histogram (PCTH) of each neuron (Methods and Fig. 6a,b). For neurons similarly engaged in accumulation and commitment, the PCTH had a ramp-to-bound profile, whereas, for neurons more engaged in commitment, the PCTH resembled a step. For neurons more engaged in accumulation, the PCTH had a ramp-and-decline profile. Even without grouping neurons, we found that the first three principal components (PCs) of the PCTHs correspond to the ramp-to-bound, step and ramp-and-decline profiles.

Fig. 6: Simplified model captures heterogeneous single-neuron temporal profiles, such as ramping and stepping, and shows functional distinctions between brain regions.

a, PCTHs for neurons grouped by relative engagement (defined in f). Neurons similarly engaged in evidence accumulation and decision commitment have ramp-to-bound profiles (centre). Neurons more engaged in decision commitment have step-like profiles (right), whereas those more engaged in evidence accumulation have ramp-and-decline profiles (left). ‘Preferred’ indicates the choice eliciting higher firing. Data are the mean across neurons and the 95% CI. b, First three PCs of PCTH differences (preferred − nonpreferred choice) across all neurons, capturing ramp-to-bound (PC1), step (PC2) and ramp-and-decline (PC3) profiles. c, Observed curved trial-averaged trajectories (projected onto the first two PCs) are captured by the MMDDM (centre) but not the single-mode DDM (right). Time from stimulus onset. Proj., projection. d, MMDDM better captures the data than the single-mode DDM (out-of-sample log likelihood: MMDDM − single-mode DDM). e, The neuron-averaged choice selectivity has different temporal profiles across brain regions: mPFC neurons are most choice selective near the beginning, whereas FOF neurons are most choice selective towards the end. f, Engagement index (EI) quantifying relative neuronal engagement in evidence accumulation versus decision commitment. PSTHs are shown for three example neurons. Shading is the 95% CI of the mean; line indicates model prediction. g, A gradient across brain regions in the strength of neural mode transitions from stronger engagement in accumulation (for example, mPFC) to more balanced engagement (for example, FOF). Marker indicates median. Overall differences in engagement index across regions were assessed using the Kruskal–Wallis test (P = 1 × 10⁻⁴⁴). Post hoc pairwise comparisons using the Tukey–Kramer test yielded P < 0.001 for mPFC versus dStr, dmFC, M1 and ventral striatum; dStr versus M1 and FOF; and dmFC versus FOF (exact P values are in the Supplementary Notes (section 2.1).

The abrupt changes at decision commitment seem inconsistent with smoothly curved trial-averaged trajectories in low-dimensional neural state space often observed in decision-making studies^2,9. Similar phenomena are observed in our data: the trial-averaged trajectories for left and right choices do not separate from each other along a straight line but rather along curved arcs (Fig. 6c). These smoothly curving arcs may result from averaging over trajectories with an abrupt turn aligned to decision commitment, which occurs at different times across trials (Fig. 5b–d). Consistent with this account, the smooth curves in low-dimensional neural state space can be captured well by the out-of-sample predictions of MMDDM but not by a one-dimensional DDM without a neural mode switch (Fig. 6c). These results indicate that the MMDDM, a simplified model of the discovered dynamics, can capture the widespread observation well of smoothly curved trial-averaged trajectories.

Mode transitions across regions

Although we generally observed dynamics with a neural mode transition across several frontal cortical and striatal areas, quantitative differences could be observed across these regions. The choice selectivity (a measure, ranging from −1 to 1, of the difference in firing rates for right-versus-left-choice trials; Extended Data Fig. 2m) averaged across neurons had different temporal profiles across brain regions (Fig. 6e). Although mPFC neurons were most choice selective near the beginning, FOF neurons were most choice selective towards the end. We found that the difference in latencies to peak choice selectivity was linked to differences in relative neuron engagement in evidence accumulation and decision commitment. Neurons that were more strongly engaged in evidence accumulation (w_EA > w_DC) tended to have a shorter latency to peak selectivity than neurons that were more strongly engaged in decision commitment (w_DC > w_EA). This result indicates that differences in choice-related encoding across frontal cortical and striatal regions can be understood in terms of relative participation in evidence accumulation versus decision commitment (Fig. 6f,g).

Discussion

How neural dynamics govern the formation of a perceptual choice has been long debated^1,2,5. Here we suggest that, for decisions on the timescale of hundreds of milliseconds to seconds, an initial input-driven regime mediates evidence accumulation and a subsequent autonomous-dominant regime subserves decision commitment. This regime transition is coupled to a rapid change in the representation of the decision process by the neural population: the initial neural mode (that is, direction in neural space) representing evidence accumulation is largely orthogonal to the subsequent mode representing decision commitment. In this sense, it is reminiscent of other covert cognitive operations, such as attentional selection, that also involve a change in neural mode⁴³.

If this coupled transition in dynamical regime and neural mode indeed corresponds to the time of decision commitment, sensory evidence presented after the transition would have minimal impact on the decision of the animal, because the animal would have already committed to a particular choice. Behavioural analysis confirmed this prediction in the experimental data (Fig. 5d), leading us to conclude that the transition is indeed a signal for covert decision commitment. We refer to the estimate of the presence and timing of such a transition in each trial, which is based on the sensory stimulus and firing rates of simultaneously recorded neurons, as nTc.

We wondered how decisions end. In reaction time paradigms of perceptual decision-making, animals are trained to respond as soon as they make a decision. The moment the animal initiates its response is then used to operationally define when it commits to a choice^44,45. In these paradigms, decision commitment is overt, as it is closely linked to the onset of the movement animals make to report their choice⁴⁵. Here, by contrast, using an experimenter-controlled duration paradigm, we found a decision commitment signal (nTc) that is covert in the sense of occurring at a time highly variable with respect to the timing of the external motor action used to report the decision, which it can precede by as much a second or more (Fig. 5c). It is also highly variable with respect to stimulus onset (Fig. 5b) or offset (Extended Data Fig. 7n). It is thus an internal signal, largely defined by coordination across neurons, not by its timing with respect to external events. The pericommitment neural responses observed here contrast sharply with the ramp-and-burst neural responses observed in animals trained to couple their decision commitment with response initiation⁴⁵ in a reaction time task.

Although the timing of the nTc signal reported here makes it very distinct from motor execution, the signal is also distinct from action preparation or planning. The beginning of action planning carries no implication as to whether sensory evidence presented subsequently will or will not be ignored. Indeed, in perceptual decision-making tasks, preliminary action preparation, driven by choice biases induced by previous trials, is often observed to begin even before the sensory stimulus, as reported previously⁴⁰ and found in our own data (Extended Data Fig. 8). By contrast, commitment to a decision suggests that evidence presented subsequently to the commitment will no longer affect the choice of the animal. Here we found that nTc corresponds to such a decision commitment moment. This was the case both at the neural level, in which it correlates with a substantial decrease in the effect of sensory inputs on neural responses in the regions we recorded (Fig. 2), and at the whole-organism behavioural level, in the sense that sensory evidence before nTc affects the choices of the animal but sensory evidence after nTc does not (Fig. 5d).

Although the behavioural DDM is a widely used model of decision-making, other frameworks are also prevalent, such as the linear ballistic accumulator⁴⁶ or urgency gating⁴⁷. It is notable that the dynamics inferred by FINDR, obtained in a data-driven, unsupervised manner from spike times and auditory click times alone, resulted in regimes that match the characteristics of the behavioural DDM but not those of the alternatives. This match led us to explore a simplified model, the MMDDM, in which a scalar latent decision variable evolves as in the DDM but is represented in different neural modes before versus after decision commitment. The neural mode change indicates that a downstream decoder of the categorical choice can improve its accuracy by selectively reading out from neurons with post-commitment weights large in magnitude. A possible mechanism for the neural mode change is an input from ascending midbrain neurons, which is suggested by a recent finding in a working memory task that midbrain neurons, in response to an external auditory cue, trigger rapid reorganization of motor cortex activity to switch from planning-related activity to a motor command that initiates movement in mice⁴⁸.

We found that the MMDDM provides a parsimonious explanation of a variety of experimental findings from several species: across primates and rodents, sensory inputs and choice are represented in separate neural dimensions^2,9,40 across time, and neither sensory responses nor the neural dimensions for optimal decoding of the choice are fixed⁹. These phenomena, along with other observations including diversity in single-neuron dynamics^39,40, curved average trajectories⁹, choice behaviour²⁴ and some vigorously debated phenomena such as a variety of single-neuron ramping versus stepping temporal profiles^3,4, are all captured by the MMDDM. However, we do not see MMDDM as a unique or a unified model of perceptual decision-making. Rather, we see it as a simple yet useful approximation, a minimally modified DDM, and a stepping stone towards a unified model of decision-making.

Single-trial trajectories, in sum, filled out the two-dimensional latent space inferred by FINDR. But when averaged over trials of a given evidence strength (Fig. 2h), they evolved along a one-dimensional curved trajectory. Looking exclusively along this one-dimensional manifold, the dynamics resemble those of the bistable attractor hypothesis¹ (Fig. 1f) in the sense of a one-dimensional unstable point at the origin, with autonomous dynamics growing stronger the farther the system is from the origin. However, the bistable attractor hypothesis and the other two hypotheses in Fig. 1g,h posit a one-dimensional manifold of slow autonomous dynamics, along which evidence accumulation evolves and towards which other states are attracted^1,23. By contrast, the FINDR-inferred dynamics (which are inferred from single trials, not averaged trials) suggest an initial two-dimensional manifold of slow autonomous dynamics. Sensory evidence inputs drive evidence accumulation along one of these slow dimensions. The other slow dimension corresponds to the decision commitment axis, along which autonomous dynamics will become dominant later in the process. We wondered why there would be slow autonomous dynamics along this second dimension. We speculate that, during initial evidence accumulation, slow autonomous dynamics along the decision commitment axis provide a mechanism for inputs driven by non-sensory factors such as trial history⁴⁹ to influence choice independent of the accumulating sensory evidence.

The authors of one recently proposed method to infer autonomous dynamics, applied to data from a task that did not require accumulating evidence over time, proposed that variety across the tuning curves of individual neurons could lead to curved one-dimensional decision manifolds¹⁴. However, the authors’ method cannot yet infer input dynamics, and thus data from tasks with evidence that arrives gradually over time cannot yet be analysed; such an extension would have to be realized before we can assess whether the curvature their approach could infer would correspond to the curvature we described here for accumulation of evidence. Importantly, inferring input dynamics in addition to autonomous dynamics was critical to our observation that a change in dynamical regime, from input dominated to autonomous dominated, seemed to coincide with the change in neural mode (Fig. 2). This observation was key for our hypothesis that this event (nTc) could correspond to decision commitment, for development of the MMDDM simplified model to estimate nTc and for experimental confirmation that nTc is indeed the moment when sensory evidence ceases to affect the decision of the animal (Fig. 5d).

Finally, our approach expands the classic repertoire of techniques used to study perceptual decision-making. We inferred decision dynamics directly from neural data rather than assuming a specific hypothesis, and we took steps to enhance the human interpretability of the discovered dynamics: the unsupervised method (FINDR) focuses on low-dimensional rather than high-dimensional decision dynamics, and the mapping from latent to neural space (before the activation function of each neuron) preserves angles and distances. On the basis of key features of the inferred latent dynamics, we developed a highly simplified, tractable model (MMDDM) that is directly relatable to the well-known DDM framework. We found that the MMDDM, despite its simplicity, could describe a broad variety of previously observed phenomena and allowed us to infer the internal decision commitment times of the animal in each trial. Pairing deep-learning-based unsupervised discovery with simplified, parsimonious models may be a promising approach for studying not only perceptual decision-making but also other complex phenomena.

Methods

Experiments

Animals

The animal procedures described in this study were approved by the Princeton University Institutional Animal Care and Use Committee and were carried out according to the standards of the National Institutes of Health (NIH). Animals consisted of 16 adult, 6–24-month-old, male Long–Evans rats (Rattus norvegicus, Hilltop Lab Animals, Taconic) that were housed in Technoplast cages in pairs with a 12-h reversed light–dark cycle. All training and testing procedures were performed during the dark cycle. The rats had free access to food, but they had restricted access to water. The amount of water that the rats obtained daily was at least 3% of their body weight. Sample sizes were chosen on the basis of previous electrophysiological studies in rats^28,29. No blinding or randomization was performed.

Behavioural task

Rats performed the behavioural task in custom-made training enclosures (Island Motion) placed inside sound- and light-attenuated chambers (IAC Acoustics). Each enclosure consisted of three straight walls and one curved wall in which three nose ports were embedded (one in the centre and one on each side). Each nose port also contained one light-emitting diode that was used to deliver visual stimuli, and the front of the nose port was equipped with an infra-red beam to detect the entrance of the nose of the rat into the port. A loudspeaker was mounted above each of the side ports and used to present auditory stimuli. Each of the side ports also contained a silicone tube that was used for water reward delivery, with the amount of water controlled by valve-opening time.

Rats performed an auditory discrimination task in which optimal performance required the gradual accumulation of auditory clicks²⁴. At the start of each trial, rats inserted their nose in the central port and maintained this placement for 1.5 s (fixation period). After a variable delay of 0.5−1.3 s, two trains of randomly timed auditory clicks were presented simultaneously: one from the left speaker and one from the right speaker. At the beginning of each click train, a click was played simultaneously from the left and right speakers (stereoclick). Regardless of onset time, the click trains ended at the end of the fixation period, resulting in stimuli ranging from 0.2 s to 1 s. The train of clicks from each speaker was generated by an underlying Poisson process, with different click rates for each side. The combined mean click rate was fixed at 40 Hz, and trial difficulty was manipulated by varying the ratio of the generative click rate between the two sides. The generative click rate ratio varied from 39:1 (easiest) to 26:14 (most difficult) clicks per s. At the end of the fixation period, the rats could orient towards the nose port on the side where more clicks were played and obtain a water reward.

Psychometric functions were calculated by grouping the trials into eight bins of similar size according to the difference in the total number of right and left clicks and, for each group, computing the fraction of trials ending in a right choice. The CI of the fraction of right responses was computed using the Clopper–Pearson method.

Electrophysiological recording

Neurons were recorded using chronically implanted Neuropixels 1.0 probes that are recoverable after the experiment⁵⁰. In four animals, a probe was implanted at 4.0 mm anterior to the bregma and 1.0 mm lateral, for a distance of 4.2 mm, and at an angle of 10° relative to the sagittal plane that intersects the insertion site (the probe tip was more medial than the probe base). In five other animals, a probe was implanted to target M1, the dStr and the ventral striatum at the site 1.0 mm anterior and 2.4 mm lateral, for a distance of 8.4 mm, and at an angle of 15° relative to the coronal plane intersecting the insertion site (the probe tip was more anterior than the probe base). In a final set of three rats, a probe was implanted to target the FOF and anterior dStr at 1.9 mm anterior and 1.3 mm lateral, for a distance of 7.4 mm, and at an angle of −10° relative to the sagittal plane intersecting the insertion site (the probe tip was more lateral than the probe base). Spikes were sorted into clusters using Kilosort2 (ref. ⁵¹), and clusters were manually curated.

Muscimol inactivation

Infusion cannulas (Invivo1) were implanted bilaterally over the dmFC (4.0 mm AP, 1.2 mm ML) in three rats. After the animal recovered from surgery, the animal was anaesthetized, and, on alternate days, a 600-nl solution of either only saline or muscimol (up to 150 ng) was infused in each hemisphere. Half an hour after the animal woke up from anaesthesia, the animal was allowed to perform the behavioural task.

Retrograde tracing

To characterize anatomical inputs into the dStr, 50 nl of cholera toxin subunit B conjugate (Thermo Fisher Scientific) was injected into the dStr at 1.9 mm AP, 2.4 ML and 3.5 mm below the cortical surface. The animal was perfused 7 days after surgery.

Histology

The rat was fully anaesthetized with 0.4 ml ketamine (100 mg ml⁻¹) and 0.2 ml xylazine (100 mg ml⁻¹) intraperitoneally, followed by transcardial perfusion of 100 ml saline (0.9% NaCl, 0.3× PBS, pH 7.0 and 0.05 ml heparin at 10,000 USP units per ml) and finally transcardial perfusion of 250 ml of 10% formalin neutral buffered solution (Sigma, HT501128). The brain was removed and postfixed in 10% formalin solution for a minimum of 7 days. Sections (100 µm) were prepared on a Leica VT1200 S vibratome and mounted on Superfrost Plus glass slides (Fisher) with Fluoromount-G (SouthernBiotech) mounting solution and glass coverslips. Images were acquired on a Hamamatsu NanoZoomer under ×4 magnification.

Autonomous and input dynamics

The class of dynamical systems we study here is specified by

$$\dot{{\bf{z}}}=F({\bf{z}},{\bf{u}})$$

(2)

for some generic function F, with z the latent decision variable and u the external input to the system from the auditory clicks in the behavioural task. At each moment, there may be no click, a click from the left or a click from the right. When time is discretized to sufficiently short steps, u is one of three values:

$${\bf{u}}=\left\{\begin{array}{ll}[0;0]={\bf{0}} & \text{representing when there is no click},\\ \left[1;0\right] & \text{representing when there is a left click or}\\ \left[0;1\right] & \text{representing when there is a right click}.\end{array}\right.$$

(3)

We define the autonomous dynamics of the system as

$${\dot{{\bf{z}}}}_{{\rm{a}}{\rm{u}}{\rm{t}}{\rm{o}}{\rm{n}}{\rm{o}}{\rm{m}}{\rm{o}}{\rm{u}}{\rm{s}}}=F({\bf{z}},{\bf{0}})$$

(4)

and the average input dynamics as

$${\dot{{\bf{z}}}}_{\overline{{\rm{input}}}}=p({\bf{u}}|{\bf{z}})(F({\bf{z}},{\bf{u}})-F({\bf{z}},{\bf{0}}))$$

(5)

and, specifically, the average left and right input dynamics as

$$\begin{array}{c}{\dot{{\bf{z}}}}_{\overline{{\rm{left}}}}=p({\bf{u}}=[1;0]|{\bf{z}})(F({\bf{z}},[1;0])-F({\bf{z}},{\bf{0}})),\\ {\dot{{\bf{z}}}}_{\overline{{\rm{right}}}}=p({\bf{u}}=[0;1]|{\bf{z}})(F({\bf{z}},[0;1])-F({\bf{z}},{\bf{0}})).\end{array}$$

(6)

The sum of autonomous dynamics and average input dynamics is equal to the expected value of $\dot{{\bf{z}}}$ computed over the distribution p(u|z):

$$\begin{array}{c}{\mathbb{E}}[\dot{{\bf{z}}}]=\sum _{{\bf{u}}}p({\bf{u}}|{\bf{z}})F({\bf{z}},{\bf{u}})\\ \,=\,p({\bf{u}}={\bf{0}}|{\bf{z}})F({\bf{z}},{\bf{0}})+p({\bf{u}}=[1;0]|{\bf{z}})F({\bf{z}},[1;0])\\ \,+\,p({\bf{u}}=[0;1]|{\bf{z}})F({\bf{z}},[0;1])\\ \,=\,(1-p({\bf{u}}=[1;0]|{\bf{z}})-p({\bf{u}}=[0;1]|{\bf{z}}))F({\bf{z}},{\bf{0}})\\ \,+\,p({\bf{u}}=[1;0]|{\bf{z}})F({\bf{z}},[1;0])+p({\bf{u}}=[0;1]|{\bf{z}})F({\bf{z}},[0;1])\\ \,=\,F({\bf{z}},{\bf{0}})+p({\bf{u}}=[1;0]|{\bf{z}})(F({\bf{z}},[1;0])-F({\bf{z}},{\bf{0}}))\\ \,+\,p({\bf{u}}=[0;1]|{\bf{z}})(F({\bf{z}},[0;1])-F({\bf{z}},{\bf{0}}))\\ \,=\,{\dot{{\bf{z}}}}_{{\rm{a}}{\rm{u}}{\rm{t}}{\rm{o}}{\rm{n}}{\rm{o}}{\rm{m}}{\rm{o}}{\rm{u}}{\rm{s}}}+{\dot{{\bf{z}}}}_{\bar{{\rm{l}}{\rm{e}}{\rm{f}}{\rm{t}}}}+{\dot{{\bf{z}}}}_{\bar{{\rm{r}}{\rm{i}}{\rm{g}}{\rm{h}}{\rm{t}}}}.\end{array}$$

(7)

Figure 2c shows a plot of ${\dot{{\bf{z}}}}_{{\rm{a}}{\rm{u}}{\rm{t}}{\rm{o}}{\rm{n}}{\rm{o}}{\rm{m}}{\rm{o}}{\rm{u}}{\rm{s}}}$, and Fig. 2e shows a plot of ${\dot{{\bf{z}}}}_{\overline{{\rm{left}}}}$ and ${\dot{{\bf{z}}}}_{\overline{{\rm{right}}}}$. F(z, left) is defined as p(u = [1; 0]|z)F(z, [1; 0]) + (1 − p(u = [1; 0]|z))F(z, 0), and F(z, right) is defined as p(u = [0; 1]|z)F(z, [0; 1]) + (1 − p(u = [0; 1]|z))(F(z, 0).

Because p(u|z) = p(z|u)p(u)/p(z) and p(z) in general do not have an analytical form, we estimate p(u|z) numerically. To do this, we train FINDR²⁰ to learn F and generate click trains for 5,000 trials in a way that is similar to how clicks are generated for the task performed by our rats. Next, we simulate 5,000 latent trajectories from the learnt F and the generated click trains. We then bin the state space of z and ask, for a single bin, how many times the latent trajectories cross that bin in total and how many of the latent trajectories when crossing that bin had u = [1;0] (or u = [0;1]). That is, we estimate p(u = [1;0]|z) with $\frac{{\rm{No.\; latent\; states\; with}}\,{\bf{u}}\,=\,[1;\,0]\,\text{in}\,{\rm{t}}{\rm{h}}{\rm{e}}\,{\rm{b}}{\rm{i}}{\rm{n}}\,{\rm{t}}{\rm{h}}{\rm{a}}{\rm{t}}\,{\rm{c}}{\rm{o}}{\rm{v}}{\rm{e}}{\rm{r}}{\rm{s}}\,{\bf{z}}\,}{{\rm{No.\; latent\; states\; in\; the\; bin\; that\; covers}}\,{\bf{z}}}$. For Fig. 2, because z is two dimensional, we use bins of eight-by-eight that cover the state space traversed by the 5,000 latent trajectories and weigh the flow arrows of the input dynamics with the estimated p(u|z). Similarly, for the background shading that quantifies the speed of input dynamics in Fig. 2, we use bins of 100-by-100 to estimate p(u|z) and apply a Gaussian filter with σ = 2 (in the units of the grid) to smooth the histogram. A similar procedure was performed for Extended Data Figs. 1 and 4 to estimate p(u|z) numerically.

Speed of autonomous and input dynamics

To compute the normalized difference in the speed of autonomous and input dynamics in Fig. 3c, similar to previous sections, we first generated latent trajectories from the learnt F for 5,000 different trials with generative click rate ratios used in our experiments with rats. Next, we computed the magnitude of the autonomous dynamics $\parallel {\dot{{\bf{z}}}}_{{\rm{a}}{\rm{u}}{\rm{t}}{\rm{o}}{\rm{n}}{\rm{o}}{\rm{m}}{\rm{o}}{\rm{u}}{\rm{s}}}\parallel$ and the magnitude of the average input dynamics $(\parallel {\dot{{\bf{z}}}}_{\bar{{\rm{l}}{\rm{e}}{\rm{f}}{\rm{t}}}}\parallel +\parallel {\dot{{\bf{z}}}}_{\bar{{\rm{r}}{\rm{i}}{\rm{g}}{\rm{h}}{\rm{t}}}}\parallel )/2$ for each time point for each of the 5,000 trajectories and then averaged across the trajectories and across time periods defined in Fig. 3b to obtain Fig. 3c.

FINDR

Detailed descriptions are provided in ref. ²⁰. Briefly, to infer velocity vector fields (or flow fields) from the neural population spike trains, we used a sequential variational autoencoder called FINDR.

FINDR minimizes a linear combination of two losses: one for neural activity reconstruction (${{\mathcal{L}}}_{1}$) and the other for vector field inference (${{\mathcal{L}}}_{2}$). To reconstruct neural activity, FINDR uses a deep neural network G that takes the spike trains of N simultaneously recorded neurons y and the sensory click inputs u in a given trial to obtain the time derivative of the d-dimensional latent decision variable z:

$${{\bf{z}}}_{t+1}={{\bf{z}}}_{t}+\Delta tG({{\bf{z}}}_{t},{{\bf{u}}}_{1:T},{{\bf{y}}}_{1:T})+{{\boldsymbol{\eta }}}_{t},\,t=1,2,3,\ldots .$$

(8)

Here, T is the number of time steps in a given trial, u_t is a two-dimensional vector representing the number of left and right clicks played in a time step (Δt = 0.01 s), y_t is an N-dimensional vector of the spike counts in a time step and η_t is noise drawn from N(0, ΔtΣ) in each time step. Σ is a d-dimensional diagonal matrix in which the diagonal elements need not be equal to each other. For each time step, FINDR infers the firing rates of N simultaneously recorded neurons r_t from z_t with

$${{\bf{r}}}_{t}={\rm{s}}{\rm{o}}{\rm{f}}{\rm{t}}{\rm{p}}{\rm{l}}{\rm{u}}{\rm{s}}(W\,{{\bf{z}}}_{t}+{{\bf{b}}}_{t}),$$

(9)

where softplus is a function approximating the firing rate–synaptic current relationship (f–I curve) of neurons, W is an N × d matrix representing the encoding weights and b_t is an N-dimensional vector representing the putatively decision-irrelevant baseline input. The baseline b_t is learnt before fitting FINDR using the procedure described in Baseline and in detail in the Supplementary Methods, section 1.2. The reconstruction loss is given by

$${{\mathcal{L}}}_{1}=-\mathop{\sum }\limits_{t=1}^{T}\text{log}\,\text{Poisson}({{\bf{y}}}_{t}| {{\bf{r}}}_{t}).$$

(10)

For vector field inference, we parametrize the vector field F with a gated feedforward neural network^20,32:

$$\dot{{\bf{z}}}\approx \frac{{{\bf{z}}}_{t}-{{\bf{z}}}_{t-\Delta t}}{\Delta t}=F({{\bf{z}}}_{t-\Delta t},{{\bf{u}}}_{t}).$$

(11)

F gives the discretized time derivative of z. We find the vector field F that captures the latent trajectories z inferred from G in equation (8) by minimizing

$${{\mathcal{L}}}_{2}=\mathop{\sum }\limits_{t\,=\,1}^{T}{(F({{\bf{z}}}_{t},{{\bf{u}}}_{t})-G({{\bf{z}}}_{t},{{\bf{u}}}_{1:T},{{\bf{y}}}_{1:T}))}^{{\rm{\top }}}{{\rm{\sum }}}^{-1}(F({{\bf{z}}}_{t},{{\bf{u}}}_{t})-G({{\bf{z}}}_{t},{{\bf{u}}}_{1:T},{{\bf{y}}}_{1:T})).$$

(12)

The total loss that is minimized by FINDR is

$${\mathcal{L}}={{\mathcal{L}}}_{1}+c{{\mathcal{L}}}_{2},$$

(13)

where c = 0.1 is a fixed hyperparameter (c = 0.0125 in Extended Data Fig. 1g). FINDR minimizes ${\mathcal{L}}$ by using stochastic gradient descent to learn W, Σ, the parameters of the neural network representing F and the parameters of the neural network G. It can be shown that ${\mathcal{L}}$ is an approximate upper bound on the marginal log likelihood of the data and that training FINDR this way is equivalent to performing inference and learning with a sequential auto-encoding variational Bayes algorithm that straightforwardly extends the standard auto-encoding variational Bayes algorithm⁵².

After training, we plot the vector field (that is, a grid of $\dot{{\bf{z}}}$) using the learnt F and generate FINDR-predicted neural responses using equation (9) and

$${{\bf{z}}}_{t}={{\bf{z}}}_{t-\Delta t}+\Delta tF({{\bf{z}}}_{t-\Delta t},{{\bf{u}}}_{t})+{{\boldsymbol{\eta }}}_{t}.$$

(14)

Equation (14) is an Euler-discretized gated neural stochastic differential equation^20,32.

Parameters

The total number of free parameters P of the FINDR model is given by

$$\begin{array}{c}P\,=\,{P}_{W}+{P}_{{\Sigma }}+{P}_{F}+{P}_{G},\\ {P}_{W}\,=\,N\times d,\\ {P}_{{\Sigma }}\,=\,d,\\ {P}_{F}\,\in \,\{90\,+(64+d)d,150+(104+d)d,300+(204+d)d\},\\ {P}_{G}\,\in \,\{15,900+300N+100x+{P}_{F},61,800+600N+200x\\ \,\,+\,{P}_{F},243,600+1,200N+400x+{P}_{F}\}.\end{array}$$

(15)

P_W is the number of parameters in the encoding weight matrix W, the dimensions of which are the number of neurons N and latent dimensionality d. P_Σ is the parameter count in the diagonal covariance Σ of the additive Gaussian noise of the latent z. The number of parameters in the neural networks parametrizing F(P_F) and G(P_G) are separate hyperparameters. Here, $x=\frac{{P}_{F}-d+{d}^{2}}{2d+3}$.

Hyperparameters

The hyperparameters that were optimized (P_F, P_G and α) include the number of parameters of the network F(P_F), the number of parameters of the network G(P_G) and the learning rate α ∈ {10⁻², 10^–1.625, 10^−1.25, 10^−0.875, 10^−0.5}. We identify the optimal values for these hyperparameters in a 3 × 3 × 5 = 45 grid search. The grid search was performed separately for each set of training data for each of five crossvalidation folds. In each training set, three-quarters of the trials were used to the optimize the parameters under a given set of hyperparameters and the remaining one-quarter was held out to evaluate the model performance for that set of hyperparameters. Test data were never used in the grid search.

Latent space transformation

Because the encoding weight matrix W is not constrained to semi-orthogonality and can take only any real values, different combinations of W and z_t can give rise to the same firing rate vector r_t, even when baseline b_t is fixed. To uniquely identify the latent trajectories (except for redundancy from rotations and reflections), after optimization, we linearly transformed the latent space z to $\mathop{{\bf{z}}}\limits^{ \sim }$:

$${\mathop{{\bf{z}}}\limits^{ \sim }}_{t}=S{V}^{{\rm{\top }}}{{\bf{z}}}_{t},$$

(16)

where S is a d × d diagonal matrix containing the singular values of W and V is a d × d matrix containing the right singular vectors

$$W=US{V}^{\top }.$$

(17)

U is an N × d matrix containing the left singular vectors of W (where N is the number of neurons). In the space of $\mathop{{\bf{z}}}\limits^{ \sim }$, the encoding weight matrix is a linear transformation that preserves angles and distances because U is semi-orthogonal and can only give rise to an isometry such as rotation and reflection.

$$\begin{array}{c}W\,{\bf{z}}=US{V}^{{\rm{\top }}}{\bf{z}}\\ =\,U\mathop{{\bf{z}}}\limits^{ \sim }\end{array}$$

(18)

To obtain meaningful axes for the transformed latent space $\mathop{{\bf{z}}}\limits^{ \sim }$, we generate 5,000 different trajectories of $\mathop{{\bf{z}}}\limits^{ \sim }$ in generative mode (that is, using F and Σ in equation (14) but not G) and perform PC analysis on the trajectories. The PCs were used to define the axes of the decision variable $\mathop{{\bf{z}}}\limits^{ \sim }$. In the main text, the PC1 axis of $\mathop{{\bf{z}}}\limits^{ \sim }$ was denoted as z₁ and the PC2 axis of $\mathop{{\bf{z}}}\limits^{ \sim }$ was denoted as z₂. In all our analyses, the latent trajectories and vector fields inferred by FINDR are shown in the transformed latent space of $\mathop{{\bf{z}}}\limits^{ \sim }$ and scaled such that the latent trajectories along PC1 lie between −1 and 1.

Sample zone

In Figs. 2 and 3, to focus on the portion of the inferred vector field that is used by the single-trial trajectories, we show only the well-sampled subregion of the state space, which is the portion occupied by at least 50 of 5,000 simulated single-trial latent trajectories of 1 s. With this definition, the sample zone is the same across time points in Fig. 2h.

Model evaluation

The goodness of fit of the PSTH was quantified using the coefficient of determination (R²) of the evidence–sign conditioned PSTH as defined in equation (34) using fivefold cross-validation. We used three-fifths of the trials in a session as the training dataset, one-fifth of the trials as the validation dataset to optimize the hyperparameters of FINDR and one-fifth of the trials as the test (that is, out-of-sample) dataset to evaluate performance of FINDR. Therefore, when we compute the goodness of fit, we also obtain five different vector fields inferred by FINDR for each fold, which we confirm are consistent across folds (Extended Data Fig. 4).

Curvature of trial-averaged trajectories

To compute the curvature of trial-averaged trajectories in Fig. 3b, as before, we first generate latent trajectories from FINDR for 5,000 different trials with generative click rate ratios used in our experiments with rats. Next, we separate the trials on the basis of whether the generative click ratio in a given trial favours a leftward choice or a rightward choice. We take the average of the latent trajectories over the left-favouring trials and then convolve the trial-averaged trajectory with a Gaussian filter with σ = 3 (in units of the time step Δt = 0.01 s). We take this smoothed trajectory to numerically compute the planar curvature. We do the same for the right-favouring trials and take the average between the curvature obtained from left-favouring trials and the curvature obtained from right-favouring trials to generate the plot in Fig. 3b.

cFINDR

The cFINDR model replaces the neural network parametrizing F in FINDR with a linear combination of affine dynamics, specified by M and N, and bistable attractor dynamics specified by φ. The dynamics are furthermore constrained to be two dimensional.

$$\begin{array}{c}\dot{{\bf{z}}}\approx \frac{{{\bf{z}}}_{t}-{{\bf{z}}}_{t-\Delta t}}{\Delta t}=F({{\bf{z}}}_{t-\Delta t},{{\bf{u}}}_{t})=M{{\bf{z}}}_{t-\Delta t}+N{{\bf{u}}}_{t}+s\times {\varphi }({{\bf{z}}}_{t-\Delta t}),\\ M=Q\Lambda {Q}^{-1},\\ Q=[\begin{array}{cc}1 & \sin (\theta )\,\\ 0 & \cos (\theta )\end{array}],\\ \Lambda =[\begin{array}{cc}0 & 0\,\\ 0 & -r\end{array}],\\ {\varphi }({{\bf{z}}}_{t})=-\exp (\,-\,{({{\bf{z}}}_{t}-{\bf{x}})}^{2}/\rho )\,\odot \,({{\bf{z}}}_{t}-{\bf{x}})\\ \,\,\,\,\,\,\,\,-\exp (\,-\,{({{\bf{z}}}_{t}+{\bf{x}})}^{2}/\rho )\,\odot \,({{\bf{z}}}_{t}+{\bf{x}}).\end{array}$$

(19)

The matrix M implements a line attractor located at z₂ = 0. The inputs u_t are the same as those in FINDR and represent the auditory clicks. The two discrete attractors are constrained such that x₂ = 0 and implemented through the function φ. The shape of the basin of attraction corresponding to each point attractor is specified by the parameter ρ. The relative contribution of the discrete attractors and the line attractor to the overall dynamics is specified by the scalar s.

The DDM line attractor hypothesis can be implemented in cFINDR by setting θ = 0. Non-normal dynamics with a line attractor² can be implemented by setting θ ≠ 0. The bistable attractor hypothesis can be implemented by increasing ρ.

As in FINDR, cFINDR learns W, Σ and parameters of G. Instead of the neural networks parametrizing F, cFINDR, learns s, θ, r, x, ρ and the 2 × 2 matrix N to approximate F, which has nine parameters. The same objective function and optimization procedure were used in cFINDR. After optimization, as in FINDR, the latent space z is linearly transformed to uniquely identify the dynamics (except for arbitrary rotations or reflections). As in the analysis of results from FINDR, the latent trajectories and vector fields inferred by cFINDR are in the transformed latent space $\mathop{{\bf{z}}}\limits^{ \sim }$.

When we fit cFINDR to the data, we experimented with the different constraints r > 0 and r > 3. The fits using r > 0 were superior to those using r > 3 and were therefore used in the comparison between cFINDR and FINDR for the data presented in Fig. 3e,f. We were motivated to try both r > 0 and r > 3 because we found that, in synthetic data, cFINDR under the constraint r > 0 could not recover the dynamics generated under the DDM line attractor hypothesis (r = 10). For this reason, Extended Data Fig. 5f shows results from synthetic data using r > 3. When fit to data, FINDR outperforms cFINDR using either r > 0 or r > 3.

FINDR models with more than two latent dimensions

For Extended Data Fig. 3j,k, we evaluated FINDR models with more than two latent dimensions to assess whether the two-dimensional manifold we found is approximately an attractor. To show that the sample zone was an approximate attractor manifold, we perturbed the latent states on the manifold along the third PC direction. When the latent states were perturbed (but not so far that the latent states went outside the range along the PC3 axis covered by the sample zone), the latent states flowed towards the manifold. To obtain the flow directions along PC3, we first generated 5,000 latent trajectories (similar to Fig. 2 for computing the sample zone). We then divided the PC1 × PC2 space into an eight-by-eight grid (the grid used for the vector field arrows in Extended Data Fig. 3i). For each cell in the grid, we identified the latent states from the 5,000 trajectories that were inside the cell and identified the highest (lowest) PC3 value ${z}_{3}^{{\rm{up}}}({z}_{3}^{{\rm{dn}}})$. This was to ensure that the perturbation along the PC3 axis was not too large. Next, we computed the flow vector using a 100-by-100 grid on the PC1 × PC2 space, assuming that ${\rm{PC3}}={z}_{3}^{{\rm{up}}}({z}_{3}^{{\rm{dn}}})$ and PC4 = 0. The space covered by each cell of the grid is coloured on the basis of the direction of the flow vector along PC3: if flowing upwards, green; if flowing downwards, pink. A Gaussian filter was applied to this heat map with σ = 2 (in units of the 100-by-100 grid), similar to the heat map for input dynamics in Fig. 2f. The resulting plot is shown on the left (right) panel. Results were similar without the Gaussian filter.

Choice decoding from FINDR

FINDR does not use the choice of the animal for reconstructing neural activity. However, after training, we can fit a logistic regression model that predicts the choice of the animal from the decision variable z at the final time step T. When we fit an ℓ₂-regularized logistic regression model using z_T from the trained network G and the choice of the animal in the representative session in Fig. 2c–h, we found that the logistic choice decoder achieves 89.7% accuracy in predicting choice in the out-of-sample dataset. We can generate choices from this decoder by generating latent trajectories using F and Σ in equation (14) as in previous sections and by supplying z_T to the trained decoder. A total of 5,000 latent trajectories and choices generated from F and the choice decoder were used for the analysis in Extended Data Fig. 4l. We used a separate logistic regression model for predicting choice from the latent trajectories truncated at time = 0.33 s projected onto PC2. Optimization of the logistic regression models was carried out using L-BFGS⁵³.

MMDDM

The MMDDM is a state-space model, comprising a dynamic model that governs the time evolution of the probability distributions of latent (that is, hidden) states and measurement models that define the conditional distributions of observations (that is, emissions) given the latent state. Additional information is provided in the Supplementary Methods, section 1.3.

Dynamic model

The latent variable z is one dimensional (that is, a scalar), and its time evolution is governed by a piecewise linear function:

$$z(t+1)=\left\{\begin{array}{l}z(t)+{u}(t)+{\eta },-B < z(t) < B\\ B\cdot {\rm{sign}}(z(t)),{\rm{otherwise.}}\end{array}\right.$$

(20)

When the absolute value of z is less than the bound height B (free parameter), its time evolution depends on momentary external input u and i.i.d. (independent and identically distributed) Gaussian noise η.

$$\eta \sim {\mathcal{N}}(0,\Delta t),$$

(21)

where Δt is the time step and set to 0.01 s. Here, ~ means ‘distributed as’. When $z$ is either less than −B or greater than B, it becomes fixed at the bound. The initial probability distribution of z is given by

$$z(t=1) \sim {\mathcal{N}}({\mu }_{0},1),$$

(22)

where the mean µ₀ is a free parameter. In time step t, the input u(t) is the total difference in the per-click input v between the right and left clicks that occurred in the time interval (t − Δt, t):

$$u(t)=\sum _{\tau \in {\rm{R}}}v(\tau ;t)-\sum _{\tau \in {\rm{L}}}v(\tau ;t),$$

(23)

where L(R) is the set of the left (right) click times and v(τ; t) is the per-click input of a click occurring at time τ and time step t. Note that $\tau \in {\mathbb{R}}$ indicates continuous time, whereas $t\in {\mathbb{N}}$ indexes a time step. The per-click input is given by

$$v(\tau ;t)=D(\tau ;t)\cdot C(\tau )\cdot {\zeta },$$

(24)

where D(τ; t) indicates the integral over the interval [t − Δt, t) of the Dirac delta function δ delayed by τ:

$$D(\tau ;t)={\int }_{t-\Delta t}^{t-\varepsilon }{\delta }(x-\tau )dx=\left\{\begin{array}{ll}1, & \,\tau \in [t-\Delta t,t)\\ 0, & {\rm{otherwise,}}\end{array}\right.$$

(25)

where ε is the machine epsilon. To account for sensory adaptation, the per-click input is depressed by preceding clicks by a time-varying scaling factor given by the function C(τ), implemented according to previous work²⁴ (Supplementary Methods, section 1.3.1). The per-click input is corrupted by i.i.d. multiplicative Gaussian noise ζ:

$${\zeta } \sim {\mathcal{N}}(1,{\sigma }_{{\rm{s}}}^{2}).$$

(26)

The free parameter ${\sigma }_{{\rm{s}}}^{2}$ is the variance of the per-click noise. Variability in the dynamic model is fit to the data through the per-click noise ζ rather than per-time step noise η on the basis of previous findings²⁴; our results are similar if we set the variance of η rather than the variance of ζ as a free parameter.

The dynamic model has three free parameters: bound height B, variance ${\sigma }_{{\rm{s}}}^{2}$ of the per-click noise and mean µ₀ of the initial state. These parameters are learnt simultaneously with the parameters of the measurement models.

Measurement model of behavioural choices

In each trial, the binary behavioural choice c (1, right; 0, left) is the sign of z in the last time step T of the trial (the earlier of 1 s after the onset of the clicks or immediately before the animal leaves the fixation port):

$$c| z(T)={\rm{sign}}(z(T)).$$

(27)

Measurement model of spike counts

In each time step t, given the value of z, the spike count y of neuron n is a Poisson random variable

$${y}^{(n)}(t)|z(t) \sim \text{Poisson}({\lambda }^{(n)}(t)\Delta t).$$

(28)

The firing rate λ is given by

$${\lambda }^{(n)}(t)|z(t)=h({w}^{(n)}\cdot z(t)+b(t)),$$

(29)

where $h(\cdot )$ is the softplus function used to approximate the neuronal frequency–current curve of a neuron:

$$h(x)=\log (1+\exp (x)).$$

(30)

The encoding weight w depends on z itself:

$${w}^{(n)}=\{\begin{array}{c}{w}_{{\rm{E}}{\rm{A}}}^{(n)},\,-B < z < B\\ {w}_{{\rm{D}}{\rm{C}}}^{(n)},\,z\in \{\,-\,B,B\}.\end{array}$$

(31)

Each neuron has two scalar weights, w_EA and w_DC, that specify the encoding of the latent variable during the evidence accumulation regime and the decision commitment regime, respectively. When the latent variable has not yet reached the bound (−B or B), all simultaneously recorded neurons are in the evidence accumulation regime and encode the latent variable through their own private w_EA. When the bound is reached, all neurons transition to the decision commitment regime and encode $z$ through their own w_DC.

The bias b accounts for factors that are putatively independent of the decision, including a component that varies only across trials and another component that varies both across and within trials:

$${b}^{(n)}(m,t)={b}_{\text{cross}}^{(n)}(m)+{b}_{\text{within}}^{(n)}(m,t).$$

(32)

The cross-trial trial component ${b}_{\text{cross}}^{(n)}$ is a function of time m from the first trial of the session, whereas t indicates time in each trial relative to the stimulus onset of that trial. The within-trial component consists of time-varying influence from spike history, post-stimulus (stim) onset and pre-movement (move) onset.

$$\begin{array}{l}{b}_{\text{within}}(m,t)={\tau }_{\text{stim}}^{(m)}({k}_{\text{stim}}\ast \delta )(t)+{\tau }_{\text{move}}^{(m)}({k}_{\text{move}}\ast \delta )(t)\\ \,\,\,\,\,\,+\,{\sum }_{i}{\tau }_{\text{spike}}^{(m,i)}({k}_{\text{spike}}\ast \delta )(t),\end{array}$$

(33)

where the symbol $\ast$ indicates convolution, τ_x indicates translation τ_xk(t) = k(t − τ_x) by the time of event x and δ is the Dirac delta function. The functions ${b}_{\text{cross}}^{(n)},{k}_{\text{stim}},{k}_{\text{move}},{k}_{\text{spike}}$ are learnt, and each is parametrized as a linear combination of radial basis functions^40,54 (Supplementary Methods, section 1.5). The measurement model of each neuron of the spike train has 19 parameters that are learnt simultaneously with the parameters of the dynamic model (that is, the model of the latent variable).

Parameter learning

All parameters, including the three parameters of the latent variable and the 19 parameters private to each neuron, are learnt simultaneously by jointly fitting to all spike trains and choices using maximum a posteriori estimation. Gaussian priors were placed on the model parameters to ensure that the optimization reached a critical point and confirmed to not change the results in separate optimizations using maximum likelihood estimation (that is, optimization without Gaussian priors). Out-of-sample predictions were computed using fivefold cross-validation.

nTc

The time step when decision commitment occurred is selected to be when the posterior probability of the latent variable at either the left bound or the right bound, given the click times, spike trains and behavioural choice, is greater than 0.8. Results were similar for other thresholds, and the threshold of 0.8 was chosen to balance between prediction accuracy and the number of trials for which commitment was predicted to have occurred. Using this definition, commitment occurred in 34.6% of trials.

Engagement index

The engagement index was computed for each neuron to quantify its involvement in evidence accumulation and decision commitment. The index was defined using w_EA and w_DC of the neuron: EI ≡ (|w_EA| − |w_DC|)/(|w_EA| + |w_DC|). It ranges from −1 to 1. A neuron with an engagement index of −1 encodes the latent variable only during decision commitment, an engagement index of 1 indicates involvement only during evidence accumulation, and an engagement index of 0 represents a similar strength of encoding the latent variable during evidence accumulation and decision commitment.

Analyses

Neuronal selection

Only neurons that meet a preselected threshold for being reliably choice selective were included for analysis. For each neuron, reliable choice selectivity was measured using the area under the receiver operating characteristic curve (auROC) indexing how well an ideal observer can classify between a left-choice trial and a right-choice trial on the basis of neuronal spike counts. Spikes were counted in four non-overlapping time windows (0.01–0.21 s, 0.21–0.4 s, 0.41–0.6 s and 0.61–0.9 s after stimulus onset), and an auROC was computed for each time window. A neuron with an auROC < 0.42 or an auROC > 0.58 for any of these windows was considered choice selective and included for other analyses. Moreover, neurons must have had an average firing rate of at least two spikes per s. Across sessions, the median fraction of neurons included under this criterion was 10.4%.

PSTH

Spike times were binned at 0.01 s and were included up to 1 s after the onset of the auditory stimulus (click trains) until 1 s after the stimulus onset or until the animal removed its nose from the central port, whichever came first. The time-varying firing rate of each neuron in each group of trials (that is, task condition) was estimated with a PSTH, which was computed by convolving the spike train on each trial with a causal Gaussian linear filter with a standard deviation of 0.1 s and a width of 0.3 s and averaging across trials. The CI of a PSTH was computed by bootstrapping across trials.

The goodness of fit of the model predictions of the PSTH was quantified using the coefficient of determination (R²), computed using fivefold crossvalidation. R² was computed by conditioning the PSTH on either the sign of the evidence (that is, whether the generative click ratio in a given trial favoured a leftward choice or a rightward choice) or the choice of the animal:

$$\begin{array}{c}{R}^{2}=1-\frac{{{\rm{SS}}}_{{\rm{res}}}}{{{\rm{SS}}}_{{\rm{tot}}}}\\ {{\rm{SS}}}_{{\rm{res}}}={\sum }_{t}({({{\rm{PSTH}}}_{{\rm{obs}}}^{{\rm{R}}}(t)-{{\rm{PSTH}}}_{{\rm{pred}}}^{{\rm{R}}}(t))}^{2}+{({{\rm{PSTH}}}_{{\rm{obs}}}^{{\rm{L}}}(t)-{{\rm{PSTH}}}_{{\rm{pred}}}^{{\rm{L}}}(t))}^{2})\\ {{\rm{SS}}}_{{\rm{tot}}}={\sum }_{t}({({{\rm{PSTH}}}_{{\rm{obs}}}^{{\rm{R}}}(t)-{{\mathbb{E}}}_{t}[{{\rm{PSTH}}}_{{\rm{obs}}}^{{\rm{R}}}(t)])}^{2}+{({{\rm{PSTH}}}_{{\rm{obs}}}^{{\rm{L}}}(t)-{{\mathbb{E}}}_{t}[{{\rm{PSTH}}}_{{\rm{obs}}}^{{\rm{L}}}(t)])}^{2}),\end{array}$$

(34)

where t is time in a trial that goes from 0 s to 1 s, with 0 s being the stimulus onset. The superscripts ‘^R’ and ‘^L’ indicate either the sign of the difference in the total number of right and left clicks or the choice of the animal. The subscripts ‘_obs’ and ‘_pred’ indicate whether the PSTH was computed using observed neural activity or model-predicted neural activity. SS_res is the residual sum of squares, and SS_tot is the total sum of squares.

A normalized PSTH was computed by dividing the PSTH by the mean firing rate of the corresponding neuron across all time steps across all trials. When PSTHs were separated by ‘preferred’ and ‘null’, the preferred task condition was defined as the group of trials with the behavioural choice when the neuron responded more strongly and a null task condition was defined as the trials associated with the other choice.

Choice selectivity

In Fig. 6 and Extended Data Fig. 2m, for each neuron and for each time step t aligned to the onset of the auditory click trains, we computed choice selectivity c(t):

$$c(t)\equiv \frac{r(t)-l(t)}{r({t}^{\ast })-l({t}^{\ast })},$$

(35)

where r and l are the PSTHs computed from trials ending in a right choice and a left choice, respectively. The time step t* is the time of the maximum absolute difference:

$${t}^{\ast }\equiv {\text{argmax}}_{t}|r(t)-l(t)|.$$

(36)

In Extended Data Fig. 2m, neurons are sorted by the centre of mass of the absolute value of the choice selectivity of each neuron.

Baseline

In FINDR, cFINDR and MMDDM, the neuronal firing rate depends on a time-varying scalar baseline. In time step t of trial m, conditioned on the value of the latents in a given time step, the spike count y of each neuron is given by

$$y(m,t)|{\bf{z}}(m,t) \sim {\rm{P}}{\rm{o}}{\rm{i}}{\rm{s}}{\rm{s}}{\rm{o}}{\rm{n}}(h\{{{\bf{w}}}^{{\rm{\top }}}{\bf{z}}(m,t)+b(m,t)\}),$$

(37)

where h is the softplus function and w is the encoding weight of the latent. The baseline b incorporates putatively decision-independent variables as input to the neural spike trains including slow drifts in firing rates across trials and faster changes in each trial that are aligned to either the time from stimulus onset or the time from the animal leaving the fixation port. The baseline is learnt using a Poisson generalized linear model fit separately to the spike counts of each neuron. Details are provided in the Supplementary Methods, section 1.2.

PCTH

In trials for which a time of decision commitment (nTc) could be inferred, the spike trains were aligned to the predicted time of commitment and then averaged across those trials. The trial average was then filtered with a causal Gaussian kernel with a standard deviation of 0.05 s. The PCTHs were averaged in each of three groups of neurons: (1) neurons that were similarly engaged in evidence accumulation and decision commitment; (2) neurons more strongly engaged in evidence accumulation; and (3) neurons more strongly engaged in decision commitment. Each neuron was assigned to one of these groups according to its engagement index. Neurons with $-\frac{1}{3}\le {\rm{EI}} < \frac{1}{3}$ are considered to be similarly engaged in evidence accumulation and decision commitment, neurons with ${\rm{EI}}\ge \frac{1}{3}$ are considered to be more strongly engaged in evidence accumulation, and those with ${\rm{EI}} < -\frac{1}{3}$ are considered to be more strongly engaged in decision commitment.

For this analysis, we focused on only the 65 of 115 sessions for which the MMDDM improved the R² of the PSTHs and for which the inferred encoding weights were reliable across cross-validation folds (R² > 0.9). From this subset of sessions, there were 1,116 neurons similarly engaged in evidence accumulation and decision commitment, 414 neurons that were more engaged in decision decision commitment and 1,529 neurons that were more engaged in evidence accumulation.

To compute the shuffled PCTH, the predicted times of commitment were shuffled among only the trials in which commitment was detected. If the randomly assigned commitment time extended beyond the length of the trial, then the time of commitment was assigned to be the last time step of that trial.

Trial-averaged trajectories in neural state space

To measure trial-averaged dynamics in neural state space, we analysed PCs in a data matrix made by concatenating the PSTHs. The data matrix X has dimensions TC-by-N, where T is the number of time steps (T = 100), C is the number of task conditions (C = 2 for choice-conditioned PSTHs and C = 4 for PSTHs conditioned on both choice and evidence strength) and N is the number of neurons. The mean across rows is subtracted from X, and singular value decomposition is performed: ${{USV}}^{\top }=X$. The principal axes correspond to the columns of the right singular matrix V, and the projections of the original data matrix X onto the principal axes correspond to the left singular matrix (U) multiplied by S, the rectangular diagonal matrix of singular values. The first two columns of the projections US are plotted as trajectories in neural state space.

Psychophysical kernel

Kernels were time locked to either nTc of each trial (Fig. 5d and Extended Data Fig. 7a–d) or the first click in each trial (Extended Data Fig. 7e–h). We extended the logistic regression model presented in ref. ⁵⁵ to include a lapse parameter (Supplementary Methods, section 1.4), and we confirmed that results were similar using generic logistic regression. A shuffling procedure was used to randomly permute the inferred time of commitment across trials without changing the behavioural choice and the times of the auditory clicks on each trial. In this randomly permuted sample, we selected trials for which the auditory stimuli were playing at least 0.2 s before and at least 0.2 s after the inferred time of commitment to compute the psychophysical kernel in the shuffled condition. For Fig. 5d, the prediction was generated using the MMDDM parameters that were fit to the data and the same set of trials in the data. For Extended Data Fig. 7, temporal basis functions were used to parametrize the kernel, and the optimal number and type of basis function were selected used crossvalidated model comparison.

Statistical tests

Binomial CIs were computed using the Clopper–Pearson method. All other CIs were computed with a bootstrapping procedure using the bias-corrected and accelerated percentile method⁵⁶. Unless otherwise specified, P values comparing medians were computed using a two-sided Wilcoxon rank-sum test, which tests the null hypothesis that two independent samples are from continuous distributions with equal medians against the alternative hypothesis that they are not.

Estimating the low-dimensional vector field without specifying a dynamical model

For Extended Data Fig. 10d, we estimated the low-dimensional velocity vector field for each session using a method that does not specify a dynamical model (model-free approach). To obtain the model-free vector field, we first estimated single-trial firing rates of individual neurons by binning the spike trains into bins of Δt = 10 ms and convolving the spike trains with a Gaussian of σ = 100 ms centred at 0. Results were similar for other values of σ around 100 ms. Next, for each neuron, we took the average across all trials in the session and subtracted this average from single-trial firing rate trajectories. These baseline-subtracted firing rate trajectories were then projected to the low-dimensional subspace spanned by the FINDR latent axes. We projected the estimated firing rates to the same subspace as FINDR to allow direct comparisons between the FINDR-inferred vector field and the model-free vector field.

We treated this low-dimensional projection of the baseline-subtracted firing rates as the latent trajectories in this model-free approach. To obtain velocity vector fields from the latent trajectories, we first estimated the instantaneous velocity $\dot{{\bf{z}}}$ at time point t by computing ${\dot{{\bf{z}}}}_{t}=({{\bf{z}}}_{t}-{{\bf{z}}}_{t-\Delta t})/\Delta t$ for all t for all latent trajectories. We then divided the two-dimensional latent space into an eight-by-eight grid. For each cell (i, j) from this eight-by-eight grid, we identified all states z_t from all trajectories that fell inside the cell (i, j). We took the corresponding ${\dot{{\bf{z}}}}_{t}$ of the identified z_t values and took the average to compute the velocity for the cell (i, j). We computed velocity vectors for all 64 cells. To compare vector fields, we took the cosine similarity between the velocity vector for cell (i, j) from FINDR and the velocity vector for cell (i, j) from the model-free approach and took the mean of these cosine similarities, S_c(FINDR, model free). In computing S_c(FINDR, model free), only cells that had a number of states greater than 1% of the total number of states were included. When the number of states used to estimate the velocity vector was less than 1% of the total number of states, we considered that cell (i, j) to be outside the sample zone, analogous to the sample zone in Fig. 2.

To compare between a random vector field and the model-free vector field, we generated 1,000 random vector fields (with each of the 64 arrows in the eight-by-eight grid going in random directions) for each session and computed S_c(random, model free) for each random vector field.

For Extended Data Fig. 10e, we estimated the autonomous dynamics vector field around the origin as a model-free way of confirming our findings in Extended Data Fig. 10a. Similar to the method for Extended Data Fig. 10d, we convolved the spike trains with a Gaussian and projected the baseline-subtracted firing rate trajectories to the low-dimensional subspace spanned by the FINDR latent axes. However, to separate autonomous dynamics from input dynamics, we used a Gaussian with a smaller σ (20 ms), with a window size ±3σ around 0, and then excluded any ${\dot{{\bf{z}}}}_{t\pm 3{\sigma }}$ with time t for which a click occurred from the estimation of the autonomous dynamics. When computing the average of (z_t − z_{t − Δt})/Δt for one of the five pie slices, we required z_{t − Δt} to be inside the pie slice. For all sessions, the circle had a radius of 0.2 (in units of z). To further ensure that we estimated the autonomous dynamics, when computing the average, we only considered the trajectories for which the number of left clicks was equal to the number of right clicks during the epoch when they were in the pie slice.

Inclusion and ethics statement

The animal procedures described in this study were approved by the Princeton University Institutional Animal Care and Use Committee.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.