Background & Summary

Projections of income distribution are becoming increasingly important for various research purposes. Income distribution is a significant factor in determining consumption and social wellbeing, as well as their uneven distribution among populations. It also closely relates to the ability of diverse populations to cope and adapt to anticipated or unexpected stressors. Scientific projections of income distribution are firstly, essential for conducting scenario analyses relevant to many important societal, economic, and environmental issues, including, but not limited to, demand assessments for a variety of commodities such as energy, water, food, and land use1,2, estimating environmental footprints3,4, cost-benefit evaluation of policies5,6, and impacts, adaptation, and vulnerability (IAV) related to climate change and other disasters7,8. In addition, income distribution projections provide an opportunity to reveal the considerable differences among populations hidden in the current aggregated national results. The use of such projections is gaining importance in multi-objectives scenario studies9,10, particularly in aligning across multiple Sustainable Development Goals (SDGs) such as poverty eradication and climate mitigation11,12.

The need for income projections is becoming more prominent, but current research and methodologies to support this are limited. Previous literature includes attempts to project future income distribution considering specific metrics such as GDP13, income inequality14, poverty rate15, or income level by deciles16. Our interest, however, is to project full income distributions. To this end, two broad approaches might be feasible, as outlined in Table 1. The top-down approach is the most commonly used method, which relies on existing projections of per capita disposable income, income inequality (measured by Gini coefficients)14 and a specific assumed form of income distribution, such as the log-normal distribution17,18, Weibull distribution, or an emerging non-parametric distribution16,19. An alternative approach is microsimulation, a bottom-up method that uses a large amount of individual/household survey data and assumptions about the dynamics of socio-demographic characteristics for a set of representative households7,20. The bottom-up approach has limitations in its application to nations and regions where access to the required survey data is less possible. In contrast, the top-down approach’s ability to generalize makes it easier to adopt at different spatial levels, as demonstrated by previous literature referenced in Table 1.

Table 1 Overview of key previous studies on income distribution projections.
Full size table

Despite the viability of the methodology for performing subnational projections, previous work on projecting income distributions is still heavily limited to the national-level, which does not fully support detailed sub-national analyses21. The foremost reason is the absence of income inequality datasets at sub-national levels, which has resulted in reliance on a published national-level dataset of Gini coefficient projections14. A recent study attempted to generate income distribution projections at the U.S. state-level based on this dataset19, but it assumed that the state-level Gini coefficients would follow the same growth rate as at the national level. This assumption undermines the heterogeneity in income distributions across states, even after accounting for the varying base year Gini coefficients of states. Additionally, previous studies usually use projections of GDP per capita as a proxy for future disposable income16,19, which inevitably leads to an overestimation of income, as GDP per capita is typically higher than household disposable income. Robust projections of disposable income and income inequality are indispensable to forecast income distribution at sub-national levels. Traditional econometric methods often used in previous studies, however, are not always reliable for making such long-term projections14. Machine learning (ML) algorithms offer an alternative to traditional econometric methods22, and have been applied to predict future socioeconomic conditions using indicators such as population23, energy demand24,25, price indices26, and consumption behaviours27.

Previous research has shown that the lack of subnational projections on income distributions is mainly due to the absence of scientific long-term projections for disposable income and income inequality, as well as a systematic framework for projecting them. Therefore, this study aims to address two sub-tasks. First, following the top-down approach, we develop a methodological framework using ML algorithms to generate income datasets of provinces based on their diverse characteristics. Then, using this approach, we project per capita disposable income, income inequality (measured by Gini coefficients), and income distributions for 31 Chinese provinces from 2020 to 2100, considering different scenarios based on China’s local circumstances. The primary data product we generate is provincial projections. Additionally, considering necessary consistency constraints between provincial, urban, and rural income datasets, for each province, we also provide results at urban and rural level as a subsidiary dataset. The focus is on China due to its growing global significance and the huge diversity among Chinese provinces, that allows for assessing the methodology’s effectiveness in capturing heterogeneities across provinces.

Methods

Model design under consistency constraints

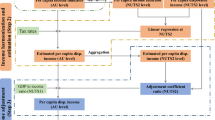
Our methodological framework mainly consists of a provincial model and urban (rural) model, as shown in Fig. 1. Each model is composed of a training and simulating module and is expected to deliver three datasets at corresponding spatial level, including per capita disposable income (PD1, SD1-1, 1-2), income inequality measured by Gini coefficient (PD2, SD2-1, 2-2), and income distribution (PD3, SD3-1,3-2). These datasets cannot be generated separately because they are not independent of each other but subject to a number of qualitative or quantitative consistency constraints.

Fig. 1
figure 1

Methodology of projecting disposable income, income inequality and income distribution.

Full size image

For disposable income, projections of provincial income are expected to keep consistent with future economic development (see e.g. this published GDP dataset13). Meanwhile, provincial, urban, and rural income need to be consistent (Eq. 1), such that the projected provincial income should equal population-weighted averages of urban and rural income. In terms of Gini coefficients, a proxy of income inequality, the consistency constraint for projections of provincial, urban, and rural Gini coefficients is described as Eq. 228. The income distributions at provincial, urban, and rural level are then generated based on the predicted per capita disposable income and Gini coefficients. The relationships between disposable income, Gini coefficients, and income distributions suggest that the factors considered for training and simulating should be derived keeping the relationships in mind and can bridge the three outcomes we require, so that we can solve for outcomes by combining the constraints and the response factors, rather than predicting them separately.

$$I={{PS}}_{{ur}}\times {I}_{{ur}}+{{PS}}_{{ru}}\times {I}_{{ru}}$$
(1)
$${ProGini}={{PS}}_{{ur}}^{2}\times \frac{{I}_{{ur}}}{I}\times {UrGini}+{{PS}}_{{ru}}^{2}\times \frac{{I}_{{ru}}}{I}\times {RuGini}+{{PS}}_{{ur}}\times {{PS}}_{{ru}}\times \frac{{I}_{{ur}}-{I}_{{ru}}}{I}$$
(2)

Where PSur and PSru represent the urban and rural population share, respectively, while Iur, Iru, and I are the per capita disposable income of urban, rural, and the whole province.

For the provincial model, the share of disposable income in GDP (Y1) and provincial Gini coefficients (Y2) are selected as factors, and the ratio between urban and rural income (Y3) and between urban and rural Gini coefficients (Y4) are chosen for the urban (rural) model. The consistency between projected provincial income and GDP is ensured by combining the factors of the provincial model with the published GDP dataset13, while the consistency between provincial, urban, and rural results is guaranteed by solving the corresponding consistency constraint for predicted urban to rural income ratio or Gini ratio.

Data acquisition and processing

Constructing and predicting the selected response factors for provincial and urban (rural) model of 31 Chinese provinces requires a range of datasets at different spatial scales (details can be found in Table 2).

Table 2 Dataset and variables used for establishing provincial and urban (rural) model.
Full size table

Household disposable income and income inequality

For the period 2007–2019, we first collect the provincial, urban, and rural per capita disposable income and GDP of 31 Chinese provinces from China’s Provincial statistical yearbooks. Then, we estimate income Gini coefficients29 of 31 Chinese provinces at provincial, urban, and rural level.

To this end, we first collected grouped household-survey data at urban and rural level from China’s Provincial statistical yearbooks. For each urban and rural income group, we used the following indicators to compute Gini coefficients - households surveyed (HN), average household size (HS), average annual per capita disposable income (PCDI). For province i at year t, the income Gini coefficients of urban (UrGini) and rural (RuGini) populations are calculated using Eq. 3. Based on UrGini and RuGini of each province, provincial income Gini coefficients (ProGini) for province i at year t are calculated using Eq. 2.

$${Gini}=1-1/\left(P\times W\right)\mathop{\sum }\limits_{j=1}^{n}\left[\left({W}_{j-1}+{W}_{j}\right)\times {P}_{j}\right]$$
(3)

Pj represents the population of urban or rural income-group j, which was obtained by multiplying HN and HS of income-group j, and P is the sum of Pj. W is the cumulative income of P, as measured by the sum of the products of Pj and PCDI of all income-groups, while Wj is the total income accumulated to income-group j.

Due to incomplete or missing data for some provinces for certain years, we also performed a series of data cleaning processes, as detailed in Tables S1–2. For example, for a few provinces, such as Guangxi between 2014 and 2019 and Chongqing between 2013 and 2015, HS data for each income group was missing, so we assumed the same HS across all income groups. Some provinces reported neither HN data nor the criteria used for dividing income groups. In this case, we set the HN of these provinces based on data for years with complete data records.

Socioeconomic and demographic variable selection

Changes in socioeconomic and demographic characteristics are understood to be related to changes in income distributions. Regarding socioeconomic features, several studies indicate that industrial structure30,31, technological progress32, employment rate33,34, and government expenditure35,36 are related to household income. For demographic features, urbanization rate, education attainment, household size, and dependency rates are shown to be related to household income37,38.

To capture changes in historical response factors, we selected a wide range of predictive variables (details in Table 2). Specifically, to reflect socioeconomic status of 31 Chinese provinces, we selected the share of value-added of industries in GDP, employment rate, and government spending on various items (including health, education, social protection, and technology), which were collected from China Statistical yearbooks. For demographic factors, we selected educational attainment (four categories: illiterate, primary, secondary, and high level), juvenile and child (J&C) dependency ratio, aged dependency ratio, average household size, and urbanization, which we retrieved from China’s Provincial statistical yearbooks and China Population and Employment Statistical Yearbooks. Notably, employment rate, household size, educational attainment, and dependency structure were collected at both provincial, urban, and rural level, while the data on other variables, was only available at the provincial level.

Modelling framework for disposable income and income inequality

This module attempted to build a general modelling framework suitable for both balanced and unbalanced panel data. Using a machine learning framework, we utilized the random forest (RF) regression algorithm to create a data-driven workflow, as shown in Fig. 2. The workflow comprised five steps, including data splitting, key feature selection, hyperparameters optimization, model comparison and baseline validation, and an additional robust validation for unbalanced data.

Fig. 2
figure 2

Workflow of modelling disposable income and income inequality.

Full size image

Dataset construction and splitting

Changes in Gini coefficients might be captured by socioeconomic and demographic variables relating to both current and past years14. Therefore, for both the provincial, and the urban, and rural level, three datasets were constructed, namely No lags (NL), First-order lag (FL), and First-order lag only (FLO) that contained information on variables considering different time periods.

To apply the RF algorithm, we need to split the dataset into a training and test set. This helps to avoid overfitting and allows us to test the predictive capability of the model. The traditional method of data splitting is sufficiently well suited for balanced panel data such as the dataset of per capital disposable income at both provincial, urban, and rural level. However, the Gini coefficient datasets for provinces, urban and rural areas were unbalanced panel data due to some provinces having incomplete or undisclosed records in certain years. This meant we had random missing datapoints, and as a result, we had to predict the Gini coefficient of province i at year t based on data from other provinces. This required the model to generalize well. So, the RF model needed to perform well both over time and across different locations. For this purpose, we split the Gini coefficients dataset into two separate sections, including a baseline set and a robust test set, as shown in Fig. 2. To build the robust set, we selected a small number of provinces, which were not used to train and test the model, while the remaining provinces were assigned to the baseline set.

For both income dataset and Gini coefficient dataset, we used the data from 2018 and 2019 for the test dataset and data from 2007 to 2017 as the training dataset. The model was first trained on the training set and tested on the test set, to ensure satisfactory performance on the time dimension. Subsequently, for the RF model of Gini coefficients, a more rigorous validation based on the spatial dimension was conducted on the robust set to evaluate the predictive capability of the trained model in predicting the Gini coefficients of provinces that it had not been trained on previously.

During the training process, a time series resampling method was used on the training dataset to create multiple resamples. Each sample was generated by splitting the data into 5-year intervals and then moving forward in 1-year steps, as shown in Fig. 2. In each resample, the first four years of data were used for training the model, and the model was then evaluated using the data from the last year. This approach assured that the model was not trained on later data and then used for predicting earlier data, and it also enhanced the model’s ability to generalize across the temporal dimension.

Key features selection

This study used the literature review to inform the selection of several socioeconomic and demographic predictors that are considered closely related to income metrics. However, it is important to empirically determine the optimal subset of predictive factors. Specifically, excluding irrelevant or redundant predictive factors through key features selection is useful not only for preventing overfitting but also for improving the generalizability of the model. This can help in achieving a better prediction performance, as detailed in Fig. 2.

Under the RF framework, we first calculated the importance of each variable, measured by the percentage increase in mean square error (%MSE), on every resample. This helped us to test the capacity of each feature in predicting response factors across multiple time windows. Then, we calculated the average %MSE of each feature across all resamples. We used a forward search approach to explore all feature combinations from the most to least important. For each combination, we fitted the RF model on every resample and calculated the resample-average of the mean absolute percentage error (MAPE) to evaluate the model’s performance. This process helped us to identify the optimal feature subset.

Hyperparameters optimization

We used two hyperparameters of the RF model, i.e., ntree and mtry, for the model training process. We performed a grid search cross-validation. Specifically, we built a hyperparameter basket and applied it to each resample. We then ran the RF model iteratively on every resample using each parameter combination in the basket. Similar to the method applied for the features selection, we chose MAPE as the performance index and calculated an average of it across all resamples to evaluate the parameter combination and the optimal parameters.

Model comparison and baseline validation

After training the model using the optimal feature subset and parameters, we used the test dataset to validate the model’s predictive capacity. In addition to the MAPE, we also calculated the root mean square error (RMSE) to assess the model’s performance in predicting future Gini coefficients. The MAPE and RMSE were estimated using Eq. 4a,b.

$${MAPE}=\frac{100 \% }{n}\times \mathop{\sum }\limits_{k=1}^{n}\left|\frac{{{Pred}}_{k}-{{Real}}_{k}}{{{Real}}_{k}}\right|$$
(4a)
$${RMSE}=\sqrt{\frac{1}{n}\times \mathop{\sum }\limits_{k=1}^{n}{\left({{Pred}}_{k}-{{Real}}_{k}\right)}^{2}}$$
(4b)

Where k represents the number of datapoints included in the test dataset, and Predk and Realk are prediction and real value of response factors for datapoint k (province i, year t) respectively, while \(\overline{{Real}}\) denotes the average real value of response factors of all datapoints.

For the provincial, urban, and rural level, we trained three RF models on the three datasets (i.e., NL, FL, FLO) and these were evaluated and compared based on MAPE and RMSE to select the model with the best predictive capacity.

Robust validation

For the optimal model of Gini coefficients selected at provincial, urban, and rural level, we then carried out a robust test to assess the generalizability of the model on the spatial dimension. Specifically, we fitted a RF model on the baseline set using the optimal feature subset and parameters trained before, and then tested this on the robust set. The robust test guaranteed the RF model with satisfactory performance in the temporal dimension (predicting a province’s future via its historical data) can also perform well on the spatial dimension (predict a province’s future via other provinces’ historical data).

Future assumptions under different scenarios

Description of different development scenarios

We developed four scenarios to describe future development of the 31 Chinese provinces with consideration of their local context, namely the high-speed development (HSD) pathway, high-quality development (HQD) pathway, business-as-usual (BAU) pathway, and the low-speed development (LSD) pathway.

We define HSD to represent an industrialized development pathway with the fastest assumed economic growth rate and characterised by a demographic future of high educational attainment and aging. We describe HQD as a high-quality economic development future. High-quality development represents a pathway that China plans to achieve, and it means shifting the growth model from crude to intensive, with a focus on innovation. In this case, the tertiary industries will play a more important role in the national economy than the secondary industries, while inevitably, some economic growth may be sacrificed. Hence, compared to HSD, we assume a slightly lower economic growth rate in HQD but similar demographic assumptions. We assume the BAU pathway follows historical development trends with moderate changes in socioeconomic and demographic characteristics. Finally, for LSD, we assume a future that is the exact opposite of HSD. The detailed assumptions for each variable in the four scenarios are shown in Table 3.

Table 3 Future assumptions regarding quantitative variables under different scenarios.
Full size table

Quantifying assumptions of predictors under different scenarios

We applied various quantitative methods to define the future values of key variables, as shown in Table 3. We first quantified the variables at the provincial level. We used predictions from two available datasets. We sourced projections of GDP and the share of value-added of industries from Jing, et al.13, and of educational attainment, urbanization, and household dependency from Chen, et al.39 Those two studies developed localized SSP storylines for China, which allow for consistent assumptions across the two datasets. We then mapped the localized SSP narratives from these two studies to our four scenarios, assuming similar demographic and economic developments as under SSP5, SSP1, SSP2, SSP3 in the HSD, HQD, BAU, and LSD pathways, respectively.

We used past growth rates to generate future employment rate trends. Under HSD and HQD, we assumed an increase in employment at the average rate of increase in employment in G7 countries over the last twenty years, which is about 0.1 percentage per year. Under BAU, we assumed the employment rate increases at the rate of 0.05 percentage per year, while under LSD we assumed the employment rate to stay at the level it was in 2019. We adopted the headship rate method40,41 to produce household size projections, based on data from the Chinese Census 2000 and 2010, and the provincial projections of population and urbanization rate39.

We did not have access to projections or commonly used quantitative methods for predicting government spending. We therefore developed and applied a regression model to create a regression-based simulation for future government spending on four specific items14. This model estimated the spending of each item using a combination of socioeconomic and demographic variables (in a first-order lag form), along with available future projections. We based our model on provincial panel data from 2007 to 2019, and included province fixed effects and a time variable (Year). The performance of the regression model can be seen in Figs. S1–4.

It is important to note that the projections of variables were done at the same spatial level as the available historical data. As a result, we projected value-added of industries, urbanization, and government spending at the provincial level. Household size and employment rate were calculated based on the respective historical provincial/urban/rural values. For educational attainment and dependency structure, we used the change rate derived from provincial projections and the historical urban and rural values in 2019 to generate projections at the urban and rural level.

Projections of disposable income, income inequality and income distribution

In this module, we first projected disposable income share of GDP (Y1) and Gini coefficients (Y2/PD2) at provincial level and the income ratio (Y3) and Gini ratio (Y4) between urban and rural populations from 2020 to 2100 under the four future scenarios. Using these projections, we then solved for the future per capita disposable income at the provincial (PD1), urban (SD1-1), and rural level (SD1-2), and urban and rural Gini coefficients (SD2-1, 2-2). The provincial/urban/rural income distributions (PD3, SD3-1, 3-2) for the 31 Chinese provinces were then projected based on future Gini coefficients and per capita GDP.

The recursive projection approach

We developed an approach using recursive projections to create annual data of Y1–Y4 from 2020 to 2100. In this approach, the RF model was trained on the most recent four years of data and then used to predict the response factors for each projected year. This process was repeated recursively from 2017 to 2099 to make projections for the years 2020 to 2100.

Solving the equality constraints

Based on the projected Y1 and Y3, available provincial projections of Chinese GDP42, and urbanization rate43, a system of linear equations was created and solved to generate the per capita disposable income at the provincial (PD1), urban (SD1-1), and rural (SD1-2) level, as shown in Eq. 5. Based on the projected provincial Gini coefficient (PD2), Y4, solved PD1 and SD1-1, 1-2, and future urbanization rate43, the projections of urban (SD2-1) and rural (SD2-2) Gini coefficients were solved annually with equations shown in Eq. 6.

$$\left\{\begin{array}{l}{Y}_{1}=\frac{I}{{GDP}}\,\\ \,\\ {Y}_{3}=\frac{{I}_{{ur}}}{{I}_{{ru}}}\,\\ \,\\ I={{PS}}_{{ur}}\times {I}_{{ur}}+{{PS}}_{{ru}}\times {I}_{{ru}}\,\end{array}\right.$$
(5)
$$\left\{\begin{array}{l}{Y}_{4}=\frac{{UrGini}}{{RuGini}}\,\\ \begin{array}{c}\\ {ProGini}={{PS}}_{{ur}}^{2}\times \frac{{I}_{{ur}}}{I}\times {UrGini}+{{PS}}_{{ru}}^{2}\times \frac{{I}_{{ru}}}{I}\times {RuGini}+{{PS}}_{{ur}}\times {{PS}}_{{ru}}\times \frac{{I}_{{ur}}-{I}_{{ru}}}{I}\\ \end{array}\end{array}\right.$$
(6)

Where PSur and PSru represent the urban and rural population share, respectively, while Iur, Iru, and I are the per capita disposable income at urban, rural, and provincial level.

Projections of income distribution

We assumed a log-normal distribution as the functional form of income distribution at the provincial, urban, and rural level. This is one of the most commonly assumed forms used in previous literature18,44. We parameterized these using the projections of per capita disposable income and Gini coefficients. Equation 7a–c describe the parameterization of the log-normal functional form16, applying a density distribution, which was defined and used for computing the income level at further different percentiles.

$$\sigma =2\times {{erf}}^{-1}\left({Gini}\right)$$
(7a)
$$\mu ={Ln}\left(I\right)-\frac{{\sigma }^{2}}{2}$$
(7b)
$${F}_{x}(x)=\varphi \left(\left({Ln}\left(x\right)-\mu \right)\,/\,\sigma \right)$$
(7c)

Where Gini represents the Gini coefficients at provincial/urban/rural level for province i in year t, and I is the respective per capita disposable income.

Data Records

The projected yearly per capita disposable income, Gini coefficients, and income distribution (includes functional parameters and income percentile), under the four localized developmental scenarios are provided at the provincial, urban, and rural levels. These are all available in the public repository Figshare45. This dataset also includes the 95% confidence intervals (CIs) of per capita disposable income and Gini coefficients for uncertainty analysis purposes. The dataset is available in the form of csv files, and Fig. 3 shows the hierarchy of data organization and file name templates.

Fig. 3
figure 3

Data organization. Dataset is available in the form of csv files.

Full size image

To store the data, we define three main folders, named “Provincial”, “Urban”, and “Rural”, pertaining to the different spatial levels. Each main folder includes three sub-folders, named “Disposable income”, “Income inequality (Gini)”, and “Income distribution”. Each sub-folder contains four new folders named after the four scenarios to store the corresponding projections under different scenarios. In the scenario folders located in folder “Disposable income”, files named “Income.csv”, “Income_High.csv”, and “Income_Low.csv” are built to store per capita disposable income data (with unit of Yuan). For the scenario folders within the sub-folder “Income inequality (Gini)”, Gini coefficients and its 95% CIs under each scenario are stored in files “Gini.csv”, “Gini_High.csv”, and Gini_Low.csv, respectively. In scenario folders of sub-folder “Income distribution”, the parameters of income distribution stored in files “Mean value.csv” and “Standard deviation.csv”. Then, sub-folders “Income percentile” are further created within each scenario folder to store the files of income percentiles. All the files of income percentiles (with unit of Yuan) are named as “ID_Province name.csv”, while ID is the number assigned to each province.

The provincial projections of per capita disposable income, Gini coefficients, and income distributions are shown in Figs. 4, 5. We distinguish the 31 provinces by three groups named tiers 1–3, based on their per capita GDP for the period 2007–2019. We then select five provinces from each tier to illustrate future disposable income and income inequality projections.

Fig. 4
figure 4

Provincial per capita disposable income (thousand yuan) of sample provinces.

Full size image
Fig. 5
figure 5

Provincial income inequality (Gini coefficient) of sample provinces.

Full size image

Technical Validation

We tested the reliability and robustness of our results in the following steps, including model performance evaluation, errors assessment for provincial disposable income, and volatility analysis for provincial Gini coefficients.

Model performance evaluation

In Tables 4, 5, we describe the predictive capacities of the provincial and urban (rural) models. For provincial model, models trained on income dataset and Gini coefficient dataset all showed outstanding performance in both baseline validation and robust validation (for only Gini coefficient model). The RMSE of the models were all below 4%, and the MAPE was all below 6%, indicating that the RF models showed excellent predictive capacity of the temporal dimension and generalization ability in terms of the spatial dimension. For further analysis, we selected the model which exhibited the best performance, i.e., the income model using the FL dataset and the Gini model using FLO dataset to perform the subsequent procedures.

Table 4 Model performance at provincial level.
Full size table
Table 5 Model performance at urban (rural) level.
Full size table

The urban (rural) level models for disposable income also showed satisfactory predictive performance across, particularly the model trained using the NL dataset, which produced a RMSE below 3% and a MAPE below 2%. However, the models trained on Gini coefficient ratio did not perform as expected. While the model trained on the FLO dataset had an acceptable performance for baseline validation, with a RMSE below 5% and a MAPE below 10%, it still did not meet expectations in the robust validation. This could be due to the uneven distributions of income equality across provinces, particularly in rural China46, which suggests that the predictive variables used in this study to build the models were limited in capturing the spatial differences in rural Gini coefficients. In literature, several variables have been highlighted as important for explaining changes in rural Gini coefficients, such as employment rates across different industries47, migration48, and land use change49. Nevertheless, data on these variables are rarely available, and their future projections carry considerable uncertainties. Therefore, we still regard the current model using the FLO dataset as the best choice for further simulation.

Error assessment for provincial disposable income

Table 6 presents the mean predictive errors from 2020 to 2023 between the provincial projections of per capital disposable income derived from per capita GDP and the provincial per capita disposable income collected from China Statistical yearbooks. The absolute percentage error (APE) is calculated based on Eq. 8 to reflect the predictive errors, where Pt represents the projected result and At represents the corresponding actual value.

$${APE}\left( \% \right)=\left|\frac{{P}_{t}-{A}_{t}}{{A}_{t}}\right|\times 100 \% $$
(8)
Table 6 The mean predictive errors from 2020 to 2023.
Full size table

The mean APE across all 31 provinces is 4%, indicating a slight difference between projected income and actual value. Specifically, 29 among 31 provinces demonstrate APEs below 10%, and 24 among those 29 provinces show APEs below 5%.

Volatility analysis for income inequality projections

We cannot directly compare our projections with others’ estimations due to the lack of similar income inequality datasets. To validate the reasonability and confidence of this dataset, we performed a volatility comparison based on provincial Gini coefficients projections. The volatility index was represented by the ratio of extreme deviation to minimum value.

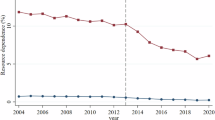
To validate the ability of our model in predicting potential fluctuations in income inequality, we performed a volatility comparison between the projected provincial Gini coefficient and the historical Gini coefficient of a few countries, including the G7 countries and China. The Gini coefficients for these countries were obtained from the World Bank (https://databank.worldbank.org/source/world-development-indicators). The comparison results are shown in Fig. 6. The volatility of Gini coefficients across eight countries ranges from 8–45%, with an average of 23%. The volatility across provinces is 5–36% (16% average) for HSD, 8–40% (20%) for HQD, 7–32% (17%) for BAU, and 3–27% (12%) for LSD. Thus, the volatility range, we observe across provinces is of the similar range as that across countries and covers the volatility seen in the past few decades (20–60 years) of most countries. This indicates this dataset can capture potential fluctuations in income inequality on a long-term temporal scale.

Fig. 6
figure 6

The volatility comparison between Chinese provinces and selected developed countries.

Full size image

Usage Notes

This study builds a methodological framework applying machine learning algorithms to project income inequality and distribution at the provincial, urban, and rural levels for 31 mainland Chinese provinces from 2020 to 2100 under different development pathways. In what follows, we discuss the potential applications of the proposed methodology and the released dataset, and we also interpret the uncertainties and limitations of this work.

Applicability of the methodology and dataset

Our products have several channels to easily interface with users’ customized demands, and some examples of such uses are shown in Fig. 7. The first strand of applications for our products is to produce datasets that caters to users’ customized demands. For example, this study provides a methodological framework to project income distribution datasets at different spatial level while considering necessary consistency constraints, which can be replicated and applied easily, as there are no strict limits on the form of data input (balanced or unbalanced panel data). Applying our methodology, users can produce similar datasets for other countries or regions at different spatial levels using their own historical datasets and assumptions regarding future scenarios.

Fig. 7
figure 7

The potential applications of the proposed methodology and released dataset.

Full size image

In addition to such direct applications, the dataset produced by this study can also serve as an input for various research domains and analyses. For instance, the income distribution can be used to carry out further micro-level simulation-based analysis at the unit of individuals or households, so as to support highly granular analyses1,50. Users can also determine specific income metrics according to their customized requirements, such as considering alternative international and national poverty thresholds, and diverse inequality metrics like the Palma ratio, or detailed income projections for all deciles. These data can serve as key input for various macro-level analyses across social, economic, and environmental domains, such as demand assessments, carbon footprint evaluations, and inequality research related to social well-being and health impacts of natural hazards. Meanwhile, this dataset can also be used in integrated assessment and computable general equilibrium models to clarify the coupled feedback between income, climate change, and economic outputs.

Uncertainties and limitations

We designed four different provincial-level pathways to explore divergent assumptions regarding future developments and related uncertainties in underlying socio-economic and demographic predictive factors. However, uncertainties still exist due to the lack of consideration of explicit policy interventions on income redistribution. While we consider indicators, such as educational expenditure, health expenditure, and social protection expenditure, as proxies for redistributive policies, we project these based on future development conditions rather than any explicit government intentions or policies to reduce inequalities. Therefore, the dataset released in this study can be regarded as a baseline reference range of disposable income, income inequality, and income distribution without taking possible policy intervention measures into account. In addition, our dataset was generated assuming a continuous development trend under each pathway, and thus does not include unforeseeable contingencies. Our dataset can be regarded as a benchmark and basis for further research that explores the impacts of specific policies, technological innovations, or events.