Abstract
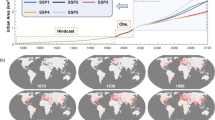
Global-scale and long-term projections of future urban 3D expansion are essential for understanding the environmental effects of future urbanization. Here, we develop a multi-task learning and end-to-end cellular automaton model for urban 3D projection (named MECA-3D). Within the MECA-3D model, the top-down component determines urban built-up volume demand based on panel data regression model and socioeconomic factors, while the bottom-up component estimates urban land suitability and built-up height by a multi-task residual neural network model. Using the MECA-3D model, for the first time, we present the global projections of future urban 3D expansion dataset (named FU3D) from 2020 to 2100 at a 1 km resolution under the five Shared Socioeconomic Pathways (SSPs). Our projections show that by 2100, global urban built-up volume will increase to about 184%–409% under the five SSPs, with the largest 3D expansion (exceeding 4000 km3) projected under the fossil-fuelled development scenario (SSP5). The validation procedures indicate that the FU3D dataset exhibits sufficient accuracy, long-term reliability and reasonable uncertainty. In general, the FU3D dataset overcomes the limitations of 2D projections, provides valuable 3D morphological information for future sustainable cities and can serve as a valuable input in relevant fields.
Similar content being viewed by others
Background & Summary
Over half of the global population currently resides in urban areas and this proportion are projected to reach 70% by 20501. The unprecedented urbanization worldwide has significantly impacted the environment, contributing to at least 70% of anthropogenic greenhouse gas emissions, 80% of natural habitat loss and over 3.4 million km² degradation of wetlands in the past centuries2,3,4, posing great challenges to the achievement of the Sustainable Development Goals (SDGs)5. Therefore, elucidating the future implications of urbanization on both the environment and human well-being is essential for advancing sustainable development in the future. Recent decades have witnessed many studies conducted to projected future urban land expansion throughout the 21st century based on cellular automata (CA) and its derived models6,7,8,9,10,11,12, which significantly enhanced the understanding of the future evolution of urban systems. The CA framework constitutes a discrete spatial modeling module wherein complex macroscopic system patterns emerge from microscopic-level cell interactions following predefined transition rules13,14,15. However, despite the extensive applications of CA models in urban simulation, an important limitation is that they cannot simultaneously simulate both horizontal and vertical expansion. Therefore, existing large-scale projections predominantly focused on horizontal 2D expansion, while the vertical 3D growth is overlooked. In the context of global change, urban 3D expansion has close relationship with sustainable land use16,17,18, public health19,20,21, energy consumption22,23, transport efficiency24, urban heat island25,26,27, natural hazards28,29,30,31 and biodiversity32,33,34,35,36. Despite the importance of the vertical building space and 3D spatial capacity in accounting for land use demands from the burgeoning urban population, they have often been overlooked. Thus, a comprehensive understanding of urban 3D expansion in the future is imperative to provide essential information for urban planning in coping with these future challenges.
Recent studies have closed this gap by simulating future urban 3D expansion. For example, Zhao et al.37 projected future urban 2D expansion while simultaneously employed a random forest algorithm to forecast the vertical growth of building height in Shenzhen, China. He et al.38 combined the CA model with a backpropagation artificial neural network to simulate future urban height in Wuhan, China. Lin et al.39 employed a predefined set of “IF-THEN” rules within a CA model to simulate built-up height growth in Guangzhou, China. Koziatek et al.40 proposed a “iCity 3D” model for forecasting vertical urban development. Chen et al.41 proposed an extended patch-based CA model to simulate horizontal and vertical urban growth under the SSPs. Despite the progress made in these preliminary studies on 3D urban simulation, most existing studies simply combined horizontal urban simulation with vertical height estimation, by which the 3D built-up space is inadequately considered for macro control. To address this limitation, recent studies employed built-up 3D volume space as top-down macro demand rather than the conventional land use demand. For example, Xu et al.42 extended the traditional FLUS model to FLUS-3D model to simulate future urban 3D expansion in three metropolitan regions of China. Wang et al.43 proposed an enhanced CA model and used built-up volume as macro control to project future urban 3D expansion in China at 1-km resolution. However, in terms of the bottom-up (spatially explicit) projections, existing studies mainly used two separate models to estimate urban land suitability and vertical height. For example, the land use suitability is mainly estimated by an Artificial Neural Network (ANN) model, while vertical height is projected by the widely used random forest model15,37,41,42,43,44. This decoupled modeling paradigm inevitably introduces structural redundancy and computational inefficiency, particularly considering the significant overlap in socioeconomic and environmental explanatory variables (e.g., population density, economic level, transportation accessibility) required for both urban land suitability and vertical height. The recent advancement of deep learning techniques presents new opportunities to overcome these limitations through multi-task learning architectures45. Multi-task learning has demonstrated superior performance across various domains by leveraging shared representations and task correlations while reducing model complexity through parameter sharing46,47,48,49. The horizontal urban land-use suitability and vertical height prediction tasks inherently exhibit strong interdependencies, that is, urban horizontal expansion patterns influence vertical intensification potential, while existing building height conversely constrains future horizontal development possibilities. This symbiotic relationship creates ideal conditions for implementing multi-task learning frameworks that can simultaneously capture these synergistic dynamics. Therefore, our study addresses this research gap by proposing an end-to-end multi-task deep learning model that seamlessly integrates urban land suitability estimation and vertical height prediction within a unified CA modeling architecture.
On the other hand, while most existing studies in terms of urban 3D projection mainly focused on some specific cities, including cities in United States, Europe and China38,39,41,44,50, knowledge gap is particularly pronounced for low- and middle-income countries which are expected to host the majority of global population growth and urbanization throughout the 21st century51,52. To the best of our knowledge, only Global Human Settlement Layer (GHSL) provides global-scale future built-up volume map53, but the projection generated by simple historical trend extrapolation is only up to 2030. Meanwhile, it does not provide SSP-consistent projections and thus does not meet the needs of the design of SSPs. Therefore, it can hardly be used in longer-term future analyses and cannot support the development of societal development pathways. That is, there is still a lack of SSP-consistent and spatially explicit 3D urban projections at a global scale that extend over the whole 21st century.
In general, the absence of global-scale, long-term and SSP-consistent 3D urban expansion products significantly limits the understanding of future urban expansion under anticipated global change and impedes advancements in urban planning. To bridge this gap, we take an important step forward to provide the first global projections of future urban 3D expansion dataset (named FU3D) from 2020 to 2100 under the five shared socioeconomic pathways (SSPs). Our study, based on the elaborating MECA-3D model (see Methods), hypothesizes the relationship between the localized SSPs and urban 3D expansion which highlights how various socioeconomic and environmental factors—such as demographic trends, economic conditions, technological advancements, and policy decisions embedded in SSP scenarios—impact urban 3D expansion and influence urban form. The five SSPs (i.e., SSP1: sustainability, SSP2: middle of the road, SSP3: regional rivalry, SSP4: inequality, and SSP5: fossil-fueled development) outline five potential pathways for the future world based on demographics and economic growth54,55,56 (Table 1). The SSP-consistent FU3D dataset with 1-km resolution can extend the applicability of urban 3D information into future scenario-based climate, environment and sustainability-related research.
Methods
Data preparation
The projection framework in this study initiates in 2015. Therefore, we first collect and fuse (by calculating their average) the global gridded built-up volume dataset from Li et al.57, Zhou et al.58, and the WSF3D dataset59, because they are the currently available global-scale 3D building products with high precision and fine resolution in (or nearby) 2015. The average built-up height is then calculated by dividing the fused built-up volume by the urban area in each cell (i.e., 1 km2). Consequently, the built-up height in this study can be considered to be a “flattened” height representing the average height of all built-up areas within a 1 km2 pixel. Thus, the value of built-up height in this study may appear to be lower than the actual “building height”42. We then mask the fused 3D maps by the urban land product collected from the European Space Agency Climate Change Initiative Land Cover products (ESA-CCI-LC, http://maps.elie.ucl.ac.be/CCI). The ESA-CCI-LC product has been widely used in many studies. For example, Chen et al.6 used the ESA-CCI-LC as the baseline of the future urban land projections. We also provide comparison with other urban land products and find that the difference is minor (Fig. 2). Historical gridded population data are retrieved from WorldPop60. Future gridded population data are provided by Li et al.61. Historical and future GDP products are collected from Chen et al.62 and Wang et al.63. Global road database is collected from the Global Roads Inventory Project (GRIP) dataset, which was generated from many different public-available sources64. Global city centers are collected from Melchiorri et al.65. Terrain data are collected from the Global Land One-kilometer Base Elevation (GLOBE) project66. We also collect global ecological reserve areas from the World Database on Protected Area project, which provides comprehensive global database of marine and terrestrial protected areas67. Global historical gridded built-up volume data from 1980 to 2010 (at 5-year intervals) are collected from GHSL68,69, which are derived based on long-term Landsat and Sentinel imageries70,71 and widely used in many studies72,73,74. Noted that they are not directly used in spatial projection but used to calculate historical built-up volume amounts in 31 subregions which are defined based on geographic location and development level. Their historical and future scenario-based GDP, population, and urbanization rate are provided by the SSP database version 2 (https://tntcat.iiasa.ac.at/SspDb). See Fig. 11C for the spatial extent of these 31 subregions.
Top-down component: determining urban built-up volume demand
Panel data regression model is used to determine the future urban built-up volume demand, which provides 3D space for population and socioeconomic activities. The panel data regression model has been widely used in estimating macro demand in urban CA models for its efficiency with limited data, model transparency and interpretability6,43,75. We use socioeconomic data attained from SSP database from 1990 to 2010 for training, and the data in 2015 for validation. We also provide comparison with Geographically and temporally weighted regression (GTWR) model76 and random forest model77. The GTWR model is mainly designed to address spatiotemporal heterogeneity, while the random forest is famous for its capacity to capture non-linear relationships. However, the results show that the panel regression model outperforms the other two models (Fig. 1), mainly due to the limited training data, which indicates that panel data regression is suitable to use in this study. Specifically, using the GHSL dataset, historical built-up volume amounts can be calculated for each subregional and then used as the dependent variable in panel data regression. However, there is obvious difference between GHSL built-up volume amount (\({D}_{2015}^{{GHSL}}\)) and the observed global amount in 2015 (\({D}_{2015})\), because \({D}_{2015}\) only includes buildings in urban area while GHSL includes buildings in both urban and rural area. To reconcile this difference, we employ an simple but effective harmonization strategy motivated by a previous study estimating historical urban land amount10. Specifically, we use the ratio \(\frac{{D}_{2015}}{{D}_{2015}^{{GHSL}}}\) to calibrate the historical built-up volume amounts of the GHSL built-up volume amounts in historical years (1980–2010) (denoted as \({D}_{t}^{{GHSL}}\)). The harmonization strategy can be expressed as follows:
where \({D}_{t}\) is the calibrated urban built-up volume demand in historical year t. Then, historical statistics of GDP per capita (GDPC) and urbanization rate (UR) from 1980 to 2010 (at 5-year interval) are used as predictors to establish the built-up volume demand model at a global scale, as shown below:
where \({{DC}}_{r,t}\) indicates per capita urban built-up volume demand in year t and region r. \(\varepsilon \) refers to the error term. \({\beta }_{{\rm{r}}}\) is a region-fixed effect term which controls for time-invariant regional differences such as geography. This term can also reflect spatial heterogeneity among the regions. Once the panel regression is established in Eq. (2), future built-up volume demand can be predicted in 31 subregions (the top-down component presented in Fig. 3). The result of the regression shows the model effectively accounts for over 98% of the variation in the data, with a statistically significant p-value < 0.001, indicating the robustness of the panel regression models and the general reliability of the projected future built-up volume demands (Table 2).
An illustration for different urban land products in Greater Bay Area, China, in 2015. (a) Building volume product from Li et al.1. (b) ESA-CCI-LC. (c). CLCD from Yang et al.2. (d) CNLULC from Liu et al.3 (e) GlobaLand30 from Chen et al.4. (f) MCQ12Q1 product. Red pixels refer to urban land, while the black lines refer to urban boundary from Li et al.5.
Bottom-up component: estimating urban land suitability and height
Urban land suitability characterizes the suitability of a non-urban pixel for development into urban pixel6,15,42. Unlike previous studies that employed separate models for predicting urban land suitability and urban height, we introduce an end-to-end multi-task deep learning model, SE-ResUNet, to simultaneously address the two tasks. Compared with single-task learning, multi-task learning shows higher learning efficiency as well as less over-fitting risk since it guides models to reach more general feature representation preferred by multiple related tasks, which can be considered as an inductive bias for the regularization of deep neural networks45. Specifically, the SE-ResUNet model adopts a residual neural network (ResNet)78 integrated with Squeeze-and-Excitation blocks (SE)79 backbone as its encoder architecture, while the decoder follows a U-Net symmetric structure80. The model employs a shared encoder but uses two independent decoders, one for urban land suitability prediction and another for urban height estimation. The ResNet backbone adopts the framework of residual learning and inserts shortcut connections into the plain neural networks, which can mitigate the training of much deeper models without degradation of performance78. SE blocks within ResNet are used, where channel-wise attention is calculated by two fully connected layers after the global average pooling on the input feature maps.
We use urban land data and urban built-up height in 2015 as ground truth data, along with a total of 7 socioeconomic and environmental variables as explanatory variables (Table 3). Specifically, population and GDP are used as they have been found to have strong relationship with urban 3D expansion41,52,53,81,82. For example, Frokling et al.82 found that building volume and GDP are positively related with R2 reaching 63%, while the GHSL building volume mapping53 found the R2 is nearly 58%. In addition, road density is also included, which is calculated as the ratio of total length of roads to the total area of each 1-km2 pixel. Distance to rivers and distance to city centers of each cell are also calculated by the Euclidean Distance tool in ArcGIS Pro software. Except for population and GDP, other variables keep static during long-term projections as we suggest they will not change a lot in the rest of the 21st century. These global 1km-resolution input data are split into tensors of shape 7 × 64 × 64 for model training. We take 80% of the data for training and the rest 20% for testing. The output of the model includes the urban land suitability and urban height, both of which are tensors of shape 1 × 64 × 64. As for loss function, the Binary Cross-Entropy (BCE) loss is used land suitability prediction (Eq. (3)), while the Mean Squared Error (MSE) loss is used for height prediction (Eq. (4)). We apply an adaptive weight scheme based on task uncertainty to combine the two loss functions (Eq. (5)). The Adaptive moment estimation (Adam) optimizer is employed83 and the initial learning rate is set as 0.001 and then decrease following the cosine annealing schedule84. The batch size is set as 16 and the number of epochs is set as 100.
where \(\hat{y}\) is the predicted value and y is the reference value. \({\sigma }_{1}^{2}\) and \({\sigma }_{2}^{2}\) are uncertainty measures for corresponding tasks and they can be treated as trainable parameters along with the parameters of the SE-ResUNet model.
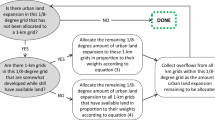
According to previous studies6,10,15,42,43, the conversion probability of a non-urban pixel changing to urban pixel (termed CP) is typically determined by four components and can be calculated as:
where \(S\) refer to the urban land suitability predicted by the SE-ResUNet model. \(N\) is the neighbor effect, which can be calculated as the percentage of existing urban land pixels within a 3 × 3 neighbor window of each pixel. \(I\) is the inertia coefficient which is calculated based on the discrepancy between projected built-up volume demand and existing developed built-up volume amount (Eq. (7)). \(P\) is set as 1 if a pixel is considered as prohibited pixel. In this study, water pixels, pixels with slopes greater than 15° and pixels within the ecological protection areas are considered as pixels prohibited from being converted to urban land.
where \({I}_{t}\) is the inertia coefficient at time t. \({D}_{t-1}\) is the difference between the projected built-up volume demand at t and the actual volume at time t-1.
MECA-3D model: projecting urban 3D expansion iteratively
Urban expansion can be simulated by the dynamic interplay between bottom-up and top-down forces43,85. The overall framework of the MECA-3D model proposed in this study to project future urban 3D expansion is presented in Fig. 3. The MECA-3D model consists of two main components: a top-down component to determine the macro built-up volume demand, and a bottom-up component to implement spatially explicit projection. The specific procedure to simulate urban 3D expansion from year t to t + 10 can be described as follows: First, the well-trained SE-ResUNet is used to predict urban land suitability and urban height in year t + 10. The built-up volume demand is also predicted by the already established panel regression model in year t + 10. Second, we update the conversion probability (CP) in year t + 10. Third, based on the updated conversion probability, we employ the random roulette selection scheme15,42,86 to determine whether or not a non-urban pixel convert to urban land in year t + 10. Fourth, the urban pixels in year t + 10 are multiplied with the corresponding predicted vertical height and accumulated to the existing built-up volume amount. The random roulette selection is implemented successively, until the accumulated built-up volume amount reaches the projected built-up volume demand in year t + 10.
Data Records
The FU3D dataset is publicly available at Zhao et al.87. It contains global gridded data of future urban land, urban built-up height and urban built-up volume at 1-km resolution, covering the years 2010 to 2020 at a 10-year interval under five SSPs. The dataset is formatted in GeoTIFF and uses the WGS1984 coordinate system. Specifically, urban built-up land is measured by a binary value (0: non-urban; 1: urban). Built-up volume is measured in km3 and built-up height is measured in meter. Data files are named according to a standardized format: “ff_yyyy_SSPx.tif,” where “ff” represents urban built-up land, urban built-up height and urban built-up volume (denoted as “urban”, “height” and “volume”, respectively); “x” represents the future SSP scenario, ranging from 1 to 5; “yyyy” represents the future year, ranging from 2020 to 2100, at a 10-year interval. The codes and programs used to generate and validate the FU3D dataset are Python (3.7) and ArcGIS Pro (3.0). Figure 4(A) provides a comprehensive view of the long-term evolution of urban built-up height in five global metropolises from 2020 to 2100 under SSP2. The five metropolises are: San Francisco in USA, Shanghai in China, Tokyo in Japan, Buenos Aires in Argentina, and Paris in France. Our FU3D dataset allows for a comprehensive 3D perspective on how these cities expand and develop over time. We can find that under SSP2, the macro built-up volume demand in Japan (JPN) will stop increasing and even decrease after 2030 (Fig. 11B). This means that the cities in Japan are expected to stop growing (Fig. 4A). For China (CHN), built-up volume demand will increase until 2060 and then stay. On the other hand, for USA and Europe, as built-up volume demands are projected to keep increasing, cities will keep growing until the end of the century.
Projected urban built-up height in the future from 2020 to 2100 under SSP2. (A) Long-term dynamics of urban built-up height in five metropolises from 2020 to 2100 under SSP2. The five metropolises are San Francisco in USA, Shanghai in China, Tokyo in Japan, Buenos Aires in Argentina, and Paris in France. (B) Urban built-up height in China, USA, and Europe in 2100 under SSP2. Note that the built-up height here can be considered to be a “flattened” height representing the average height of all built-up areas within a 1 km2 pixel. Thus, the value of built-up height in this study may appear to be lower than the actual “building height”.
Technical Validation
Validation measurements
The receiver operating characteristic (ROC) curve is used to evaluate the overall performance of the SE-ResUNet. The area under the curves (AUC) value ranges from 0 to 1. A completely random model yields an AUC value of 0.5, while a perfect model yields an AUC value of 188. The performance of 2D urban expansion is quantified by overall accuracy (OA), Kappa coefficient (Kappa), and figure of merit (FoM). OA is a measure of the proportion of pixels that are accurately simulated. Kappa ranges from −1 to 1, with a value of 0 indicating that model performance is equivalent to a random model, while a value approaching 1 indicating that model performance is perfect. FoM is designed for evaluating how much correct changes can be simulated by a cellular automaton-based model. It ranges from 0 to 1, with a value of approximately 0.2 considered as a favourable accuracy according to previous studies15,89. FoM can be calculated as follows:
where A represents the non-urban pixels correctly simulated to change to urban pixel. B denotes the observed changed pixels but fail to be projected to change. C denotes the observed non-changed pixels that are incorrectly projected as changed. We also use error decomposition-based method. In specific, the overall disagreement between the actual and simulated urban land can be decomposed into the quantity disagreement (QD) and the allocation disagreement (termed AD)90,91,92,93,94, which can be calculated as follows:
where \({p}_{i}\) and \({r}_{i}\) represent the binary value (urban: 1; non-urban: 0) of pixels in the projected and actual urban land data, respectively. \({FP}\) (false positive) and \({FN}\) (false negative) are commission and omission errors in the confuse matrix, respectively.
The performance of 3D urban expansion is evaluated by three metrics, i.e., squared-correlation coefficient (R2), Root Mean Square Error (RMSE) and Mean Absolute Error (MAE) are used to evaluate the overall agreement, which are expressed as follows:
where \({y}_{i}\), \({\hat{y}}_{i}\) and \({\bar{y}}_{i}\) are the reference value, predicted value and the average of predicted values.
Model evaluation
The AUC value for land use suitability exceeds 0.96 (Fig. 5A), suggesting that the estimated urban land suitability is well accounted for by the chosen input variables. What’s more, the validation conducted on independent test set shows that the overall accuracy of predicting urban land suitability reaches 0.97, while the RMSE and MAE reach 0.2 m and 0.06 m (Table S2). These results indicate that the SE-ResUNet achieves satisfactory performance after 100 training epochs (Fig. 5B).
Performance of the FU3D dataset in 2020
We compare the spatial patterns of urban land projected in FU3D dataset with the ESA-CCI-LC 2020 product and three similar global 2D urban projections, i.e., Chen et al.6, Li et al.10, and Gao et al.95. As shown in Fig. 6, the projected urban land of FU3D shows the most similarity with ESA-CCI-LC product. Further validations including spatial agreement analysis and error decomposition show that the OA across the four datasets is similar (nearly 0.99), while the Kappa, FoM, QD and AD of FU3D dataset outperform the other three existing products (Table 4). Moreover, the other three existing products have only horizontal attributes, while the FU3D has vertical height attributes. Generally, the methodological advancements of our study are achieved by two aspects: (1) we use built-up volume as the proxy of macro demand, while the compared benchmark studies only used urban land. The built-up volume can better represent the 3D space that supports human activities and thus provides more accurate macro control for urban expansion in a CA model. (2) The MECA-3D proposed in this study leverages state-of-the-art multi-task residual deep learning technique, enhancing the performance of the spatially explicit projection.
For the projected urban built-up height, we collect three global-scale built-up height datasets, i.e., GHSL53, GLAMOUR96 and GBH97. GLAMOUR dataset is derived from Sentinel imagery that captures the average building height and footprint at a resolution of 0.0009° across urbanized areas worldwide96. GBH dataset provides a 150-m global urban building height map around 2020 by combining the spaceborne lidar (GEDI), multi-sourced data (Landsat-8, Sentinel-2, and Sentinel-1), and topographic data97. The 1km-resolution GHSL built-up volume map in 2020 is generated by integrating multi-source satellite imagery (Landsat, Sentinel-2) and DEM datasets (AW3D30/SRTM), while the built-up volume map in 2030 is generated by extrapolating the historical trends53. To avoid possible misunderstanding, it should be noted that the gridded GHSL volume datasets (both historical and future) are not directly used to train the bottom-up component (the SE-ResUNet). In this study, the validation procedure is conducted in ten regions determined by the World Bank. Within each region, 5000 sample points are randomly allocated. The results demonstrate that our projections generally align with the selected datasets, as shown in Figs. 7–10. We find that the R² between FU3D and the GHSL dataset is around 80%, while the overall R² with the GLAMOUR and GBH datasets is approximately 45% and 60%, respectively. It should be noted that since the urban built-up height projected in FU3D is a “flattened-height” (as mentioned in the Data Preparation section), it is relatively underestimated compared to the vertical heights in the three compared datasets, similar with Xu et al.42.
Except for global-scale datasets, we also provide comparisons against several regional datasets. For example, we collect building footprints of 68 Chinese cities with height information (expressed as floor numbers) in 2020 from Amap (https://ditu.amap.com/). Height of each floor is assumed as 3 meter according to previous studies98,99. The results show that the overall R2 is 74% with the RMSE value 0.93 m (Table S3). Then, for Europe, EUBBCCO v0.1 dataset is collected100, which includes nearly 202 million buildings across the 27 European Union countries by combining newest multi-source government achieves and the records from OpenStreetMap100. Because the EUBBCCO v0.1 dataset is too large to use all the records for validation, 8 representative countries are chosen. In each country, 10,000 sample points are randomly generated for validation. Results show that the FU3D height in 2020 show a good agreement with the EUBBCCO dataset, with R2 nearly 78% (Table S4). Note that since both datasets are building vector datasets, we calculate the “flattened height” before the comparison with FU3D. Specifically, we compute the total building volume within each 1 km² pixel and then divided it directly by the pixel area to derive the so-called “flattened height”.
Uncertainty analysis
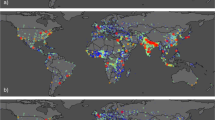
Uncertainty in the FU3D dataset can be categorized into three types: spatial heterogeneity uncertainty, parameter uncertainty and stochastic uncertainty. To mitigate spatial heterogeneity uncertainty, regional-fixed effect is included in the panel data regression for projecting future built-up demand. This approach accounts for spatial heterogeneity by assigning distinct intercepts to different subregions. However, it should be noted that while panel regression with individual fixed effects improves model fit, as reflected in higher R² value, this approach relies on the assumption that regional heterogeneity remains time-invariant, which may be untenable for long-term projections spanning decades to 2100, as socioeconomic and environmental conditions typically evolve nonlinearly. Future work could address this limitation through time-varying fixed effects or hybrid modeling approaches101. For parameter uncertainty, the input parameter uncertainty primarily stems from variations in per capita GDP and urbanization rates. We quantify it by calculating the 95% confidence intervals of the regression coefficients in the panel data regression, which are shown in Table S1. How parameter uncertainty impacts the projected demand are also depicted in Fig. 11. Then, to quantify stochastic uncertainty, we perform 100 simulations for each SSP during the future projections. Since we employ the random roulette selection method in the MECA-3D model, the results from multiple repeated experiments can effectively capture the model’s stochastic uncertainty. By overlaying the results of these simulations6, stochastic uncertainty can be clearly quantified (Figs. 13, 14). What’s more, by comparing the different spatial patterns across the SSPs, we can clearly see how macro socioeconomic variable variations across different SSPs ultimately affect the projected outcomes in 2100. The resulting urban spatial patterns align well with those reported in previous studies6,10,95.
Global and regional built-up volume demand during historical period (1980–2010) and the future under five SSPs (2020–2100). The shaded areas represent the 95% confidence intervals estimated by panel data regression. (A) Global built-up volume demand. (B) Built-up volume demands of the 31 subregions. (C) Distribution of the 31 subregions.
Uncertainty of projected urban land in five metropolises in 2100 under five SSPs. The five metropolises are San Francisco in USA, Shanghai in China, Tokyo in Japan, Buenos Aires in Argentina, and Paris in France. This figure shows the likelihood of each non-urban pixel becoming urban which is estimated by overlapping the results of 100 simulations.
Usage Notes
To understand the environmental impacts of future urbanization and human activities, it is crucial to have global-scale and long-term projections of urban 3D expansion. Currently, such projections are missing. Our research addresses this gap by presenting the first comprehensive global-scale projections of urban 3D growth for the 21st century. The projected urban 3D growth patterns in this study under SSPs comply with the relative literal meanings of the five SSPs (Fig. 11). For example, by 2100, global urban built-up volume will increase to nearly 184%–409% under the five SSPs, with the largest 3D expansion exceeding 4000 km3 projected under SSP5, which reflects the dramatic global economic growth. The SSP3 and SSP4 show minimal changes, owing to the projected economic deceleration6 (Fig. 12). Despite severe global population decline8,56, SSP5 anticipates continued urbanization due to ongoing economic development, which maintains high demand for built-up space throughout the 21st century.
With the support of the FU3D dataset, researchers can further understand how cities will grow and which pattern they follow (e.g., outward or upward102) in the future under different scenarios. Moreover, the FU3D dataset is also highly valuable for advancing research in several areas such as urban public health103,104, infrastructure resilience to natural hazards105,106,107, urban heat island effects108,109, CO2 emission estimates110,111, and local climate zone mapping108,112,113. In urban planning, the FU3D dataset is a critical resource for policymakers. It helps refine development strategies for sustainable growth by evaluating factors such as energy consumption, urban heat islands, and biodiversity under different SSP scenarios. This enables the creation of policies that mitigate negative impacts and enhance sustainability, for example, understanding future vertical development patterns helps cities improve resilience to climate change impacts, such as sea-level rise and extreme weather events, promoting adaptive and sustainable urban development. For climate modelling, recent studies have demonstrated the importance of spatially explicit 3D urban information. For example, Kamath et al.114 found that incorporating 3D urban information can significantly improve the accuracy (55% in RMSE) of the urban Weather Research and Forecasting (WRF-Urban) model compared to the traditional table-based local climate zone approach. Melissa et al.115 found that high-resolution 3D urban morphological parameters into the WRF model reduced extreme precipitation simulation errors by nearly 18%. Therefore, we believe the long-term future 3D information provided by FU3D dataset can also serve as crucial input parameters for future urban climate modelling. The incorporation of FU3D can help more accurately capture future urban climate and weather extremes under different SSPs, thereby enabling local governments to develop targeted adaptation strategies for sustainable urban development.
There are also several limitations in the FU3D dataset. First, to ensure the projections is consistent with the SSPs storyline, the macro urban built-up volume demand is calculated in each subregion, due to the lack of country-level (or finer-scale) urban built-up and socioeconomic data for all countries. Second, the impact of future climate change on the evolution of urban 3D forms is not considered. Projections considering climate factors are also needed. This limitation will be addressed in future work by incorporating projections based on the integrated scenarios of SSP and Representative Concentration Pathway (RCP). Third, we neglect the urban renewal during long-term urbanization. Although it is reasonable for a 10-year interval, our future work is expected to produce annual datasets by considering more complicated rules to include urban renewal. Fourth, the MECA-3D model is only trained and calibrated in 2015, due to the lack of long-term and accurate historical data. In further research, long-term historical 3D urban expansion data can be considered for the calibration and validation of urban 3D growth simulations.
Code availability
Executable codes for the MECA-3D model to produce FU3D dataset are publicly available at Zhao et al.116. Additional materials related to this work can be requested from the authors.
References
Affairs, U. N. D. of E. and S. World Urbanization Prospects: The 2018 Revision. https://doi.org/10.18356/b9e995fe-en (United Nations, 2019).
Hopkins, F. M. et al. Mitigation of methane emissions in cities: How new measurements and partnerships can contribute to emissions reduction strategies. Earth’s Future 4, 408–425 (2016).
Ke, X. et al. Direct and indirect loss of natural habitat due to built-up area expansion: A model-based analysis for the city of Wuhan, China. Land Use Policy 74, 231–239 (2018).
Fluet-Chouinard, E. et al. Extensive global wetland loss over the past three centuries. Nature 614, 281–286 (2023).
Nations, U. Transforming our world: The 2030 agenda for sustainable development. New York: United Nations, Department of Economic and Social Affairs (2015).
Chen, G. et al. Global projections of future urban land expansion under shared socioeconomic pathways. Nat Commun 11, 537 (2020).
Luo, M. et al. 1 km land use/land cover change of China under comprehensive socioeconomic and climate scenarios for 2020–2100. Sci Data 9, 110 (2022).
Gao, J. & O’Neill, B. C. Mapping global urban land for the 21st century with data-driven simulations and Shared Socioeconomic Pathways. Nat Commun 11, 2302 (2020).
He, W. et al. Global urban fractional changes at a 1km resolution throughout 2100 under eight scenarios of Shared Socioeconomic Pathways (SSPs) and Representative Concentration Pathways (RCPs). Earth System Science Data 15, 3623–3639 (2023).
Li, X. et al. Global urban growth between 1870 and 2100 from integrated high resolution mapped data and urban dynamic modeling. Commun Earth Environ 2, 1–10 (2021).
Klein Goldewijk, K., Beusen, A., Doelman, J. & Stehfest, E. Anthropogenic land use estimates for the Holocene – HYDE 3.2. Earth System Science Data 9, 927–953 (2017).
Li, X., Zhou, Y., Eom, J., Yu, S. & Asrar, G. R. Projecting Global Urban Area Growth Through 2100 Based on Historical Time Series Data and Future Shared Socioeconomic Pathways. Earth’s Future 7, 351–362 (2019).
Li, X., Chen, Y., Liu, X., Li, D. & He, J. Concepts, methodologies, and tools of an integrated geographical simulation and optimization system. International Journal of Geographical Information Science 25, 633–655 (2011).
Santé, I., García, A. M., Miranda, D. & Crecente, R. Cellular automata models for the simulation of real-world urban processes: A review and analysis. Landscape and Urban Planning 96, 108–122 (2010).
Liu, X. et al. A future land use simulation model (FLUS) for simulating multiple land use scenarios by coupling human and natural effects. Landscape and Urban Planning 168, 94–116 (2017).
Grace Wong, K. M. Vertical cities as a solution for land scarcity: the tallest public housing development in Singapore. Urban Des Int 9, 17–30 (2004).
Rao, Y., Zhou, J., Zhou, M., He, Q. & Wu, J. Comparisons of three-dimensional urban forms in different urban expansion types: 58 sample cities in China. Growth and Change 51, 1766–1783 (2020).
Zhou, Y. & Lu, Y. Spatiotemporal evolution and determinants of urban land use efficiency under green development orientation: Insights from 284 cities and eight economic zones in China, 2005–2019. Applied Geography 161, 103117 (2023).
Southerland, V. A. et al. Global urban temporal trends in fine particulate matter (PM2·5) and attributable health burdens: estimates from global datasets. The Lancet Planetary Health 6, e139–e146 (2022).
Yu, W. et al. Global estimates of daily ambient fine particulate matter concentrations and unequal spatiotemporal distribution of population exposure: a machine learning modelling study. The Lancet Planetary Health 7, e209–e218 (2023).
Rao, S. et al. Future air pollution in the Shared Socio-economic Pathways. Global Environmental Change 42, 346–358 (2017).
Güneralp, B. et al. Global scenarios of urban density and its impacts on building energy use through 2050. Proceedings of the National Academy of Sciences 114, 8945–8950 (2017).
You, K., Ren, H., Cai, W., Huang, R. & Li, Y. Modeling carbon emission trend in China’s building sector to year 2060. Resources, Conservation and Recycling 188, 106679 (2023).
Fu, X. et al. Co-benefits of transport demand reductions from compact urban development in Chinese cities. Nat Sustain 1–11 https://doi.org/10.1038/s41893-024-01271-4 (2024).
Liu, H. et al. The influence of urban form on surface urban heat island and its planning implications: Evidence from 1288 urban clusters in China. Sustainable Cities and Society 71, 102987 (2021).
Shao, L. et al. Drivers of global surface urban heat islands: Surface property, climate background, and 2D/3D urban morphologies. Building and Environment 242, 110581 (2023).
Yuan, B. et al. Global distinct variations of surface urban heat islands in inter- and intra-cities revealed by local climate zones and seamless daily land surface temperature data. ISPRS Journal of Photogrammetry and Remote Sensing 204, 1–14 (2023).
Li, Y., Schubert, S., Kropp, J. P. & Rybski, D. On the influence of density and morphology on the Urban Heat Island intensity. Nat Commun 11, 2647 (2020).
Zhang, W., Villarini, G., Vecchi, G. A. & Smith, J. A. Urbanization exacerbated the rainfall and flooding caused by hurricane Harvey in Houston. Nature 563, 384–388 (2018).
Feng, B., Zhang, Y. & Bourke, R. Urbanization impacts on flood risks based on urban growth data and coupled flood models. Nat Hazards 106, 613–627 (2021).
Xi, Z., Li, C., Zhou, L., Yang, H. & Burghardt, R. Built environment influences on urban climate resilience: Evidence from extreme heat events in Macau. Science of The Total Environment 859, 160270 (2023).
Goddard, M. A. et al. A global horizon scan of the future impacts of robotics and autonomous systems on urban ecosystems. Nat Ecol Evol 5, 219–230 (2021).
Ren, Q. et al. Impacts of urban expansion on natural habitats in global drylands. Nat Sustain 5, 869–878 (2022).
Strona, G. & Bradshaw, C. J. A. Coextinctions dominate future vertebrate losses from climate and land use change. Science Advances 8, eabn4345 (2022).
Simkin, R. D., Seto, K. C., McDonald, R. I. & Jetz, W. Biodiversity impacts and conservation implications of urban land expansion projected to 2050. Proceedings of the National Academy of Sciences 119, e2117297119 (2022).
Li, G. et al. Global impacts of future urban expansion on terrestrial vertebrate diversity. Nat Commun 13, 1628 (2022).
Zhao, L., Liu, X., Xu, X., Liu, C. & Chen, K. Three-Dimensional Simulation Model for Synergistically Simulating Urban Horizontal Expansion and Vertical Growth. Remote Sensing 14, 1503 (2022).
He, Q., Liu, Y., Zeng, C., Chaohui, Y. & Tan, R. Simultaneously simulate vertical and horizontal expansions of a future urban landscape: a case study in Wuhan, Central China. International Journal of Geographical Information Science 31, 1907–1928 (2017).
Lin, J., Huang, B., Chen, M. & Huang, Z. Modeling urban vertical growth using cellular automata—Guangzhou as a case study. Applied Geography 53, 172–186 (2014).
Koziatek, O. & Dragićević, S. iCity 3D: A geosimualtion method and tool for three-dimensional modeling of vertical urban development. Landscape and Urban Planning 167, 356–367 (2017).
Chen, Y. An extended patch-based cellular automaton to simulate horizontal and vertical urban growth under the shared socioeconomic pathways. Computers, Environment and Urban Systems 91, 101727 (2022).
Xu, X., Ding, D. & Liu, X. A three-dimensional future land use simulation (FLUS-3D) model for simulating the 3D urban dynamics under the shared socio-economic pathways. Landscape and Urban Planning 250, 105135 (2024).
Wang, K., He, T., Xiao, W. & Yang, R. Projections of future spatiotemporal urban 3D expansion in China under shared socioeconomic pathways. Landscape and Urban Planning 247, 105043 (2024).
Chen, Y. & Feng, M. Urban form simulation in 3D based on cellular automata and building objects generation. Building and Environment 226, 109727 (2022).
Ruder, S. An Overview of Multi-Task Learning in Deep Neural Networks. Preprint at https://doi.org/10.48550/arXiv.1706.05098 (2017).
Li, R., Sun, T., Tian, F. & Ni, G.-H. SHAFTS (v2022.3): a deep-learning-based Python package for simultaneous extraction of building height and footprint from sentinel imagery. Geoscientific Model Development 16, 751–778 (2023).
Cipolla, R., Gal, Y. & Kendall, A. Multi-task Learning Using Uncertainty to Weigh Losses for Scene Geometry and Semantics. in 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition 7482–7491. https://doi.org/10.1109/CVPR.2018.00781 (IEEE, Salt Lake City, UT, USA, 2018).
Vandenhende, S. et al. Multi-Task Learning for Dense Prediction Tasks: A Survey. IEEE Transactions on Pattern Analysis and Machine Intelligence 44, 3614–3633 (2022).
Sener, O. & Koltun, V. Multi-Task Learning as Multi-Objective Optimization. in Advances in Neural Information Processing Systems vol. 31 (Curran Associates, Inc., 2018).
Pazos Perez, R. I., Carballal, A., Rabuñal, J. R., Mures, O. A. & García-Vidaurrázaga, M. D. Predicting Vertical Urban Growth Using Genetic Evolutionary Algorithms in Tokyo’s Minato Ward. Journal of Urban Planning and Development 144, 04017024 (2018).
Demuzere, M. et al. A global map of local climate zones to support earth system modelling and urban-scale environmental science. Earth System Science Data 14, 3835–3873 (2022).
Mahtta, R. et al. Urban land expansion: the role of population and economic growth for 300+ cities. npj Urban Sustain 2, 1–11 (2022).
European Commission. Joint Research Centre. GHSL Data Package 2023. (Publications Office, LU, 2023).
Bauer, N. et al. Shared Socio-Economic Pathways of the Energy Sector – Quantifying the Narratives. Global Environmental Change 42, 316–330 (2017).
Jiang, L. & O’Neill, B. C. Global urbanization projections for the Shared Socioeconomic Pathways. Global Environmental Change 42, 193–199 (2017).
Riahi, K. et al. The Shared Socioeconomic Pathways and their energy, land use, and greenhouse gas emissions implications: An overview. Global Environmental Change 42, 153–168 (2017).
Li, M., Wang, Y., Rosier, J. F., Verburg, P. H. & van Vliet, J. Global maps of 3D built-up patterns for urban morphological analysis. International Journal of Applied Earth Observation and Geoinformation 114, 103048 (2022).
Zhou, Y. et al. Satellite mapping of urban built-up heights reveals extreme infrastructure gaps and inequalities in the Global South. Proceedings of the National Academy of Sciences 119, e2214813119 (2022).
Esch, T. et al. World Settlement Footprint 3D - A first three-dimensional survey of the global building stock. Remote Sensing of Environment 270, 112877 (2022).
Tatem, A. J. WorldPop, open data for spatial demography. Sci Data 4, 170004 (2017).
Li, M. et al. Spatiotemporal dynamics of global population and heat exposure (2020–2100): based on improved SSP-consistent population projections. Environ. Res. Lett. 17, 094007 (2022).
Chen, J. et al. Global 1 km × 1 km gridded revised real gross domestic product and electricity consumption during 1992–2019 based on calibrated nighttime light data. Sci Data 9, 202 (2022).
Wang, T. & Sun, F. Global gridded GDP data set consistent with the shared socioeconomic pathways. Sci Data 9, 221 (2022).
Meijer, J. R., Huijbregts, M. A. J., Schotten, K. C. G. J. & Schipper, A. M. Global patterns of current and future road infrastructure. Environ. Res. Lett. 13, 064006 (2018).
Melchiorri, M. The global human settlement layer sets a new standard for global urban data reporting with the urban centre database. Front. Environ. Sci. 10, (2022).
National Geophysical Data Center. Global Land One-kilometer Base Elevation (GLOBE), version 1. National Geophysical Data Center, NOAA https://doi.org/10.7289/V52R3PMS (1999).
Bingham, H. C. et al. Sixty years of tracking conservation progress using the World Database on Protected Areas. Nat Ecol Evol 3, 737–743 (2019).
Pesaresi, M. & Politis, P. GHS-BUILT-V R2023A - GHS built-up volume grids derived from joint assessment of Sentinel2, Landsat, and global DEM data, multitemporal (1975-2030). https://doi.org/10.2905/AB2F107A-03CD-47A3-85E5-139D8EC63283 (2023).
Pesaresi, M. et al. Advances on the global human settlement layer by joint assessment of earth observation and population survey data. International Journal of Digital Earth 17, 2390454 (2024).
Pesaresi, M. et al. Assessment of the Added-Value of Sentinel-2 for Detecting Built-up Areas. Remote Sensing 8, 299 (2016).
Liu, F. et al. Accuracy assessment of Global Human Settlement Layer (GHSL) built-up products over China. PLOS ONE 15, e0233164 (2020).
Ma, X. et al. A global product of fine-scale urban building height based on spaceborne lidar.
Ma, X. et al. Mapping fine-scale building heights in urban agglomeration with spaceborne lidar. Remote Sensing of Environment 285, 113392 (2023).
Sarker, T. et al. Impact of Urban built-up volume on Urban environment: A Case of Jakarta. Sustainable Cities and Society 105, 105346 (2024).
Hou, Y. et al. Simulating the dynamics of urban land quantity in China from 2020 to 2070 under the Shared Socioeconomic Pathways. Applied Geography 159, 103094 (2023).
Fotheringham, A. S., Crespo, R. & Yao, J. Geographical and Temporal Weighted Regression (GTWR). Geographical Analysis 47, 431–452 (2015).
Athey, S., Tibshirani, J. & Wager, S. Generalized Random Forests. Preprint at https://doi.org/10.48550/arXiv.1610.01271 (2018).
He, K., Zhang, X., Ren, S. & Sun, J. Deep Residual Learning for Image Recognition. in 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 770–778. https://doi.org/10.1109/CVPR.2016.90 (2016).
Hu, J., Shen, L. & Sun, G. Squeeze-and-Excitation Networks. in 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition 7132–7141. https://doi.org/10.1109/CVPR.2018.00745 (2018).
Olaf, R. P. et al. Medical Image Computing and Computer-Assisted Intervention – MICCAI. 18th International Conference Munich Germany October 5-9. Proceedings Part III U-Net: Convolutional Networks for Biomedical Image Segmentation International. Publishing Cham 234-241 (2015).
Wu, W.-B. et al. A first Chinese building height estimate at 10 m resolution (CNBH-10 m) using multi-source earth observations and machine learning. Remote Sensing of Environment 291, 113578 (2023).
Frolking, S., Mahtta, R., Milliman, T. & Seto, K. C. Three decades of global trends in urban microwave backscatter, building volume and city GDP. Remote Sensing of Environment 281, 113225 (2022).
Kingma, D. P. & Ba, J. Adam: A Method for Stochastic Optimization. Preprint at https://doi.org/10.48550/arXiv.1412.6980 (2017).
Loshchilov, I. & Hutter, F. SGDR: Stochastic Gradient Descent with Warm Restarts. Preprint at https://doi.org/10.48550/arXiv.1608.03983 (2017).
Yang, J. et al. Simulating urban expansion using cellular automata model with spatiotemporally explicit representation of urban demand. Landscape and Urban Planning 231, 104640 (2023).
Liang, X., Liu, X., Li, D., Zhao, H. & Chen, G. Urban growth simulation by incorporating planning policies into a CA-based future land-use simulation model. International Journal of Geographical Information Science 32, 2294–2316 (2018).
Zhao, Q. FU3D: the first global projections of future urban three-dimensional (3D) expansion for the 21st century under shared socioeconomic pathways. 2411065693 Bytes https://doi.org/10.6084/M9.FIGSHARE.26795932.V2 (2025).
Bolin, J. H. Review of Introduction to Mediation, Moderation, and Conditional Process Analysis: A Regression-Based Approach. Journal of Educational Measurement 51, 335–337 (2014).
Chen, Y., Li, X., Liu, X. & Ai, B. Modeling urban land-use dynamics in a fast developing city using the modified logistic cellular automaton with a patch-based simulation strategy. International Journal of Geographical Information Science 28, 234–255 (2014).
Pontius, R. G. Jr & Millones, M. Death to Kappa: birth of quantity disagreement and allocation disagreement for accuracy assessment. International Journal of Remote Sensing 32, 4407–4429 (2011).
Warrens, M. J. Properties of the quantity disagreement and the allocation disagreement. International Journal of Remote Sensing 36, 1439–1446 (2015).
Pickard, B., Gray, J. & Meentemeyer, R. Comparing Quantity, Allocation and Configuration Accuracy of Multiple Land Change Models. Land 6, 52 (2017).
Pickard, B. R. & Meentemeyer, R. K. Validating land change models based on configuration disagreement. Computers, Environment and Urban Systems 77, 101366 (2019).
Zhang, Y., Li, X., Liu, X. & Qiao, J. Self-modifying CA model using dual ensemble Kalman filter for simulating urban land-use changes. International Journal of Geographical Information Science 29, 1612–1631 (2015).
Gao, J. & Pesaresi, M. Downscaling SSP-consistent global spatial urban land projections from 1/8-degree to 1-km resolution 2000–2100. Sci Data 8, 281 (2021).
Li, R., Sun, T., Ghaffarian, S., Tsamados, M. & Ni, G. GLAMOUR: GLobAl building MOrphology dataset for URban hydroclimate modelling. Sci Data 11, 618 (2024).
Ma, X. et al. A global product of 150-m urban building height based on spaceborne lidar. Sci Data 11, 1387 (2024).
Huang, H. et al. Estimating building height in China from ALOS AW3D30. ISPRS Journal of Photogrammetry and Remote Sensing 185, 146–157 (2022).
He, T. et al. Global 30 meters spatiotemporal 3D urban expansion dataset from 1990 to 2010. Sci Data 10, 321 (2023).
Milojevic-Dupont, N. et al. EUBUCCO v0.1: European building stock characteristics in a common and open database for 200+ million individual buildings. Sci Data 10, 147 (2023).
Wang, X., Jin, S., Li, Y., Qian, J. & Su, L. On time-varying panel data models with time-varying interactive fixed effects. Journal of Econometrics 249, 105960 (2025).
Frolking, S., Mahtta, R., Milliman, T., Esch, T. & Seto, K. C. Global urban structural growth shows a profound shift from spreading out to building up. Nat Cities 1–12, https://doi.org/10.1038/s44284-024-00100-1 (2024).
Yang, J. et al. Air pollution dispersal in high density urban areas: Research on the triadic relation of wind, air pollution, and urban form. Sustainable Cities and Society 54, 101941 (2020).
Zhang, A., Xia, C. & Li, W. Exploring the effects of 3D urban form on urban air quality: Evidence from fifteen megacities in China. Sustainable Cities and Society 78, 103649 (2022).
Armenakis, C., Du, E. X., Natesan, S., Persad, R. A. & Zhang, Y. Flood Risk Assessment in Urban Areas Based on Spatial Analytics and Social Factors. Geosciences 7, 123 (2017).
Paprotny, D., Kreibich, H., Morales-Nápoles, O., Terefenko, P. & Schröter, K. Estimating exposure of residential assets to natural hazards in Europe using open data. Natural Hazards and Earth System Sciences 20, 323–343 (2020).
Vamvakeridou-Lyroudia, L. S. et al. Assessing and visualising hazard impacts to enhance the resilience of Critical Infrastructures to urban flooding. Science of The Total Environment 707, 136078 (2020).
Wu, W.-B., Yu, Z.-W., Ma, J. & Zhao, B. Quantifying the influence of 2D and 3D urban morphology on the thermal environment across climatic zones. Landscape and Urban Planning 226, 104499 (2022).
Luo, P. et al. How 2D and 3D built environments impact urban surface temperature under extreme heat: A study in Chengdu, China. Building and Environment 231, 110035 (2023).
Lin, J., Lu, S., He, X. & Wang, F. Analyzing the impact of three-dimensional building structure on CO2 emissions based on random forest regression. Energy 236, 121502 (2021).
Lan, T., Shao, G., Xu, Z., Tang, L. & Dong, H. Considerable role of urban functional form in low-carbon city development. Journal of Cleaner Production 392, 136256 (2023).
Zhou, L. et al. Understanding the effects of 2D/3D urban morphology on land surface temperature based on local climate zones. Building and Environment 208, 108578 (2022).
Fung, K. Y., Yang, Z.-L. & Niyogi, D. Improving the local climate zone classification with building height, imperviousness, and machine learning for urban models. Comput.Urban Sci. 2, 16 (2022).
Kamath, H. G. et al. GLObal Building heights for Urban Studies (UT-GLOBUS) for city- and street- scale urban simulations: Development and first applications. Sci Data 11, 886 (2024).
Allen-Dumas, M. R. et al. Sensitivity of mesoscale modeling to urban morphological feature inputs and implications for characterizing urban sustainability. npj Urban Sustain 4, 1–11 (2024).
Zhao, Q. Codes for MECA-3D model to produce FU3D dataset. 5681927532 Bytes https://doi.org/10.6084/M9.FIGSHARE.26795902.V2 (2025).
Linke, S. et al. Global hydro-environmental sub-basin and river reach characteristics at high spatial resolution. Sci Data 6, 283 (2019).
Lehner, B., Messager, M. L., Korver, M. C. & Linke, S. Global hydro-environmental lake characteristics at high spatial resolution. Sci Data 9, 351 (2022).
Acknowledgements
This research is financially supported by the National Natural Science Foundation of China Major Program (42192580, 42192581), the National Natural Science Foundation of China (52209118), the Science and Technology Development Fund, Macau SAR (File Nos. 001/2024/SKL, 0029/2022/A1, 0033/2024/RIA1), UM Research Grant (File Nos. MYRG-GRG2023-00052-IOTSC-UMDF, MYRG2022-00090-IOTSC), Shenzhen Science and Technology Innovation Committee (SGDX20210823103805043), the FY-3 Lot 03 Meteorological Satellite Engineering Ground Application System Ecological Monitoring and Assessment Application Project (Phase I): ZQC-R22227, and CORE. CORE is a joint research center for ocean research between Laoshan Laboratory and HKUST. The authors would like to greatly acknowledge all these financial supports.
Author information
Authors and Affiliations
Contributions
Qikang Zhao: Conceptualization, Data curation, Methodology, Visualization, Validation, Writing- original draft preparation, Writing - review and editing; Qingyan Meng: Supervision, Conceptualization, Validation, Writing- reviewing and editing, Project administration, Funding acquisition; Liang Gao: Supervision, Writing- reviewing and editing, Project administration, Funding acquisition. Mingming Zhu: Writing- reviewing and editing.
Corresponding authors
Ethics declarations
Competing interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Zhao, Q., Meng, Q., Gao, L. et al. FU3D: the first global projections of future urban three-dimensional (3D) expansion for the 21st century under shared socioeconomic pathways. Sci Data 12, 1555 (2025). https://doi.org/10.1038/s41597-025-05711-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41597-025-05711-4