Background & Summary

In 2023, middle-aged adults aged 36 to 55 represented approximately 25% of the United States population and 41% of its workforce1,2. Despite their substantial representation in the population and workforce, there exists a stark disparity between the demographic representation of this cohort and the available research data dedicated to them3. A review of the one hundred most recent, original research articles from the Journal of Biomechanics (available online between January 22, 2025, and April 12, 2025) reveals that 14% of articles recruited at least one group of participants with an average age between 36 and 55. For the journal Gait & Posture (available online between December 13, 2024, and April 25, 2025), 17% of articles had at least one group within the same age bracket. Most of those participants were not recruited deliberately but as age-matched controls for a clinical population of interest. Alarmingly, only 2.5% of those two hundred studies intentionally recruited middle-aged adults or split their analysis to include a middle-aged adult category. The convenience of studying healthy college-aged adults, combined with the well-known—and well-funded—focus on older adults and clinical groups, has stunted our understanding of this critical period of life.

The lack of research dedicated to the middle-aged population is particularly concerning, as midlife marks a transformative period in the biological and physiological development of an adult. There are reductions in perceptuomotor learning rates and signs of cognitive decline as early as the third decade of life4,5,6. Muscle quality and muscle strength begin to deteriorate between ages 40 and 50 in both the upper and lower extremities, potentially leading to sarcopenia by age 50 and changes to gait7,8,9. There are also very clearly many changes to gait that coincide with increasing age10,11,12,13,14. Specific age-related gait changes can include reduced walking speed, altered knee kinematics, and impaired ankle function, particularly when walking at maximum speed, among other subtle changes15,16,17. Moreover, the postural stability of gait begins to deteriorate after age 45, resulting in a threefold increase in fall incidence18,19. Despite this handful of biomechanical changes, the subtle fluctuations that occur between each stride remain insufficiently characterized in this age cohort20,21,22,23.

The insufficient prioritization of middle-aged gait research presents a challenge in developing comprehensive models of how gait dynamics evolve from an individual’s first to final step in life. The present Nonlinear Analysis Core (NONAN) GaitPrint dataset helps bridge this research gap by providing gait characteristics and data on healthy middle-aged adults, completing our series of three databases that also include healthy young and older adults24,25. We also statistically compared a nonlinear analysis of these individuals’ gait patterns across our datasets to understand how gait variability changes with age. Our final contribution to our healthy adult database is not just a scientific imperative but also a societal one. NONAN GaitPrint delivers a wealth of quantitative biomechanical measures to inform the health and well-being of a critical demographic: middle-aged adults. This group represents a significant portion of the population, dominates the workforce, and is now on the cusp of gait deterioration.

Methods

Subjects and ethics statement

The study enlisted the participation of 50 middle-aged adults (36–55 years old; 21 men and 29 women; age: 46.1 ± 5.9 years; height: 173.43 ± 8.42 cm; body mass: 87.14 ± 18.87 kg). Recruitment methods included word of mouth, campus-wide emails, community flyer distribution, and engagement through social media channels. Each participant received $20 compensation per session for their involvement.

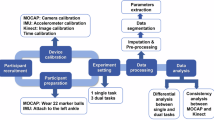
Eligibility for participation was determined based on the following criteria: (i) capability to provide informed consent, (ii) ability to walk independently without the aid of assistive devices, (iii) no self-reported diagnosis of neurological disease, (iv) no self-reported diagnosis of any lower limb disability, injury, or disease. Before involvement, subjects had to provide verbal and written informed consent under the University of Nebraska Medical Center Institutional Review Board (Approval ID: 0762-21-EP). Participants consented to data sharing but not explicitly in the format for Nature Scientific Data. The subject recruitment, compensation, and screening criteria are identical to the NONAN Gaitprint database of young adults and similar to the NONAN Gaitprint database of older adults24,25. The remainder of the methods for this set of participants are identical to the two other published databases24,25.

Setup and procedures

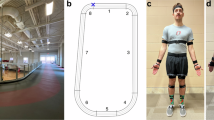
During the first session, each participant’s anthropometric data was obtained for the biomechanical gait model in the MyoResearch software (version 3.18.126). The specific anthropometric measures encompassed skull height (measured from the chin to the top of the head), shoulder width (inter-acromion joint distance), lumbar + thoracic length (from the seventh cervical vertebra to the first sacral vertebra), pelvis width (the distance between the anterior superior iliac spines), upper arm length (acromion process to lateral humeral epicondyle), forearm length (lateral humeral epicondyle to radial styloid process), hand length (ulnar notch to the tip of the third phalange), thigh length (greater trochanter to lateral femoral epicondyle), shank length (lateral femoral epicondyle to lateral malleolus), and foot length (the length of the shoe). Following those measurements, we placed 16 inertial measurement units (IMUs) affixed to the head, upper thoracic region, lower thoracic region, pelvis, upper arms, forearms, hands, thighs, shanks, and feet (Fig. 1). These body measurements and IMU arrangement ensured comprehensive and accurate kinematic data captured during the overground walking sessions according to Noraxon’s recommendations.

Fig. 1
figure 1

Experimental setup. (a) Data collection environment. Image taken from segment 2 in b. (b) Layout of the indoor track. Segments 1–8 were measured at a distance of 21.03, 10.96, 50.83, 21.71, 12.19, 21.83, 51.86, 9.71 meters, respectively, with lane widths of 0.9 meters. All trials started on the blue X. (c) Anterior and posterior views of the first author (who consents to the open publication of this image; Not a participant) wearing the Noraxon Ultium Motion IMU sensors to replicate those used in the experiment. (e) The front (top) and back (bottom) of an IMU and its local coordinate system. All sensors in (c,d) were placed such that the X-axis points away from the ground (Blue hexagon is facing upwards). Notably, the feet follow a different orientation and the X-axis can be seen pointing toward the toes (Blue hexagon pointing towards the toes). The orientation of the X-axis in relation to the IMU’s blue hexagon is consistent for all sensors.

Full size image

Kinematic data was acquired through self-paced, overground walking trials. Prior to each trial, a functional walking calibration was performed to ensure accurate kinematic measurements. The calibration began with participants standing still for 2.5 seconds, with arms relaxed at their side, and feet positioned approximately hip to shoulder-width apart. Participants then completed an approximately 15-second walking segment at a self-selected pace, which included a deliberate 180° left turn, a return to the starting point, and a final 2.5-second period of standing still in the initial posture. The data obtained during this calibration procedure are not included in the dataset. The subjects then received explicit instructions that they would walk for four minutes and maintain a comfortable pace. Following the conclusion of each trial, participants received verbal instruction to stop walking, stand at their starting position for calibration, and repeat the same procedure for the next trial. Each session consisted of nine walking trials (each with a calibration) with the autonomy to take up to a five-minute break after the third and sixth trials (end of block one and two, respectively) for a maximum time of up to five minutes. The kinematic data during each overground walking trial was recorded at a sampling rate of 200 Hz. Seven days later, subjects returned to the lab and completed another nine walking trials with the same walking instructions as their first session.

The seven-day interval was deliberately chosen to support the primary objectives for investigating Gaitprints, a set of kinematic variables that can identify an individual, and assessing consistency of nonlinear analyses in the Technical Validation across walking bouts and data collection sessions26.

Screening and consent procedures occurred at the Center for Research in Human Movement Variability (MOVCENTR), within the Biomechanics Research Building at the University of Nebraska at Omaha. Subjects were outfitted in comfortable athletic clothing and walking-appropriate shoes, if necessary. All participants returned to their second session with the same shoes as their first session. The direction of subjects’ movement, either clockwise or counterclockwise, adhered to the established track rules. Specifically, trials conducted on Monday, Wednesday, Friday, and Sunday mandated clockwise walking, while counterclockwise walking occurred on the remaining days of the week. These directions were set by the Health & Kinesiology Building that maintains the 200 m indoor track. This directional information is documented in GaitPrint_Trial_Characteristics.csv, revealing that out of the 891 walked trials, 531 trials (60%) followed a clockwise direction, and 360 trials (40%) followed a counterclockwise trajectory. One participant (S122) did not return for their second session. Four participants (S044, S115, S175, S186) returned for their second session at a time greater than one week after their first session (18, 9, 62, 17 days, respectively). All participants walked in the same direction for both sessions and started from the same location on the track (including both trials and calibrations).

Data processing and extraction of foot placement variables

Before exporting the data to the current database, the Noraxon MyoResearch 3.18.126 software applied specific post-processing options to optimize the quality and accuracy of the recorded data. These options were as follows:

  • The processing fusion mode was set to “standard” the default setting utilizing an adaptive filtering technique. This technique aims to optimize sensor tracking while considering the cleanliness of the magnetometer data during recording.

  • Course Stabilization was configured as “Foot, Shank, Thigh, Spine”. This setting employs a high-pass filtering operation on the secondary joint angles, utilizing a ten-second sliding window. Its purpose is to eliminate sensor drift, particularly when severe magnetic interference affects the entire body, by stabilizing the foot, shank, and thigh from top to bottom and the upper and lower spine segments relative to the pelvis.

  • The progression setting was set to “translation” following personal communication and recommendation from Noraxon.

  • Acceleration was set to “sensor-based”, ensuring the capture of acceleration data with respect to the coordinate frame of each sensor.

  • The software used gyroscope and accelerometer data from foot sensors to detect heel contacts, allowing for the determination of stance and swing as an on/off signal.

  • Noraxon’s software also offered an anti-wobbling correction to smooth the data at 5 Hz, with a residual duration of 300 ms. This correction was intended to eliminate soft tissue artifacts and improve data quality.

As we have done before, gait parameters were computed through a MATLAB script GaitPrint_Spatiotemporal_Calculation.m (Mathworks, Inc., Natick, MA) to accompany the dataset. Using the filtered time series, Noraxon’s foot contact events, and custom code provided with the data, we calculated the following gait parameters (units in parenthesis):

Spatial parameters

  • Step length (cm)—the distance from one heel strike to the next heel strike of the opposite foot.

  • Stride length (cm)—the distance between two consecutive heel strikes of the same foot.

  • Step width (cm)—the lateral distance between the heel center of one heel strike and the line joining the heel center of two consecutive heel strikes of the opposite foot.

  • Distance traveled (m)—the distance the participant traveled as tracked by the pelvis sensor.

Temporal parameters

  • Cadence (steps/min)—the number of steps per minute, also called step rate.

  • Step time (s)—the time elapsed from one foot’s initial contact to the opposite foot’s initial contact.

  • Stride time (s)—the time elapsed between the initial contacts of two consecutive footfalls of the same foot.

  • Stance time (s)—the time elapsed between the first and last contacts of a single footfall (the stance phase starts at heel contact and ends at toe-off of the same foot).

  • Swing time (s)—the time elapsed between the current footfall’s last contact and the following footfall’s first contact (the swing phase starts with toe-off and ends with the first contact of the same foot).

  • Single support time (s)—the total time one foot is in contact with the ground throughout the gait cycle.

  • Double support time (s)—the total time both feet are simultaneously in contact with the ground throughout the gait cycle.

Temporophasic parameters

  • Stance time (%Stride time)—stance time normalized to stride time.

  • Swing time (%Stride time)—swing time normalized to stride time.

  • Single support time (%Stride time)—single support time normalized to stride time.

  • Double support time (%Stride time)—double support time normalized to stride time.

Spatiotemporal parameters

  • Gait speed (m/s)—the ratio of distance walked and trial time.

  • Stride speed (m/s)—the ratio of stride length and stride time.

Data Records

All data is available using Figshare27. Gaitprint_Subject_Characteristics.csv provides information about the screening outcomes, age, sex, body mass, height, hand and foot dominance, shoe make and model, and anthropometrics. GaitPrint_Trial_Characteristics.csv provides information about the session date and start time, shoe make and model, walking direction, start time, the first step taken, and any notes taken during the trial. All kinematic data is grouped into subject-specific folders and .csv files including the subject’s alphanumeric code (e.g., S###_G02_D01_B01_T01) with the following tabular structure:

ID. This field codes the subject number. It is labeled “S041”, “S042”, “S043,” … for the 50 subjects.

Group. This field codes the study population (middle-age). It is labeled “G02” for the current dataset.

Day. This field codes whether the data was collected during the first or second day. It is labeled “D01” and “D02” for Day 1 and Day 2, respectively.

Block. This field codes the block number within a session. It is labeled as “B01,” “B02,” and “B03” for Block 1, Block 2, and Block 3, respectively.

Trial. This field codes the trial number within a block. It is labeled as “T01,” “T02,” and “T03” for Trial 1, Trial 2, and Trial 3, respectively.

S###.zip (IMU Data)

These folders contain one .csv file for each trial (Fig. 2). For example, S041.zip contains 18 .csv files, each as a table providing all the raw data from that subject’s trial. The data has been arranged in a matrix of 48,000 by 321 columns, with one row per timestamp. The first column, “Time” provides the timestamps in milliseconds. The next 320 columns each provide the kinematic variables exported by the Noraxon MyoResearch 3.18.126 software including, but not limited to, the acceleration, velocity, position, and orientation of each sensor, body segment, and joint.

Fig. 2
figure 2

After following the reference link to the Figshare database, select one of the participant’s zipped folders (i.e., S041.zip) to download one .csv file per walking trial. Each .csv contains 321 columns of IMU data for the duration of the specific trial. Alternatively, the entire database can be downloaded with the ‘Download all’ button.

Full size image

Spatiotemporal_Variables.zip

In addition, we pre-calculated spatiotemporal variables and extracted raw data for each trial in distinct .csv files compressed into subject-specific subfolders (S###.zip) housed within a final compressed folder Spatiotemporal_Variables.zip. Each file includes 26 columns of spatiotemporal characteristics and each row indicates a stride taken by the subject. A compressed folder (Template_Scripts.zip) includes example MATLAB, Python, and R scripts as examples to manipulate the results and help ease the barrier for entry into our dataset.

Technical Validation

In this validation, because the dataset marks the completion of our recruitment of healthy adults, we compare young (n = 35; Age = 24.6 ± 2.7 years; Height = 173.73 ± 7.76 cm; Weight = 72.44 ± 15.04 kg), middle-aged (n = 50; Age = 46.1 ± 5.9 years; Height = 173.43 ± 8.42 cm; Weight = 87.14 ± 18.87 kg), and older adults (n = 41; Age = 64.7 ± 7.5 years; Height = 170.89 ± 9.85 cm; Weight = 81.08 ± 17.76 kg), all of whom followed the exact same walking protocol24,25. Because we were interested in comparing all groups, Bayesian independent samples t-tests were used for pairwise comparisons, unless stated otherwise. All alternative hypotheses assume the compared groups have different gait kinematics whereas the null hypothesis assumes the same, or similar, values. Instead of obtaining a p-value like in frequentist statistics, Bayesian tests obtain a BayesFactor expressed as BF10, and quantifies the evidence in favor of one hypothesis compared to another28. BF10 is the likelihood of the data under the alternative hypothesis divided by the likelihood of the data under the null hypothesis. As informal rules of thumb, we considered BF10 equal to 1 to be no evidence, BF10 from 1–3 to be anecdotal, from 3–10 to be moderate evidence, BF10 from 10–30 to be strong evidence, BF10 from 30–100 to be very strong evidence and BF10 greater than 100 to be extreme evidence in support of the alternative hypothesis29,30,31. The reciprocal of the BF10 (BF01) values are considered as strength of evidence in support of the null hypothesis. The code and results for all analyses are provided in the supplementary material for the following sections of our technical validation.

Bayesian statistical parametric mapping

We conducted Bayesian Statistical Parametric Mapping (SPM) to compare right hip, knee, and ankle kinematics between the three healthy age groups32. For each person’s overground walking trial, we took a 101 datapoint ensemble average of their lower body joint angles. Ensembled gait cycles were averaged within each participant’s trial. To interpret our results, we chose an arbitrary posterior probability of 0.95 that conceptually conforms to the Frequentist’s interpretation of a significant result. Probabilities greater than 0.95 were interpreted as evidence supporting a difference between two groups, probabilities below 0.05 were interpreted as evidence supporting no difference between the two groups, and all other probabilities were considered to be no evidence for or against either hypothesis. For brevity, we only report and interpret posterior probability values over 0.95. We compared young to middle-aged adults (Fig. 3), young to older adults (Fig. 4), and middle-aged adults to older adults (Fig. 5).

Fig. 3
figure 3

Column 1 outlines hip, knee, and ankle joint angles as the mean ± 95% credible interval for young (Red) and middle-aged (Blue) adults across the gait cycle. Positive values on the y-axis represent hip, knee, or ankle dorsiflexion. Column 2 outlines each joint’s posterior probability map testing the hypotheses that gait kinematics are similar or different between the tested groups for each percent of the gait cycle. The horizontal dashed lines at 0.05 and 0.95 depict the thresholds for which the data supports similar or different gait kinematics, respectively.

Full size image
Fig. 4
figure 4

Column 1 outlines hip, knee, and ankle joint angles as the mean ± 95% credible interval for young (Red) and older (Brown) adults across the gait cycle. Positive values on the y-axis represent hip, knee, or ankle dorsiflexion. Column 2 outlines each joint’s posterior probability map testing the hypotheses that gait kinematics are similar or different between the tested groups for each percent of the gait cycle. The horizontal dashed lines at 0.05 and 0.95 depict the thresholds for which the data supports similar or different gait kinematics, respectively.

Full size image
Fig. 5
figure 5

Column 1 outlines hip, knee, and ankle joint angles as the mean ± 95% credible interval for middle-aged (Blue) and older (Brown) adults across the gait cycle. Positive values on the y-axis represent hip, knee, or ankle dorsiflexion. Column 2 outlines each joint’s posterior probability map testing the hypotheses that gait kinematics are similar or different between the tested groups for each percent of the gait cycle. The horizontal dashed lines at 0.05 and 0.95 depict the thresholds for which the data supports similar or different gait kinematics, respectively.

Full size image

For young adults compared to middle-aged adults, hip kinematics were different at 52–68% and 97–98% of the gait cycle. At the knee, gait kinematics were different at 62–85% and 97–98% of the gait cycle. At the ankle, gait kinematics were different at 0–56% and 78–100% of the gait cycle. For young adults compared to older adults, hip kinematics were not different across the gait cycle. At the knee, gait kinematics were different at 5–17% and 45–92% of the gait cycle. At the ankle, gait kinematics were different at 29–52%, 66–67%, and 86–97% of the gait cycle. For middle-aged adults compared to older adults, hip kinematics were different at 58–65% of the gait cycle. At the knee, gait kinematics were different at 1–16% and 70–93% of the gait cycle. At the ankle, gait kinematics were different at 0–21% and 87–100% of the gait cycle. Ankle joint angles differed across nearly the entire gait cycle between young and middle-aged adults, the ankle showed more variable differences between young and older adults and diverged primarily around heel contact between middle-aged and older adults. Notably, we often observed group differences at heel strike and mid-swing at the hip and knee, suggesting that subtle shifts in foot placement control may begin to emerge by mid-life. At the hip and knee, most group differences were concentrated around the loading response and mid-swing phases, indicating that each age group may employ slightly different strategies to manage ground reaction forces and prepare for the next heel strike during swing.

Our application of SPM between age groups showed clear differences across portions of the gait cycle at the hip, knee, and ankle joints. In comparison to similar literature, one study found differences in hip joint angles along 26–46% of the gait cycle between young and older adults, a finding not corroborated by our results33. A second study found almost no differences in hip, knee, and ankle angles across the gait cycle, findings with which our results did not always support34. A third study found significant differences between young and middle-aged adults walking with added mass on a treadmill; however, that study did not include a control condition (i.e., no added mass) and grouped the added mass conditions together during age group comparisons, thereby making age-related changes unclear35. The lack of agreement between our results and the first two referenced SPM applications could be due to differences in motion capture equipment, environment, walking duration, and sample size. The first issue (equipment) is a large point of contention in biomechanics: SPM is frequently used to detect discrepancies in joint-angle measurements between systems (e.g., IMUs and optical motion capture) and might be contributing to some degree of unexplained disagreement between studies36. Overall, studies comparing healthy gait kinematics across the lifespan are sparse (many studies can be found with clinical groups), therefore making adequate comparisons between studies and age groups challenging using SPM. The contradicting evidence outlined in the referenced literature, in comparison to the present study, suggests a call for additional data comparing healthy groups, especially the underrepresented middle-aged adults.

Nonlinear analysis of human movement

In these analyses, we conducted Bayesian independent samples t-tests between the three age groups (Table 1). The final 174 right strides of each participant’s gait data were used for each analysis, unless otherwise stated. In addition, nonlinear analyses were nearly identical to the procedures outlined in our older adult database25. All results can be found in Table 1 or Fig. 6.

Table 1 Mean ± standard deviation of the young, middle, and older adults’ Hurst exponent, sample entropy, and recurrence quantification analysis (RQA) percent determinism at each kinematic measurement.
Full size table
Fig. 6
figure 6

A series of gait metrics used to compare our young, middle, and older adult databases. The y-axis in the first subplot represents the relative phase between the left and right leg at the thigh, shank, and foot. The y-axis in the second and third subplot represents the nonlinear variable characterizing time series of stride lengths, stride intervals, and the range of motion at the hip, knee, and ankle. The y-axis in the fourth subplot represents the percent determinism of the thigh, shank, and foot segment angles. Age groups are colored and denoted on the x axis. Colored points and error bars represent the group mean and standard deviation, respectively. Black points are individual data, each representing a single trial.

Full size image

Relative phase

Relative phase measures how coordinated two coupled oscillators are by describing whether their respective rhythms are in sync or out of sync. In healthy gait, the limbs move in a nearly perfect anti-phase rhythm (180°)37,38,39. Using the entire four minutes of overground walking (except the first five strides), the average circular relative phase of the right thigh compared to the left thigh, the right shank compared to the left shank, and the right foot compared to the left foot were calculated40,41. A multilevel Bayesian circular regression, including random participant effects, was performed for the coupled limb segments to compare the coordination between the three groups. As alluded to in the introduction, changes to human movement inevitably occur with aging. Therefore, we expected to find evidence that young, middle, and older adults would demonstrate differences in coordination, most notably between young and older adults—but this was not the case in our study (Table 1; Fig. 6).

The relative phase measured between each thigh, shank, and foot were not different for all comparisons between young, middle, and older adults (Table 2). In fact, each group’s relative phase at the thigh, shank, and foot were similar and centered around 180°, implying a near-perfect anti-phase pattern indicative of healthy gait patterns37,38,39. Because gait is strongly symmetric unless interrupted by a physiological or mechanical perturbation, it is understandable to find lacking in statistical support. We did find, however, the left foot lags slightly behind the right foot. If clinical populations—such as stroke survivors whom we are actively recruiting for the same protocol, or older adults in palliative care—were compared, then a relative phase deviating from 180° would be expected.

Table 2 Bayesian Regression output including each regression coefficient’s Estimate, Estimated Error, Lower and Upper 95% Credibility Intervals.
Full size table

Regarding the larger literature, plenty of studies are available using healthy controls as a baseline for the relative phase of clinical groups, but none solely intended to characterize changes across all ages. There is, however, an exploratory study on inter-limb coordination throughout the developmental years into young adulthood38. Overtime, the relative phase of the thigh’s angular displacement gradually increases from 173.9° (2.9 to 5.9 years old), to 174.7° (6 to 9.9 years old), 175.1° (10 to 13.9 years old), 175.4° (14 to 18.9 years old), and finally 175.4° (19 to 35.2 years old)38. While their data deviated approximately 5° from 180°, our data was mostly centered around 180°. This discrepancy may be influenced by using different time series or asymmetric limb movement during initial accelerations over the course of the two to ten strides they monitored over a 10 meter walkway38. In contrast, our longer time series would wash out those effects of acceleration and be more representative of average limb coordination. Regardless, our two findings provide evidence that lower limb coordination matures quite quickly toward anti-phasic behavior near 180° over the course of motor development as the system self-organizes into an optimally efficient state for walking that persists into older adulthood. Our results are also similar to another study suggesting that the relative phase between limbs is typically within a “dead zone” that requires no control from approximately 171° to 189°37,39. By that criterion, the average relative phase at the thigh for 32 trials (8 young, 15 middle-aged, and 9 older adults) and at the foot for 171 trials (29 young, 56 middle-aged, and 86 older adults), fell outside this proposed dead zone. Notably, at the thigh, one young adult had seven of their trials fall outside the dead zone and one middle-aged adult had thirteen trials outside the dead zone. These individuals might be demonstrating difficulty coordinating limb movements even under stable walking conditions. At the foot, half of one young adult’s trials fell outside the dead zone, five middle-aged adults had about half of their trials outside the dead zone, and one older adult had nearly half their trials outside the dead zone. Additionally, three other older adults each had at least 15 trials fall outside this zone. Although we did not find an age difference in the aggregate, our results hint towards asymmetric coordination of the feet becoming more prevalent as age increases on an individual basis.

Hurst exponent

The Hurst exponent (H), which quantifies the strength of long-range correlations (LRCs) in a time series, was estimated on time series of right stride intervals, stride lengths, and range of motion at the hip, knee, and ankle. A newer Bayesian approach was applied by taking the median of 200 posterior samples of H to obtain a point estimate used to compare groups42,43. Based on previous literature, it was expected that young, middle, and older adults would experience weaker LRCs with increasing age for all analyzed time series21.

Stride length H was identical for young and middle-aged adults, with extreme and very strong evidence that H was lower in older adults (Table 1; Fig. 6). Stride interval H peaked in middle age but was lowest for older adults. Only the comparison between the young and middle-aged adults lacked evidence supporting the alternative hypothesis. The weakest hip range of motion LRCs and the strongest evidence supporting the alternative hypothesis were observed in young adults, while the difference between middle-aged and older adults provided strong support for the null hypothesis. The LRCs calculated for the knee range of motion were identical. Finally, the ankle range of motion was either extremely or very strongly in support of the alternative hypothesis except for the comparison between young and older adults, which anecdotally supported the null hypothesis.

Stride intervals and stride lengths are two of the most common gait characteristics used to calculate H21. Only stride lengths followed our predicted pattern of weakened LRCs with increasing age. Roughly half of the Bayes Factors suggested differences in H across all five time series compared between our three age groups. Young and middle-aged stride lengths had the strongest LRCs out of all age groups and time series. We also investigated the variability of time series derived from the range of motion at the hip, knee, and ankle, in contrast to stride intervals and stride lengths, which are commonly assessed in nonlinear analyses of human movement. At the knee and ankle, range of motion H values were nearly identical between all three groups in contrast to the increasingly strengthened LRCs found at the hip with older age. The observed increase in hip LRCs with age may reflect a compensatory reliance on proximal lower-body musculature, which is better suited to maintaining locomotion as distal control (e.g., ankle function) declines44,45,46. Additionally, some evidence suggests that physical activity helps preserve LRCs as individuals age47. LRCs have been found to range between 0.6 to 0.92 for young adults and 0.68 to 0.87 for older adults across a variety of methodologies according to a systematic review on Detrended Fluctuations Analysis, a different method of calculating LRCs that is conceptually the same as H21. All H values in Table 1 reside within the expected range for young adults. Middle-aged H values also reside within the range defined for their cohort. Three of our older adults’ H values fell below their age group’s expected range. There are, however, substantial inconsistencies in papers reporting LRCs as well as the LRCs between the time series selected in our technical validation Table 121. Considering that LRCs did not uniformly become weaker with age, and we found a large range of Bayes factors for the alternative hypothesis, additional studies will need to create a list of physiological time series that best describe age-related declines in gait variability.

Sample entropy

Sample entropy (SampEn), which quantifies the unpredictability of a time series, was calculated from the same list of time series as H48. Similar to H, we expected that gait patterns would become progressively more unpredictable with age49.

Stride lengths were strongly or extremely supportive of the alternative hypothesis when young adults were compared to middle and older adults, respectively (Table 1; Fig. 6). When comparing middle and older adults, anecdotal evidence supported the null hypothesis that SampEn was similar between groups. H and SampEn are complementary analyses that only shared extreme evidence supporting the alternative hypothesis for young and older adult stride lengths as well as middle-aged and older adult stride intervals. SampEn calculated from hip and knee range of motion never supported the alternative hypothesis. Ankle SampEn extremely supported the alternative hypothesis between young and older adults only; otherwise, the remaining two comparisons provided moderate or anecdotal evidence. In the interpretations of the previous section, there were some expected and unexpected findings regarding the Hurst exponent that rely on additional context provided by SampEn. The results for stride intervals demonstrate a relationship with SampEn’s unpredictability, which peaks when H is 0.5. Specifically, middle-aged adults had the strongest LRC accompanied by the lowest SampEn, whereas older adults exhibited the lowest H and the highest SampEn50,51,52. However, because the unpredictability of the hip, knee, and ankle range of motion was relatively unchanged for all three groups, increases in hip LRCs could be interpreted purely as changes in the available strategies of the young, middle, and older adults’ gait, rather than the coupled movement between H and SampEn.

Our analysis of SampEn on gait patterns revealed small age-related changes alongside other studies. One study measured stride length SampEn values of young adults (1.96) and older adults (2.01) while they walked overground indoors49. A second study found similar SampEn values, depending on the input parameters for a time series of step times, in young adults walking overground (approximately 1.8)53. Calculations of SampEn on discrete gait metrics, such as joint ROM, are rare. However, one study monitoring young adults walking on a treadmill found SampEn values between 1.5 and 3 at the hip, knee, and ankle, which are similar to our results in Table 154. Additionally, our results align with those of older adults who walked on a treadmill over two sessions, resulting in stride interval SampEn values of 2.06 and 2.11, respectively (knee osteoarthritis data was not separated from the healthy data)55. Another study found that, in young adults walking on a treadmill, the stride length and interval SampEn values were approximately 0.5 bits lower than in our overground results using a similar sampling rate56. This difference in SampEn is acceptable considering that treadmills constrain gait toward more predictable patterns53. However, as with H, the magnitude of differences observed between healthy age groups—and the degree to which those differences are clinically meaningful—remains unclear.

Recurrence quantification analysis percent determinism

The final technical validation calculated percent determinism using recurrence quantification analysis, which tallies the proportion of recurrent trajectories that pass through similar areas of a reconstructed state space compared to those that do not, on right thigh, shank, and foot segment angles57,58,59. After creating individually reconstructed state spaces for each walking trial and time series, we dynamically adjusted our threshold for classifying a recurrent point to achieve a recurrence rate of 5%. We also considered a diagonal line to be at least 60% of a trial’s average stride interval. We predicted that increasing age leads to less deterministic gait patterns.

Following our prediction, as our age groups became older, the thigh became slightly less deterministic (Table 1; Fig. 6). Only the percent determinism of the thigh in young adults compared to older adults was extremely supportive of the alternative hypothesis, in contrast to the other two age group comparisons.

Percent determinism calculated at the shank was highest for older adults, despite pairwise comparisons mostly supporting the null hypothesis. Finally, foot percent determinism was highest for young adults, and the evidence was strong in favor of the alternative hypothesis compared to middle-aged adults and very strong when compared to older adults. The shank was far less deterministic than the thigh and foot for all groups. It is also worth noting that the range of values obtained at the foot was quite tight compared to the large spread of values found at the thigh and shank. The compact percent determinism values at the foot might be attributable to the fact that a large portion of the foot is in stance throughout the gait cycle; consequently, the foot angle remains static, resulting in potentially more recurrent trajectories. Although some evidence did support the alternative hypothesis, the average difference between any two age groups was no greater than 5%. Whether or not this small difference is clinically relevant from the perspective of natural aging or should be considered a minimal detectable change needs to be investigated. To keep our technical validation consistent, the sagittal plane was chosen for all nonlinear analyses in this dataset, but greater age-related differences could be revealed along the frontal plane body segments. We also only statistically compared percent determinism instead of all other metrics that can be derived from a recurrence plot. Those metrics were calculated but not analyzed because they are rarely reported in the literature and can be found in supplementary material.

Both the thigh (to swing the distal segments of the leg forward) and the foot (to ensure a stable surface during heel contact and stance) play an active role in locomotion. In contrast, the shank’s role is to provide a stable structure to translate the center of mass forward across the ankle and knee joint, and its low deterministic behavior is worth noting. One potential reason for the low percent determinism of the shank is that because it passively serves as a support structure for the thigh and foot, its deterministic properties are governed by those segments. Further investigation is needed into the recurrence quantification of the lower-body limb segments due to the scarcity of publications in this area. The scarcity of publications was readily apparent during a literature search that revealed no comparable analysis incorporating our kinematic measures (thigh, shank, and foot segment angle) across the lifespan. Therefore, we assert that our technical validation offers a new comparison that requires additional investigation. However, while differences across studies and nonlinear analyses may stem from variations in study design or specific gait variables analyzed, the overall pattern remains clear: aging is associated with changes in gait’s temporal structure across all analyses in this technical validation.

Strengths and limitations

The present dataset exhibits distinctive strengths that differentiate it from existing gait datasets, starting with lengthy time series at 48,000 samples per walking trial. This extended duration facilitates the application of nonlinear analytical methods, making it unique from data sets characterized by significantly shorter series. Additionally, the dataset incorporates a substantial number of recordings (n = 18) for each subject, which significantly bolsters modeling efforts to evaluate the uniqueness of individual gait patterns26. This comprehensive exploration of an individual’s distinctive “gaitprint” has promising potential to offer important clues about disease prediction, physiological declines, and improvements in rehabilitation strategies60,61.

The present dataset has two unavoidable limitations. First, the IMU system’s dependence on the Earth’s magnetic field for horizontal motion detection introduces the potential for drift and phantom changes in direction due to the surrounding metal around the track. Extensive pilot testing shaped our final procedure that is consistent across all three datasets. Participants walked within a dedicated lane for four minutes, a duration and path chosen to minimize artifacts caused by the surrounding metal supporting the indoor track. To curb sensor drift and support high-quality data, each trial began with a dynamic calibration, followed immediately by a visual check of the participant’s virtual model and real-time joint angles to determine if a recalibration was required. Following Noraxon’s guidelines, all sensors were zeroed before the participant arrived. Second, while not strictly a limitation, users of our data must be aware that the track does not feature a symmetrically oval design and may introduce inherent asymmetry that may influence gait dynamics (Fig. 1). Previous literature demonstrates that curved walking drives numerous changes to gait kinematics, kinetics, and stability with differential effects according to age62,63,64,65,66. The influence of these paths on the Hurst exponent, sample entropy, and recurrence quantification analysis are not established. An upcoming manuscript explores these relationships and finds that clockwise and counterclockwise walking patterns result in subtle changes to gait’s long-range correlations and, thus, should be an experimental consideration.

Clear from our technical validation is that some methods detected age-related changes in gait kinematics better than others. SPM and relative phase are both common in the literature but generally failed to reveal consistent age-related differences, the implication being that inter-limb coordination remains generally stable over the lifespan, at least until a notable change in health status occurs (e.g., stroke or injury) occurs. If one assumes that nonlinear metrics should distinguish age groups, we found that H and SampEn succeeded, whereas RQA was less sensitive. Their discriminative power, however, depended on the variable: hip ROM assessed with SampEn and knee ROM assessed with either metric failed to reveal age-related effects. Our application of RQA used a dynamic algorithm that fixed the recurrence rate and the specification that a diagonal line was at least 60% of the gait cycle. This approach highlighted clear differences in thigh pitch between young and older adults, but an upcoming report is sweeping the algorithm’s parameters to establish optimal settings for more reliable deployment. Similar optimizations are underway for H and SampEn43,67,68. For the former, taking the median of 200 posterior samples produces reliable group differences. Increasing the sample count will yield more precise LRCs at the cost of runtime. As a preview of those forthcoming results, preliminary sweeps for SampEn indicate that a vector length (m) of 11 (rather than 2) and a tolerance (r) of 10% (rather than 25%) of the time-series standard deviation may better separate healthy age groups.

Usage Notes

The present gait dataset is structured within subject-specific folders, encompassing raw data, pre-calculated spatiotemporal variables for each trial, and scripts designed to facilitate analyses in MATLAB, Python, and R. Nearly all functions used in the technical validation are available on the GitHub repository associated with the Nonlinear Analysis Core of the Department of Biomechanics at the University of Nebraska at Omaha (https://github.com/Nonlinear-Analysis-Core/NONANLibrary). This online repository has recently been optimized using C++ with example data from our database and is now better suited for many datasets other than gait.

Within a larger project, our middle-aged adult dataset is encouraged to be used with our publicly accessible datasets featuring healthy young adults aged between 19 and 35 years and older adults greater than 5524,25. Those two cohorts underwent an identical experimental protocol described in the current paper (identified as G01 and G03, respectively, in all data)24,25. The remainder of this larger project is actively compiling a dataset for three clinical populations:

  • Group 4: Lower-limb amputees

  • Group 5: Post-stroke patients

  • Group 6: Patients with peripheral arterial disease

The composition of our six gait datasets forms an accessible and comprehensive repository spanning healthy adults of all ages and three clinical groups for collaboration among researchers, clinicians, and therapists aiming to discern variations among our sample. Furthermore, our dataset serves as a record of human movement that becomes increasingly identifiable due to advances in machine learning26,69,70,71,72. The current dataset includes nonconsecutive subject IDs due to the simultaneous recruitment of multiple groups. The finality of our Gaitprint project, including six databases, will eventually include consecutive IDs, barring excluded participants.