Introduction

Suspended sediment transport is a very important part of both the catchment and global geochemical cycle1, which has a great influence on many respects such as pollution and degradation2,3,4. So suspended sediment modeling is crucial for catchment management and operation of water resources projects5,6,7. However, the transportation of sediment is a complex process, which includes fluid-sediment interaction and the characteristics of both flow and sediment. This makes the sediment modeling quite difficult by using physically-based models, which are high computational costs and have a high demand for input data5,8,9.

The AI (Artificial Intelligence) and computational approaches such as artificial neural networks (ANNs) have the effective ability with regard to the high non-linear nature and complexity of the employed data10,11. It has been developed and widely used for hydrologic modeling recently12,13,14,15,16. Specifically, in the field of sediment prediction and forecasting, there are many AI techniques and methods that have been used, such as artificial neural network (ANN), support vector machine (SVM), fuzzy logic (FL), and numerous search optimization and statistical learning method12,13,14,15,16. For example, Kisi et al.17 modeled the suspended sediment using genetic programming. Cobaner et al.18 estimated suspended sediment concentration by adaptive neuro-fuzzy and neural network approaches. Singh and Panda19 simulated daily suspended sediment load using artificial neural networks and cross validation method for a small agricultural watershed.

Long Short-Term Memory (LSTM) networks are a special type of recurrent neural networks with an internal memory, which has the ability to learn and store long-term dependencies of the input–output relationship20,21. So it has great capability in capturing highly complex data distributions for predictions than traditional neural networks without explicit cell memory10,20,22,23. Such a superiority and efficiency of the LSTM model has been reported in the fields of flood forecasting24, runoff modeling20, groundwater level simulation25, and sediment modeling26,27,28. Kratzert et al.20 simulated rainfall-runoff and the results revealed that LSTM could recognize the long-term relation of inputs and targets. Nourani and Behfar 28 proposed two new seasonal-based LSTM models for runoff-sediment modeling, and the results showed that the models had good performances. Huang et al.22 adopted LSTM and other neural networks for real-time forecasting of suspended sediment concentrations reservoirs, and the results showed that LSTM was superior to those other machine learning models. Kaveh et al.29 evaluated the efficiency of LSTM model in estimating suspended sediment concentration in a river in the United States, and it indicated that LSTM model led to more accurate results.

Although LSTM network can extract the complex relationship patterns of data, yet it still could not effectively capture data with thresholds. Thresholds and other non-linear behaviors are quite common inhydrologic and geomorphic systems30, and they can occur at different levels of complexity and may limit the predictability of hydrological processes31,32,33. Rainfall threshold is one of the most key controlling factors for runoff, sediment and landslide33,34,35,36,37,38,39. For example, Guzzetti et al.40 studied the rainfall thresholds for the initiation of landslides worldwide. Western and Grayson 41 found that surface runoff was a threshold process controlled by catchment wetness conditions. Castillo et al.34 explored the role of antecedent soil water content in the runoff response of semiarid catchments, and results showed that the antecedent soil water content was important for controlling runoff during medium and low-intensity storms.

The role of rainfall threshold and soil moisture was found especially obvious in semiarid and arid environments42,43.Soil erosion is accelerated on land where erosive rain falls on landscapes and an obvious sediment process will occur when rainfall over some threshold4,44,45. Different runoff and sediment will produce under different rainfall conditions46. Meng et al.44 explored the impact of rainfall patterns on the soil loss of the hillslope, and results showed that the soil erosion was quite different under moderate, heavy and storm rainfall patterns.

The Loess Plateau, which is located in the arid/semiarid regions of North China, is highly fragmented by gullies and has suffered severe soil erosion47,48,49.The catchment in this study (Heimutouchuan, HMTC) is a small semiarid catchment and flows down the Loess Plateau. It is noticed that the suspended sediment transport rate would increase when a certain rainfall amount is exceeded, which indicated the inherent rainfall-sediment mechanism and relationship changes when reaching or exceeding some rainfall threshold. So it is necessary to explore the rainfall-sediment patterns and the role of rainfall threshold in sediment prediction.

The main objective of this study is to improve the suspended sediment prediction of semiarid catchments through (1) exploring the rainfall thresholds based on rainfall both on the given day and antecedent days, (2) integrating rainfall thresholds in the LSTM model for improving sediment modeling. This study is expected to provide a better understanding and modeling of the sediment processes of semiarid catchments.

Methodology

Study area and data

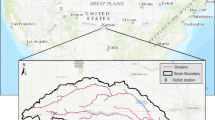
HMTC catchment is a tributary river of the Yellow River and flows down the Loess Plateau. Figure 1 shows location of the catchment. HMTC lies between 109°15′–109°37′ E longitude and 37°44′–38°00′ N latitude. The location of rain and flow gauges is also showed in Fig. 1. There are three rain gauges and one flow (sediment) gauge in HMTC catchment. Data used in this study are daily runoff (Qt), daily areal rainfall (Pt, weighted by Thiessen polygon method for the three rainfall stations) and daily suspended sediment transport rate (St) in 1980–2010 (July to October).

Figure 1
figure 1

Location of the study area and stations (map generated using ArcMap 10.4(10.4.1)50 using ASTER GDEM digital elevation model 30 m resolution51).

Full size image

The catchment area of HMTC is 327km2 and the characteristics of the catchment for the present study are given in Table1. The average annual rainfall is 260 mm and the average annual temperature is 8.6 °C. The daily average runoff is between 0.1 and 67.1 m3/s, and the daily sediment transport rate changes widely from 0.001 to 30,100 kg/s, which mainly occurs in summer (July to August). The soil type and land use are shown in Fig. 2. The soil type of HMTC is mainly PLe and FLd (FAO90, HWSD) (Fig. 2). The area contribution of the HMTC catchment is 52.76% under arid land, 45.72% under grass cover, 0.54% under forest land, 0.14% under other construction land, and 0.45% for under unutilized land with a remaining 0.38% underwater bodies for the year (Table 2).

Table 1 Characteristics of the study catchment.
Full size table
Figure 2
figure 2

Soil type (a) and land use (b) of the study area.

Full size image
Table 2 Soil and land use types in the study area.
Full size table

LSTM model

The LSTM model is one of the deep learning techniques which shows the great ability for dealing with time series problems by considering information selections and long-term dependencies21. LSTM can capture highly complex data distributions through memory units (Fig. 3), composed of a forget gate, an input gate and an output gate. The addition of the memory unit in the hidden layer enables the LSTM to learn the state characteristics of the long-period sequence data, making the memory information in the time series controllable, thereby solving the problem of the disappearance or explosion of the traditional RNN (Recurrent Neural Network) gradient10,20.

Figure 3
figure 3

Structure of LSTM neural network model (\(f_{t}\), \(i_{t}\), and \(o_{t}\) are forget gate, input gate and output gate respectively; \(\sigma\) and \(\tanh\) are activation functions; \(\otimes\) is matrix and element product, \(\oplus\) is addition).

Full size image

LSTM introduces a new internal state variable \(c_{t}\) dedicated to linear cyclical information transmission, and at the same time non-linearly outputs information to the external state of the hidden layer \(h_{t}\), \(c_{t}\) and \(h_{t}\) the calculation formula is as follows:

$$c_{t} = f_{t} \otimes c_{t - 1} + i_{t} \otimes \tilde{c}_{t}$$
(1)
$$h_{t} = o_{t} \otimes \tanh (c_{t} )$$
(2)

\(\tilde{c}_{t}\) is the candidate state variable obtained by the nonlinear function:

$$\tilde{c}_{t} = \tanh (W_{c} x_{t} + U_{c} h_{t - 1} + b_{c} )$$
(3)

LSTM introduces a gating mechanism to control the path of information transmission. The calculation formula for the three gates \(i_{t}\), \(f_{t}\), \(o_{t}\) and the memory unit are:

$$i_{t} = \sigma (W_{i} x_{t} + U_{i} h_{t - 1} + b_{i} )$$
(4)
$$f_{t} = \sigma (W_{f} x_{t} + U_{f} h_{t - 1} + b_{f} )$$
(5)
$$o_{t} = \sigma (W_{o} x_{t} + U_{o} h_{t - 1} + b_{o} )$$
(6)

LSTM network introduces the gating mechanism to control the path of information transmission, the cell state vector ensures a continuously updated long-term memory52,53. In such a method, the forget and input bits respectively decide (i) whether to reset the cell states from the previous time-stamp and forget the past and (ii) whether to increment the cell states from the previous time-stamp to incorporate new information into long-term memory52,53. Therefore, in the memory unit, not only a piece of certain key information can be captured at sometime through the forget gate, and the key information can be saved for a certain time interval, but also the historical information can be directly emptied through the forget gate. In this way, the LSTM neural network can selectively retain or forget previous information.

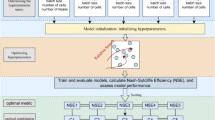
In this study, the rainfall thresholds are integrated in the LSTM model for improving sediment modeling.The sediments modeling is developed based on LSTM model without threshold (LSTM scheme) and with the rainfall threshold (C-LSTM scheme). The training of C-LSTM after data classification means a part of forgetting and selection in advance according to the mechanism. For example, when the input and output data corresponding to high sediment appears in the model operation, the previous low sediment content will be forgotten, and the high sediment content retains more information. In this way, the C-LSTM method would get the useful information and not miss the essentials.

Antecedent rainfall model

Rainfall threshold is affected by rainfall on the given day and antecedent days. Antecedent rainfall is usually estimated by an empirical approach through an index (the Antecedent Precipitation Index, API) based on the cumulated rainfall with a short period preceding the event50. Several antecedent rainfall models have been proposed52,53, which are as follows:

$$P_{a,t} = KP_{t - 1} + K^{2} P_{t - 2} + \cdots + K^{n} P_{t - n}$$
(7)
$$P_{a,t} = P_{t - 1} + 2^{d} P_{t - 2} + 3^{d} P_{t - 3} + \cdots + n^{d} P_{t - n}$$
(8)

where \({P}_{a,t}\) is antecedent rainfall (mm) for day t; K is a constant coefficient, usually about 0.8–0.9; \({P}_{t-n}\) is the rainfall (mm) on the nth day before 0, and n is usually 5-15d; d is the recession curve coefficient, which can be derived from the hydrograph (d < 0)51.

Equation (8) considers the fast drainage of soils and results in a shift of the distribution of the daily rainfall magnitudes to lower antecedent daily rainfall values54. HMTC catchment is located in the semiarid areas and does not have large long-term water storage capacity, so the Eq. (8) with lower antecedent daily rainfall is more appropriate for estimation of soil moisture conditions in the study catchment.

The recession curve coefficient d has a strong influence on the magnitude of antecedent rainfall. The larger the absolute value of the exponent, the faster water drains from the soil, thus lowering the time interval of effective antecedent rainfall influence to the critical water content required to sediment.

Evaluation of model performances

Nash–Sutcliffe efficiency (NSE), the coefficient of determination (R2), root mean square error (RMSE), and relative bias (BIAS) are used to evaluate the accuracy of sediment simulation results, which are defined as follows:

$$NSE = 1 - \frac{{\sum {(S_{obs} (i) - S_{sim} (i))^{2} } }}{{\sum {(S_{obs} (i) - S_{obs,mean} )^{2} } }}$$
(9)
$$R^{2} = \frac{{\left( {\sum\nolimits_{i = 1}^{n} {(S_{obs} (i) - S_{obs,mean} )(S_{sim} (i) - S_{sim,mean} )} } \right)^{2} }}{{n\sum\nolimits_{i = 1}^{n} {(S_{obs} (i) - S_{obs,mean} )^{2} \cdot } \sum\nolimits_{i = 1}^{n} {(S_{sim} (i) - S_{sim,mean} )^{2} } }}$$
(10)
$$RMSE = \sqrt {\frac{{\sum\nolimits_{i = 1}^{n} {(S_{obs} (i) - S_{sim} (i))^{2} } }}{{S_{mean} }}}$$
(11)
$$BIAS = \frac{{\sum\nolimits_{i = 1}^{n} {\left| {S_{sim} (i) - S_{obs} (i)} \right|} }}{n}$$
(12)

where \(S_{obs}\) and \(S_{sim}\) are observed and modeled daily sediment respectively, \(S_{obs,mean}\), \(S_{sim,mean}\) are the arithmetic mean of the observed and modeled daily sediment, \(i\) is the ith sample, and n is the number of samples.

Results and discussion

Rainfall threshold and rainfall pattern

To derive rainfall thresholds, the rainfall-sediment relationship under different rainfall conditions was investigated to identify patterns in behaviors. Both rainfall on the given day (P) and antecedent days (Pa) were considered to link to the sediment (Fig. 4). Antecedent rainfall of HMTC was estimated by Eq. (8). After calculation, the recession curve coefficients, i.e., d = − 1.65, and n = 5 days, were used in this study for HMTC catchment.

Figure 4
figure 4

Relationship of rainfall (P + Pa) to sediment (S).

Full size image

Figure 4 displays the relationship between sediment rate S, and rainfall P + Pa. The red dots were related to rainfall (P + Pa) > 10 mm, and the blue dots relating to rainfall (P + Pa) < 10 mm. It was noticed that rainfall-sediment relationships undergone changes with rainfall over 10 mm. This indicated sediment process would change when rainfall exceeds 10 mm threshold. So the rainfall-sediment relationships can be mainly grouped into two patterns by rainfall threshold 10 mm. Pattern 1 was associated with medium and high daily rainfall (P + Pa > 10 mm) mainly leading to medium and high suspended sediment, while Pattern 2 was low rainfall (P + Pa < 10 mm) leading to low sediment.

Comparison of the two schemes for suspended sediment prediction

The sediment modeling in this study is developed based on LSTM model without threshold (LSTM scheme) and with the rainfall threshold (C-LSTM scheme). The same data set were used in both LSTM and C-LSTM schemes for acomparative study. C-LSTM scheme modeled high sediment and low sediment separately, and LSTM scheme simulated all sediments. Qt, Pt and Pa,t were used as input data for modeling in this study. Data of 20 years (1980–1999) were used for model calibration, and data of 11 years (2000–2010) were used for validation.

The performances of the two schemes were examined using the calibration and validation data set. The obtained results of the C-LSTM were compared to LSTM scheme for evaluating the predictive capability. The NSE values of the two schemes are presented in Table 3. It was observed that the C-LSTM scheme showed better performances in predicting the daily sediment in the study catchment. In Pattern 1 for medium and high sediment simulation, the NSE of LSTM was 0.925 and 0.911 for calibration and validation, while the NSE using C-LSTM was 0.934 and 0.924, respectively (Table 3). The results showed the simulation was marginally improved.

Table 3 NSE evaluation of simulation results of two schemes.
Full size table

Moreover, in Pattern 2 with rainfall P + Pa < 10 mm for low sediment simulation, the improvement was more significant. It was observed that the LSTM scheme was unable to capture the low suspended sediment rate as it was very clear a negative NSE value was predicted during low sediment data. The NSE of LSTM was -0.375 and 0.171 for calibration and validation, and was improved to 0.738 and 0.797 by C-LSTM. Results suggested that the C-LSTM scheme was much better than LSTM scheme based on NSE as performance evaluation criteria.

Figure 5 and Table 4 further compared simulation results for the calibration and validation periods in terms of BIAS. The median BIAS in Pattern 1 for the two schemes (LSTM and C-LSTM) was 771.7 kg/s and 757.9 kg/s for calibration, as well as, 968.7 kg/s and 811.1 kg/s for validation, respectively; The median BIAS in Pattern 2 for the two schemes was 56.3 kg/s and 12.4 kg/s for calibration, while 47.4 kg/s and 16.7 kg/s for validation, respectively. The BIAS results also suggested that the C-LSTM scheme was better than the LSTM scheme.

Figure 5
figure 5

Box plot of BIAS indicator for Patten1 (a) and Patten2 (b).

Full size image
Table 4 BIAS evaluation for the study catchment (Q1, the lower quartile; Q2, the median; and Q3, the higher quartile).
Full size table

Further comparisons of the two schemes are shown in the form of a hydrograph in Fig. 6. In pattern 1 for medium and high sediment (Fig. 6a), the hydrographs indicated that the modeled suspended sediment rate by both models followed the variation in the observed data. In pattern 2, the C-LSTM scheme results showed much better performance than that of LSTM scheme. It was seen from the hydrograph that observed and model sediment yielded by LSTM scheme was not followed closely, and the hydrographs indicated that LSTM scheme overestimated the sediment in pattern 2 during the low rainfall days (Fig. 6b).

Figure 6
figure 6

Comparison between observed and estimated sediment using the two schemes for Patten1 (a) and Patten2 (b).

Full size image

Similarly, in the scatter plot, it was observed that results in pattern 1 were closer to the 1:1 line, and the data points were scattered around the 1:1 line (Fig. 7a). The RMSE between the observed and modeled sediments obtained from the C-LSTM scheme (1047.93 kg/s) was less than that from LSTM scheme (1188.40 kg/s), and the R2 was raised from 0.92 to 0.93. Results exhibited that the C-LSTM scheme slightly outperformed LSTM scheme for medium and high sediment simulation. In Pattern 2 (Fig. 7b), the RMSE from the C-LSTM scheme (27.22 kg/s) was less than that from LSTM scheme (54.22 kg/s). The R2 was raised from 0.28 to 0.75, which also suggested that C-LSTM scheme was much better than the LSTM scheme for low sediment simulation.

Figure 7
figure 7

Scatter plot of observed and simulated of sediment for Patten1 (a) and Patten2 (b).

Full size image

Limitations and uncertainties

Results in this study showed that rainfall threshold was a potentially useful factor for sediment modeling in semiarid areas such as the Loess Plateau of China. However, there were still some limitations and uncertainties if only rainfall amount was considered in suspended sediment modeling. For example, there were still some events not following the rainfall threshold (Fig. 4). This was mainly because there were some other factors which may influence the sediment process such as rainfall intensity (PI)48,55.

The role of rainfall intensity was analyzed and displayed in Table 5. It showed that some high-intensity rainstorms produce high sediment. For example, the rainfall amount in HMTC on August 8, 1982 (P = 10.01 mm, Pa = 1.72 mm) and September 27, 1984 (P = 10.20 mm, Pa = 1.69 mm) was almost the same, but the former had a greater PI (10.5 mm/h) which led to the higher sediment (1190 kg/s), while PI of the latter was 3.9 mm/h, leading to a lower sediment flux (81.7 kg/s) (Table 5a). This demonstrated high-intensity rainfall would increase soil erosion and sediment response. Another comparison was made between July 7, 2000 and July 19, 1999 (Table 5b). The former had a lower rainfall amount (27.65 mm) but higher sediment (3130 kg/s) because of the higher PI (30.6 mm/h), while the later led to a lower sediment flux (2310 kg/s) because of the lower PI (11.5 mm/h). These indicated that the rainfall intensity had great effects on sediment, and including rainfall intensity as a key factor would be helpful for the reduction of sediment predictive uncertainty. Also, there were still some other factors such as land use and land cover, which may influence the sediment and need to be further considered in the future55.

Table 5 Relationship between sediment, rainfall amount and rainfall intensity (hourly).
Full size table

Conclusions

This study investigated the effectiveness of integrating rainfall thresholds in the sediment modeling in a small semiarid catchment in China. The results showed that coupling antecedent rainfall could lead to better rainfall thresholds. Evaluation of the accuracies of results produced by the C-LSTM and LSTM scheme showed that C-LSTM had much better performances for predicting sediment, especially for low rainfall conditions. This demonstrated the C-LSTM scheme had a better suspended sediment simulation capability compared to LSTM scheme, which indicated the advances of integrating rainfall thresholds for suspended sediment modeling. The results highlighted the importance of integrating rainfall thresholds in sediment prediction in semiarid areas such as the Loess Plateau of China. However, the rainfall intensity, land use, and land cover, which were also very important for the sediment processes, have not been incorporated in the present study and will be included in future research to further improve the estimation capability of suspended sediment.