Different estimation techniques for constant-partially accelerated life tests of chen distribution using complete data

Abstract

The issue of various estimation techniques in constant partially accelerated life tests with complete data is the main subject of this research. The Chen distribution is regarded as an item’s lifetime under use conditions. To estimate the distribution parameters and the acceleration factor, maximum likelihood estimation, least square estimation, weighted least square estimation, Cramér Von–Mises estimation, Anderson–Darling estimation, right-tail Anderson–Darling estimation, percentile estimation, and maximum product of spacing estimation are presented for classical estimation. For illustrative purposes, two real data sets are analyzed. The investigation of the two real data sets reveals that the suggested techniques are practical and can be used to solve some engineering-related issues. In order to compare the results of the several estimation techniques that have been offered based on mean square error and absolute average bias, a simulation study is presented at the end. When adopting the smallest values for mean square error and absolute average bias, this study demonstrates that maximum product of spacing estimation is the technique that is most effective among the alternatives in most cases.

Introduction

The rapid and successive technological developments in various engineering fields have led to an increase in the demand for products with high reliability. These products are difficult to test for reliability during the lifetime test period due to the high cost, which makes it difficult to collect failure information under the use conditions. Therefore, accelerated lifetime tests (ALT) are used to collect failure time data for test products in much less time and at a lower cost. In accelerated life tests, the experiment can either start under accelerated conditions and continue under these conditions, or under use conditions and then apply the accelerated conditions to those units that did not fail within the predetermined time under the influence of use conditions. Accordingly, there are two main types of ALT: fully ALT, which are suitable for the first case, and partially accelerated life tests (PALT), which are suitable for the latter case.

One of the most popular models that has received a lot of attention in the literature on fully ALT is the constant accelerated life tests (CALT). Numerous statisticians have addressed the issue of various estimation techniques based on CALT using complete data, including^1,2,3,4,5.

The two most significant PALT models in the literature are step-stress PALT and constant (CPALT). Goel⁶ investigated, in a step-stress PALT, the MLE technique for parameter estimation for exponential and uniform distributions utilizing complete data. To estimate the exponential distribution’s parameters in a step-stress PALT with complete data, Bayesian technique was utilized, see⁷.

According to⁸, the CPALT only performs each item under the use or accelerated conditions. Additionally, the authors used type-I censored data to investigate the CPALT issue for exponential distributions. Subsequent studies addressed the issue of CPALT estimation under various censored data utilizing various distributions. Using CPALT with type-I censored data, Bai et al.⁹ investigated the of estimation and optimal design for the log-normal distribution. Abdel-Hamid¹⁰ investigated the problem of estimation for Burr type-II distribution based on CPALT using progressive type-II. In CPALT, the optimal design problem for the inverse Weibull distribution utilizing type-I censored data has been studied by¹¹. Using a unified hybrid censoring data, Lone et al.¹² have taken into account the prediction issue in CPALT for the Gompertz distribution. The estimation for the two-parameter Gompertz distribution using CPALT under an adaptive progressive hybrid censoring scheme was introduced in¹³. In accordance with an adaptive type-II progressive censoring scheme, Almalki et al.¹⁴ introduced parameter estimation for the Kumaraswamy distribution using CPALT. Mahmoud et al.¹⁵ proposed parameter estimation for the inverted generalized linear exponential distribution under CPALT using a progressive type-II censoring scheme. parameter estimation for the Nadarajah–Haghighi distribution based on the progressive type-II censoring scheme was investigated by¹⁶. For the modified Kies exponential distribution, Nassar and Alam¹⁷ examined parameter estimation based on the CPALT utilizing a type-II censoring data. Based on progressive first failure type-II censored using CPALT, Eliwa and Ahmed¹⁸ conducted a reliability analysis of the Lomax model.

On the other hand, the issue of various estimation techniques based on CPALT using complete data, which is the focus of this study, has not been adequately addressed. Additionally, a variety of natural phenomena, engineering problems, and clinical treatment produce a large amount of complete real data that are extremely important to our life. According to the aforementioned, the issue of various estimation methodologies based on CPALT and employing complete real data is of considerable relevance.

With an increasing or bathtub-shaped hazard rate function (HRF), Chen¹⁹ suggested a two-parameter lifetime distribution. Due to the fact that the bathtub-shaped HRF serves as a useful conceptual model for electronic and machinery industries, it has received consideration from numerous researchers; see^20,21,22,23.

The Chen distribution has some distinctive properties compared to other models with two parameters such as the fact that its HRF is bathtub-shaped and also the confidence intervals for the shape parameter and the joint confidence regions for the two parameters have closed form. Therefore, many researchers have studied its statistical inference based on ALT and PALT, see^24,25,26.

The main objective of this research is to provide eight techniques of estimations for CPALT of Chen distribution based on the complete data, namely: maximum likelihood estimation (MLE), least square estimation (LSE), weighted least square estimation (WLSE), Cramér Von–Mises estimation (CVME), Anderson–Darling estimation (ADE), right-tail Anderson–Darling estimation (RADE), percentile estimation (PE), and maximum product of spacing estimation (MPSE). To illustrate the importance of the model in resolving various engineering issues, two complete real data sets are used. A simulation study is conducted to assess the performance of the suggested methods. Small, medium, and large sample sizes were used to compare the mean squared errors (MSE) and the absolute average bias (AAB) of the estimators’ performances.

The sections of this study are arranged as follows. “Basic assumptions and model description” presents the main concepts of CPALT. The MLE of Chen distribution using CPALT is studied in “Maximum likelihood estimation”. “Least square and weighted least square estimations” discusses the estimation of Chen distribution using CPALT based on LSE and WLSE. The CVME is studied for Chen distribution under CPALT in “Cramér Von–Mises estimation”. In “Anderson–Darling and right-tail Anderson–Darling estimations”, the ADE and RTADE are presented to estimate the unknown parameters and accelerated factor of Chen distribution using CPALT. PE using CPALT for Chen distribution is studied in “Percentile estimation”. In “Maximum product of spacing estimation”, the MPSE is presented for Chen distribution under CPALT. Two uncensored real data sets are analyzed in “Numerical computations”. In “Simulation study”, the simulation study is covered. Conclusion remarks are reported in “Conclusion”.

Basic assumptions and model description

Basic assumptions

• Under use conditions, the lifetimes of test units follow the Chen distribution and are independent and identically distributed. The probability density function (PDF) and the cumulative distribution function (CDF) of Chen distribution are given by

  $$\begin{aligned} f_{1}(t;\lambda ,\xi ) =\lambda \ \xi \ e^{t^{\xi }} \ t^{\xi -1} \ e^{\lambda (1-e^{t^{\xi }})}, \qquad \lambda>0, \ \xi>0, \ t>0. \end{aligned}$$

  (1)

  and

  $$\begin{aligned} F_{1}(t;\lambda ,\xi ) = 1- e^{\lambda (1-e^{t^{\xi }})}, \qquad t>0. \end{aligned}$$

  (2)

  respectively. The survival function (SF) and HRF are given by:

  $$\begin{aligned} S_{1}(t;\lambda ,\xi ) =e^{\lambda (1-e^{t^{\xi }})}, \end{aligned}$$

  (3)

  and

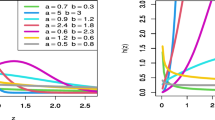
  $$\begin{aligned} h_{1}(t;\lambda ,\xi ) = \lambda \ \xi \ e^{t^{\xi }} \ t^{\xi -1}. \end{aligned}$$

  (4)

  respectively. Equation (4) can be used to demonstrate how the hazard rate function for the Chen distribution can have two different shapes: an increasing shape for $\xi \ge 1$ and $\lambda >0$ and a bathtub shape for $\xi <1$ and $\lambda >0$ with change point at $t^*=\left( \frac{1-\xi }{\xi }\right) ^{1/\xi }$. For additional properties, see²⁷.

• Under the acceleration condition, the lifetimes of test units follow the Chen distribution and are independent and identically distributed. The HRF of test unit can be given by $h_{2}(t)=\varphi \ h_{1}(t)$, where $\varphi >1$ is the acceleration factor. Then the HRF, SF, CDF, and PDF can be written as

  $$\begin{aligned} h_{2}(t;\lambda ,\xi ,\varphi )= & {} \lambda \ \varphi \ \xi \ e^{t^{\xi }} \ t^{\xi -1}, \end{aligned}$$

  (5)
  $$\begin{aligned} S_{2}(t;\lambda ,\xi ,\varphi )= & {} e^{\int _{0}^{t}h_{2}(x;\lambda ,\xi ,\varphi )}=e^{\lambda \ \varphi (1-e^{t^{\xi }})}, \end{aligned}$$

  (6)
  $$\begin{aligned} F_{2}(t;\lambda ,\xi ,\varphi )= & {} 1- e^{\lambda \ \varphi (1-e^{t^{\xi }})}, \end{aligned}$$

  (7)

  and

  $$\begin{aligned} f_{2}(t;\lambda ,\xi ,\varphi ) = \lambda \ \xi \ \varphi \ e^{t^{\xi }} \ t^{\xi -1} \ e^{\lambda \ \varphi (1-e^{t^{\xi }})}, \end{aligned}$$

  (8)

respectively.

Model description

Upon using the CPALT, the total size of units is divided into two groups: $m_{1}$ units for use condition and $m_{2}$ units for accelerated condition. Let the lifetime $T_{ji}$, $i=1,\ldots ,m_{j}$, $j=1,2$ be two complete samples from Chen distribution. The lifetime of an item tested at use conditions is denoted by $T_{1i}$, while the lifetime of an item tested at accelerated conditions is denoted by $T_{2i}$. The two lifetimes $T_{1i}$ and $T_{2i}$ are pairwise statistically independent.

Point estimation

The MLE, LSE, WLSE, CVME, ADE, RADE, PE, and MPSE estimation methods under CPALT for Chen distribution utilizing complete data are explored in this section.

Maximum likelihood estimation

The MLEs of parameters and accelerated factor of Chen distribution under complete data using CPALT are discussed in this subsection. The likelihood function of CPALT for Chen distribution under complete data can be obtained as:

$$\begin{aligned} L(\lambda ,\xi ,\varphi |{\textbf {t}})= \prod _{j=1}^{2} \ \prod _{i=1}^{m_{j}} \ f_{j}(t_{ji};\lambda , \xi , \varphi ). \end{aligned}$$

(9)

Upon using (1) and (8), the log-likelihood function $\ell =\log \ L(\lambda ,\xi ,\varphi |{\textbf {t}})$ can be written as

$$\begin{aligned} \ell (\lambda ,\xi ,\varphi |{\textbf {t}})= & {} (m_{1}+m_{2}) \log {\lambda }+(m_{1}+m_{2}) \log { \xi }+m_{2}\log {\varphi } +(\xi -1)\sum _{i=1}^{m_{1}} \ \log {t_{1i}}+\sum _{i=1}^{m_{1}} \ t_{1i}^\xi \nonumber \\{} & {} \,+ \sum _{i=1}^{m_{1}} \ \lambda \ (1-e^{t_{1i}^\xi }) + (\xi -1)\sum _{i=1}^{m_{2}} \ \log {t_{2i}}+\sum _{i=1}^{m_{2}} \ t_{2i}^\xi +\sum _{i=2}^{m_{2}} \ \lambda \ \varphi \ (1-e^{t_{2i}^\xi }). \end{aligned}$$

(10)

The normal equations of the unknown parameters and the accelerated factor can be given as:

$$\begin{aligned} \frac{\partial \ell }{\partial \lambda }= & {} \frac{m_{1}+m_{2}}{\lambda }+\sum _{i=1}^{m_{1}} \ (1-e^{t_{1i}^\xi })+ \sum _{i=1}^{m_{2}} \ \varphi \ (1-e^{t_{2i}^\xi })=0, \end{aligned}$$

(11)

$$\begin{aligned} \frac{\partial \ell }{\partial \xi }= & {} \frac{m_{1}+m_{2}}{\xi }+\sum _{i=1}^{m_{1}} \ \log {t_{1i}}+\sum _{i=1}^{m_{1}} \ t_{1i}^\xi \ \log {t_{1i}} -\sum _{i=1}^{m_{1}} \ \lambda \ t_{1i}^\xi \ \log {t_{1i}} \ e^{t_{1i}^\xi } \nonumber \\{} & {} \,+ \sum _{i=1}^{m_{2}} \ \log {t_{2i}}+\sum _{i=1}^{m_{2}} \ t_{2i}^\xi \ \log {t_{2i}} -\sum _{i=1}^{m_{2}} \ \lambda \ \varphi \ t_{2i}^\xi \ \log {t_{2i}} \ e^{t_{2i}^\xi } =0, \end{aligned}$$

(12)

and

$$\begin{aligned} \frac{\partial \ell }{\partial \varphi }= & {} \frac{m_{2}}{\varphi }+\sum _{i=1}^{m_{2}} \ \lambda \ (1-e^{t_{2i}^\xi })=0. \end{aligned}$$

(13)

The three aforementioned equations do not have a closed-form solution, hence the MLEs can be obtained using a numerical methodology by employing FindRoot[] in Mathematica or by using Newton–Raphson algorithm. The MLEs of $\lambda$, $\xi$, and $\varphi$ can be denoted as ${\hat{\lambda }}$, ${\hat{\xi }}$, and ${\hat{\varphi }}$.

Least square and weighted least square estimations

LSE and WLSE are presented for estimating the beta distribution’s parameters in the paper by²⁸. With the use of CPALT, these techniques will be used to estimate the unknown parameters and the accelerated factor of Chen distribution under complete data. For this purpose, take lifetimes $T_{(ji)}$, $i=1,\ldots ,m_{j}$, $j=1,2$ to be two complete ordered samples from Chen distribution under CPALT. Then the LSE of the unknown parameters and the accelerated factor can be obtained by minimizing the following function

$$\begin{aligned} S= \sum _{j=1}^2 \ \sum _{i=1}^{m_{j}} \left( \ F_{j}(t_{(ji)};\lambda , \xi , \varphi )-\frac{ i}{ m_{j}+1} \right) ^2 \ \end{aligned}$$

(14)

w.r.t. the unknown parameters $\lambda$, $\xi$, and the accelerated factor $\varphi$. Upon using (2) and (7), the equation (14) can be written as

$$\begin{aligned} S= \sum _{i=1}^{m_{1}} \left( 1- e^{\lambda \left( \ 1-e^{t_{(1i)}^{\xi }}\right) \ }-\frac{ i}{ m_{1}+1} \right) ^2 \ +\sum _{i=1}^{m_{2}} \left( 1- e^{\lambda \ \varphi \left( \ 1-e^{t_{(2i)}^{\xi }}\right) \ }-\frac{ i}{ m_{2}+1} \right) ^2 \ \end{aligned}$$

Additionally, the following non-linear equations can be solved to yield the LSEs of the unknown parameters and the accelerated factor.

$$\begin{aligned} \frac{\partial S}{\partial \lambda }= & {} \sum _{i=1}^{m_{1}} \ \left( 1- e^{\lambda \left( 1-e^{t_{(1i)}^{\xi }}\right) \ }-\frac{ i}{ m_{1}+1} \right) \ \delta _{1}(t_{(1i)};\lambda , \xi ) \\{} & {} \,+\sum _{i=1}^{m_{2}} \ \left( 1- e^{\lambda \ \varphi \left( \ 1-e^{t_{(2i)}^{\xi }}\right) \ }-\frac{ i}{ m_{2}+1} \right) \ \delta _{2}(t_{(2i)};\lambda , \xi , \varphi ) =0, \\ \frac{\partial S}{\partial \xi }= & {} \sum _{i=1}^{m_{1}} \ \left( 1- e^{\lambda \left( 1-e^{t_{(1i)}^{\xi }}\right) \ }-\frac{ i}{ m_{1}+1} \right) \ \delta _{3}(t_{(1i)};\lambda , \xi )\\{} & {} \,+\sum _{i=1}^{m_{2}} \ \left( 1- e^{\lambda \ \varphi \left( \ 1-e^{t_{(2i)}^{\xi }}\right) \ }-\frac{ i}{ m_{2}+1} \right) \ \delta _{4}(t_{(2i)};\lambda , \xi , \varphi ) =0, \end{aligned}$$

and

$$\begin{aligned} \frac{\partial S}{\partial \varphi }= \sum _{i=1}^{m_{2}} \ \left( \ 1- e^{\lambda \ \varphi \left( 1-e^{t_{(2i)}^{\xi }}\right) \ }-\frac{ i}{ m_{2}+1} \right) \ \delta _{5}(t_{(2i)};\lambda , \xi , \varphi )=0, \end{aligned}$$

where

$$\begin{aligned} \delta _{1}(t_{(1i)};\lambda , \xi )=- e^{\lambda \left( \ 1-e^{t_{(1i)}^{\xi }}\right) \ } \left( 1-e^{t_{(1i)}^{\xi }}\right) \, \end{aligned}$$

(15)

$$\begin{aligned} \delta _{2}(t_{(2i)};\lambda , \xi , \varphi )=-\varphi \ e^{\lambda \ \varphi \left( 1-e^{t_{(2i)}^{\xi }}\right) \ } \left( \ 1-e^{t_{(2i)}^{\xi }}\right) \, \end{aligned}$$

(16)

$$\begin{aligned} \delta _{3}(t_{(1i)};\lambda , \xi )= e^{\lambda \left( \ 1-e^{t_{(1i)}^{\xi }}\right) \ } \ \lambda \ t_{(1i)}^\xi \ \log {t_{(1i)}} \ e^{t_{(1i)}^\xi }, \end{aligned}$$

(17)

$$\begin{aligned} \delta _{4}(t_{(2i)};\lambda , \xi , \varphi )= e^{\lambda \ \varphi \left( 1-e^{t_{(2i)}^{\xi }}\right) \ } \ \lambda \ \varphi \ t_{(1i)}^\xi \ \log {t_{(1i)}} \ e^{t_{(1i)}^\xi }, \end{aligned}$$

(18)

and

$$\begin{aligned} \delta _{5}(t_{(2i)};\lambda , \xi , \varphi )= -\lambda \ e^{\lambda \ \varphi \left( 1-e^{t_{(2i)}^{\xi }}\right) \ } \left( \ 1-e^{t_{(2i)}^{\xi }}\right) . \end{aligned}$$

(19)

One can obtain WLSEs for Chen distribution using CPALT under complete data by minimizing the following function

$$\begin{aligned} W=\sum _{j=1}^2 \ \sum _{i=1}^{m_{j}} \ \frac{ (m_{j} + 2) (m_{j} + 1)^2}{i \ (m_{j} - i + 1)} \ \left( \ F_{j}(t_{(ji)};\lambda , \xi , \varphi )-\frac{ i}{ m_{j}+1} \right) ^2 \end{aligned}$$

w.r.t. the unknown parameters $\lambda$, $\xi$, and the accelerated factor $\varphi$ or by finding the solution to the non-linear equations

$$\begin{aligned} \frac{\partial W}{\partial \lambda }= & {} \sum _{i=1}^{m_{1}} \ \frac{ (m_{1} + 2) (m_{1} + 1)^2}{i \ (m_{1} - i + 1)} \ \left( 1- e^{\lambda \left( 1-e^{t_{(1i)}^{\xi }}\right) \ }-\frac{ i}{ m_{1}+1} \right) \ \delta _{1}(t_{(1i)};\lambda , \xi ) \\{} & {} \, + \sum _{i=1}^{m_{2}} \ \frac{ (m_{2} + 2) (m_{2} + 1)^2}{i \ (m_{2} - i + 1)} \ \left( 1- e^{\lambda \ \varphi \left( \ 1-e^{t_{(2i)}^{\xi }}\right) \ }-\frac{ i}{ m_{2}+1} \right) \ \delta _{2}(t_{(2i)};\lambda , \xi , \varphi ) =0, \\ \frac{\partial W}{\partial \xi }= & {} \sum _{i=1}^{m_{1}} \ \frac{ (m_{1} + 2) (m_{1} + 1)^2}{i \ (m_{1} - i + 1)} \ \left( 1- e^{\lambda \left( 1-e^{t_{(1i)}^{\xi }}\right) \ }-\frac{ i}{ m_{1}+1} \right) \ \delta _{3}(t_{(1i)};\lambda , \xi )\\ {}{} & {} \, +\sum _{i=1}^{m_{2}} \ \frac{ (m_{2} + 2) (m_{2} + 1)^2}{i \ (m_{2} - i + 1)} \ \left( \ 1- e^{\lambda \ \varphi \left( 1-e^{t_{(2i)}^{\xi }}\right) \ }-\frac{ i}{ m_{2}+1} \right) \ \delta _{4}(t_{(2i)};\lambda , \xi , \varphi ) =0, \end{aligned}$$

and

$$\begin{aligned} \frac{\partial W}{\partial \varphi }= \sum _{i=1}^{m_{2}} \ \frac{ (m_{2} + 2) (m_{2} + 1)^2}{i \ (m_{2} - i + 1)} \ \left( \ 1- e^{\lambda \ \varphi \left( 1-e^{t_{(2i)}^{\xi }}\right) \ }-\frac{ i}{ m_{2}+1} \right) \ \delta _{5}(t_{(2i)};\lambda , \xi , \varphi )=0, \end{aligned}$$

where $\delta _{1}(t_{(1i)};\lambda , \xi )$, $\delta _{2}(t_{(2i)};\lambda , \xi , \varphi )$, $\delta _{3}(t_{(1i)};\lambda , \xi )$, $\delta _{4}(t_{(2i)};\lambda , \xi , \varphi )$ and $\delta _{5}(t_{(2i)};\lambda , \xi , \varphi )$ are given by (15), (16), (17), (18) and (19) respectively.

Cramér Von–Mises estimation

A study by²⁹ revealed that the bias of CVME is lower than that of the other minimum distance estimator. In this subsection, CVME is applied to Chen distribution using CPALT based on complete data. Then the CVME of the unknown parameters and the accelerated factor can be given by minimizing the following function

$$\begin{aligned} C=\frac{1}{12 \ (m_{1}+m_{2})} +\sum _{j=1}^2 \ \sum _{i=1}^{m_{j}} \left( F_{j}(t_{(ji)};\lambda , \xi , \varphi )-\frac{2 \ i-1}{2 \ m_{j}} \right) ^2 \ \end{aligned}$$

w.r.t. the unknown parameters $\lambda$, $\xi$, and the accelerated factor $\varphi$ or by solving the following non-linear equations

$$\begin{aligned} \frac{\partial C}{\partial \lambda }= & {} \sum _{i=1}^{m_{1}} \ \left( 1- e^{\lambda \left( \ 1-e^{t_{(1i)}^{\xi }}\right) \ }-\frac{2 \ i-1}{2 \ m_{1}} \right) \ \delta _{1}(t_{(1i)};\lambda , \xi )\\{} & {} \,+\sum _{i=1}^{m_{2}} \ \left( 1- e^{\lambda \ \varphi \left( 1-e^{t_{(2i)}^{\xi }}\right) \ }-\frac{2 \ i-1}{2 \ m_{2}} \right) \ \delta _{2}(t_{(2i)};\lambda , \xi , \varphi ) =0, \\ \frac{\partial C}{\partial \xi }= & {} \sum _{i=1}^{m_{1}} \ \left( 1- e^{\lambda \left( 1-e^{t_{(1i)}^{\xi }}\right) \ }-\frac{2 \ i-1}{2 \ m_{1}} \right) \ \delta _{3}(t_{(1i)};\lambda , \xi )\\{} & {} \, +\sum _{i=1}^{m_{2}} \ \left( 1- e^{\lambda \ \varphi \left( 1-e^{t_{(2i)}^{\xi }}\right) \ }-\frac{2 \ i-1}{2 \ m_{2}} \right) \ \delta _{4}(t_{(2i)};\lambda , \xi , \varphi ) =0, \end{aligned}$$

and

$$\begin{aligned} \frac{\partial C}{\partial \varphi }= \sum _{i=1}^{m_{2}} \ \left( 1- e^{\lambda \ \varphi \left( 1-e^{t_{(2i)}^{\xi }}\right) \ }-\frac{2 \ i-1}{2 \ m_{2}} \right) \ \delta _{5}(t_{(2i)};\lambda , \xi , \varphi )=0, \end{aligned}$$

where $\delta _{1}(t_{(1i)};\lambda , \xi )$, $\delta _{2}(t_{(2i)};\lambda , \xi , \varphi )$, $\delta _{3}(t_{(1i)};\lambda , \xi )$, $\delta _{4}(t_{(2i)};\lambda , \xi , \varphi )$ and $\delta _{5}(t_{(2i)};\lambda , \xi , \varphi )$ are given by (15), (16), (17), (18) and (19) respectively.

Anderson–Darling and right-tail Anderson–Darling estimations

As an alternative to previous statistical tests for identifying sample distributions deviating from normality, Anderson and Darling³⁰ created the Anderson–Darling test. Boos³¹ examined the characteristics of ADE in a different investigation. Using his results, the ADE of Chen distribution using CPALT can be obtained by minimizing the following function

$$\begin{aligned} A= -(m_{1}+m_{2})-\sum _{j=1}^2 \ \sum _{i=1}^{m_{j}} \ \frac{(2 \ i-1)}{m_{j}} \left( \log {F_{j}(t_{(ji)};\lambda , \xi , \varphi )} - \log { \left( 1-F_{j}(t_{(m_{j}+1-ji)};\lambda , \xi , \varphi ) \right) \ } \right) \, \end{aligned}$$

w.r.t. the unknown parameters $\lambda$, $\xi$, and the accelerated factor $\varphi$ or by solving the following non-linear equations:

$$\begin{aligned} \frac{\partial A}{\partial \lambda }= & {} - \sum _{i=1}^{m_{1}} \frac{(2 \ i-1)}{m_{1}} \ \left( \ \frac{\delta _{1}(t_{(1i)};\lambda , \xi )}{ 1- e^{\lambda \left( \ 1-e^{t_{(1i)}^{\xi }} \right) \ }} -\frac{\delta _{1}(t_{(m_{1}+1-1i)};\lambda , \xi )}{ e^{\lambda \left( 1-e^{t_{(m_{1}+1-1i)}^{\xi }} \right) \ }} \right) \ \\ {}{} & {} \, - \sum _{i=1}^{m_{2}} \frac{(2 \ i-1)}{m_{2}} \ \left( \ \frac{\delta _{2}(t_{(2i)};\lambda , \xi , \varphi )}{ 1- e^{\lambda \ \varphi \left( 1-e^{t_{(2i)}^{\xi }} \right) \ }} -\frac{\delta _{2}(t_{(m_{2}+1-2i)};\lambda , \xi , \varphi )}{ e^{\lambda \ \varphi \left( 1-e^{t_{(m_{2}+1-2i)}^{\xi }} \right) \ }} \right) \ =0, \\ \frac{\partial A}{\partial \xi }= & {} - \sum _{i=1}^{m_{1}} \frac{(2 \ i-1)}{m_{1}} \ \left( \ \frac{\delta _{3}(t_{(1i)};\lambda , \xi )}{ 1- e^{\lambda \left( \ 1-e^{t_{(1i)}^{\xi }} \right) \ }} -\frac{\delta _{3}(t_{(m_{1}+1-1i)};\lambda , \xi )}{ e^{\lambda \left( 1-e^{t_{(m_{1}+1-1i)}^{\xi }} \right) \ }} \right) \ \\ {}{} & {} \, - \sum _{i=1}^{m_{2}} \frac{(2 \ i-1)}{m_{2}} \ \left( \ \frac{\delta _{4}(t_{(2i)};\lambda , \xi , \varphi )}{ 1- e^{\lambda \ \varphi \left( 1-e^{t_{(2i)}^{\xi }} \right) \ }} -\frac{\delta _{4}(t_{(m_{2}+1-2i)};\lambda , \xi , \varphi )}{ e^{\lambda \ \varphi \left( 1-e^{t_{(m_{2}+1-2i)}^{\xi }} \right) \ }} \right) \ =0, \end{aligned}$$

and

$$\begin{aligned} \frac{\partial A}{\partial \varphi }=- \sum _{i=1}^{m_{2}} \frac{(2 \ i-1)}{m_{2}} \ \left( \ \frac{\delta _{5}(t_{(2i)};\lambda , \xi , \varphi )}{ 1- e^{\lambda \ \varphi \left( 1-e^{t_{(2i)}^{\xi }} \right) \ }} -\frac{\delta _{5}(t_{(m_{2}+1-2i)};\lambda , \xi , \varphi )}{ e^{\lambda \ \varphi \left( 1-e^{t_{(m_{2}+1-2i)}^{\xi }} \right) \ }} \right) \ =0, \end{aligned}$$

where $\delta _{1}(t_{(1i)};\lambda , \xi )$, $\delta _{2}(t_{(2i)};\lambda , \xi , \varphi )$, $\delta _{3}(t_{(1i)};\lambda , \xi )$, $\delta _{4}(t_{(2i)};\lambda , \xi , \varphi )$ and $\delta _{5}(t_{(2i)};\lambda , \xi , \varphi )$ are given by (15), (16), (17), (18) and (19), respectively.

The RTADE of Chen distribution using CPALT can be given by minimizing the following function

$$\begin{aligned} R= \frac{(m_{1}+m_{2})}{2}-2 \ \sum _{j=1}^2 \ \sum _{i=1}^{m_{j}} \ F_{j}(t_{(ji)};\lambda , \xi , \varphi ) - \sum _{j=1}^2 \ \sum _{i=1}^{m_{j}} \ \frac{(2 \ i-1)}{m_{j}} \left( \ \log { \left( 1-F_{j}(t_{(m_{j}+1-ji)};\lambda , \xi , \varphi ) \right) \ } \right) ,\ \end{aligned}$$

w.r.t. the unknown parameters $\lambda$, $\xi$, and the accelerated factor $\varphi$ or by solving the following non-linear equations:

$$\begin{aligned} \frac{\partial A}{\partial \lambda }= & {} -2 \sum _{i=1}^{m_{1}} \ \left( \delta _{1}(t_{(1i)};\lambda , \xi ) - \frac{(2 \ i-1)}{m_{1}} \ \frac{\delta _{1}(t_{(m_{1}+1-1i)};\lambda , \xi )}{ e^{\lambda \left( \ 1-e^{t_{(m_{1}+1-1i)}^{\xi }} \right) \ }} \right) \ \\ {}{} & {} \, - 2 \sum _{i=1}^{m_{2}} \ \left( \delta _{2}(t_{(2i)};\lambda , \xi , \varphi ) - \frac{(2 \ i-1)}{m_{2}} \ \frac{\delta _{2}(t_{(m_{2}+1-2i)};\lambda , \xi , \varphi )}{ e^{\lambda \ \varphi \left( 1-e^{t_{(m_{2}+1-2i)}^{\xi }} \right) \ }} \right) \ =0, \\ \frac{\partial A}{\partial \xi }= & {} -2 \sum _{i=1}^{m_{1}} \ \left( \delta _{3}(t_{(1i)};\lambda , \xi , ) - \frac{(2 \ i-1)}{m_{1}} \ \frac{\delta _{3}(t_{(m_{1}+1-1i)};\lambda , \xi )}{ e^{\lambda \left( 1-e^{t_{(m_{1}+1-1i)}^{\xi }} \right) \ }} \right) \ \\ {}{} & {} \, - 2 \sum _{i=1}^{m_{2}} \ \left( \ \delta _{4}(t_{(2i)};\lambda , \xi , \varphi ) - \frac{(2 \ i-1)}{m_{2}} \ \frac{\delta _{4}(t_{(m_{2}+1-2i)};\lambda , \xi , \varphi )}{ e^{\lambda \ \varphi \left( 1-e^{t_{(m_{2}+1-2i)}^{\xi }} \right) \ }} \right) \ =0, \end{aligned}$$

and

$$\begin{aligned} \frac{\partial A}{\partial \varphi }=- 2 \sum _{i=1}^{m_{2}} \ \left( \delta _{5}(t_{(2i)};\lambda , \xi , \varphi ) - \frac{(2 \ i-1)}{m_{2}} \ \frac{\delta _{5}(t_{(m_{2}+1-2i)};\lambda , \xi , \varphi )}{ e^{\lambda \ \varphi \left( 1-e^{t_{(m_{2}+1-2i)}^{\xi }} \right) \ }} \right) \ =0, \end{aligned}$$

where $\delta _{1}(t_{(1i)};\lambda , \xi )$, $\delta _{2}(t_{(2i)};\lambda , \xi , \varphi )$, $\delta _{3}(t_{(1i)};\lambda , \xi )$, $\delta _{4}(t_{(2i)};\lambda , \xi , \varphi )$ and $\delta _{5}(t_{(2i)};\lambda , \xi , \varphi )$ are given by (15), (16), (17), (18) and (19), respectively.

Percentile estimation

Kao³² was the one who first proposed the PE, which has been used to estimate the unknown parameters of Weibull distribution. In order to apply this technique in this subsection to obtain the PE of Chen distribution using CPALT, the following equation needs to be minimized

$$\begin{aligned} P=\sum _{j=1}^2 \ \sum _{i=1}^{m_{j}} \left( \ t_{(ji)}-t_{P_{ji}} \right) ^2 \ \end{aligned}$$

where

$$\begin{aligned} t_{P_{1i}}= \Bigg ( \log { \Bigg ( 1- \frac{ \log { \Bigg ( 1-P_{1i}} \Bigg ) }{ \lambda }} \Bigg ) \Bigg )^{\frac{1}{\xi }} \quad t_{P_{2i}}= \Bigg (\log { \Bigg (1- \frac{ \log { \Bigg ( 1-P_{2i}} \Bigg ) }{ \lambda \varphi }} \Bigg ) \Bigg )^{\frac{1}{\xi }}, \quad P_{ji}= \frac{i}{m_{j}+1}. \end{aligned}$$

w.r.t. the unknown parameters $\lambda$, $\xi$, and the accelerated factor $\varphi$ or by solving the following non-linear equations:

$$\begin{aligned} \frac{\partial P}{\partial \lambda }= & {} -2 \sum _{i=1}^{m_{1}} \frac{ \Big (t_{(1i)}-t_{P_{1i}} \Big )\ \log {(1-P_{1i})} \ \Bigg (\log { \Bigg ( 1- \frac{ \log { \Big (\ 1-P_{1i}} \Big )\ }{ \lambda }} \Bigg )\ \Bigg )^{\frac{1}{\xi }-1} \ }{ \lambda ^2 \ \xi \left( 1-\frac{\log \left( 1-P_{1i}\right) }{\lambda }\right) } \\ {}{} & {} \,- 2 \sum _{i=1}^{m_{2}} \frac{ \Big (\ t_{(2i)}-t_{P_{2i}} \Big )\ \log {(1-P_{2i})} \ \Bigg ( \log { \Bigg (\ 1- \frac{ \log { \Big (1-P_{2i}} \Big )\ }{ \lambda \ \varphi }} \Bigg )\ \Bigg )^{\frac{1}{\xi }-1} \ }{ \lambda ^2 \ \xi \ \varphi \left( 1-\frac{\log \left( 1-P_{2i}\right) }{\lambda \ \varphi }\right) }=0, \\ \frac{\partial P}{\partial \xi }= & {} -2 \sum _{i=1}^{m_{1}} \frac{ \Big (t_{(1i)}-t_{P_{1i}} \Big )\ \log { \Bigg (\log { \Bigg (\ 1- \frac{ \log { \Big (1-P_{1i}} \Big )\ }{ \lambda }} \Bigg )\ \Bigg )\ } \ \Bigg (\log { \Bigg (1- \frac{ \log { \Big (1-P_{1i}} \Big )\ }{ \lambda }} \Bigg )\ \Bigg )^{\frac{1}{\xi }} \ }{ \xi ^2 } \\ {}{} & {} \, - 2 \sum _{i=1}^{m_{2}} \frac{ \Big (\ t_{(2i)}-t_{P_{2i}} \Big )\ \log {\Bigg (\log { \Bigg (1- \frac{ \log { \Big (1-P_{2i}} \Big )\ }{ \lambda \ \varphi }} \Bigg )\ \Bigg )\ } \ \Bigg (\log { \Bigg (1- \frac{ \log { \Big (1-P_{2i}} \Big )\ }{ \lambda \ \varphi }} \Bigg )\ \Bigg )^{\frac{1}{\xi }} \ }{ \xi ^2}=0, \end{aligned}$$

and

$$\begin{aligned} \frac{\partial P}{\partial \varphi }=- 2 \sum _{i=1}^{m_{2}} \frac{ \Big (t_{(2i)}-t_{P_{2i}} \Big )\ \log {(1-P_{2i})} \ \Bigg (\log { \Bigg (1- \frac{ \log { \Big (\ 1-P_{2i}} \Big )\ }{ \lambda \ \varphi }} \Bigg )\ \Bigg )^{\frac{1}{\xi }-1} \ }{ \lambda \ \xi \ \varphi ^2 \left( 1-\frac{\log \left( 1-P_{2i}\right) }{\lambda \ \varphi }\right) }=0, \end{aligned}$$

Maximum product of spacing estimation

The method of MPSE developed by^33,34 is applied in this subsection to estimate the Chen distribution using CPALT under complete data. To obtain the MPSE of Chen distribution under CPALT, the following function

$$\begin{aligned} M=\sum _{j=1}^2 \ \sum _{i=1}^{m_{j}+1} \frac{ \log {D_{ji}}}{m_{j}+1}, \end{aligned}$$

(20)

needs to maximize w.r.t. the unknown parameters $\lambda$, $\xi$, and the accelerated factor $\varphi$, where $D_{ji}$ is the uniform spacings of a random sample from the Chen distribution under CPALT and defined by

$$\begin{aligned} D_{ji}=F_{j}(t_{(ji)};\lambda , \xi , \varphi )-F_{j}(t_{(ji-1)};\lambda , \xi , \varphi ), \quad F_{j}(t_{(j0)};\lambda , \xi , \varphi )=0, \quad F_{j}(t_{(jm_{j}+1)};\lambda , \xi , \varphi )=1. \end{aligned}$$

Upon using Eqs. (2) and (7) into Eq. (20), one can show that

$$\begin{aligned} M= & {} \frac{ 1}{m_{1}+1} \ \Biggr [\ \sum _{i=2}^{m_{1}} \log { \Bigg (e^{\lambda \Big (1-e^{t_{(1i-1)}^{\xi }} \Big )\ }- e^{\lambda \Big (1-e^{t_{(1i)}^{\xi }} \Big )\ } \Bigg )\ }\\{} & {} \, + \log \Bigg (1- e^{\lambda \Big (1-e^{t_{11}^{\xi }} \Big )\ } \Bigg )\ + \log { e^{\lambda \Big (1-e^{t_{1m_{1}}^{\xi }} \Big )\ }} \Biggr ]\\ {}{} & {} \, + \frac{ 1}{m_{2}+1} \ \Biggr [\ \sum _{i=2}^{m_{2}} \log { \Bigg (e^{\lambda \ \varphi \Big (\ 1-e^{t_{(2i-1)}^{\xi }} \Big )\ }- e^{\lambda \ \varphi \Big (\ 1-e^{t_{(2i)}^{\xi }} \Big )\ } \Bigg )\ }\\ {}{} & {} \, + \log \Bigg (\ 1- e^{\lambda \ \varphi \Big (1-e^{t_{21}^{\xi }} \Big )\ } \Bigg )\ + \log { e^{\lambda \ \varphi \Big (1-e^{t_{2m_{2}}^{\xi }} \Big )\ }} \Biggr ].\ \end{aligned}$$

So, the MPSE of Chen distribution using CPALT can be obtained also by solving the following non-linear equations $\frac{\partial M}{\partial \lambda }=0$, $\frac{\partial M}{\partial \xi }=0$, and $\frac{\partial M}{\partial \varphi }=0$.

Numerical computations

To illustrate the computation of methods presented in the previous section, two real life data sets are presented.

Data set 1: ordered times to failure

The data presented in³⁵ expressing the required failure times for ten steel samples under the influence of four stress levels are used in this subsection. Accordingly, only two levels of stress, 0.87 and 0.99 ($10^6$ psi), are used as the use condition and the accelerated condition after being modified to meet the problem being examined, see Table 1.

Table 1 The ordered times to failure under two stress levels.

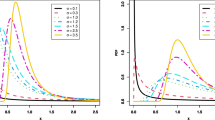
First, the MLE is used under complete data to check the validity of the Chen D to fit the data set for use and accelerated conditions. The Kolmogorov–Smirnov (K–S) distance and the corresponding p value are obtained for use and accelerated conditions. The results are summarized in Table 2. From Table 2, the Chen distribution provides a good fit to the data under use and accelerated conditions. Figure 1 also displays the empirical CDF and the fitted CDF of the Chen distribution using MLE in the use and accelerated conditions.

Table 2 The ML estimates of parameters, the K–S values and the associated p values under use and accelerated conditions.

Figure 1

(a) The fitted CDF of Chen distribution under use condition for ordered times to failure data. (b) The fitted CDF of Chen distribution under accelerated condition for ordered times to failure data.

The estimation methods, which are given in “Maximum likelihood estimation” to “Maximum product of spacing estimation”, are used to obtain the estimates of the unknown parameters and the accelerated factor under CPALT using the ordered times to failure data. The estimates based on real data sets under different methods of estimation are tabulated in Table 3.

Table 3 The different methods of estimations for $(\lambda ,\mu ,\theta ,\gamma )$ using real data.

Data set 2: oil breakdown times of insulating fluid

The data set from³⁶ that details the insulating fluid’s oil breakdown times under high test voltages are considered in this subsection after being modified to meet the problem being examined. Accordingly, only two levels of stress, 30 and 32 kV, are used as the use condition and the accelerated condition, see Table 4.

Table 4 Oil breakdown times of insulating fluid.

First, the MLE is used under complete data to check the validity of the Chen distribution to fit the data set for use and accelerated conditions. The Kolmogorov–Smirnov (K–S) distance and the corresponding p value are obtained for use and accelerated conditions. The results are summarized in Table 5. From Table 5, the Chen distribution provides a good fit to the data under use and accelerated conditions. The empirical CDF and the fitted CDF of the Chen distribution using MLE under use and accelerated conditions are also shown in Fig. 2.

Table 5 The ML estimates of parameters, the K–S values and the associated p values under use and accelerated temperatures.

Figure 2

(a) The fitted CDF of Chen distribution under use condition for oil breakdown times of insulating fluid. (b) The fitted CDF of Chen distribution under accelerated condition for oil breakdown times of insulating fluid data.

The estimation methods, which are given in “Maximum likelihood estimation” to “Maximum product of spacing estimation”, are used to obtain the estimates of the unknown parameters and the accelerated factor under CPALT using the oil breakdown times of insulating fluid data. The estimates based on real data sets under different methods of estimation are tabulated in Table 6.

Table 6 The different methods of estimations for $(\lambda ,\mu ,\theta ,\gamma )$ using real data.

Simulation study

The principal reason for this section is to compare the estimators of the parameters by utilizing MSE and AAB. For varying values of $m_{1}$ and $m_{2}$ (number of two samples for use and accelerated conditions), a large number $N=10{,}000$ of complete samples are generated from Chen distribution under use and accelerated conditions. Take the true values of $\lambda$, $\xi$, and $\varphi$ as $(\lambda ,\xi ,\varphi )=(1.5,1.5,2)$, $(\lambda ,\xi ,\varphi )=(1.5,2,1.5)$, $(\lambda ,\xi ,\varphi )=(1.5,2,2)$ $(\lambda ,\xi ,\varphi )=(2,4,3)$, $(\lambda ,\xi ,\varphi )=(2,3,4)$, and $(\lambda ,\xi ,\varphi )=(2,3,3)$. To carry out the numerical study, the following steps are required:

• 1 Generate two independent random samples of sizes $m_{1}$ and $m_{2}$ from Uniform (0,1) distribution using RandomReal[] in mathematica $(U_{j1}, U_{j2}, \ldots , U_{jm_{j}}), j=1,2$. With different choice of $m_{1}$, $m_{2}$, and different values of the parameters and accelerated factor, the two complete samples are generated from the inverse CDFs $F_{1}(t)$ and $F_{2}(t)$ for use and accelerated conditions respectively as follow: $t_{1i}=\Bigg (\ \log { \Bigg (\ 1- \frac{ \log { \Big (\ 1-U_{1i}} \Big )\ }{ \lambda }} \Bigg )\ \Bigg )^{\frac{1}{\xi }}$ and $t_{2i}= \Bigg (\ \log { \Bigg (\ 1- \frac{ \log { \Big (\ 1-U_{2i}} \Big )\ }{ \lambda \ \varphi }} \Bigg )\ \Bigg )^{\frac{1}{\xi }}$, where $i=1,2,3,\ldots ,m_{j}$

• 2 Across using the results obtained in “Maximum likelihood estimation” to “Maximum product of spacing estimation”, the different estimates of the unknown parameters and accelerated factor are calculated. using the package FindRoot[] in Mathematica or using the Newton–Raphson algorithm.

• 3 Repeat Steps $1-2$, $N=10{,}000$ times.

• 4 Calculate the AEs, MSEs and AABs of the unknown parameters and accelerated factor from $AE=\frac{1}{N} \ \sum _{l=1}^{N}({\hat{\Theta }})$, $MSE=\frac{1}{N} \ \sum _{l=1}^{N}({\hat{\Theta }}-\Theta )^2$, and $AAB=\frac{1}{N} \ \sum _{l=1}^{N}|{\hat{\Theta }}-\Theta |$. where, ${\hat{\Theta }}$ is the parameter estimation for $\Theta$.

The results obtained from the numerical comparison study between different methods based on MSEs and AABs for all estimates are presented in Tables 7, 8, 9, 10, 11 and 12. These tables amply demonstrate that:

• It is clear from Tables 7, 8, 9, 10, 11 and 12 that with an increase in $m_{1}$, $m_{2}$, the MSEs and AABs decrease for all estimates as expected.

• It is clear also that MLE improves for the better in terms of small values of MSE and AAB and becomes one of the best estimates for large sample in relation to the parameter $\lambda$.

• We also find that the MPSE outperforms alternative techniques in most cases for parameter $\lambda$.

• For the parameter $\xi$, we find that MLE is the best estimate based on the lowest values of MSE and AAB.

• As for the parameter $\varphi$, we find that MPSE is the best estimate, followed by MLE according to MSE and AAB.

• Taking MSE and AAB into consideration, the MPSE technique outperforms alternative techniques in most cases.

• In view of the results of the simulation study, we recommend the use of MPSE, MLE, PE and ADE to estimate CPALT under the complete data when taking MSE and AAB into consideration.

Table 7 The average estimators, the mean square error, and the absolute average bias of different methods of estimations (1.5,1.5,2).

Table 8 The average estimators, the mean square error, and the absolute average bias of different methods of estimations (1.5,2,1.5).

Table 9 The average estimators, the mean square error, and the absolute average bias of different methods of estimations (1.5,2,2).

Table 10 The average estimators, the mean square error, and the absolute average bias of different methods of estimations (2,4,3).

Table 11 The average estimators, the mean square error, and the absolute average bias of different methods of estimations (2,3,4).

Table 12 The average estimators, the mean square error, and the absolute average bias of different methods of estimations (2,3,3).

Conclusion

In this paper, the problem of various techniques of estimations under complete sample in CPALT has been studied. Eight methodologies of classical estimation, namely, MLEs, LSEs, WLSEs, CVMEs, ADEs, RTADEs, PEs, and MPSEs, have been considered to estimate the unknown parameters and the accelerated factor of Chen distribution under CPALT. The proposed methodologies were demonstrated using two real data sets, demonstrating their applicability as they can be applied to address several engineering-related problems. Additionally, in order to compare these methodologies with various sample sizes and various sets of the unknown parameters, and the accelerated factor, a comprehensive simulation analysis has been carried out. The AEs, MSEs, and AAB under complete data using CPALT have been calculated. According to the MSEs and AABs values computed from the simulation study, the MPSE is the most effective methodology among the alternatives in most cases for all parameters. Based on the results of the simulation study, it can be demonstrated that the MPSE, MLE, PE, and ADE methods can be recommended for estimating the parameters and accelerated factor for the CPALT of Chen distribution when complete data is available.

With the help of the suggested methodology and the results of this investigation, some future studies can be presented, such as:

• Other distributions with different shapes for HRF can be analyzed.

• Additionally, other real data with various phenomena, engineering problems, and clinical treatments can be applied.

• Actually, 6 value sets of the parameters and accelerated factor have been used in the simulation study. Therefore, a number of additional value sets can be used to extend the simulation study and examine their influence on the MSEs and AABs values.