Introduction

Nonlinear partial differential equation (NLPDE)1,2,3,4,5,6,7,8,9,10,11,12,13 plays a very important role in the fields of natural science and engineering technology. In the study of NLPDEs, the construction of soliton solutions and the study of dynamic behavior are currently hot topics. Many experts and scholars are committed to this research, and many very important methods have been proposed. For example, the extended the \((\frac{G'}{G})\)-expansion method14,15, the Hirota bilinear method16, the extended Kudryashov’s method17, the Sine-Gordon expansion method18, the Khater II method19.

With the maturity of fractional calculus theory, fractional partial differential equations(FPDEs)20,21,22,23,24 can better describe mathematical models with memory and genetic properties in the field of natural sciences. The research on FPDEs mainly focuses on numerical solution25, soliton solution26 and qualitative analysis27. This type of FPDE is a (2+1)-dimensional Heisenberg ferro-magnetic spin chains model with beta fractional derivative, which usually is described as follows28

$$\begin{aligned} i_{0}^{A}D_{t}^{\beta }F+\Omega _{1}F_{xx}+\Omega _{2}F_{yy}+\Omega _{3}F_{xy}-\Omega _{4}|F|^{2}F=0, \end{aligned}$$
(1)

where \(F=F(x,y,t)\) is an unknown function. \(\Omega _{1}\), \(\Omega _{2}\) and \(\Omega _{3}\) are real numbers. \(_{0}^{A}D_{t}^{\beta }(\cdot )\) is the M-fractional derivative. Equation (1) is commonly applied in fluid mechanics, nonlinear optical system and biological molecular system. In Ref.28, Khatun and his collaborators studied the solion solutions of Eq. (1) by using the extended simple method. However, research on the dynamic behavior of such equations has not yet been reported. Moreover, more general Jacobian function solutions are still under study.

The remaining sections of research are as follows. In “Soliton solutions of Eq. (1)” section, Eq. (1) is transformed into the ordinary differential equation. Moreover, the soliton solutions of Eq. (1) are presented by using the second-order complete discriminant system. In “Dynamical analysis” section, the dynamical analysis of dynamical system and its disturbance systems are studied. In “Conclusion” section, a brief conclusion is given.

Soliton solutions of Eq. (1)

Mathematical derivation

In this section, we consider the complex envelope wave structure (see Refs.28,29)

$$\begin{aligned} F(x,y,t)=\psi (\xi )e^{i\chi }, \xi =k_{1}x+l_{1}y+\frac{v}{\beta }\left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta }, \chi =k_{2}x+l_{2}y-\frac{w}{\beta }\left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta }. \end{aligned}$$
(2)

Plugging wave transformation (2) into Eq. (1) and splitting the imaginary and real parts yield

$$ \left\{ {\begin{array}{l} {(w - \Omega _{1} k_{2}^{2} - \Omega _{2} l_{2}^{2} - \Omega _{3} k_{2} l_{2} )\psi + (\Omega _{1} k_{1}^{2} + \Omega _{2} l_{1}^{2} + \Omega _{3} k_{1} l_{1} )\psi ^{{\prime \prime }} - \Omega _{4} \psi ^{3} = 0,} \hfill \\ {[2\Omega _{1} k_{1} k_{2} + 2\Omega _{2} l_{1} l_{2} + \Omega _{3} (k_{1} l_{2} + k_{2} l_{1} ) + v]\psi ^{\prime} = 0} \hfill \\ \end{array} } \right. $$
(3)

From the second equation of Eq. (3), we have

$$\mathcalligra{v}=-2\Omega _{1}k_{1}k_{2}-2\Omega _{2}l_{1}l_{2}-\Omega _{3}(k_{1}l_{2}+k_{2}l_{1}).$$

From the first equation of Eq. (3), we obtain

$$\begin{aligned} \psi ^{\prime \prime }=4a_{4}\psi ^{3}+2a_{2}\psi , \end{aligned}$$
(4)

where \(a_{4}=\frac{\Omega _{4}}{4(\Omega _{1}k_{1}^{2}+\Omega _{2}l_{1}^{2}+\Omega _{3}k_{1}l_{1})}\), \(a_{2}=-\frac{w-\Omega _{1}k_{2}^{2}-\Omega _{2}l_{2}^{2}-\Omega _{3}k_{2}l_{2}}{2(\Omega _{1}k_{1}^{2}+\Omega _{2}l_{1}^{2}+\Omega _{3}k_{1}l_{1})}\).

Soliton solutions of Eq. (1)

Multiplying two sides of Eq. (4) by \(\psi '\), we obtain

$$\begin{aligned} (\psi ^{\prime })^{2}=a_{4}\psi ^{4}+a_{2}\psi ^{2}+a_{0}, \end{aligned}$$
(5)

where \(a_{0}\) is an integral constant.

Next, we make some assumptions

$$\begin{aligned} \psi =\pm \sqrt{(4a_{4})^{-\frac{1}{3}}\Psi },\ \ b_{1}=4a_{2}(4a_{4})^{-\frac{2}{3}},\ \ b_{0}=4a_{0}(4a_{4})^{-\frac{1}{3}},\ \ \xi _{1}=(4a_{4})^{-\frac{1}{3}}\xi . \end{aligned}$$
(6)

Substituting Eq. (6) into Eq. (5), we have

$$\begin{aligned} \Psi _{\xi _{1}}^{2}=\Psi (\Psi ^{2}+b_{1}\Psi +b_{0}), \end{aligned}$$
(7)

and its integral expression is

$$\begin{aligned} \pm (\xi _{1}-\xi _{0})=\int \frac{d\Psi }{\sqrt{\Psi (\Psi ^{2}+b_{1}\Psi +b_{0})}}, \end{aligned}$$
(8)

here, the complete discriminant system30 for Eq. (8) is

$$\begin{aligned} F(\Psi )=\Psi ^{2}+b_{1}\Psi +b_{0}. \end{aligned}$$
(9)

Next, we assume that \(\Delta =b_{1}^{2}-4b_{0}\).

Case I \(\Delta =0\), \(\Psi >0\)

If \(b_{1}<0\), we obtain the solution of Eq. (1)

$$\begin{aligned} \begin{aligned} F_{1}(x,y,t)&=\frac{2(w-\Omega _{1}k_{2}^{2}-\Omega _{2}l_{2}^{2}-\Omega _{3}k_{2}l_{2})(2\Omega _{4})^{-\frac{2}{3}}}{(\Omega _{1}k_{1}^{2}+\Omega _{2}l_{1}^{2}+\Omega _{3}k_{1}l_{1})^{-\frac{1}{3}}}\tanh ^{2}\left( \sqrt{\frac{(w-\Omega _{1}k_{2}^{2}-\Omega _{2}l_{2}^{2}-\Omega _{3}k_{2}l_{2})(2\Omega _{4})^{-\frac{2}{3}}}{2(\Omega _{1}k_{1}^{2}+\Omega _{2}l_{1}^{2}+\Omega _{3}k_{1}l_{1})^{-\frac{1}{3}}}}\right. \\&\left. \left( \bigg (\frac{2\Omega _{4}}{(\Omega _{1}k_{1}^{2}+\Omega _{2}l_{1}^{2}+\Omega _{3}k_{1}l_{1})}\right) ^{-\frac{1}{3}}\bigg (k_{1}x+l_{1}y+\frac{v}{\beta }\left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta }\bigg )-\xi _{0})e^{i\big (k_{2}x+l_{2}y-\frac{w}{\beta }\left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta }\big )}\right. , \end{aligned} \end{aligned}$$
(10)
$$\begin{aligned} \begin{aligned} F_{2}(x,y,t)&=\frac{2(w-\Omega _{1}k_{2}^{2}-\Omega _{2}l_{2}^{2}-\Omega _{3}k_{2}l_{2})(2\Omega _{4})^{-\frac{2}{3}}}{(\Omega _{1}k_{1}^{2} +\Omega _{2}l_{1}^{2}+\Omega _{3}k_{1}l_{1})^{-\frac{1}{3}}}\coth ^{2}\left( \sqrt{\frac{(w-\Omega _{1}k_{2}^{2}-\Omega _{2}l_{2}^{2} -\Omega _{3}k_{2}l_{2})(2\Omega _{4})^{-\frac{2}{3}}}{2(\Omega _{1}k_{1}^{2}+\Omega _{2}l_{1}^{2}+\Omega _{3}k_{1}l_{1})^{-\frac{1}{3}}}}\right. \\&\left. \left( \frac{2\Omega _{4}}{(\Omega _{1}k_{1}^{2}+\Omega _{2}l_{1}^{2}+\Omega _{3}k_{1}l_{1})}\right) ^{-\frac{1}{3}}\left( k_{1}x+l_{1}y+\frac{v}{\beta }\left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta }\right) -\xi _{0})e^{i\left( k_{2}x+l_{2}y-\frac{w}{\beta }(t+\frac{1}{\Gamma (\beta )})^{\beta }\right) }\right. . \end{aligned} \end{aligned}$$
(11)

If \(b_{1}>0\), we have the solution of Eq. (1)

$$\begin{aligned} \begin{aligned} F_{3}(x,y,t)&=\frac{2(\Omega _{1}k_{2}^{2}+\Omega _{2}l_{2}^{2}+\Omega _{3}k_{2}l_{2}-w)(2\Omega _{4})^{-\frac{2}{3}}}{(\Omega _{1}k_{1}^{2} +\Omega _{2}l_{1}^{2}+\Omega _{3}k_{1}l_{1})^{-\frac{1}{3}}}\tan ^{2}\left( \sqrt{\frac{(\Omega _{1}k_{2}^{2}+\Omega _{2}l_{2}^{2} +\Omega _{3}k_{2}l_{2}-w)(2\Omega _{4})^{-\frac{2}{3}}}{2(\Omega _{1}k_{1}^{2}+\Omega _{2}l_{1}^{2}+\Omega _{3}k_{1}l_{1})^{-\frac{1}{3}}}}\right. \\&\left. \left( \frac{2\Omega _{4}}{(\Omega _{1}k_{1}^{2}+\Omega _{2}l_{1}^{2}+\Omega _{3}k_{1}l_{1})}\right) ^{-\frac{1}{3}}\left( k_{1}x+l_{1}y+\frac{v}{\beta }\left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta }\right) -\xi _{0})e^{i\left( k_{2}x+l_{2}y-\frac{w}{\beta }\left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta }\right) }\right. \end{aligned} \end{aligned}$$
(12)

If \(b_{1}=0\), we obtain the solution of Eq. (1)

$$\begin{aligned} F_{4}(x,y,t)=\frac{4}{((\frac{2\Omega _{4}}{(\Omega _{1}k_{1}^{2}+\Omega _{2}l_{1}^{2} +\Omega _{3}k_{1}l_{1})})^{-\frac{1}{3}}(k_{1}x+l_{1}y+\frac{v}{\beta }(t+\frac{1}{\Gamma (\beta )})^{\beta })-\xi _{0})^{2}}e^{i\big (k_{2}x+l_{2}y-\frac{w}{\beta }(t+\frac{1}{\Gamma (\beta )})^{\beta }\big )}. \end{aligned}$$
(13)

Case II \(\Delta >0\), \(b_{0}=0\)

If \(\Psi >-b_{1}\), \(b_{1}>0\), we obtain the solution of Eq. (1)

$$\begin{aligned} \begin{aligned} F_{5}(x,y,t)&=\bigg (\frac{2(-w+\Omega _{1}k_{2}^{2}+\Omega _{2}l_{2}^{2}+\Omega _{3}k_{2}l_{2})(2\Omega _{4})^{-\frac{2}{3}}}{(\Omega _{1}k_{1}^{2} +\Omega _{2}l_{1}^{2}+\Omega _{3}k_{1}l_{1})^{-\frac{1}{3}}}\tanh ^{2}\left( \sqrt{\frac{(-w+\Omega _{1}k_{2}^{2}+\Omega _{2}l_{2}^{2}+\Omega _{3}k_{2}l_{2})(2\Omega _{4})^{-\frac{2}{3}}}{2(\Omega _{1}k_{1}^{2}+\Omega _{2}l_{1}^{2}+\Omega _{3}k_{1}l_{1})^{-\frac{1}{3}}}}\right. \\&\left. \left( \frac{2\Omega _{4}}{(\Omega _{1}k_{1}^{2}+\Omega _{2}l_{1}^{2}+\Omega _{3}k_{1}l_{1})}\right) ^{-\frac{1}{3}}\left( k_{1}x+l_{1}y+\frac{v}{\beta }\left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta }\right) -\xi _{0})-b_{1})e^{i\left( k_{2}x+l_{2}y-\frac{w}{\beta }\left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta }\right) },\right. \\ \end{aligned} \end{aligned}$$
(14)
$$\begin{aligned} \begin{aligned} F_{6}(x,y,t)&=\bigg (\frac{2(-w+\Omega _{1}k_{2}^{2}+\Omega _{2}l_{2}^{2}+\Omega _{3}k_{2}l_{2})(2\Omega _{4})^{-\frac{2}{3}}}{(\Omega _{1}k_{1}^{2} +\Omega _{2}l_{1}^{2}+\Omega _{3}k_{1}l_{1})^{-\frac{1}{3}}}\coth ^{2}\left( \sqrt{\frac{(-w+\Omega _{1}k_{2}^{2}+\Omega _{2}l_{2}^{2}+\Omega _{3}k_{2}l_{2})(2\Omega _{4})^{-\frac{2}{3}}}{2(\Omega _{1}k_{1}^{2}+\Omega _{2}l_{1}^{2}+\Omega _{3}k_{1}l_{1})^{-\frac{1}{3}}}}\right. \\&\left. \left( \frac{2\Omega _{4}}{(\Omega _{1}k_{1}^{2}+\Omega _{2}l_{1}^{2}+\Omega _{3}k_{1}l_{1})}\right) ^{-\frac{1}{3}}\left( k_{1}x+l_{1}y+\frac{v}{\beta }\left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta }\right) -\xi _{0})-b_{1})e^{i\left( k_{2}x+l_{2}y-\frac{w}{\beta }\left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta }\right) }\right. . \end{aligned} \end{aligned}$$
(15)

If \(b_{1}<0\), we obtain the solution of Eq. (1)

$$\begin{aligned} \begin{aligned} F_{7}(x,y,t)&=\frac{2(w-\Omega _{1}k_{2}^{2}-\Omega _{2}l_{2}^{2}-\Omega _{3}k_{2}l_{2})(2\Omega _{4})^{-\frac{2}{3}}}{(\Omega _{1}k_{1}^{2}+\Omega _{2}l_{1}^{2} +\Omega _{3}k_{1}l_{1})^{-\frac{1}{3}}}\tan ^{2}\left( \sqrt{\frac{(w-\Omega _{1}k_{2}^{2}-\Omega _{2}l_{2}^{2}-\Omega _{3}k_{2}l_{2})(2\Omega _{4})^{-\frac{2}{3}}}{2(\Omega _{1}k_{1}^{2} +\Omega _{2}l_{1}^{2}+\Omega _{3}k_{1}l_{1})^{-\frac{1}{3}}}}\right. \\&\left. \left( \frac{2\Omega _{4}}{(\Omega _{1}k_{1}^{2}+\Omega _{2}l_{1}^{2}+\Omega _{3}k_{1}l_{1})}\right) ^{-\frac{1}{3}}\left( k_{1}x+l_{1}y+\frac{v}{\beta }\left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta }\right) -\xi _{0})-b_{1}) e^{i\left( k_{2}x+l_{2}y-\frac{w}{\beta }\left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta }\right) }\right. \end{aligned} \end{aligned}$$
(16)

Case III \(\Delta >0\), \(b_{0}\ne 0\)

If \(\alpha<\beta <k\) and \(\alpha<\Psi <\beta \), we obtain the solution of Eq. (1)

$$\begin{aligned} \begin{aligned} F_{8}(x,y,t)&=\left[ \alpha +(\beta -\alpha )\textbf{sn}^{2}\left( \frac{\sqrt{k-\alpha }}{2}((\frac{2\Omega _{4}}{(\Omega _{1}k_{1}^{2} +\Omega _{2}l_{1}^{2}+\Omega _{3}k_{1}l_{1})}\right) ^{-\frac{1}{3}}\left( k_{1}x+l_{1}y+\frac{v}{\beta }\left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta }\right) -\xi _{0}),m)\right] \\&e^{i(k_{2}x+l_{2}y-\frac{w}{\beta }(t+\frac{1}{\Gamma (\beta )})^{\beta })}. \end{aligned} \end{aligned}$$
(17)

If \(\Psi >k\), we obtain the solution of Eq. (1)

$$\begin{aligned} \begin{aligned} F_{9}(x,y,t)&=\frac{-\beta \textbf{sn}^{2}\left( \sqrt{k-\alpha }((\frac{2\Omega _{4}}{(\Omega _{1}k_{1}^{2}+\Omega _{2}l_{1}^{2}+\Omega _{3}k_{1}l_{1})}\right) ^{-\frac{1}{3}}\left( k_{1}x+l_{1}y+\frac{v}{\beta }\left( t +\frac{1}{\Gamma (\beta )}\right) ^{\beta }\right) -\xi _{0})/2,m)+k}{\textbf{cn}^{2}\left( \sqrt{k-\alpha }((\frac{2\Omega _{4}}{(\Omega _{1}k_{1}^{2} +\Omega _{2}l_{1}^{2}+\Omega _{3}k_{1}l_{1})}\right) ^{-\frac{1}{3}}\left( k_{1}x+l_{1}y+\frac{v}{\beta }\left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta }\right) -\xi _{0})/2,m)}\\&e^{i\left( k_{2}x+l_{2}y-\frac{w}{\beta }\left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta }\right) }, \end{aligned} \end{aligned}$$
(18)

where \(m^{2}=(\beta -\alpha )/(k-\alpha )\).

Case iv \(\Delta <0\)

If \(\Psi >0\), we obtain the solution of Eq. (1)

$$\begin{aligned} \begin{aligned} F_{10}(x,y,t)&=\left[ \frac{2\sqrt{b_{0}}}{1+\textbf{cn}(b_{0}^{1/4}((\frac{2\Omega _{4}}{(\Omega _{1}k_{1}^{2} +\Omega _{2}l_{1}^{2}+\Omega _{3}k_{1}l_{1})})^{-\frac{1}{3}}(k_{1}x+l_{1}y+\frac{v}{\beta }(t+\frac{1}{\Gamma (\beta )})^{\beta })-\xi _{0}),m)}-\sqrt{b_{0}}\right] \\&\quad \times e^{i(k_{2}x+l_{2}y-\frac{w}{\beta }(t+\frac{1}{\Gamma (\beta )})^{\beta })}, \end{aligned} \end{aligned}$$
(19)

where \(m^{2}=\frac{1-b_{1}/2\sqrt{b_{0}}}{2}\).

Numerical simulation

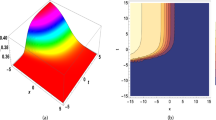
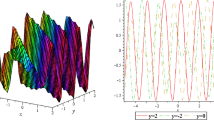
In this section, we use mathematical software of Maple 2022 to draw three-dimensional, two-dimensional, and contour plots of the modulus of solutions \(F_{1}(t,x,y)\) and \(F_{5}(t,x,y)\) of Eq. (1) when we choose different parameters. From Figs. 1 and 2, it can be seen that the mode length diagrams of these solutions are all dark soliton solutions.

Figure 1
figure 1

The solution \(F_{1}(t,x,y)\) of (1) with \(k_{1}=1,k_{2}=1,l_{1}=1,l_{2}=1,\Omega _{1}=1,\Omega _{2}=1,\Omega _{3}=-1,\Omega _{4}=1,w=\frac{7}{2},v=-2\).

Full size image
Figure 2
figure 2

The solution \(F_{5}(t,x,y)\) of (1) with \(k_{1}=1,k_{2}=1,l_{1}=1,l_{2}=1,\Omega _{1}=1,\Omega _{2}=1,\Omega _{3}=-1,\Omega _{4}=\frac{1}{2},w=\frac{1}{2},v=-3\).

Full size image

Dynamical analysis

In this section, the two-dimensional dynamic system (4)31,32 can be described as

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{d\psi }{d\xi }=z,\\ \frac{dz}{d\xi }=4a_{4}\psi ^{3}+2a_{2}\psi , \end{array}\right. } \end{aligned}$$
(20)

its first integral is

$$\begin{aligned} H(\psi ,z)=\frac{1}{2}z^{2}-a_{4}\psi ^{4}-a_{2}\psi ^{2}=h, \end{aligned}$$
(21)

where h is the constant. In this section, we plotted the phase diagram of the system (20) under given parameter conditions as shown in Fig. 3.

Figure 3
figure 3

2D phase portraits of (20).

Full size image

Next, in system (20), we add a small disturbance

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{d\psi }{d\xi }=z,\\ \frac{dz}{d\xi }=4a_{4}\psi ^{3}+2a_{2}\psi +A\sin (\varpi \xi ). \end{array}\right. } \end{aligned}$$
(22)

By using mathematical software, we can draw the phase diagrams of (22) when considering different initial values and parameters as shown in Figs. 4 and 5.

Figure 4
figure 4

Phase portraits of (22) when \(a_{4}<0\), \(a_{2}<0\).

Full size image
Figure 5
figure 5

Phase portraits of (22) when \(a_{4}>0\), \(a_{2}<0\).

Full size image

Conclusion

In this article, we study the dynamical analysis and the soliton solutions of Eq. (1), respectively. On the one hand, we obtained the soliton solution of Eq. (1). On the other hand, the phase portrait of (20) and its disturbance system was drawn by using mathematical software and dynamic system analysis theory. What’s more, we use mathematical software to draw three-dimensional, two-dimensional, and contour plots of the modulus of solutions \(F_{1}(t,x,y)\) and \(F_{5}(t,x,y)\) of Eq. (1) when we choose different parameters. Compared with reference28, we not only obtained the dynamic behavior of Eq. (1), but also constructed a more general Jacobian function solution. In future research, we will still study soliton solutions and dynamics of FPDEs.