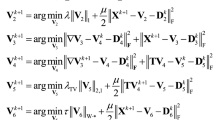Abstract
Based on double-compressed sampling, a hyperspectral spectral unmixing algorithm (SU_DCS) is proposed, which could directly complete the endmember extraction and abundance estimation. On the basis of the linear mixed model (LMM), we designed spatial and spectral sampling matrices, obtained spatial and spectral measurement data, and constructed a joint unmixing model containing endmember and abundance information. By using operator separation and Lagrangian multiplier algorithm, the endmember matrix, abundance matrix and remixing image can be quickly obtained by matrix operation. The parameters of the unmixing algorithm, including regularization parameter, convergence threshold and spatial sampling rate, are determined using synthetic simulated hyperspectral data. The proposed algorithm is applied to two kinds of real hyperspectral data, with or without ground truth, in order to verify the effectiveness and reliability of the algorithm. Firstly, we provide the performance of the algorithm on real datasets without ground truth. Compared with algorithm VCA_FCLS and algorithm CPPCA_VCA_FCLS, the endmember spectral curve extracted by the proposed SU_DCS is almost consistent with that obtained by VCA_FCLS, and is more smooth than that of obtained by CPPCA_VCA_FCLS. Additionally, the abundance estimation map estimated by the SU_DCS has consistency with the results obtained by VCA_FCLS. Moreover, the proposed SU_DCS has higher peak signal-to-noise ratio (PSNR) for remixing images with higher computational efficiency. Secondly, we provide the performance of the proposed algorithm on four real datasets with ground truth, including dataset Cuprite, dataset Samson, dataset Jasper and dataset Urban. We provide the results of endmember extraction and abundance estimation from the compressed data under different sampling rate conditions. The extracted endmember maintains good consistency with the true spectral curves, and the estimated abundance map can also maintain good spatial consistency with the ground truth. The comparison results with other four comparative algorithms also indicate that the proposed algorithm can obtain relatively accurate endmembers and abundance information from compressed data, the reliability and validity of the proposed algorithm have been proved. In summary, the main innovation of the proposed algorithm is that it can extract endmembers and estimate abundance with high accuracy from a small amount of measurement data.
Similar content being viewed by others
Hyperspectral images (HSIs) contain rich spatial geometric information and spectral feature information1, and are suitable for terrain reconnaissance2, target detection and recognition3,4,5, vegetation classification6,7 and other military and civilian fields. Research on imaging spectrometer8,9, image data analysis and processing10, and image interpretation11,12,13,14,15 have become hot research fields. The data obtained by the hyperspectral imager contains the spectral information of each pixel, and the corresponding spectral response characteristics of different ground substances are different. Due to the insufficient spatial resolution, Liu proposed a two-stream fusion network (TFNet)16 and Zhang proposed spatial-spectral reconstruction network (SSR-NET)17 to obtain the high resolution images, named as hyperspectral fusion. Then the high resolution fusion images can be used for classification and target detection. There are also other scholars to study the spectral mixing characteristics18,19, especially the linear mixture model (LMM), which is the basis of spectral unmixing. The endmember information and abundance information obtained can be used for target detection and classification research20,21,22,23.
Aimed at the endmember extraction of hyperspectral images, researchers have proposed many practical extraction methods from different perspectives, including SiMultaneous Endmember Extraction Algorithm (SM-EEA)24 and SeQuential Endmember Extraction Algorithm (SQ-EEA)24. The SM-EEA includes the pixel purity index (PPI) algorithm25, the NFINDR algorithm26, the Automated Morphological Endmember Extraction algorithm27, the Minimum Volume Simplex Analysis28. The advantage of these algorithms is that the endmembers are independent of each other. However, due to the simultaneous extraction of all endmembers, the computation is heavy.
The SQ-EEA includes Neville's Iterative Error Analysis (IEA)29, Nascimento's Vertex Component Analysis (VCA)30 and Chang's Simplex Growing Algorithm31. The well-designed SQ-EEA can achieve the same results as the SM-EEA, and the SQ-EEA can significantly reduce the computational complexity. In particular, VCA algorithm finds the orthogonal vector formed by the extracted terminal elements repeatedly, and has low computational complexity and fast extraction speed32.
Abundance estimation mainly includes the algorithms based on least squares and the algorithms based on convex geometry theory. The Fully Constrained Least Square (FCLS)33 considers the Abundance Sum to one Constraint (ASC) and the Abundance Non-Negativity Constraint (ANC). It regards the abundance estimation as the least square problem under the physical constraint of abundance, and obtains the abundance matrix through numerical iteration. It is the most widely used abundance estimation method. The methods based on convex geometry theory mainly include: OSP algorithm34, non-convex sparse and low-rank constraint with dictionary pruning35. The algorithms based on the theory of convex geometry do not have constraints, but they involve matrix operations, dimension reduction operations and high computational complexity.
The decomposition of mixed pixels can realize the unmixing, including the independent component analysis36, and sparse unmixing algorithms via variable splitting augmented Lagrangian37,38,39. The sparse unmixing by variable splitting and augmented Lagrangian (SUnSAL) algorithm40 applies the alternating direction method of multipliers (ADMM) to solve the constrained sparse recursion problem of abundance estimation, and obtains good estimation results. The simplex projection unmixing41 algorithm depends on the geometry of a single shape. The nonnegative matrix factorization42 transformed the unmxing problem to the matrix decomposition, which obtains wide application. Feng proposed a non-negative matrix decomposition-based unmixing method43, Zhang proposed an adaptive region division-based unmixing method44, Hong proposed a low-rank characteristic-based unmixing method45, and Ozkan proposed an unmixing method based on neural network46.
Furthermore, to make full use of the spatial information of hyperspectral images, convolutional neural networks (CNNs) have also been applied in hyperspectral unmixing. Zhang et al.47 used the CNN to achieve good unmixing results for the first time, demonstrating its great potential in the field of spectral unmixing, but the algorithm utilized requires training samples, which limits its application potential. Palsson et al.48 proposed a CNN-based blind spectral unmixing method that combines the CNN and autoencoder for the first time. SUnCNN is the first deep learning-based technique proposed for sparse unmixing proposed by Rasti49, the deep network learns in an unsupervised manner to map a fixed input into the sparse optimum abundances. the limitation in this algorithm is that it needs to generate the abundances relying on a spectral library. Gao et al.50 proposed the cycle-consistency unmixing network by learning cascaded autoencoders (CyCU-Net), by learning two cascaded autoencoders in an end-to-end fashion, to enhance the unmixing performance more effectively. Some researchers have divided images into cubic patches and used 3-D-CNN to jointly learn spatial and spectral features51, but the size of the cube will affect the accuracy of the unmixing drastically. Inspired by the two-stream network structure, Chen et al.52 proposed a spatial–spectral adaptive nonlinear unmixing network (SSANU-Net) in which the spatial-spectral information of hyperspectral imagery is effectively learned using the two-stream encoder, followed by the simulation of the linear–nonlinear scattering component of photons using a two-stream decoder.
The above algorithms can obtain better estimation results for the endmember extraction and abundance estimation of the whole hyperspectral data. However, the amount of hyperspectral data is large and limited to storage and transmission. Using compressed sensing theory to process hyperspectral data could solve this problem. The traditional mode is compression sampling and reconstruction first, and then spectral unmixing. For example, we can utilize the compressive-projection principal component analysis (CPPCA)53 to complete the compress and reconstruct process, then use the reconstruction information for unmixing. Given the endmember information, the abundance coefficient estimation is completed directly54 or with the help of preserving the intrinsic structure invariant55 or sparse representation56,57. The challenge is that we do not have complete endmember information before unmxing, then the scholars consider other methods, such as extracting terminal elements from the original hyperspectral data58, adding endmember regularization terms59, using endmember library60, and utilizing the L1 sparse regularization61, to achieve the spectral unmixing.
The disadvantage of using traditional mode to complete unmixing is that, the reconstruction process has very high computational complexity, resulting in a very slow interpretation process. What's more, the reconstruction result has lost some effective information, and the accuracy will be affected if the dimension reduction and unmixing are carried out based on the reconstruction result. In actual hyperspectral image unmixing processing, researchers sometimes cannot measure true pure pixel information due to economic, environmental, policy and other factors, which increases the difficulty of accurately extracting endmembers and estimating abundance.
Therefore, the research motivation of this paper is how to estimate the endmember and abundance information at the same time through compressed sensing theory, to achieve high-precision and high-efficient unmixing. Realizing high-precision and efficient unmixing can significantly improve the accuracy and reliability of remote sensing image data, and provide more accurate and comprehensive land cover information. High precision hyperspectral unmixing technology can provide technical support for markets such as large-scale farm evaluation, forest tree species identification, water environment monitoring, mineral identification and mapping, and garbage classification, promoting the rapid development of hyperspectral remote sensing industry.
Aiming at the problem of unmixing hyperspectral images, we propose the spectral unmixing algorithm based on double-compressed sampling (SU_DCS). The contribution of this paper is, the proposed algorithm can obtain endmember and abundance information with high accuracy from a small amount of sampled data, solving the storage and transmission challenges of hyperspectral images under large quantities of conditions.
Spectral mixing characteristics
To achieve unmixing of hyperspectral images, it is necessary to understand the mechanism of spectral mixing. The imaging spectrometer collects hyperspectral data, and each pixel reflects the spectral information of surface materials, with different types of ground objects having different spectral responses. Usually, due to low spatial resolution, each pixel collected may correspond to a larger ground spatial area, which may contain more than one type of ground object. The spectral response of these different ground objects is mixed in a certain proportion, resulting in mixed pixels. According to the different mixing modes of mixed pixels, we choose the linear mixing model (LMM) to analyze the data characteristics of hyperspectral images.
Using LMM theory, the hyperspectral image is decomposed into endmember matrix and abundance matrix62.
where \({\varvec{X}} \in R^{L \times N}\) is the hyperspectral image, \(N\) is the pixels included in each band, \(L\) represents the number of all bands. \({\varvec{E}} \in R^{L \times P}\) is the endmember matrix, where, \(P\) is the number of endmembers, the spectral vector of the \(p\)-th endmember is \({\varvec{E}}_{p}\). \({\varvec{S}} = \left[ {{\varvec{s}}_{1} ,{\varvec{s}}_{2} ,...,{\varvec{s}}_{N} } \right] \in R^{P \times N}\) is the abundance matrix, \({\varvec{s}}_{n} \in R^{P \times 1}\) is the abundance vector for the \(n\)-th pixel.
The \(n\)-th pixel vector can be approximately represented by the linear mixture of each endmember.
Since the hyperspectral remote sensing imaging area only contains several types of ground objects, the dimension of the endmember matrix and abundance matrix will be much smaller than the dimension of the original hyperspectral data matrix.
According to the physical meaning of the abundance vector, it should satisfy ASC and ANC.
where \({\mathbf{1}}_{P}\) and \({\mathbf{1}}_{N}\) represents the a column vector with all 1, \(\left( \cdot \right)^{{\text{T}}}\) is the transpose operation, and whose dimensions are \(P\) and \(N\), respectively.
Spectral unmixing scheme
In this section, we use compressive sensing method to compress hyperspectral images, and propose a spectral unmixing method in the compressed domain.
Compression processing can effectively reduce the amount of hyperspectral data, thereby accelerating the speed of image processing. Compared with other compressed methods, we have chosen the compressive sensing method, which has the following advantages. Firstly, compressive sensing theory can achieve the integration of collection and compression, greatly reducing the amount of data stored and transmitted. Secondly, the sampling rate in compressed sensing is lower than the traditional Nyquist sampling rate, which helps to reduce the sampling and computational costs of the sampler. This asymmetry in compression and decompression is precisely suitable for the characteristics of hyperspectral compression, which is particularly important for scenarios with limited resources such as spaceborne devices. In addition, compressive sensing algorithms can maintain good performance even in the presence of noise and data loss.
The illustration of proposed SU_DCS framework is shown in Fig. 1. At the sampling end, the hyperspectral image is spatially and spectral sampled to obtain spatial and spectral measurements, denoted as double-compressed sampling (DCS). In the unmixing end, we mainly use the LMM model satisfied by the mixed spectrum to complete unmixing, which is referred to as spectral unmixing (SU). We establish a joint optimization model according to the characteristics of endmember information and abundance information. The operator splitting and alternate iteration are used to solve the unmixing model, and finally complete the endmember extraction and abundance estimation. According to the process of sampling and unmixing, our proposed algorithm is denoted as SU_DCS.
Illustration of the proposed SU_DCS framework.
Double-compressed sampling
In this section, we provide a detailed description of the double-compressed sampling process, including spectral sampling and spatial sampling. We also analyzed the characteristics of the measurement data, to ensure that it contains rich endmember and abundance information, which can be used for the unmixing process.
Spectral sampling
In this subsection, we describe the spectral sampling process, and analyzed the characteristics of the spectral measurement data.
By using spectral compression sampling to reduce the amount of spectral data, the sampled data is a linear combination of the original pixel vectors, without losing all absorption features of a certain frequency band. Therefore, we can use spectral measurement data to estimate abundance coefficients.
The spectral measurement data is,
where \({\mathbf{Y}}_{{{\text{spe}}}} \in R^{{L_{{{\text{spe}}}} \times N}}\) is the spectral measurement data, \(L_{{{\text{spe}}}}\) is the sampling points from each pixel vector, \({\varvec{\varPhi}}_{{{\text{spe}}}} \in R^{{L_{{{\text{spe}}}} \times L}}\) is the spectral sampling matrix.
The spectral sampling rate is expressed as,
Analyzing the spectral measurement data, we found the compressed measurement data still contains all kinds of original ground objects, therefore the number of endmembers can be estimated from spectral measurement data. At the same time, we found that spectral measurement data can provide complete abundance information, which is beneficial for abundance estimation.
Through analysis, we found that spectral sampling does not require the design of a special sampling matrix. According to compressive sensing theory, the random sampling matrix must meet the RIP condition63, and the random Gaussian matrix can meet this condition. Therefore, when sampling between spectral bands, we choose a random Gaussian matrix to obtain spectral measurement data.
Spatial sampling
In this subsection, we describe the spatial sampling process, and analyzed the characteristics of the spatial measurement data.
Spatial compression sampling means that the random measurement matrix is used to sample images of each band, and the amount of measurement data in the spatial dimension will be greatly reduced, while the spectral dimension remains unchanged.
The spatial measurement data is,
where \({\mathbf{Y}}_{{{\text{spa}}}} \in R^{{L \times N_{{{\text{spa}}}} }}\) is the spatial measurement data, \(N_{{{\text{spa}}}}\) is the sampling points from each band image, \({{\varvec{\Phi}}}_{{{\text{spa}}}} \in R^{{N_{{{\text{spa}}}} \times N}}\) is the spatial sampling matrix.
The spatial sampling rate is expressed as,
According to the LMM model, we represent the measurement data as,
Compared with Eq. (1), we found that the measurement data \({\mathbf{Y}}_{{{\text{spa}}}} \in R^{{L \times N_{{{\text{spa}}}} }}\) also includes the endmember matrix \({\mathbf{E}} \in R^{L \times P}\), but due to the presence of spatial measurement matrix, the abundance matrix has changed.
Let \({\mathbf{S}}_{{{\text{CS}}}} = {\mathbf{S\Phi }}_{{{\text{spa}}}}\) represent the compressed abundance matrix, and the spatial sampling can be rewritten as,
Through this operation, we found that the spatial measurements can be separated into compressed abundance matrix and original endmember matrix46. We can assume that, if the compressed abundance matrix can meet constraints of ACS and ANC,
where \({\mathbf{1}}_{P}\) and \({\mathbf{1}}_{{N_{{{\text{spa}}}} }}\) represents the a column vector whose elements are all 1 and whose dimensions are \(P\) and \(N_{{{\text{spa}}}}\), respectively.
Then the spatial measurement values meet LMM, thus we can utilize mature endmember extraction algorithms to extract endmembers from spatial measurements. The problem is transformed into how to design a special spatial sampling matrix, so that the spatial measurements could meet the LMM. Only in this way, the spatial measurement data can be used for the unmixing process.
Spatial sampling matrix design
In this subsection, we need to design a spatial sampling matrix to ensure that spatial measurement data provides usable endmember information for unmixing. Our focus is on analyzing the composition of the matrix \({\mathbf{S}}_{{{\text{CS}}}} = {\mathbf{S\Phi }}_{{{\text{spa}}}}\), to ensure that it satisfies ASC and ANC.
Let \({\mathbf{S}}\left( {p,n} \right)\) represent the element of row \(p\), column \(n\) in \({\mathbf{S}}\), the ASC and ANC constraints can be described as,
The element of row \(p\), column \(k\) in \({\mathbf{S}}_{{{\text{CS}}}}\) is described as,
where \({\varvec{\varPhi}}_{{{\text{spa}}}} \left( {n,k} \right)\) is the element of row \(n\), column \(k\) in \({{\varvec{\Phi}}}_{{{\text{spa}}}}\).
Firstly, ANC constraint indicates that each element of \({\mathbf{S}}_{{{\text{CS}}}}\) is nonnegative. If each element \({{\varvec{\Phi}}}_{{{\text{spa}}}} \left( {n,k} \right)\) of the spatial measurement matrix is positive, and multiplied by the original abundance matrix \({\mathbf{S}}\), it can ensure that each element of \({\mathbf{S}}_{{{\text{CS}}}}\) is positive. That is to say, the first condition of the spatial measurement matrix is that each element is a positive number.
Secondly, ASC constraint indicates that the sum of each row in \({\mathbf{S}}_{{{\text{CS}}}}\) is 1. We calculate the sum of column \(k\),
Analyze Eq. (13), the sum of column \(k\) in \({\mathbf{S}}_{{{\text{CS}}}}\) equals to the sum of column \(k\) in \({{\varvec{\Phi}}}_{{{\text{spa}}}}\). In other words, if \({\mathbf{S}}_{{{\text{CS}}}}\) is required to meet ASC, the sum of each row in matrix \({{\varvec{\Phi}}}_{{{\text{spa}}}}\) is required to be 1. The second condition of the spatial measurement matrix is that the sum of each row is 1.
Based on the above analysis, we conclude that when the spatial measurement matrix satisfies the following conditions, the compressed abundance matrix can satisfy ASC and ANC. Based on the analysis in Sect. “Spectral sampling”, at this point, the spatial measurement data can meet the LMM requirements. And mature endmember extraction algorithms can be used to complete endmember extraction, providing necessary conditions for unmixing.
There are many matrices that meet the required conditions required by Eq. (14), such as identity matrices. The sum of each row in the identity matrix is 1, and each element is non negative. According to the requirements of the spatial measurement matrix, we choose any \(N_{{{\text{spa}}}}\) rows from the identity matrix as the spatial sampling matrix \({{\varvec{\Phi}}}_{{{\text{spa}}}}\). The advantage of this choice is that there are many zero elements in the matrix, which can save storage space.
After spatial sampling of each band with such measurement matrix, it can ensure that the spatial measurement data \({\mathbf{Y}}_{{{\text{spa}}}}\) still meet LMM, and then the spatial measurement data can provide sufficient endmember information for unmixing.
Looking back at the design process of the spatial measurement matrix, our original intention was to provide sufficient endmember information for the unmixing process using spatial measurement data. Mature endmember extraction algorithms are all used for the raw hyperspectral data which satisfies LMM. Therefore, we envision that if spatial measurement data can satisfy LMM, existing endmember extraction algorithms can be utilized. Then, we analyzed how the spatial measurement data can meet the conditions of LMM, and found that the compressed abundance matrix is required to meet ASC and ANC. Subsequently, through analysis, we found that if the compressed abundance matrix can satisfy ASC and ANC, the spatial measurement matrix is required to satisfy the conditions of nonnegative and each row is summed to 1. Finally, we consider the factor of storing the measurement matrix space, and select several rows from the identity matrix as the spatial measurement matrix. In this way, we have completed the design of the spatial measurement matrix, ensuring that the spatial measurement data can provide sufficient endmember information for subsequent unmixing.
Spectral unmixing algorithm
This section gives a detailed introduction to the spectral unmixing algorithm. Firstly, we utilize spatial and spectral measurement data, as well as LMM, to construct a spectral unmixing model. Secondly, we use the ADMM method to solve the unmixing model. Finally, we present the process of the unmixing algorithm.
Unmixing model construction
In this subsection, we present the construction process of the spectral unmixing model. According to the algorithm framework shown in Fig. 1, we found that three key elements are required for unmixing, namely, the endmember number, the endmember matrix and the abundance matrix.
In the unmixing end, the known information we have is that, spatial measurement data can provide rich endmember information. Spectral measurement data includes all types of land cover, which can be used to estimate the endmember number, and it also provides sufficient information for abundance estimation. We also know that the product of the endmember matrix and the abundance matrix is the original hyperspectral data, which satisfies LMM. Based on these information, we have listed the following equation.
Combined with the mathematical description of raw hyperspectral data, the endmember matrix and abundance matrix should meet the following requirements at the same time.
Analyze the unmixing model in Eq. (16), it is a constrained optimization problem. We transformed it into an unconstrained optimization problem using the Lagrange multiplier method. For the obtained multivariate functions, by taking the partial derivative of each variable, we can obtain a local optimal solution that is consistent with the original constrained function.
Therefore, we take the endmember matrix \({\mathbf{E}}\) and abundance matrix \({\mathbf{S}}\) as optimization variables, and introduce auxiliary variable \({\mathbf{X}}\) to establish a joint optimization unmixing model.
Where, \(\lambda_{1}\) and \(\lambda_{2}\) are the regularization optimization parameters of the unmixing model for the spatial measurement data and the interspectral measurement data. In the calculation process, if the value of the abundance coefficient is negative, we set this value to 0 to ensure that the abundance coefficient meets the ANC. We adopted the method proposed by Lu64 to ensure that the abundance coefficient meets the ASC constraint.
Unmixing model solution
In this subsection, we provide a detailed introduction to the solution process of the spectral unmixing optimization model.
The analysis of Eq. (17) shows that the joint optimization unmixing model contains three unknowns, namely, \({\mathbf{X}}\), \({\mathbf{E}}\) and \({\mathbf{S}}\), with high computational complexity. Using the idea of operator splitting, the model is divided into three sub problems, and the three unknowns are updated by alternating direction iteration. In other words, we utilize the ADMM method for solving this unmixing model.
Assuming the current number of iterations is \(t\), optimize \({\mathbf{X}}\), \({\mathbf{E}}\) and \({\mathbf{S}}\), respectively. Through iterative optimization, we can obtain endmember matrix, abundance matrix and remixing image by matrix operation.
According to the analysis in Sect. “Spectral sampling”, the spectral measurement data includes all types of ground objects in the hyperspectral image. We used the HySime algorithm to estimate the number of endmembers, and the detailed process can be found in reference63.
We use VCA algorithm to obtain the initial value of endmember matrix.
The spectral measurement process can be rewritten as,
Under the condition that the measurement data \({\mathbf{Y}}_{{{\text{spe}}}}\), measurement matrix \({{\varvec{\Phi}}}_{{{\text{spe}}}}\) and endmember matrix \({\hat{\mathbf{E}}}^{0}\) are known, solving the abundance matrix \({\mathbf{S}}\) belongs to solution of overdetermined equations. We obtain the initial estimate value of abundance matrix using the least square method.
The initial estimate of hyperspectral image is,
The iterative optimization process is as follows.
a) Fix \({\mathbf{X}}\) and \({\mathbf{S}}\) to solve \({\mathbf{E}}\). The unconstrained form of the endmember information optimization problem is,
Let \(L\left( {\hat{\varvec{S}}^{t} ,{\varvec{E}},\hat{\varvec{X}}^{t} } \right)\) rewrite as,
Let the derivative \(\frac{{\partial L\left( {\hat{\varvec{S}}^{t} ,{\varvec{E}},\hat{\varvec{X}}^{t} } \right)}}{{\partial {\varvec{E}}}} = 0\), the solution of Eq. (24) can be obtained, namely,
We sort out Eq. (27) and get,
To solve Eq. (29), we make,
Then rewrite Eq. (30) as follows.
To solve Eq. (31), we first determine the dimensions of each matrix. From the above analysis, the dimension of each matrix is: \({\mathbf{X}} \in R^{L \times N}\), \({\mathbf{S}} \in R^{P \times N}\), \({\varvec{\varPhi}}_{{{\text{spa}}}} \in R^{{N \times N_{{{\text{spa}}}} }}\), \({\mathbf{Y}}_{{{\text{spa}}}} \in R^{{L \times N_{{{\text{spa}}}} }}\), \({\varvec{\varPhi}}_{{{\text{spe}}}} \in R^{{L_{{{\text{spe}}}} \times L}}\), \({\mathbf{Y}}_{{{\text{spe}}}} \in R^{{L_{{{\text{spe}}}} \times N}}\), \({\varvec{C}} \in R^{{L \times \left( {N + N_{spa} } \right)}}\), \({\varvec{D}} \in R^{{P \times \left( {N + N_{spa} } \right)}}\), \({\varvec{A}} \in R^{L \times L}\), \({\varvec{B}} \in R^{P \times P}\), \({\varvec{F}} \in R^{L \times P}\). According to the dimensions of matrix and the characteristics of equation, we find that the equation described in Eq. (31) belongs to Sylvester equation, which can be solved by Bartels–Stewart algorithm. The update endmember matrix is expressed as,
b) Fix \({\varvec{X}}\) and \({\varvec{E}}\) to solve \({\varvec{S}}\). The unconstrained form of the abundance information optimization problem is expressed as,
Let \(L\left( {{\varvec{S}},\hat{\varvec{E}}^{t + 1} ,\hat{\varvec{X}}^{t} } \right)\) rewrite as,
Let the derivative \(\frac{{\partial L\left( {{\varvec{S}},\hat{\varvec{E}}^{t + 1} ,\hat{\varvec{X}}^{t} } \right)}}{{\partial {\varvec{S}}}} = 0\), the solution of Eq. (33) can be obtained, namely,
We sort out Eq. (36) and get,
To solve Eq. (38), we make,
Then rewrite Eq. (39) as follows,
To solve Eq. (40), we first determine the dimensions of each matrix. From the above analysis, the dimension of each matrix is: \({\varvec{H}} \in R^{{\left( {L + L_{{{\text{spe}}}} } \right) \times N}}\),\({\varvec{Q}} \in R^{{\left( {L + L_{{{\text{spe}}}} } \right) \times P}}\), \({\varvec{W}} \in R^{P \times P}\),\({\varvec{V}} \in R^{N \times N}\), \({\varvec{J}} \in R^{P \times N}\). According to the dimensions of matrix and the characteristics of equation, we find that the equation described in Eq. (40) belongs to Sylvester equation, which can be solved by Bartels–Stewart algorithm. The update abundance matrix is expressed as,
3) Fix \({\varvec{E}}\) and \({\varvec{S}}\) to update \({\varvec{X}}\). The unconstrained form of the hyperspectral image optimization problem is expressed as,
Let the derivative \(\frac{{\partial L\left( {\hat{\varvec{S}}^{t + 1} ,\hat{\varvec{E}}^{t + 1} ,{\varvec{X}}} \right)}}{{\partial {\varvec{X}}}} = 0\), the solution of Eq. (42) can be obtained, namely:
Then the hyperspectral image is updated as,
There are two termination criteria for algorithms. The first is to terminate the iteration when the relative change \(r_{{{\text{elchg}}}}\) between two iterations is less than the convergence threshold \(T_{{\text{h}}}\).
The second is to terminate the iteration when the maximum number of iterations is reached.
The setting of convergence threshold and maximum number of iterations will be discussed and analyzed in Sect. “Convergence threshold selection experiment”.
Execution process of unmixing algorithm
In this subsection, the realization process of SU_DCS is summarized as follows.
SU_DCS
We analyze the computational complexity of the SU_DCS algorithm. The computation time of SU_DCS is primarily dominated by the computations of the endmember extraction in Step 5 and the abundance estimation in Step 6. We utilize Bartels–Stewart algorithm to optimize the unmixing process, and its computational complexity is \(O\left( {P^{3} } \right)\), the computational complexity of Step 7 is \(O\left( {LPN} \right)\). The complexity of one loop is \(O\left( {2P^{3} + LPN} \right)\), after \(T\) iterations, the total computational complexity is \(O\left( {2TP^{3} + LPNT} \right)\). In the case of \(2P^{3} < LPN\), the total computational complexity could be simplified as \(O\left( {LPNT} \right)\).
Experimental results and analysis of simulated hyperspectral data
In this section, we conducted some experiments on simulated hyperspectral data using the proposed algorithm to verify its feasibility and robustness. Firstly, we provide the construction of simulated hyperspectral data and the evaluation indicators of the algorithm. Then, algorithm parameters experiments are conducted, including regularization parameters, convergence threshold, spatial sampling rate, etc., to determine the parameters when the algorithm achieves optimal performance. Finally, we present the experimental results of the proposed algorithm SU_DCS on simulated hyperspectral data and analyze them.
Simulated hyperspectral data and evaluation indicators
In this subsection, we provide the construction of simulated hyperspectral data, and indicators for evaluating algorithm performance.
The simulated hyperspectral data is composed of the endmember spectral curve multiplied by abundance matrix, added Gaussian white noise. We choose some spectral curves from USGS spectral database65 as the endmembers for the simulated hyperspectral data.
According to the analysis in Sect. “Spectral mixing characteristics”, the abundance matrix needs to satisfy ASC and ANC. That is to say, each element of the abundance matrix is nonnegative, and the sum of each row is 1. According to the definition of the Dirichlet distribution function, the matrix elements it generates are nonnegative and the sum of each row is 1, satisfying ASC and ANC. Therefore, we can use the matrix generated by the Dirichlet distribution as the abundance coefficient to synthesize hyperspectral data.
In the simulated hyperspectral data, the image size is 256 × 256, the number of bands is 224, and four minerals (Carnallite, Ammonioalunite, Biotite, Actinolite) were selected as endmembers, and the abundance matrix obeyed Dirichlet distribution.
We use the spectral angle distance (SAD) to evaluate the accuracy of the endmember information extracted,
where \({\varvec{E}}_{p}\) and \(\hat{\varvec{E}}_{p}\) represent the \(p\)-th true endmember vector and the estimated endmember vector, respectively.
We use the root mean square error of the abundance (RMSE) to evaluate the accuracy of the abundance estimation.
where \({\varvec{S}}_{p}\) and \(\hat{\varvec{S}}_{p}\) represent the true abundance matrix and the estimated matrix for the \(p\)-th endmember, respectively.
According to the above unmixing algorithm execution process, utilizing the endmember matrix and abundance matrix estimated by SU_DCS can obtain the remixing image. In the absence of true endmember information and abundance information of hyperspectral image, we can also use peak signal-to-noise ratio (PSNR) and structural similarity (SSIM)46 to measure accuracy of the algorithm. The PSNR is defined as,
where \({\varvec{X}}_{l}\) and \(\hat{\varvec{X}}_{l}\) are the original image and remixing image for the \(l\)-th band, \(\max \left( {{\varvec{X}}_{l} } \right)\) is the peak value of \({\varvec{X}}_{l}\), and \({\text{MSE}}\,\,\left( {{\varvec{X}}_{l} ,\hat{\varvec{X}}_{l} } \right)\) is the mean square error,
SSIM is defined in Eq. (51), the parameters can be referred to Ref.46.
Parameter selection experiment on SU_DCS algorithm
In this subsection, we conducted experiments using SU_DCS on simulated hyperspectral data to analyze the effects of regularization parameters, convergence threshold, and spatial sampling rate on algorithm performance. Based on the experimental results, we have decided on the parameter selection when the algorithm achieves optimal performance.
Regularization parameter selection experiment
In the unmixing model, \(\lambda_{1}\) and \(\lambda_{2}\) is selected as the regularization optimization parameter of spatial measurement data and interspectral measurement data. The influence of regularization parameters on the algorithm is tested through regularization parameter selection experiment. Using the unmixing algorithm SU_DCS samples and unmixes simulated hyperspectral data.
The range of two sampling rates is 0.1–0.5, the interval is 0.1, the maximum number of iterations is set to 20, and the algorithm iteration ends after the maximum number of iterations. The variation range of the regularization parameter is \(10^{ - 5}\)–\(10^{5}\), with an interval of 10. The SAD of the estimated and true endmember spectrum, the RMSE of the estimated and true abundance matrix, and the PSNR results of remixing image are shown in Fig. 2. At this time, the two sampling rates are both 0.1, and the regularization parameters are expressed in logarithmic coordinates.
Regularization parameters performance on unmixing algorithm. (a) SAD, (b) RMSE, (c) PSNR.
Seen from Fig. 2a, under the condition that the regularization parameter \(\lambda_{2}\) is fixed, the SAD increases with the increase of \(\lambda_{1}\). Under condition of \(\lambda_{1}\) fixed, SAD decreases with the increase of \(\lambda_{1}\), and tends to be stable when it reaches the order of magnitude \(10^{2}\), indicating that smaller \(\lambda_{1}\) should be selected. By comparing Fig. 2a,b, it is found that the influence of regularization parameters on the accuracy RMSE of abundance estimation is consistent with that on the accuracy SAD of endmember estimation.
Seen from Fig. 2c, when the regularization parameter \(\lambda_{1}\) is fixed, the PSNR of the remixing image increases with the increase of \(\lambda_{2}\). When the magnitude order of \(\lambda_{2}\) is selected as \(10^{2}\), the PSNR tends to be stable. According to the experimental results in Fig. 2 (a), (b), (c) and other sampling rate conditions, when the magnitude order of \(\lambda_{2}\) is selected as \(10^{2}\) and the parameter \(\lambda_{1}\) is selected as \(10^{ - 1}\), the accuracy of endmember, abundance and remixing images can reach the optimum. In the subsequent experiments, we selected \(\lambda_{1} = 0.1\) and \(\lambda_{2} = 100\) as the regularization parameters of unmixing algorithm.
Convergence threshold selection experiment
Using the unmixing algorithm SU_DCS samples and unmixes the simulated hyperspectral images, and studies the impact of convergence threshold on the algorithm performance. The range of two sampling rates is 0.1–0.5, the regularization parameter is set to \(\lambda_{1} = 0.1\) and \(\lambda_{2} = 100\), the maximum iteration number is 30, and the iteration ends after 30 iterations. When the two sampling rates are both 0.5, the SAD, the RMSE, and the PSNR results of the remixing image are shown in Fig. 3.
Convergence threshold performance on unmixing algorithm. (a) SAD, (b) RMSE, (c) PSNR, (d) Relchg.
With the increase of iteration times, the SAD of extracted endmember spectrum and true spectral curve is kept within \(9 \times 10^{ - 4}\), which indicates that the initial value of endmember obtained from spatial measurement data for the first time is very accurate. The RMSE of the estimated abundance matrix is kept within \(3 \times 10^{ - 2}\), indicating that iteration is helpful to improve the accuracy of the abundance estimation. As the number of iterations increases, the PSNR of the remixing image increases. After 20 iterations, it gradually becomes stable, and the relative change of the adjacent remixing image gradually reduces to \(10^{ - 14}\). Considering the accuracy of the unmixing, the maximum iteration number is set to \(T = {20}\), and the convergence threshold is set to \(T_{{\text{h}}} = 10^{ - 14}\).
Spatial sampling rate selection experiment
From the results of convergence threshold selection experiment, we find that VCA algorithm can effectively extract accurate endmember data from spatial measurement data. Therefore, we consider conducting spatial sampling rate selection experiment to analyze the impact of spatial sampling rate on the unmixing accuracy. In the experiment, the spatial sampling rate is 0.005 ~ 0.1, the interval is 0.005, and the spectral sampling rate is 0.1–0.5, the interval is 0.1.
Under different spectral sampling rates, the SAD and RMSE results versus the spatial sampling rate are shown in Fig. 4. When the spatial sampling rate increases from 0.005 to 0.015, SAD decreases greatly, followed by small amplitude oscillation, and reaches a new minimum after sampling rate increases to 0.045. RMSE reaches the first minimum after the spatial sampling rate increases to 0.02, and then keeps a small amplitude oscillation. Under the condition of different spectral sampling rates, the accuracy of the endmember and abundance estimation can be kept at a high level. The experimental results can show that even if hyperspectral images are sampled at a lower spatial sampling rate, the measured data can still contain accurate endmember information for endmember extraction. Therefore, in the subsequent experiments, we set the spatial sampling rate to \(SR_{{{\text{spa}}}} = 0.05\), and then consider the effect of spectral sampling rate on the unmixing accuracy.
Spatial sampling rate performance on unmixing algorithm. (a) SAD, (b) RMSE.
Pure pixel ratio experiment
The premise assumption of the endmember extraction algorithm is that hyperspectral images contain available pure pixels. We define the ratio of pure pixel number to all pixels as pure pixel ratio, denoted as PPR. If the pure pixel ratio is high, that is, the mixing degree of hyperspectral images is not strong, the difficulty of extracting endmembers is relatively low. Since the accuracy of endmember extraction will further affect the accuracy of abundance coefficient estimation, we firstly analyze the impact of pure pixel ratio on endmember extraction.
Now we generate a set of simulated datasets with different pure pixel ratio. The image size is 256 × 256, the number of bands is 224, and four minerals (Carnalite, Ammonioalute, Biotite, Actinolite) were selected as endmembers. The abundance matrix should satisfy the condition that each element is positive and the sum of each row is 1. Each row of the abundance matrix represents the component coefficients of each type of feature in the pixel. When one element in a row of the abundance matrix is significantly larger than the other elements, it is considered as a pure pixel. Therefore, we change the pure pixel ratio of the simulated data by changing the abundance matrix. To increase the PPR from 10 to 100%, SU_DCS was used to perform endmember extraction and abundance estimation, and studies the impact of pure pixel ratio on the algorithm performance.
The four endmember spectral curves we selected are shown in Fig. 5a. When the pure pixel ratio is 0.1, according to our definition of pure pixel ratio, the number of pure pixels in the image is 6554, indicating that there are 6554 pixels containing only one type of terrain, and the other pixels are mixed pixels. We use different colors to distinguish different types of pixels, and the abundance scatterplot map is shown in Fig. 5b. In order to display the distribution positions of the four types of pure pixels and mixed pixels more clearly, we provided a 36 * 36 subgraph in the upper left corner shown in Fig. 5c, and marked the pixel types represented by each color.
The simulated dataset (a) four endmember spectral curves from USGS, (b) scatterplot of the fractional abundances, (c) the enlarged subgraph with pure pixel marked.
To test the robustness of the algorithm, we added Gaussian white noise to the spatial measurement data and tested the accuracy of the algorithm in extracting endmembers under different signal-to-noise ratio (SNR). In the experiment, the SNR ranged from 10 to 50 dB with intervals of 10 dB. The regularization parameters are selected as \(\lambda_{1} = 0.1\) and \(\lambda_{2} = 100\), the maximum iteration number is \(T = {20}\), the convergence threshold is \(T_{{\text{h}}} = 10^{ - 14}\), and the spatial sampling rate is \(SR_{{{\text{spa}}}} = 0.05\).
At sampling rates of 0.1, 0.3, and 0.5, the variation of SAD with PPR and SNR is shown in Fig. 6. Seen from Fig. 6a, in this case the sampling rate is lower, when the SNR is as low as 10 dB, there is a significant error between the endmember spectrum extracted by the algorithm and the true spectrum, the maximum SAD is approximately 0.26. As the SNR increases to 30 dB, the error can be reduced to \(7 \times 10^{ - 3}\). When the signal-to-noise ratio increases to 50 dB, the error can be reduced to \(4 \times 10^{ - 4}\). At the same time, we can also observe that when the sampling rate is low, the error of endmember extraction changes slightly with the change of PPR.
Spatial sampling rate performance on unmixing algorithm. (a) sampling rate is 0.1, (b) sampling rate is 0.3, (c) sampling rate is 0.5
When the sampling rate increases to 0.3, as the SNR increases, the accuracy of endmember extraction increases, as shown in Fig. 6b. At this time, as the pure pixel ratio increases, the accuracy of endmember extraction also continuously increases, and the maximum SAD is approximately below 0.17. When the sampling rate increases to 0.5, as shown in Fig. 6c, the maximum SAD is small and can be reduced to below 0.09. The results also indicate that as the sampling rate increases, the information contained in the measurement data will also increase, and the endmember extraction will be more accurate.
The comparison between the endmember spectrum extracted by SU_DCS and the true spectral curve from USGS is shown in Fig. 7, in these figures, the sampling rate during the unmixing is 0.1 and the SNR is 10 dB. The pure pixel ratio is 0.1, 0.4, 0.7 and 0.9. From the graph, it can be seen that there are differences between the extracted endmember spectrum and the true spectrum under different pure pixel ratios. Comparing the curves of the four endmembers, it is found that Carnalite and Biotite can be accurately extracted, and the trend of the extracted spectrum and the true spectral curves is basically consistent. For the endmember Ammonioalute, the higher the pure pixel ratio, the more consistent the trend with the true curve. When the pure pixel ratio is lower, the error will be larger such as PPR = 0.4. For endmember Actinolite, when the pure pixel ratio is as low as 0.1, the extracted spectral lines are inaccurate, resulting in significant errors. This is because when the ratio is too low, there are fewer pure pixels in the hyperspectral dataset, resulting in inaccurate extraction of Actinolite spectral information. However, analyzing the extraction effects of the other three types of features, at a ratio of 0.1, the extracted spectral information is still quite consistent with the spectral information in the USGS library. When the pure pixel ratio increases, the errors will be smaller in most cases.
Comparison between the estimated and true endmember spectral curve with different pure pixel ratio under SNR = 10 dB. (a) Carnallite, (b) Ammonioalunite, (c) Biotite, (d) Actinolite.
Figure 8 shows the comparison curve under the condition of SNR = 20 dB. For each endmember, the extracted spectral curve is already very close to the true spectral curve. Compared with Fig. 7, the error has decreased significantly, indicating that the SNR also has a significant impact on algorithm accuracy.
Comparison between the estimated and true endmember spectral curve with different pure pixel ratio under SNR = 20 dB. (a) Carnallite, (b) Ammonioalunite, (c) Biotite, (d) Actinolite.
Utilizing VCA, PPI and NFINDR algorithm performs endmember extraction on simulated hyperspectral data which includes 4 endmembers. The PPI algorithm and NFINDR algorithm perform endmember extraction on raw hyperspectral data, while the VCA algorithm performs endmember extraction on measurement data with a sampling rate of 0.1. The comparison of the results of four extracted endmembers is shown in Fig. 9. From the graph, it can be seen that the endmember curves extracted by the three algorithms are relatively consistent with the real endmember curves, with only slight differences. This indicates that for simulated data, the proposed algorithm can accurately extract endmember information. In the following experiments, we would use the proposed algorithm to conduct endmember extraction experiments on real hyperspectral data to verify its effectiveness.
Endmember extraction comparison between VCA, PPI and NFINDR algorithms. (a) Carnallite, (b) Ammonioalunite, (c) Biotite, (d) Actinolite.
Experimental results of simulated hyperspectral data
In this subsection, we conducted experiments using the SU_DCS algorithm on simulated hyperspectral data (the simulated data is from Sect. “Simulated hyperspectral data and evaluation indicators”) using the determined algorithm parameters. Analyze the experimental results and evaluate the performance of the proposed algorithm in endmember extraction, abundance estimation, and image remixing.
According to the above experiments, we can determine the parameters of SU_DCS. The regularization parameters are selected as \(\lambda_{1} = 0.1\) and \(\lambda_{2} = 100\), the maximum iteration number is \(T = {20}\), the convergence threshold is \(T_{{\text{h}}} = 10^{ - 14}\), and the spatial sampling rate is \(SR_{{{\text{spa}}}} = 0.05\). The unmixing experiment is conducted on the synthetic hyperspectral data to complete the endmember extraction and abundance estimation.
At this point, we only have measured spatial and spectral data. In this case, it is necessary to find reliable endmember and abundance to complete the evaluation of algorithm performance. VCA can quickly extract endmember, with strong reliability and high accuracy. The abundance matrix estimated by the FCLS algorithm33 is closer to the global optimal solution and has a fast iteration speed. Therefore, we use the VCA_FCLS algorithm to extract endmembers and estimate abundance from the raw hyperspectral data, and use the results as a benchmark to evaluate our proposed algorithm.
The comparison between the endmember spectrum extracted by two algorithms and the true spectral curve of the USGS is shown in Fig. 10. At this time, the simulated hyperspectral data includes four spectral substances, namely, Carnallite, Ammonioalunite, Biotite and Actinolite. The sampling rate during the unmixing is 0.1. Whether VCA_FCLS algorithm or SU_DCS algorithm, the extracted endmember spectral curve is very consistent with the true spectral curve, which fully shows that even if there is only 10% of the measured data, the algorithm SU_DCS can still extract accurate endmember spectral information.
Comparison between the estimated and true endmember spectral curve with different algorithms. (a) Carnallite, (b) Ammonioalunite, (c) Biotite, (d) Actinolite.
Table 1 lists the endmember extraction accuracy (SAD), abundance estimation accuracy (RMSE) and remixing image accuracy (PSNR) obtained by different algorithms, when the endmember number is 4, 5, 6 and 7. Analyzing the experimental data in the table, the accuracy of algorithm VCA_FCLS performed on the full hyperspectral data is the highest, keeping the error on the order of \(10^{ - 6}\) magnitude. The endmember extraction accuracy is on the order of \(10^{ - 4}\) magnitude, the abundance estimation accuracy is on the order of \(10^{ - 3}\) magnitude, and the PSNR for remixing image could be about 80 dB in our proposed algorithm SU_DCS. The result shows that adopting SU_DCS algorithm on simulated hyperspectral data could get high unmixing accuracy.
Given that hyperspectral datasets may be large and computationally intensive, let's now consider the impact of dataset size on algorithm computational efficiency and scalability. Select 4, 5, 6, and 7 objects from the USGS spectral library, to construct simulated hyperspectral datasets, with image sizes of 64 * 64, 128 * 128, 256 * 256, 512 * 512 and 1024 * 1024. The sampling rate is 0.1 ~ 0.5, with an interval of 0.1. Record the calculation time of the algorithm for different image sizes, as shown in Fig. 11.
Impact of dataset size on algorithm computational efficiency. (a) Endmember number is 4, (b) Endmember number is 5, (c) Endmember number is 6, (d) Endmember number is 7.
From the results, it can be seen that for smaller datasets, the algorithm can quickly complete the task of unmixing, which requires less computer resources and has a lighter computational burden. As the size of the dataset increases, the computational complexity of the algorithm also increases, resulting in longer computation time. When the image size is 1024 * 1024, the calculation time can still be controlled within the square order of 10, indicating that the algorithm has the ability to handle large datasets. If high-performance computers can be utilized, data can be processed faster and algorithm efficiency can be improved. The results in the figure also indicate that the algorithm can handle datasets of different sizes, whether they are small or large. As the size of the dataset expands, algorithms can maintain stable performance and adapt to the growth of data volume.
In the simulated data unmixing results mentioned above, we utilize endmember extraction accuracy (SAD), abundance estimation accuracy (RMSE) and remixing image accuracy (PSNR) to evaluate the accuracy and feasibility for the proposed algorithm. By comparing with other algorithms, we found that the proposed algorithm can accurately extract endmember information and abundance information from simulated data. Algorithms can handle datasets of different sizes while maintaining stable performance. We will use the proposed algorithm to perform unmixing processing on real hyperspectral data.
Experimental results and analysis of real hyperspectral data
In this section, we conducted some experiments on two kinds real hyperspectral data using the proposed algorithm to evaluate its performance. Firstly, we provide the performance of the algorithm on real datasets without ground truth, in other words, we do not have the endmembers or abundance included in the datasets. Secondly, we provide the performance of the algorithm on real datasets with ground truth, namely, we have the true endmembers or abundance. In two situations, we analyze the accuracy of endmember extraction, abundance estimation, and remixing images, and compare the computational efficiency of the algorithms.
Experimental results of real hyperspectral data without groundtruth
In this subsection, we present the performance of the algorithm on six hyperspectral datasets, and compare it with other algorithms to evaluate their accuracy and efficiency.
Real hyperspectral data and evaluation indicators
The source hyperspectral data cube is obtained from66,67, the basic situation of the six datasets is shown in Table 2, and the details for them can refer to Ref.63. Selecting three bands of hyperspectral images as RGB primary colors, the synthesized pseudo-color images are shown in Fig. 12. The satellite images obtained through calculation and processing were all created using Octave software68.
Pseudo color images of hyperspectral data created using Octave software68. (a) Cuprite1, (b) Cuprite2, (c) Cuprite3, (d) Indian Pines, (e) Pavia University, (f) Botswana.
Three methods are used to perform unmixing experiments. (1) The VCA algorithm is used for endmember extraction from original hyperspectral data, the FCLS algorithm is used for abundance estimation, and the algorithm is denoted as VCA_FCLS. (2) The classic CPPCA53 algorithm is used to compress and reconstruct hyperspectral data, then utilize VCA and FCLS algorithm for unmixing, and the method is denoted as CPPCA_VCA_FCLS. (3) Adopting the proposed algorithm SU_DCS, directly extracts the endmember and estimates the abundance from compressed sampling data.
Due to the lack of endmember information for real hyperspectral data, the VCA_FCLS results are used as the standard, to evaluate performance of other algorithms. The endmember accuracy is evaluated by SAD, and the abundance matrix is evaluated by RMSE. The extracted endmember matrix and abundance matrix are used to synthesize the remixing image, and the PSNR and SSIM are used to evaluate the algorithm efficiency, and the execution time is used to evaluate the algorithm efficiency.
Results and analysis of endmember extraction
The endmember spectral curves extracted by three algorithms are shown in Fig. 13. We give nine endmember results extracted from scene Cuprite3, and the sampling rate of CPPCA_VCA_FCLS and SU_DCS is 0.2. The trend of the endmember spectral curves extracted by different algorithms is generally consistent, which indicates that these algorithms can effectively extract the endmember. From the perspective of the smoothness of the spectral curve, the spectral curve obtained by the CPPCA_VCA_FCLS has many burrs, and the trend of spectral curve at some wavebands has deviation. Proposed algorithm SU_DCS has a smoother spectral curve, which is more consistent with that of VCA_FCLS algorithm, indicating that SU_DCS algorithm extracts the endmember with high reliability.
Endmember spectral curve comparison between three algorithms. (a) Endmember 1, (b) Endmember 2, (c) Endmember 3, (d) Endmember 4, (e) Endmember 5, (f) Endmember 6, (g) Endmember 7, (h) Endmember 8, (i) Endmember 9.
Using the endmember curve extracted by VCA_ FCLS as the standard, calculate the SAD between endmember spectral curve extracted by different algorithms and the standard curve, and record these experimental results in Table 3. With the case of the SAD of SU_DCS less than CPPCA_VCA_FCLS, the result will be displayed in bold. It can be found from the data in the table that in most cases, the SAD of SU_DCS is at a low level, indicating that the algorithm can accurately extract the endmember information, which is consistent with the conclusion in Fig. 11.
Results and analysis of abundance estimation
The abundance matrix estimated by the three algorithms is shown in Fig. 14, which is consistent with the nine endmembers corresponding to Fig. 13. It can be seen that for most endmembers, the abundance matrices estimated by different algorithms are consistent, and few abundance matrices have little biased. Using the results of VCA_FCLS as the standard, the RMSE results of the other two algorithms are recorded in Table 4. The smaller the RMSE, the smaller the mean square deviation between the estimated abundance matrix and the standard abundance. It can be found from the data that in most cases, the RMSE of SU_DCS is at a low level, which indicates that the algorithm can accurately estimate abundance matrix, which is consistent with the conclusion in Fig. 13.
Abundance matrix comparison between three algorithms created using Octave software68. (a) Endmember 1, (b) Endmember 2, (c) Endmember 3, (d) Endmember 4, (e) Endmember 5, (f) Endmember 6, (g) Endmember 7, (h) Endmember 8, (i) Endmember 9.
Accuracy comparison for remixing images
The extracted endmember and abundance matrix were used to synthesize the remixing image, and the accuracy of the remixing image was evaluated. The comparison of PSNR experimental data is shown in Fig. 15. Obviously, the proposed algorithm SU_DCS has the highest PSNR, indicating that this unmixing framework has high accuracy. The comparison of SSIM experimental data for the structural similarity of the three algorithms is shown in Fig. 16. The structural similarity of the remixing images obtained by three algorithms are all close to 1, indicating that the structure of the remixing images obtained by three algorithms is very consistent with the original image.
PSNR comparison of remixing images. (a) Cuprite1, (b) Cuprite2, (c) Cuprite3, (d) Indian Pines, (e) Pavia University, (f) Botswana.
SSIM comparison of remixing images. (a) Cuprite1, (b) Cuprite2, (c) Cuprite3, (d) Indian Pines, (e) Pavia University, (f) Botswana.
The results of Indian Pines, Pavia University and Botswana comparing with algorithm, TFNet16 and SSR-NET17 using PSNR, are listed in Table 5. The two algorithms obtained the reconstruction hyperspectral images using image fusion from hyperspectral and multispectral images. For the proposed SU_DCS, we list the result reconstructed from the measurement data, namely, the sampling rate is 0.1 ~ 0.5. For Indian Pines, the PSNR of SU_DCS algorithm can achieve the accuracy of TFNet at the sampling rate of 0.3, and achieve the accuracy of SSR-NET algorithm at a sampling rate of 0.4. For Pavia University, the SU_DCS could achieve the accuracy of TFNet and SSR-NET algorithms at a lower sampling rate of 0.2, while for the Botswana dataset, the sampling rate could be further reduced to 0.1. This indicates that our algorithm is feasible in reconstructing raw data from measurement data and can ensure reconstruction accuracy.
The comparison between the original image and remixing images is shown in Fig. 17 (the band used by the pseudo color image is the same as that in Fig. 12), and the sampling rate is 0.2. The remixing image obtained by three unmixing algorithms is consistent with the original image. Surprisingly, we find that the remixing images obtained by SU_DCS has a higher degree of coincidence with the real image, which shows that the endmember and abundance extracted by the algorithm are reliable.
Comparison between Remixing Image and Original Image created using Octave software68. (a) Cuprite1, (b) Cuprite2, (c) Cuprite3, (d) Indian Pines, (e) Pavia University, (f) Botswana.
Algorithm efficiency comparison
The execution time of the three unmixing algorithms is recorded in Fig. 18. The results show that although the execution efficiency of three algorithms is on the same order of magnitude, the amount of data required is different. Compared with VCA_FCLS algorithm, the SU_DCS only needs 10% of measurement data to meet the same accuracy. Compared with CPPCA_VCA_FCLS algorithm, although the efficiency of SU_DCS has only a slight advantage, the endmember accuracy, abundance accuracy and remixing image accuracy have great advantages. To sum up, the algorithm SU_ DCS has a significant advantage of unmixing accuracy and efficiency.
Comparison of algorithm efficiency. (a) Cuprite1, (b) Cuprite2, (c) Cuprite3, (d) Indian Pines, (e) Pavia University, (f) Botswana.
Experimental results of real hyperspectral data with groundtruth
In this subsection, we present the performance of the algorithm on two hyperspectral datasets with real endmembers or abundance. Compare the extracted endmembers and estimated abundance with the real ground truth, to verify the reliability of the proposed algorithm.
Results and analysis for dataset cuprite
Cuprite dataset69 covers the Cuprite in Las Vegas, NV, U.S. There are 224 channels, ranging from 370 to 2480 nm. After removing the noisy channels (1–2 and 221–224) and water absorption channels (104–113 and 148–167), we remain 188 channels. A region of 250 × 190 pixels is considered in the experiment. Due to the USGS spectral library is recorded in 1995, while the Cuprite data was collected in 1997, variations between minerals occur during this period, resulting in changes in spectral curves. The pseudo-color image and its mineral map are shown in Fig. 19. We combined the mineral map of Cuprite to determine the reference spectral map of this dataset. We determine the number of endmembers is 12, which are summarized as follows "#1 Alunite", "#2 Andradite", "#3 Buddingtonite", "#4 Dumortierite", "#5 Kaolinite1", "#6 Kaolinite2", "#7 Muscovite", "#8 Montmorillonite", "#9 Nontronite", "#10 Pyrope", "#11 Sphene", "#12 Chalcedony". The reference spectral signatures of this dataset from USGS is shown in Fig. 20.
The pseudo-color image of Cuprite and its mineral map. (a) Cuprite, (b) USGS mineral map of Cuprite mining district.
The USGS library mineral spectral signatures.
We use the proposed algorithm SU_DCS to perform unmixing processing on the dataset. Noted that it is not possible to directly match the set with the smallest SAD between the estimated value and the true value of the endmember. It is also necessary to visually interpret it in conjunction with the reference spectral curve shown in Fig. 20. Considering that the USGS spectral curve is obtained under ideal conditions, while hyperspectral data may be affected by atmospheric interference and other environmental factors during collection. The endmember extracted by the proposed algorithm is estimated from randomly measured hyperspectral data, and there is inevitably a difference between the estimated value and the true value.
Figure 21 shows the endmember curve and abundance map estimated by the proposed algorithm under the condition of a sampling rate of 0.3. From the abundance estimation map, compared with the mineral distribution map shown in Fig. 19, the estimated 8 types of features can have good spatial consistency with the mineral distribution map. Although the estimated endmember curve has some deviation from the curve in the USGS library, it still has good consistency from the trend of the spectral curve.
Comparison between endmembers extracted by the SU_DCS algorithm and the spectral curve from USGS library, and the corresponding estimated abundance map for each endmember created using Octave software68. (a) #1 Alunite, (b) #3 Buddingtonite, (c) #5 Kaolinite1, (d) #6 Kaolinite2, (e) #7 Muscovite, (f) #9 Nontronite, (g) #11 Sphene, and (h) #12 Chalcedony.
Results and analysis for dataset Samson
In this Samson dataset69, there are 952 × 952 pixels. Each pixel is recorded at 156 channels covering the wavelengths from 401 to 889 nm. The spectral resolution is highly up to 3.13 nm. As the original image is too large, which is very expensive in terms of computational cost, a region of 95 × 95 pixels is used in the experiment. It starts from the (252,332)-th pixel in the original image. This data is not degraded by the blank channel or badly noised channels. Specifically, there are three targets in this image, i.e. "#1 Soil", "#2 Tree" and "#3 Water" respectively. The pseudo-color image and its ground truth are shown in Fig. 22.
The pseudo-color image of Samson and its ground truth created using Octave software68. (a) Samson, (b) GT: Endmembers, (c) GT: #1 Soil, (d) GT: #2 Tree, (e) GT: #3 Water.
We conducted an unmixing experiment on the Samson dataset using the proposed SU_DCS algorithm, with a sampling rate of 0.1–0.5. Under different sampling conditions, we use SAD and RMSE to evaluate the accuracy of endmember extraction and abundance estimation, respectively. Table 6 quantifies the experimental results of the proposed algorithm and other four comparative algorithms on dataset Samson, including the sparse convolutional unmixing network (SUnCNN)49, the cycle-consistency unmixing network by learning cascaded autoencoders (CyCU-Net)50, the 3-DCNN unmixing frame considering SV (3DCNN-var)51, and the spatial-spectral adaptive nonlinear unmixing network (SSANU-Net)52.
The difference between the other algorithms and the proposed algorithm is that, the proposed algorithm estimate endmembers and abundance information from compressed data, while other algorithms perform unmixing on the raw hyperspectral data. From the perspective of endmember extraction, the proposed algorithm has an accuracy between the algorithm SUnCNN and the algorithm CyCU-net, and is superior to the 3DCNN-var algorithm. From the perspective of abundance estimation accuracy, the proposed algorithm is comparable to the algorithm SUnCNN and superior to the CyCU-net algorithm. Although the accuracy of the proposed algorithm is inferior to that of the SSANU-Net algorithm, its advantage lies in the ability to recover endmember and abundance information from a lower amount of data, making it suitable for application scenarios that do not require high unmixing accuracy but require high transmission rates.
Figure 23 shows the comparison between the extracted endmember spectral curve and the true curve at a sampling rate of 0.3, and provides the corresponding abundance estimation graph. Observing the results in the graph, although the extracted endmember spectral curve has some deviations from the true spectral curves, in most bands, the two spectral curves have good consistency. The estimated abundance map may have some deviations compared to the true abundance map in Fig. 22, but it can accurately reflect the spatial distribution of each type of feature. These comparison results can demonstrate that the proposed algorithm can accurately perform spectral unmixing, and has good reliability.
The comparison between extracted endmember spectral curve and the truth spectral curve (left column), the corresponding estimated abundance (right column) created using Octave software68. (a) Endmember: #1 Soil, (b) Abundance: #1 Soil, (c) Endmember: #2 Tree, (d) Abundance: #2 Tree, (e) Endmember: #3 Water, (f) Abundance: #3 Water.
Results and analysis for dataset Jasper
In this Jasper dataset69, there are 512 × 614 pixels. Each pixel is recorded at 224 channels ranging from 380 to 2500 nm. The spectral resolution is up to 9.46 nm. Since this hyperspectral image is too complex to get the ground truth, we consider a subimage of 100 × 100 pixels. The first pixel starts from the (105,269)-th pixel in the original image. After removing the channels 1–3, 108–112, 154–166 and 220–224 (due to dense water vapor and atmospheric effects), we remain 198 channels. There are four endmembers latent in this data: "#1 Road", "#2 Soil", "#3 Water" and "#4 Tree". The pseudo-color image and its ground truth are shown in Fig. 24.
The pseudo-color image of Jasper and its ground truth created using Octave software68. (a) Jasper, (b) GT: Endmembers, (c) GT: #1 Tree, (d) GT: #2 Water, (e) GT: #3 Soil, (f) GT: #4 Road.
We conducted an unmixing experiment on the Jasper dataset using the proposed SU_DCS algorithm, with a sampling rate of 0.1–0.5. Under different sampling conditions, we use SAD and RMSE to evaluate the accuracy of endmember extraction and abundance estimation, respectively. Table 7 quantifies the experimental results of the proposed algorithm and other four comparative algorithms on dataset Jasper. From the perspective of endmember extraction, the accuracy of proposed algorithm is comparable to the algorithm 3DCNN-var and superior to the CyCU-net algorithm. From the perspective of abundance estimation, the five algorithms have the similar accuracy. This indicates that the proposed algorithm has highly competitive in terms of endmember extraction and abundance estimation.
Figure 25 shows the comparison between the extracted endmember spectral curve and the true curve at a sampling rate of 0.3, and provides the corresponding abundance estimation graph. The geographic environment of Jasper data is more complex than Samson data, and the spectral curves of the endmember Tree and endmember Soil are somewhat similar. Moreover, the tree and soil belong to a highly mixed state in space, which brings some difficulties to unmixing. Nevertheless, the abundance map estimated by the proposed algorithm still exhibits spatial similarity with the ground truth.
The comparison between extracted endmember spectral curve and the truth spectral curve (left column), the corresponding estimated abundance (right column) created using Octave software68. (a) Endmember: #1 Tree, (b) Abundance: #1 Tree, (c) Endmember: #2 Water, (d) Abundance: #2 Water, (e) Endmember: #3 Soil, (f) Abundance: #3 Soil, (g) Endmember: #4 Road, (h) Abundance: #4 Road.
Results and analysis for dataset urban
In this Urban dataset69, there are 307 × 307 pixels, each of which corresponds to a 2 × 2 m2 area. In this image, there are 210 wavelengths ranging from 400 to 2500 nm, resulting in a spectral resolution of 10 nm. After the channels 1–4, 76, 87, 101–111, 136–153 and 198–210 are removed (due to dense water vapor and atmospheric effects), we remain 162 channels. There are four endmembers latent in this data: "#1 Asphalt", "#2 Grass", "#3 Tree" and "#4 Roof". The pseudo-color image and its ground truth are shown in Fig. 26.
The pseudo-color image of Urban and its ground truth created using Octave software68. (a) Jasper, (b) GT: Endmembers, (c) GT: #1 Asphalt, (d) GT: #2 Grass, (e) GT: #3 Tree, (f) GT: #4 Roof.
We conducted an unmixing experiment on the Urban dataset using the proposed SU_DCS algorithm, with a sampling rate of 0.1 ~ 0.5. Under different sampling conditions, we use SAD and RMSE to evaluate the accuracy of endmember extraction and abundance estimation, respectively. Table 8 quantifies the experimental results of the proposed algorithm and other four comparative algorithms on dataset Urban. The proposed algorithm has the similar endmember extraction accuracy with algorithm SUnCNN, and has the similar abundance estimation accuracy with algorithm CyCU-net.
Compared to the Samson and Jasper datasets using indicators SAD and RMSE, the accuracy of the extracted endmembers and estimated abundance are slightly lower, especially with significant deviations in the endmember Asphalt. The reasons for this bad result might lie in the following two aspects. On the one hand, the Urban dataset has a more complex geographical environment than the Samson and Jasper datasets, the spectral characteristics of different endmembers can be quite similar, which increases the difficulty of spectral unmixing. On the other hand, the proposed algorithm extracts endmembers and estimates abundance information from compressed data. The compression process leads to partial loss of data information, further increasing the difficulty of unmixing and affecting the accuracy of unmixing.
Figure 27 shows the comparison between the extracted endmember spectral curve and the true curve at a sampling rate of 0.3, and provides the corresponding abundance estimation graph. Comparing the abundance map in Fig. 27 and the ground truth map in Fig. 26, it can be seen that the spatial distribution of endmember Grass, endmember Tree, and endmember Roof is still consistent with the ground truth, indicating that the proposed algorithm can still effectively obtain endmember and abundance information from compressed measured data.
The comparison between extracted endmember spectral curve and the truth spectral curve (left column), the corresponding estimated abundance (right column) created using Octave software68. (a) Endmember: #1 Asphalt, (b) Abundance: #1 Asphalt, (c) Endmember: #2 Grass, (d) Abundance: #2 Grass, (e) Endmember: #3 Tree, (f) Abundance: #3 Tree, (g) Endmember: #4 Roof, (h) Abundance: #4 Roof.
We will continue to study how to achieve high-precision unmixing from such complex environments.
Algorithm performance analysis and discussions
Analyzing the above experimental results, we discuss the performance of the proposed algorithm on different types of datasets.
The Cuprite dataset belongs to mineralogy data, which has extremely diverse lithological and chemical composition and structural characteristics, forming complex surface images. Due to the influence of environmental factors on the chemical composition, crystal structure, or physical state of minerals, the spectral characteristics measured using a spectrometer may be inaccurate. From the experimental results, it can be seen that the estimated spectrum is consistent with the basic trend of the measured spectrum curve, but there may be some numerical errors. Moreover, chemical reactions or molecular drift may occur between minerals, leading to some deviation between the estimated abundance and the ground truth.
The Samson dataset uses a single image with relatively simple components, which only includes three types of land cover: soil, trees, and water. The spectral curves of these three types of land cover have significant differences. From the experimental results, it can be seen that the estimated spectral curve and land distribution are consistent with the ground truth.
The sub image blocks used in the Jasper dataset contain four types of land cover, namely # 1 Road, # 2 Soil, # 3 Water, and # 4 Tree. The spectral curves of the four types of land cover differ greatly. From the experimental results, the estimated spectral curves and land cover distribution are consistent with the ground truth.
The Urban dataset contains four types of features, including Asphalt, Grass, Tree, and Roof. The spectral curves of grasslands and trees are similar, and the Asphalt undergoes an aging process during use, which leads to changes in its chemical composition and physical properties, thereby affecting its spectral characteristics. This increases the difficulty of endmember extraction and abundance estimation. From the experimental results, it can be seen that the extraction of the spectral curve of Asphalt is not accurate enough, and there is a significant difference between the abundance map and the actual distribution of land cover. The other three types of features, including grass, trees, and roofs, follow the same trend as the ground truth.
Overall, the proposed algorithm can extract endmembers that maintain good consistency with the given true endmember spectral curves. The estimated abundance map can also maintain good spatial consistency with the spatial distribution of real objects. The comparison results with other algorithms also indicate that the proposed algorithm can obtain relatively accurate endmembers and abundance information from compressed data, the reliability and validity of the proposed algorithm have been proved.
Conclusions
Based on the measured data in the compressed sampling domain and the characteristics of the endmember and abundance matrix, a spectral unmixing algorithm based on double-compressed sampling (SU_DCS) is proposed. The hyperspectral image is spatially coherent sampled and inter spectral compressed sampled, and the joint optimization model of endmember and abundance is constructed. The endmember extraction and abundance estimation are optimized using ADMM algorithm to realize spectral unmixing. Using USGS spectral library and Dirichlet distribution to construct simulated hyperspectral dataset, the parameter selection of SU_DCS algorithm is determined.
We utilize SU_DCS algorithm for conducting unmixing experiments on two kinds of real hyperspectral datasets, and evaluates the endmember extraction and abundance estimation using SAD and RMSE. The first kind dataset is without ground truth, and the experimental results are compared with VCA_FCLS to evaluate the performance of the algorithm in extracting endmember information and estimating abundance. Use PSNR and SSIM to evaluate the accuracy of re-mixing images, the remixing images obtained by SU_DCS are very consistent with the original image, which further illustrates the algorithm SU_DCS has high unmixing accuracy. Moreover, by comparing the execution time, it is found that SU_DCS has high unmixing efficiency. Due to the second kind dataset with ground truth, including dataset Cuprite, dataset Samson, dataset Jasper and dataset Urban, we provided the comparison between the extracted endmember and the ground truth. From the comparison results, it can be seen that the proposed algorithm can accurately extract endmember information from compressed data and estimate abundance map, thus proving the effectiveness of SU_DCS. Comparing the proposed algorithm with other algorithms, including SUnCNN, CyCU-Net, 3DCNN-var and SSANU-Net, it was found that the proposed algorithm can obtain relatively accurate endmember and abundance information from compressed data, fully demonstrating the reliability and effectiveness of the algorithm. We will continue to study the application of the unmixing results in hyperspectral image classification in the future.
Data availability
Data is provided within the manuscript.
References
Aburaed, N. et al. A review of spatial enhancement of hyperspectral remote sensing imaging techniques. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 16, 2275–2300. https://doi.org/10.1109/JSTARS.2023.3242048 (2023).
Wang, B. et al. Multichannel interconnection decomposition for hyperspectral LiDAR waveforms detected from over 500 m. IEEE Trans. Geosci. Remote Sens. 60, 1–14. https://doi.org/10.1109/TGRS.2021.3108160 (2022).
Chang, C. I. Hyperspectral anomaly detection: A dual theory of hyperspectral target detection. IEEE Trans. Geosci. Remote Sens. 60, 1–20. https://doi.org/10.1109/TGRS.2021.3086768 (2022).
Freitas, S., Silva, H. & Silva, E. Remote hyperspectral imaging acquisition and characterization for marine litter detection. Remote Sens. 13(13), 2536. https://doi.org/10.3390/rs13132536 (2021).
Matteoli, S. & Theiler, J. Bayesian target detection algorithms for solid subpixel targets in hyperspectral images. IEEE Trans. Geosci. Remote Sens. 61, 1–14. https://doi.org/10.1109/TGRS.2023.3292067 (2023).
Hong, D. et al. Graph convolutional networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 59, 5966–5978. https://doi.org/10.1109/TGRS.2020.3015157 (2021).
Boateng, R. et al. Remote vegetation diagnostics in Ghana with a hyperspectral fluorescence lidar. IEEE J. Quantum Electron. 29(4), 1–7. https://doi.org/10.1109/JSTQE.2023.3234022 (2023).
Smith, W. L. et al. Hyperspectral satellite radiance atmospheric profile information content and its dependence on spectrometer technology. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 14, 4720–4736. https://doi.org/10.1109/JSTARS.2021.3073482 (2021).
Cristóbal, J. et al. Airborne hyperspectral data acquisition and processing in the arctic: A pilot study using the hyperspectral imaging spectrometer for wetland mapping. Remote Sens. 13(6), 1178. https://doi.org/10.3390/rs13061178 (2021).
Wang, L. & Wang, W. Hyperspectral image compressed processing: evolutionary multiobjective optimization sparse decomposition. PLOS ONE 17(4), e0267754. https://doi.org/10.1371/journal.pine.0267754 (2022).
Perera, C. J., Premachandra, C. & Kawanaka, H. Low pixel resolution hyperspectral image mosaics generation using learning-based feature matching. IEEE Access 11, 104084–104093. https://doi.org/10.1109/ACCESS.2023.3315769 (2023).
Li, W. et al. Asymmetric feature fusion network for hyperspectral and SAR image classification. IEEE Trans. Neural Netw. Learn. Syst. 34(10), 8057–8070. https://doi.org/10.1109/TNNLS.2022.3149394 (2023).
Song, X. Y. et al. Spectral-spatial anomaly detection of hyperspectral data based on improved isolation forest. IEEE Trans. Geosci. Remote Sens. 60, 1–16. https://doi.org/10.1109/TGRS.2021.3104998 (2021).
Liang, H. et al. HSI-mixer: hyperspectral image classification using the spectral–spatial mixer representation from convolutions. IEEE Geosci. Remote Sens. Lett. 19, 1–5. https://doi.org/10.1109/LGRS.2022.3200145 (2022).
Zare, M. et al. Hyperspectral and multispectral image fusion using coupled non-negative tucker tensor decomposition. Remote Sens. 13(15), 2930. https://doi.org/10.3390/rs13152930 (2021).
Liu, X., Liu, Q. & Wang, Y. Remote sensing image fusion based on two-stream fusion network. Inf. Fusion 55, 1–15. https://doi.org/10.1016/j.inffus.2019.07.010 (2020).
Zhang, X., Huang, W., Wang, Q. & Li, X. SSR-NET: spatial–spectral reconstruction network for hyperspectral and multispectral image fusion. IEEE Trans. Geosci. Remote Sens. 59(7), 5953–5965. https://doi.org/10.1109/TGRS.2020.3018732 (2021).
Jouni, M. et al. MultiHU-TD: multifeature hyperspectral unmixing based on tensor decomposition. IEEE Trans. Geosci. Remote Sens. 61, 1–21. https://doi.org/10.1109/TGRS.2023.3314218 (2023).
Wei, Y. et al. A multiobjective group sparse hyperspectral unmixing method with high correlation library. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 15, 7114–7127. https://doi.org/10.1109/JSTARS.2022.3200693 (2022).
Li, C. Z., Chen, X. H. & Zhang, Y. Hyperspectral subpixel unmixing via an integrative framework. Int J Remote Sens. 41(22), 8778–8807. https://doi.org/10.1080/01431161.2020.1783711 (2020).
Feng, S. S. & Fan, F. L. Analyzing the effect of the spectral interference of mixed pixels using hyperspectral imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 14, 1434–1446. https://doi.org/10.1109/JSTARS.2020.3045712 (2020).
Ye, Z. et al. Few-shot learning using residual channel attention and prototype domain adaptation for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 20, 1–5. https://doi.org/10.1109/LGRS.2023.3320406 (2023).
Shang, X. D. et al. Interference-suppressed and cluster-optimized hyperspectral target extraction based on density peak clustering. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 14, 4999–5014. https://doi.org/10.1109/JSTARS.2021.3078452 (2021).
Chang, C. I: Hyperspectral data processing: algorithm design and analysis. Copyright © 2013 John Wiley & Sons, Inc. (2013) https://doi.org/10.1002/9781118269787
González, C. et al. FPGA implementation of the pixel purity index algorithm for remotely sensed hyperspectral image analysis. EURASIP J. Adv. Signal Process. 2010, 969806. https://doi.org/10.1155/2010/969806 (2010).
Winter, M. E. N-finder: An algorithm for fast autonomous spectral endmember determination in hyperspectral data. Proc. Image Spectrom V 3753, 266–277. https://doi.org/10.1117/12.366289 (1999).
Plaza, A., Martinez, P., Perez, R. & Plaza, J. Spatial/spectral endmember extraction by multidimensional morphological operations. IEEE Trans. Geosci. Remote Sens. 40(9), 2025–2041. https://doi.org/10.1109/TGRS.2002.802494 (2002).
Craig, M. D: Minimum-volume transforms for remotely sensed data. IEEE Trans. Geosci. Remote Sens. 32(3), 542–552. https://doi.org/10.1109/36.297973 (1994).
Neville, R. A., Staenz, K. & Szeredi, T., et al.: Automatic endmember extraction from hyperspectral data for mineral exploration. Proc. 4th Int. Airborne Remote Sens. Conf. and Exhib./21st Can. Symp. Remote Sens., Ottawa, ON, Canada, 21–24. (1999)
Nascimento, J. M. P. & Dias, J. M. Vertex component analysis: A fast algorithm to unmix hyperspectral data. IEEE Trans. Geosci. Remote Sens. 43(4), 898–910. https://doi.org/10.1109/TGRS.2005.844293 (2005).
Chang, C. I. et al. A new growing method for simplex-based endmember extraction algorithm. IEEE Trans. Geosci. Remote Sens. 44(10), 2804–2819. https://doi.org/10.1109/TGRS.2006.881803 (2006).
Song, D. M. et al. Fast unmixing of noisy hyperspectral images based on vertex component analysis and singular spectrum analysis algorithms. Can J Remote Sens 46(1), 34–48. https://doi.org/10.1080/07038992.2020.1726735 (2020).
Heinz, D. C. & Chang, C. I. Fully constrained least squares linear spectral mixture analysis method for material quantification in hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 39(3), 529–545. https://doi.org/10.1109/36.911111 (2001).
Chang, C. I., Cao, H. & Song, M. Orthogonal subspace projection target detector for hyperspectral anomaly detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 14, 4915–4932. https://doi.org/10.1109/JSTARS.2021.3068983 (2021).
Han, H. W. et al. Hyperspectral unmixing via nonconvex sparse and low-rank constraint. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 13, 5704–5718. https://doi.org/10.1109/JSTARS.2020.3021520 (2020).
Chen, S. B. et al. Geometrical constrained independent component analysis for hyperspectral unmixing. Int J Remote Sens. 41(17), 6783–6804. https://doi.org/10.1080/01431161.2020.1750732 (2020).
Kong, F. et al. Deep interpretable fully CNN structure for sparse hyperspectral unmixing via model-driven and data-driven integration. IEEE Trans. Geosci. Remote Sens. 61, 1–16. https://doi.org/10.1109/TGRS.2023.3324018 (2023).
Chen, T. et al. Superpixel-based collaborative and low-rank regularization for sparse hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 60, 5529216. https://doi.org/10.1109/TGRS.2022.3177636 (2022).
Sun, L. et al. Mixed noise removal for hyperspectral images based on global tensor low-rankness and nonlocal SVD-aided group sparsity. IEEE Trans. Geosci. Remote Sens. 61, 1–17. https://doi.org/10.1109/TGRS.2023.3257851 (2023).
Parente, M., Iordache, M. D. Sparse unmixing of hyperspectral data: the legacy of SUnSAL. International Geoscience and Remote Sensing Symposium IGARSS, IEEE, Brussels, Belgium, 11–16 July, 21–24. (2021) https://doi.org/10.1109/IGARSS47720.2021.9553723
Ding, M., Fu, X., Huang, T. Z., et al.: Constrained block-term tensor decomposition-based hyperspectral unmixing via alternating gradient projection. 29th European Signal Processing Conference (EUSIPCO), IEEE, Dublin, Ireland, 23–27 August, 1060–1064. (2021) https://doi.org/10.23919/EUSIPCO54536.2021.9616213
Wang, Z. L. et al. Semi-NMF-based reconstruction for hyperspectral compressed sensing. IEEE J Sel. Top. Appl. Earth Obs. Remote Sens. https://doi.org/10.1109/JSTARS.2020.3010332 (2020).
Feng, X. et al. Hyperspectral unmixing using sparsity-constrained deep nonnegative matrix factorization with total variation. IEEE Trans. Geosci. Remote Sens. 56(10), 6245–6257. https://doi.org/10.1109/TGRS.2018.2834567 (2018).
Zhang, X. et al. Hybrid unmixing based on adaptive region segmentation for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 56(7), 3861–3875. https://doi.org/10.1109/TGRS.2018.2815044 (2018).
Hong, D. & Zhu, X. X. SULoRA: Subspace unmixing with low-rank attribute embedding for hyperspectral data analysis. IEEE J. Sel. Top. Signal Process. 12(6), 1351–1363. https://doi.org/10.1109/JSTSP.2018.2877497 (2018).
Ozkan, S., Kaya, B. & Akar, G. B. EndNet: sparse auto encoder network for endmember extraction and hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 57(1), 482–496. https://doi.org/10.1109/TGRS.2018.2856929 (2019).
Zhang, X. et al. Hyperspectral unmixing via deep convolutional neural networks. IEEE Geosci. Remote Sens. Lett. 15(11), 1755–1759. https://doi.org/10.1109/LGRS.2018.2857804 (2018).
Palsson, B., Ulfarsson, M. O. & Sveinsson, J. R. Convolutional autoencoder for spectral–Spatial hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 59(1), 535–549. https://doi.org/10.1109/TGRS.2020.2992743 (2021).
Rasti, B. & Koirala, B. SUnCNN: Sparse unmixing using unsupervised convolutional neural network. IEEE Geosci. Remote Sens. Lett. 19, 5508205. https://doi.org/10.1109/LGRS.2021.3100992 (2022).
Gao, L. et al. CyCU-Net: Cycle-consistency unmixing network by learning cascaded autoencoders. IEEE Trans. Geosci. Remote Sens. 60, 5503914. https://doi.org/10.1109/TGRS.2021.3064958 (2022).
Zhao, M. et al. A 3-D-CNN framework for hyperspectral unmixing with spectral variability. IEEE Trans. Geosci. Remote Sens. 60, 5521914. https://doi.org/10.1109/TGRS.2022.3141387 (2022).
Chen, X. et al. An improved hyperspectral unmixing approach based on a spatial–spectral adaptive nonlinear unmixing network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 16, 9680–9696. https://doi.org/10.1109/JSTARS.2023.3323748 (2023).
Fowler, J. E. Compressive-projection principal component analysis. IEEE Trans. Image Process. 18(10), 2230–2242. https://doi.org/10.1109/TIP.2009.2025089 (2009).
Yuan, Y., Dong, L. & Li, X. L. Hyperspectral unmixing using nonlocal similarity-regularized low-rank tensor factorization. IEEE Trans. Geosci. Remote Sens. 60, 5507614. https://doi.org/10.1109/TGRS.2021.3095488 (2021).
Li, C. & Chen, X. A staged approach with structural sparsity for hyperspectral unmixing. IEEE Sens. J. 23(12), 13248–13260. https://doi.org/10.1109/JSEN.2023.3270885 (2023).
Sun, L. et al. Weighted nonlocal low-rank tensor decomposition method for sparse unmixing of hyperspectral images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 13, 1174–1188. https://doi.org/10.1109/JSTARS.2020.2980576 (2020).
Ling, Q. et al. Hyperspectral detection and unmixing of subpixel target using iterative constrained sparse representation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 15, 1049–1063. https://doi.org/10.1109/JSTARS.2022.3140389 (2022).
Wang, Z. L. & Xiao, H. Distributed compressed hyperspectral sensing imaging based on spectral unmixing. Sensors 20(8), 2305. https://doi.org/10.3390/s20082305 (2020).
Ding, M., Fu, X. & Zhao, X. L. Fast and structured block-term tensor decomposition for hyperspectral unmixing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 16, 1691–1709. https://doi.org/10.1109/JSTARS.2023.3238653 (2023).
Xiao, H., Wang, Z. L. & Cui, X. Y. Distributed compressed sensing of hyperspectral images according to spectral library matching. IEEE Access 9, 112994–113006. https://doi.org/10.1109/ACCESS.2021.3104025 (2021).
Song, F. X. & Deng, S. W. First-order graph trend filtering for sparse hyperspectral unmixing. IEEE Geosci. Remote Sens. Lett. 20, 1–5. https://doi.org/10.1109/LGRS.2023.3307891 (2023).
Bioucas-Dias, J. M. et al. Hyperspectral unmixing overview: geometrical, statistical, and sparse regression-based approaches. IEEE J. Sel. Topics Appl. Earth Obs. Remote Sens. 5(2), 354–379. https://doi.org/10.1109/JSTARS.2012.2194696 (2012).
Wang, L. et al. Compressed sensing reconstruction of hyperspectral images based on spectral unmixing. IEEE J. Sel. Top. Signal Process. 11(4), 1266–1284. https://doi.org/10.1109/JSTARS.2017.2787483 (2018).
Lu, X. Q., Wu, H. & Yuan, Y. Double constrained NMF for hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 52(5), 2746–2758. https://doi.org/10.1109/tgrs.2013.2265322 (2014).
USGS Digital Spectral Libraries. Available online: http://speclab.cr.usgs.gov/spectral-lib.html
Hyperspectral Remote Sensing Scenes. Available online: http://www.ehu.eus/ccwintco/index.php?title=Hyperspectral_Remote_Sensing_Scenes.
AVIRIS free data. Available online: http://aviris.jpl.nasa.gov/data/free_data.html.
Octave. Version 8.1.0. https://ftp.gnu.org/gnu/octave/windows/
Acknowledgements
We greatly acknowledge the Shaanxi Province Key Laboratory of Aerobat Multi-Modal Heterogeneous Information Intelligent Perception and Processing Technology for providing the necessary equipment for this study.
Funding
This research was funded by Research and Development Program of Shaanxi (Grant no. 2024JC-YBQN-0644), National Natural Science Foundation of China (Grant nos. 61901350 and 12004293), and was funded by Aeronautical Science Foundation (Grant no. 2019ZH0T7001), and was funded by Key Research and Development Program of Shaanxi (Grant nos. 2023YBGY019 and 2024GX-YBXM-262).
Author information
Authors and Affiliations
Contributions
Conceptualization, L.W.; methodology, L.W; software, W.W.; validation, L.W. and W.W.; resources, Y.B.; data curation, J.L.; writing—original draft preparation, L.W.; writing—review and editing, L.W.; visualization, W.W.; funding acquisition, L.W. and Y.B. All authors have read and agreed to the published version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Wang, L., Bi, Y., Wang, W. et al. Endmember extraction and abundance estimation algorithm based on double-compressed sampling. Sci Rep 14, 17934 (2024). https://doi.org/10.1038/s41598-024-68382-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-68382-y
