Introduction

Heat flow in soil is related to soil thermal conductivity that is used in studying the soil temperature distribution, energy balance at soil surface, the artificial heating of soils for enhanced crop production and heat flow away from industrial installations in the ground1.

Heat conduction in moist soil (soil solid particle + soil water) is occurred due to heat transfer by soil solid particles and solid-water interaction (liquid and vapor). Therefore, soil thermal conductivity is considered as apparent thermal conductivity (λ). The apparent thermal conductivity of a soil is dependent on the thermal properties of the solid materials, soil texture, pore size distribution, bulk density/porosity, water content, and the temperature of the soil2,3,4. Among these parameters, soil water content (θ) is varied greatly in field conditions. Accurate values of λ are important for soil heat process determination5. However, field measurement of λ as function of θ, i.e., λ(θ) is time consuming and costly efforts and impractical for large-scale application3,6. Therefore, different models have been proposed to predict λ(θ) by many investigators1,2,3,7,8,9,10. The soil thermal conductivity models are classified into two types: physical-based models and empirical models1,2,10,11,12. A physically based model was developed by de vries2. It was used by Campbell et al.13 and Sepaskhah and Boersma1 to predict λ(θ) in different soil temperatures and soil textures. However, it requires appropriate critical soil water content and shape factor for accurate prediction of λ(θ)14,15. With the continuous development of the model, although the physical mechanism considered by those models are becoming more and more comprehensive, the increase in parameters increases the computational difficulty of the model, limits the use of model in practice and improves the accuracy to a limited extent. Therefore, a new model proposed by Xiong et al.5 that described the relationship between soil thermal conductivity and degree of saturation, furthermore, dry soil thermal conductivity and saturated soil thermal conductivity were described using a linear expression and geometric mean model, respectively. Also, a quadratic function with one constant was added to calculate λ beyond the lower λdry and upper λsat limit conditions. However, they used a constant value that should be different for different soil textures that are not given for all different soil textures.

Different empirical models for λ(θ) prediction have been proposed by Kersten16, Campbell8, Johansen7, Chung and Horton18, and Lu et al.10. Kersten16 proposed an empirical model that requires bulk density (ρb). However, it is not appropriate for prediction of λ at low soil water contents. An empirical model [λ(θ)] with two parameters (i.e., soil bulk density and clay content) was proposed by Campbell8 to estimate the soil λ for silt, loam soils and forest litter, that is not appropriate for all soil textures. Therefore, as the thermal conductivity accounts for the tortuosity of the soil, it is described with a non-linear simple empirical equation presented by Chung and Horton17. This equation has been used in models for simulation of heat and water flow in soil such as HYDRUS model18. In this model, they used soil measured temperature and soil water content to inversely solve for the coefficients of the empirical equation for λ(θ). However, this procedure is required to measure the soil water content and temperature in field that is time consuming and costly for different soil textures.

Johansen7 introduced a simple empirical model for λ(θ) that is based on normalized thermal conductivity (Ke), degree of saturation (Sr) and soil mineral compositions. Many investigators used the Johansen7 model to predict λ(θ) for many soils accurately10,14. Later on, Cote and Konrad9 improved the Johansen7 model by using an empirical relationship between Ke and Sr. However, the modified Johansen7 model by Cote and Konrad9 was not able to predict λ(θ) accurately at lower soil water contents, especially in fine-textured soils10. Therefore, it was modified further to be applicable for lower soil water contents and fine-textured soils10. However, the modified model by Lu et al.10 showed high sensitivity to sand fraction (quartz), especially at soil water content higher than 0.2 cm3 cm−3. Therefore, this modified model needs further verification for different soil textures.

Sigmoidal model (i.e., logistic growth curve) initially was used for describing population growth. Logistic growth equation is a sigmoidal curve that can be used to model growth that increases gradually at first, more rapidly in the middle, slowly at the end and leveling off at a maximum value after some period of time. It has been widely used in biomass accumulation, crop height, leaf area expansion and crop yield prediction19,20,21,22,23. Also, soil thermal conductivity depends mostly on the soil particles and soil pores size distribution that is filled variably with air and water in different soil water contents. On the other hand, the soil particles and soil pores size distribution follow simple sigmoidal function24. Therefore, the λ(θ) function could be shown by a sigmoidal model1,2. On the other hand, field measurement of λ(θ) is time consuming, costly effort and not practical for large scale application. Therefore, a sigmoidal model should be developed for λ(θ).

The objective of this study was to develop a simple empirical model based on the logistic equation for λ(θ) at room temperature for entire soil water content range and soil textures. Further, the performance of the new empirical model along with Johansen7, Lu et al.10 and Xiong et al.5 was evaluated by comparing the predicted thermal conductivity with the measured thermal conductivity for different soil textures.

Method and materials

Soil thermal conductivity measurement

Six soils from Fars province, I.R. of Iran were used in the new model development. The physical properties of these soils are presented in Table 1. Soil particle size distribution was determined by hydrometer method25. Soil textures determined based on soil particle size distribution using USDA procedure.

Table 1 Physical properties of soils used in model development and validation.
Full size table

The soil samples were prepared by adding the amount of water required to bring a pre-packed, air-dried sample to the desired water content. The air-dried soil was packed in glass jars (97 mm in diameter and 100 mm in length, partially filled with soil to a height of 70 mm) which were tapped twice on the top of the laboratory bench with each scoop of sample poured into it. The number of scoop and the filled volume per jar was the same for each sample in order to obtain unique soil bulk density for each soil texture (Table 1). Bulk density of the samples was determined by dividing the weight of dry soil to the soil volume in the jar. Pre-determined quantities of water were applied to the samples such that no water was pond on the soil surface. This method of water application prevented trapping of air in the samples. Soil samples with low water content were prepared by pouring air dried soil on a plastic sheet and spreading it evenly in a thin layer. Required amounts of water were sprinkled onto the soil which was then shaken in a plastic bag to distribute the water uniformly and packed into jars. The containers were capped with a lid to prevent water loss by evaporation during storage. The containers were kept in an empty ice box in laboratory with a room temperature about 20 ± 1 °C for 24 h. Thermal conductivity (λ) measurement made at the same time during different days for having similar air temperature during the λ measurement. Apparent thermal conductivity was measured with a cylindrical heat probe with 60 mm length and 1.28 mm diameter (kd2, Decagon Device, Inc, Pullman, WA, USA). The heat probe was inserted in soil samples contained in glass jars. Immediately after removing the cap, the probe was inserted into the soil samples carefully to measure the λ and probe temperature with three replications after 1.5 min. of turning on the kd2 apparatus. The mean values of three replications were considered as soil λ. After λ measurement, soil water contents of samples were measured by gravimetric procedure in oven with 105 °C for 24 h. The gravimetric soil water content was multiplied by soil bulk density to determine the volumetric water content.

Model development

Johansen model

The concept of normalized thermal conductivity, Ke (i.e., the Kersten number) was proposed by Johansen7 and he used a relationship between λ and Ke as follows:

$$ \lambda = \left( {{\lambda_{sat}} - {\lambda_{dry}}} \right){K_e} + {\lambda_{dry}} $$
(1)

where, λdry and λsat are the thermal conductivity of dry and saturated soils (w m−1 K−1), respectively. The values of λdry and λsat were determined as follows:

$$ {\lambda_{sat}} = {\lambda_s}^{1 - n}{\lambda_w}^n $$
(2)

and

$$ {\lambda_{dry}} = \left( {0.135{\rho_b} + 64.7} \right)/\left( {2700 - 0.947{\rho_b}} \right) $$
(3)

where, n is the soil porosity, λw is the thermal conductivity of water (0.594 w m−1 K−1 at 20 °C), ρb is the soil bulk density (kg m−3), and λs is the effective thermal conductivity of soil solid particles (w m−1 K−1). The values of λs are calculated by the following equation as a geometric mean:

$$ {\lambda_s} = {\lambda_q}^q{\lambda_o}^{1 - q} $$
(4)

where, λq is the thermal conductivity of quartz (sand) (7.7 w m−1 K−1), q is the quartz (sand) content (fraction), λo is the thermal conductivity of other soil particles content (2.0 w m−1 K−1 for soils with q > 0.2 and 3.0 w m−1 K−1 for soils with q ≤ 0.2). Furthermore, Johansen (1975) proposed empirical relationships between Ke and normalized soil water content for different soil textures as follows:

$$ {K_e} = 0.7log{S_r} + 1.0\quad \left( {{S_r} > 0.05} \right)\,{\text{for}}\,{\text{coarse}}\,{\text{ - textured}}\,{\text{soils}} $$
(5)
$$ {K_e} = log{S_r} + 1.0\quad \left( {{S_r} > 0.1} \right)\,{\text{for fine - textured}}\,{\text{soils}} $$
(6)

where, Sr is the normalized soil water content as θ/θs where θ and θs are the soil water content and saturated soil water content (cm3 cm−3), respectively.

Modified Cote and Konrad model

Although Cote and Konrad9 improved the Johansen7 model, however their modified model was not accurate in λ prediction for fine-textured soils at lower water contents. Therefore, Lu et al.10 proposed the following equation for Ke estimation across the entire range of soil water content:

$$ {K_e} = exp\left\{ {\alpha \left[ {1 - {S_r}^{(\alpha - 1.33)}} \right]} \right\} $$
(7)

where, α is the soil texture dependent parameter (α = 0.96 for coarse-textured soils and α = 0.27 for fine-textured soils, respectively) and 1.33 is a shape factor.

Furthermore, Lu et al.10 used a simple empirical linear relationship between λdry and soil porosity (n) as follows:

$$ {\lambda_{dry}} = - an + b $$
(8)

where a and b are constants as a = 0.56 and b = 0.51 for 0.0 < n < 0.6, and n is the soil porosity. The value of λsat was calculated according to Eq. (2) used in Johansen7 model.

New Xiong et al. model

The proposed model by Xiong et al.5 is as follows:

$$ \lambda = P + Q{S_r}^R + S\left\{ {exp\left[ {{S_r}\left( {1 - {S_r}} \right)} \right]} \right\} $$
(9a)
$$ P = \, {\lambda_{dry}} = 0.51 - 0.6n $$
(9b)
$$ Q = \, {\lambda_{sat}} - \, {\lambda_{dry}} = {\left( { \, {\lambda_q}^q{\lambda_o}^{1 - q}} \right)^{1 - n}}{\left( {\lambda_w} \right)^n}\left( {0.51 - 0.6n} \right) $$
(9c)
$$ S = 1.5\left( {{S_r} - {S_r}^2} \right) $$
(9d)

where, n is the soil porosity (–), Sr is the degree of soil saturation as θ/θs (%), λq is the thermal conductivity of quartz (sand) (7.7 w m−1 K−1), q is the quartz (sand) content (fraction), λo is the thermal conductivity of other soil particles content (2.0 w m−1 K−1 for soils with q > 0.2 and 3.0 w m−1 K−1 for soils with q ≤ 0.2), λw is the thermal conductivity of water (0.594 w m−1 K−1) and the value of R is 1.2 for sand, 1.5 for the fine-textured soils, and 2.0 for clay. However, the values of R for fine-textured soils are not well designated for different fine-textured soils.

Sigmoidal model

Sigmoidal model (i.e., logistic equation) to describe the soil thermal conductivity as a function of soil water content is as follows:

$$ \lambda = K/\left[ {1 + Aexp\left( { - B\theta } \right)} \right] $$
(10)

where, λ is the soil thermal conductivity (w m−1 K−1), θ is the soil volumetric water content (cm3 cm−3), K is the upper most asymptote implies the upper limits of soil thermal conductivity, and A and B are coefficients as taken of initial stage and total accretion rate.

Measured soil thermal conductivities at different soil water contents for six soils with different textures were used in Eq. (10) to determine the values of K, A, and B by Solver tool in EXCEL software. Then, the values of K, A, and B were used in multiple linear regression analysis in EXCEL software to obtain an empirical model to estimate the values of K, A, and B based on soil physical parameters. These parameters were sand, silt, and clay contents, soil bulk density, soil porosity. Among these parameters sand content and soil bulk density entered in the empirical multiple linear regression as follows:

$$ K = {a_o} + {a_1}q + {a_2}{\rho_b} $$
(11)
$$ A = {b_{o + }}{b_1}q + {b_2}{\rho_b} $$
(12)
$$ B = {c_o} + {c_1}q + {c_2}{\rho_b} $$
(13)

where, ao, a1, a2, bo, b1, b2, co, c1, and c2 are constants, q is the sand particle content (%), and ρb is the soil bulk density (g cm−3). The entrance of soil bulk density and sand content is due to the fact that the thermal conductivity of sand (instead of quartz) is much higher than the clay and silt particles and it contributes much more to the λ value of soil, and value of bulk density indicates the compaction of soil, soil pores distribution and extend the contact of the soil particles to cause the soil thermal conductance.

Using the measured values of λ in sigmoidal model (Eq. 10) and Solver tool in EXCEL software, the values of K, A, and B were determined for six different soil textures (Table 2). These values were used in Eq. (10) to estimate λ(θ) for different soil water contents.

Table 2 The estimated values of the logistic equation (K, A, and B) for the sigmoidal model development and model validation.
Full size table

Sigmoidal model validation

For validation of the new model, measured data from Lu et al.10 for three different soil textures are used (Table 1). By use of the empirical multi-linear equations (Eqs. 11, 12, and 13), the values of the empirical-logistic constants (K, A, and B) were estimated. Based on these coefficients the values of λ(θ) were estimated. Then, the estimated values of λ(θ) were compared with the measured values reported by Lu et al.10.

Statistical analysis

The outputs of the model were compared by the measured values using following statistical parameters:

$$ NRMSE = {\left( {1/N{\Sigma^n}_{i = 1}{{\left( {{X_i} - {Y_i}} \right)}^2}} \right)^{0.5}}/O $$
(14)

where, NRMSE is the normalized root mean square error, N is the number of observations, X is the measured values, Y is the estimated values and O is the mean values of measured data. The value of NRMSE approaches 0.0 for the accurate estimation. The closer the NRMSE is to 0, the model is more accurate. Linear relationship between the measured and predicted values is compared with 1:1 line with slope and intercept of 1.0 and 0, respectively by using Fisher F-test.

Results and discussion

Measured thermal conductivity

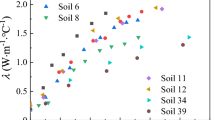
Measured λ as a function of θ for six different soil textures are shown in Fig. 1. The values of λ for different soil textures are different. For given value of θ, the values of λ for coarse-textured soils (sandy loam, and loamy sand) are higher than those values for medium-textured soil (loam) and λ of medium textured soil are higher than those for fine-textured soils (silty clay). The main reason for this finding is greater soil porosity in fine-textured soil (Table 1). By increasing porosity, λ is decreased due to higher air and water content in fine-textured soils with much lower λ value for air and water1. Of course, the sand content (quartz) in coarse-textured soil is higher with higher λ values than those in fine-texture soil with low values of sand/higher values of clay with lower values of λ (Table 1). Therefore, the values of λ in coarse textured soils are higher than those in fine-textured soils.

Figure 1
figure 1

Measured soil thermal conductivity at different water contents for different soil textures.

Full size image

Furthermore, for given soil texture, λ value increased by increasing soil volumetric water content. However, the value of λ remained unchanged as the θ values increased from zero to 0.05–0.06 cm3 cm−3 for medium textured soil (loam) to fine-textured soils (silt loam, clay loam, and silty clay) (Fig. 1). This is occurred because the fine-textured soils showed large surface area26, therefore higher water content is needed to form water bridge between soil particles. By increasing the soil water content higher than the critical soil water content, the λ was increased faster as θ was increased. This increase in λ was higher in coarse-textured soils than in fine-textured soils. This increase in λ is due to the formation of wedges of water at the points where soil particles make contact. With further addition of water, soil pores gradually are filled and the increase of λ with each increment of water added becomes smaller. Furthermore, it is indicated that λ is increased by soil bulk density due to increase in number of soil particles in unit volume of soil and consequently increase in the number of contacts between soil particles that increase the heat conduction.

Figure 1 indicated that λ(θ) curve could be grouped into two different soil textures as coarse-textured soils (sandy loam, and loamy sand) with sand content > 40%, and fine-textured soils (loam, silty loam, clay loam, and silty clay) with sand fraction of ≤ 40% that is corresponding to those findings reported by Lu et al.10.

Sigmoidal model development

The estimated λ(θ) and the measured λ are shown in Fig. 2. It is indicated that the estimated values of λ by logistic equation are very close to those of measured values, especially in low and high soil water content, that the accuracy of estimation is higher.

Figure 2
figure 2

Measured and predicted soil thermal conductivity with logistic equation (Eq. 10) for different soil textures: (a) Clay loam, (b) Silty clay, (c) Silty loam, )d) Loam, )e) Loamy sand, (f) Sandy loam.

Full size image

The values of K, A, and B for six different soils were used to develop linear-multiple regression equation to relate these values to different soil physical properties, i.e., sand, silt, clay, bulk density, porosity, geometric mean diameter, and geometric standard deviation by multiple regression analysis. According to the ANOVA Table and probability level statistics for the coefficients of linear multiple regression (data not shown), the sand particle content and soil bulk density were included in the linear-multiple regression as follows:

$$ K = 0.0035q + 0.878{\rho_b} $$
(15)

N = 6, R2 = 0.999, SE = 0.028, p < 0.0001

$$ A = - 0.0935q + 7.458{\rho_b} $$
(16)

N = 6, R2 = 0.990, SE = 0.666, p = 0.0007

$$ B = - 34.66 - 0.219q + 47.56{\rho_b} $$
(17)

N = 6, R2 = 0.956, SE = 1.277, p = 0.009,

where, q is the sand content (%), ρb is the bulk density (g cm−3), N is the number of observations, R2 is the coefficient of determination, SE is the standard error, and p is the level of probability. The statistical parameters indicated that Eqs. (15)–(17) have acceptable accuracy. Therefore, by using these equations and sand content and soil bulk density of different soils, the values of K, A, and B can be estimated. Then, by using these constants in Eq. (10), the values of λ for different soil water contents can be estimated. To show the accuracy of these estimations, the estimated λ and the measured λ for the six different soils used in the model development are presented in Fig. 3. In this Figure, relationship between the measured λ (λm) and the predicted λ (λp) were compared with 1:1 line by Fisher F-test. It is indicated that the slope and intercept of the linear relationships are close to 1.0 and 0.0, respectively and the estimation of λ are accurate.

Figure 3
figure 3

Comparison between measured soil thermal conductivity (λm) and predicted values (λp) by the sigmoidal model for different soil textures: (a) Loamy sand, (b) Sandy loam, (c) Loam, (d) Silt loam, (e) Clay loam, (f) Silty clay.

Full size image

Sigmoidal model validation

For validation of the sigmoidal model, the measured λ(θ) of three different soil textures presented by Lu et al.10 was used. The physical properties of these soils are shown in Table 1. Initially, the values of K, A, and B were estimated by the sand content and ρb of the soils presented by Lu et al.10, then the estimated values of K, A, and B (Table 2) were used in Eq. (10) and λ(θ) was estimated. The estimated λ(θ) and the measured values of λ by Lu et al.10 are shown in Fig. 4. It is shown that in a wide range of soil water contents the estimated values of λ are very close to the measured values. However, in saturation water content the estimated λ is lower than the measured values. This difference is more pronounced in coarse-textured soil (sand), however this difference is not significant. Relationship between the measured and estimated λ was compared with 1:1 lone in Fig. 5. Comparison between the slopes and intercepts by Fisher F-test indicated that there are non-significant differences between the slope and 1.0 and the intercept and 0.0 (p > 0.05). The linear relationships are as follows:

$$ {\lambda_m} = 1.03{\lambda_p},\;\;\;{R^2} = 0.993\quad {\text{For}}\,{\text{silt}}\,{\text{loam}}\,{\text{soil}} $$
(18)
$$ {\lambda_m} = 1.05{\lambda_p},\;\;\;{R^2} = 0.988\quad {\text{For}}\,{\text{loam}}\,{\text{soil}} $$
(19)
$$ {\lambda_m} = 1.16{\lambda_p},\;\;\;{R^2} = 0.991\quad {\text{For}}\,{\text{sand}}\,{\text{soil}} $$
(20)

where λm and λp are the measured and predicted λ, respectively (w m−1 K−1). Therefore, the estimated λ are accurate, however there is 16% under-estimation of λ by the sigmoidal model for sand soil at soil water content near saturation (Figs. 4, and 5).

Figure 4
figure 4

Measured soil thermal conductivity (λm) by Lu et al.10 and predicted values (λp) for validation of the sigmoidal model for different soil textures: (a) Silt loam, (b) Loam, (c) Sand.

Full size image
Figure 5
figure 5

Comparison between measured soil thermal conductivity (λm) by Lu et al.10 and predicted values (λp) by the sigmoidal model for different soil texture: (a) Silt loam, (b) Loam, (b) Sand.

Full size image

Evaluation of different models

The physical parameters of six soils used in developing the new model (Table 1) and three soils used in Lue et al.10 (Table 1) were used to evaluate the models of Johansen7 [Eqs. (1)–(6)], Lu et al.10 [Eqs. (7)–(8)] and the sigmoidal model proposed in this study [Eqs. (10)–(13)]. Classification of soil texture as coarse or fine is critical in Johansen7 and Lu et al.10 models to estimate Ke. Therefore, in this evaluation the loam soil was considered as coarse/fine texture to evaluate the suitability of this selection. Results of these evaluations are presented in Figs. 6, and 7. Comparison between the measured and predicted λ is evaluated by NRMSE (Eq. 14) (Table 3). Classification of loam soil in Johansen7 and Lu et al.10 models as a fine-textured soil for estimation of Ke value indicated that NRMSE of this selection is lower as 0.107. Whereas, based on classification as coarse-textured soil, this selection is more critical in Johansen7 model with higher value of NRMSE as 0.916 for coarse-textured selection in comparison to 0.107 for fine-textured soil selection. However, this classification in Lu et al.10 model is not very critical due to NRMSE of 0.133 for coarse-textured selection in comparison to 0.107 for fine-textured soil selection.

Figure 6
figure 6

Measured soil thermal conductivity (λm) and predicted values (λp) by different prediction models for different soil textures: (a) Clay loam, (b) Silty clay, (c) Silt loam, (d) Loam, (e) Sandy loam, (f) Loamy sand.

Full size image
Figure 7
figure 7

Measured soil thermal conductivity by Lu et al.10 and predicted values by different prediction models for different soil textures: (a) Silt loam, (b) Loam, (c) Sand.

Full size image
Table 3 Statistical parameter (NRMSE) for evaluation of different model to estimate soil thermal conductivity at different water content.
Full size table

Johansen7 and Lu et al.10 models resulted in lower λ than the measured values for loam and silt loam soils in a wide range of soil water contents (Figs. 6, and 7), while the sigmoidal model predicted λ accurately. On the other hand, for light-textured soils (sandy loam and loamy sand) the Johansen7 and Lu et al.10 model prediction of λ was higher than the measured values, especially at water contents higher than 0.30 cm3 cm−3, while the sigmoidal model predicted λ with a good accuracy. This difference might be due to the fact that sand particle in soil is assumed as quartz with a higher λ compared with other minerals in soil that is used in prediction of λ. Therefore, small error in this assumption results in higher estimation of λ compared with the measured values.

The values of NRMSE indicated that Lu et al.10 predicted λ for most of soil textures with higher accuracy than those predicted by Johansen7 model (Table 3). For sand, the sigmoidal model was not superior to those of Johansen7 and Lu et al.10 models. In general, the sigmoidal model was superior to the other two models in prediction of λ for wide range of soil textures, except sand.

Results of predicted soil λ values based on Xiong et al.5 model for different soil textures are shown in Fig. 8. Also, the measured values are shown in this Figure. It is indicated that for soil textures of loam, silty loam and clay loam Xiong et al.5 model predicted λ values accurately. This is shown in Fig. 9 that presented the relationships between the measured and predicted values. These relationships for loam, silty loam and clay loam with slopes of near to 1.0 are similar to 1:1 line with slope of 1.0 and intercept of 0.0. Whereas, for loamy sand, sandy loam and silty clay soils Xiong et al.5 model was not able to predict λ values. These discrepancies are mainly due to uncertainties in designating appropriate values of R in Eq. (9a) for different soil textures.

Figure 8
figure 8

The predicted, λp5, and measured soil thermal conductivities (λm) as a function of soil volumetric water contents.

Full size image
Figure 9
figure 9

Relationships between the measured (λm) and predicted, λ5, soil thermal conductivities at different soil volumetric water contents.

Full size image

Considerations on sigmoidal model

Soil thermal conductivity (λ) is non-linear with many influencing factors, and a simple derivation using only multivariate linear analyses is feasible in some sense, but does not focus on temperature, a factor that has a significant effect. This point may be most valid in high soil temperature condition where water vapor flow occurs in the soil in a greater extent that should be considered in soil thermal conductivity as reported by Sepaskhah and Boersma1. However, in low soil temperature this phenomenon can be ignored for simplicity.

In Figs. 4 and 5 we validated the performance of the sigmoidal model by using available data from Lu et al.10 for the given soil textures as silt loam, loam and sand that cover heavy to light textures. In Fig. 5, the linear relationships between λm and λp [Eqs. (18) (19) and (20)] were compared with the 1:1 line. In these relationships the intercepts are 0.0 and the slopes are close to 1.0 indicated that the λm and λp values are statistically close together, except for sand soil at soil water content near saturation with 16% under-estimation.

The implications of Multiple Linear Regression may fail to capture nonlinear relationships and performs poorly for complex data patterns. Whether interpolation using multiple linear regression is a reasonable way to derive the proposed model may not be convincing and other methods may be used. In terms of model validation, of course it is better to validate the λp by simulation with models such as HYDRUS, however, in our study the soil temperature and water flow such as infiltration rate has not been measured that is required for validation of λp in HYDRUS model as reported by Nakhaei and Simunek18. Therefore, the used procedure in this study is the possible way to validate the λp.

Conclusions

A sigmoidal model was developed for predicting soil thermal conductivity from its water content based on a logistic equation that its constants are estimated based on the proposed empirical equations by using soil sand content and bulk density. The sigmoidal model was validated with good accuracy for a wide range of soil textures. Comparison of the sigmoidal model with Johansen and Lu et al. models indicated that the sigmoidal model was superior to the other two models in prediction of λ for a wide range of soil textures and soil water contents. Furthermore, comparison with a recently proposed model by Xiong et al. indicated that our sigmoidal model is superior.