Introduction

Concrete has become the prevalent building material in modern society due to its affordability, ease of casting, and substantial compressive strength after hardening1. In 2017, the global annual consumption of concrete reached 30 billion tons, and projections indicate a 50% increase by 20502. To ensure the quality of construction, it is imperative to measure the compressive strength of concrete to guarantee the structural reliability of concrete. The traditional methods involve testing specimens in a specialized laboratory, encompassing several stages: ingredient preparation, mixing, curing, and compression testing3. Among these stages, achieving the desired concrete strength and optimal workability in the laboratory requires technicians to thoroughly study various admixtures. If the test results fall short of the required strength in the concrete mix design, the entire concrete design process must be reinitiated, leading to an extended testing cycle and a delay in obtaining timely compressive strength data.

Due to the crucial role of concrete compressive strength testing in engineering construction, researchers have developed numerous methods for testing compressive strength. Currently, the primary testing methods include non-destructive testing and micro-damage testing4,5. Specifically, the non-destructive testing method quantifies the strength of concrete based on its relevant physical properties, inferring the relationship between strength and these properties without causing damage to the concrete components. These methods primarily comprise rebound6, ultrasonic pulse velocity7, and the ray method8. The rebound method, for instance, employs a rebound instrument to measure concrete hardness, inferring its compressive strength based on carbonation depth. In comparison to other methods, this technique is simple and flexible, yet its accuracy is relatively low6. Ultrasonic pulse velocity measures concrete strength by observing changes in ultrasonic waves. Nevertheless, variations in materials, moisture content, and age significantly affect the relationship between ultrasonic wave propagation speed and concrete strength, posing challenges in determining compressive strength7. While γ rays can be employed for detecting concrete compressive strength, their engineering use is rare due to radiation concerns8. The primary advantage of non-destructive concrete testing is its ability to measure compressive strength without causing damage, facilitating quick and easy testing. Nevertheless, the accuracy of this method requires improvement.

Micro-damage testing assesses the strength and defects of concrete structures through systematic testing. In contrast to non-destructive testing of concrete, micro-damage testing boasts high detection accuracy. Micro-damage detection methods encompass core drilling9, Pull-out10, Nail shooting11, and others. The core drilling method involves drilling core samples from concrete components, followed by calculating concrete strength through destructive tests. While this method yields highly accurate experimental results, it suffers from the drawbacks of relatively complex operation and high cost9. The Pull-out method involves pre-embedding riveted parts in structural components, recording external force magnitudes and the destructive force borne by the concrete during specimen extraction, and estimating compressive strength by establishing a relationship between obtained data and compressive strength. In comparison to traditional core drilling methods, the Pull-out method offers advantages such as simplicity of operation, low cost, and easy implementation. Nevertheless, the Pull-out method is influenced by numerous experimental factors, potentially leading to lower accuracy compared to the core drilling method10. The Nail shooting method involves using a hammer shaft to shoot a test nail into the concrete, then using a dial gauge to measure the depth of injection into the concrete, and estimating compressive strength based on this depth. However, establishing its correlation formula necessitates conducting a substantial number of concrete specimen failure tests before employing this method for strength detection11. Furthermore, the aforementioned methods are exclusively employed for detecting concrete compressive strength during the usage stage. If a method could predict compressive strength with varying factor ratios in the early design stage, it would significantly expedite industrial construction progress and diminish compressive strength testing costs.

Machine learning has found extensive applications across various fields12,13,14,15,16, with numerous algorithms utilized to predict concrete compressive strength. These algorithms include gene expression programming (GEP), support vector regressor (SVR), decision tree (DT), adaboost, randomforest (RF), artificial neural network (ANN), and extreme learning machine (ELM). Notably, Gholampour et al. employed GEP to predict the 28-day compressive strength of recycled aggregate concrete, constructing a database for performance testing17. Javed et al. applied GEP to predict the compressive strength of Bagasse Ash-based concrete, achieving an R2 value exceeding 0.8 between observed and predicted values18. Yang et al. utilized GEP to predict the compressive strength of concrete blended with carbon nanotubes, evaluating the contribution of different features through shapley analysis19. The advantage of GEP lies in its ability to generate formulas in a visible manner, making them easy to understand. However, a disadvantage is that optimizing GEP parameters can be challenging, necessitating efforts to enhance its prediction accuracy. Ling et al. combined SVR with k-fold cross-validation to predict the compressive strength of concrete in marine environments. Nevertheless, this model is a black-box model lacking interpretability20. Farooq et al. applied adaboost and RF to predict the compressive strength of high-performance concrete (HPC), demonstrating that the integrated model can enhance the performance of compressive strength prediction21. Network connectivity-based models, including ANN and ELM, have been widely employed for predicting concrete compressive strength. Yeh utilized ANN to predict the compressive strength of HPC, validating their model’s performance through a set of trial batches22. Additionally, Keshavarz and Torkian used ANN to predict compressive strength with different mixing ratios, revealing that while ANN can effectively predict concrete compressive strength, its efficacy is inferior to that of adaptive Neuro Fuzzy Inference23. ELM, a relatively recent addition to the ANN family, was employed by Al-Shamiri et al. to predict the compressive strength of high-strength concrete (HSC). The prediction results of the ELM-based model surpassed those of ANN24. The advantage of ANN lies in its intricate nonlinear mapping capability, though it comes with the drawback of requiring a substantial amount of data and being susceptible to falling into local optima. Deepforest, an integrated model proposed by Zhou et al. in 201725, amalgamates the strengths of RF and deep ANN. It deeply integrates traditional tree-based models (like RF) through a cascaded forest structure, endowing it with robust learning ability and enhancing the nonlinear mapping ability of the model through multi-grained scanning. Furthermore, in comparison to deep neural networks, Deepforest requires fewer hyperparameters and is easier to train.

The objective of this study is to introduce the latest machine learning algorithm and comprehensively evaluate the predictive performance of various machine learning algorithms in predicting the compressive strength of concrete. To identify the optimal combination of factors, the study compared the model’s performance with various factor combinations and ultimately determined the optimal subset, comprising blast furnace slag, superplasticizer, age, cement, and water. On this basis, 12 distinct machine learning algorithms were employed for modeling and parameter optimization. Ultimately, results on the independent testing dataset demonstrated that the Deepforest-based model yielded the most effective predictions for concrete compressive strength, making it a more efficient predictor.

Methods

Dataset construction

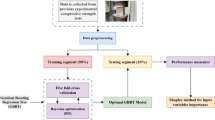
The dataset used in this study consists of a total of 1030 concrete samples (Downloaded from https://archive.ics.uci.edu/dataset/165/concrete+compressive+strength). It was randomly divided into the training dataset and the independent testing dataset, maintaining an approximate ratio of 8:2. Consequently, 822 samples were utilized for model training, and 208 samples were designated for performance evaluation. Each sample comprises eight factors, namely blast furnace slag, fly ash, water, superplasticizer, coarse aggregate, fine aggregate, age, and cement. The statistical analysis of the sample data is presented in Table 1.

Table 1 Statistical analysis for the sample data.
Full size table

Correlation between different factors and concrete compressive strength

Correlation analysis is a statistical method used to understand the interactions between different factors and delve deeper into their impact on a specific variable26. To investigate the correlation between compressive strength and different factors, all 1030 samples in the benchmark dataset were used for analysis, and the sample distribution of different factors relative to compressive strength is shown in Fig. 1. The compressive strength of each sample ranges from 2.33 to 82.6. As for the different factors—blast furnace slag, fly ash, water, superplasticizer, coarse aggregate, fine aggregate, age, and cement—their values range from 0 to 359.4, 0 to 200.1, 121.8 to 247, 0 to 32.2, 801 to 1145, 594 to 992.6, 1 to 365, and 102 to 540, respectively. Owing to the substantial difference between the values of different factors, the model may exhibit bias towards factors with larger values. Hence, normalizing different characteristic factors is necessary before the follow-up process. Additionally, we observed that the median values of blast furnace slag, fly ash, and high-efficiency water reducing agent in 45.73%, 54.79%, and 36.80% of the samples were 0, respectively. This may be attributed to the non-utilization of these elements or the presence of missing records. If records are missing, it can impact the accuracy and reliability of the machine learning model. Hence, strategies such as deletion, mean/median interpolation, or regression-based interpolation (such as K-Nearest Neighbors, KNN) can be employed to enhance data integrity.

Figure 1
figure 1

Sample distribution of different factors relative to concrete compressive strength.

Full size image

To further investigate the correlation between different factors, the correlation coefficient between each factor was calculated. As shown in Fig. 2, the correlation coefficient of compressive strength and each factor—blast furnace slag, fly ash, water, superplasticizer, coarse aggregate, fine aggregate, age, and cement—were 0.13, − 0.11, − 0.29, 0.37, − 0.16, − 0.17, 0.33, and 0.5, respectively. The superplasticizer factor has the strongest correlation with compressive strength. Furthermore, we also observed that the correlation coefficient between fly ash, water, coarse aggregate, and fine aggregate was negative, suggesting that we should reasonably control the addition of these elements during the experiments.

Figure 2
figure 2

Correlation analysis of different factors. The meanings of different correlation coefficient values are as follows: 0.1–0.3 stands for weak correlation; 0.3–0.5 represents moderate correlation; 0.5–1.0 is strongly correlated.

Full size image

Normalization

Normalization is employed to convert data into a unified proportional range, thereby eliminating dimensional differences between different factors27. By utilizing normalization, data can be mapped to a specific range, such as [0, 1] or [− 1, 1], ensuring that different factors have similar numerical ranges. Some machine learning algorithms, such as ANN and SVR, are sensitive to the numerical range of the input data. If the numerical range of the input data varies significantly, it may lead to slower convergence speed in the model training process. In this study, the maximum-minimum normalization method was applied to map different factors to [0, 1], and the specific calculation formula is as follows:

$$x^{*} = \frac{{x - {\text{min}}\left( x \right)}}{{\max \left( x \right) - {\text{min}}\left( x \right)}}$$
(1)

where \(x\) is the factor value of each sample, \(\text{min}(x)\),\(\text{max}\left(x\right)\) are the minimum and maximum values of the factor for all samples, respectively. \({x}^{*}\) stands for the normalized factor for each sample.

RandomForest and ExtraTrees

Randomforest (RF) is an ensemble learning algorithm introduced by Breiman et al. in 2001, integrating multiple CART decision trees for prediction28. It excels in handling nonlinear, high-dimensional complex problems. To augment the number of decision trees in RF, researchers frequently employ multiple random vectors to construct each decision tree in RF. The algorithmic process of the random forest is as follows:

Algorithm 1
figure a

The algorithm of randomforest.

Full size image

ExtraTrees is a variant of RF29. The distinction between ExtraTrees and RF lies in the determination of the training set for each decision tree: bootstrap sampling is used in RF, while the original training set is employed in ExtraTrees. Moreover, RF selects an optimal factor partition point, similar to the traditional decision tree. However, ExtraTrees will randomly select a factor value to partition the decision tree. Due to the random selection of factor partition points rather than the optimal position, the size of the decision tree generated by ExtraTrees is generally larger than that of the decision tree generated by RF. In other words, the variance of the model is further reduced relative to RF, but the bias is increased relative to RF. At certain times, the generalization ability of ExtraTrees is superior to that of RF.

Deepforest

Deepforest, also known as cascade forest, was initially proposed by Zhou et al. in 201725. To comprehensively integrate the distinct advantages of RF and ExtraTrees, each layer of Deepforest comprises two RF-based models and two ExtraTrees-based models (Fig. 3). The prediction of concrete compressive strength for each cascade layer is the average of the four models.

Figure 3
figure 3

Schematic diagram of Deepforest.

Full size image

During model training, the model performs layer-by-layer calculations, transferring the calculation results from the previous layer to the next layer, and assessing the difference between the prediction error of each layer and the preceding layer. If the prediction error of the current layer decreases compared to the previous layer, the calculation of the next layer continues. However, if the prediction error of this layer is higher than that of the previous layer, the calculation of the next layer is halted. Subsequently, the layer with the lowest prediction error is selected as the output layer to generate the prediction result.

The optimal number of the tth layer of Deepforest should minimize the prediction error of the model when the tth layer was served as the output layer. Therefore, the optimal level number \(\hat{t}\) of Deepforest should be obtained by the following formula.

$$\begin{array}{*{20}l} { \mathop {\min }\limits_{t} MSE = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left( {y_{i} - G\left( {{\varvec{x}}_{{\varvec{i}}} } \right)} \right)^{2} } \hfill \\ {s.t.\quad G\left( {{\varvec{x}}_{{\varvec{i}}} } \right) = \left\{ {\begin{array}{*{20}l} {C_{1} \left( {{\varvec{x}}_{{\varvec{i}}} } \right),} \hfill & {t = 1} \hfill \\ {C_{t} \left( {\left[ {{\varvec{x}}_{{\varvec{i}}} ,C_{t - 1} \left( {{\varvec{x}}_{{\varvec{i}}} } \right)} \right]} \right),} \hfill & {t > 1} \hfill \\ \end{array} } \right.} \hfill \\ { \quad \quad C_{t} \left( {{\varvec{x}}_{{\varvec{i}}} } \right) = \frac{1}{4}\left[ {F_{t,1} \left( {{\varvec{x}}_{{\varvec{i}}} } \right) + F_{t,2} \left( {{\varvec{x}}_{{\varvec{i}}} } \right) + CF_{t,1} \left( {{\varvec{x}}_{{\varvec{i}}} } \right) + CF_{t,2} \left( {{\varvec{x}}_{{\varvec{i}}} } \right)} \right]} \hfill \\ \end{array}$$
(2)

where \(MSE\) is the mean square error, \({\varvec{x}}_{{\varvec{i}}}\) stands for the ith sample, \(y_{i}\) represents the label of the ith sample, \(N\) is the size of the training dataset. \(G\left( {{\varvec{x}}_{{\varvec{i}}} } \right)\) is the predicted result on the ith sample. \(C_{t} \left( {{\varvec{x}}_{{\varvec{i}}} } \right)\) is the prediction result of the ith sample at the tth layer. Each layer was made up of two Randomforests \(\left( {F_{t,1} \;{\text{and}}\;F_{t,2} } \right)\) and two ExtraTrees \(\left( {CF_{t,1} \;{\text{and}}\;CF_{t,2} } \right)\). For each sample \({\varvec{x}}_{{\varvec{i}}}\), the prediction of concrete compressive strength of each cascade layer \(C_{t} \left( {{\varvec{x}}_{{\varvec{i}}} } \right)\) is the average of the above-mentioned four models.

Performance evaluation

12 different regressors, including Linear30, KNN31, DT32, SVR33, Least absolute shrinkage and selection operator (LASSO)34, Multilayer Perceptron (MLP)35, ExtraTrees29, RF28, AdaBoost36, GradientBoosting37, Bagging38 and Deepforest25, were implemented using Python. For model training, Grid search39 was applied to find the optimized hyperparameter of the different models.

Fivefold cross-validation was employed to assess the performance of different models. The training dataset is approximately divided into 5 folds, wherein each fold uses 4 folds for training, leaving one fold for testing. Subsequently, the average results of the 5 tests are computed to evaluate the model’s performance. For a more objective evaluation of different models, this study derived 4 standard indicators: coefficient of determination (R2)40, mean square error (MSE)41, mean absolute error (MAE)42, and root mean square error (RMSE)43. Among these indicators, the range of R2 is (− ∞, 1], and the compressive strength predictor achieves optimal performance when the values of these indicators are equal to 1. Regarding MSE, MAE, and RMSE, the closer the value is to 0, the smaller the prediction error. The indicators can be defined as follows.

$$\left\{ {\begin{array}{*{20}l} {R^{2} = 1 - \frac{{\frac{1}{N}\mathop \sum \nolimits_{i = 1}^{N} \left( {y_{i} - \hat{y}_{i} } \right)^{2} }}{{\frac{1}{N}\mathop \sum \nolimits_{i = 1}^{N} \left( {y_{i} - \overline{y}} \right)^{2} }}} \hfill \\ {MSE = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left( {\hat{y}_{i} - y_{i} } \right)^{2} } \hfill \\ {MAE = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left| {y_{i} - \hat{y}_{i} } \right|} \hfill \\ {RMSE = \sqrt {\frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left( {\hat{y}_{i} - y_{i} } \right)^{2} } } \hfill \\ \end{array} } \right.$$
(3)

where \(\hat{y}_{i}\) and \(y_{i}\) are the predicted and actual value of the ith sample, respectively. \(\overline{y}\) is the average compressive strength of all samples. \(N\) is the size of the training dataset. Using graphic approaches can provide an intuitive vision to study concrete compressive strength prediction. Thus, the framework of our model is shown in Fig. 4.

Figure 4
figure 4

The framework of our model.

Full size image

Results

Model performance with different characteristic factors

To determine the optimized factor subset, various combinations of factors, blast furnace slag, fly ash, water, superplasticizer, coarse aggregate, fine aggregate, age, and cement, were employed to train a DT-based model on the training dataset. For the evaluation of our model with different factor subsets, fivefold cross-validation was utilized, and standard indicators were introduced for comparison. As indicated in Table 2, our model achieved the best performance with an R2 of 0.39 when using the age factor alone for model training. This outcome underscores the significance of age as the most crucial factor in predicting the compressive strength of concrete. In the early stages of age, the compressive strength of concrete experiences rapid growth, but this growth gradually slows down with the extension of age. Moreover, the water and cement factors also exhibited superior performance compared to other factors, with R2 values of 0.22 and 0.24, respectively. The pronounced impact of water and cement on predicting the compressive strength of concrete can be attributed to the hydration reaction between water and cement, leading to the formation of hardened cement stone that binds the aggregates, resulting in concrete with a certain strength. Consequently, the amount of water used and its compatibility with cement significantly influence the compressive strength of concrete, necessitating their consideration in prediction models. Through the judicious selection and control of factors such as water-cement ratio, cement variety, and strength grade, the strength and durability of concrete can be enhanced. Furthermore, despite the lowest correlation coefficient of − 0.29 between the water factor and compressive strength, it outperformed blast furnace slag, fly ash, superplasticizer, coarse aggregate, and fine aggregate in terms of prediction performance. This indicates a negative correlation between water factors and compressive strength, implying that compressive strength decreases with increasing water content. Our model achieved the highest R2 of 0.83 using the blast furnace slag, superplasticizer, age, cement, and water factors, surpassing the performance of the single-factor predictor (with the age factor achieving the highest R2 of 0.39). These results underscore the necessity of comprehensively considering the influence of various factors when predicting concrete strength. Consequently, the blast furnace slag, superplasticizer, age, cement, and water factors were identified as the optimized subset for concrete compressive strength prediction.

Table 2 Performance comparison with different factor combinations.
Full size table

Model performance on the training dataset

To obtain the best regressor, the training dataset was used to train the above-mentioned 12 regressors (Linear, KNN, DT, SVR, LASSO, MLP, ExtraTrees, RF, AdaBoost, GradientBoosting, Bagging and Deepforest) and the optimized feature subset, blast furnace slag, superplasticizer, age, cement, and water, was selected into the 12 different regressors. To compare the performance of different regressors fairly, fivefold cross-validation was used on the training dataset with the same fold. The optimized parameters of each model were shown in Table 3.

Table 3 Parameter optimization on the training dataset using fivefold cross-validation.
Full size table

To identify the best regressor, the aforementioned 12 regressors were trained on the entire training dataset with their optimized parameters. As indicated in Table 4, the Deepforest-based regressor exhibited the best performance with an R2 of 0.91, MSE of 26.32, MAE of 3.60, and RMSE of 5.11, respectively. Additionally, the RF-based model secured a second-place score with an R2 of 0.90, MSE of 28.00, MAE of 3.71, and RMSE of 5.26, respectively. Furthermore, it was observed that the ANN-based model, MLP, achieved the poorest performance among all models, suggesting that the neural network-based model is not suitable for addressing this issue.

Table 4 Performance comparison with different regressors on the training dataset.
Full size table

Model comparison on the independent testing dataset

To further evaluate the performance of our model, the whole training dataset was used to train the 12 regressors with their best hyperparameters, and then the performance of each model were compared on the independent testing dataset. As shown in Table 5, the Deepforest-based model achieved the highest R2 of 0.91. What’s more, we also noticed that the tree-based models, ExtraTrees, RF, Bagging and Deepforest, achieved higher performance (R2 greater than 0.90) than the LASSO-based model (got the lowest R2 of 0.61, MSE of 109.09, MAE of 8.22, and RMSE of 10.44), which suggest that the tree-based models are better suited to predict concrete compressive strength. The reason for this result is that tree-based models can automatically select the most relevant features for prediction, which is particularly useful for determining which features are most important for prediction. In addition, tree-based models have a certain degree of robustness against noise and outliers, as they perform data filtering and dimensionality reduction during the process of constructing trees.

Table 5 Performance comparison with different regressors on the independent testing dataset.
Full size table

The absolute difference for each sample in the independent testing dataset was shown in Fig. 5. For 31.3% (65/208) of the samples, the absolute difference between the predicted strength and the true strength was within 1. For 80.3% (167/208) of the samples, the absolute difference between the predicted strength and the true strength was within 5. Only 5.8% (12/208) of the samples had an absolute difference greater than 10 between their true strength and predicted strength, indicating the superiority of our model.

Figure 5
figure 5

Absolute difference for each sample in the independent testing dataset.

Full size image

Compared with the state-of-the-art predictors

To further explore the performance of the Deepforest-based regressor, we compared our model with the State-of-the-art predictors. These models are constructed based on GEP17, RF21, SVR20, and ELM24, respectively. For a fair comparison, all models were trained on the same training dataset and tested on the same independent test dataset. Although these models target concrete materials and have different input factors, we compared the performance of the models on our optimized subset. As shown in Fig. 6, the correlation coefficient of our model is greater than 0.95, and the central RMS error and standard deviation are the smallest among the five models, which suggest that our model is most suitable for concrete strength prediction.

Figure 6
figure 6

Performance comparison with the State-of-the-art Predictors.

Full size image

Performance validation using existing data

Due to the difficulty in obtaining experimental data, it is difficult to find a dataset that is completely consistent with our modeling dataset. In this study, we used the dataset from44 for validation, which collected compressive strength data of the machine-made sand concrete mixed with different amounts of super absorbent polymer. Although the dataset is not exactly the same as our modeling dataset, it contains four of our optimal subsets, namely superplasticizer, age, cement, and water factors. Therefore, we reconstructed the concrete strength prediction model on our training dataset based on these four factors and random selected 15 of their test data for prediction. As shown in Table 6, our prediction bias are within 13% for samples with an age of 3 or 7, while our prediction ability is limited, with a bias of around 20% for samples with an age of 28. These results indicate that despite the different additives in concrete, our model still has a certain predictive ability. However, different additives may cause certain changes in the mechanical properties of concrete. Therefore, establishing specific models for different additives can better predict the compressive strength of concrete45,46. For the convenience of researchers, we packaged the model developed in this article using wxpython and pyinstaller. The software includes Feature selection, Regressor selection, Model construction, Model validation and Sample Prediction modules (https://github.com/NWAFU-LiuLab/CCS-Predictor). Researchers can not only use our software for prediction, but also use it for secondary development, exploring optimization combinations of different training datasets, features, and regressors. It should be noted that due to the different random number seeds used to partition the training and testing sets, the software’s predicted results may differ slightly from the results in the article.

Table 6 Concrete compressive strength prediction using other existing data.
Full size table

Limitations of the study and recommendation for future research

However, our method still has some limitations. Firstly, the dataset utilized in this study dates back to 2007, and the recent trend of using auxiliary cement-based materials (SCM) may change the dataset and thus alter the prediction results47. Secondly, only a feature subset was used for modeling, and complex feature engineering was not undertaken in this study. For small datasets, considering the use of pre-trained models in other related fields (such as models trained on other concrete datasets) for transfer learning is possible. Transfer learning can expedite model convergence on new datasets and may enhance prediction accuracy. Although the raw data may lack complex features, more meaningful features can be extracted through feature engineering techniques such as principal component analysis, feature combination, feature selection, etc. Additionally, considering the incorporation of other characteristics related to concrete strength, such as the chemical composition of raw materials, certain parameters during the production process, etc., is feasible. However, it should be noted that these methods may not necessarily be effective in all situations, so in practical applications, selection and adjustment may need to be based on specific circumstances.

Conclusions

So far, research on concrete strength prediction based on machine learning has made some progress, but the identification accuracy remains insufficient, and the hyperparameter adjustment process of the model is complex. Consequently, a Deepforest-based model was developed in this study. For model training, blast furnace slag, superplasticizer, age, cement, and water factors were selected for the aforementioned 12 regressors, and grid search was employed for hyperparameter optimization. Rigorous validation experiments led to the selection of Deepforest as the optimized regressor, achieving an R2 of 0.91 on the independent testing dataset. The results demonstrate the effectiveness of our model in predicting concrete strength.

According to the experimental results, age is the most crucial factor affecting the strength of concrete, followed by cement. With the addition of other factors, the prediction accuracy of concrete strength gradually improves. Among them, blast furnace slag, superplasticizer, age, cement, and water factors proved to be the best indexes for predicting the strength of concrete. However, it was observed that R2 did not improve when coarse aggregate and fine aggregate were added, indicating that these two factors have no significant effect on enhancing the prediction accuracy of concrete. Compared with other models, the Deepforest-based regressor achieved superior results on the training set and the independent testing dataset and does not require explicit hyperparameter adjustments, reducing the difficulty of model optimization.

In this study, machine learning algorithms are utilized to learn and analyze a substantial amount of experimental data. The advantages of this model include: (1) Establishing a more accurate concrete strength prediction model, thereby enhancing the accuracy of concrete strength prediction; (2) Determining the concrete mix proportion more precisely, thereby optimizing the performance and cost of concrete; (3) Controlling key parameters more accurately in the production process, thereby improving production efficiency and quality. Additionally, implementing machine learning-based models for predicting concrete strength in the real world may also require addressing the following challenges: (1) High-quality data is the foundation of machine learning algorithms, so ensuring the accuracy and completeness of experimental data is necessary; (2) Different machine learning algorithms may be suitable for different datasets and problems, so choosing the appropriate algorithm based on the actual situation is necessary. (3) Machine learning models require extensive training and validation to achieve high prediction accuracy, necessitating sufficient time and resources to be invested. (4) Applying machine learning-based concrete strength prediction models in the real world also requires considering various challenges in practical applications, such as data collection, model deployment, and maintenance.