Introduction

Wireless communication has become a vital element in the ever-changing realm of modern technology, significantly transforming how people connect and interact with their environment. Wireless Sensor Networks (WSNs) have driven technological advancements within the transformative paradigm. They have greatly facilitated the integration of wireless communication into numerous aspects of our daily lives. Environmental monitoring, healthcare, and industrial automation are just a few areas that have discovered their widespread use. The limitations of conventional power sources restrict the autonomy of wireless sensors, as they are naturally limited in supply1. To effectively address the growing need for sustainable and self-sufficient energy systems, it is imperative to explore innovative solutions. With the increasing demand for energy and the urgent need to adopt sustainable practices, there is a growing focus on researching and advancing inventive and efficient energy-harvesting technologies2. Conventional power systems rely heavily on finite resources, resulting in adverse environmental impacts. Hence, it is imperative to shift towards alternative sources of energy. Energy harvesting is a concept that involves capturing energy from the surrounding environment and converting it into electrical power for practical purposes3. This approach has the potential to significantly increase the lifespan of wireless sensor nodes while also minimizing their environmental impact.

The study of metamaterials (MMs) holds great potential in pursuing sustainable energy solutions4. MMs are artificial structures endowed with electromagnetic (EM) characteristics that are absent in natural materials. These materials exhibit outstanding properties such as negative refraction and EM cloaking in their remarkable capacity to manipulate EM radiation. MMs possess distinctive attributes that render them an appealing and promising alternative for addressing the obstacles faced by conventional power systems.

Metamaterial absorbers (MMAs) represent a captivating and cutting-edge research domain within the MMs field. The materials with specific properties have been carefully engineered to interact with EM waves efficiently. Subwavelength structures, like resonators, are used to achieve remarkably high absorption efficiency within specific frequency ranges. MMAs have emerged as a promising technology that has the potential to revolutionize energy harvesting methods, particularly in applications such as wireless sensor networks. These absorbers are highly effective in capturing and dissipating EM energy, offering a distinct approach to enhance the efficiency and sustainability of power systems. This discovery marks a significant milestone in the quest for innovative, eco-friendly energy solutions.

Recent research has brought attention to the significant potential of MM perfect absorbers (MPA) in the field of energy harvesting applications5,6,7. An EM energy harvesting application using MMs operating at 2.40 GHz, a widely used frequency band, was proposed in8. The design incorporated a square ring resonator that utilized resistors for power delivery. According to theoretical analysis, the energy harvesting efficiency (E-HE) was 83.6%. Furthermore, the study showcased the versatility of the temperature sensor configuration by demonstrating its applicability to a wide range of sensing applications beyond just energy harvesting. In9, researchers proposed an ultrathin dual-layer MMA for RF energy harvesting. This absorber consists of concentric annular structures made from copper foil on a flexible neoprene rubber sheet. The absorber exhibited three distinct absorption peaks at 1.75 GHz, 2.17 GHz, and 2.6 GHz, with 96.91%, 96.41%, and 90.12%, respectively. Numerical simulations and experiments have confirmed that the device exhibits robust RF performance in various conditions. This makes it a promising candidate for energy harvesting, as it demonstrates improved absorption values when subjected to different resistive loading scenarios. An absorber with concentric ring resonators is investigated in the research10, which demonstrates near-perfect absorption over a range of frequencies. Three efficiencies were proposed by analyzing the relationship between absorption characteristics and energy harvesting capability through numerical research on modifications in dimensions and geometry. The study focuses on multiband absorption and draws attention to converting half of the incoming wave energy (0.25 W) at 5.88 GHz utilizing resistive loads. This design has great promise for use in wireless communication and power systems. In11, the authors conducted a study on RF energy harvesting for long-term power supply of electronic systems. They proposed a compact absorber based on a tilted split ring multiband MM. The absorber is designed to work effectively in LTE2350, WiFi2450, and LTE2600 frequency bands. It utilizes a split ring technique based on MM. The high-frequency structure simulator software simulations unveiled resonances at 2.35 GHz, 2.45 GHz, and 2.6 GHz frequencies. The corresponding return loss values were also obtained. The absorber's compact structure, measuring 35 mm × 35 mm × 1.67 mm, and its multiband features make it a highly promising solution for RF energy harvesting applications. A metasurface (MS) with two bands, one for 2.4 GHz and one for 5.4 GHz, was proposed in12 for effective EM energy harvesting. With a circular split ring resonator on a low-loss substrate with an air layer, the MS unit cell could attain near-unity efficiency of 97% at 2.4 GHz and 94% at 5.4 GHz, respectively. The MS utilized a single harvesting port, simplifying the power network design. Experimental validation of a 5 × 5-unit cell MS harvester confirmed its high efficiency and suitability for diverse microwave applications, including energy harvesting and wireless power transfer. A MPA combined with Schottky diodes was developed in13 for harvesting high-efficiency radio frequency (RF) energy. By capitalizing on Fabry–Perot (FP) cavity resonance to enhance energy absorption, the MPA-based rectenna effectively converted RF waves to DC power. Particularly at low intensities, incorporating FP resonance increased the voltage and Q-factor across Schottky diodes, enhancing rectification efficiency. In14, the authors developed a perfect, triple-band MS absorber that efficiently harvests RF energy. The absorber was designed with a three-layer meta-atom structure of cross-shaped and slotted square-shaped metallic patches. In total, there were 9 × 9 meta-atoms in the design. This absorber could operate in both S- and C-bands, with resonant frequencies at 3.06, 3.9, and 5.97 GHz. The experiment demonstrated nearly perfect absorption at various incident angles, and the results closely matched the simulations. The absorber demonstrated a high E-HE, achieving 94.4% and 84% at frequencies of 3.07 and 5.97 GHz, respectively. The MMA described by the authors in15 featured resistive loads and a multi-type split coin resonator. The design mentioned above demonstrated angle insensitivity by attaining an absorption efficiency of over 80% for transverse EM waves within the frequency range of 3 to 8 GHz. A blend of experimental validations and numerical simulations supported the conclusions drawn by the researchers. The absorber was effectively utilized in energy harvesting applications, demonstrating significant efficiencies in absorption (82.21%) and harvesting (46.07%). A MMA structure designed for microwave energy harvesting was proposed in16. The structure was comprised of four-wheel resonators, each possessing distinct dimensions. The chosen frequency range corresponds to the commonly used wireless communication signals. The dimensions were optimized for achieving a wideband absorption response through the utilization of a parametric study and genetic algorithm. Study results showed substantial absorption ratios in the 3–5.9 GHz and 7.3–8 GHz frequency ranges, with values ranging from 80 to 99%. Furthermore, the E-HE in the 2–5 GHz range surpassed 0.8, indicating a highly effective process. In17, the authors proposed an MS for energy harvesting applications. Their design was composed of subwavelength electrical small ring resonators operating at 2.5 GHz. The resonators were organized in a two-dimensional array, which allowed for efficient energy harvesting. The MS demonstrated 90% E-HE when subjected to varying polarization and incidence angles. A 9 × 9 MS energy harvesting array prototype was manufactured and tested, and its efficiency for incident waves with arbitrary polarizations and broad angle was found to be over 80%.

Extensive research in EM harvesting utilizing MMs has propelled the field forward significantly. However, it is imperative to acknowledge the inherent constraints and limitations within current designs. It is worth mentioning that certain designs result in MMs structures that are quite large8,9,10,11,12,13,14,15,16,17, making them unsuitable for applications with strict size and weight limitations. Additionally, many existing designs are confined to a limited range of absorption frequency bands8,13,17, restricting their capacity to harness energy from a broader spectrum of EM waves and diminishing overall versatility. In addition, it is necessary to focus on developing smaller, more flexible, and more efficient MMs structures for EM energy harvesting applications.

This study introduces a new energy harvester, measuring 10 × 10 mm2, based on MMs. Its compact size not only helps to reduce costs but also enhances manufacturability. Additionally, its compact design allows for precise and cost-effective fabrication. The product seamlessly integrates into current systems, improving their portability and versatility. This broadens the range of applications and fosters innovation in MM technology.

Furthermore, the MM harvester's multiband functionality enables it to efficiently capture energy from different frequency bands simultaneously, maximizing its utilization of ambient EM waves. This adaptability makes it perfect for urban environments with crowded communication networks, enabling strong and self-sufficient wireless sensor networks and IoT devices. It emphasizes energy efficiency and sustainability by minimizing the need for frequent battery replacements or wired power sources, benefiting a wide range of technological applications.

The proposed energy harvester has four resonance frequencies at 3.7 GHz, 6.3 GHz, 9.9 GHz, and 14.2 GHz. The design effectively showcases negative (permittivity and permeability) within specific frequency ranges. It is firmly established as a double negative (DNG) MM. The energy harvester demonstrates exceptional absorption efficiencies across multiple frequencies. The absorption efficiency at 3.7 GHz is remarkably high, reaching 99.96%. At frequencies of 6.3 GHz, 9.9 GHz, and 14.2 GHz, the absorption efficiencies are 99.87%, 99.88%, and 99.87%, respectively. The proposed structure has shown its effectiveness in capturing EM power from different incident angles, as evidenced by computational simulations and experimental results. The EM harvesting efficiency reaches 95.3% at 3.7 GHz. At 6.3 GHz, 9.9 GHz, and 14.2 GHz, it attained 96.5%, 95%, and 95.2% under normal incidence, respectively. Our novel energy harvester has distinct advantages over established methodologies, making it highly valuable in practical applications. Our design has the potential to revolutionize various industries, making it highly appealing.

Design layout

The resonators within each layer exhibit resonance at frequencies that are closely spaced but distinct from one another due to variations in their dimensions. By combining the overlapping frequency responses of each layer, one can determine the overall response of the structure18. Moreover, the design's absorption and frequency response depend upon several aspects. These criteria encompass the number of resonators, their geometric measurements, the widths, and the diameters of the split gaps19.

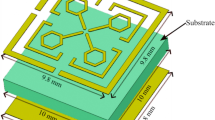
The front and back views of the proposed unit cell design layout are shown in Fig. 1a and b. Additionally, Fig. 1c displays the design layout of the 3 × 3 array structure. The unit cell consists of a split ring resonator (SRR), two strip lines, and two split strip lines. The strip lines that connect the ring's edges are the same width. The inner split strips, which have the same widths, are connected to the middle of the ring resonator. The resonators are made of annealed copper, with a thickness of 0.035 mm and a conductivity (σ) of 5.8 × 107 S/m. The split gaps are connected to the lumped elements (resistive loads), specifically R1, R2, and R3. The proposed unit cell has an overall size of (10 × 10) mm2, while the 3 × 3 array structure has a size of (30 × 30) mm2. Compared to other designs documented in the literature, the proposed one is comparatively smaller. Furthermore, the split ring resonator's 45° inclination is another distinguishing characteristic of the design, significantly enhancing its bandwidth.

Figure 1
figure 1

Schematic structure (a) Unit cell front-view (b) Unit cell Back-view c Prospective view of 3 × 3 array structure.

Full size image

Furthermore, the dielectric loss tangent measures the loss level in a dielectric substance. It demonstrates how EM energy within the material is turned into heat. Consequently, RF losses are more significant, and the absorption bandwidth is broader due to a higher loss tangent, which signifies a greater amount of energy being lost20. Consequently, the Rogers RT 5880 substrate is employed in the proposed design to reduce energy losses effectively. The substrate's permittivity (ε) is 2.2, and its loss tangent (δ) is 0.0009. It has a thickness of 1.575 mm. Table 1 displays the optimal structure dimensions as obtained by a parametric study.

Table 1 The geometric dimensions of the proposed structure.
Full size table

A parametric analysis was conducted to ascertain the configuration of the top-layer metal pattern. The Scattering parameters were evaluated using five separate designs. The final design met all the required characteristics, which dictated the top layer's shape. Figure 2 illustrates the various designs of top-layer structures, whereas Fig. 3 shows the S11 values for these designs.

Figure 2
figure 2

Parametric analysis of the proposed design.

Full size image
Figure 3
figure 3

Reflection coefficient (S11) for various designs.

Full size image

The proposed device's equivalent circuit model is constructed in ADS, and its outcomes are compared to those obtained by CST. Figure 4 depicts the equivalent circuit model. Furthermore, Fig. 5 presents the Scattering parameters data for the ADS and CST. Figure 5 shows a remarkable resemblance in the S11 values between CST and ADS values.

Figure 4
figure 4

The equivalent circuit model of the proposed MM harvester.

Full size image
Figure 5
figure 5

Reflection coefficient from CST and ADS.

Full size image

Furthermore, as illustrated in Fig. 6, the scattering parameters were examined using two distinct substrate materials: Rogers RT 5880 and FR4. The S11 results are optimized for Rogers RT 5880 due to its lower loss tangent than FR4. As a result, the substrate chosen for the proposed device was Rogers RT 5880.

Figure 6
figure 6

Reflection coefficient for FR4 and Rogers RT 5880.

Full size image

Analysis of the proposed harvester's absorption and scattering parameters

The numerical simulations use Microwave Studio, a Computer Simulation Technology (CST) software. CST provides investigations in the microwave frequency band utilizing genetic and parametric algorithms. Each of the three axes represents different boundary conditions: electric, magnetic, and open. We assume the E-field and H-field components are x- and y-polarized to facilitate numerical analysis. Furthermore, it is postulated that the propagation occurs in the z-direction. The absorption of the proposed unit cell is calculated using the equation below21.

$$A \left(\omega \right)=1- {\left|{S}_{11}\left(\omega \right)\right|}^{2} - {\left|{S}_{21}(\omega )\right|}^{2}$$
(1)

where \({S}_{11}\left(\omega \right)\) denotes the overall structure's reflection coefficient and \({S}_{21}\left(\omega \right)\) denotes its transmission coefficient. To optimize the absorption of structure, it is important to minimize both the reflection \({S}_{11}\left(\omega \right)\) and the transmission \({S}_{21}\left(\omega \right)\) at the operating frequency. As the backside of the back layer is entirely covered with copper, the absorption coefficient may be determined using the following equation:

$$A \left(\omega \right)=1- {\left|{S}_{11}\left(\omega \right)\right|}^{2}$$
(2)

The following equations can be used to compute the scattering parameters, specifically the reflection coefficient (S11) and the transmission coefficient (S21)22:

$${S}_{11}= \frac{{R}_{01}(1-{e}^{i2n{k}_{0}d})}{1- {{R}_{01}}^{2}{e}^{i2{k}_{0}d}}$$
(3)
$${S}_{21}= \frac{(1-{{R}_{01}}^{2}){e}^{in{k}_{0}d}}{1- {{R}_{01}}^{2}{e}^{i2{k}_{0}d}}$$
(4)

where \({R}_{01}= z-1/z+1 .\) The impedance, represented by the symbol z, can be determined through the utilization of the following equation:

$$z= \pm \sqrt{\frac{{(1+{S}_{11})}^{2}-{S}_{21}^{2}}{{(1-{S}_{11})}^{2}-{S}_{21}^{2}}}$$
(5)
$${e}^{in{k}_{0}d}=X\pm i\sqrt{1-{X}^{2}}$$
(6)
$$X= \frac{1}{2{S}_{21}(1-{S}_{11}^{2}+{S}_{21}^{2})}$$
(7)

Figure 7 displays the simulated results for S11 and S21, respectively. Four resonance frequencies are depicted in the Figure: 3.7 GHz, 6.3 GHz, 9.9 GHz, and 14.2 GHz. At these resonance frequencies, the S11 values are − 34 dB, − 29 dB, − 27 dB, and − 38 dB, respectively. The S21 values are − 0.10 dB, − 0.16 dB, − 0.20 dB, and − 0.13 dB. The N5227A model of a Vector Network Analyzer (VNA) is utilized to evaluate the S-parameters and validate the simulation results. The VNA was prepared using the calibration kit (Agilent N4694-60001). After careful consideration, a waveguide was selected to operate effectively within the 2–16 GHz frequency range. Two coaxial cables, one for transmission and one for reception, connected the VNA to the waveguides. Five distinct waveguide models were considered to find the S-parameters. The unit cell is inserted into these waveguides sequentially. The PRN file format was used to record the measured values for S11 and S21 obtained from the VNA. The graph plotting process was completed by importing the (PRN) data into Excel and Origin. The measurement setup is illustrated in Fig. 8a, and the fabricated unit cell and array structure is shown in Fig. 8b. Figure 9 presents the simulated and measured S11.

Figure 7
figure 7

Scattering parameters, S11 and S21 vs frequency.

Full size image
Figure 8
figure 8

(a) Measurement setup for a unit cell using a vector network analyzer (VNA). (b) Fabricated unit cell and array structure.

Full size image
Figure 9
figure 9

The measure and simulated reflection coefficient, S11 (dB) versus frequency (GHz).

Full size image

The absorption of the proposed unit cell with lumped elements is calculated using Eq. (2). Figure 10 illustrates the absorption of the proposed unit cell at four distinct resonance frequencies. The absorption rate is 99.96% at 3.7 GHz, 99.87%, 99.88%, and 99.87% at 6.3 GHz, 9.9 GHz, and 14.2 GHz, respectively. Nearly perfect absorption and near-zero reflection are observed at the four resonance frequencies.

Figure 10
figure 10

Absorption & reflection of the proposed unit cell with resistive loads at four distinct resonance frequencies.

Full size image

The analysis of the absorption of an MM harvester in different Transverse Electric (TE) and Transverse Magnetic (TM) modes for energy harvesting presents significant advantages. This computational method enhances the design of the harvester, guaranteeing maximum energy conversion efficiency by precisely adjusting its interaction with various modes. The ability to customize to a higher degree allows for tailored adaptation to specific operating conditions. This is crucial for achieving optimal performance in various environments and addressing variations in EM waves.

Figures 11 and 12 depict the absorption responses of the proposed design for TE and TM modes. The incident angles (θinc) vary from 0° to 75°, with a step size of 15°. In the case of TE and TM modes, the polarization angle (ϕ) remains fixed at 0°. In TE mode, the electric field (E-field) is perpendicular to the direction of wave propagation and remains fixed in that perpendicular plane. In contrast, the magnetic field (H-field) has components that are perpendicular and parallel to the direction of wave propagation.

Figure 11
figure 11

Absorption in (%) versus frequency for varying incident angles (θinc) (TE-polarization mode).

Full size image
Figure 12
figure 12

Absorption in (%) versus frequency for varying incident angles (θinc) (TM- polarization mode).

Full size image

Conversely, in TM mode, the magnetic field (H-field) is perpendicular to the direction of wave propagation. It remains fixed in that perpendicular plane, while the electric field (E-field) exhibits both perpendicular and parallel components to the direction of wave propagation. The figures show that the absorption responses from 0° to 45° are almost identical to those at 0°. However, as the incident angle increases from 45° to 60° and 75°, there is a clear reduction in absorption and a shift in the resonance point.

To optimize the performance, versatility, and reliability of MM harvesters, it is crucial to investigate the absorption responses at various polarization angles. Ensuring they can perform effectively in multiple applications and operating conditions is essential. Figure 13 illustrates the effect of changing the polarization angle (ϕ) on the absorption response when the incidence is normal. The absorption remains constant for the polarization angles of 75° and 60°. Nevertheless, for angles of 15°, 30°, and 45°, there is a minor reduction in the extent of absorption and a modest change in the frequency at which resonance occurs. In general, the proposed MM harvester seems to be impervious to polarization.

Figure 13
figure 13

Absorption versus frequency for varying polarization angles (ϕ) under normal incident.

Full size image

Assessment of the proposed design's E-HE

The simulated E-HE of the MM was calculated using CST Studio Suite. The simulation required the creation of a three-dimensional model that included specific parameters and detailed specifications for incident wave properties. The simulated E-HE (η) in percentage can be calculated using the equation below:

$$\eta = \left(\frac{{P}_{load}}{{P}_{incident}}\right)\times 100$$
(8)

Therefore, the total power delivered to the loads is denoted by, \({P}_{load}= {P}_{absorbed}-{P}_{loss}\). Meanwhile, \({P}_{incident }\) represents the whole incident energy that the MM device received at that time. Figure 14 shows the proposed design's simulated E-HE. The efficiency at 3.7 GHz is 95.2%, while at 6.3 GHz, 9.9 GHz, and 14.2 GHz, it is 94.84%, 96.11%, and 94.41%, respectively. Figure 15 presents a detailed analysis of the power delivered to loads for TE modes, considering oblique incidence angles ranging from 0 to 60°. The Figure demonstrates the power transfer efficiency to the load, highlighting its remarkable effectiveness. The transfer process demonstrates high efficiency, with minimal dissipation within the copper and dielectric substrate. The device shows exceptional efficiency at normal incidence (0°), exceeding 95%, indicating its superior performance under standard conditions. In addition, the study's findings demonstrate a sustained level of optimal performance, even when the angle of incidence is raised to 45°. Nevertheless, once the incident angle reaches 60°, there is a noticeable decline in efficiency. This observation indicates a potential drawback in the device's performance when used at higher incidence angles, emphasizing the significance of taking the angle of incidence into account when aiming to enhance power transfer efficiency.

Figure 14
figure 14

Simulated E-HE versus frequency.

Full size image
Figure 15
figure 15

Simulated E-HE for varying incident (θinc) angles (TE-polarization mode).

Full size image

Integrating the lumped elements (resistive loads) is vital in designing the EM energy harvester. The study examines the effectiveness of harvesting by adjusting the resistive loads connected from (50 to 200Ω), as depicted in Fig. 16. The unit cell demonstrates an impressive efficiency of nearly 95% when connected to a resistor load of 50 Ω, almost identical to the input impedance of the proposed harvester. In addition, the efficiency exceeds 85% at all resonant frequencies for resistive loads of 100 Ω. For resistive loads of 150 Ω and 500 Ω, the efficiency is 80% and 65%, respectively.

Figure 16
figure 16

Efficiency vs. frequency for different resistive loads.

Full size image

It is critical to conduct precise measurements of the magnetic field (H-field), surface current, and electric field (E-field) of an MM harvester to analyze its functionality, refine its design, and resolve any potential problems. These measurements serve multiple purposes, including identifying hotspots, validating simulation models, and customizing the harvester for various conditions. This enhances the versatility of the harvester. The analysis conducted here thoroughly comprehends the EM phenomena within the structure at different resonance frequencies.

The current distribution at resonance frequencies is independently measured in Fig. 17, which reveals an anti-parallel current flow. An intense current is generated in the outer SRR at a frequency of 3.7 GHz. The current is focused in the center and then sent to the resistor load, resulting in almost perfect absorption. At a frequency of 6.3 GHz, the inner two split strip lines show a significant increase in current intensity. Similarly, at 9.9 GHz and 14.2 GHz frequencies, the corner strip lines demonstrate elevated current levels.

Figure 17
figure 17

Surface current distribution at all four resonance frequencies.

Full size image

In Fig. 18, the E-field distributions exhibit clear and distinct patterns at the resonance frequencies. At a frequency of 3.7 GHz, both outer SRR and inner split strip lines demonstrate a high concentration of E-field intensity. When transitioning to a frequency of 6.3 GHz, the E-field is concentrated within the inner split strip lines that contain resistive loads. At a frequency of 9.9 GHz, the concentration of the E-field shifts towards the inner split strip lines and outer SRR. Similarly, at a frequency of 14.2 GHz, both the corner strip lines and outer SRR exhibit an intensified E-field.

Figure 18
figure 18

Distribution of the E-field at each of the four resonance frequencies.

Full size image

Figure 19 provides additional analysis by presenting H-field distributions. Significant fields are observed at the inner split strip lines, particularly at a resonance frequency of 3.7 GHz and 6.3 GHz. At a frequency of 6.3 GHz, the outer SRR demonstrates concentrated fields on the lower side. At a frequency of 9.9 GHz, the H-field intensity becomes concentrated in the upper and lower sides of the inner split strip lines. At a frequency of 14.2 GHz, the corner strip lines exhibit the highest intensity of the H-field.

Figure 19
figure 19

Distribution of the H-field at each of the four resonance frequencies.

Full size image

The proposed design undergoes initial validation through simulations and subsequent experimental verification using the fabricated 3 × 3 array structure. Figures 20 and 21 show the schematic diagram and experimental setup, respectively. The efficiency of the array structure is determined through a comprehensive evaluation conducted in an anechoic chamber. The experimental setup ensures that external interference is kept to a minimum, which enables precise measurements of the array's performance. The experiment utilized an RF signal generator, spectrum analyzer, horn antennas, and adapters. The input ports of the horn antenna were connected to the signal generator to guarantee that it could produce the correct frequency for testing. Next, a spectrum analyzer measured the received power after the array was attached to the transmitting horn antenna and positioned in the far-field zone. Equation (9) can be used to calculate the necessary separation distance between the transmitter antenna and the array sample for optimal excitation of the array by a plane wave in the far-field area23:

Figure 20
figure 20

Schematic diagram of the measurement setup for the 3 × 3 array harvester in an anechoic chamber.

Full size image
Figure 21
figure 21

The actual measurement setup for the 3 X 3 array harvester inside an anechoic chamber.

Full size image
$$R= \frac{2{D}^{2}}{\lambda }$$
(9)

Concerning this context, R denotes the distance between the array sample and the horn antenna, D represents the aperture of the antenna, and λ denotes the wavelength. Using the following equation, we can get the array structure's total RF-to-AC efficiency24:

$${\eta }_{\left(RF-AC\right)}= \frac{{P}_{load}}{{P}_{incident}}\times 100$$
(10)
$$ P_{{load}} = \mathop \sum \limits_{{n = 1}}^{N} {\raise0.7ex\hbox{${V_{i} ^{2} }$} \!\mathord{\left/ {\vphantom {{V_{i} ^{2} } {R_{i} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${R_{i} }$}} $$
(11)

The voltage across the resistance of each collector is denoted as \({V}_{i}\), is determined by \({R}_{i}\), while \(N\) represents the total number of cross-dipole elements.

$${P}_{incident}={P}_{t}{G}_{t}\left(\frac{A}{4\pi {R}^{2}}\right)$$
(12)

\({P}_{t} \text{and} {G}_{t}\) indicate the power and gain of the transmitting antenna, respectively, whereas \(A\) represents the functional surface area of the unit cell perpendicular to the incidence plane.

The array structure's simulated and measured E-HE under normal incidence is shown in Fig. 22. The peak efficiency of the measure was 95.3% at 3.7 GHz. At 6.3 GHz, 9.9 GHz, and 14.2 GHz, it reached 96.5%, 95%, and 95.2%, respectively. The fabrication process, measurement port losses, and calibration errors indicate a slight discrepancy between the simulated and measured outcomes. Overall, the results strongly agree with the measurement data and the simulation outputs.

Figure 22
figure 22

Comparison of simulated and measured E-HE of the proposed harvester.

Full size image

Due to several important factors, using a Rogers 5880 substrate and copper resonator dramatically improved our harvesting system. Rogers 5880's low dielectric constant and loss tangent reduce energy loss. However, copper's high electrical conductivity reduces resistive losses and optimizes energy transfer. Rogers 5880's thermal stability and dielectric properties ensure reliable operation in various temperature and frequency settings. Advanced fabrication procedures compatible with Rogers 5880 allow accurate copper resonator patterning, improving MM EM characteristics. This combination enables optimal impedance matching, reducing reflection losses and maximizing E-HE.

Furthermore, the power efficiency is calculated using the following equation25:

$$Efficiency= \frac{{P}_{harvested}}{{P}_{\text{transmitter}}}\times 100$$
(13)
$${P}_{harvested}= {P}_{\text{received}}\times \eta $$
(14)
$${P}_{received}= {P}_{\text{transmitter}}-FSPL$$
(15)

where \(\eta \) is the efficiency of the MM array at the respective resonance frequency. The Free Space Path Loss (FSPL) is determined using the equation below26:

$$FSPL=20{\text{log}}_{10}(d)+ 20{\text{log}}_{10}(f)+20 {\text{log}}_{10}(\frac{4\pi }{c})$$
(16)

The distance between the transmitter and the receiver is denoted by d, measured in meters; the frequency is represented by f, measured in Hz, and the speed of light is denoted by c, equal to 3 × 108 m/s.

Figure 23 illustrates the power efficiency at four distinct resonance frequencies, measured at varying distances ranging from 0.5 to 2 m. This distance represents the separation between the signal source and the harvester device. The power efficiency is significant up to 1 m.

Figure 23
figure 23

Power efficiency (%) versus distance (meter).

Full size image

Table 2 compares the proposed harvester to other efforts in the field and gives a thorough description of its features and performance. The proposed harvester showcased a more compact design and improved E-HE in comparison to previously published research works 14,17,27,28,29,30,31,32,33,34,35,36. Despite the smaller sizes of the works presented in 37 and 38, their E-HE is lower than the efficiency achieved by the proposed harvester.

Table 2 Comparison of the proposed harvester E-HE with other published work.
Full size table

Conclusion

This article presents a compact, wide-angle, and polarization-insensitive MM harvester with multiband. The harvester underwent a comprehensive numerical analysis using CST Microwave Studio, revealing a superior absorption ratio, excellent angular stability, and enhanced efficiency at resonance frequencies (3.7 GHz, 6.3 GHz, 9.9 GHz, and 14.2 GHz). Simulation results showcase the harvester's ability to efficiently capture EM power across incident angles, achieving over 95% E-HE at all resonance frequencies. A 3 × 3 array structure was fabricated and tested in an anechoic chamber to validate accuracy, demonstrating strong agreement between simulated and measured outcomes. Our proposed compact harvester has various practical uses, particularly for microelectronic devices. The small dimensions of this device make it well-suited for Internet of Things (IoT) devices, wearable health monitors, and smart home sensors. It allows for uninterrupted operation without the need for frequent recharging. Remote sensing utilizes it to provide consistent power to environmental and animal monitoring devices. This device's multiband and polarization-insensitive design allows it to efficiently gather energy from several sources, making it an ideal choice for autonomous wireless sensors and low-power communication devices. This harvester prolongs the lifespan of electronics by utilizing ambient EM energy, hence decreasing dependence on conventional power sources and advocating for environmentally friendly technologies. Future research will explore advanced materials, optimize fabrication processes, and integrate with other technologies. Collaborations with industry and academia will accelerate innovation and practical deployment.